Abstract
Local self-government has the task of enabling stable economic development, in addition to enabling a normal quality of life for citizens. This is why the state government should provide guidelines that will improve the local business climate, and by doing so enable local economic development. This can be done through the introduction of a business-friendly certification procedure, which is influenced by uncertain inputs and influences many output factors. Each local government has the important task of determining its rank of efficiency in this process. A number of methodologies developed to solve this problem are generally divided into two groups: Parametric and non-parametric. These two groups of methodologies could provide quite different results. Therefore, the purpose of this paper was to create a model using both approaches to achieve a balanced symmetrical approach that produces better results than each approach individually. For this purpose, the paper describes a multicriteria decision aid-based model of optimization to evaluate the effectiveness of this process, integrating classification, data envelopment analysis, and stochastic frontier analysis, as well as its application in a case study of business-friendly certification in the Republic of Serbia.
1. Introduction
The constant monitoring and quantification of the effects of a job in modern society is a necessary element of its successful implementation, no matter what type of process it is and from which field of human activity it originates from. Logistics processes are crucial for achieving this, and the basic indicator is the definition of the relationship between the results achieved and the resources invested, which is called efficiency [1]. Measuring and increasing efficiency is a necessary prerequisite for the implementation of efficient logistics systems, which is why it is a significant scientific discipline represented in the world literature and practice [2,3,4].
Depending on the criteria defined, efficiency in logistics can be divided in different ways. In this respect, it is possible to distinguish between logistics efficiency at the strategic, tactical, and operational levels. Depending on the type of indicators used to describe efficiency, several types of efficiency emerge. When it comes to logistics efficiency, the most commonly referred to is operational efficiency or operations efficiency. In addition to operational efficiency, the most commonly encountered are cost (financial) efficiency, environmental or eco-efficiency, energy efficiency, qualitative efficiency, city efficiency, etc. From the type of logistics system and process point of view, as one of the most important criteria, it is possible to distinguish several types of efficiency: Distributive efficiency, transport efficiency, warehouse efficiency, efficiency of the picking process, efficiency of the inventory management process, etc. [5].
The main problem of monitoring efficiency in practice is the misunderstanding and use of partial indicators that often, for example, do not represent an appropriate measure of efficiency. In most logistics systems, the emphasis is on costs and financial indicators that do not provide sufficient information on efficiency, so corrective action is taken to determine appropriate indicators. This problem can be solved both through the use of expert knowledge and the discovery of knowledge from data by the use of appropriate artificial intelligence methods, one of which is a well-known classification, which can provide the selection of essential criteria and thus optimize the procedure to ensure its better performance.
For the purpose of measuring the efficiency of a process, four methodologies are available [6]: Econometric average response estimation, index numbers, data wrapping analysis (for example, data envelopment analysis, DEA), and stochastic boundary analysis (for example, stochastic frontier analysis, SFA). Today, with the advent of artificial intelligence, machine learning methods can also be used to measure efficiency.
All the above-mentioned methodologies belong to a broad group of so-called multi-criteria decision aid (MCDA) methodologies [7,8], which primarily address the solution of four underlying multi-criteria decision problems: Problem description, the choice of the best alternative, the ranking of alternatives, and the classification of alternatives [9]. Therefore, we aimed to address two main research questions in this paper: 1. Is it possible to successfully integrate the efficiency evaluation parametric of non-parametric methods with machine learning? 2. Does problem dimensionality reduction by a machine learning method have an effect on the quality of the efficiency evaluation results?
We propose the integration of the efficiency evaluation methods DEA and SFA, with a machine learning method, classification into the procedure of efficiency measurement, which we have not encountered in the literature. Namely, it is generally known and evident from the content of this introduction and literature review that the most commonly used methods for determining different types of efficiency are the non-parametric DEA method and the parametric SFA method. Symmetry in the approach of using those two methods, and their complementary advantages and disadvantages were the starting points for their simultaneous application. The integration of DEA and SFA with classification methods is done while having in mind the possibilities of the dimensionality reduction, which might lead to more suitable results being obtained.
The aforementioned new procedure was applied for solving the univariate problem of determining the efficiency of the business-friendly certification (BFC) process of local governments in the Republic of Serbia, considering the amount of investment per capita as an output performance indicator. The proposed model for determining the process efficiency of BFC cities determines not only the competitiveness of local self-governments in attracting direct investment as an essential precondition for competitiveness in the market but also improves the efficiency of the planning of their local economic development (LED) [10]. The efficiency determination of the BFC process incorporates the effects of the selected criteria and their individual importance, defined by the appropriate professional organization in the Republic of Serbia, the National Alliance for Local Economic Development (NALED) [11]. This process belongs to a group of problems with the input factors burdened with uncertainty, imprecision, and subjective influence. The fulfillment of conditions related to the established criteria is a prerequisite for obtaining the certificate. The efficiency of the BFC process can be evaluated by different performance, such as the aforementioned average investment per capita, the number of new employees, the average salary of employees, etc. In the general case, solving the described real-world problem leads a complex multivariate problem being solved. Consequently, we decided to deal with a specific but very indicative output indicator: The average amount of investment per capita.
In order to present the subject and achieve the set goal, the paper is organized into the following chapters: In addition to this introduction, the second chapter is an overview of the published studies related to the subject of this work; the third chapter describes the BFC process; the fourth chapter, in the three subchapters of the DEA, classification, and SFA method, describes three methods whose integration addresses the problem of process efficiency evaluation; The fifth chapter is organized in two subchapters which discusses motivation and integration of the DEA, classification and SFA method. Sixth chapter describes the new proposed integrated method in two subchapters, through the case study and seventh chapter is discussion of obtained results. The eight chapter provides the conclusion. In the end, the references chapter provides the literature used in the paper.
2. Literature Review
The multi-criteria decision aid-based model for measuring efficiency as well as the methods used in it are represented in the world literature primarily because of the importance of problem solving and its global representation in many areas of human life.
As we outlined in the introduction, the most commonly used methodologies for determining efficiency are DEA and SFA, and they all belong to a broad group of so-called MCDA methodologies. The papers [12,13] discuss DEA as an MCDA methodology and [14] discusses SFA as an MCDA methodology. The authors of [15] provide evidence of DEA and SFA as MCDA methodology, and [16] discusses two MCDA classifiers. MCDA has been applied in many different fields of human activities [17], which can be found in the literature, such as healthcare [18,19], finance and banking [20], environmental protection [21], construction and manufacturing [22], computer science [23], tourism [24], emergency management [25], logistics [26], electricity supply [27] and others [28,29].
When it comes to efficiency and its measurement, there are widespread applications in the same areas of human activity, such as healthcare [30], finance and banking [31], environmental conservation [32], construction and manufacturing [33], computer science and robotics [34], tourism [35], emergency management [36], logistics [37], electricity supply [38] and others [39,40].
As far as the BFC process is concerned, it is not specific for the Republic of Serbia, in which, as we have already stated in the introduction, it is implemented by NALED. It should be noted that more than 90 local governments from Bosnia and Herzegovina, Montenegro, Croatia, Macedonia, and Serbia are improving their business environment by up to 70% through the BFC South-East Europe (SEE) certification program [41].
Specifically, with the support of the German Agency for International Cooperation (GIZ) and the Open Regional Fund for the Modernization of Municipal Services, the BFC SEE program was launched and implemented through the regional network of institutions in order to establish a unique standard of business environment quality for the SEE local self-governments. The regional network brings together various governmental and non-governmental institutions [11,41].
The literature on the evaluation of LED in the Republic of Serbia can be found in [42,43] and on the NALED BFC process in the Republic of Serbia in [44].
Different aggregations of individual MCDA methodologies for assessing the importance of individual criteria have been discussed in [45,46]. When it comes to evaluating the efficiency of local governments, classical approaches, such as parametric DEA or non-parametric SFA methods, are most commonly used. The parametric SFA method was used for the analysis of the efficiency expenditure indicators in the Republic of Serbia’s local governments [47]. The conclusion was that local self-governments could not effectively resolve issues, such as demographic and socioeconomic constraints. The efficiency of municipalities in Portugal was evaluated in two phases: SFA and Tobit regression [48]. DEA has been also used for the regions efficiency evaluation [49,50]. The comparative analysis of the cost-effectiveness of Belgian local governments was performed by FDH, DEA, and econometric approaches in [51] while authors in [52] dealt with the public sector’s efficiency in German municipalities. Another technical efficiency evaluation of major Italian municipalities by the DEA method can be found in [53]. Furthermore, a cost efficiency evaluation of Australian local governments was conducted by using mathematical programming and econometric approaches [54] while DEA was also used in the case of South African local government’s efficiency measurement [55].
In his book, Rao [56] provides a comprehensive description of the DEA methodological approach and Cooper, Seiford, and Zhu provide an overview of the DEA in their articles [57,58,59]. The DEA methodology was also used to create a meaningful multiple criteria decision-making platform that was used for evaluating the performance of engineering schools, but in [60], a user-written data envelopment analysis command for the Stata software tool is presented. In the literature, different integrations of DEA with other MCDA methods also exist, such as for, example, with the analytical hierarchy process (AHP) [61,62]. An overview of the SFA methodology can be found in [63,64,65]. User-written SFA commands for the Stata software tool are given in [66]. SFA has been integrated with other MCDA methods, such as TOPSIS, in order to obtain a method with better characteristics [67].
We should note that in the literature review, there are many attempts to integrate SFA and DEA methods [68,69,70,71], as well as integrate them with some other methods from the MCDA group [72,73], especially in order to obtain better quality methods for evaluating the efficiency of different processes. Finally, it should be noted that there are a number of SFA and DEA integrations with data mining methods in the literature [74,75,76,77].
3. BFC Process Efficiency
Considering today’s level of development of human society, it can be said that when it comes to the city, or local self-government, two of the main functions are service and production. The product group of functions can be classified as crafts, industry, construction, etc. while the service group should cover all service activities that take place in the city or local government area. Of great importance for the development of the city are the so-called basic functions, which include the functions of those services and production activities directly used by the population inside and outside the city, including the population of the wider local government, including the functions of providing and planning the economic basis for the functioning of the city and its future development. These basic functions influence the creation and planning of appropriate city infrastructure, job creation, etc. However, for the life of the people in the city, it is necessary to provide additional social functions, such as information, education, recreation, and so on. The above two types of functions of one city and the local government indicate that they are in fact a conglomerate of several basic and social functions exercised in the area. As for the competitiveness of cities and local governments, the basic functions are the ones that are of greater importance and there is a need to evaluate their value in that domain.
Local self-governments and cities must provide the best possible environment in which the realization of bigger direct investments will provide conditions for job creation and an improvement of salaries of already employed people and thus better overall life of the population. Local governments must create LED plans that allow them to compete competitively in the local through to regional and national context to the global environment.
As it is well known, uneven regional development is one of the biggest problems Serbia faces. Investments represent one of the indicators of these regional differences between cities and local governments in Serbia.
Namely, investors are interested in cities and local self-governments, having in mind several important characteristics starting from the geographical location, infrastructure of the existing production, personnel profiles, and work of the local self-government to successful examples of implemented investments. For this reason, local governments must constantly improve their investment conditions and thus increase their competitiveness.
Following the best practices of the European Union, in 2007, NALED launched a program for the certification of municipalities, cities and local governments with a favorable business environment in order to a create positive business environment and increase the level of investment in local governments, the number of employees, the average salary of employees, etc. The project was made possible with the institutional support of the Ministry of Economy and Regional Development of the Republic of Serbia, with the aim of familiarizing local self-governments with the standards they need to meet in order to be eligible and certified.
BFC is a procedure that introduces rules and enables tools for assessing the quality of services to businesses by municipalities. The certification is intended for all municipalities, cities and local governments in the Republic of Serbia who want to improve the conditions for business in their communities, attract new investments, and stimulate the development of the local economy.
In addition to the financial benefits, communication with the local administration, professional and accurate behavior, as well as a positive expectation of partnership in the future are also important for business. Investors appreciate the most realistic picture of the environment in cities and municipalities, which implies predictability of the duration and cost of all individual procedures, starting from the construction of facilities and its traffic and energy connections for general infrastructure supply through to labor employment and company registration to the payment of all duties.
Twelve criteria were established as a basis for evaluation of whether and to what extent a municipality [78], i.e., the city, met the standards of a favorable business environment. These twelve criteria, which are used in BFC process in the Republic in Serbia, are as follows [79]:
- C1: A strategic approach in development planning.
- C2: Organizational capacity for support of the local economy.
- C3: Involvement of the economy in the work of the local government (economic council).
- C4: An effective system for issuing building permits.
- C5: Availability of information for investment.
- C6: Promotion of investment.
- C7: Creditworthiness and financial stability.
- C8: Promotion of employment and development.
- C9: Encouraging private–public partnerships.
- C10: Adequate infrastructure.
- C11: Transparent policy of taxes and incentives.
- C12: Application of information technologies.
A favorable business environment is provided by those municipalities, i.e., cities, that meet 75% of the above criteria. The official certificate is issued by NALED and the Ministry of Economy and Regional Development of the Republic of Serbia, as a document that investors use, like a proof, showing that a particular local government offers everything for a successful start-up.
Today, more than one-third of all local self-governments in the Republic of Serbia are improving their business environment and participating in NALED’s certification program, and more than 20 municipalities have earned the Certificate of Favorable Business Environment.
The certification criteria give clear guidance to municipalities and cities on the type and quality of services they should offer well as recommendations on what reforms they need to implement. The ultimate goal of the certification is to strengthen the competitiveness, promote investments, increase employment, and, as a final goal, raise the standard of living in the Republic of Serbia.
The establishment of the criteria is a process that takes place in real time and involves upgrading them both in quality and quantity. Given the rapid development of human society at the beginning of the 21st century in the era of the fourth industrial revolution, the BFC certification process itself is therefore subject to constant evaluation and mandatory recertification every two years.
The certification program for municipalities with a positive business environment is unique in the Republic of Serbia and includes several activities.
In the BFC process, at the beginning of each current year, NALED defines the significance of the criteria as the average score of the previous levels of assessment, which is often referred to as the relative importance of the observed criteria Ci (i = 1,…,12) [10,44,45,61]. It is given in Table 1 by NALED’s criterion validity rating.

Table 1.
NALED’s evaluation criteria importance of the BFC process in Republic of Serbia.
Using the assessment of the fulfillment of the criteria of each local government in certification by experts and the established formula that it is necessary to meet at least 75% for each criterion, it is possible to determine which city, i.e., local government, deserves certification. Additionally, since it is very useful to plan the intensity of investment required for local economic development and to achieve this in the coming period, the evaluation of the criteria by the NALED experts given in Table 1 is useful in determining the rank of each local government, which can be done using some of the known methods of MCDM.
As it is mentioned in this introduction, this paper aimed to evaluate the efficiency of this BFC process, considering the amount of investment per capita as an output criterion. The investment per capita is one of the most important attributes in measuring local economic development success. In our case, this output was chosen in order to make a comparative analysis of the ability of local governments to attract direct investment as well as to determine whether efficiency is related to the level of fulfillment of defined input criteria.
4. Background
As we already indicated in the introduction, we will consider the integration of different multicriteria methods in order to evaluate the efficiency of the BFC certification process of cities and local governments in the Republic of Serbia. The integration procedure of the DEA, SFA, and classification method is proposed to improve the features of the individual methods. The case study of the efficiency evaluation of BFC process in the Republic of Serbia cities is used to verify the goodness of the proposed procedure. However, it could be generally applied in other cases of evaluating the efficiency of a univariate or multivariate process, aforementioned in Section 3 (BFC process).
Namely, it is known that within the MCDA, we generally identify at least one decision maker (DM), who is solely responsible for making the decision, whatever it may be. The DM chooses one of several alternative decisions, judging them by a set of criteria, attributes, or points of view, and which are most often opposed to each other. The DM may express some preferences regarding the alternatives and criteria offered and use the MCDA algorithms as parameters to find a solution to the problem. These problems, as the ultimate implication of a decision, fall into various possible categories:
- -
- Choice (determining the “best” alternative);
- -
- Ranking (ranking the alternatives); and
- -
- Sorting (assigning alternatives to predefined and ordered classes).
MCDA is applied in many different fields of human activity as we already stated in Section 2 [17,18,19,20,21,22,23,24,25,26,27,28,29].
The process of MCDA is often complex and depends on the specific area where it is applied and whether it has and what are the preferences of the decision maker. As a result, many different algorithms and their implementations have arisen [80,81]. Several papers have dealt with more or less successful attempts to simplify decision-making by choosing the best algorithm for MCDA problems [82].In one of them [83], this procedure is divided into several steps. We look at inputs and outputs as attributes or criteria for evaluating the decision-making unit (DMU), while minimizing inputs and/or maximizing results as associated goals. With this approach, we can practically consider this process as one ranking that leads to a classification of basically two possible groups, MCDA and DEA formulations [12,13,84].Additionally, the classification of basically two possible efficient and inefficient groups and SFA coincides if we consider the input and output attributes as single function variables [14]. Luckily, in the literature, classifications can be encountered using DEA and SFA together with other MCDA methodologies, such as Promethee’s multicriteria decision-making (MCDM) [23].
The DEA and SFA methods can be used to solve the problem of determining the efficiency of the BFC process of cities and municipalities in the Republic of Serbia. For this purpose, a synthetic summary indicator should be created, taking into account all input and output attributes used to accomplish the BFC process itself. The DEA efficiency measure is defined as the ratio of the weighted output t to the weighted input. The efficiency measure enables the aggregation of all the observed inputs (outputs) into one virtual input (output) representing the sum of the product of the coefficients and values of the inputs or outputs, which is necessary, which implies solving the problem of expressing the input and output data in ranges of values that are mutually comparable.
4.1. DEA
As it is aforementioned, the DEA has been widely used for assessing the relative efficiency of decision-making units (DMUs)in an observing set. All DMUs use the same multiple commensurate inputs to produce multiple commensurate outputs. The original efficiency definition is given in [85] and it generalizes single-input to single-output ratios in the definition of efficiency, as the ratio of the sum of weighted outputs to the sum of weighted inputs. Let us suppose that we have a set of n DMUs (DMUj, j = 1,…,n), which uses inputs xij (i = 1,…,m) to produce outputs yrj (r = 1,…,s). The absolute efficiency measure model is as follows [86]:
where vi (i = 1,…,m) are input multipliers and ur (r = 1,…,s) are output multipliers (weights). The above definition corresponds to a discrete MCDM. The determination of weights is a very sensitive and complicated process. The idea behind the DEA model is to avoid a priori weights determination. The authors of the DEA model in Charnes et al. [87] allowed each DMU to choose the most appropriate set of weights, with the goal of becoming as efficient as possible compared with the other units in the observing set. The linear programming (LP) weighted form of the basic constant return to scale model (DEA CCR or DEA CRS) with output orientation [87] is as follows:
such that:
The optimal efficiency scores hk are obtained by solving the linear model of Equations (1)–(5) n—times (once for each DMU with the goal of comparing it with other DMUs). As a solution of basic Charnes, Cooper, and Rhodes (CCR) DEA models [87], all efficient units are assessed with the even efficiency scores hk(k = 1,…,n) equal to 1 while the other inefficient ones are assessed with a score greater than 1 (it is usually calculated as the reciprocal value less than one). All inefficient units are enveloped by the production frontier, consisting of efficient DMUs. The efficient DMUs are composed of real-efficient or virtual-composite peer units(lying on the efficient frontier) for each of the inefficient DMUS. This model is transformed into the so-called Banker, Charnes and Cooper (BCC) model, which is described in [88], to incorporate the variable return to scale assumption. Namely, with respect to the DEA CRS model, the DEA BCC or DEA VRS model has an additional variable u* that defines the position of the auxiliary hyperplane lying above or at each DMU included in the analysis and checks that the specified DMU has reached the desired output level with minimum input engagement and that all possible overlapping hyperplanes of all DMUs are selected from the one that has the least horizontal distance from the observed DMU to this hyperplane. For u* = 0, the BCC model is reduced to the CCR model:
such that:
It must be noted on this place that, from these two basic DEA CCR and DEA BCC models, many other variants and extensions of DEA have been developed to solve real-world problems.
4.2. SFA
Stochastic frontier analysis is a parametric approach to efficiency measurement introduced by Aigner, Lovell, and Schmidt [89] and Meeusen and Van den Broeck [90]. It takes into account the error of measurement in estimating the efficiency of the firm under observation.
Let us assume that firm j (j = 1,…,n) produces the output level by using inputs given as a vector . The production function is given as , where β is a parameter vector to be estimated. The output level is also under the effect of the efficiency and random error . Finally, output production for the firm j is given by the form:
Since represents the level of efficiency for firm i, it must be in the (0; 1]. The firm is efficient if = 1; otherwise, it is inefficient. The aim is to estimate the vector parameters and , so as to maximize the of the firm under observation. For this purpose, the natural logs of Equation (11) together with the assumption that the production function of k inputs is linear in logs are taken as:
where represents the level of inefficiency, while represents identically and independently the distributed random error. A stochastic frontier is given by , while indicates the inefficiency level.
After estimating the parameters [91] for the given Equation (11), the technical efficiency of firm i can easily be calculated as a relative distance of the actual output to the estimated stochastic frontier:
4.3. Classification
Classification is an important technique, commonly used in expert systems in order to support the domain experts to identify knowledge within the large volume of data.
Classification is considered the task of supervised learning of data mining (DM) and machine learning (ML), where the dataset is divided into classes (two and more) and each instance of the set has a tag identifying the class to which it belongs. Supervised machine learning algorithms are used to induce a classifier from a set of properly classified instances, i.e., expensive training. The test set, as a set of properly classified data instances, is used to measure the quality of a classifier obtained through the training process. Different types of models are used to represent classifiers and there are numerous algorithms available to induce classifiers from data: Logistic regression, decision trees, neuron network, k-nearest neighbor, and support vector machines, usually named neural networks [92,93,94]. For our case study, we chose naïve Bayes.
Bayesian classifiers imply that the knowledge of an event is described by the probability of its occurrence. The naïve Bayes classifier requires a small amount of training data, so this classifier could be easy implemented, and experience to date shows that in the case if independent predictors, better results are provided as compared to other classifiers [95,96,97].
The basic measure of classifier success is the confusion matrix, which is given in Figure 1. Additionally, apart from the confusion matrix, it is useful to define several other measures of classification success, such as the accuracy, precision, recall, F measure and area under the receiver operating characteristics (ROC) curve.
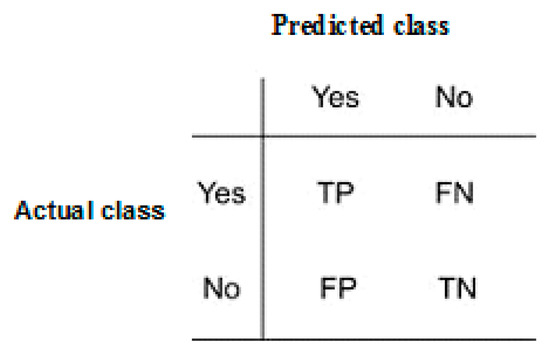
Figure 1.
Confusion matrix for the classification process.
Accuracy = (TP + TN)/N, Precision = TP/(TP + FP), Recall = TP/(TP + FN), wherein TP-True Positive; TN-True Negative and N-total number of samples (instances) in a dataset.
The accuracy measure is unreliable in the case of a very unequal distribution of instances between classes (so-called skewed classes). Therefore, it is necessary to make a compromise between the measures of precision and recall in practice. The F measure combines precision and recall measures and the so-called F1 is an F measure, which gives equal importance to both of these two measures so F1 measure = 2 × Precision × Recall/(Precision + Recall).
The ROC curve illustrates the diagnostic ability of a binary classifier system using a comparison of recall (sensitivity) and FPR(specificity) = TN/(TN + FP).
Algorithms for the selection of the optimal feature subset perform a search within the space of feasible solutions. Most of the commonly used classification methods are very sensitive to the dimension of dataset and the instance/feature ratio [98].
The selection algorithm searches for a subset of attributes that provide the best result. The concept of feature ranking is limited and oriented to those classifiers that are very sensitive to the initial ordering of the input features. We proposed a ranker evaluation approach for the detection of attributes because it ranks the attributes by its importance. Weka is software that reduces the information volume [99], reducing it by the application of various algorithms and techniques, respectively, that could be suggested as the ranking approach in the previous sentence.
Ranking methods for optimal feature selection evaluate a single feature by using various metrics and assign a rank, based on its performance. The evaluation metrics are commonly founded on features ‘statistical properties or their expected potential. The reduction of the dimensionality of data is based on those properties [100]. Attribute selection algorithms can be broken down into filters and prior learning methods. In this paper, we chose to use three algorithms from the filter group, the measure gain ratio, which is practically derived from the measure information gain (InfoGain) and Relief-F, which perform the individual attribute ranking and was originally intended to be classified into only two classes, which is the case that we solve in this paper and the case because we are interested in whether the BFC process is effective or not.
The complexity of group correlation analysis derives from the huge number of combinations of the attributes in which interactions should be taken into consideration O(2N), where N is the number of attributes in the model [98]. The entropy commonly used in the information theory [101], which represents the “purity” of an arbitrary collection of examples. The entropy measures the system’s unpredictability. The entropy of Y is given by Equation (13):
where p(y) is defined as the marginal probability density function for the random variable Y. Let us assume that Y and X are random variables in the training set S. If the entropy of Y with respect to the partitions induced by X is less than the entropy of Y prior to partitioning, the conditional entropy function is given by Equation(14):
where p(y|x) is the conditional probability of y conditional to the knowledge of x.
The entropy can be considered as a criterion of impurity in thetraining set S. Therefore, we can define a measure of the amount by which the entropy of attribute decreases to gain additional information about the attribute provided by the class [102]. This measure is known as information gain: InfoGain. InfoGain evaluates the worth of an attribute by measuring the information gain with respect to the class, according to Equation (15):
where H represents the information entropy.
InfoGain (Class,Attribute) = H(Class) − H(Class | Attribute),
The information gain ratio or GainRatio is the non-symmetrical measure, introduced to compensate for the bias of the InfoGain [103] by reducing it on high-branch attributes. GainRatio should be more significant when data is evenly spread or smaller when all data belong to one branch. GainRatio, which takes the number and size of branches into account when choosing an attribute, is given by Equation (16):
Equation (16) represents the normalization of the InfoGain, by dividing it with the entropy of class. Due to normalization, the GainRatio values fall in the range [0, 1]. The knowledge of the class fully predicts the attribute if the GainRatio is equal to 1. On the other hand, if the GainRatio is equal to 0, one can conclude that there is no relation between attribute and class. The decision tree classification methods C4.5 [104] and ID3 [105] employ the GainRatio as a criterion of the attribute selection at every node.
One of the possible filtering methods with the proceedings of the attribute ranking is ReliefF, based on the procedure of the nearest neighbors (k-nearest neighbors or k-NN).
The algorithm estimates and ranks each attribute with the global grade function [−1,…, 1]. Weight calculation is based on the probability of the nearest neighbors form two different classes with different values for the attributes and probability that form two neighbors from the same class with the same value of attributes.
The function diff(Attribute; Instance1; Instance2) computes the difference of the attribute’s values obtained in two instances. For discrete attributes, the difference is either 1 (different values) or 0 (the same values), while for continuous attributes the differences are normalized on the interval [0, 1]. Kononenko [106] notes that the higher the number of instances, the more reliable ReliefF’s estimates but the running time also increases. The ReliefF algorithm is given in Figure 2. We used Weka software [99] to perform the feature selection algorithms.

Figure 2.
Relief algorithm.
5. Methodology
According to Stewart [13], the MCDA formulation corresponds to the DEA formulation. The inputs and outputs are seen as attributes or criteria for DMUs’ efficiency evaluation, where the associated objective is to minimize the inputs and/or to maximize the outputs. Practically, we can consider DEA as a non-parametric method, which leads to classification in basically two groups of efficient and inefficient decision-making units. Another option is to use a parametric SFA method, which considers inputs and outputs as variables of the production function.
Classification is a methodology for dividing the dataset into two or more classes. The ReliefF is a classifier for attribute ranking, which enables future selection and reduction of the dimensionality of the database by selecting the only necessary attributes. The future selection process offers the following positive effects:
- Fulfillment of the necessary condition for DEA application, i.e., strong relation between the number of input and outputs and DMUs. According to the literature [107], the general rule of thumb is as follows: ((number of inputs + number of outputs) × 3 <Number of DMUs. There are also milder conditions, set by authors in [107], which requires two DMUs for each input and output;
- Eliminating the noise in the data;
- Increases the readability of the results; and
- Speeds up the calculation.
These are the reasons for proposing an algorithm that integrates efficiency assessment methods with classification methods into a framework that shows better characteristics than each of the methods used individually.
5.1. Basic Motivation for Integrating DEA and SFA with Classification
This paper attempts to optimize the process of solving the considered univariate problem of determining the efficiency of certification (BFC) of local governments in the Republic of Serbia. The authors had in mind four underlying motives, i.e., reasons for building one model that integrates DEA, SFA, and classification methods to obtain a method with better characteristics than each model individually:
1. The results obtained with the group of DEA methods and with the group of SFA methods very often differ significantly. In our case, we classified the efficiency of BFC processes into two classes, Efficient and inefficient cities, which implies using one type of informational n-redundancy (n ≥ 3). This means using at least three different methods from the mandatory groups of DEA and SFA methods (in our case DEA CCR, DEA BCC and SFA) and classifying as efficient only those DMUs that are evaluated as efficient by at least two out of these three methods.
2. Classification algorithms can be useful to assess the essential parameters, before and after the attribute selection, to determine and assess the improvement of classification obtained by reducing attributes. In our case, the naïve Bayes classifier was chosen as the most suitable for the set of a small number of training units.
3. The fact that DEA as one of the most commonly used methods requires that the ratio of the total number of DMUs and input and output attributes should be at least 3 (milder condition is 2). This classification can be useful in the case of the necessity of problem dimensionality reduction.
4. Using a well-known attribute selection procedure might be helpful in the reduction of the number of attributes, which solves the previously mentioned limitations of the DEA, as well as the problem of reducing noise in the data. The ReliefF algorithm, as one from the group of Relief algorithms, is selected to estimate the weights of attributes and rank them. In addition, for example, in [108], one can find a number of conclusions that justify using the ReliefF algorithm.
5.2. Integration of the Classification and Efficiency Evaluation
The proposed new model for evaluating the efficiency of the certification process involves the integration of non-parametric DEA and parametric SFA models with the classification into the following algorithm shown in Figure 3.
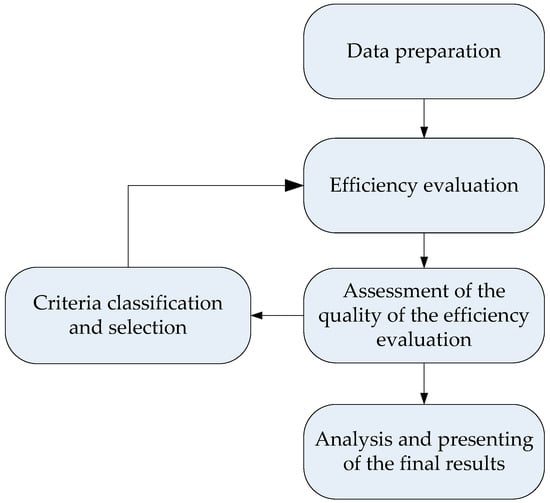
Figure 3.
Efficiency evaluation model that integrates three methods: DEA, classification and SFA.
According to Figure 3, the algorithm’s steps in the proposed frameworks are:
1. Data preparations assume defining DMUs and criteria of the efficiency evaluation, collecting and cleaning necessary data and handling missing values.
2. Determining the efficiency scores using the three models (DEA CRS, DEA VRS and SFA). Using models with different assumptions allows deeper insight into inefficiency sources and result verifications. The DMUs are classified into two classes (efficient and inefficient subsets) and partially ranked within the class of inefficient ones.
3. Using the obtained efficiency scores as a two-class classification attribute (efficient and inefficient) for the assessment of the essential parameters characterizing the quality of classification, precision, and accuracy by the F-measure [109]. The naive Bayes classification model is selected, like the most appropriate one for the small-set classification [110]. If the quality measures are satisfactory, go to step 5; otherwise, go to step 4.
4. The attribute selection process uses the ReliefF classifier, as the one that individually evaluates each of the attributes and rank them. This ranking provides a base for selecting a subset of parameters that are relevant and checks the eligibility conditions for applying DEA methods by checking the allowed ratio of the number of attributes and units. Go to step 2.
Steps 2, 3 and 4 can be repeated until satisfactory results have been obtained.
5. The definitive ranking of DMUs and analyzing the final results.
6. Case Study: Evaluating of the Effectiveness of the BFC Process
As we mentioned, the authors aimed to propose one new model for determining the efficiency of a successful BFC process in attracting foreign direct investments. The BFC process has been carried out since 2007. It was completed successfully in 21 cities and municipalities in the Republic of Serbia until 2013. The main idea was to evaluate the efficiency of the BFC process in those cities and municipalities using the model given in Figure 3. The efficiency was assessed as the success of attracting investments taking into account the achieved level of the 12 certification criteria given in Section 3.
6.1. Data
The cities and municipalities that completed the BFC process, excluding one outlier, are considered as 20 DMUs in the efficiency evaluation (j = 1,…,20). The 12 relevant BFC criteria, according to NALED’s methodology and their importance, are given in Table 1 in Section 3. In the efficiency evaluation, the average values of these 12 criteria (C1–C12) are used as inputs (xij, i = 1,…12, j = 1,…20), while the amount of investment per capita is used as an output (yj, j = 1,…20). The case study of the efficiency evaluation of the BFC process of cities and local governments in the Republic of Serbia uses data, provided by NALED. The input and output criteria database together with BFC scores and ranking according to NALED’s methodology (normalized value of Ci × wi, i = 1,…,12) are presented in Table 2.

Table 2.
Descriptive statistics on data and NALED’s evaluation.
The descriptive statistics show that the input criteria values drop into a relatively small range of 0.46 to 1.09, with a standard deviation from 0.02 to 0.15. Therefore, the BFC process accomplishment is evaluated with scores 0.81 to 0.98. The municipalities are expected to attract a relatively even amount of investments considering the BFC process evaluation. However, the investments per capita range from 111.78 to 995.82, which is expected to make an impact on the efficiency evolution.
6.2. Efficiency Evaluation: Preliminary Results and Classification
The preliminary results of the efficiency evaluation of BFC process in the 20 municipalities, according to the criteria given in Table 2, are given in Table 3. The second and third columns show the efficiency results obtained using the DEA model of Equations (2)–(5) with the assumption of a constant to return (CRS) economy. The CRS assumption is stricter than a variable to return economy assumption imposed in the DEA VRS model (Equations (6)–(9)), with the results given in the fourth and fifth columns. The results of the parametric SFA model are given in the last two columns of Table 3.

Table 3.
Scores, ranks and descriptive statistics (12 input criteria).
As we already mentioned, all three methods provide classification into subsets of efficient and inefficient municipalities. Nevertheless, the size of the subsets varies depending on the used methodology. The DEA CCR model produces the subset of four efficient municipalities (municipality 6, 7, 10 and 15), with an average efficiency score of 0.684 and standard deviation of 0.275. On the other hand, only 6 out of 20 municipalities are assessed as inefficient, with a mean value of 0.927. All municipalities assessed as inefficient according to the DEA CRS model exhibit increasing returns to scale. The size of the SFA efficient subset lies between the two obtained by DEA. It consists of nine municipalities, while the average efficiency score of the whole set is 0.759 (stdev = 0.241).
The most unrealistic results are obtained using the DEA VRS model, which allows the highest degrees of freedom among the three used efficiency evaluation methods. Those results are expected, taking into account that the number of 13 criteria (inputs and outputs) is too big in comparison with 20 DMUs. The optimal number of DMUs for DEA efficiency evaluation should be greater or equal to (12+1) × 3 = 39 according to the rule of thumb given in the literature [107]. On the contrary, the number of criteria for the 20 DMUs should be a maximum of 7. Therefore, in step two, we performed the classification using the naive Bayes algorithm in order to check the data model’s validity and the results are given in Table 4.

Table 4.
Bayes classification results based on the DEA CRS score (four efficient DMUs).
Instep three, we performed feature selection using only the Belief classifier because the InfoGain and GainRatio classifiers give only one attribute as important: C12. The results, which are given in Table 5, show that only five attributes, i.e., the input criteria, are in the group of important ones: C12, C6, C2, C8 and C9, respectively. In this procedure of criteria selection, all those criteria that have a value of at least an order of magnitude lower than the previous one were rejected and treated as insignificant.

Table 5.
Feature selection using the Belief classifier.
In step four, we reapplied the three redundant methodology for efficiency evolution (DEA CRS, DEA VRS, and SFA). Based on the obtained results, given in Table 6, we conclude that now we have only two municipalities (7 and 15) that belong to the efficient subset according to the DEA CRS model, while the DEA VRS model classifies six municipalities into the efficient subset. Once again, SFA proves the middle way, with a subset of five efficient municipalities.

Table 6.
Scores, ranks and descriptive statistics (5 attributes).
In this step, we also repeated classification using the naïve Bayes algorithm. The results and parameters for classification with five input criteria, given in Table 7, clearly show better values are achieved for all parameters than in the case of the efficiency evaluation with 12 criteria. The precision at this stage is 0.9 (in comparison to 0.778), recall is equal to 1 (former value was 0.875), and consequently the F-measure is almost 1 (0.978 in comparison to 0.824). Those results are obvious indications that attribute (criteria) selection and reduction of the problem dimensionality led to a positive improvement.

Table 7.
Bayes classification results based on the DEA CRS score (two efficient DMUs).
The results presented in Table 6 might be considered as the final.
7. Results Discussion
The subset of five criteria selection is justified by the increased parameters of quality evaluation after problem dimensionality reduction. The correlation between the ranks obtained before and after reduction shows that the DEA CRS model is the most robust (correlation coefficient is equal to 97.47% at the significance level of 0.001). The correlations for the other two models (DEA VRS and SFA) are 46.79% and 49.39% with no statistical significance. The degrees of freedom together with criteria values are important factors for DEA efficiency evaluation (less criteria led to less efficient DMUs as proven by the obtained results). On the other hand, SFA as a measure of the central tendency also relies also on the criteria values and it is very sensitive to their selection.
To analyze the rank similarity between the final individual efficiency scores obtained by using the three models (Table 6), we computed Spearman’s rank correlation between them. We found a DEA rank correlation of 59.96% with no statistical significance at 0.01levels due to different economy of scale assumptions. Actually, all efficient municipalities under the constant return to scale (CRS) assumption remain efficient under the variable return to scale (VRS) assumptions, but the number of efficient DMUs increased. The diversity in the ranks of the individual DMUs might be better explained by introducing the NELED’s ranks given in Table 3. For example, municipality 5 is ranked in 19th place according to NALED. It is efficient under VRS but ranked in 15th place under the CRS assumption. By comparing it with municipality 18 (NALEDs top-ranked DMU), we can conclude that municipality 5 attracted more investment per capita (315.95) than municipality 18 295.83. Therefore, municipality 5 is a benchmark DMU for municipality 18. At the same time, NALED’s bottom-ranked municipality 17 attracted a smaller amount of investments per capita and cannot be benchmark for municipality 5 if the model considers scale of economy as an important factor in the efficiency evaluation.
When it comes to the correlation between the parametric and nonparametric rankings, there is a correlation of 48.58% between the DEA CRS and SFA ranks and a correlation of 50.79% between the DEA VRS and SFA ranks with no statistical significance, which is in line with a previous study [111]. The authors of [112] stressed that the contradictory results obtained by DEA and SFA might be expected since they have different degrees of dispersion and perform rankings differently. The former one is a frontier deterministic method while the latter one is a central tendency stochastic method, which takes statistical errors into account. The implication of this divergence is given in [113], where the authors stated that the application of only one methodology for ranking may lead to misuse, especially in the case when there is no significant correlation between different models.
8. Conclusions
The initial hypothesis from which the main goal of this paper arose was it is possible to construct an efficiency assessment model that integrates different methods and produces better characteristics than any of the methods involved? This paper proposed a framework for integrating the efficiency assessment non-parametric DEA CRS and DEA VRS and parametric SFA models with the machine learning algorithm for classification and quality evaluation. It was checked and justified by implementing it on the real-world case study of BFC certification of cities in the Republic of Serbia.
Having in mind the existence of the real-world problem of efficiency evaluation, such as evaluation of the BFC process, which includes a large number of influencing factors in comparison with the number of units of local governments, there is an expressed need to reduce the problem dimensions in order to obtain better results. In such a case, the classification method in synergy with the future selection of attributes is realistically the right choice.
In this paper, we successfully integrated representative methods of the two most commonly used approaches in assessing efficiency, DEA as non-parametric and SFA as parametric, with a machine learning classification method to reduce the number of criteria. Therefore, the novel model takes advantage of the excellent characteristics of each of employed method and eliminates the bad ones using dimension optimization:
- -
- Enables proper use of the DEA methodology with appropriate degrees of freedom;
- -
- Reduces noise in the data; and
- -
- Provides better quality results as proved by naïve Bayes classification.
The suggestion is to use the DEA CRS model as the most robust and strict one for result verification. DEA, as a non-parametric model with no a priori weight assignment, is a very suitable method for efficiency evaluation in the presence of multiple inputs and outputs [81]. It is also a primary choice if there is a lack of some input and output criteria, which might be compensated by the advantages of another one. Therefore, criteria classification and selection are essential. SFA is the method of choice for when numerous criteria exist and in the case of the necessity of inclusion of the stochastic nature of the parameters. All in all, these two methodologies (DEA and SFA) might be imposed as corrective factors to one another.
It is important to remark on the possible uncertainty, imprecision, and subjectivity of input data determination, which is the case in the considered BFC process, and implies the necessity of adding methodologies, which decreases the impact of this deficiency on the results obtained with the proposed methodology. This is, for example, the case with the methodologies based on the fuzzy, interval rough set and interval neutrosophic rough set theory, which are considered in the papers [114,115,116,117,118,119,120]. This could be the subject of future work of the authors.
Author Contributions
Conceptualization: M.J.; Project administration: S.N.; Writing—original draft, Validation: M.R.; Writing—review and editing, Formal analysis: G.S.; Software: V.S.; Investigation: V.S.; Supervision, Methodology: D.R. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Ministry of Education, Science and Technological Development, Republic of Serbian, grants number III44007.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Verbruggen, F.; Sutherland, J.; Werf, J.M.; Brinkkemper, S.; Sutherland, A. Process Efficiency—Adapting Flow to the Agile Improvement Effort. In Proceedings of the 52nd Hawaii International Conference on System Sciences (HICSS), Grand Wailea, Maui, 8–11 January 2019; pp. 1–7. [Google Scholar]
- Farell, M.J. The Measurement of Productive Efficiency. J. R.Stat. Soc. Ser. A Stat.Soc. 1957, 120, 253–290. [Google Scholar] [CrossRef]
- Office of the Finanacial Managemnet, State of the Washington. Performance Measure Guide. Available online: http://www.ofm.wa.gov/budget/instructions/other/2009performancemeasureguide.pdf (accessed on 1 June 2020).
- Kaplan, R.S.; Norton, D.P. Translating Strategy into Action—The Balanced ScoreCard; Harward Bussines School Press: Boston, MA, USA, 1996. [Google Scholar]
- Dario, C.; Simar, L. Advaced Robust and Nonparametric Methods in Efficiency Analysis Methodology and Applications; Springer: New York, NY, USA, 2007; ISBN 987-0-387-35155-1. [Google Scholar]
- Coelli, T.J.; Rao, D.S.P.; O’Donnell, C.J.; Battese, G.E. An Introduction to Efficiency and Productivity Analysis; Springer: New York, NY, USA, 2005; ISBN 978-0-387-25895-9. [Google Scholar]
- Doumpos, M.; Zouponidis, C. Multicriteria Decision Aid Classification Methods (Applied Optimization); Springer: New York, NY, USA, 2002; ISBN 1402008058 (ISBN13: 9781402008054). [Google Scholar]
- Zopounidis, C.; Doumpos, M. Multicriteria classification and sorting methods: A literature review. Eur. J. Oper. Res. 2002, 138, 229–246. [Google Scholar] [CrossRef]
- Yeveyeva, I. Solving Classification Problems with Multicriteria Decision Aiding Approaches. Ph.D. Thesis, Faculty of Information Technology, University of Jyvaskyla, Jyväskylä, Finland, 2007. [Google Scholar]
- Ranđelović, M.; Stanković, J.; Savić, G.; Kuk, K.; Ranđelović, D. An Approach to Determining the Importance of Criteria in the Process of Certifying a City as a Business-Friendly Environment. Interfaces 2018, 48, 156–165. [Google Scholar] [CrossRef]
- NALED. Business Friendly Certification BFC SEE. Available online: https://naled.rs/certifikacija-opstina-bfc-see (accessed on 1 June 2020).
- Sarkis, J. A comparative analysis of DEA as a discrete alternative multiplecriteria decision tool. Eur. J. Oper. Res. 2000, 123, 543–557. [Google Scholar] [CrossRef]
- Stewart, T.J. Relationships between data envelopment analysis and multicriteria decision analysis. J. Oper. Res. Soc. 1996, 47, 654–665. [Google Scholar] [CrossRef]
- Prado, J.; Heijungs, R. Implementation of stochastic multi attribute analysis (SMAA) in comparative environmental assessments. Environ. Model. Softw. 2018, 109, 223–231. [Google Scholar] [CrossRef]
- Ploskas, N.; Stiakakis, E.; Fouliras, P. Assessing Computer Network Efficiency Using Data Envelopment Analysis and Multicriteria Decision Analysis Techniques. J. Multi-Criteria Decis. Anal. 2014, 22. [Google Scholar] [CrossRef]
- Bigaret, S.; Hodgett, R.E.; Meyer, P. Supporting the Multi-Criteria Decision Aiding process: R and the MCDA package. EURO J. Decis. Process. 2017, 5, 169–194. [Google Scholar] [CrossRef]
- Brasil, A.T.; Pinheiro, R.P.; Coelho, L.V.A.; Costa, C.N. Comparison of Two MCDA Classification Methods over the Diagnosis of Alzheimer’s Disease. In Rough Sets and Knowledge Technology. RSKT 2009; Wen, P., Li, Y., Polkowski, L., Yao, Y., Tsumoto, S., Wang, G., Eds.; Springer: Berlin/Heidelberg, Germany, 2009; Volume 5589, pp. 334–341. [Google Scholar]
- Longaray, A.; Ensslin, L.; Ensslin, S.; Alves, G.; Dutra, A.; Munhoz, P. Using MCDA to evaluate the performance of the logistics process in public hospitals: The case of a Brazilian teaching hospital. Int. Trans. Oper. Res. 2018, 25, 133–156. [Google Scholar] [CrossRef]
- Roy, J.; Adhikary, K.; Kar, S.; Pamucar, D. A rough strength relational DEMATEL model for analysing the key success factors of hospital service quality. Decis. Mak. Appl. Manag. Eng. 2018, 1, 121–142. [Google Scholar] [CrossRef]
- Figueira, J.; Greco, S.; Ehrgott, M. (Eds.) Multiple Criteria Decision Analysis: State of the Art Surveys; International Series in Operations Research & Management Science; Springer: Boston, MA, USA, 2005. [Google Scholar]
- Lahdelma, R.; Salminen, P.; Hokkanen, J. Using Multicriteria Methods in Environmental Planning and Management. Environ. Manag. 2014, 26, 595–605. [Google Scholar] [CrossRef] [PubMed]
- Coutinho-Rodrigues, J.; Simao, A.; Antunes, C.H. A gis-based multicriteriaspatial decision support system for planning urban infrastructures. Decis. Support Syst. 2011, 51, 720–726. [Google Scholar] [CrossRef]
- Bagherikahvarin, M.; De Stem, Y. Using the A ranking method based on DEA and PROMETHEE II (a rank based on DEA & PR.II). Measurement 2016, 89, 333–342. [Google Scholar]
- Botti, L.; Peypoch, N. Multi-criteria ELECTRE method and destination competitiveness. Tour. Manag. Perspect. 2013, 6, 108–113. [Google Scholar] [CrossRef]
- Papamichail, K.N.; French, S. 25 years of MCDA in nuclear emergency management. IMA J. Manag. Math. 2013, 24, 481–503. [Google Scholar] [CrossRef]
- Sawicka, H.; Węglinski, S.; Witort, P. Application of multiple criteria decision aid methods in logistic systems. LogForum 2010, 6, 3–10. [Google Scholar]
- Biswas, P.; Pal, B.B. A fuzzy goal programming method to solve congestion management problem using genetic algorithm. Decis. Mak. Appl. Manag. Eng. 2019, 2, 36–53. [Google Scholar] [CrossRef]
- Belacel, N. Multicriteria assignment method PROAFTN: Methodology and medical applications. Eur. J. Oper. Res. 2000, 125, 175–183. [Google Scholar] [CrossRef]
- Brasil, A.T.; Pinheiro, P.R.; Coelho, A.L.V. The impact of the prototype selectionon a multicriteria decision aid classification algorithm. In Innovations and Advances in Computer Sciences and Engineering; Springer: New York, NY, USA, 2010; Volume 1, pp. 379–382. [Google Scholar]
- Jacobs, R.; Smith, P.; Street, A. Measuring Efficiency in Health Care; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Berger, A.N.; Hunter, W.C.; Timme, S.G. The Efficiency of Financial Institutions: AReview and Preview of Research Past, Present, and Future. J. Bank. Financ. 1993, 17, 221–249. [Google Scholar] [CrossRef]
- Sarkis, J.; Talluri, S. Eco-efficiency measurement using data envelopment analysis: Research data practitioner issues. Integr. Environ. Assess. Manag. 2004, 6, 91–123. [Google Scholar] [CrossRef]
- Carlsson, B. The Measurement of Efficiency in Production: An Application to Swedish Manufacturing Industries 1968. Swedish J. Econ. 1972, 74, 468–485. [Google Scholar] [CrossRef]
- Klimchik, A.; Ambiehl, A.; Garnier, S.; Furet, B.; Pashkevich, A. Efficiency evaluation of robots in machining applications using industrial performance measure. Robot. Comput.-Integr Manuf. 2017, 48, 12–29. [Google Scholar] [CrossRef]
- Peypoch, N.; Solonandrasana, B. Research note: Technical efficiency in the tourism industry. Tour. Econ. 2006, 12, 653–657. [Google Scholar] [CrossRef]
- Haar, S.; Segers, R.M.; Jehn, K. Measuring the effectiveness of emergency management teams: Scale development and validation. Int. J. Emerg. Manag. 2013, 9, 258. [Google Scholar] [CrossRef]
- Andrejić, M.; Kilibarda, M. The problems of measuring efficiency in logistics. Vojnotehnicki glasnik 2013, 61. [Google Scholar] [CrossRef]
- Filippini, M.; Farsi, M. Regulation and Measuring Cost-Efficiency with Panel Data Models: Application to Electricity Distribution Utilities. Rev. Ind. Organ. 2004, 25, 1–19. [Google Scholar]
- Ferrera, J.; Pedraja-Chaparro, F.; Salinas-Jimenez, J. Measuring Efficiency in Education: An Analysis of Different Approaches for Incorporating Non-discretionary Inputs. Appl. Econ. 2008, 40, 1323–1339. [Google Scholar] [CrossRef]
- Liket, K.C.; Maas, K. Nonprofit organizational effectiveness: Analysis of best practices. Nonprofit Volunt. Sect. Q. 2015, 44, 268–296. [Google Scholar] [CrossRef]
- BFC SEE Network. Available online: http://bfc-see.org/about-bfc-see-network (accessed on 1 June 2020).
- Radukić, S.; Stanković, J. Evaluation of Local Business Environment in the Republic of Serbia. ProcediaEcon. Financ. 2015, 19, 353–363. [Google Scholar] [CrossRef][Green Version]
- Stojanović, B.; Stanković, J.; Ranđelović, M. The City of Niš Competitiveness Analysis in the Field of Foreign Direct Investment. Econ. Enterp. 2012, 60, 167–178. [Google Scholar] [CrossRef]
- Ranđelović, D.; Stanković, J.; Anđelković, M.; Ranđelović, M. Application of AHP method in cities certification process. Management 2014, 69, 75–84. [Google Scholar]
- Ranđelović, M.; Stanković, J.; Ranđelović, D.; Suknović, M. Methods for determination weights in multi-criteria model of cities certification methods for determination weights in multi-criteria model of cities certification. Tech. Technol. Educ. Manag. 2013, 8, 1404–1412. [Google Scholar]
- Randjelović, D.; Janjić, J.; Stanković, J.; Randjelović, M.; Pešić, M. Weights determination in MCDM model combining the techniques of mathematical and statistical analysis. Metal. Int. 2013, XVIII, 217–221. [Google Scholar]
- Radulovic, B.; Dragutinovic, S. Efficiency of local self-governments in Serbia: An SFA approach. Industrija 2015, 43, 123–142. [Google Scholar] [CrossRef]
- Afonso, A.; Fernandes, S. Assessing and Explaining the Relative Efficiency of Local Government. J. Socio-Econ. 2008, 37, 1946–1979. [Google Scholar] [CrossRef]
- Balaguer, M.T.; Prior, D.; Tortosa, E. On the determinants of local government performance: A two-stage nonparametric approach. Eur. Econ. Rev. 2007, 51, 425–451. [Google Scholar] [CrossRef]
- Sousa, M.D.C.S.D.; Stošić, B. Technical Efficiency of the Brazilian Municipalities: Correcting Nonparametric Frontier Measurements for Outliers. J. Product. Anal. 2005, 24, 157–181. [Google Scholar] [CrossRef]
- De Borger, B.; Kerstens, K. Cost Efficiency of Belgian Local Governments: A Comparative analysis of FDH, DEA, and econometric approaches. Reg. Sci. Urban Econ. 1996, 26, 145–170. [Google Scholar] [CrossRef]
- Geys, B.; Heinemann, F.; Kalb, A. Voter involvement, fiscal autonomy and public sector efficiency: Evidence from German municipalities. Eur. J. Political Econ. 2010, 26, 265–278. [Google Scholar] [CrossRef]
- Lo Storto, C. Evaluating technical efficiency of Italian major municipalities: A data envelopment analysis model. Procedia Soc. Behav. Sci. 2013, 81, 346–350. [Google Scholar] [CrossRef]
- Worthington, A.C. Cost Efficiency in Australian Local Government: A Comparative Analysis of Mathematical Programming and Econometric Approaches. Financ. Account. Manag. 2000, 16, 201–223. [Google Scholar] [CrossRef]
- Westhuizen, G.; Dollery, B. South African Local Government Efficiency Measurement; Working Paper Series 4.1-19; Centre for Local Government, School of Business, Economics and Public Policy, University of New England: Armidale, Australia, 2009. [Google Scholar]
- Ray, S. Data Envelopment Analysis; Cambridge University Press: Cambridge, UK, 2004; ISBN 0-521-80256-3. [Google Scholar]
- Charnes, A.; Cooper, W.; Lewin, A.Y.; Seiford, L.M. Data Envelopment Analysis Theory, Methodology and Applications. J. Oper. Res. Soc. 1997, 48, 332–333. [Google Scholar] [CrossRef]
- Cooper, W.W.; Seiford, L.M.; Zhu, J. Data Envelopment Analysis, Handbook on Data Envelopment Analysis; Springer: Boston, MA, USA, 2004; ISBN 978-1-4020-7798-2. [Google Scholar]
- Kongar, E.; Pallis, J.; Sobh, T. Non-parametric Approach for Evaluating the Performance of Engineering Schools. Int. J. Eng. Educ. 2010, 26, 1210–1219. [Google Scholar]
- Ji, Y.; Lee, C. Data envelopment analysis. Stata J. 2010, 2, 267–280. [Google Scholar] [CrossRef]
- Stanković, J.; Radenković;-Jocić, D. The role of business environment in the promotion of investment activities: Case study and municipalities in the Republic of Serbia. Teme 2017, XLI, 457–473. [Google Scholar]
- Beiragh, R.; Alizadeh, R.; Shafiei Kaleibari, S.; Cavallaro, F.; Zolfani, S.; Bausys, R.; Mardani, A. An integrated Multi-Criteria Decision Making Model for Sustainability Performance Assessment for Insurance Companies. Sustainability 2020, 12, 789. [Google Scholar] [CrossRef]
- Kumbhakar, S.; Parmeter, C.; Zelenyuk, V. Stochastic Frontier Analysis: Foundations and Advances; Working Papers 2017-10; Department of Economics, University of Miami: Coral Gables, FL, USA, 2017. [Google Scholar]
- Seale, J., Jr. Stochastic Frontier Analysis. J. Econ. Lit. 2000, 38, 936–938. [Google Scholar]
- Battese, G.; Corra, G. Estimation of a production frontier model: With application to the pastoral zone of eastern Australia. Aust. J. Agric. Resour. Econ. 1977, 21, 169–179. [Google Scholar] [CrossRef]
- Belotti, F.; Daidone, S.; Ilardi, G.; Atella, V. Stochastic Frontier Analysis Using Stata. Stata J. 2012, 13, 719–758. [Google Scholar] [CrossRef]
- Chitnis, A.; Vaidya, O. Efficiency ranking method using SFA and TOPSIS (ERM-ST): Case of Indian banks. Benchmarking Int. J. Res. 2018, 25, 471–488. [Google Scholar] [CrossRef]
- Johnson, A.; Kuosmanen, T. An Introduction to CNLS and StoNED Methods for Efficiency Analysis: Economic Insights and Computational Aspects and Formulations. In Benchmarking for Performance Evaluation: A Production Frontier Approach; Ray, S., Kumbhakar, S., Dua, P., Eds.; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Thoraneenitiyan, N.; Avkiran, K.N. Measuring the impact of restructuring and country-specific factors on the efficiency of post-crisis East Asian banking systems:Integrating DEA with SFA. Socio.-Econ. Plan. Sci. 2009, 43, 240–252. [Google Scholar] [CrossRef]
- Bezat-Jarzebowska, A. A concept of technical efficiency measurement based on the integrated use of the SFA and DEA methods. Sci. Works Wrocław University Econ. 2012, 261, 11–24. [Google Scholar]
- François-Seck, F.; Al-Mouksit, A.; Wassongma, H. DEA and SFA research on the efficiency of microfinance institutions: A meta-analysis. World Dev. 2018, 107, 176–188. [Google Scholar]
- Bogetoft, P.; Otto, L. Stochastic Frontier Analysis SFA. In Benchmarking with DEA, SFA, and R; Operations Research Management Science Series 157; Springer: Berlin/Heidelberg, Germany, 2011; pp. 197–231. [Google Scholar] [CrossRef]
- Azadeh, A.; Ghaderi, S.F.; Omrani, H.; Eivazy, H. An integrated DEA-COLS-SFA algorithm for optimization and policy making of electricity distribution units. Energy Policy 2009, 37, 2605–2618. [Google Scholar] [CrossRef]
- Anouze, A.L.; Bou-Hamad, I. Data envelopment analysis and data mining to efficiency estimation and evaluation. Int. J. Islamic Middle East. Financ. Manag. 2019, 12, 169–190. [Google Scholar] [CrossRef]
- Azadeh, A.; Saberi, M.; Moghaddam, R.; Javanmardi, L. An integrated data envelopment analysis-artificial neural network-rough set algorithm for assessment of personnel efficiency. Expert Syst. Appl. 2011, 38, 1364–1373. [Google Scholar] [CrossRef]
- Antonuccia, L.; Crocettaa, C.; D’Ovidio, F. Evaluation of Italian Judicial System. Procedia Econ. Financ. 2014, 17, 121–130. [Google Scholar] [CrossRef][Green Version]
- Fethi, M.; Pasiouras, F. Assessing bank efficiency and performance with operational research and artificial intelligence techniques: A survey. Eur. J. Oper. Res. 2010, 204, 189–198. [Google Scholar] [CrossRef]
- Swinburn, G.; Goga, S.; Murphy, F. Local Economic Development: A Primer Developing and Implementing Local Economic Development Strategies and Action Plan; The World Bank: Washington, DC, USA, 2006; Available online: http://siteresources.worldbank.org/INTLED/423069-1099670772921/20738133/led_primer.pdf (accessed on 1 June 2020).
- Ranđelović, M.; Nedeljković, S.; Jovanović, M.; Čabarkapa, M.; Stojanović, V.; Aleksić, A.; Ranđelović, D. Use of Determination of the Importance of Criteria in Business-Friendly Certification of Cities as Sustainable Local Economic Development Planning Tool. Symmetry 2020, 12, 425. [Google Scholar] [CrossRef]
- Keeney, R.; Raiffa, H. Decisions with Multiple Objectives: Preferences and Value Tradeoffs; J. Wiley: New York, NY, USA, 1976. [Google Scholar]
- Koksalan, M.; Wallenius, J.; Zionts, S. Multiple Criteria Decision Making: _From Early History to 21th Century; World Scientific: Singapore, 2011; ISBN 978-981-4335-58-4. [Google Scholar]
- Ishizaka, A.; Nemery, P. Multi-Criteria Decision Analysis: Methods and Software; J. Wiley: New York, NY, USA, 2013. [Google Scholar]
- Tsoukiàs, A. From decision theory to decision aiding methodology. Eur. J. Oper. Res. 2008, 187, 138–161. [Google Scholar] [CrossRef]
- Belton, V.; Vickers, S.P. Demystifying DEA—A visual interactive approach based on multi criteria analysis. J. Oper. Res. Soc. 1993, 44, 883–896. [Google Scholar]
- Cooper, W.W.; Seiford, L.M.; Tone, K. Data Envelopment Analysis: A Comprehensive Text with Models, Applications, References and DEA-Solver Software; Kluwer Academic Publishers: Boston, MA, USA, 2000. [Google Scholar]
- Podinovski, V.V. Side effects of absolute weight bounds in DEA models. Eur. J. Oper. Res. 1999, 115, 583–595. [Google Scholar] [CrossRef]
- Charnes, A.; Cooper, W.W.; Rhodes, E. Measuring the efficiency of decision making units. Eur. J. Oper. Res. 1978, 2, 429–444. [Google Scholar] [CrossRef]
- Banker, R.D.; Charnes, A.; Cooper, W.W. Some Models for Estimating Technical and Scale Inefficiencies in Data Envelopment Analysis. Manag. Sci. 1984, 30, 1078–1092. [Google Scholar] [CrossRef]
- Aigner, D.; Lovell, C.A.K.; Schmidt, P. Formulation and estimation of stochastic frontier production function models. J. Econ. 1977, 6, 21–37. [Google Scholar] [CrossRef]
- Meeusen, W.; Van Den Broeck, J. Efficiency estimation from Cobb–Douglas production functions with composed error. Int.Econ. Rev. 1977, 18, 435–444. [Google Scholar] [CrossRef]
- Kumbhakar, S.C.; Lovell, C.A.K. Stochastic Frontier Analysis; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- MacKay, D. Information Theory, Inference, and Learning Algorithms; CambridgeUniversity Press: Cambridge, UK, 2003. [Google Scholar]
- Mitchell, T. Machine Learning; McGraw-Hill Science/Engineering/Math: New York, NY, USA, 1997. [Google Scholar]
- Haykin, S. Neural Networks. A Comprehensive Foundation, 2nd ed.; Prentice Hall: Upper Saddle River, NJ, USA, 2005. [Google Scholar]
- Russell, S.; Norvig, P. Artificial Intelligence: A Modern Approach; Prentice Hall: Upper Saddle River, NJ, USA, 2003. [Google Scholar]
- Langley, P.; Iba, W.; Thompson, K. An analysis of Bayesian classifiers. In Proceedings of the Tenth National Conference on Artificial Intelligence, San Jose, CA, USA, 12–16 July 1992; pp. 399–406. [Google Scholar]
- Friedman, N.; Geiger, D.; Goldszmidt, M. Bayesian network classifiers. Mach. Learn. 1997, 29, 131–163. [Google Scholar] [CrossRef]
- Almuallim, H.; Dietterich, T.G. Learning with many irrelevant features. In Proceedings of the Ninth National Conference on Artificial Intelligence, Anaheim, CA, USA, 14–19 July 1991; pp. 547–552. [Google Scholar]
- Weka (University of Waikato: New Zealand). Available online: http://www.cs.waikato.ac.nz/ml/weka (accessed on 1 June 2020).
- Liu, H.; Motoda, H. Feature Selection for Knowlegde Discovery and Data Mining; Kluwer Academic Publishers: London, UK, 1998. [Google Scholar]
- Abe, N.; Kudo, M. Entropy criterion for classifier-independent feature selection. Lect. Notes Comput. Sci. 2005, 3684, 689–695. [Google Scholar]
- Hall, M.A.; Smith, L.A. Practical feature subset selection for machine learning. In Proceedings of the 21st Australian Computer Science Conference (ACSC’98), Perth, Australia, 4–6 February1998; pp. 181–191. [Google Scholar]
- Moriwal, R.; Prakash, V. An efficient info-gain algorithm for finding frequent sequential traversal patterns from web logs based on dynamic weight constraint. In Proceedings of the CUBE International Information Technology Conference (CUBE’12), Pune, India, 3–5 September2012; pp. 718–723. [Google Scholar]
- Quinlan, J.R. C4.5: Programs for Machine Learning; Morgan Kaufmann Publishers: San Francisco, CA, USA, 1993. [Google Scholar]
- Thakur, D.; Markandaiah, N.; Raj, D.S. Re optimization of ID3 and C4.5 decision tree. Proceedingsof the International Conference on Computer and Communication Technology (ICCCT), Allahabad, India, 17–19 September 2010; pp. 448–450. [Google Scholar]
- Kononenko, I. Estimating attributes: Analysis and extensions of relief. In Machine Learning: ECML-94; Springer: Berlin/Heidelberg, Germany, 1994; pp. 171–182. [Google Scholar]
- Cooper, W.; Seiford, L.; Tone, K. Data Envelopment Analysis; Springer: New York, NY, USA, 2000. [Google Scholar]
- Urbanowicz, R.; Meeker, M.; La Cava, W.; Olson, R.; Moore, J. Relief-based feature selection: Introduction and review. J. Biomed. Inform. 2018, 85, 189–203. [Google Scholar] [CrossRef]
- Powers, D. Evaluation: From precision, recall and F-measure to ROC, informedness, markedness & correlation. J. Mach. Learn. Technol. 2011, 2, 2229–3981. [Google Scholar] [CrossRef]
- Domingos, P.; Pazzani, M. On the optimality of the simple Bayesian classifier under zero-one loss. Mach. Learn. 1997, 29, 103–130. [Google Scholar] [CrossRef]
- Silva, T.C.; Tabak, B.M.; Cajueiro, D.O.; Dias, M.V.B. A comparison of DEA and SFA using micro-and macro-level perspectives: Efficiency of Chinese local banks. Phys. A 2017, 469, 216–223. [Google Scholar] [CrossRef]
- Popović, M.; Savić, G.; Kuzmanović, M.; Martić, M. Using Data Envelopment Analysis and Multi-Criteria Decision-Making Methods to Evaluate Teacher Performance in Higher Education. Symmetry 2020, 12, 563. [Google Scholar]
- Dong, Y.; Hamilton, R.; Tippett, M. Cost efficiency of the Chinese banking sector: A comparison of stochastic frontier analysis and data envelopment analysis. Econ. Model. 2014, 36, 298–308. [Google Scholar] [CrossRef]
- Shumaiza, A.M.; Alcantud, J.C.R. An m-Polar Fuzzy PROMETHEE Approach for AHP-Assisted Group Decision-Making. Math. Comput. Appl. 2020, 25, 26. [Google Scholar]
- Đalić, I.; Stević, Ž.; Karamasa, C.; Puška, A. A novel integrated fuzzy PIPRECIA—Interval rough SAW model: Green supplier selection. Decis. Mak. Appl. Manag. Eng. 2020, 3, 126–145. [Google Scholar] [CrossRef]
- Pamučar, D. Fuzzy-dea model for measuring the efficiency of the transport quality. Mil. Tech. Cour. 2011, LIX, 40–61. [Google Scholar] [CrossRef]
- Stojić, G.; Sremac, S.; Vasiljković, I. A fuzzy model for determining the justifiability of investing in a road freight vehicle fleet. Oper. Res. Eng. Sci. Theory Appl. 2018, 1, 62–75. [Google Scholar] [CrossRef]
- Liu, F.; Aiwu, G.; Lukovac, V.; Vukic, M. A multicriteria model for the selection of the transport service provider: A single valued neutrosophic DEMATEL multicriteria model. Decis. Mak. Appl. Manag. Eng. 2018, 1, 121–130. [Google Scholar] [CrossRef]
- Kevkić, T.S.; Odalović, M.T.; Petković, D.M. A stochastic model of gamma-ray induced oxide charge distribution and threshold voltage shift of MOS transistors. Nucl. Technol. Radiat. 2012, 27, 33–39. [Google Scholar] [CrossRef]
- Kevkić, T.; Stojanović, V.; Joksimović, D. Application of the Generalized Logistic Functions in the Surface Potential Based MOSFET Modeling. J. Comput. Electron. 2017, 16, 90–97. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).