On Valency-Based Molecular Topological Descriptors of Subdivision Vertex-Edge Join of Three Graphs

Abstract

In the studies of quantitative structure–activity relationships (QSARs) and quantitative structure–property relationships (QSPRs), graph invariants are used to estimate the biological activities and properties of chemical compounds. In these studies, degree-based topological indices have a significant place among the other descriptors because of the ease of generation and the speed with which these computations can be accomplished. In this paper, we give the results related to the first, second, and third Zagreb indices, forgotten index, hyper Zagreb index, reduced first and second Zagreb indices, multiplicative Zagreb indices, redefined version of Zagreb indices, first reformulated Zagreb index, harmonic index, atom-bond connectivity index, geometric-arithmetic index, and reduced reciprocal Randić index of a new graph operation named as “subdivision vertex-edge join” of three graphs.

1. Introduction

In mathematical chemistry and chemical graph theory, a topological index is a numerical criterion that is computed based on the molecular graph of a chemical structure. In the study of QSARs/QSPRs, several topological indices (TIs) are frequently applied to gain the correlations between various properties of molecules or the biological activity with their shape [1,2,3]. TIs have also been used in spectral graph theory to quantify the robustness and resilience of complex networks [4]. TIs are two-dimensional descriptors, which consider the internal atomic setting of compounds and give the facts in the numerical form regarding the branching, molecular size, shape, existence of multiple bonds, and heteroatoms. TIs have gained appreciable significance in the previous few years because of the ease of generation and the speed with which these assessments can be accomplished.

There are several graphical invariants, which are valuable in theoretical chemistry and nanotechnology. Thereby, the computation of these TIs is one of the effective lines of research. Suppose that T represents the set of all finite, simple, and connected graphs. Then, a function $F:T\to R^{+}$ is called a topological index if, for any set of two isomorphic graphs $G_1$ and $G_2$, we have $F\left(G_1\right)=F\left(G_2\right)$. Some impressive types of TIs of graphs are distance-based, spectral-based, degree-based, and counting-related graphs. Among these, degree-based are the most eye-catching and can perform the leading rule to characterize the chemical compounds and predict their different physiochemical properties such as density, refractive index, boiling point, molecular weight, etc. For the comprehensive discussions of these indices and other well-known TIs, we refer the reader to [5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25].

Throughout this article, we assume that all graphs are finite, simple, and connected. For a graph $\mathcal{Z}$, $\mathcal{V}\left(\mathcal{Z}\right)$ and $\mathcal{E}\left(\mathcal{Z}\right)$ represent the vertex and edge sets, respectively. For a given graph $\mathcal{Z}$, the order and size are represented by n and e, respectively. An edge with end vertices ${\mathrm{z}}_i$ and ${\mathrm{z}}_j$ is denoted by ${\mathrm{z}}_i{\mathrm{z}}_j\in \mathcal{E}\left(\mathcal{Z}\right)$. For a vertex $\mathrm{z}\in \mathcal{V}\left(\mathcal{Z}\right),$ the number of edges having $\mathrm{z}$ as an end vertex is called the degree of $\mathrm{z}$ in $\mathcal{Z}$ and it is expressed by ${deg}_{\mathcal{Z}}\left(\mathrm{z}\right)$, and, if $\mathrm{z}={\mathrm{z}}_1{\mathrm{z}}_2\in \mathcal{E}\left(\mathcal{Z}\right),$ then ${deg}_{\mathcal{Z}}\left(\mathrm{z}\right)={deg}_{\mathcal{Z}}\left({\mathrm{z}}_1\right)+{deg}_{\mathcal{Z}}\left({\mathrm{z}}_2\right)$ with ${\mathrm{z}}_1,{\mathrm{z}}_2\in \mathcal{V}\left(\mathcal{Z}\right),$. The notations ${\delta }_{\mathcal{Z}}$ and ${▵}_{\mathcal{Z}}$ stand for the minimum and maximum degrees of a graph $\mathcal{Z}$, respectively. We denote the path, cycle, and complete graph, each of order n, by $P_n$, $C_n$, and $K_n$, respectively.

Using graph operations, one can construct a new graph from the given graphs, and it is established that some chemically interesting graphs can be achieved as an outcome of graph operations of some simple graphs. From the relations of various TIs of graph operations in the form of TIs of their components, it is beneficial to determine the TIs of some nanostructures and molecular graphs.

There are several studies regarding TIs of different graph operations (see, e.g., [26,27,28,29,30,31,32]). Very recently, another graph operation, named as the subdivision vertex-edge join (SVE-join), has been introduced [33]. For a graph ${\mathcal{Z}}_1$, $\mathcal{S}\left({\mathcal{Z}}_1\right)$ is the subdividing graph of ${\mathcal{Z}}_1$ whose vertex set has two portions: the original set of vertices $\mathcal{V}\left({\mathcal{Z}}_1\right)$ and the set $\mathcal{I}\left({\mathcal{Z}}_1\right)$ consisting of the inserting vertices that are end vertices of the edges of ${\mathcal{Z}}_1$. Let ${\mathcal{Z}}_2$ and ${\mathcal{Z}}_3$ are the two other disjoint graphs. The $SVE-join$ of ${\mathcal{Z}}_1$ with ${\mathcal{Z}}_2$ and ${\mathcal{Z}}_3$, denoted by ${\mathcal{Z}}_1^{\mathcal{S}}⊳({\mathcal{Z}}_2^{\mathcal{V}}\cup {\mathcal{Z}}_3^{\mathcal{I}})$, is the graph consisting of $\mathcal{S}\left({\mathcal{Z}}_1\right)$, ${\mathcal{Z}}_2$ and ${\mathcal{Z}}_3$, all vertex-disjoint, then joining the ith vertex of $\mathcal{V}\left({\mathcal{Z}}_1\right)$ to every vertex in $\mathcal{V}\left({\mathcal{Z}}_2\right)$ and the ith vertex of $\mathcal{I}\left({\mathcal{Z}}_1\right)$ to each vertex in $\mathcal{V}\left({\mathcal{Z}}_3\right)$. Furthermore, we see that ${\mathcal{Z}}_1^{\mathcal{S}}⊳({\mathcal{Z}}_2^{\mathcal{V}}\cup {\mathcal{Z}}_3^{\mathcal{I}})$ is ${\mathcal{Z}}_1\dot{\vee }{\mathcal{Z}}_2$ (is obtained from $\mathcal{S}\left({\mathcal{Z}}_1\right)$ and ${\mathcal{Z}}_2$ by linking each vertex of $\mathcal{V}\left({\mathcal{Z}}_1\right)$ to every vertex of $\mathcal{V}\left({\mathcal{Z}}_2\right)$ [34]) if ${\mathcal{Z}}_3$ is the null graph, and is ${\mathcal{Z}}_1\underline{\vee }{\mathcal{Z}}_3$ (is obtained from $\mathcal{S}\left({\mathcal{Z}}_1\right)$ and ${\mathcal{Z}}_3$ by linking each vertex of $\mathcal{I}\left({\mathcal{Z}}_1\right)$ to every vertex of $\mathcal{V}\left({\mathcal{Z}}_3\right)$ [34]) if ${\mathcal{Z}}_2$ is the null graph. The graphs $P_4\dot{\vee }{C}_3$, $P_4\underline{\vee }{K}_4$ and $P_4^{\mathcal{S}}⊳(C_3^{\mathcal{V}}\cup K_4^{\mathcal{I}})$ are illustrated in Figure 1.

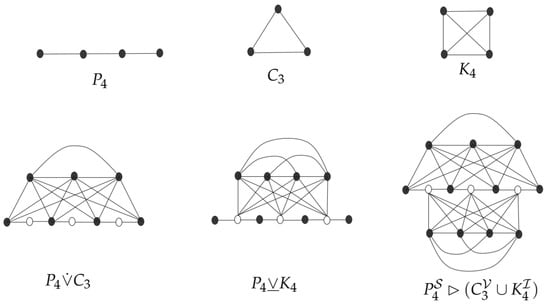
Figure 1. $P_4\dot{\vee }{C}_3$, $P_4\underline{\vee }{K}_4$ and $P_4^{\mathcal{S}}⊳(C_3^{\mathcal{V}}\cup K_4^{\mathcal{I}})$.

The Zagreb indices are well considered molecular structure descriptors, and they have appreciable applications in chemistry. In 1972, Gutman and Trinajstić [1] introduced the first Zagreb index based on the degree of vertices of $\mathcal{Z}.$ The first and second Zagreb indices of a graph $\mathcal{Z}$ can be defined in the following way:

$$\begin{array}{cc}\hfill {\mathcal{M}}_1\left(\mathcal{Z}\right)=\sum _{\mathrm{z}\in \mathcal{V}\left(\mathcal{Z}\right)}{deg}_{\mathcal{Z}}^2\left(\mathrm{z}\right),& {\mathcal{M}}_2\left(\mathcal{Z}\right)=\sum _{{\mathrm{z}}_1{\mathrm{z}}_2\in \mathcal{E}\left(\mathcal{Z}\right)}{deg}_{\mathcal{Z}}\left({\mathrm{z}}_1\right){deg}_{\mathcal{Z}}\left({\mathrm{z}}_2\right).\hfill \end{array}$$

(1)

The third Zagreb index (also called irregular index) [35] of $\mathcal{Z}$ can be stated as:

$${\mathcal{M}}_3\left(\mathcal{Z}\right)=\sum _{{\mathrm{z}}_1{\mathrm{z}}_2\in \mathcal{E}\left(\mathcal{Z}\right)}\left|{deg}_{\mathcal{Z}}\left({\mathrm{z}}_1\right)-{deg}_{\mathcal{Z}}\left({\mathrm{z}}_2\right)\right|.$$

(2)

Inspired by the first and second Zagreb indices, Furtula and Gutman [36] proposed the forgotten topological index (or F-index) of $\mathcal{Z}$ in the following way:

$$\mathcal{F}\left(\mathcal{Z}\right)=\sum _{\mathrm{z}\in \mathcal{V}\left(\mathcal{Z}\right)}{deg}_{\mathcal{Z}}^3\left(\mathrm{z}\right).$$

(3)

Shirdel et al. [37] put forward a new degree based Zagreb index of $\mathcal{Z}$ in 2013 and they named it “hyper-Zagreb index”, which is specified as follows:

$$\mathcal{HM}\left(\mathcal{Z}\right)=\sum _{{\mathrm{z}}_1{\mathrm{z}}_2\in \mathcal{E}\left(\mathcal{Z}\right)}{({deg}_{\mathcal{Z}}\left({\mathrm{z}}_1\right)+{deg}_{\mathcal{Z}}\left({\mathrm{z}}_2\right))}^2=\mathcal{F}\left(\mathcal{Z}\right)+2{\mathcal{M}}_2\left(\mathcal{Z}\right).$$

(4)

The reduced first Zagreb index of $\mathcal{Z}$, introduced by Ediz [38], and the reduced second Zagreb index, defined by Furtula et al. [39], are as follows:

$$\begin{array}{cc}\hfill {\mathcal{RM}}_1\left(\mathcal{Z}\right)=\sum _{\mathrm{z}\in \mathcal{V}\left(\mathcal{Z}\right)}{({deg}_{\mathcal{Z}}\left(\mathrm{z}\right)-1)}^2,& {\mathcal{RM}}_2\left(\mathcal{Z}\right)=\sum _{{\mathrm{z}}_1{\mathrm{z}}_2\in \mathcal{E}\left(\mathcal{Z}\right)}({deg}_{\mathcal{Z}}\left({\mathrm{z}}_1\right)-1)({deg}_{\mathcal{Z}}\left({\mathrm{z}}_2\right)-1).\hfill \end{array}$$

(5)

In 2010, Todeshine et al. [40,41] proposed the multiplicative variants of ordinary Zagreb indices of $\mathcal{Z}$, which are defined as follows:

$$\begin{array}{cc}\hfill \prod _1\left(\mathcal{Z}\right)=\prod _{\mathrm{z}\in \mathcal{V}\left(\mathcal{Z}\right)}{deg}_{\mathcal{Z}}^2\left(\mathrm{z}\right),& \prod _2\left(\mathcal{Z}\right)=\prod _{{\mathrm{z}}_1{\mathrm{z}}_2\in \mathcal{E}\left(\mathcal{Z}\right)}{deg}_{\mathcal{Z}}\left({\mathrm{z}}_1\right){deg}_{\mathcal{Z}}\left({\mathrm{z}}_2\right).\hfill \end{array}$$

(6)

The first, second, and third redefined versions of Zagreb indices of $\mathcal{Z}$ brought by Ranjini et al. [42] and Usha et al. [43] are, respectively:

$$\mathcal{R}e\mathcal{Z}{e}_1\left(\mathcal{Z}\right)=\sum _{{\mathrm{z}}_1{\mathrm{z}}_2\in \mathcal{E}\left(\mathcal{Z}\right)}{\displaystyle \frac{{deg}_{\mathcal{Z}}\left({\mathrm{z}}_1\right)+{deg}_{\mathcal{Z}}\left({\mathrm{z}}_2\right)}{{deg}_{\mathcal{Z}}\left({\mathrm{z}}_1\right){deg}_{\mathcal{Z}}\left({\mathrm{z}}_2\right)}}.$$

(7)

$$\mathcal{R}e\mathcal{Z}{e}_2\left(\mathcal{Z}\right)=\sum _{{\mathrm{z}}_1{\mathrm{z}}_2\in \mathcal{E}\left(\mathcal{Z}\right)}{\displaystyle \frac{{deg}_{\mathcal{Z}}\left({\mathrm{z}}_1\right){deg}_{\mathcal{Z}}\left({\mathrm{z}}_2\right)}{{deg}_{\mathcal{Z}}\left({\mathrm{z}}_1\right)+{deg}_{\mathcal{Z}}\left({\mathrm{z}}_2\right)}}.$$

(8)

$$\mathcal{R}e\mathcal{Z}{e}_3\left(\mathcal{Z}\right)=\sum _{{\mathrm{z}}_1{\mathrm{z}}_2\in \mathcal{E}\left(\mathcal{Z}\right)}{deg}_{\mathcal{Z}}\left({\mathrm{z}}_1\right){deg}_{\mathcal{Z}}\left({\mathrm{z}}_2\right)({deg}_{\mathcal{Z}}\left({\mathrm{z}}_1\right)+{deg}_{\mathcal{Z}}\left({\mathrm{z}}_2\right)).$$

(9)

In [44], Milićević et al. introduced new versions of Zagreb indices called reformulated Zagreb indices. The first reformulated Zagreb index of $\mathcal{Z}$ is as follows:

$${\mathcal{EM}}_1\left(\mathcal{Z}\right)=\sum _{\mathrm{f}\in \mathcal{E}\left(\mathcal{Z}\right)}{deg}_{\mathcal{Z}}{\left(\mathrm{f}\right)}^2=\sum _{\mathrm{f}={\mathrm{z}}_1{\mathrm{z}}_2\in \mathcal{E}\left(\mathcal{Z}\right)}{({deg}_{\mathcal{Z}}\left({\mathrm{z}}_1\right)+{deg}_{\mathcal{Z}}\left({\mathrm{z}}_2\right)-2)}^2.$$

(10)

For a graph $\mathcal{Z}$, the harmonic index was presented by Fajtlowicz [45] as:

$$\mathcal{H}\left(\mathcal{Z}\right)=\sum _{{\mathrm{z}}_1{\mathrm{z}}_2\in \mathcal{E}\left(\mathcal{Z}\right)}{\displaystyle \frac{2}{{deg}_{\mathcal{Z}}\left({\mathrm{z}}_1\right)+{deg}_{\mathcal{Z}}\left({\mathrm{z}}_2\right)}}.$$

(11)

Estrada [46] described atom-bond connectivity index of $\mathcal{Z}$ as follows:

$$\mathcal{ABC}\left(\mathcal{Z}\right)=\sum _{{\mathrm{z}}_1{\mathrm{z}}_2\in \mathcal{E}\left(\mathcal{Z}\right)}\sqrt{{\displaystyle \frac{{deg}_{\mathcal{Z}}\left({\mathrm{z}}_1\right)+{deg}_{\mathcal{Z}}\left({\mathrm{z}}_2\right)-2}{{deg}_{\mathcal{Z}}\left({\mathrm{z}}_1\right){deg}_{\mathcal{Z}}\left({\mathrm{z}}_2\right)}}}.$$

(12)

The geometric-arithmetic index of $\mathcal{Z}$ was defined by Vukičević et al. [47] as:

$$\mathcal{GA}\left(\mathcal{Z}\right)=\sum _{{\mathrm{z}}_1{\mathrm{z}}_2\in \mathcal{E}\left(\mathcal{Z}\right)}{\displaystyle \frac{2\sqrt{{deg}_{\mathcal{Z}}\left({\mathrm{z}}_1\right){deg}_{\mathcal{Z}}\left({\mathrm{z}}_2\right)}}{{deg}_{\mathcal{Z}}\left({\mathrm{z}}_1\right)+{deg}_{\mathcal{Z}}\left({\mathrm{z}}_2\right)}}.$$

(13)

Reduced reciprocal Randić index ($\mathcal{RRR}$ index) of $\mathcal{Z}$ was introduced by Gutman et al. in [48] as follows:

$$\mathcal{RRR}\left(\mathcal{Z}\right)=\sum _{{\mathrm{z}}_1{\mathrm{z}}_2\in \mathcal{E}\left(\mathcal{Z}\right)}\sqrt{({deg}_{\mathcal{Z}}\left({\mathrm{z}}_1\right)-1)({deg}_{\mathcal{Z}}\left({\mathrm{z}}_2\right)-1)}.$$

(14)

Now, we state certain properties of the subdivision vertex-edge join of three graphs in the next lemma.

Lemma 1

([33]). Let ${\mathcal{Z}}_1$, ${\mathcal{Z}}_2$, and ${\mathcal{Z}}_3$ be graphs. Then, we have:

• $|\mathcal{V}({\mathcal{Z}}_1^{\mathcal{S}}⊳({\mathcal{Z}}_2^{\mathcal{V}}\cup {\mathcal{Z}}_3^{\mathcal{I}}))|=n_1+e_1+n_2+n_3$ and $|\mathcal{E}({\mathcal{Z}}_1^{\mathcal{S}}⊳({\mathcal{Z}}_2^{\mathcal{V}}\cup {\mathcal{Z}}_3^{\mathcal{I}}))|=2e_1+n_1{n}_2+e_1{n}_3+e_2+e_3$.
• ${deg}_{{\mathcal{Z}}_1^{\mathcal{S}}⊳({\mathcal{Z}}_2^{\mathcal{V}}\cup {\mathcal{Z}}_3^{\mathcal{I}})}\left(z\right)=\left\{\begin{array}{cc}{deg}_{{\mathcal{Z}}_1}\left(z\right)+n_2,\hfill & z\in \mathcal{V}\left({\mathcal{Z}}_1\right),\hfill \\ n_3+2,\hfill & z\in \mathcal{I}\left({\mathcal{Z}}_1\right),\hfill \\ {deg}_{{\mathcal{Z}}_2}\left(z\right)+n_1,\hfill & z\in \mathcal{V}\left({\mathcal{Z}}_2\right),\hfill \\ {deg}_{{\mathcal{Z}}_3}\left(z\right)+e_1,\hfill & z\in \mathcal{V}\left({\mathcal{Z}}_3\right).\hfill \end{array}\right.$

By using these graph operation, one can construct new (chemical) graphs from existing graphs. Therefore, it is important to know which physico-chemical properties are carried from original graphs to the newly constructed graph via this new operation. Moreover, many molecular characteristics of newly formed compound via this operation can be predicted by computing the expression for their additive degree-based indices.

2. Applications of Topological Indices

The atom-bond connectivity $\left(\mathcal{ABC}\right)$ index provides a very good correlation for the stability of linear alkanes as well as the branched alkanes and for computing the strain energy of cyclo alkanes [49]. The Randić index is a topological descriptor that has correlated with a lot of chemical characteristics of the molecules and has been found to the parallel to computing the boiling point and Kovats constants of the molecules. To correlate with certain physico-chemical properties, $\mathcal{GA}$ index has much better predictive power than the predictive power of the Randić connectivity index [50]. The Zagreb indices were found to occur for the computation of the total $\pi$-electron energy of the molecules within specific approximate expressions [51]. These are among the graph invariants which were proposed for the measurement of the skeleton of the branching of the carbon atom [52].

3. Main Results

The present section provides the results related to the first, second, and third Zagreb indices, forgotten index, hyper Zagreb index, reduced first and second Zagreb indices, multiplicative Zagreb indices, redefined version of Zagreb indices, first reformulated Zagreb index, harmonic index, atom-bond connectivity index, geometric-arithmetic index, and reduced reciprocal Randić index of the subdivision vertex-edge join of three graphs.

In the following theorem, we present the closed formulae for the first, second, and third Zagreb indices of subdivision vertex-edge join for three graphs.

Theorem 1.

Let ${\mathcal{Z}}_1$, ${\mathcal{Z}}_2$ and ${\mathcal{Z}}_3$ be three graphs. Then, we have

• ${\mathcal{M}}_1({\mathcal{Z}}_1^{\mathcal{S}}⊳({\mathcal{Z}}_2^{\mathcal{V}}\cup {\mathcal{Z}}_3^{\mathcal{I}}))={\mathcal{M}}_1\left({\mathcal{Z}}_1\right)+{\mathcal{M}}_1\left({\mathcal{Z}}_2\right)+{\mathcal{M}}_1\left({\mathcal{Z}}_3\right)+n_1{n}_2(n_1+n_2)+4(n_2{e}_1+n_1{e}_2)+n_3{e}_1(e_1+n_3)+4e_1(1+e_3+n_3).$
• ${\mathcal{M}}_2({\mathcal{Z}}_1^{\mathcal{S}}⊳({\mathcal{Z}}_2^{\mathcal{V}}\cup {\mathcal{Z}}_3^{\mathcal{I}}))={\mathcal{M}}_2\left({\mathcal{Z}}_2\right)+{\mathcal{M}}_2\left({\mathcal{Z}}_3\right)+(n_3+2){\mathcal{M}}_1\left({\mathcal{Z}}_1\right)+n_1{\mathcal{M}}_1\left({\mathcal{Z}}_2\right)+e_1{\mathcal{M}}_1\left({\mathcal{Z}}_3\right)+2n_1{n}_2(e_1+e_2)+e_1(n_3+2)(2e_3+n_3{e}_1+2n_2)+n_1^2(e_2+n_2^2)+e_1(4e_2+e_1{e}_3).$
• ${\mathcal{M}}_3({\mathcal{Z}}_1^{\mathcal{S}}⊳({\mathcal{Z}}_2^{\mathcal{V}}\cup {\mathcal{Z}}_3^{\mathcal{I}}))\le {\mathcal{M}}_3\left({\mathcal{Z}}_2\right)+{\mathcal{M}}_3\left({\mathcal{Z}}_3\right)+{\mathcal{M}}_1\left({\mathcal{Z}}_1\right)+n_1{n}_2(n_1+n_2)+2n_1(e_2+e_3)+e_1{n}_3(n_3+e_1+2)+2e_1(2n_2+n_3+2).$

Proof. 

• By using Lemma 1 in Equation (1), we get

  $$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\mathcal{M}}_1({\mathcal{Z}}_1^{\mathcal{S}}⊳({\mathcal{Z}}_2^{\mathcal{V}}\cup {\mathcal{Z}}_3^{\mathcal{I}}))& =\sum _{\mathrm{z}\in \mathcal{V}\left({\mathcal{Z}}_1\right)}({deg}_{{\mathcal{Z}}_1}^2\left(\mathrm{z}\right)+n_2^2+2n_2{deg}_{{\mathcal{Z}}_1}\left(\mathrm{z}\right))+\sum _{\mathrm{z}\in \mathcal{I}\left({\mathcal{Z}}_1\right)}(n_3^2+4+4n_3)\hfill \\ & +\sum _{\mathrm{z}\in \mathcal{V}\left({\mathcal{Z}}_2\right)}({deg}_{{\mathcal{Z}}_2}^2\left(\mathrm{z}\right)+n_1^2+2n_1{deg}_{{\mathcal{Z}}_2}\left(\mathrm{z}\right))+\sum _{\mathrm{z}\in \mathcal{V}\left({\mathcal{Z}}_3\right)}({deg}_{{\mathcal{Z}}_3}^2\left(\mathrm{z}\right)+e_1^2\hfill \\ & +2e_1{deg}_{{\mathcal{Z}}_3}\left(\mathrm{z}\right))\hfill \\ & ={\mathcal{M}}_1\left({\mathcal{Z}}_1\right)+n_2^2{n}_1+4n_2{e}_1+e_1(n_3^2+4+4n_3)+{\mathcal{M}}_1\left({\mathcal{Z}}_2\right)+n_1^2{n}_2\hfill \\ & +4n_1{e}_2+{\mathcal{M}}_1\left({\mathcal{Z}}_3\right)+e_1^2{n}_3+4e_1{e}_3.\hfill \end{array}\end{array}$$

  After some simplifications, we get the required result.
• By using Lemma 1 in Equation (1), we obtain

  $$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\mathcal{M}}_2({\mathcal{Z}}_1^{\mathcal{S}}⊳({\mathcal{Z}}_2^{\mathcal{V}}\cup {\mathcal{Z}}_3^{\mathcal{I}}))& =\sum _{{\mathrm{z}}_1{\mathrm{z}}_2\in \mathcal{E}\left({\mathcal{Z}}_2\right)}({deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_1\right)+n_1)({deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_2\right)+n_1)+\sum _{{\mathrm{z}}_1{\mathrm{z}}_2\in \mathcal{E}\left({\mathcal{Z}}_3\right)}({deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_1\right)\hfill \\ & +e_1)({deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_2\right)+e_1)+\sum _{{\mathrm{z}}_1\in \mathcal{V}\left({\mathcal{Z}}_1\right)}\sum _{{\mathrm{z}}_2\in \mathcal{V}\left({\mathcal{Z}}_2\right)}({deg}_{{\mathcal{Z}}_1}\left({\mathrm{z}}_1\right)+n_2)({deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_2\right)\hfill \\ & +n_1)+\sum _{{\mathrm{z}}_1\in \mathcal{I}\left({\mathcal{Z}}_1\right)}\sum _{{\mathrm{z}}_2\in \mathcal{V}\left({\mathcal{Z}}_3\right)}(n_3+2)({deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_2\right)+e_1)\hfill \\ & +\sum _{\begin{array}{c}{\mathrm{z}}_1{\mathrm{z}}_2\in \mathcal{E}\left(\mathcal{S}\left({\mathcal{Z}}_1\right)\right),\\ {\mathrm{z}}_1\in \mathcal{V}\left({\mathcal{Z}}_1\right),{\mathrm{z}}_2\in \mathcal{I}\left({\mathcal{Z}}_1\right)\end{array}}({deg}_{{\mathcal{Z}}_1}\left({\mathrm{z}}_1\right)+n_2)(n_3+2)\hfill \\ & ={\mathcal{M}}_2\left({\mathcal{Z}}_2\right)+n_1{\mathcal{M}}_1\left({\mathcal{Z}}_2\right)+n_1^2{e}_2+{\mathcal{M}}_2\left({\mathcal{Z}}_3\right)+e_1{\mathcal{M}}_1\left({\mathcal{Z}}_3\right)+e_1^2{e}_3+4e_1{e}_2\hfill \\ & +2n_1{n}_2{e}_2+2n_1{n}_2{e}_1+n_1^2{n}_2^2+(n_3+2)(2e_1{e}_3+n_3{e}_1^2)+(n_3+2)\hfill \\ & ({\mathcal{M}}_1\left({\mathcal{Z}}_1\right)+2n_2{e}_1).\hfill \end{array}\end{array}$$

  After some simplifications, we acquire the required result.
• By using Lemma 1 in Equation (2), we get

  $$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\mathcal{M}}_3({\mathcal{Z}}_1^{\mathcal{S}}⊳({\mathcal{Z}}_2^{\mathcal{V}}\cup {\mathcal{Z}}_3^{\mathcal{I}}))& =\sum _{{\mathrm{z}}_1{\mathrm{z}}_2\in \mathcal{E}\left({\mathcal{Z}}_2\right)}\left|{deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_1\right)-{deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_2\right)\right|\hfill \\ & +\sum _{{\mathrm{z}}_1{\mathrm{z}}_2\in \mathcal{E}\left({\mathcal{Z}}_3\right)}\left|{deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_1\right)-{deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_2\right)\right|\hfill \\ & +\sum _{{\mathrm{z}}_1\in \mathcal{V}\left({\mathcal{Z}}_1\right)}\sum _{{\mathrm{z}}_2\in \mathcal{V}\left({\mathcal{Z}}_2\right)}\left|{deg}_{{\mathcal{Z}}_1}\left({\mathrm{z}}_1\right)-{deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_2\right)-n_1+n_2\right|\hfill \\ & +\sum _{{\mathrm{z}}_1\in \mathcal{I}\left({\mathcal{Z}}_1\right)}\sum _{{\mathrm{z}}_2\in \mathcal{V}\left({\mathcal{Z}}_3\right)}\left|{deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_2\right)+e_1-n_3-2\right|\hfill \\ & +\sum _{\begin{array}{c}{\mathrm{z}}_1{\mathrm{z}}_2\in \mathcal{E}\left(\mathcal{S}\left({\mathcal{Z}}_1\right)\right),\\ {\mathrm{z}}_1\in \mathcal{V}\left({\mathcal{Z}}_1\right),{\mathrm{z}}_2\in \mathcal{I}\left({\mathcal{Z}}_1\right)\end{array}}\left|{deg}_{{\mathcal{Z}}_1}\left({\mathrm{z}}_1\right)+n_2-n_3-2\right|\hfill \\ & \le {\mathcal{M}}_3\left({\mathcal{Z}}_2\right)+{\mathcal{M}}_3\left({\mathcal{Z}}_3\right)+2e_1{n}_2+2e_2{n}_1+n_1^2{n}_2+n_1{n}_2^2+2e_3{n}_1+e_1^2{n}_3\hfill \\ & +n_3^2{e}_1+2e_1{n}_3+\sum _{\mathrm{z}\in \mathcal{V}\left({\mathcal{Z}}_1\right)}{deg}_{{\mathcal{Z}}_1}\left({\mathrm{z}}_1\right)\left|{deg}_{{\mathcal{Z}}_1}\left(\mathrm{z}\right)+n_2-n_3-2\right|\hfill \\ & \le {\mathcal{M}}_3\left({\mathcal{Z}}_2\right)+{\mathcal{M}}_3\left({\mathcal{Z}}_3\right)+2e_1{n}_2+n_1{n}_2(n_1+n_2)+2n_1(e_2+e_3)\hfill \\ & +e_1{n}_3(n_3+e_1+2)+{\mathcal{M}}_1\left({\mathcal{Z}}_1\right)+2n_2{e}_1+2e_1(n_3+2).\hfill \end{array}\end{array}$$

This completes the proof. □

Now, we set up the precise value of the F-index of subdivision vertex-edge join for three graphs.

Theorem 2.

Let ${\mathcal{Z}}_1$, ${\mathcal{Z}}_2$ and ${\mathcal{Z}}_3$ be three graphs. Then, we have

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \mathcal{F}({\mathcal{Z}}_1^S⊳({\mathcal{Z}}_2^V\cup {\mathcal{Z}}_3^E))& =\mathcal{F}\left({\mathcal{Z}}_1\right)+\mathcal{F}\left({\mathcal{Z}}_2\right)+\mathcal{F}\left({\mathcal{Z}}_3\right)+3(n_2{\mathcal{M}}_1\left({\mathcal{Z}}_1\right)+n_1{\mathcal{M}}_1\left({\mathcal{Z}}_2\right)+e_1{\mathcal{M}}_1\left({\mathcal{Z}}_3\right))\hfill \\ & +n_1{n}_2(n_1^2+n_2^2)+n_3{e}_1(n_3^2+e_1^2)+6(n_2^2{e}_1+n_1^2{e}_2+e_1^2{e}_3)+8e_1+6n_3{e}_1(n_3+2).\hfill \end{array}\end{array}$$

Proof. 

By Lemma 1 in Equation (3), we get

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \mathcal{F}({\mathcal{Z}}_1^S⊳({\mathcal{Z}}_2^{\mathcal{V}}\cup {\mathcal{Z}}_3^{\mathcal{I}}))& =\sum _{\mathrm{z}\in \mathcal{V}({\mathcal{Z}}_1)}({deg}_{{\mathcal{Z}}_1}^3(z)+n_2^3+3n_2{deg}_{{\mathcal{Z}}_1}^2\left(z\right)+3n_2^2{deg}_{{\mathcal{Z}}_1}\left(z\right))+\sum _{\mathrm{z}\in \mathcal{I}({\mathcal{Z}}_1)}(n_3^3+8\hfill \\ & +6n_3^2+12n_3)+\sum _{\mathrm{z}\in \mathcal{V}\left({\mathcal{Z}}_2\right)}({deg}_{{\mathcal{Z}}_2}^3\left(z\right)+n_1^3+3n_1{deg}_{{\mathcal{Z}}_2}^2\left(z\right)+3n_1^2{deg}_{{\mathcal{Z}}_2}\left(z\right))\hfill \\ & +\sum _{\mathrm{z}\in \mathcal{V}\left({\mathcal{Z}}_3\right)}({deg}_{{\mathcal{Z}}_3}^3\left(z\right)+e_1^3+3e_1{deg}_{{\mathcal{Z}}_3}^2\left(z\right)+3e_1^2{deg}_{{\mathcal{Z}}_3}\left(z\right))\hfill \\ & =\mathcal{F}\left({\mathcal{Z}}_1\right)+n_2^3{n}_1+3n_2{\mathcal{M}}_1\left({\mathcal{Z}}_1\right)+6n_2^2{e}_1+e_1(n_3^3+8+6n_3^2+12n_3)+\mathcal{F}\left({\mathcal{Z}}_2\right)\hfill \\ & +n_1^3{n}_2+3n_1{\mathcal{M}}_1\left({\mathcal{Z}}_2\right)+6n_1^2{e}_2+\mathcal{F}\left({\mathcal{Z}}_3\right)+e_1^3{n}_3+3e_1{\mathcal{M}}_1\left({\mathcal{Z}}_3\right)+6e_1^2{e}_3.\hfill \end{array}\end{array}$$

This finishes the proof. □

Now, we give the exact expression for the hyper-Zagreb index of subdivision vertex-edge join for three graphs.

Theorem 3.

Let ${\mathcal{Z}}_1$, ${\mathcal{Z}}_2$ and ${\mathcal{Z}}_3$ be three graphs. Then, we have

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \mathcal{HM}({\mathcal{Z}}_1^{\mathcal{S}}⊳({\mathcal{Z}}_2^{\mathcal{V}}\cup {\mathcal{Z}}_3^{\mathcal{I}}))& =\mathcal{F}\left({\mathcal{Z}}_1\right)+\mathcal{F}\left({\mathcal{Z}}_2\right)+\mathcal{F}\left({\mathcal{Z}}_3\right)+2({\mathcal{M}}_2\left({\mathcal{Z}}_2\right)+{\mathcal{M}}_2\left({\mathcal{Z}}_3\right))+{\mathcal{M}}_1\left({\mathcal{Z}}_1\right)(3n_2\hfill \\ & +2n_3+4)+5n_1{\mathcal{M}}_1\left({\mathcal{Z}}_2\right)+5e_1{\mathcal{M}}_1\left({\mathcal{Z}}_3\right)+n_1{n}_2{(n_1+n_2)}^2+4n_1{n}_2(e_1+e_2)\hfill \\ & +n_3{e}_1{(n_3+e_1)}^2+4e_1{e}_3(n_3+2e_1+2)+4n_3{e}_1(n_2+e_1)+8e_2(n_1^2+e_1)\hfill \\ & +8e_1+2n_2{e}_1(4+3n_2)+6n_3{e}_1(n_3+2).\hfill \end{array}\end{array}$$

Proof. 

By definition of hyper-Zagreb index, we have $\mathcal{HM}({\mathcal{Z}}_1^{\mathcal{S}}⊳({\mathcal{Z}}_2^{\mathcal{V}}\cup {\mathcal{Z}}_3^{\mathcal{I}}))=\mathcal{F}({\mathcal{Z}}_1^{\mathcal{S}}⊳({\mathcal{Z}}_2^{\mathcal{V}}\cup {\mathcal{Z}}_3^{\mathcal{I}}))+2{\mathcal{M}}_2({\mathcal{Z}}_1^{\mathcal{S}}⊳({\mathcal{Z}}_2^{\mathcal{V}}\cup {\mathcal{Z}}_3^{\mathcal{I}}))$. Hence, the result follows from Theorems 1 and 2. □

In the next result, we provide the closed formulas of the reduced first and second Zagreb indices of subdivision vertex-edge join for three graphs.

Theorem 4.

Let ${\mathcal{Z}}_1$, ${\mathcal{Z}}_2$ and ${\mathcal{Z}}_3$ be three graphs. Then, we have

• ${\mathcal{RM}}_1({\mathcal{Z}}_1^{\mathcal{S}}⊳({\mathcal{Z}}_2^{\mathcal{V}}\cup {\mathcal{Z}}_3^{\mathcal{I}}))={\mathcal{RM}}_1\left({\mathcal{Z}}_1\right)+{\mathcal{RM}}_1\left({\mathcal{Z}}_2\right)+{\mathcal{RM}}_1\left({\mathcal{Z}}_3\right)+n_1{n}_2(n_1+n_2-4)+4(n_2{e}_1+n_1{e}_2)+e_1{(n_3+1)}^2+e_1(e_1{n}_3+4e_3-2n_3).$
• ${\mathcal{RM}}_2({\mathcal{Z}}_1^{\mathcal{S}}⊳({\mathcal{Z}}_2^{\mathcal{V}}\cup {\mathcal{Z}}_3^{\mathcal{I}}))={\mathcal{RM}}_2\left({\mathcal{Z}}_2\right)+{\mathcal{RM}}_2\left({\mathcal{Z}}_3\right)+(n_3+1){\mathcal{M}}_1\left({\mathcal{Z}}_1\right)+n_1{\mathcal{M}}_1\left({\mathcal{Z}}_2\right)+e_1{\mathcal{M}}_1\left({\mathcal{Z}}_3\right)+e_1(n_3+1)(2e_3+n_3(e_1-1)+2(n_2-1))+n_1{e}_2(n_1-2)+e_1{e}_3(e_1-2)+(2e_1+n_1(n_2-1))(2e_2+n_2(n-1)).$

Proof. 

By using Lemma 1 in Equation (5), we get

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\mathcal{RM}}_1({\mathcal{Z}}_1^{\mathcal{S}}⊳({\mathcal{Z}}_2^{\mathcal{V}}\cup {\mathcal{Z}}_3^{\mathcal{I}}))& =\sum _{\mathrm{z}\in \mathcal{V}\left({\mathcal{Z}}_1\right)}{({deg}_{{\mathcal{Z}}_1}\left(z\right)+n_2-1)}^2+\sum _{\mathrm{z}\in \mathcal{I}\left({\mathcal{Z}}_1\right)}{(n_3+2-1)}^2\hfill \\ & +\sum _{\mathrm{z}\in \mathcal{V}\left({\mathcal{Z}}_2\right)}{({deg}_{{\mathcal{Z}}_2}\left(z\right)+n_1-1)}^2+\sum _{\mathrm{z}\in \mathcal{V}\left({\mathcal{Z}}_3\right)}{({deg}_{{\mathcal{Z}}_3}\left(z\right)+e_1-1)}^2\hfill \\ & =\sum _{\mathrm{z}\in \mathcal{V}\left({\mathcal{Z}}_1\right)}({({deg}_{{\mathcal{Z}}_1}\left(z\right)-1)}^2+n_2^2+2n_2({deg}_{{\mathcal{Z}}_1}\left(z\right)-1))+\sum _{\mathrm{z}\in \mathcal{I}\left({\mathcal{Z}}_1\right)}{(n_3+1)}^2\hfill \\ & +\sum _{\mathrm{z}\in \mathcal{V}\left({\mathcal{Z}}_2\right)}({({deg}_{{\mathcal{Z}}_2}\left(z\right)-1)}^2+n_1^2+2n_1({deg}_{{\mathcal{Z}}_2}\left(z\right)-1))\hfill \\ & +\sum _{\mathrm{z}\in \mathcal{V}\left({\mathcal{Z}}_3\right)}({({deg}_{{\mathcal{Z}}_3}\left(z\right)-1)}^2+e_1^2+2e_1({deg}_{{\mathcal{Z}}_3}\left(z\right)-1))\hfill \\ & ={\mathcal{RM}}_1\left({\mathcal{Z}}_1\right)+n_2^2{n}_1+2n_2(2e_1-n_1)+e_1{(n_3+1)}^2+{\mathcal{RM}}_1\left({\mathcal{Z}}_2\right)+n_1^2{n}_2\hfill \\ & +2n_1(2e_2-n_2)+{\mathcal{RM}}_1\left({\mathcal{Z}}_3\right)+e_1^2{n}_3+2e_1(2e_3-n_3).\hfill \end{array}\end{array}$$

By means of some simplifications, we get the required result. Now, using Lemma 1 in Equation (5), we have

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\mathcal{RM}}_2({\mathcal{Z}}_1^{\mathcal{S}}⊳({\mathcal{Z}}_2^{\mathcal{V}}\cup {\mathcal{Z}}_3^{\mathcal{I}}))& =\sum _{{\mathrm{z}}_1{\mathrm{z}}_2\in \mathcal{E}\left({\mathcal{Z}}_2\right)}({deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_1\right)+n_1-1)({deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_2\right)+n_1-1)+\sum _{{\mathrm{z}}_1{\mathrm{z}}_2\in \mathcal{E}\left({\mathcal{Z}}_3\right)}\hfill \\ & ({deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_1\right)+e_1-1)({deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_2\right)+e_1-1)+\sum _{{\mathrm{z}}_1\in \mathcal{V}\left({\mathcal{Z}}_1\right)}\sum _{{\mathrm{z}}_2\in \mathcal{V}\left({\mathcal{Z}}_2\right)}({deg}_{{\mathcal{Z}}_1}\left({\mathrm{z}}_1\right)\hfill \\ & +n_2-1)({deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_2\right)+n_1-1)+\sum _{{\mathrm{z}}_1\in \mathcal{I}\left({\mathcal{Z}}_1\right)}\sum _{{\mathrm{z}}_2\in \mathcal{V}\left({\mathcal{Z}}_3\right)}(n_3+2-1)\hfill \\ & ({deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_2\right)+e_1-1)+\sum _{\begin{array}{c}{\mathrm{z}}_1{\mathrm{z}}_2\in \mathcal{E}\left(\mathcal{S}\left({\mathcal{Z}}_1\right)\right),\\ {\mathrm{z}}_1\in \mathcal{V}\left({\mathcal{Z}}_1\right),{\mathrm{z}}_2\in \mathcal{I}\left({\mathcal{Z}}_1\right)\end{array}}({deg}_{{\mathcal{Z}}_1}\left({\mathrm{z}}_1\right)+n_2-1)(n_3+2-1)\hfill \\ & =\sum _{{\mathrm{z}}_1{\mathrm{z}}_2\in \mathcal{E}\left({\mathcal{Z}}_2\right)}(({deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_1\right)-1)({deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_2\right)-1)+n_1({deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_1\right)+{deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_2\right))\hfill \\ & -2n_1+n_1^2)+\sum _{{\mathrm{z}}_1{\mathrm{z}}_2\in \mathcal{E}\left({\mathcal{Z}}_3\right)}(({deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_1\right)-1)({deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_2\right)-1)+e_1({deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_1\right)\hfill \\ & +{deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_2\right))-2e_1+e_1^2)+\sum _{{\mathrm{z}}_1\in \mathcal{V}\left({\mathcal{Z}}_1\right)}\sum _{{\mathrm{z}}_2\in \mathcal{V}\left({\mathcal{Z}}_2\right)}({deg}_{{\mathcal{Z}}_1}\left({\mathrm{z}}_1\right){deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_2\right)+(n_1-1)\hfill \\ & {deg}_{{\mathcal{Z}}_1}\left({\mathrm{z}}_1\right)+(n_2-1){deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_2\right)+(n_1-1)(n_2-1))+(n_3+1)\hfill \\ & \sum _{{\mathrm{z}}_1\in \mathcal{I}\left({\mathcal{Z}}_1\right)}\sum _{{\mathrm{z}}_2\in \mathcal{V}\left({\mathcal{Z}}_3\right)}({deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_2\right)+e_1-1)+(n_3+1)\sum _{\mathrm{z}\in \mathcal{V}\left({\mathcal{Z}}_1\right)}{deg}_{{\mathcal{Z}}_1}\left(z\right)({deg}_{{\mathcal{Z}}_1}\left(z\right)\hfill \\ & +n_2-1)\hfill \\ & ={\mathcal{RM}}_2\left({\mathcal{Z}}_2\right)+n_1{\mathcal{M}}_1\left({\mathcal{Z}}_2\right)+e_2{n}_1(n_1-2)+{\mathcal{RM}}_2\left({\mathcal{Z}}_3\right)+e_1{\mathcal{M}}_1\left({\mathcal{Z}}_3\right)\hfill \\ & +e_3{e}_1(e_1-2)+4e_1{e}_2+2n_2{e}_1(n_1-1)+2n_1{e}_2(n_2-1)+n_1{n}_2(n_1-1)(n_2\hfill \\ & -1)+(n_3+1)(2e_1{e}_3+n_3{e}_1(e_1-1))+(n_3+1)({\mathcal{M}}_1\left({\mathcal{Z}}_1\right)+2e_1(n_2-1))\hfill \end{array}\end{array}$$

By means of some simplifications, we obtain the required result. This finishes the proof. □

Now, we give the following lemma that is used in the proof of next result.

Lemma 2

((AM-GM inequality) [53]). Let ${\mathrm{b}}_1,{\mathrm{b}}_2,\dots ,{\mathrm{b}}_n$ be non-negative numbers. Then,

$${\displaystyle \frac{{\mathrm{b}}_1+{\mathrm{b}}_2+\cdots +{\mathrm{b}}_n}{n}}\ge \sqrt[n]{{\mathrm{b}}_1{\mathrm{b}}_2\dots {\mathrm{b}}_n}$$

holds with equality if and only if ${\mathrm{b}}_1={\mathrm{b}}_2=\cdots ={\mathrm{b}}_n$.

In the upcoming result, we give the upper bounds of multiplicative Zagreb indices of subdivision vertex-edge join for three graphs.

Theorem 5.

Let ${\mathcal{Z}}_1$, ${\mathcal{Z}}_2$ and ${\mathcal{Z}}_3$ be three graphs. Then,

• $\prod _1({\mathcal{Z}}_1^{\mathcal{S}}⊳({\mathcal{Z}}_2^{\mathcal{V}}\cup {\mathcal{Z}}_3^{\mathcal{I}}))\le {\displaystyle \frac{{\left(n_3+2\right)}^{2e_1}}{n_1^{n_1}{n}_2^{n_2}{n}_3^{n_3}}}{\left({\mathcal{M}}_1\left({\mathcal{Z}}_1\right)+n_2^2{n}_1+4n_2{e}_1\right)}^{n_1}{\left({\mathcal{M}}_1\left({\mathcal{Z}}_2\right)+n_1^2{n}_2+4n_1{e}_2\right)}^{n_2}$
  ${\left({\mathcal{M}}_1\left({\mathcal{Z}}_3\right)+e_1^2{n}_3+4e_1{e}_3\right)}^{n_3},$
• $\prod _2({\mathcal{Z}}_1^{\mathcal{S}}⊳({\mathcal{Z}}_2^{\mathcal{V}}\cup {\mathcal{Z}}_3^{\mathcal{I}}))\le {(n_3+2)}^{n_3+2e_1}{\left({\displaystyle \frac{2e_3+n_3{e}_1}{e_1{n}_3}}\right)}^{n_3}{\left({\displaystyle \frac{{\mathcal{M}}_2\left({\mathcal{Z}}_2\right)+n_1{\mathcal{M}}_1\left({\mathcal{Z}}_1\right)+n_1^2{e}_2}{e_2}}\right)}^{e_2}$
  ${\left({\displaystyle \frac{2e_1+n_2}{2e_1}}\right)}^{2e_1}{\left({\displaystyle \frac{{\mathcal{M}}_2\left({\mathcal{Z}}_3\right)+e_1{\mathcal{M}}_1\left({\mathcal{Z}}_3\right)+e_1^2{e}_3}{e_3}}\right)}^{e_3}{\left({\displaystyle \frac{4e_1{e}_2+2n_1{n}_2(e_1+e_2)+n_1^2{n}_2^2}{n_1{n}_2}}\right)}^{n_1{n}_2},$

holds with equality if and only if ${\mathcal{Z}}_1$, ${\mathcal{Z}}_2$ and ${\mathcal{Z}}_3$ are regular graphs.

Proof. 

By Equation (6) and Lemma 1, we have

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \prod _1({\mathcal{Z}}_1^{\mathcal{S}}⊳({\mathcal{Z}}_2^{\mathcal{V}}\cup {\mathcal{Z}}_3^{\mathcal{I}}))& =\prod _{\mathrm{z}\in \mathcal{V}\left({\mathcal{Z}}_1\right)}{({deg}_{{\mathcal{Z}}_1}\left(z\right)+n_2)}^2\prod _{\mathrm{z}\in \mathcal{I}\left({\mathcal{Z}}_1\right)}{(n_3+2)}^2\prod _{\mathrm{z}\in \mathcal{V}\left({\mathcal{Z}}_2\right)}{({deg}_{{\mathcal{Z}}_2}\left(z\right)+n_1)}^2\hfill \\ & \prod _{\mathrm{z}\in \mathcal{V}\left({\mathcal{Z}}_3\right)}{({deg}_{{\mathcal{Z}}_3}\left(z\right)+e_1)}^2\hfill \\ & \le {\left({\displaystyle \frac{{\displaystyle \sum _{\mathrm{z}\in \mathcal{V}\left({\mathcal{Z}}_1\right)}}({deg}_{{\mathcal{Z}}_1}^2\left(z\right)+n_2^2+2n_2{deg}_{{\mathcal{Z}}_1}\left(z\right))}{n_1}}\right)}^{n_1}{\left({\displaystyle \frac{{\displaystyle \sum _{\mathrm{z}\in \mathcal{I}\left({\mathcal{Z}}_1\right)}}{(n_3+2)}^2}{e_1}}\right)}^{e_1}\hfill \\ & {\left({\displaystyle \frac{{\displaystyle \sum _{\mathrm{z}\in \mathcal{V}\left({\mathcal{Z}}_2\right)}}({deg}_{{\mathcal{Z}}_2}^2\left(z\right)+n_1^2+2n_1{deg}_{{\mathcal{Z}}_2}\left(z\right))}{n_2}}\right)}^{n_2}\hfill \\ & {\left({\displaystyle \frac{{\displaystyle \sum _{\mathrm{z}\in \mathcal{V}\left({\mathcal{Z}}_3\right)}}({deg}_{{\mathcal{Z}}_3}^2\left(z\right)+e_1^2+2e_1{deg}_{{\mathcal{Z}}_3}\left(z\right))}{n_3}}\right)}^{n_3}\hfill \end{array}\end{array}$$

(15)

By means of some simplifications, we obtain the required result. Now, by Equation (6) and Lemma 1, we have

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \prod _2({\mathcal{Z}}_1^{\mathcal{S}}⊳({\mathcal{Z}}_2^{\mathcal{V}}\cup {\mathcal{Z}}_3^{\mathcal{I}}))& =\prod _{{\mathrm{z}}_1{\mathrm{z}}_2\in \mathcal{E}\left({\mathcal{Z}}_2\right)}({deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_1\right)+n_1)({deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_2\right)+n_1)\prod _{{\mathrm{z}}_1{\mathrm{z}}_2\in \mathcal{E}\left({\mathcal{Z}}_3\right)}({deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_1\right)+e_1)\hfill \\ & ({deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_2\right)+e_1)\prod _{{\mathrm{z}}_1\in \mathcal{V}\left({\mathcal{Z}}_1\right)}\prod _{{\mathrm{z}}_2\in \mathcal{V}\left({\mathcal{Z}}_2\right)}({deg}_{{\mathcal{Z}}_1}\left({\mathrm{z}}_1\right)+n_2)({deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_2\right)+n_1)\hfill \\ & \prod _{{\mathrm{z}}_1\in \mathcal{I}\left({\mathcal{Z}}_1\right)}\prod _{{\mathrm{z}}_2\in \mathcal{V}\left({\mathcal{Z}}_3\right)}(n_3+2)({deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_2\right)+e_1)\prod _{\begin{array}{c}{\mathrm{z}}_1{\mathrm{z}}_2\in \mathcal{E}\left(\mathcal{S}\left({\mathcal{Z}}_1\right)\right),\\ {\mathrm{z}}_1\in \mathcal{V}\left({\mathcal{Z}}_1\right),{\mathrm{z}}_2\in \mathcal{I}\left({\mathcal{Z}}_1\right)\end{array}}({deg}_{{\mathcal{Z}}_1}\left({\mathrm{z}}_1\right)+n_2)\hfill \\ & (n_3+2).\hfill \end{array}\end{array}$$

By Lemma 2, we get

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \prod _2({\mathcal{Z}}_1^{\mathcal{S}}⊳({\mathcal{Z}}_2^{\mathcal{V}}\cup {\mathcal{Z}}_3^{\mathcal{I}}))& \le {\left({\displaystyle \frac{{\mathcal{M}}_2\left({\mathcal{Z}}_2\right)+n_1{\mathcal{M}}_1\left({\mathcal{Z}}_2\right)+n_1^2{e}_2}{e_2}}\right)}^{e_2}{\left({\displaystyle \frac{{\mathcal{M}}_2\left({\mathcal{Z}}_3\right)+e_1{\mathcal{M}}_1\left({\mathcal{Z}}_3\right)+e_1^2{e}_3}{e_3}}\right)}^{e_3}\hfill \\ & {\left({\displaystyle \frac{4e_1{e}_2+2n_1{n}_2{e}_1+2n_1{n}_2{e}_2+n_1^2{n}_2^2}{n_1{n}_2}}\right)}^{n_1{n}_2}{\left({\displaystyle \frac{e_1(n_3+2)(2e_3+n_3{e}_1)}{e_1{n}_3}}\right)}^{e_1{n}_3}\hfill \\ & {\left({\displaystyle \frac{(n_3+2){\displaystyle \sum _{\mathrm{z}\in \mathcal{V}\left({\mathcal{Z}}_1\right)}}{deg}_{{\mathcal{Z}}_1}\left(z\right)({deg}_{{\mathcal{Z}}_1}\left({\mathrm{z}}_1\right)+n_2)}{2e_1}}\right)}^{2e_1}\hfill \\ & ={\left({\displaystyle \frac{{\mathcal{M}}_2\left({\mathcal{Z}}_2\right)+n_1{\mathcal{M}}_1\left({\mathcal{Z}}_2\right)+n_1^2{e}_2}{e_2}}\right)}^{e_2}{\left({\displaystyle \frac{{\mathcal{M}}_2\left({\mathcal{Z}}_3\right)+e_1{\mathcal{M}}_1\left({\mathcal{Z}}_3\right)+e_1^2{e}_3}{e_3}}\right)}^{e_3}\hfill \\ & {\left({\displaystyle \frac{4e_1{e}_2+2n_1{n}_2{e}_1+2n_1{n}_2{e}_2+n_1^2{n}_2^2}{n_1{n}_2}}\right)}^{n_1{n}_2}{\left({\displaystyle \frac{e_1(n_3+2)(2e_3+n_3{e}_1)}{e_1{n}_3}}\right)}^{e_1{n}_3}\hfill \\ & {\left({\displaystyle \frac{(n_3+2)({\mathcal{M}}_1\left({\mathcal{Z}}_1\right)+2n_2{e}_1)}{2e_1}}\right)}^{2e_1}\hfill \end{array}\end{array}$$

(16)

After some simplifications, we get the required result. Additionally, if ${\mathcal{Z}}_1$, ${\mathcal{Z}}_2$, and ${\mathcal{Z}}_3$, are regular graphs, then the equalities in Equations (15) and (16) hold. □

In the next three theorems, we give the upper and lower bounds of the redefined versions of Zagreb indices of subdivision vertex-edge join for three graphs.

Theorem 6.

Let ${\mathcal{Z}}_1$, ${\mathcal{Z}}_2$ and ${\mathcal{Z}}_3$ be three graphs. Then,

$$\begin{array}{c}\hfill \begin{array}{c}{\displaystyle \frac{{\delta }_{{\mathcal{Z}}_2}^2}{{({△}_{{\mathcal{Z}}_2}+n_1)}^2}}\mathcal{R}e\mathcal{Z}{e}_1\left({\mathcal{Z}}_2\right)+{\displaystyle \frac{2n_1{e}_2}{{({△}_{{\mathcal{Z}}_2}+n_1)}^2}}+{\displaystyle \frac{{\delta }_{{\mathcal{Z}}_3}^2}{{({△}_{{\mathcal{Z}}_3}+e_1)}^2}}\mathcal{R}e\mathcal{Z}{e}_1\left({\mathcal{Z}}_3\right)+{\displaystyle \frac{2e_1{e}_3}{{({△}_{{\mathcal{Z}}_3}+e_1)}^2}}\hfill \\ +n_1{n}_2\left({\displaystyle \frac{{\delta }_{{\mathcal{Z}}_1}+{\delta }_{{\mathcal{Z}}_2}+n_1+n_2}{({△}_{{\mathcal{Z}}_1}+n_2)({△}_{{\mathcal{Z}}_2}+n_1)}}\right)+e_1{n}_3\left({\displaystyle \frac{{\delta }_{{\mathcal{Z}}_3}+e_1+n_3+2}{({△}_{{\mathcal{Z}}_3}+e_1)(n_3+2)}}\right)+2e_1\left({\displaystyle \frac{{\delta }_{{\mathcal{Z}}_1}+n_2+n_3+2}{({△}_{{\mathcal{Z}}_1}+n_2)(n_3+2)}}\right)\le \hfill \\ \mathcal{R}e\mathcal{Z}{e}_1({\mathcal{Z}}_1^{\mathcal{S}}⊳({\mathcal{Z}}_2^{\mathcal{V}}\cup {\mathcal{Z}}_3^{\mathcal{I}}))\le {\displaystyle \frac{{△}_{{\mathcal{Z}}_2}^2}{{({\delta }_{{\mathcal{Z}}_2}+n_1)}^2}}\mathcal{R}e\mathcal{Z}{e}_1\left({\mathcal{Z}}_2\right)+{\displaystyle \frac{2n_1{e}_2}{{({\delta }_{{\mathcal{Z}}_2}+n_1)}^2}}+{\displaystyle \frac{{△}_{{\mathcal{Z}}_3}^2}{{({\delta }_{{\mathcal{Z}}_3}+e_1)}^2}}\mathcal{R}e\mathcal{Z}{e}_1\left({\mathcal{Z}}_3\right)\hfill \\ +{\displaystyle \frac{2e_1{e}_3}{{({\delta }_{{\mathcal{Z}}_3}+e_1)}^2}}+n_1{n}_2\left({\displaystyle \frac{{△}_{{\mathcal{Z}}_1}+{△}_{{\mathcal{Z}}_2}+n_1+n_2}{({\delta }_{{\mathcal{Z}}_1}+n_2)({\delta }_{{\mathcal{Z}}_2}+n_1)}}\right)+e_1{n}_3\left({\displaystyle \frac{{△}_{{\mathcal{Z}}_3}+e_1+n_3+2}{({\delta }_{{\mathcal{Z}}_3}+e_1)(n_3+2)}}\right)\hfill \\ +2e_1\left({\displaystyle \frac{{△}_{{\mathcal{Z}}_1}+n_2+n_3+2}{({\delta }_{{\mathcal{Z}}_1}\left({\mathrm{z}}_1\right)+n_2)(n_3+2)}}\right).\hfill \end{array}\end{array}$$

hold with equalities if and only if ${\mathcal{Z}}_1$, ${\mathcal{Z}}_2$ and ${\mathcal{Z}}_3$ are regular graphs.

Proof. 

By using Lemma 1 in Equation (7), we get

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \mathcal{R}e\mathcal{Z}{e}_1({\mathcal{Z}}_1^{\mathcal{S}}⊳({\mathcal{Z}}_2^{\mathcal{V}}\cup {\mathcal{Z}}_3^{\mathcal{I}}))& =\sum _{{\mathrm{z}}_1{\mathrm{z}}_2\in \mathcal{E}\left({\mathcal{Z}}_2\right)}{\displaystyle \frac{{deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_1\right)+{deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_2\right)+2n_1}{({deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_1\right)+n_1)({deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_2\right)+n_1)}}\hfill \\ & +\sum _{{\mathrm{z}}_1{\mathrm{z}}_2\in \mathcal{E}\left({\mathcal{Z}}_3\right)}{\displaystyle \frac{{deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_1\right)+{deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_2\right)+2e_1}{({deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_1\right)+e_1)({deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_2\right)+e_1)}}\hfill \\ & +\sum _{{\mathrm{z}}_1\in \mathcal{V}\left({\mathcal{Z}}_1\right)}\sum _{{\mathrm{z}}_2\in \mathcal{V}\left({\mathcal{Z}}_2\right)}{\displaystyle \frac{{deg}_{{\mathcal{Z}}_1}\left({\mathrm{z}}_1\right)+{deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_2\right)+n_1+n_2}{({deg}_{{\mathcal{Z}}_1}\left({\mathrm{z}}_1\right)+n_2)({deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_2\right)+n_1)}}\hfill \\ & +\sum _{{\mathrm{z}}_1\in \mathcal{I}\left({\mathcal{Z}}_1\right)}\sum _{{\mathrm{z}}_2\in \mathcal{V}\left({\mathcal{Z}}_3\right)}{\displaystyle \frac{{deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_2\right)+e_1+n_3+2}{({deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_2\right)+e_1)(n_3+2)}}\hfill \\ & +\sum _{\begin{array}{c}{\mathrm{z}}_1{\mathrm{z}}_2\in \mathcal{E}\left(\mathcal{S}\left({\mathcal{Z}}_1\right)\right),\\ {\mathrm{z}}_1\in \mathcal{V}\left({\mathcal{Z}}_1\right),{\mathrm{z}}_2\in \mathcal{I}\left({\mathcal{Z}}_1\right)\end{array}}{\displaystyle \frac{{deg}_{{\mathcal{Z}}_1}\left({\mathrm{z}}_1\right)+n_2+n_3+2}{({deg}_{{\mathcal{Z}}_1}\left({\mathrm{z}}_1\right)+n_2)(n_3+2)}}.\hfill \end{array}\end{array}$$

(17)

Now,

$$\begin{array}{cc}{\displaystyle \frac{{deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_1\right)+{deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_2\right)+2n_1}{({deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_1\right)+n_1)({deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_2\right)+n_1)}}\hfill & ={\displaystyle \frac{{deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_1\right)+{deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_2\right)}{{deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_1\right){deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_2\right)}}\times {\displaystyle \frac{{deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_1\right){deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_2\right)}{({deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_1\right)+n_1)({deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_2\right)+n_1)}}\hfill \\ & +{\displaystyle \frac{2n_1}{({deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_1\right)+n_1)({deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_2\right)+n_1)}}\hfill \\ & \le {\displaystyle \frac{{△}_{{\mathcal{Z}}_2}^2}{{({\delta }_{{\mathcal{Z}}_2}+n_1)}^2}}\times {\displaystyle \frac{{deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_1\right)+{deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_2\right)}{{deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_1\right){deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_2\right)}}+{\displaystyle \frac{2n_1}{{({\delta }_{{\mathcal{Z}}_2}+n_1)}^2}}.\hfill \end{array}$$

(18)

Similarly,

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\displaystyle \frac{{deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_1\right)+{deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_2\right)+2e_1}{({deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_1\right)+e_1)({deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_2\right)+e_1)}}& \le {\displaystyle \frac{{△}_{{\mathcal{Z}}_3}^2}{{({\delta }_{{\mathcal{Z}}_3}+e_1)}^2}}\times {\displaystyle \frac{{deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_1\right)+{deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_2\right)}{{deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_1\right){deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_2\right)}}+{\displaystyle \frac{2e_1}{{({\delta }_{{\mathcal{Z}}_3}+e_1)}^2}}.\hfill \end{array}\end{array}$$

(19)

By using Equations (18) and (19) in Equation (17), we obtain

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \mathcal{R}e\mathcal{Z}{e}_1({\mathcal{Z}}_1^{\mathcal{S}}⊳({\mathcal{Z}}_2^{\mathcal{V}}\cup {\mathcal{Z}}_3^{\mathcal{I}}))& \le \sum _{{\mathrm{z}}_1{\mathrm{z}}_2\in \mathcal{E}\left({\mathcal{Z}}_2\right)}\left({\displaystyle \frac{{△}_{{\mathcal{Z}}_2}^2}{{({\delta }_{{\mathcal{Z}}_2}+n_1)}^2}}\times {\displaystyle \frac{{deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_1\right)+{deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_2\right)}{{deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_1\right){deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_2\right)}}+{\displaystyle \frac{2n_1}{{({\delta }_{{\mathcal{Z}}_2}+n_1)}^2}}\right)\hfill \\ & +\sum _{{\mathrm{z}}_1{\mathrm{z}}_2\in \mathcal{E}\left({\mathcal{Z}}_3\right)}\left({\displaystyle \frac{{△}_{{\mathcal{Z}}_3}^2}{{({\delta }_{{\mathcal{Z}}_3}+e_1)}^2}}\times {\displaystyle \frac{{deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_1\right)+{deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_2\right)}{{deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_1\right){deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_2\right)}}+{\displaystyle \frac{2e_1}{{({\delta }_{{\mathcal{Z}}_3}+e_1)}^2}}\right)\hfill \\ & +\sum _{{\mathrm{z}}_1\in \mathcal{V}\left({\mathcal{Z}}_1\right)}\sum _{{\mathrm{z}}_2\in \mathcal{V}\left({\mathcal{Z}}_2\right)}{\displaystyle \frac{{△}_{{\mathcal{Z}}_1}+{△}_{{\mathcal{Z}}_2}+n_1+n_2}{({\delta }_{{\mathcal{Z}}_1}+n_2)({\delta }_{{\mathcal{Z}}_2}+n_1)}}\hfill \\ & +\sum _{{\mathrm{z}}_1\in \mathcal{I}\left({\mathcal{Z}}_1\right)}\sum _{{\mathrm{z}}_2\in \mathcal{V}\left({\mathcal{Z}}_3\right)}{\displaystyle \frac{{△}_{{\mathcal{Z}}_3}+e_1+n_3+2}{({\delta }_{{\mathcal{Z}}_3}+e_1)(n_3+2)}}\hfill \\ & +\sum _{\begin{array}{c}{\mathrm{z}}_1{\mathrm{z}}_2\in \mathcal{E}\left(\mathcal{S}\left({\mathcal{Z}}_1\right)\right),\\ {\mathrm{z}}_1\in \mathcal{V}\left({\mathcal{Z}}_1\right),{\mathrm{z}}_2\in \mathcal{I}\left({\mathcal{Z}}_1\right)\end{array}}{\displaystyle \frac{{△}_{{\mathcal{Z}}_1}+n_2+n_3+2}{({\delta }_{{\mathcal{Z}}_1}+n_2)(n_3+2)}}\hfill \\ & ={\displaystyle \frac{{△}_{{\mathcal{Z}}_2}^2}{{({\delta }_{{\mathcal{Z}}_2}+n_1)}^2}}\mathcal{R}e\mathcal{Z}{e}_1\left({\mathcal{Z}}_2\right)+{\displaystyle \frac{2n_1{e}_2}{{({\delta }_{{\mathcal{Z}}_2}+n_1)}^2}}+{\displaystyle \frac{{△}_{{\mathcal{Z}}_3}^2}{{({\delta }_{{\mathcal{Z}}_3}+e_1)}^2}}\mathcal{R}e\mathcal{Z}{e}_1\left({\mathcal{Z}}_3\right)\hfill \\ & +{\displaystyle \frac{2e_1{e}_3}{{({\delta }_{{\mathcal{Z}}_3}+e_1)}^2}}+n_1{n}_2\left({\displaystyle \frac{{△}_{{\mathcal{Z}}_1}+{△}_{{\mathcal{Z}}_2}+n_1+n_2}{({\delta }_{{\mathcal{Z}}_1}+n_2)({\delta }_{{\mathcal{Z}}_2}+n_1)}}\right)\hfill \\ & +e_1{n}_3\left({\displaystyle \frac{{△}_{{\mathcal{Z}}_3}+e_1+n_3+2}{({\delta }_{{\mathcal{Z}}_3}+e_1)(n_3+2)}}\right)+2e_1\left({\displaystyle \frac{{△}_{{\mathcal{Z}}_1}+n_2+n_3+2}{({\delta }_{{\mathcal{Z}}_1}\left({\mathrm{z}}_1\right)+n_2)(n_3+2)}}\right).\hfill \end{array}\end{array}$$

Similarly, we can compute

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \mathcal{R}e\mathcal{Z}{e}_1({\mathcal{Z}}_1^{\mathcal{S}}⊳({\mathcal{Z}}_2^{\mathcal{V}}\cup {\mathcal{Z}}_3^{\mathcal{I}}))& \ge {\displaystyle \frac{{\delta }_{{\mathcal{Z}}_2}^2}{{({△}_{{\mathcal{Z}}_2}+n_1)}^2}}\mathcal{R}e\mathcal{Z}{e}_1\left({\mathcal{Z}}_2\right)+{\displaystyle \frac{2n_1{e}_2}{{({△}_{{\mathcal{Z}}_2}+n_1)}^2}}+{\displaystyle \frac{{\delta }_{{\mathcal{Z}}_3}^2}{{({△}_{{\mathcal{Z}}_3}+e_1)}^2}}\mathcal{R}e\mathcal{Z}{e}_1\left({\mathcal{Z}}_3\right)\hfill \\ & +{\displaystyle \frac{2e_1{e}_3}{{({△}_{{\mathcal{Z}}_3}+e_1)}^2}}+n_1{n}_2\left({\displaystyle \frac{{\delta }_{{\mathcal{Z}}_1}+{\delta }_{{\mathcal{Z}}_2}+n_1+n_2}{({△}_{{\mathcal{Z}}_1}+n_2)({△}_{{\mathcal{Z}}_2}+n_1)}}\right)\hfill \\ & +e_1{n}_3\left({\displaystyle \frac{{\delta }_{{\mathcal{Z}}_3}+e_1+n_3+2}{({△}_{{\mathcal{Z}}_3}+e_1)(n_3+2)}}\right)+2e_1\left({\displaystyle \frac{{\delta }_{{\mathcal{Z}}_1}+n_2+n_3+2}{({△}_{{\mathcal{Z}}_1}\left({\mathrm{z}}_1\right)+n_2)(n_3+2)}}\right).\hfill \end{array}\end{array}$$

Furthermore, if ${\mathcal{Z}}_1$, ${\mathcal{Z}}_2$, and ${\mathcal{Z}}_3$ are regular graphs, then the above equalities hold. This finishes the proof. □

Theorem 7.

Let ${\mathcal{Z}}_1$, ${\mathcal{Z}}_2$, and ${\mathcal{Z}}_3$ be three graphs. Then,

$$\begin{array}{c}\hfill \begin{array}{c}{\displaystyle \frac{{\delta }_{{\mathcal{Z}}_2}}{{△}_{{\mathcal{Z}}_2}+n_1}}\mathcal{R}e\mathcal{Z}{e}_2\left({\mathcal{Z}}_2\right)+{\displaystyle \frac{n_1}{2({△}_{{\mathcal{Z}}_2}+n_1)}}{\mathcal{M}}_1\left({\mathcal{Z}}_2\right)+{\displaystyle \frac{n_1^2{e}_2}{2({△}_{{\mathcal{Z}}_2}+n_1)}}+{\displaystyle \frac{{\delta }_{{\mathcal{Z}}_3}}{{△}_{{\mathcal{Z}}_3}+e_1}}\mathcal{R}e\mathcal{Z}{e}_2\left({\mathcal{Z}}_3\right)\hfill \\ +{\displaystyle \frac{e_1}{2({△}_{{\mathcal{Z}}_3}+e_1)}}{\mathcal{M}}_1\left({\mathcal{Z}}_3\right)+{\displaystyle \frac{e_1^2{e}_3}{2({△}_{{\mathcal{Z}}_3}+e_1)}}+n_1{n}_2\left({\displaystyle \frac{({\delta }_{{\mathcal{Z}}_1}+n_2)({\delta }_{{\mathcal{Z}}_2}+n_1)}{{△}_{{\mathcal{Z}}_1}+{△}_{{\mathcal{Z}}_2}+n_1+n_2}}\right)+e_1{n}_3\left({\displaystyle \frac{({\delta }_{{\mathcal{Z}}_3}+e_1)(n_3+2)}{{△}_{{\mathcal{Z}}_3}+e_1+n_3+2}}\right)\hfill \\ +2e_1\left({\displaystyle \frac{({\delta }_{{\mathcal{Z}}_1}+n_2)(n_3+2)}{{△}_{{\mathcal{Z}}_1}+n_2+n_3+2}}\right)\le \mathcal{R}e\mathcal{Z}{e}_2({\mathcal{Z}}_1^{\mathcal{S}}⊳({\mathcal{Z}}_2^{\mathcal{V}}\cup {\mathcal{Z}}_3^{\mathcal{I}}))\le {\displaystyle \frac{{△}_{{\mathcal{Z}}_2}}{{\delta }_{{\mathcal{Z}}_2}+n_1}}\mathcal{R}e\mathcal{Z}{e}_2\left({\mathcal{Z}}_2\right)\hfill \\ +{\displaystyle \frac{n_1}{2({\delta }_{{\mathcal{Z}}_2}+n_1)}}{\mathcal{M}}_1\left({\mathcal{Z}}_2\right)+{\displaystyle \frac{n_1^2{e}_2}{2({\delta }_{{\mathcal{Z}}_2}+n_1)}}+{\displaystyle \frac{{△}_{{\mathcal{Z}}_3}}{{\delta }_{{\mathcal{Z}}_3}+e_1}}\mathcal{R}e\mathcal{Z}{e}_2\left({\mathcal{Z}}_3\right)+{\displaystyle \frac{e_1}{2({\delta }_{{\mathcal{Z}}_3}+e_1)}}{\mathcal{M}}_1\left({\mathcal{Z}}_3\right)+{\displaystyle \frac{e_1^2{e}_3}{2({\delta }_{{\mathcal{Z}}_3}+e_1)}}\hfill \\ +n_1{n}_2\left({\displaystyle \frac{({△}_{{\mathcal{Z}}_1}+n_2)({△}_{{\mathcal{Z}}_2}+n_1)}{{\delta }_{{\mathcal{Z}}_1}+{\delta }_{{\mathcal{Z}}_2}+n_1+n_2}}\right)+e_1{n}_3\left({\displaystyle \frac{({△}_{{\mathcal{Z}}_3}+e_1)(n_3+2)}{{\delta }_{{\mathcal{Z}}_3}+e_1+n_3+2}}\right)+2e_1\left({\displaystyle \frac{({△}_{{\mathcal{Z}}_1}+n_2)(n_3+2)}{{\delta }_{{\mathcal{Z}}_1}+n_2+n_3+2}}\right).\hfill \end{array}\end{array}$$

hold with equalities if and only if ${\mathcal{Z}}_1$, ${\mathcal{Z}}_2$, and ${\mathcal{Z}}_3$ are regular graphs.

Proof. 

By using Lemma 1 in Equation (8), we get the following

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \mathcal{R}e\mathcal{Z}{e}_2({\mathcal{Z}}_1^{\mathcal{S}}⊳({\mathcal{Z}}_2^{\mathcal{V}}\cup {\mathcal{Z}}_3^{\mathcal{I}}))& =\sum _{{\mathrm{z}}_1{\mathrm{z}}_2\in \mathcal{E}\left({\mathcal{Z}}_2\right)}{\displaystyle \frac{({deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_1\right)+n_1)({deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_2\right)+n_1)}{{deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_1\right)+{deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_2\right)+2n_1}}\hfill \\ & +\sum _{{\mathrm{z}}_1{\mathrm{z}}_2\in \mathcal{E}\left({\mathcal{Z}}_3\right)}{\displaystyle \frac{({deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_1\right)+e_1)({deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_2\right)+e_1)}{{deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_1\right)+{deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_2\right)+2e_1}}\hfill \\ & +\sum _{{\mathrm{z}}_1\in \mathcal{V}\left({\mathcal{Z}}_1\right)}\sum _{{\mathrm{z}}_2\in \mathcal{V}\left({\mathcal{Z}}_2\right)}{\displaystyle \frac{({deg}_{{\mathcal{Z}}_1}\left({\mathrm{z}}_1\right)+n_2)({deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_2\right)+n_1)}{{deg}_{{\mathcal{Z}}_1}\left({\mathrm{z}}_1\right)+{deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_2\right)+n_1+n_2}}\hfill \\ & +\sum _{{\mathrm{z}}_1\in \mathcal{I}\left({\mathcal{Z}}_1\right)}\sum _{{\mathrm{z}}_2\in \mathcal{V}\left({\mathcal{Z}}_3\right)}{\displaystyle \frac{({deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_2\right)+e_1)(n_3+2)}{{deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_2\right)+e_1+n_3+2}}\hfill \\ & +\sum _{\begin{array}{c}{\mathrm{z}}_1{\mathrm{z}}_2\in \mathcal{E}\left(\mathcal{S}\left({\mathcal{Z}}_1\right)\right),\\ {\mathrm{z}}_1\in \mathcal{V}\left({\mathcal{Z}}_1\right),{\mathrm{z}}_2\in \mathcal{I}\left({\mathcal{Z}}_1\right)\end{array}}{\displaystyle \frac{({deg}_{{\mathcal{Z}}_1}\left({\mathrm{z}}_1\right)+n_2)(n_3+2)}{{deg}_{{\mathcal{Z}}_1}\left({\mathrm{z}}_1\right)+n_2+n_3+2}}.\hfill \end{array}\end{array}$$

(20)

Now,

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\displaystyle \frac{({deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_1\right)+n_1)({deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_2\right)+n_1)}{{deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_1\right)+{deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_2\right)+2n_1}}& ={\displaystyle \frac{{deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_1\right){deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_2\right)+n_1({deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_1\right)+{deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_2\right))+n_1^2}{{deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_1\right)+{deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_2\right)+2n_1}}\hfill \end{array}\end{array}$$

By multiplying and dividing the first term of above expression by ${deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_1\right)+{deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_2\right)$, we get

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\displaystyle \frac{({deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_1\right)+n_1)({deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_2\right)+n_1)}{{deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_1\right)+{deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_2\right)+2n_1}}& ={\displaystyle \frac{{deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_1\right){deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_2\right)}{{deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_1\right)+{deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_2\right)}}\times {\displaystyle \frac{{deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_1\right)+{deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_2\right)}{{deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_1\right)+{deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_2\right)+2n_1}}\hfill \\ & +{\displaystyle \frac{n_1({deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_1\right)+{deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_2\right))}{({deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_1\right)+{deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_2\right)+2n_1}}+{\displaystyle \frac{n_1^2}{{deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_1\right)+{deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_2\right)+2n_1}}\hfill \end{array}\end{array}$$

By using ${△}_{\mathcal{Z}}\le {deg}_{\mathcal{Z}}\left(\mathrm{z}\right)\le {\delta }_{\mathcal{Z}}$, we acquire following

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\displaystyle \frac{({deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_1\right)+n_1)({deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_2\right)+n_1)}{{deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_1\right)+{deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_2\right)+2n_1}}& \le {\displaystyle \frac{{deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_1\right){deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_2\right)}{{deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_1\right)+{deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_2\right)}}\times {\displaystyle \frac{{△}_{{\mathcal{Z}}_2}}{{\delta }_{{\mathcal{Z}}_2}+n_1}}\hfill \\ & +{\displaystyle \frac{n_1({deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_1\right)+{deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_2\right))}{2({\delta }_{{\mathcal{Z}}_2}+n_1)}}+{\displaystyle \frac{n_1^2}{2({\delta }_{{\mathcal{Z}}_2}+n_1)}}.\hfill \end{array}\end{array}$$

(21)

Similarly,

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\displaystyle \frac{({deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_1\right)+e_1)({deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_2\right)+e_1)}{{deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_1\right)+{deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_2\right)+2e_1}}& \le {\displaystyle \frac{{△}_{{\mathcal{Z}}_3}}{{\delta }_{{\mathcal{Z}}_3}+e_1}}\times {\displaystyle \frac{{deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_1\right){deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_2\right)}{{deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_1\right)+{deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_2\right)}}\hfill \\ & +{\displaystyle \frac{e_1({deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_1\right)+{deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_2\right))}{2({\delta }_{{\mathcal{Z}}_2}+e_1)}}+{\displaystyle \frac{e_1^2}{2({\delta }_{{\mathcal{Z}}_3}+e_1)}}.\hfill \end{array}\end{array}$$

(22)

By using Equations (21) and (22) in Equation (20), we obtain

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \mathcal{R}e\mathcal{Z}{e}_2({\mathcal{Z}}_1^{\mathcal{S}}⊳({\mathcal{Z}}_2^{\mathcal{V}}\cup {\mathcal{Z}}_3^{\mathcal{I}}))& \le \sum _{{\mathrm{z}}_1{\mathrm{z}}_2\in \mathcal{E}\left({\mathcal{Z}}_2\right)}({\displaystyle \frac{{△}_{{\mathcal{Z}}_2}}{{\delta }_{{\mathcal{Z}}_2}+n_1}}\times {\displaystyle \frac{{deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_1\right){deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_2\right)}{{deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_1\right)+{deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_2\right)}}\hfill \\ & +{\displaystyle \frac{n_1({deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_1\right)+{deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_2\right))}{2({\delta }_{{\mathcal{Z}}_2}+n_1)}}+{\displaystyle \frac{n_1^2}{2({\delta }_{{\mathcal{Z}}_2}+n_1)}})\hfill \\ & +\sum _{{\mathrm{z}}_1{\mathrm{z}}_2\in \mathcal{E}\left({\mathcal{Z}}_3\right)}({\displaystyle \frac{{△}_{{\mathcal{Z}}_3}}{{\delta }_{{\mathcal{Z}}_3}+e_1}}\times {\displaystyle \frac{{deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_1\right){deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_2\right)}{{deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_1\right)+{deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_2\right)}}\hfill \\ & +{\displaystyle \frac{e_1({deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_1\right)+{deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_2\right))}{2({\delta }_{{\mathcal{Z}}_3}+e_1)}}+{\displaystyle \frac{e_1^2}{2({\delta }_{{\mathcal{Z}}_3}+e_1)}})\hfill \\ & +\sum _{{\mathrm{z}}_1\in \mathcal{V}\left({\mathcal{Z}}_1\right)}\sum _{{\mathrm{z}}_2\in \mathcal{V}\left({\mathcal{Z}}_2\right)}{\displaystyle \frac{({△}_{{\mathcal{Z}}_1}+n_2)({△}_{{\mathcal{Z}}_2}+n_1)}{{\delta }_{{\mathcal{Z}}_1}+{\delta }_{{\mathcal{Z}}_2}+n_1+n_2}}\hfill \\ & +\sum _{{\mathrm{z}}_1\in \mathcal{I}\left({\mathcal{Z}}_1\right)}\sum _{{\mathrm{z}}_2\in \mathcal{V}\left({\mathcal{Z}}_3\right)}{\displaystyle \frac{({△}_{{\mathcal{Z}}_3}+e_1)(n_3+2)}{{\delta }_{{\mathcal{Z}}_3}+e_1+n_3+2}}\hfill \\ & +\sum _{\begin{array}{c}{\mathrm{z}}_1{\mathrm{z}}_2\in \mathcal{E}\left(\mathcal{S}\left({\mathcal{Z}}_1\right)\right),\\ {\mathrm{z}}_1\in \mathcal{V}\left({\mathcal{Z}}_1\right),{\mathrm{z}}_2\in \mathcal{I}\left({\mathcal{Z}}_1\right)\end{array}}{\displaystyle \frac{({△}_{{\mathcal{Z}}_1}+n_2)(n_3+2)}{{\delta }_{{\mathcal{Z}}_1}+n_2+n_3+2}}\hfill \\ & ={\displaystyle \frac{{△}_{{\mathcal{Z}}_2}}{{\delta }_{{\mathcal{Z}}_2}+n_1}}\mathcal{R}e\mathcal{Z}{e}_2\left({\mathcal{Z}}_2\right)+{\displaystyle \frac{n_1}{2({\delta }_{{\mathcal{Z}}_2}+n_1)}}{\mathcal{M}}_1\left({\mathcal{Z}}_2\right)+{\displaystyle \frac{n_1^2{e}_2}{2({\delta }_{{\mathcal{Z}}_2}+n_1)}}\hfill \\ & +{\displaystyle \frac{{△}_{{\mathcal{Z}}_3}}{{\delta }_{{\mathcal{Z}}_3}+e_1}}\mathcal{R}e\mathcal{Z}{e}_2\left({\mathcal{Z}}_3\right)+{\displaystyle \frac{e_1}{2({\delta }_{{\mathcal{Z}}_3}+e_1)}}{\mathcal{M}}_1\left({\mathcal{Z}}_3\right)+{\displaystyle \frac{e_1^2{e}_3}{2({\delta }_{{\mathcal{Z}}_3}+e_1)}}\hfill \\ & +n_1{n}_2\left({\displaystyle \frac{({△}_{{\mathcal{Z}}_1}+n_2)({△}_{{\mathcal{Z}}_2}+n_1)}{{\delta }_{{\mathcal{Z}}_1}+{\delta }_{{\mathcal{Z}}_2}+n_1+n_2}}\right)+e_1{n}_3\left({\displaystyle \frac{({△}_{{\mathcal{Z}}_3}+e_1)(n_3+2)}{{\delta }_{{\mathcal{Z}}_3}+e_1+n_3+2}}\right)\hfill \\ & +2e_1\left({\displaystyle \frac{({△}_{{\mathcal{Z}}_1}+n_2)(n_3+2)}{{\delta }_{{\mathcal{Z}}_1}+n_2+n_3+2}}\right).\hfill \end{array}\end{array}$$

(23)

Similarly, we calculate

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \mathcal{R}e\mathcal{Z}{e}_2({\mathcal{Z}}_1^{\mathcal{S}}⊳({\mathcal{Z}}_2^{\mathcal{V}}\cup {\mathcal{Z}}_3^{\mathcal{I}}))& \ge {\displaystyle \frac{{\delta }_{{\mathcal{Z}}_2}}{{△}_{{\mathcal{Z}}_2}+n_1}}\mathcal{R}e\mathcal{Z}{e}_2\left({\mathcal{Z}}_2\right)+{\displaystyle \frac{n_1}{2({△}_{{\mathcal{Z}}_2}+n_1)}}{\mathcal{M}}_1\left({\mathcal{Z}}_2\right)+{\displaystyle \frac{n_1^2{e}_2}{2({△}_{{\mathcal{Z}}_2}+n_1)}}\hfill \\ & +{\displaystyle \frac{{\delta }_{{\mathcal{Z}}_3}}{{△}_{{\mathcal{Z}}_3}+e_1}}\mathcal{R}e\mathcal{Z}{e}_2\left({\mathcal{Z}}_3\right)+{\displaystyle \frac{e_1}{2({△}_{{\mathcal{Z}}_3}+e_1)}}{\mathcal{M}}_1\left({\mathcal{Z}}_3\right)+{\displaystyle \frac{e_1^2{e}_3}{2({△}_{{\mathcal{Z}}_3}+e_1)}}\hfill \\ & +n_1{n}_2\left({\displaystyle \frac{({\delta }_{{\mathcal{Z}}_1}+n_2)({\delta }_{{\mathcal{Z}}_2}+n_1)}{{△}_{{\mathcal{Z}}_1}+{△}_{{\mathcal{Z}}_2}+n_1+n_2}}\right)+e_1{n}_3\left({\displaystyle \frac{({\delta }_{{\mathcal{Z}}_3}+e_1)(n_3+2)}{{△}_{{\mathcal{Z}}_3}+e_1+n_3+2}}\right)\hfill \\ & +2e_1\left({\displaystyle \frac{({\delta }_{{\mathcal{Z}}_1}+n_2)(n_3+2)}{{△}_{{\mathcal{Z}}_1}+n_2+n_3+2}}\right).\hfill \end{array}\end{array}$$

Additionally, the above equalities hold if and only if ${\mathcal{Z}}_1$, ${\mathcal{Z}}_2$, and ${\mathcal{Z}}_3$ are regular graphs. This finishes the proof. □

Theorem 8.

Let ${\mathcal{Z}}_1$, ${\mathcal{Z}}_2$ and ${\mathcal{Z}}_3$ be three graphs. Then,

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \mathcal{R}e\mathcal{Z}{e}_3({\mathcal{Z}}_1^{\mathcal{S}}⊳({\mathcal{Z}}_2^{\mathcal{V}}\cup {\mathcal{Z}}_3^{\mathcal{I}}))& =\mathcal{R}e\mathcal{Z}{e}_3\left({\mathcal{Z}}_2\right)+\mathcal{R}e\mathcal{Z}{e}_3\left({\mathcal{Z}}_3\right)+n_1{\mathcal{HM}}_1\left({\mathcal{Z}}_2\right)+e_1{\mathcal{HM}}_1\left({\mathcal{Z}}_3\right)+2n_1{\mathcal{M}}_2\left({\mathcal{Z}}_2\right)\hfill \\ & +2e_1{\mathcal{M}}_2\left({\mathcal{Z}}_3\right)+(3n_1+2e_1+n_1{n}_2){\mathcal{M}}_1\left({\mathcal{Z}}_2\right)+(3n_1+e_1(n_3+2)){\mathcal{M}}_1\left({\mathcal{Z}}_3\right)\hfill \\ & +(n_3+2)\mathcal{F}\left({\mathcal{Z}}_1\right)+(2e_2+n_1{n}_2+(n_3+2)(2n_2+n_3+2)){\mathcal{M}}_1\left({\mathcal{Z}}_1\right)+2n_1^3{e}_2\hfill \\ & +2e_1^3{e}_3+(8e_1{e}_2+n_1^2{n}_2^2)(n_1+n_2)+2n_1{n}_2(n_1+n_2)(e_1+e_2)+2n_1{n}_2(n_2{e}_1\hfill \\ & +n_1{e}_2)+e_1(n_3+2)(e_1+n_3+2)(2e_3+n_3{e}_1)+2e_1^2{e}_3(n_3+2)\hfill \\ & +2n_2{e}_1(n_2+n_3+2).\hfill \end{array}\end{array}$$

Proof. 

By using Lemma 1 in Equation (9), we get the following:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \mathcal{R}e\mathcal{Z}{e}_3({\mathcal{Z}}_1^{\mathcal{S}}⊳({\mathcal{Z}}_2^{\mathcal{V}}\cup {\mathcal{Z}}_3^{\mathcal{I}}))& =\sum _{{\mathrm{z}}_1{\mathrm{z}}_2\in \mathcal{E}\left({\mathcal{Z}}_2\right)}({deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_1\right){deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_2\right)({deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_1\right)+{deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_2\right))\hfill \\ & +2n_1{deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_1\right){deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_2\right)+n_1{({deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_1\right)+{deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_2\right))}^2\hfill \\ & +3n_1^2({deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_1\right)+{deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_2\right))+2n_1^3)+\sum _{{\mathrm{z}}_1{\mathrm{z}}_2\in \mathcal{E}\left({\mathcal{Z}}_3\right)}({deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_1\right)\hfill \\ & {deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_2\right)({deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_1\right)+{deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_2\right))+2e_1{deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_1\right){deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_2\right)\hfill \\ & +e_1{({deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_1\right)+{deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_2\right))}^2+3e_1^2({deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_1\right)+{deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_2\right))+2e_1^3)\hfill \\ & +\sum _{{\mathrm{z}}_1\in \mathcal{V}\left({\mathcal{Z}}_1\right)}\sum _{{\mathrm{z}}_2\in \mathcal{V}\left({\mathcal{Z}}_2\right)}({deg}_{{\mathcal{Z}}_1}^2\left({\mathrm{z}}_1\right)({deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_2\right)+n_1)+{deg}_{{\mathcal{Z}}_2}^2\left({\mathrm{z}}_2\right)({deg}_{{\mathcal{Z}}_1}\left({\mathrm{z}}_1\right)\hfill \\ & +n_2)+2(n_1+n_2){deg}_{{\mathcal{Z}}_1}\left({\mathrm{z}}_1\right){deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_2\right)+(n_1+n_2)(n_1{deg}_{{\mathcal{Z}}_1}\left({\mathrm{z}}_1\right)\hfill \\ & +n_2{deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_2\right))+n_1{n}_2({deg}_{{\mathcal{Z}}_1}\left({\mathrm{z}}_1\right)+{deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_2\right))+n_1{n}_2(n_1+n_2))\hfill \\ & +(n_3+2)\sum _{{\mathrm{z}}_1\in \mathcal{I}\left({\mathcal{Z}}_1\right)}\sum _{{\mathrm{z}}_2\in \mathcal{V}\left({\mathcal{Z}}_3\right)}({deg}_{{\mathcal{Z}}_3}^2\left({\mathrm{z}}_2\right)+{deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_2\right)(n_3+2e_1+2)\hfill \\ & +e_1(n_3+e_1+2))+(n_3+2)\sum _{\begin{array}{c}{\mathrm{z}}_1{\mathrm{z}}_2\in \mathcal{E}\left(\mathcal{S}\left({\mathcal{Z}}_1\right)\right),\\ {\mathrm{z}}_1\in \mathcal{V}\left({\mathcal{Z}}_1\right),{\mathrm{z}}_2\in \mathcal{I}\left({\mathcal{Z}}_1\right)\end{array}}({deg}_{{\mathcal{Z}}_1}^2\left({\mathrm{z}}_2\right)+{deg}_{{\mathcal{Z}}_1}\left({\mathrm{z}}_2\right)\hfill \\ & (2n_2+n_3+2)+(n_2+n_3+2))\hfill \\ & =\mathcal{R}e\mathcal{Z}{e}_3\left({\mathcal{Z}}_2\right)+2n_1{\mathcal{M}}_2\left({\mathcal{Z}}_2\right)+n_1{\mathcal{HM}}_1\left({\mathcal{Z}}_2\right)+3n_1{\mathcal{M}}_1\left({\mathcal{Z}}_2\right)+2n_1^3{e}_2\hfill \\ & +\mathcal{R}e\mathcal{Z}{e}_3\left({\mathcal{Z}}_3\right)+2e_1{\mathcal{M}}_2\left({\mathcal{Z}}_3\right)+e_1{\mathcal{HM}}_1\left({\mathcal{Z}}_3\right)+3n_1{\mathcal{M}}_1\left({\mathcal{Z}}_3\right)+2e_1^3{e}_3\hfill \\ & +(2e_2+n_1{n}_2){\mathcal{M}}_1\left({\mathcal{Z}}_1\right)+(2e_1+n_1{n}_2){\mathcal{M}}_1\left({\mathcal{Z}}_2\right)+8e_1{e}_2(n_1+n_2)\hfill \\ & +2n_1{n}_2(n_1+n_2)(e_1+e_2)+2n_1{n}_2(n_2{e}_1+n_1{e}_2)+n_1^2{n}_2^2(n_1+n_2)\hfill \\ & +(n_3+2)(e_1{\mathcal{M}}_1\left({\mathcal{Z}}_3\right)+2e_1{e}_3(2e_1+n_3+2)+n_3{e}_1^2(e_1+n_3+2))\hfill \\ & +(n_3+2)(\mathcal{F}\left({\mathcal{Z}}_1\right)+{\mathcal{M}}_1\left({\mathcal{Z}}_1\right)(2n_2+n_3+2)+2n_2{e}_1(n_2+n_3+2)).\hfill \end{array}\end{array}$$

This completes the proof. □

In the following theorem, we present the exact value of first reformulated Zagreb index of subdivision vertex-edge join for three graphs.

Theorem 9.

Let ${\mathcal{Z}}_1$, ${\mathcal{Z}}_2$ and ${\mathcal{Z}}_3$ be three graphs. Then, we have

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\mathcal{EM}}_1({\mathcal{Z}}_1^{\mathcal{S}}⊳({\mathcal{Z}}_2^{\mathcal{V}}\cup {\mathcal{Z}}_3^{\mathcal{I}}))& ={\mathcal{EM}}_1\left({\mathcal{Z}}_2\right)+{\mathcal{EM}}_1\left({\mathcal{Z}}_3\right)+5n_1{\mathcal{M}}_1\left({\mathcal{Z}}_2\right)+5e_1{\mathcal{M}}_1\left({\mathcal{Z}}_3\right)+\mathcal{F}\left({\mathcal{Z}}_1\right)+(3n_2\hfill \\ & +2n_3){\mathcal{M}}_1\left({\mathcal{Z}}_1\right)+4n_1{e}_2(n_1-2)+4e_1{e}_3(e_1-2)+8e_1{e}_3+4(n_1+n_2+2)\hfill \\ & (n_2{e}_1+n_1{e}_2)+n_1{n}_2{(n_1+n_2+2)}^2+e_1{n}_3{(e_1+n_3)}^2+4e_1{e}_3(e_1+n_3)\hfill \\ & +2e_1{(n_2+n_3)}^2.\hfill \end{array}\end{array}$$

Proof. 

By using Lemma 1 in Equation (10), we get the following:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\mathcal{EM}}_1({\mathcal{Z}}_1^{\mathcal{S}}⊳({\mathcal{Z}}_2^{\mathcal{V}}\cup {\mathcal{Z}}_3^{\mathcal{I}}))& =\sum _{{\mathrm{z}}_1{\mathrm{z}}_2\in \mathcal{E}\left({\mathcal{Z}}_2\right)}({({deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_1\right)+{deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_2\right)-2)}^2+4n_1^2+4n_1({deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_1\right)\hfill \\ & +{deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_1\right))-8n_1)+\sum _{{\mathrm{z}}_1{\mathrm{z}}_2\in \mathcal{E}\left({\mathcal{Z}}_3\right)}({({deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_1\right)+{deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_2\right)-2)}^2+4e_1^2\hfill \\ & +4e_1({deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_1\right)+{deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_1\right))-8e_1)+\sum _{{\mathrm{z}}_1\in \mathcal{V}\left({\mathcal{Z}}_1\right)}\sum _{{\mathrm{z}}_2\in \mathcal{V}\left({\mathcal{Z}}_2\right)}({deg}_{{\mathcal{Z}}_1}^2\left({\mathrm{z}}_1\right)\hfill \\ & +{deg}_{{\mathcal{Z}}_2}^2\left({\mathrm{z}}_2\right)+2{deg}_{{\mathcal{Z}}_1}\left({\mathrm{z}}_1\right){deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_2\right)+2(n_1+n_2-2)({deg}_{{\mathcal{Z}}_1}\left({\mathrm{z}}_1\right)\hfill \\ & +{deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_2\right))+{(n_1+n_2-2)}^2)+\sum _{{\mathrm{z}}_1\in \mathcal{I}\left({\mathcal{Z}}_1\right)}\sum _{{\mathrm{z}}_2\in \mathcal{V}\left({\mathcal{Z}}_3\right)}({deg}_{{\mathcal{Z}}_3}^2\left({\mathrm{z}}_2\right)+{(e_1+n_3)}^2\hfill \\ & +2(e_1+n_3){deg}_{{\mathcal{Z}}_3}({\mathrm{z}}_2))+\sum _{\mathrm{z}\in \mathcal{V}\left({\mathcal{Z}}_1\right)}{deg}_{{\mathcal{Z}}_1}(\mathrm{z})({deg}_{{\mathcal{Z}}_1}^2\left(\mathrm{z}\right)+{(n_2+n_3)}^2\hfill \\ & +2(n_2+n_3){deg}_{{\mathcal{Z}}_1}\left(\mathrm{z}\right))\hfill \\ & ={\mathcal{EM}}_1\left({\mathcal{Z}}_2\right)+4e_2{n}_1^2+4n_1{\mathcal{M}}_1\left({\mathcal{Z}}_2\right)-8n_1{e}_2+{\mathcal{EM}}_1\left({\mathcal{Z}}_3\right)+4e_3{e}_1^2\hfill \\ & +4e_1{\mathcal{M}}_1\left({\mathcal{Z}}_3\right)-8e_1{e}_3+n_2{\mathcal{M}}_1\left({\mathcal{Z}}_1\right)+n_1{\mathcal{M}}_1\left({\mathcal{Z}}_2\right)+8e_1{e}_2+4(n_1+n_2+2)\hfill \\ & (n_2{e}_1+n_1{e}_2)+n_1{n}_2{(n_1+n_2+2)}^2+e_1{\mathcal{M}}_1\left({\mathcal{Z}}_3\right)+e_1{n}_3{(e_1+n_3)}^2+4e_1{e}_3(e_1\hfill \\ & +n_3)+\mathcal{F}\left({\mathcal{Z}}_1\right)+2e_1{(n_2+n_3)}^2+2(n_2+n_3){\mathcal{M}}_1\left({\mathcal{Z}}_1\right).\hfill \end{array}\end{array}$$

After some simplifications, we get the required result. This completes the proof. □

In the following theorem, we provide the lower and upper bounds of the Harmonic index of subdivision vertex-edge join for three graphs.

Theorem 10.

Let ${\mathcal{Z}}_1$, ${\mathcal{Z}}_2$ and ${\mathcal{Z}}_3$ be three graphs. Then,

$$\begin{array}{c}\hfill \begin{array}{c}{\displaystyle \frac{{\delta }_{{\mathcal{Z}}_2}}{{△}_{{\mathcal{Z}}_2}+n_1}}\mathcal{H}\left({\mathcal{Z}}_2\right)+{\displaystyle \frac{{\delta }_{{\mathcal{Z}}_3}}{{△}_{{\mathcal{Z}}_3}+e_1}}\mathcal{H}\left({\mathcal{Z}}_3\right)+{\displaystyle \frac{2n_1{n}_2}{{△}_{{\mathcal{Z}}_1}+{△}_{{\mathcal{Z}}_2}+n_1+n_2}}+{\displaystyle \frac{2e_1{n}_3}{{△}_{{\mathcal{Z}}_3}+e_1+n_3+2}}\hfill \\ +{\displaystyle \frac{4e_1}{{△}_{{\mathcal{Z}}_1}+n_2+n_3+2}}\le \mathcal{H}({\mathcal{Z}}_1^{\mathcal{S}}⊳({\mathcal{Z}}_2^{\mathcal{V}}\cup {\mathcal{Z}}_3^{\mathcal{I}}))\le {\displaystyle \frac{{△}_{{\mathcal{Z}}_2}}{{\delta }_{{\mathcal{Z}}_2}+n_1}}\mathcal{H}\left({\mathcal{Z}}_2\right)+{\displaystyle \frac{{△}_{{\mathcal{Z}}_3}}{{\delta }_{{\mathcal{Z}}_3}+e_1}}\mathcal{H}\left({\mathcal{Z}}_3\right)\hfill \\ +{\displaystyle \frac{2n_1{n}_2}{{\delta }_{{\mathcal{Z}}_1}+{\delta }_{{\mathcal{Z}}_2}+n_1+n_2}}+{\displaystyle \frac{2e_1{n}_3}{{\delta }_{{\mathcal{Z}}_3}+e_1+n_3+2}}+{\displaystyle \frac{4e_1}{{\delta }_{{\mathcal{Z}}_1}+n_2+n_3+2}},\hfill \end{array}\end{array}$$

hold with equalities if and only if ${\mathcal{Z}}_1$, ${\mathcal{Z}}_2$ and ${\mathcal{Z}}_3$ are regular graphs.

Proof. 

By using Lemma 1 in Equation (11), we get the following:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \mathcal{H}({\mathcal{Z}}_1^{\mathcal{S}}⊳({\mathcal{Z}}_2^{\mathcal{V}}\cup {\mathcal{Z}}_3^{\mathcal{I}}))& =\sum _{{\mathrm{z}}_1{\mathrm{z}}_2\in \mathcal{E}\left({\mathcal{Z}}_2\right)}{\displaystyle \frac{2}{{deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_1\right)+{deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_2\right)+2n_1}}\hfill \\ & +\sum _{{\mathrm{z}}_1{\mathrm{z}}_2\in \mathcal{E}\left({\mathcal{Z}}_3\right)}{\displaystyle \frac{2}{{deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_1\right)+{deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_2\right)+2e_1}}\hfill \\ & +\sum _{{\mathrm{z}}_1\in \mathcal{V}\left({\mathcal{Z}}_1\right)}\sum _{{\mathrm{z}}_2\in \mathcal{V}\left({\mathcal{Z}}_2\right)}{\displaystyle \frac{2}{{deg}_{{\mathcal{Z}}_1}\left({\mathrm{z}}_1\right)+{deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_2\right)+n_1+n_2}}\hfill \\ & +\sum _{{\mathrm{z}}_1\in \mathcal{I}\left({\mathcal{Z}}_1\right)}\sum _{{\mathrm{z}}_2\in \mathcal{V}\left({\mathcal{Z}}_3\right)}{\displaystyle \frac{2}{{deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_2\right)+e_1+n_3+2}}\hfill \\ & +\sum _{\begin{array}{c}{\mathrm{z}}_1{\mathrm{z}}_2\in \mathcal{E}\left(\mathcal{S}\left({\mathcal{Z}}_1\right)\right),\\ {\mathrm{z}}_1\in \mathcal{V}\left({\mathcal{Z}}_1\right),{\mathrm{z}}_2\in \mathcal{I}\left({\mathcal{Z}}_1\right)\end{array}}{\displaystyle \frac{2}{{deg}_{{\mathcal{Z}}_1}\left({\mathrm{z}}_1\right)+n_2+n_3+2}}\hfill \\ \hfill \mathcal{H}({\mathcal{Z}}_1^{\mathcal{S}}⊳({\mathcal{Z}}_2^{\mathcal{V}}\cup {\mathcal{Z}}_3^{\mathcal{I}}))& =\sum _{{\mathrm{z}}_1{\mathrm{z}}_2\in \mathcal{E}\left({\mathcal{Z}}_2\right)}{\displaystyle \frac{2}{{deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_1\right)+{deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_2\right)}}\times {\displaystyle \frac{{deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_1\right)+{deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_2\right)}{{deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_1\right)+{deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_2\right)+2n_1}}\hfill \\ & +\sum _{{\mathrm{z}}_1{\mathrm{z}}_2\in \mathcal{E}\left({\mathcal{Z}}_3\right)}{\displaystyle \frac{2}{{deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_1\right)+{deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_2\right)}}\times {\displaystyle \frac{{deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_1\right)+{deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_2\right)}{{deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_1\right)+{deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_2\right)+2e_1}}\hfill \\ & +\sum _{{\mathrm{z}}_1\in \mathcal{V}\left({\mathcal{Z}}_1\right)}\sum _{{\mathrm{z}}_2\in \mathcal{V}\left({\mathcal{Z}}_2\right)}{\displaystyle \frac{2}{{deg}_{{\mathcal{Z}}_1}\left({\mathrm{z}}_1\right)+{deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_2\right)+n_1+n_2}}\hfill \\ & +\sum _{{\mathrm{z}}_1\in \mathcal{E}\left({\mathcal{Z}}_1\right)}\sum _{{\mathrm{z}}_2\in \mathcal{V}\left({\mathcal{Z}}_3\right)}{\displaystyle \frac{2}{{deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_2\right)+e_1+n_3+2}}\hfill \\ & +\sum _{\begin{array}{c}{\mathrm{z}}_1{\mathrm{z}}_2\in \mathcal{E}\left(\mathcal{S}\left({\mathcal{Z}}_1\right)\right),\\ {\mathrm{z}}_1\in \mathcal{V}\left({\mathcal{Z}}_1\right),{\mathrm{z}}_2\in \mathcal{I}\left({\mathcal{Z}}_1\right)\end{array}}{\displaystyle \frac{2}{{deg}_{{\mathcal{Z}}_1}\left({\mathrm{z}}_1\right)+n_2+n_3+2}}\hfill \\ & \le {\displaystyle \frac{{△}_{{\mathcal{Z}}_2}}{{\delta }_{{\mathcal{Z}}_2}+n_1}}\mathcal{H}\left({\mathcal{Z}}_2\right)+{\displaystyle \frac{{△}_{{\mathcal{Z}}_3}}{{\delta }_{{\mathcal{Z}}_3}+e_1}}\mathcal{H}\left({\mathcal{Z}}_3\right)+{\displaystyle \frac{2n_1{n}_2}{{\delta }_{{\mathcal{Z}}_1}+{\delta }_{{\mathcal{Z}}_2}+n_1+n_2}}\hfill \\ & +{\displaystyle \frac{2e_1{n}_3}{{\delta }_{{\mathcal{Z}}_3}+e_1+n_3+2}}+{\displaystyle \frac{4e_1}{{\delta }_{{\mathcal{Z}}_1}+n_2+n_3+2}}.\hfill \end{array}\end{array}$$

Similarly, we have

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \mathcal{H}({\mathcal{Z}}_1^{\mathcal{S}}⊳({\mathcal{Z}}_2^{\mathcal{V}}\cup {\mathcal{Z}}_3^{\mathcal{I}}))& \ge {\displaystyle \frac{{\delta }_{{\mathcal{Z}}_2}}{{△}_{{\mathcal{Z}}_2}+n_1}}\mathcal{H}\left({\mathcal{Z}}_2\right)+{\displaystyle \frac{{\delta }_{{\mathcal{Z}}_3}}{{△}_{{\mathcal{Z}}_3}+e_1}}\mathcal{H}\left({\mathcal{Z}}_3\right)+{\displaystyle \frac{2n_1{n}_2}{{△}_{{\mathcal{Z}}_1}+{△}_{{\mathcal{Z}}_2}+n_1+n_2}}\hfill \\ & +{\displaystyle \frac{2e_1{n}_3}{{△}_{{\mathcal{Z}}_3}+e_1+n_3+2}}+{\displaystyle \frac{4e_1}{{△}_{{\mathcal{Z}}_1}+n_2+n_3+2}}.\hfill \end{array}\end{array}$$

Additionally, if ${\mathcal{Z}}_1$, ${\mathcal{Z}}_2$, and ${\mathcal{Z}}_3$ are regular graphs, then the above equalities hold. □

In the next result, we give the lower and upper bounds of the $\mathcal{ABC}$ index of subdivision vertex-edge join for three graphs.

Theorem 11.

Let ${\mathcal{Z}}_1$, ${\mathcal{Z}}_2$ and ${\mathcal{Z}}_3$ be three graphs. Then,

$$\begin{array}{c}\hfill \begin{array}{c}\left|{\displaystyle \frac{{\delta }_{{\mathcal{Z}}_2}}{{△}_{{\mathcal{Z}}_2}+n_1}}\mathcal{ABC}\left({\mathcal{Z}}_2\right)-{\displaystyle \frac{\sqrt{2n_1}{e}_2}{{△}_{{\mathcal{Z}}_2}+n_1}}\right|+\left|{\displaystyle \frac{{\delta }_{{\mathcal{Z}}_3}}{{△}_{{\mathcal{Z}}_3}+e_1}}\mathcal{ABC}\left({\mathcal{Z}}_3\right)-{\displaystyle \frac{\sqrt{2e_1}{e}_3}{{△}_{{\mathcal{Z}}_3}+e_1}}\right|\hfill \\ +n_1{n}_2\sqrt{{\displaystyle \frac{{\delta }_{{\mathcal{Z}}_1}+{\delta }_{{\mathcal{Z}}_2}+n_1+n_2-2}{({△}_{{\mathcal{Z}}_1}+n_2)({△}_{{\mathcal{Z}}_2}+n_1)}}}{e}_1{n}_3\sqrt{{\displaystyle \frac{{\delta }_{{\mathcal{Z}}_3}+e_1+n_3}{({△}_{{\mathcal{Z}}_3}+e_1)(n_3+2)}}}+2e_1\sqrt{{\displaystyle \frac{{\delta }_{{\mathcal{Z}}_1}+n_2+n_3}{({△}_{{\mathcal{Z}}_1}+n_2)(n_3+2)}}}\hfill \end{array}\end{array}$$

$$\begin{array}{c}\hfill \begin{array}{c}\le \mathcal{ABC}({\mathcal{Z}}_1^{\mathcal{S}}⊳({\mathcal{Z}}_2^{\mathcal{V}}\cup {\mathcal{Z}}_3^{\mathcal{I}}))\le {\displaystyle \frac{{△}_{{\mathcal{Z}}_2}}{{\delta }_{{\mathcal{Z}}_2}+n_1}}\mathcal{ABC}\left({\mathcal{Z}}_2\right)+{\displaystyle \frac{{△}_{{\mathcal{Z}}_3}}{{\delta }_{{\mathcal{Z}}_3}+e_1}}\mathcal{ABC}\left({\mathcal{Z}}_3\right)+{\displaystyle \frac{\sqrt{2n_1}{e}_2}{{\delta }_{{\mathcal{Z}}_2}+n_1}}+{\displaystyle \frac{\sqrt{2e_1}{e}_3}{{\delta }_{{\mathcal{Z}}_3}+e_1}}\hfill \\ +n_1{n}_2\sqrt{{\displaystyle \frac{{△}_{{\mathcal{Z}}_1}+{△}_{{\mathcal{Z}}_2}+n_1+n_2-2}{({\delta }_{{\mathcal{Z}}_1}+n_2)({\delta }_{{\mathcal{Z}}_2}+n_1)}}}+e_1{n}_3\sqrt{{\displaystyle \frac{{△}_{{\mathcal{Z}}_3}+e_1+n_3}{({\delta }_{{\mathcal{Z}}_3}+e_1)(n_3+2)}}}+2e_1\sqrt{{\displaystyle \frac{{△}_{{\mathcal{Z}}_1}+n_2+n_3}{({\delta }_{{\mathcal{Z}}_1}+n_2)(n_3+2)}}}.\hfill \end{array}\end{array}$$

hold with equalities if and only if ${\mathcal{Z}}_1$ is a regular graph and ${\mathcal{Z}}_2={\mathcal{Z}}_3=P_2$.

Proof. 

By using Lemma 1 in Equation (12), we get the following:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \mathcal{ABC}({\mathcal{Z}}_1^{\mathcal{S}}⊳({\mathcal{Z}}_2^{\mathcal{V}}\cup {\mathcal{Z}}_3^{\mathcal{I}}))& =\sum _{{\mathrm{z}}_1{\mathrm{z}}_2\in \mathcal{E}\left({\mathcal{Z}}_2\right)}\sqrt{{\displaystyle \frac{{deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_1\right)+{deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_2\right)+2n_1-2}{({deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_1\right)+n_1)({deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_2\right)+n_1)}}}\hfill \\ & +\sum _{{\mathrm{z}}_1{\mathrm{z}}_2\in \mathcal{E}\left({\mathcal{Z}}_3\right)}\sqrt{{\displaystyle \frac{{deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_1\right)+{deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_2\right)+2e_1-2}{({deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_1\right)+e_1)({deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_2\right)+e_1)}}}\hfill \\ & +\sum _{{\mathrm{z}}_1\in \mathcal{V}\left({\mathcal{Z}}_1\right)}\sum _{{\mathrm{z}}_2\in \mathcal{V}\left({\mathcal{Z}}_2\right)}\sqrt{{\displaystyle \frac{{deg}_{{\mathcal{Z}}_1}\left({\mathrm{z}}_1\right)+{deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_2\right)+n_1+n_2-2}{({deg}_{{\mathcal{Z}}_1}\left({\mathrm{z}}_1\right)+n_2)({deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_2\right)+n_1)}}}\hfill \\ & +\sum _{{\mathrm{z}}_1\in \mathcal{I}\left({\mathcal{Z}}_1\right)}\sum _{{\mathrm{z}}_2\in \mathcal{V}\left({\mathcal{Z}}_3\right)}\sqrt{{\displaystyle \frac{{deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_2\right)+e_1+n_3+2-2}{({deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_2\right)+e_1)(n_3+2)}}}\hfill \\ & +\sum _{\begin{array}{c}{\mathrm{z}}_1{\mathrm{z}}_2\in \mathcal{E}\left(\mathcal{S}\left({\mathcal{Z}}_1\right)\right),\\ {\mathrm{z}}_1\in \mathcal{V}\left({\mathcal{Z}}_1\right),{\mathrm{z}}_2\in \mathcal{I}\left({\mathcal{Z}}_1\right)\end{array}}\sqrt{{\displaystyle \frac{{deg}_{{\mathcal{Z}}_1}\left({\mathrm{z}}_1\right)+n_2+n_3+2-2}{({deg}_{{\mathcal{Z}}_1}\left({\mathrm{z}}_1\right)+n_2)(n_3+2)}}}.\hfill \end{array}\end{array}$$

Now,

$$\begin{array}{cc}{\displaystyle \frac{{deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_1\right)+{deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_2\right)+2n_1-2}{({deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_1\right)+n_1)({deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_2\right)+n_1)}}\hfill & ={\displaystyle \frac{{deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_1\right)+{deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_2\right)-2}{{deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_1\right){deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_2\right)}}\times {\displaystyle \frac{{deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_1\right){deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_2\right)}{({deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_1\right)+n_1)({deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_2\right)+n_1)}}\hfill \\ \hfill & +{\displaystyle \frac{2n_1}{({deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_1\right)+n_1)({deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_2\right)+n_1)}}\hfill \\ \hfill & \le {\displaystyle \frac{{△}_{{\mathcal{Z}}_2}^2}{{({\delta }_{{\mathcal{Z}}_2}+n_1)}^2}}\times {\displaystyle \frac{{deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_1\right)+{deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_2\right)-2}{{deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_1\right){deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_2\right)}}+{\displaystyle \frac{2n_1}{{({\delta }_{{\mathcal{Z}}_2}+n_1)}^2}}.\hfill \end{array}$$

(24)

Since $\sqrt{a+b}\le \sqrt{a}+\sqrt{b}$ with equality if and only if $a=0$ or $b=0$. Therefore,

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \sqrt{{\displaystyle \frac{{deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_1\right)+{deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_2\right)+2n_1-2}{({deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_1\right)+n_1)({deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_2\right)+n_1)}}}& \le {\displaystyle \frac{{△}_{{\mathcal{Z}}_2}}{{\delta }_{{\mathcal{Z}}_2}+n_1}}\sqrt{{\displaystyle \frac{{deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_1\right)+{deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_2\right)-2}{{deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_1\right){deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_2\right)}}}+{\displaystyle \frac{\sqrt{2n_1}}{{\delta }_{{\mathcal{Z}}_2}+n_1}}.\hfill \end{array}\end{array}$$

Equality holds if and only if ${deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_1\right)={deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_2\right)=1$. Similarly, we have

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \sqrt{{\displaystyle \frac{{deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_1\right)+{deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_2\right)+2e_1-2}{({deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_1\right)+e_1)({deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_2\right)+e_1)}}}& \le {\displaystyle \frac{{△}_{{\mathcal{Z}}_3}}{{\delta }_{{\mathcal{Z}}_3}+e_1}}\sqrt{{\displaystyle \frac{{deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_1\right)+{deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_2\right)-2}{{deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_1\right){deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_2\right)}}}+{\displaystyle \frac{\sqrt{2e_1}}{{\delta }_{{\mathcal{Z}}_3}+e_1}}.\hfill \end{array}\end{array}$$

Equality holds if and only if ${deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_1\right)={deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_2\right)=1$. By the above calculations, we get

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \mathcal{ABC}({\mathcal{Z}}_1^{\mathcal{S}}⊳({\mathcal{Z}}_2^{\mathcal{V}}\cup {\mathcal{Z}}_3^{\mathcal{I}}))& \le \sum _{{\mathrm{z}}_1{\mathrm{z}}_2\in \mathcal{E}\left({\mathcal{Z}}_2\right)}\left({\displaystyle \frac{{△}_{{\mathcal{Z}}_2}}{{\delta }_{{\mathcal{Z}}_2}+n_1}}\sqrt{{\displaystyle \frac{{deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_1\right)+{deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_2\right)-2}{{deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_1\right){deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_2\right)}}}+{\displaystyle \frac{\sqrt{2n_1}}{{\delta }_{{\mathcal{Z}}_2}+n_1}}\right)\hfill \\ & +\sum _{{\mathrm{z}}_1{\mathrm{z}}_2\in \mathcal{E}\left({\mathcal{Z}}_3\right)}\left({\displaystyle \frac{{△}_{{\mathcal{Z}}_3}}{{\delta }_{{\mathcal{Z}}_3}+e_1}}\sqrt{{\displaystyle \frac{{deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_1\right)+{deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_2\right)-2}{{deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_1\right){deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_2\right)}}}+{\displaystyle \frac{\sqrt{2e_1}}{{\delta }_{{\mathcal{Z}}_3}+e_1}}\right)\hfill \end{array}\end{array}$$

$$\begin{array}{c}\hfill \begin{array}{cc}& +\sum _{{\mathrm{z}}_1\in \mathcal{V}\left({\mathcal{Z}}_1\right)}\sum _{{\mathrm{z}}_2\in \mathcal{V}\left({\mathcal{Z}}_2\right)}\sqrt{{\displaystyle \frac{{△}_{{\mathcal{Z}}_1}+{△}_{{\mathcal{Z}}_2}+n_1+n_2-2}{({\delta }_{{\mathcal{Z}}_1}+n_2)({\delta }_{{\mathcal{Z}}_2}+n_1)}}}\hfill \\ & +\sum _{{\mathrm{z}}_1\in \mathcal{I}\left({\mathcal{Z}}_1\right)}\sum _{{\mathrm{z}}_2\in \mathcal{V}\left({\mathcal{Z}}_3\right)}\sqrt{{\displaystyle \frac{{△}_{{\mathcal{Z}}_3}+e_1+n_3}{({\delta }_{{\mathcal{Z}}_3}+e_1)(n_3+2)}}}\hfill \\ & +\sum _{\begin{array}{c}{\mathrm{z}}_1{\mathrm{z}}_2\in \mathcal{E}\left(\mathcal{S}\left({\mathcal{Z}}_1\right)\right),\\ {\mathrm{z}}_1\in \mathcal{V}\left({\mathcal{Z}}_1\right),{\mathrm{z}}_2\in \mathcal{I}\left({\mathcal{Z}}_1\right)\end{array}}\sqrt{{\displaystyle \frac{{△}_{{\mathcal{Z}}_1}+n_2+n_3}{({\delta }_{{\mathcal{Z}}_1}+n_2)(n_3+2)}}}\hfill \\ \hfill \mathcal{ABC}({\mathcal{Z}}_1^{\mathcal{S}}⊳({\mathcal{Z}}_2^{\mathcal{V}}\cup {\mathcal{Z}}_3^{\mathcal{I}}))& ={\displaystyle \frac{{△}_{{\mathcal{Z}}_2}}{{\delta }_{{\mathcal{Z}}_2}+n_1}}\mathcal{ABC}\left({\mathcal{Z}}_2\right)+{\displaystyle \frac{\sqrt{2n_1}{e}_2}{{\delta }_{{\mathcal{Z}}_2}+n_1}}+{\displaystyle \frac{{△}_{{\mathcal{Z}}_3}}{{\delta }_{{\mathcal{Z}}_3}+e_1}}\mathcal{ABC}\left({\mathcal{Z}}_3\right)+{\displaystyle \frac{\sqrt{2e_1}{e}_3}{{\delta }_{{\mathcal{Z}}_3}+e_1}}\hfill \\ & +n_1{n}_2\sqrt{{\displaystyle \frac{{△}_{{\mathcal{Z}}_1}+{△}_{{\mathcal{Z}}_2}+n_1+n_2-2}{({\delta }_{{\mathcal{Z}}_1}+n_2)({\delta }_{{\mathcal{Z}}_2}+n_1)}}}+e_1{n}_3\sqrt{{\displaystyle \frac{{△}_{{\mathcal{Z}}_3}+e_1+n_3}{({\delta }_{{\mathcal{Z}}_3}+e_1)(n_3+2)}}}\hfill \\ & +2e_1\sqrt{{\displaystyle \frac{{△}_{{\mathcal{Z}}_1}+n_2+n_3}{({\delta }_{{\mathcal{Z}}_1}+n_2)(n_3+2)}}}.\hfill \end{array}\end{array}$$

Now,

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill {\displaystyle \frac{{deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_1\right)+{deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_2\right)+2n_1-2}{({deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_1\right)+n_1)({deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_2\right)+n_1)}}& \ge {\displaystyle \frac{{\delta }_{{\mathcal{Z}}_2^2}}{{({△}_{{\mathcal{Z}}_2}+n_1)}^2}}{\displaystyle \frac{{deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_1\right)+{deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_2\right)-2}{{deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_1\right){deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_2\right)}}+{\displaystyle \frac{2n_1}{{({△}_{{\mathcal{Z}}_2}+n_1)}^2}}.\hfill \end{array}\end{array}$$

Since $\sqrt{a+b}\ge |\sqrt{a}-\sqrt{b}|$ with equality if and only if $a=0$ or $b=0$,

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \sqrt{{\displaystyle \frac{{deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_1\right)+{deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_2\right)+2n_1-2}{({deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_1\right)+n_1)({deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_2\right)+n_1)}}}& \ge \left|{\displaystyle \frac{{\delta }_{{\mathcal{Z}}_2}}{{△}_{{\mathcal{Z}}_2}+n_1}}\sqrt{{\displaystyle \frac{{deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_1\right)+{deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_2\right)-2}{{deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_1\right){deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_2\right)}}}-{\displaystyle \frac{\sqrt{2n_1}}{{△}_{{\mathcal{Z}}_2}+n_1}}\right|.\hfill \end{array}\end{array}$$

Equality holds if and only if ${deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_1\right)={deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_2\right)=1$. By a similar argument as those are given above, we get:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \sqrt{{\displaystyle \frac{{deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_1\right)+{deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_2\right)+2e_1-2}{({deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_1\right)+e_1)({deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_2\right)+e_1)}}}& \ge \left|{\displaystyle \frac{{\delta }_{{\mathcal{Z}}_3}}{{△}_{{\mathcal{Z}}_3}+e_1}}\sqrt{{\displaystyle \frac{{deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_1\right)+{deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_2\right)-2}{{deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_1\right){deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_2\right)}}}-{\displaystyle \frac{\sqrt{2e_1}}{{△}_{{\mathcal{Z}}_3}+e_1}}\right|.\hfill \end{array}\end{array}$$

Equality holds if and only if ${deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_1\right)={deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_2\right)=1$. By the above calculations, we get

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \mathcal{ABC}({\mathcal{Z}}_1^{\mathcal{S}}⊳({\mathcal{Z}}_2^{\mathcal{V}}\cup {\mathcal{Z}}_3^{\mathcal{I}}))& \ge \sum _{{\mathrm{z}}_1{\mathrm{z}}_2\in \mathcal{E}\left({\mathcal{Z}}_2\right)}\left(\left|{\displaystyle \frac{{\delta }_{{\mathcal{Z}}_2}}{{△}_{{\mathcal{Z}}_2}+n_1}}\sqrt{{\displaystyle \frac{{deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_1\right)+{deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_2\right)-2}{{deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_1\right){deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_2\right)}}}-{\displaystyle \frac{\sqrt{2n_1}}{{△}_{{\mathcal{Z}}_2}+n_1}}\right|\right)\hfill \\ & +\sum _{{\mathrm{z}}_1{\mathrm{z}}_2\in \mathcal{E}\left({\mathcal{Z}}_3\right)}\left(\left|{\displaystyle \frac{{\delta }_{{\mathcal{Z}}_3}}{{△}_{{\mathcal{Z}}_3}+e_1}}\sqrt{{\displaystyle \frac{{deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_1\right)+{deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_2\right)-2}{{deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_1\right){deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_2\right)}}}-{\displaystyle \frac{\sqrt{2e_1}}{{△}_{{\mathcal{Z}}_3}+e_1}}\right|\right)\hfill \\ & +\sum _{{\mathrm{z}}_1\in \mathcal{V}\left({\mathcal{Z}}_1\right)}\sum _{{\mathrm{z}}_2\in \mathcal{V}\left({\mathcal{Z}}_2\right)}\sqrt{{\displaystyle \frac{{\delta }_{{\mathcal{Z}}_1}+{\delta }_{{\mathcal{Z}}_2}+n_1+n_2-2}{({△}_{{\mathcal{Z}}_1}+n_2)({△}_{{\mathcal{Z}}_2}+n_1)}}}\hfill \\ & +\sum _{{\mathrm{z}}_1\in \mathcal{I}\left({\mathcal{Z}}_1\right)}\sum _{{\mathrm{z}}_2\in \mathcal{V}\left({\mathcal{Z}}_3\right)}\sqrt{{\displaystyle \frac{{\delta }_{{\mathcal{Z}}_3}+e_1+n_3}{({△}_{{\mathcal{Z}}_3}+e_1)(n_3+2)}}}\hfill \\ & +\sum _{\begin{array}{c}{\mathrm{z}}_1{\mathrm{z}}_2\in \mathcal{E}\left(\mathcal{S}\left({\mathcal{Z}}_1\right)\right),\\ {\mathrm{z}}_1\in \mathcal{V}\left({\mathcal{Z}}_1\right),{\mathrm{z}}_2\in \mathcal{I}\left({\mathcal{Z}}_1\right)\end{array}}\sqrt{{\displaystyle \frac{{\delta }_{{\mathcal{Z}}_1}+n_2+n_3}{({△}_{{\mathcal{Z}}_1}+n_2)(n_3+2)}}}\hfill \\ & =\left|{\displaystyle \frac{{\delta }_{{\mathcal{Z}}_2}}{{△}_{{\mathcal{Z}}_2}+n_1}}\mathcal{ABC}\left({\mathcal{Z}}_2\right)-{\displaystyle \frac{\sqrt{2n_1}{e}_2}{{△}_{{\mathcal{Z}}_2}+n_1}}\right|+\left|{\displaystyle \frac{{\delta }_{{\mathcal{Z}}_3}}{{△}_{{\mathcal{Z}}_3}+e_1}}\mathcal{ABC}\left({\mathcal{Z}}_3\right)-{\displaystyle \frac{\sqrt{2e_1}{e}_3}{{△}_{{\mathcal{Z}}_3}+e_1}}\right|\hfill \\ & +n_1{n}_2\sqrt{{\displaystyle \frac{{\delta }_{{\mathcal{Z}}_1}+{\delta }_{{\mathcal{Z}}_2}+n_1+n_2-2}{({△}_{{\mathcal{Z}}_1}+n_2)({△}_{{\mathcal{Z}}_2}+n_1)}}}+e_1{n}_3\sqrt{{\displaystyle \frac{{\delta }_{{\mathcal{Z}}_3}+e_1+n_3}{({△}_{{\mathcal{Z}}_3}+e_1)(n_3+2)}}}\hfill \\ & +2e_1\sqrt{{\displaystyle \frac{{\delta }_{{\mathcal{Z}}_1}+n_2+n_3}{({△}_{{\mathcal{Z}}_1}+n_2)(n_3+2)}}}.\hfill \end{array}\end{array}$$

Additionally, if ${\mathcal{Z}}_1$ is a regular graph and ${\mathcal{Z}}_2={\mathcal{Z}}_3=P_2$, then the above equalities hold. This completes the proof. □

In the following theorem, we give the lower and upper bounds of the $\mathcal{GA}$ index of subdivision vertex-edge join for three graphs.

Theorem 12.

Let ${\mathcal{Z}}_1$, ${\mathcal{Z}}_2$, and ${\mathcal{Z}}_3$ be three graphs. Then,

$$\begin{array}{c}\hfill \begin{array}{c}{\displaystyle \frac{e_2({\delta }_{{\mathcal{Z}}_2}+n_1)}{{△}_{{\mathcal{Z}}_2}+n_1}}+{\displaystyle \frac{e_3({\delta }_{{\mathcal{Z}}_3}+e_1)}{{△}_{{\mathcal{Z}}_3}+e_1}}+{\displaystyle \frac{2n_1{n}_2\sqrt{({\delta }_{{\mathcal{Z}}_1}+n_2)({\delta }_{{\mathcal{Z}}_2}+n_1)}}{{△}_{{\mathcal{Z}}_1}+{△}_{{\mathcal{Z}}_2}+n_1+n_2}}+{\displaystyle \frac{2e_1{n}_3\sqrt{({\delta }_{{\mathcal{Z}}_3}+e_1)(n_3+2)}}{{△}_{{\mathcal{Z}}_3}+e_1+n_3+2}}\hfill \\ +{\displaystyle \frac{4e_1\sqrt{({\delta }_{{\mathcal{Z}}_3}+e_1)(n_3+2)}}{{△}_{{\mathcal{Z}}_3}+e_1+n_3+2}}\le \mathcal{GA}({\mathcal{Z}}_1^{\mathcal{S}}⊳({\mathcal{Z}}_2^{\mathcal{V}}\cup {\mathcal{Z}}_3^{\mathcal{I}}))\le {\displaystyle \frac{e_2({△}_{{\mathcal{Z}}_2}+n_1)}{{\delta }_{{\mathcal{Z}}_2}+n_1}}+{\displaystyle \frac{e_3({△}_{{\mathcal{Z}}_3}+e_1)}{{\delta }_{{\mathcal{Z}}_3}+e_1}}\hfill \\ +{\displaystyle \frac{2n_1{n}_2\sqrt{({△}_{{\mathcal{Z}}_1}+n_2)({△}_{{\mathcal{Z}}_2}+n_1)}}{{\delta }_{{\mathcal{Z}}_1}+{\delta }_{{\mathcal{Z}}_2}+n_1+n_2}}+{\displaystyle \frac{2e_1{n}_3\sqrt{({△}_{{\mathcal{Z}}_3}+e_1)(n_3+2)}}{{\delta }_{{\mathcal{Z}}_3}+e_1+n_3+2}}+{\displaystyle \frac{4e_1\sqrt{({△}_{{\mathcal{Z}}_1}+n_2)(n_3+2)}}{{\delta }_{{\mathcal{Z}}_1}+n_2+n_3+2}}.\hfill \end{array}\end{array}$$

hold with equalities if and only if ${\mathcal{Z}}_1$, ${\mathcal{Z}}_2$, and ${\mathcal{Z}}_3$ are regular graphs.

Proof. 

By using Lemma 1 in Equation (13), we get the following:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \mathcal{GA}({\mathcal{Z}}_1^{\mathcal{S}}⊳({\mathcal{Z}}_2^{\mathcal{V}}\cup {\mathcal{Z}}_3^{\mathcal{I}}))& =\sum _{{\mathrm{z}}_1{\mathrm{z}}_2\in \mathcal{E}\left({\mathcal{Z}}_2\right)}{\displaystyle \frac{2\sqrt{({deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_1\right)+n_1)({deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_2\right)+n_1)}}{{deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_1\right)+{deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_2\right)+2n_1}}\hfill \\ & +\sum _{{\mathrm{z}}_1{\mathrm{z}}_2\in \mathcal{E}\left({\mathcal{Z}}_3\right)}{\displaystyle \frac{2\sqrt{({deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_1\right)+e_1)({deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_2\right)+e_1)}}{{deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_1\right)+{deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_2\right)+2e_1}}\hfill \\ & +\sum _{{\mathrm{z}}_1\in \mathcal{V}\left({\mathcal{Z}}_1\right)}\sum _{{\mathrm{z}}_2\in \mathcal{V}\left({\mathcal{Z}}_2\right)}{\displaystyle \frac{2\sqrt{({deg}_{{\mathcal{Z}}_1}\left({\mathrm{z}}_1\right)+n_2)({deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_2\right)+n_1)}}{{deg}_{{\mathcal{Z}}_1}\left({\mathrm{z}}_1\right)+{deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_2\right)+n_1+n_2}}\hfill \\ & +\sum _{{\mathrm{z}}_1\in \mathcal{I}\left({\mathcal{Z}}_1\right)}\sum _{{\mathrm{z}}_2\in \mathcal{V}\left({\mathcal{Z}}_3\right)}{\displaystyle \frac{2\sqrt{({deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_2\right)+e_1)(n_3+2)}}{{deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_2\right)+e_1+n_3+2}}\hfill \\ & +\sum _{\begin{array}{c}{\mathrm{z}}_1{\mathrm{z}}_2\in \mathcal{E}\left(\mathcal{S}\left({\mathcal{Z}}_1\right)\right),\\ {\mathrm{z}}_1\in \mathcal{V}\left({\mathcal{Z}}_1\right),{\mathrm{z}}_2\in \mathcal{I}\left({\mathcal{Z}}_1\right)\end{array}}{\displaystyle \frac{2\sqrt{({deg}_{{\mathcal{Z}}_1}\left({\mathrm{z}}_1\right)+n_2)(n_3+2)}}{{deg}_{{\mathcal{Z}}_1}\left({\mathrm{z}}_1\right)+n_2+n_3+2}}\hfill \\ & \le {\displaystyle \frac{e_2({△}_{{\mathcal{Z}}_2}+n_1)}{{\delta }_{{\mathcal{Z}}_2}+n_1}}+{\displaystyle \frac{e_3({△}_{{\mathcal{Z}}_3}+e_1)}{{\delta }_{{\mathcal{Z}}_3}+e_1}}+{\displaystyle \frac{2n_1{n}_2\sqrt{({△}_{{\mathcal{Z}}_1}+n_2)({△}_{{\mathcal{Z}}_2}+n_1)}}{{\delta }_{{\mathcal{Z}}_1}+{\delta }_{{\mathcal{Z}}_2}+n_1+n_2}}\hfill \\ & +{\displaystyle \frac{2e_1{n}_3\sqrt{({△}_{{\mathcal{Z}}_3}+e_1)(n_3+2)}}{{\delta }_{{\mathcal{Z}}_3}+e_1+n_3+2}}+{\displaystyle \frac{4e_1\sqrt{({△}_{{\mathcal{Z}}_1}+n_2)(n_3+2)}}{{\delta }_{{\mathcal{Z}}_1}+n_2+n_3+2}}.\hfill \end{array}\end{array}$$

Similarly,

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \mathcal{GA}({\mathcal{Z}}_1^{\mathcal{S}}⊳({\mathcal{Z}}_2^{\mathcal{V}}\cup {\mathcal{Z}}_3^{\mathcal{I}}))& \ge {\displaystyle \frac{e_2({\delta }_{{\mathcal{Z}}_2}+n_1)}{{△}_{{\mathcal{Z}}_2}+n_1}}+{\displaystyle \frac{e_3({\delta }_{{\mathcal{Z}}_3}+e_1)}{{△}_{{\mathcal{Z}}_3}+e_1}}+{\displaystyle \frac{2n_1{n}_2\sqrt{({\delta }_{{\mathcal{Z}}_1}+n_2)({\delta }_{{\mathcal{Z}}_2}+n_1)}}{{△}_{{\mathcal{Z}}_1}+{△}_{{\mathcal{Z}}_2}+n_1+n_2}}\hfill \\ & +{\displaystyle \frac{2e_1{n}_3\sqrt{({\delta }_{{\mathcal{Z}}_3}+e_1)(n_3+2)}}{{△}_{{\mathcal{Z}}_3}+e_1+n_3+2}}+{\displaystyle \frac{4e_1\sqrt{({\delta }_{{\mathcal{Z}}_3}+e_1)(n_3+2)}}{{△}_{{\mathcal{Z}}_3}+e_1+n_3+2}}.\hfill \end{array}\end{array}$$

Additionally, if ${\mathcal{Z}}_1$, ${\mathcal{Z}}_2$, and ${\mathcal{Z}}_3$ are regular graphs, then the above equalities hold. This completes the proof. □

Finally, we set up the lower and upper bounds of the reduced reciprocal Randić index of subdivision vertex-edge join for three graphs.

Theorem 13.

Let ${\mathcal{Z}}_1$, ${\mathcal{Z}}_2$, and ${\mathcal{Z}}_3$ be three graphs. Then,

$$\begin{array}{c}\hfill \begin{array}{c}\left|\mathcal{RRR}\left({\mathcal{Z}}_2\right)-n_1{e}_2-\sqrt{2n_1({\delta }_{{\mathcal{Z}}_2}-1)}\right|+\left|\mathcal{RRR}\left({\mathcal{Z}}_3\right)-e_1{e}_3-\sqrt{2e_1({\delta }_{{\mathcal{Z}}_3}-1)}\right|\hfill \\ +e_1{n}_3\sqrt{({\delta }_{{\mathcal{Z}}_3}+e_1-1)(n_3+1)}+n_1{n}_2\sqrt{({\delta }_{{\mathcal{Z}}_1}+n_2-1)({\delta }_{{\mathcal{Z}}_2}+n_1-1)}\hfill \\ +2e_1\sqrt{({\delta }_{{\mathcal{Z}}_1}+n_2-1)(n_3+1)}\le \mathcal{RRR}({\mathcal{Z}}_1^{\mathcal{S}}⊳({\mathcal{Z}}_2^{\mathcal{V}}\cup {\mathcal{Z}}_3^{\mathcal{I}}))\le \mathcal{RRR}\left({\mathcal{Z}}_2\right)+n_1{e}_2+\sqrt{2n_1({△}_{{\mathcal{Z}}_2}-1)}\hfill \\ +\mathcal{RRR}\left({\mathcal{Z}}_3\right)+e_1{e}_3+\sqrt{2e_1({△}_{{\mathcal{Z}}_3}-1)}+n_1{n}_2\sqrt{({△}_{{\mathcal{Z}}_1}+n_2-1)({△}_{{\mathcal{Z}}_2}+n_1-1)}\hfill \\ +e_1{n}_3\sqrt{({△}_{{\mathcal{Z}}_3}+e_1-1)(n_3+1)}+2e_1\sqrt{({△}_{{\mathcal{Z}}_1}+n_2-1)(n_3+1)}.\hfill \end{array}\end{array}$$

hold with equalities if and only if ${\mathcal{Z}}_1$ is a regular graph and ${\mathcal{Z}}_2={\mathcal{Z}}_3=P_2$.

Proof. 

By using Lemma 1 in Equation (14), we get the following:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \mathcal{RRR}({\mathcal{Z}}_1^{\mathcal{S}}⊳({\mathcal{Z}}_2^{\mathcal{V}}\cup {\mathcal{Z}}_3^{\mathcal{I}}))& =\sum _{{\mathrm{z}}_1{\mathrm{z}}_2\in \mathcal{E}\left({\mathcal{Z}}_2\right)}\sqrt{({deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_1\right)+n_1-1)({deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_2\right)+n_1-1)}\hfill \\ & +\sum _{{\mathrm{z}}_1{\mathrm{z}}_2\in \mathcal{E}\left({\mathcal{Z}}_3\right)}\sqrt{({deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_1\right)+e_1-1)({deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_2\right)+e_1-1)}\hfill \\ & +\sum _{{\mathrm{z}}_1\in \mathcal{V}\left({\mathcal{Z}}_1\right)}\sum _{{\mathrm{z}}_2\in \mathcal{V}\left({\mathcal{Z}}_2\right)}\sqrt{({deg}_{{\mathcal{Z}}_1}\left({\mathrm{z}}_1\right)+n_2-1)({deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_2\right)+n_1-1)}\hfill \\ & +\sum _{{\mathrm{z}}_1\in \mathcal{I}\left({\mathcal{Z}}_1\right)}\sum _{{\mathrm{z}}_2\in \mathcal{V}\left({\mathcal{Z}}_3\right)}\sqrt{({deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_2\right)+e_1-1)(n_3+2-1)}\hfill \\ & +\sum _{\begin{array}{c}{\mathrm{z}}_1{\mathrm{z}}_2\in \mathcal{E}\left(\mathcal{S}\left({\mathcal{Z}}_1\right)\right),\\ {\mathrm{z}}_1\in \mathcal{V}\left({\mathcal{Z}}_1\right),{\mathrm{z}}_2\in \mathcal{I}\left({\mathcal{Z}}_1\right)\end{array}}\sqrt{({deg}_{{\mathcal{Z}}_1}\left({\mathrm{z}}_1\right)+n_2-1)(n_3+2-1)}.\hfill \end{array}\end{array}$$

However, $\sqrt{a+b}\le \sqrt{a}+\sqrt{b}$, with equality if and only if $a=0$ or $b=0$. Therefore,

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \sqrt{({deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_1\right)+n_1-1)({deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_2\right)+n_1-1)}& \le \sqrt{({deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_1\right)-1)({deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_2\right)-1)}+n_1\hfill \\ & +\sqrt{n_1}\sqrt{{deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_1\right)+{deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_2\right)-2}.\hfill \end{array}\end{array}$$

Equality holds if and only if ${deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_1\right)={deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_2\right)=1$. Similarly,

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \sqrt{({deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_1\right)+e_1-1)({deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_2\right)+e_1-1)}& \le \sqrt{({deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_1\right)-1)({deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_2\right)-1)}+e_1\hfill \\ & +\sqrt{e_1}\sqrt{{deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_1\right)+{deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_2\right)-2}.\hfill \end{array}\end{array}$$

Equality holds if and only if ${deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_1\right)={deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_2\right)=1$.

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \mathcal{RRR}({\mathcal{Z}}_1^{\mathcal{S}}⊳({\mathcal{Z}}_2^{\mathcal{V}}\cup {\mathcal{Z}}_3^{\mathcal{I}}))& \le \sum _{{\mathrm{z}}_1{\mathrm{z}}_2\in \mathcal{E}\left({\mathcal{Z}}_2\right)}(\sqrt{({deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_1\right)-1)({deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_2\right)-1)}+n_1\hfill \\ & +\sqrt{n_1}\sqrt{{deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_1\right)+{deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_2\right)-2})\hfill \\ & +\sum _{{\mathrm{z}}_1{\mathrm{z}}_2\in \mathcal{E}\left({\mathcal{Z}}_3\right)}(\sqrt{({deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_1\right)-1)({deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_2\right)-1)}\hfill \\ & +e_1+\sqrt{e_1}\sqrt{{deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_1\right)+{deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_2\right)-2})\hfill \\ & +\sum _{{\mathrm{z}}_1\in \mathcal{V}\left({\mathcal{Z}}_1\right)}\sum _{{\mathrm{z}}_2\in \mathcal{V}\left({\mathcal{Z}}_2\right)}\sqrt{({△}_{{\mathcal{Z}}_1}+n_2-1)({△}_{{\mathcal{Z}}_2}+n_1-1)}\hfill \\ & +\sum _{{\mathrm{z}}_1\in \mathcal{I}\left({\mathcal{Z}}_1\right)}\sum _{{\mathrm{z}}_2\in \mathcal{V}\left({\mathcal{Z}}_3\right)}\sqrt{({△}_{{\mathcal{Z}}_3}+e_1-1)(n_3+1)}\hfill \\ & +\sum _{\begin{array}{c}{\mathrm{z}}_1{\mathrm{z}}_2\in \mathcal{E}\left(\mathcal{S}\left({\mathcal{Z}}_1\right)\right),\\ {\mathrm{z}}_1\in \mathcal{V}\left({\mathcal{Z}}_1\right),{\mathrm{z}}_2\in \mathcal{I}\left({\mathcal{Z}}_1\right)\end{array}}\sqrt{({△}_{{\mathcal{Z}}_1}+n_2-1)(n_3+1)}\hfill \\ & \le \mathcal{RRR}\left({\mathcal{Z}}_2\right)+n_1{e}_2+\sqrt{2n_1({△}_{{\mathcal{Z}}_2}-1)}+\mathcal{RRR}\left({\mathcal{Z}}_3\right)+e_1{e}_3\hfill \\ & +\sqrt{2e_1({△}_{{\mathcal{Z}}_3}-1)}+n_1{n}_2\sqrt{({△}_{{\mathcal{Z}}_1}+n_2-1)({△}_{{\mathcal{Z}}_2}+n_1-1)}\hfill \\ & +e_1{n}_3\sqrt{({△}_{{\mathcal{Z}}_3}+e_1-1)(n_3+1)}+2e_1\sqrt{({△}_{{\mathcal{Z}}_1}+n_2-1)(n_3+1)}.\hfill \end{array}\end{array}$$

However, $\sqrt{a+b}\le |\sqrt{a}-\sqrt{b}|$, with equality if and only if $a=0$ or $b=0$. Therefore,

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \sqrt{({deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_1\right)+n_1)({deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_2\right)+n_1)}& \ge |\sqrt{({deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_1\right)-1)({deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_2\right)-1)}-n_1\hfill \\ & -\sqrt{n_1({deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_1\right)+{deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_2\right)-2)}|.\hfill \end{array}\end{array}$$

Equality holds if and only if ${deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_1\right)={deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_2\right)=1$. By a similar argument as those are given above, we get:

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \sqrt{({deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_1\right)+n_1)({deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_2\right)+e_1)}& \ge |\sqrt{({deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_1\right)-1)({deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_2\right)-1)}-e_1\hfill \\ & -\sqrt{e_1({deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_1\right)+{deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_2\right)-2)}|.\hfill \end{array}\end{array}$$

Equality holds if and only if ${deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_1\right)={deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_2\right)=1$. By using the above calculation, we obtain

$$\begin{array}{c}\hfill \begin{array}{cc}\hfill \mathcal{RRR}({\mathcal{Z}}_1^{\mathcal{S}}⊳({\mathcal{Z}}_2^{\mathcal{V}}\cup {\mathcal{Z}}_3^{\mathcal{I}}))& \ge \sum _{{\mathrm{z}}_1{\mathrm{z}}_2\in \mathcal{E}\left({\mathcal{Z}}_2\right)}|\sqrt{({deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_1\right)-1)({deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_2\right)-1)}-n_1-\sqrt{n_1}\hfill \\ & \sqrt{{deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_1\right)+{deg}_{{\mathcal{Z}}_2}\left({\mathrm{z}}_2\right)-2}|\hfill \\ & +\sum _{{\mathrm{z}}_1{\mathrm{z}}_2\in \mathcal{E}\left({\mathcal{Z}}_3\right)}|\sqrt{({deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_1\right)-1)({deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_2\right)-1)}\hfill \\ & -e_1-\sqrt{e_1}\sqrt{{deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_1\right)+{deg}_{{\mathcal{Z}}_3}\left({\mathrm{z}}_2\right)-2}|\hfill \\ & +\sum _{{\mathrm{z}}_1\in \mathcal{V}\left({\mathcal{Z}}_1\right)}\sum _{{\mathrm{z}}_2\in \mathcal{V}\left({\mathcal{Z}}_2\right)}\sqrt{({\delta }_{{\mathcal{Z}}_1}+n_2-1)({\delta }_{{\mathcal{Z}}_2}+n_1-1)}\hfill \\ & +\sum _{{\mathrm{z}}_1\in \mathcal{I}\left({\mathcal{Z}}_1\right)}\sum _{{\mathrm{z}}_2\in \mathcal{V}\left({\mathcal{Z}}_3\right)}\sqrt{({\delta }_{{\mathcal{Z}}_3}+e_1-1)(n_3+1)}\hfill \\ & +\sum _{\begin{array}{c}{\mathrm{z}}_1{\mathrm{z}}_2\in \mathcal{E}\left(\mathcal{S}\left({\mathcal{Z}}_1\right)\right),\\ {\mathrm{z}}_1\in \mathcal{V}\left({\mathcal{Z}}_1\right),{\mathrm{z}}_2\in \mathcal{I}\left({\mathcal{Z}}_1\right)\end{array}}\sqrt{({\delta }_{{\mathcal{Z}}_1}+n_2-1)(n_3+1)}\hfill \\ & =\left|\mathcal{RRR}\left({\mathcal{Z}}_2\right)-n_1{e}_2-\sqrt{2n_1({\delta }_{{\mathcal{Z}}_2}-1)}\right|\hfill \\ & +\left|\mathcal{RRR}\left({\mathcal{Z}}_3\right)-e_1{e}_3-\sqrt{2e_1({\delta }_{{\mathcal{Z}}_3}-1)}\right|\hfill \\ & +n_1{n}_2\sqrt{({\delta }_{{\mathcal{Z}}_1}+n_2-1)({\delta }_{{\mathcal{Z}}_2}+n_1-1)}+e_1{n}_3\sqrt{({\delta }_{{\mathcal{Z}}_3}+e_1-1)(n_3+1)}\hfill \\ & +2e_1\sqrt{({\delta }_{{\mathcal{Z}}_1}+n_2-1)(n_3+1)}.\hfill \end{array}\end{array}$$

Furthermore, if ${\mathcal{Z}}_1$ is a regular graph and ${\mathcal{Z}}_2={\mathcal{Z}}_3=P_2$, then the above equalities hold. This finishes the proof. □

4. Conclusions

In this article, we compute additive degree-based topological indices for new graph operation subdivision vertex-edge join of three graphs. By using these graph operation, one can construct new (chemical) graphs from existing graphs. Therefore, it is important to know which physico-chemical properties are carried from original graphs to the newly constructed graph via this new operation.

Recently, the Zagreb indices and their variants have been used for studying the complexity of molecular graphs while overall Zagreb indices have shown a potential applicability for deriving multilinear regression models. Zagreb indices have also been used by various researchers in their QSPR and QSAR studies. The first and second Zagreb indices are useful for the computation of the total $\pi$-electron energy of molecules. The expression for Zagreb type indices for subdivision vertex-edge join will be useful in study of QSPR and QSAR analysis of new compound formed by this operations.

The Randic index is a topological descriptor that correlates with many chemical characteristics of molecules such as boiling point. The expression obtained for subdivision vertex-edge join of three graphs would be useful and applicable for correlating many chemical properties of new molecular compounds.

The atom-bond connectivity (ABC) index exhibits a very good correlation for computing the strain energy of molecular graphs. Hence, the results obtained for ABC index can be used for correlation of computing the strain energy of new molecules formed by this new introduced operations. Sometimes, the GA index has as much predictive power as that of the Randic index, so the GA index is more useful than the Randic index in some cases as it has more predictive power for certain chemical compounds.