Asymmetrical Velocity Distribution in the Drag-Reducing Channel Flow of Surfactant Solution Caused by an Injected Ultrathin Water Layer
Abstract
1. Introduction
2. Experiments
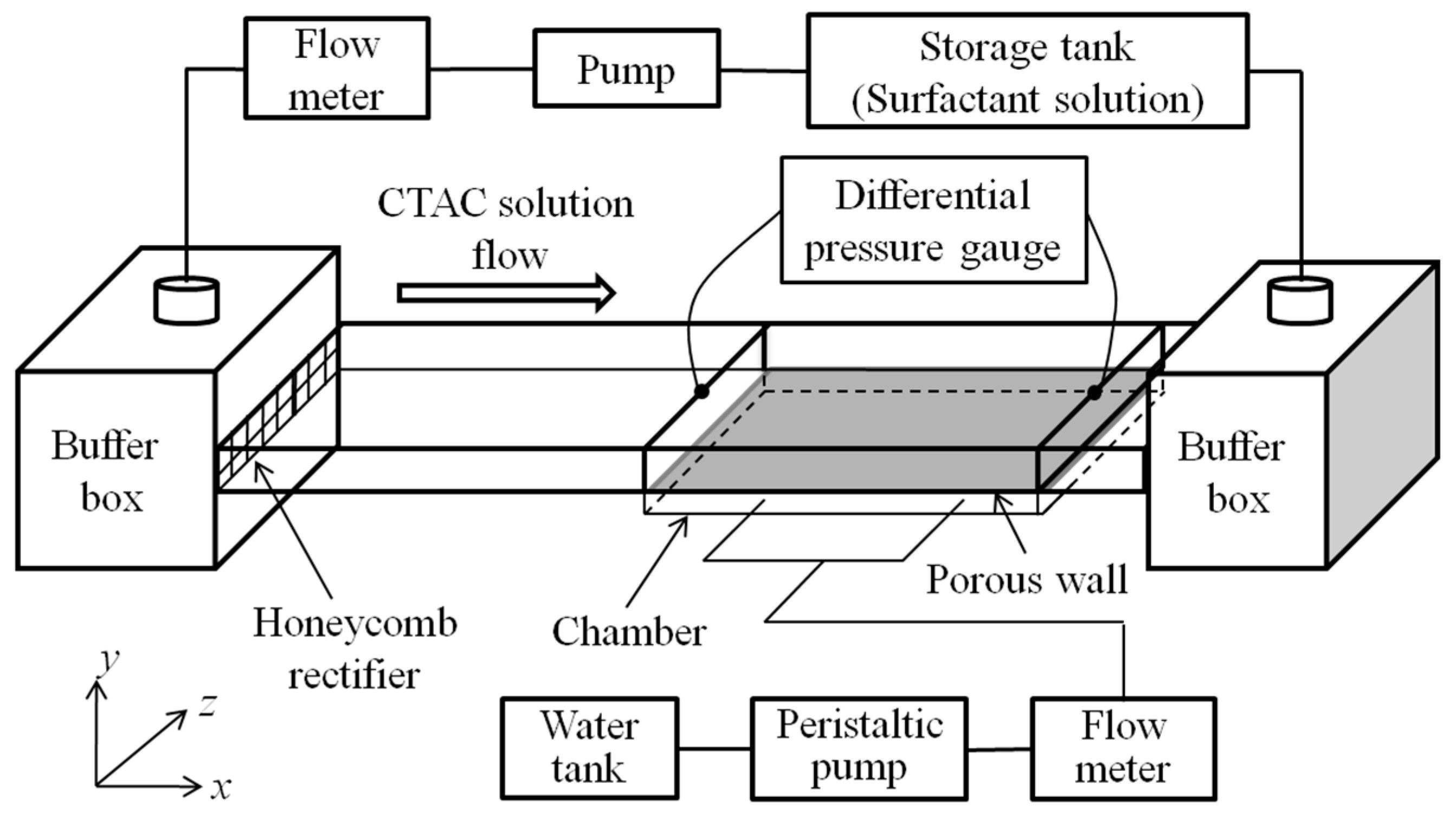
2.1. Experimental Equipment
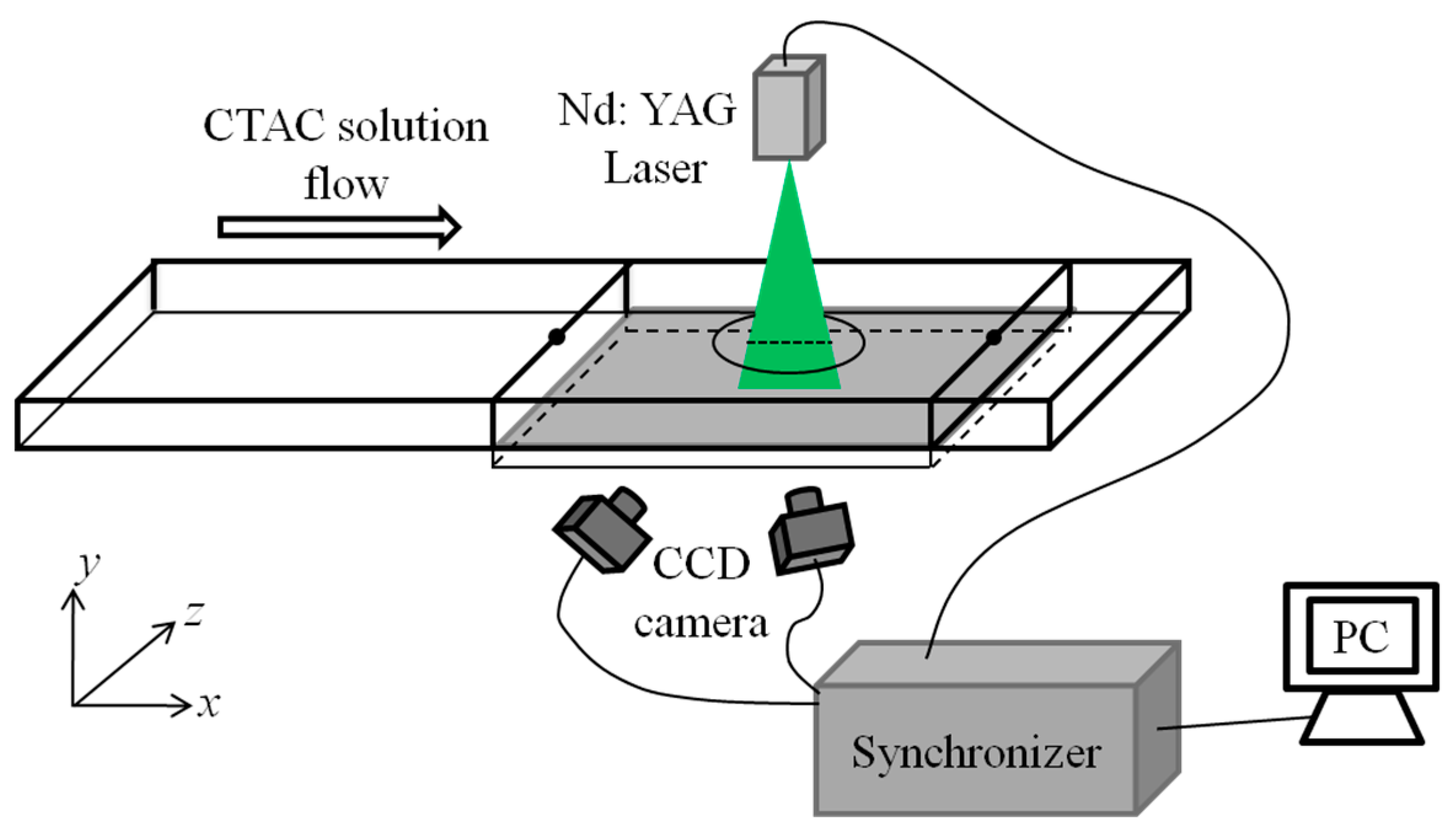
2.2. PIV/PLIF Arrangements
2.3. Experimental Conditions
3. Results and Discussion
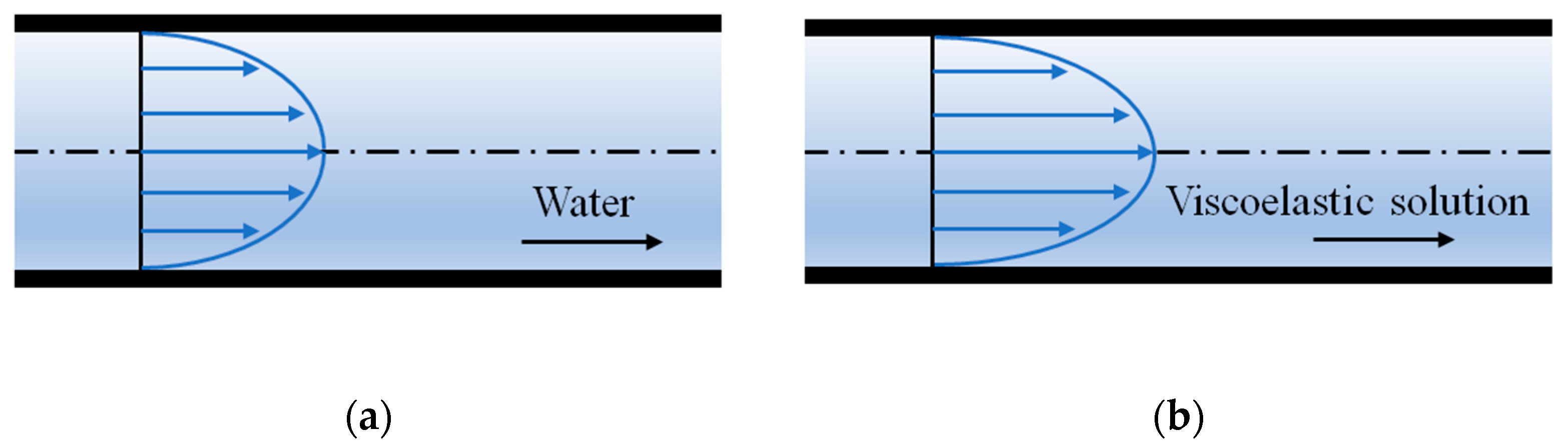
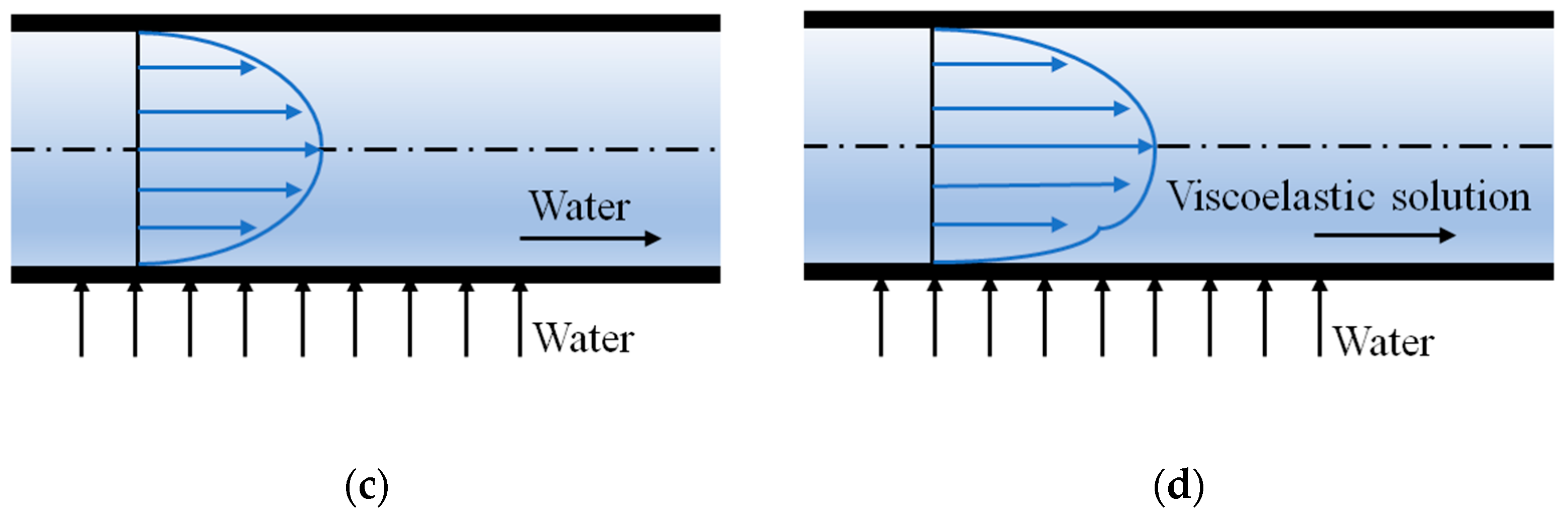
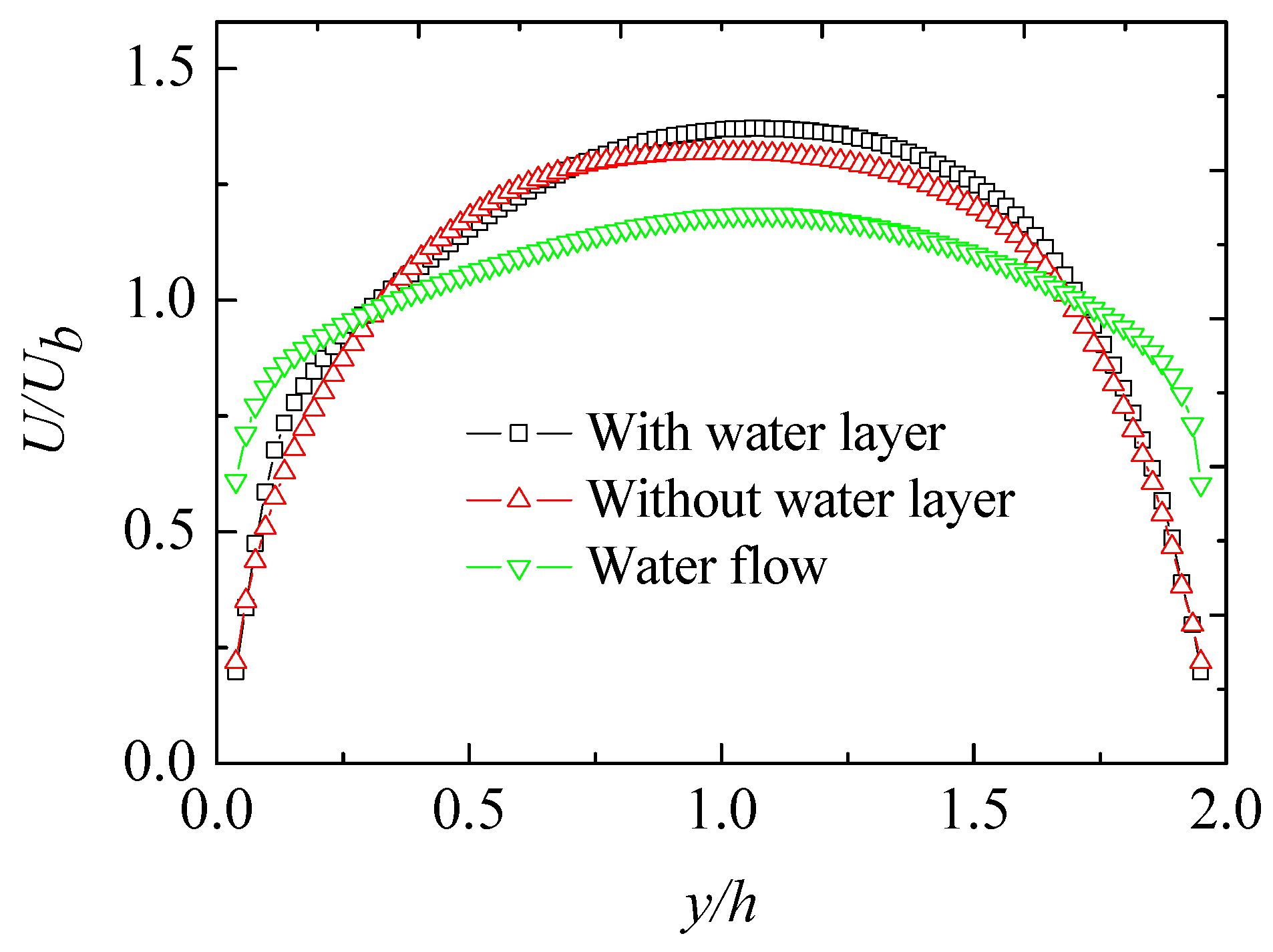
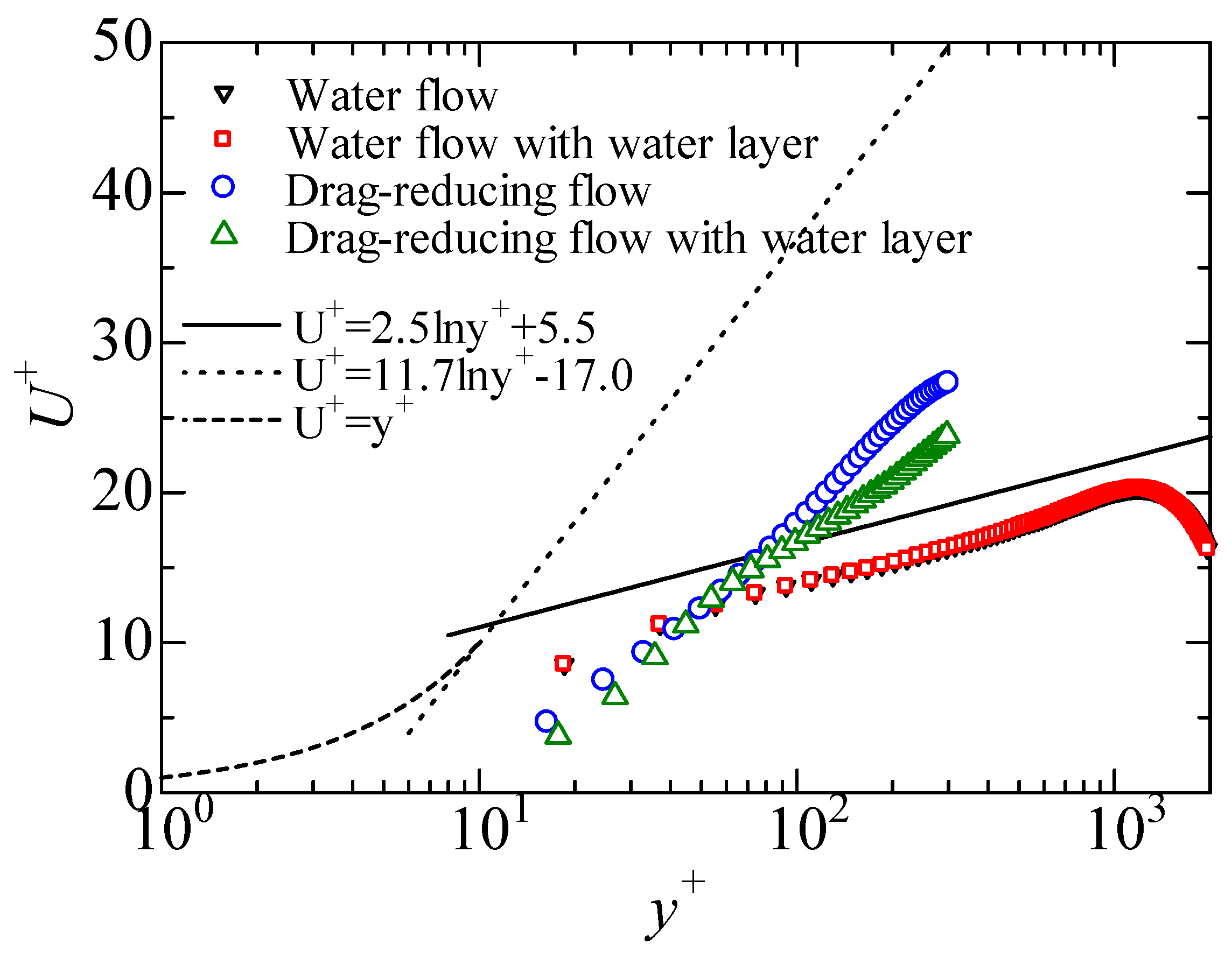
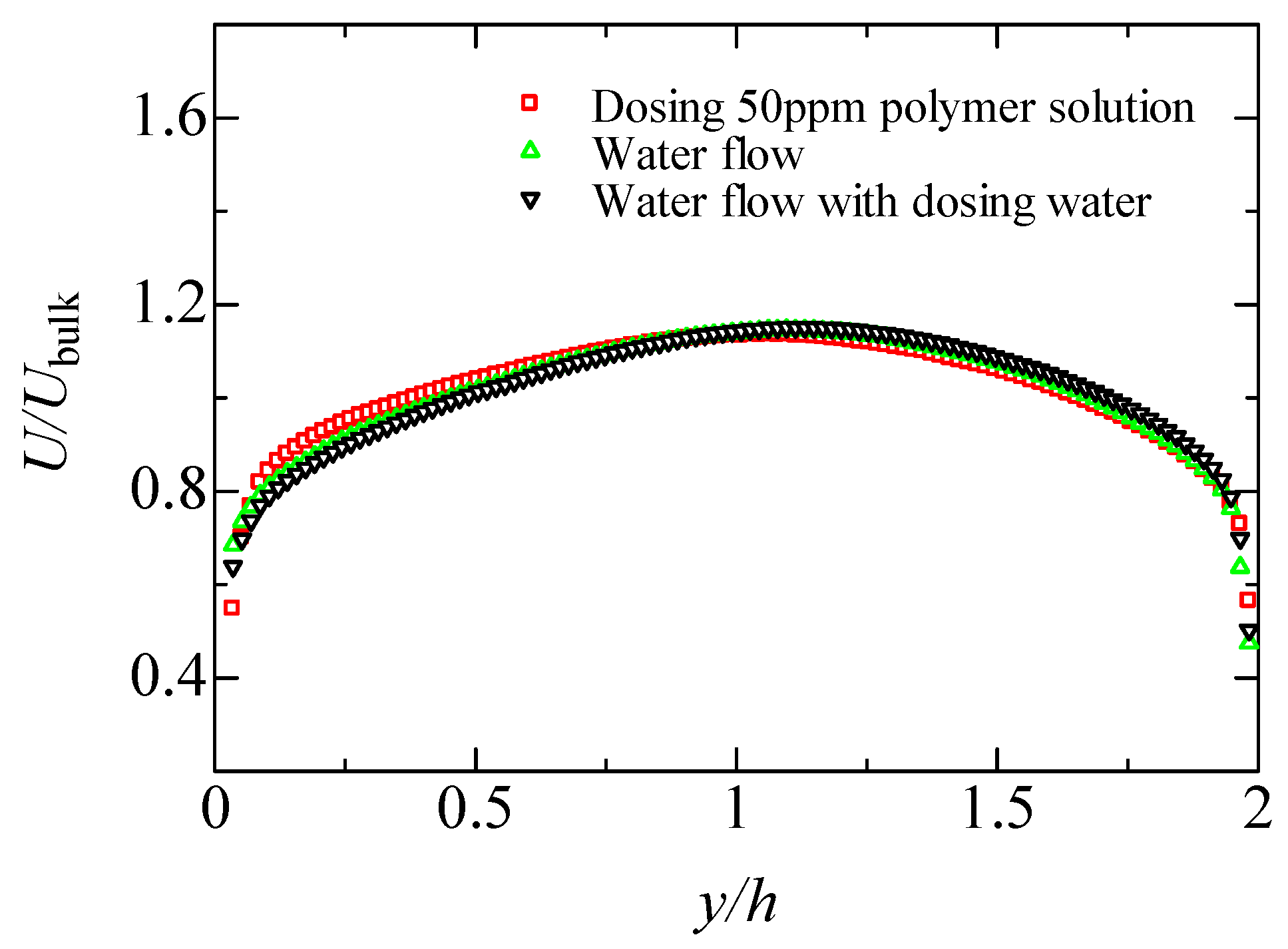
3.1. Asymmetrical Velocity Distribution
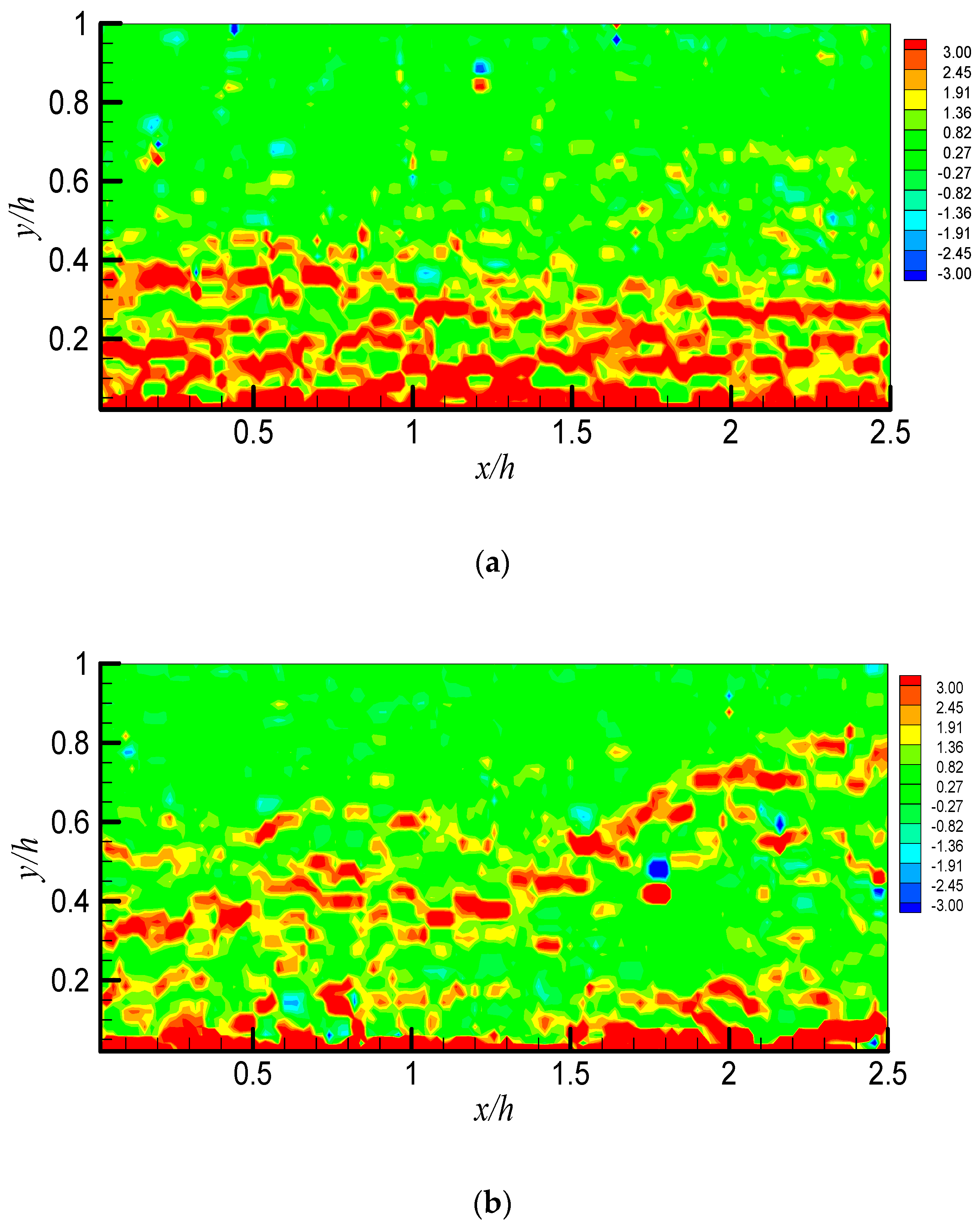
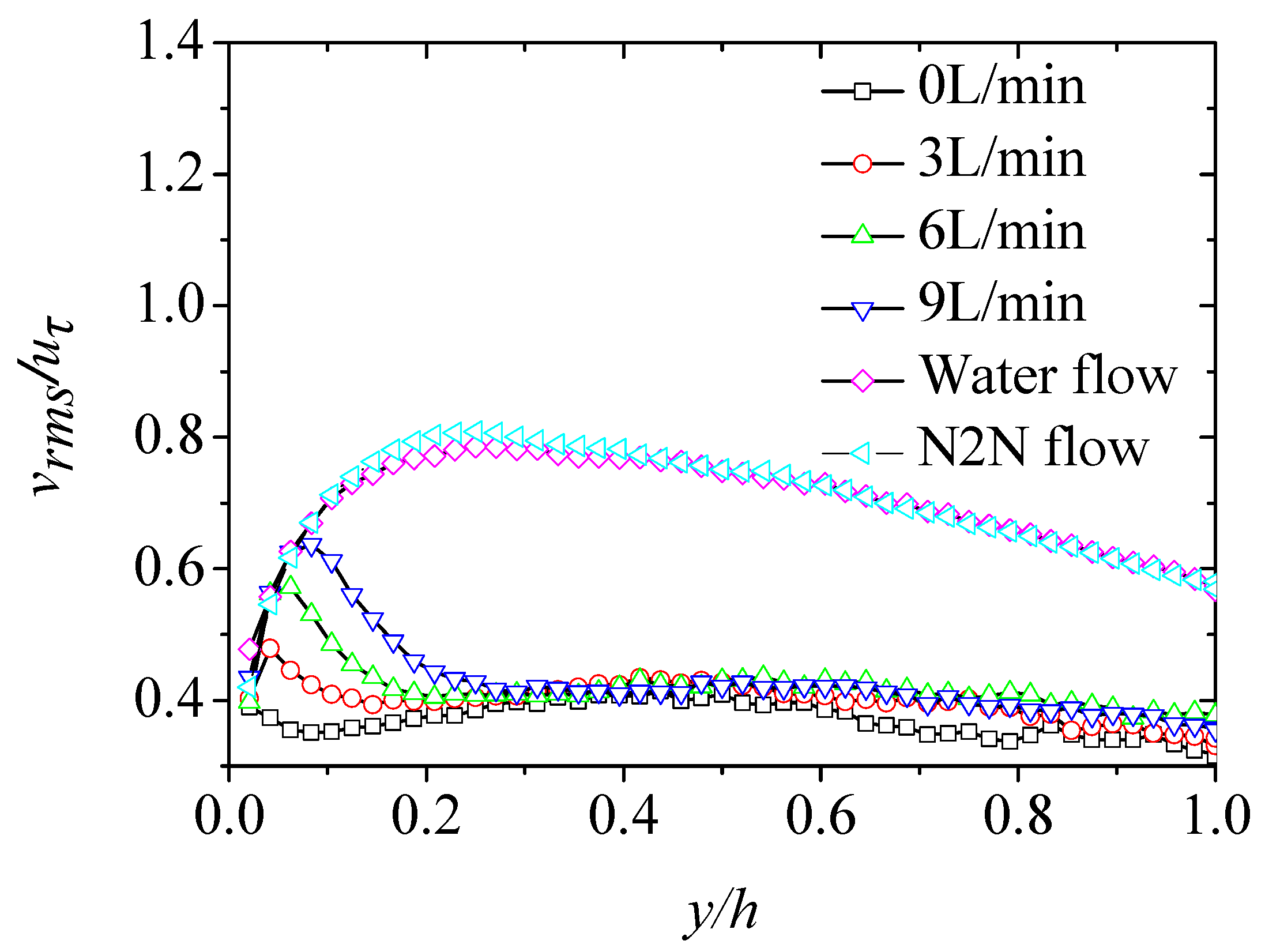
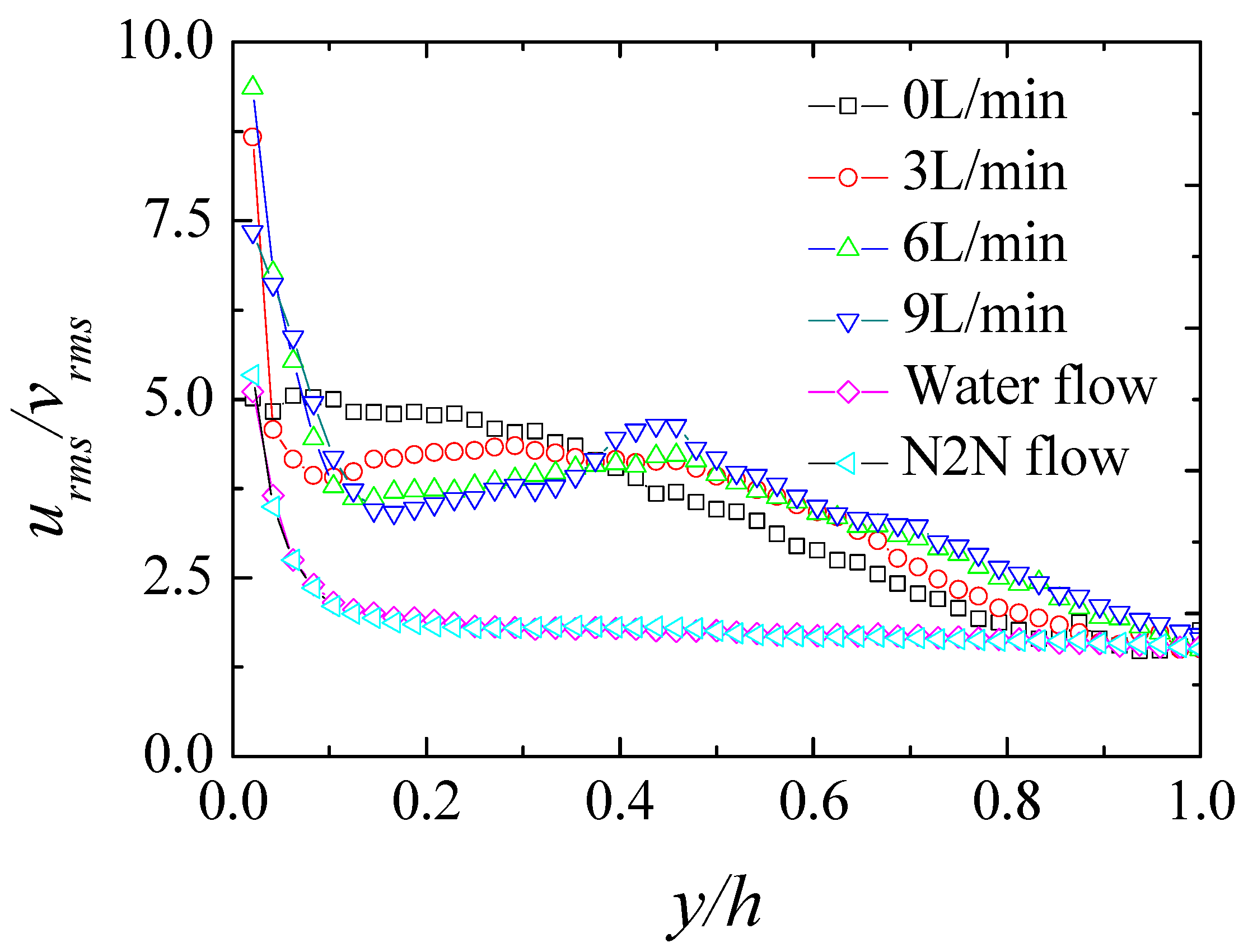
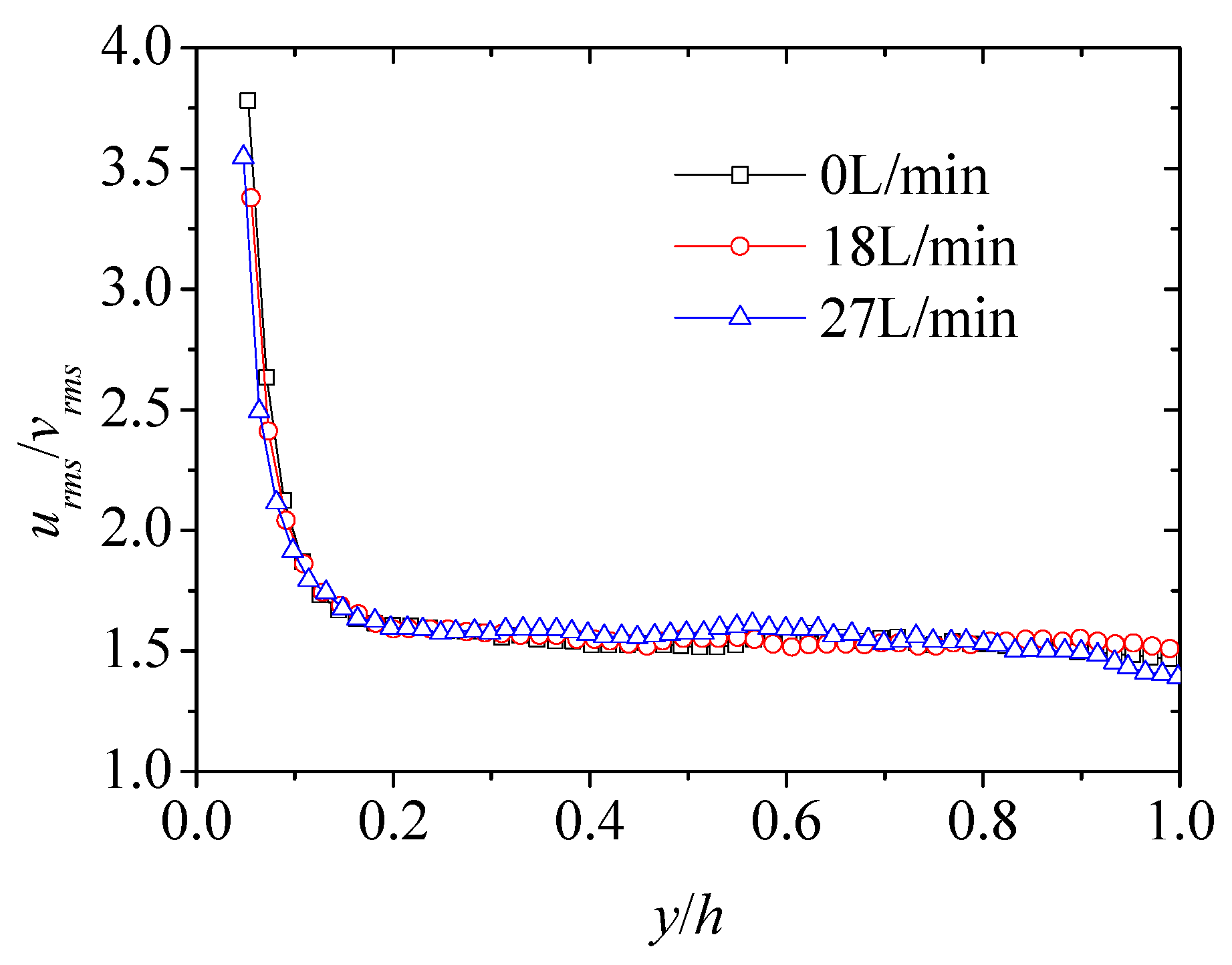
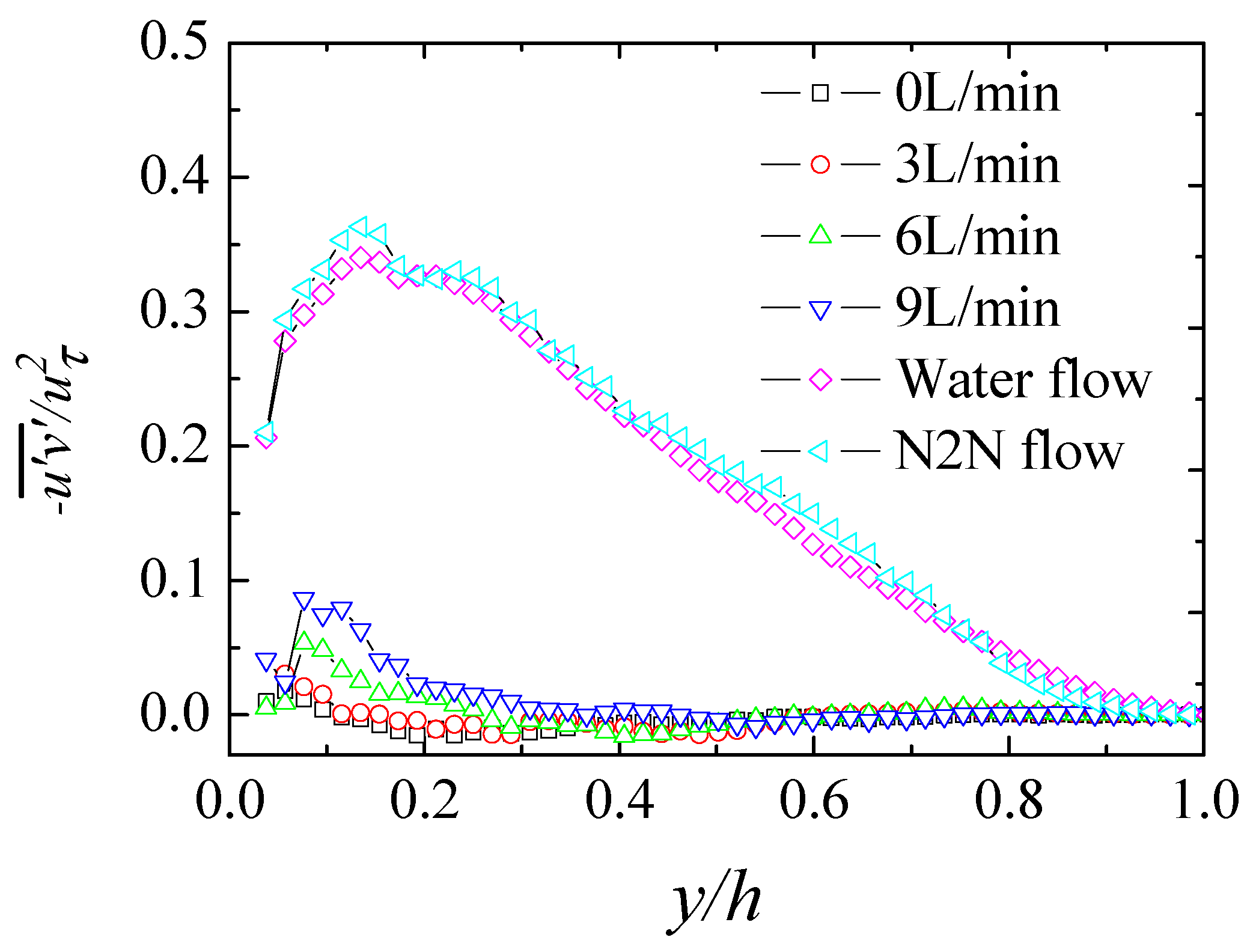
3.2. Turbulence Intensity and Anisotropy
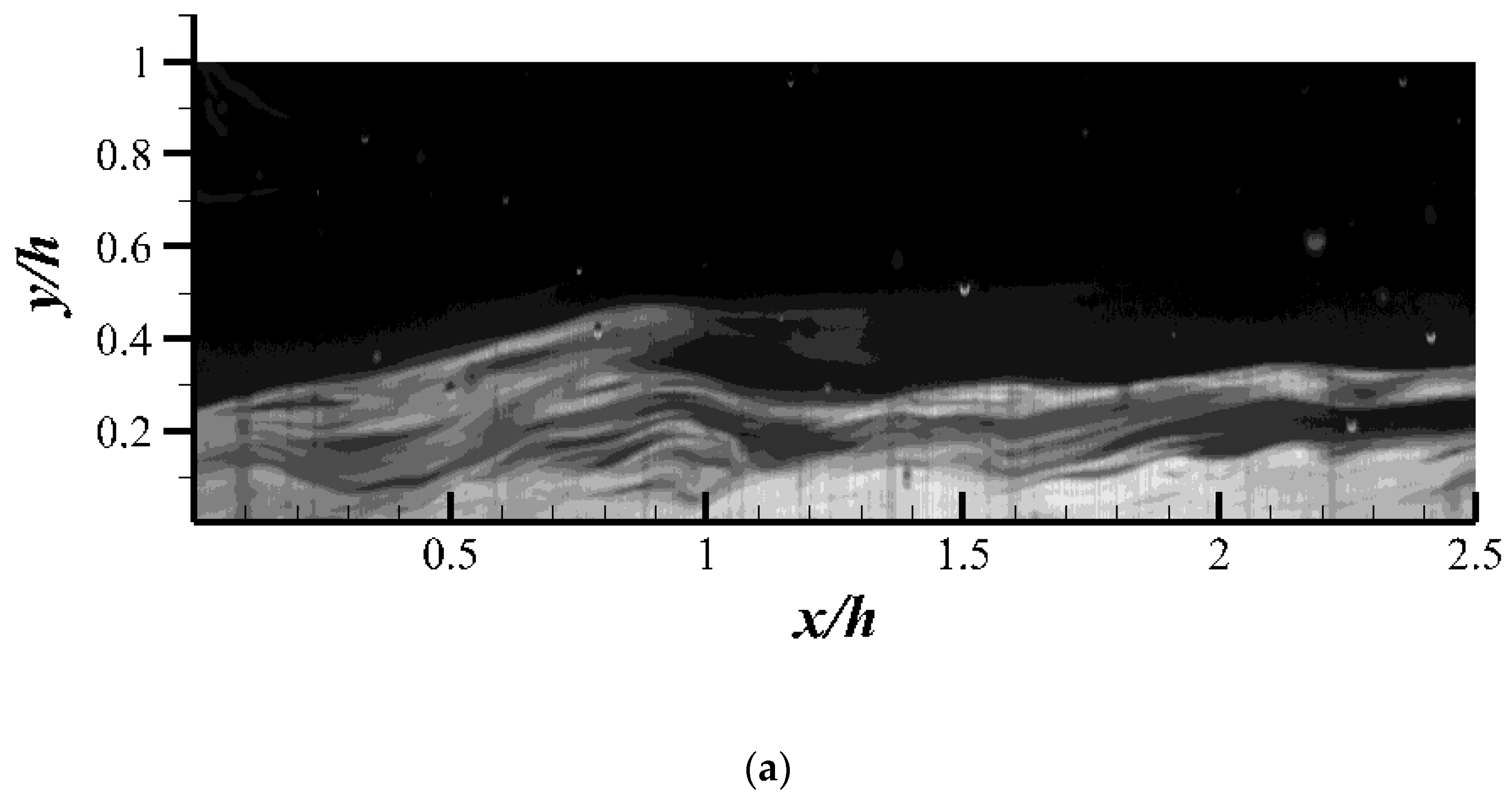
3.3. Discussion of the Possible Cause
4. Conclusions
- Under the experimental conditions, the injected ultrathin water layer breaks the symmetry of the mean velocity distribution about the channel centerline. The normalized velocity in the logarithmic layer is descended, and the near-wall structure of the shear layer indicted by the velocity gradient is modified in the viscoelastic drag-reducing flow with the water layer when compared with the case without water layer.
- The injected water layer leads to the enhancement of turbulence fluctuation intensity. The turbulence anisotropy in the drag-reducing flow with the injected water layer is also promoted while it does not change in the water flow with the injection of the water layer. The change of the viscoelastic solution near the wall plays a key role.
- Under the influence of the ultrathin water layer, the viscoelastic drag-reducing flow presents the zonal characteristics of layers of water and viscoelastic solution in the wall-normal direction with a wavy boundary. The redistributed viscoelastic solution in the near-wall region causes the modification of stress distribution. The near-wall Reynolds shear stress is increased in the drag-reducing flow. This redistributed stress results in the break of the symmetric velocity and the related structure.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Toms, B. Some observations on the flow of linear polymer solutions through straight tubes at large Reynolds numbers. In Proceedings of the 1st International Congress on Rheology, Amsterdam, The Netherlands, 17 January 1948; pp. 135–141. [Google Scholar]
- Luo, Y.; Wang, L.; Green, L.; Song, K.; Wang, L.; Smith, R. Advances of drag-reducing surface technologies in turbulence based on boundary layer control. J. Hydrodyn. 2015, 27, 473–487. [Google Scholar] [CrossRef]
- Burger, E.; Chorn, L.; Perkins, T. Studies of drag reduction conducted over a broad range of pipeline conditions when flowing Prudhoe bay crude oil. J. Rheology 1980, 24, 603–626. [Google Scholar] [CrossRef]
- Fu, Z.; Kawaguchi, Y. A short review on drag-reduced turbulent flow of inhomogeneous polymer solutions. Adv. Mech. Eng. 2015, 5, 432949. [Google Scholar] [CrossRef]
- White, C.; Mungal, M. Mechanics and prediction of turbulent drag reduction with polymer additives. Annu. Rev. Fluid Mech. 2008, 40, 235–256. [Google Scholar] [CrossRef]
- Tsurumi, D.; Tsukahara, T.; Kawaguchi, Y. Experimental analysis of turbulent structure of viscoelastic fluid flow in downstream of two-dimensional orifice. In Proceedings of the Seventh International Symposium on Turbulence Heat and Mass Transfer, Palermo, Italy, 24–27 September 2012. [Google Scholar]
- Peng, S. Numerical Study of Flows over Bluff Bodies in Viscoelastic Fluid; Huazhong University of Science and Technology: Wuhan, China, 2018. [Google Scholar]
- Zhang, H.; Li, F.; Cao, Y.; Kunugi, T.; Yu, B. Direct numerical simulation of elastic turbulence and its mixing-enhancement effect in a straight channel flow. Chin. Phys. B 2013, 22, 24703. [Google Scholar] [CrossRef]
- Li, D.; Zhang, H.; Cheng, J.; Li, X.; Li, F.; Qian, S. Numerical simulation of heat transfer enhancement by elastic turbulence in a curvy channel. Microfluid. Nanofluidics 2017, 21, 21–25. [Google Scholar] [CrossRef]
- Iwamoto, K.; Fukagata, K.; Kasagi, N.; Suzuki, Y. Friction drag reduction achievable by near-wall turbulence manipulation at high Reynolds numbers. Phys. Fluids 2005, 17, 73–76. [Google Scholar] [CrossRef]
- Fukagata, K.; Iwamoto, K.; Kasagi, N. Contribution of Reynolds stress distribution to the skin friction in wall-bounded flows. Phys. Fluids 2002, 14, 73–76. [Google Scholar] [CrossRef]
- Motozawa, M.; Ishitsuka, S.; Iwamoto, K.; Ando, H.; Senda, T.; Kawaguchi, Y. Experimental investigation on turbulent structure of drag reducing channel flow with blowing polymer solution from the wall. Flow Turbul. Combust. 2012, 88, 121–141. [Google Scholar] [CrossRef]
- Fu, Z.; Otsuki, T.; Motozawa, M.; Kurosawa, T.; Yu, B.; Kawaguchi, Y. Experimental investigation of polymer diffusion in the drag-reduced turbulent channel flow of inhomogeneous solution. Int. J. Heat Mass Transf. 2014, 77, 860–873. [Google Scholar] [CrossRef]
- Okamura, Y.; Sugioka, H.; Kawaguchi, Y. Enhancement of Turbulent Shear Stress and Mass Transfer in Wall Turbulence accompanied with wall blowing. In Proceedings of the ASME 2016 Fluids Engineering Division Summer Meeting collocated with the ASME 2016 Heat Transfer Summer Conference and the ASME 2016 14th International Conference on Nanochannels, Microchannels, and Minichannels, Washington DC, USA, 10–14 July 2016. [Google Scholar]
- Okamura, Y.; Kurose, T.; Kawaguchi, Y. Modification of near-wall turbulent structure in channel flow by dosing a small amount of polymer solution. In Proceedings of the ASME Fluids Engineering Division Summer Meeting, Hawaii, HI, USA, 30 July–3 August 2017. [Google Scholar]
- Sugioka, H.; Fu, Z.; Tsukahara, T.; Kawaguchi, Y. PIV-PLIF Experiment on modification of turbulent scalar diffusion near the wall by uniform blowing. In Proceedings of the ASME Joint Fluids Engineering Conference, Seoul, Korea, 26–31 July 2015. [Google Scholar]
- Yu, B.; Li, F.; Kawaguchi, Y. DNS of drag-reducing turbulent channel flow with coexisting Newtonian and non-Newtonian fluid. Fluids Eng. 2005, 127, 929–935. [Google Scholar] [CrossRef]
- Fu, Z.; Iwaki, Y.; Motozawa, M.; Tsukahara, T.; Kawaguchi, Y. Characteristic turbulent structure of a modified drag-reduced surfactant solution flow via dosing water from channel wall. Int. J. Heat Fluid Flow 2015, 53, 135–145. [Google Scholar] [CrossRef]
- Suga, K.; Matsumura, Y.; Ashitaka, Y.; Tominaga, S.; Kaneda, M. Effects of wall permeability on turbulence. Int. J. Heat Fluid Flow 2010, 31, 974–984. [Google Scholar] [CrossRef]
- White, C.; Dubief, Y.; Klewicki, J. Re-examing the logarithmic dependence of the mean velocity distribution in polymer drag reduced wall-bounded flow. Phys. Fluids 2012, 24, 021701. [Google Scholar] [CrossRef]
- Jovanovic, J.; Frohnapfel, B.; Durst, F.; Koskinen, J.; Koskinen, K. On the mechanism responsible for turbulent drag reduction by dilute addition of high polymers: Theory, experiments, simulations, and predictions. Fluids Eng. 2006, 128, 118–130. [Google Scholar] [CrossRef]
- Iwaki, Y.; Motozawa, M.; Tsukahara, T.; Kawaguchi, Y. Enhanced drag reduction in surfactant flow by dosing water from the wall: Investigation of turbulent statistics by PIV and PLIF. In Proceedings of the 8th World Conference on Experimental Heat Transfer, Fluid Mechanics, and Thermodynamics, Lisbon, Portugal, 16–20 June 2013. [Google Scholar]
- Xi, L. Turbulent drag reduction by polymer additives: Fundamentals and recent advances. Phys. Fluids 2019, 31, 121302. [Google Scholar]

© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fu, Z.; Liang, X.; Zhang, K. Asymmetrical Velocity Distribution in the Drag-Reducing Channel Flow of Surfactant Solution Caused by an Injected Ultrathin Water Layer. Symmetry 2020, 12, 846. https://doi.org/10.3390/sym12050846
Fu Z, Liang X, Zhang K. Asymmetrical Velocity Distribution in the Drag-Reducing Channel Flow of Surfactant Solution Caused by an Injected Ultrathin Water Layer. Symmetry. 2020; 12(5):846. https://doi.org/10.3390/sym12050846
Chicago/Turabian StyleFu, Zaiguo, Xiaotian Liang, and Kang Zhang. 2020. "Asymmetrical Velocity Distribution in the Drag-Reducing Channel Flow of Surfactant Solution Caused by an Injected Ultrathin Water Layer" Symmetry 12, no. 5: 846. https://doi.org/10.3390/sym12050846
APA StyleFu, Z., Liang, X., & Zhang, K. (2020). Asymmetrical Velocity Distribution in the Drag-Reducing Channel Flow of Surfactant Solution Caused by an Injected Ultrathin Water Layer. Symmetry, 12(5), 846. https://doi.org/10.3390/sym12050846



