Swarm Intelligence Algorithms for Weapon-Target Assignment in a Multilayer Defense Scenario: A Comparative Study

Abstract

Weapon-target assignment (WTA) is a kind of NP-complete problem in military operations research. To solve the multilayer defense WTA problems when the information about enemy’s attacking plan is symmetric to the defender, we propose four heuristic algorithms based on swarm intelligence with customizations and improvements, including ant colony optimization (ACO), binary particle swarm optimization (BPSO), integer particle swarm optimization (IPSO) and sine cosine algorithm (SCA). Our objective is to assess and compare the performance of different algorithms to determine the best algorithm for practical large-scale WTA problems. The effectiveness and performance of various algorithms are evaluated and compared by means of a benchmark problem with a small scale, the theoretical optimal solution of which is known. The four algorithms can obtain satisfactory solutions to the benchmark problem with high quality and high robustness, while IPSO is superior to BPSO, ACO and SCA with respect to the solution quality, algorithmic robustness and computational efficiency. Then, IPSO is applied to a large-scale WTA problem, and its effectiveness and performance are further assessed. We demonstrate that IPSO is capable of solving large-scale WTA problems with high efficiency, high quality and high robustness, thus meeting the critical requirements of real-time decision-making in modern warfare.

1. Introduction

Dynamic command, control and battle management functions require fast and effective decision aids to provide the optimal allocation of resources for effective engagement and real-time battle damage assessment. Allocating weapons appropriately to targets is considered an important planning task. The weapon-target assignment (WTA) is a fundamental issue in the realm of military operations research, which concerns how to allocate weapons properly to targets to ensure maximum value of survival assets. Studies on WTA began in the 1950s, when the WTA modeling issues were originally confronted [1,2]. In those days, due to limited computing power, scholars were forced to make a set of simplification assumptions in modeling and could only tackle some small-scale WTA problems by using classic discrete optimization methods, such as the dynamic programming or branch and bound method. In the past 30 years, many scholars and practitioners have continuously extended and improved WTA models and solving algorithms, including extending from single-layer to multilayer defense scenarios; from static allocation to dynamic allocation situations; from considering only the availability of weapons to considering more constraints, including manpower, budget and space availability; and from developing exact algorithms for small-scale WTA problems to developing heuristic algorithms for large-scale WTA problems.

WTA is a combinatorial optimization problem with constraints. The WTA problem for multi-type weapons is proved to be NP-complete [3]. An exact algorithm based on mathematical programming usually leads to an exponential increase in computational requirements, regardless of the size of the problem. Therefore, exact algorithms focus only on static WTA problems, with some constraints, such as that all weapons are of the same type or that the target can only be attacked by one type of weapon [4,5]. Recent research has focused on the dynamic situation [6], and some up-to-date researches put forward some new WTA schemes which can be solved by modern heuristic algorithms [7,8,9]. It is of great significance to effectively solve the WTA problem in military operations research. The reason is that the problem must be solved in real time in a fighting situation. The huge combinatorial complexity of the problem means that even with supercomputers now available, exact optimal solutions cannot be obtained in real time. So, researchers have focused on developing modern heuristic algorithms such as the genetic algorithm (GA), simulated annealing algorithm (SA), ant colony optimization (ACO), particle swarm optimization (PSO) and sine cosine algorithm (SCA), as well as some variant algorithms [10]. These heuristic algorithms have been developed and are widely used as search algorithms in a variety of applications. In addition, some researchers have tried to adopt a distributed framework to improve the computational efficiency [11].

This paper deliberates the multi-constraint WTA problem in the context of multilayer defense [12,13]. The multilayer, multi-constraint WTA problem has been approached using heuristic algorithms, with the dual intentions of developing a method for real-time situations and of providing an optimal defense plan for the higher-level problem of capability planning. To solve the multilayer, multi-constraint WTA problem, some heuristic algorithms such as GA [14], SA [15], and the hybrid algorithm of GA and SA were adopted as solving tools [16]. The algorithms adopted by these researchers belong to the category of early-developed heuristic algorithms before the 1990s.

Subsequently, a new optimization technique using an analogy of the swarm behavior of natural creatures began in the early 1990s. ACO was developed based mainly on social insects, especially the ant metaphor [17,18], in which each individual implicitly exchanges information through pheromones. PSO was developed based on the analogy of swarms of birds and schools of fish [19], in which each individual exchanges previous experiences. These two types of heuristic algorithms are called swarm intelligence algorithms [20,21,22]. Swarm intelligence algorithms have also been widely developed and applied recently. ACO was utilized to reconfigure a given shipboard power system (SPS) network [23]. A formulated mathematical model was solved by using PSO to determine the optimal operation sequence [24]. An example-based learning PSO (ELPSO) was proposed to overcome the shortcomings of a canonical PSO [25], which was proven by mathematical and numerical results. In recent years, some researchers have adopted swarm intelligence algorithms to solve the WTA-related problems. For example, ACO was used to solve the WTA problem [26], and a combination of GA and ACO was developed to solve a resource allocation problem [27]. PSO was adopted PSO to solve the WTA problem in the context of multilayer defense [28]. The biologically inspired architectures such as GA, a reinforcement algorithm and PSO were proposed and implemented to solve the WTA problem in a multilayer defense scenario [29], where the mathematical model concerns the battle management/command, control and communication (BM/C³) problem. The proposed schemes were implemented in MATLAB, and PSO was shown to converge rapidly and result in saving more assets with a faster convergence for learning. A novel GA was proposed to solve the sensor-weapon-target assignment problem [30]. Some up-to-date swarm intelligence algorithms have also been developed to solve complex problems, including SCA and the modified backtracking search algorithm (MBSA) [31,32]. Moreover, some swarm intelligence algorithms have been applied in the financial market and image segmentation [33,34].

In this paper, we adopt three kinds of heuristic algorithms inspired by swarm intelligence, including PSO, ACO and SCA, to solve the multi-constraint WTA problem in the context of multilayer defense, wherein we develop two discrete versions of PSO, i.e., integer PSO (IPSO) and binary PSO (BPSO). Taking a small-scale WTA problem as the benchmark, the effectiveness of different algorithms is evaluated and the performance is compared. Furthermore, we apply the IPSO algorithm to solve a large-scale WTA along with further assessment of its performance. Our objective is to compare the performance of different swarm intelligence algorithms when solving multilayer defense WTA problems and to identify the most promising algorithm that is applicable to practical large-scale WTA problems in a time-sensitive battlefield environment.

Our contributions to the research on WTA problems are summarized as follows. First, in the existing literature, although there are many theoretical researches on WTA problems, there are few discussions on how to solve large-scale WTA problems efficiently. Our research promotes the study of efficient algorithms for solving large-scale WTA problems at the application level, thus providing a powerful tool for real-time battlefield decision making. Second, in terms of the applicable solution method, to adapt to the characteristics of WTA problems in a multilayer defense scenario, we propose four swarm intelligence algorithms, ACO, BPSO, IPSO and SCA, and present improved algorithmic procedures and optimal parameter settings. Third, from multiple dimensions, we evaluate and compare the performance of different algorithms comprehensively and rigorously based on a benchmark WTA problem, thereby finding the most promising algorithm for practical large-scale WTA problems. We demonstrate that IPSO is capable of solving large-scale WTA problems with very high efficiency and high quality, thus meeting the critical requirements of real-time decision-making in modern warfare. Fourth, for an instance of a large-scale WTA in the context of multilayer defense, we present the best solution found by IPSO, which provides a foundation for researchers to evaluate and compare different algorithms.

The remainder of this paper is organized as follows: Section 2 describes a general model of the multilayer defense WTA problem and presents a small-scale benchmark problem and its optimal solution. In Section 3, the solving methods, especially the implementation schemes of ACO, BPSO, IPSO and SCA are illustrated in detail. In Section 4, we present the solving results of the four algorithms for the benchmark problem and evaluate and compare the performance of different algorithms. Then, in Section 5, we adopt IPSO to solve a large-scale WTA instance, present the solving results and further discussion on the performance of IPSO. Section 6 provides some concluding remarks.

2. Multilayer Defense WTA Model and Benchmark Problem

2.1. WTA Model under Multilayer Defense

Suppose that a defender builds a defense system with multiple layers that comprises D types of defensive weapons to safeguard S strategic assets. The enemy (attacker), who possesses A types of offensive weapons, will attack these assets. Typically, each layer of the defense system is equipped with only the same type of intercept weapon. For instance, ballistic missiles can be deployed in a space layer, surface-to-air missiles can be deployed in a high-altitude layer, and flak guns can be deployed in a low-altitude layer. In consideration of this military practice, we assume that the number of defense layers is equal to the number of defensive weapon types. Apparently, S strategic assets become the targets that the defense system intends to protect; on the other hand, offensive weapons are the targets that the defense system intends to intercept. Assume that the information about the attacking plan and the destruction probabilities of various attacking weapons is symmetric, that is, the information is known to the defender.

The WTA problem can be described as follows: to defend the target assets s (s = 1,2,…,S) to be the most powerful on the whole, how many weapons of type d (d = 1,2,…,D) should be allocated to intercept the offensive weapons of type a (a = 1,2,…,A)? The notations to be used are as follows:

Decision variable x_dsa: the number of weapons of type d deployed to intercept the offensive weapons of type a to protect asset s (i.e., the defense plan).

The number of decision variables x_dsa is equal to D × S × A.

Table 1. Notation definitions.

νs: Value of asset s	Gs: Ground area available at asset s
kdsa: Probability of successful interception by one defending weapon of type d deployed to defend an asset s against an attacking weapon of type a (effectiveness)	cd: Cost of operating one defending weapon of type d
nsa: Number of attacking weapons of type a aimed at asset s (attack plan)	Cmax: Maximum operating cost of weapons deployed
gsa: Probability that a single offensive weapon of type a can penetrate the defense system and destroy asset s (probability of damage)	md: Manpower required for operating each defensive weapon of type d
Bd: Number of defending weapons of type d	Md: Maximum available manpower to operate defending weapons of type d
td: Ground area occupied by deploying each defensive weapon of type d

lists the other notations used in the model.

The following expressions constitute a general WTA model under multilayer defense, which can be simplified or extended to model various WTA problems.

While maximizing objective function:

$$\max f(X)={\displaystyle \sum _{s=1}^S{v}_s}{\displaystyle \prod _{a=1}^A{\left\{1-\left[{\displaystyle \prod _{d=1}^D{(1-k_{dsa})}^{x_{dsa/n_{sa}}}}\right]g_{sa}\right\}}^{n_{sa}}}$$

(1)

satisfying constraints:

$${\displaystyle \sum _{s=1}^S{\displaystyle \sum _{a=1}^A{x}_{dsa}}}\le B_d,d=1,2,\cdots ,D.$$

(2)

$${\displaystyle \sum _{d=1}^D{\displaystyle \sum _{a=1}^A{t}_d{x}_{dsa}}}\le G_s,s=1,2,\cdots ,S$$

(3)

$${\displaystyle \sum _{d=1}^D{\displaystyle \sum _{s=1}^S{\displaystyle \sum _{a=1}^A{c}_d{x}_{dsa}}}}\le C_{\max }$$

(4)

$${\displaystyle \sum _{s=1}^S{\displaystyle \sum _{a=1}^A{m}_d{x}_{dsa}}}\le M_d,d=1,2,\cdots ,D.$$

(5)

The objective represented by Equation (1) is to make the expected survival value of all protected assets as large as possible. Constraint (2) mandates that the total number of defensive weapons of type d deployed cannot exceed the number available. Constraint (3) states that the ground area occupied by deploying defensive weapons at asset s must be no more than the space available at asset s. Constraint (4) states that the total cost for procuring, deploying and operating defensive weapons cannot exceed the available budget. Constraint (5) states that the manpower required for defensive weapons of type d cannot exceed the available manpower. The above WTA model is essentially an integer programming problem featured with high dimension and nonlinearity. In theory, it is impossible for a large-scale problem of this kind to find its optimal solution in a reasonable time by using an exact algorithm based on the traditional mathematical programming theory.

2.2. Benchmark Problem and Optimal Solution

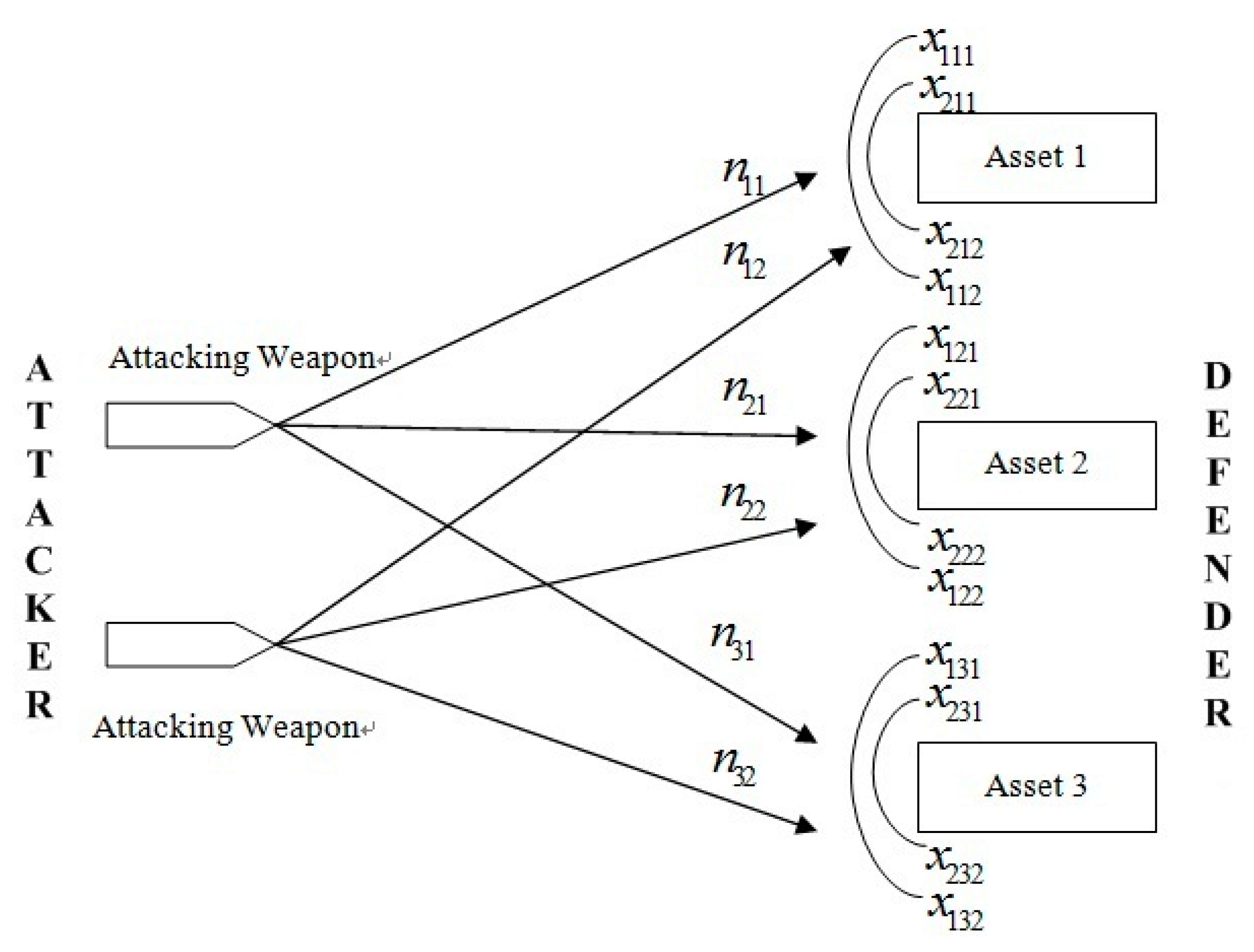
An instantiated WTA problem with a small scale of 2 × 3 × 2 is presented in [35], where two types of defensive weapons are deployed against two types of offensive weapons to protect three assets, i.e., D = 2, S = 3 and A = 2. Figure 1 depicts this defense scenario. We present a slightly different instance by modifying some data in this problem, the theoretical optimal solution of which can be found and is used as the baseline to assess and compare the performance of different algorithms. We call this modified instance a “benchmark problem” with the following parameter settings.

The number of available defensive weapons; B₁ = 100 and B₂ = 50.

The number of offensive weapons of type 1 and 2 is 50 and 29, respectively.

The value of three assets; ν₁ = 400, ν₂ = 300 and ν₃ = 200.

The attacking plan is known as n₁₁ = 5, n₁₂ = 9, n₂₁ = 25, n₂₂ = 7, n₃₁ = 20 and n₃₂ = 13.

The areas available at three assets; G₁ = 2250, G₂= 1500 and G₃ = 1950.

The area required by deploying defending weapons; t₁ = 34 and t₁ = 51.

The cost of defensive weapons; C₁ = 20 and C₁ = 30, while the total budget C_max = 3800.

The available manpower for operating defensive weapons of type 1 and 2; M_max1 = 350 and M_max2 = 320, respectively, while the manpower required for operating each defending weapon of type 1 and 2 is M₁ = 5 and M₂ = 4, respectively.

The interception probabilities of the defensive weapons and the damage probabilities of offensive weapons with respect to different weapon-asset combinations can be found in [35].

Since the benchmark problem contains only 12 decision variables, its theoretical optimal solution is easy to obtain by using optimization software LINGO 11.0. The maximum objective function to the benchmark problem f* = 537.516, or represented as a normalized value, $f^{*}=\frac{537.516}{{{\displaystyle \sum }}_{s=1}^3{\nu }_s}=0.59724$. The optimal solution is:

$$x_{111}=0,x_{112}=43,x_{121}=0,x_{122}=0,x_{131}=27,x_{132}=0$$

$$x_{211}=6,x_{212}=0,x_{221}=29,x_{222}=0,x_{231}=0,x_{232}=15$$

The optimal number of defending weapons of type 1 to be deployed is 70, and that of type 2 is 50. Of course, all of the constraints are met, in which only both constraints on the available weapons of type 2 and the available manpower for weapons of type 1 are tight. Note that the available weapons of type 1 are not exhausted, which arises due to the bottleneck resulting from insufficient manpower operating this type of weapons. This insufficiency can guide how to improve the defense system. For example, the expected survival value of assets can be increased by reducing weapons of type 1, thereby increasing weapons of type 2 with the saved resource, or by increasing the number of professionals operating weapons of type 1.

3. Solving Methods

In this section, we describe the four modern heuristic optimization methods based on swarm intelligence that we use to solve the WTA problem with focus on their implementation schemes. The first ACO algorithm was proposed in 1992 [17]. ACO is a meta-heuristic approach for combinatorial optimization problems that belongs to biologically inspired heuristic algorithms, which were developed mainly based on the observations of the foraging behavior of real ants. In ACO algorithms, a set of artificial ants cooperate to find the solution to a combinatorial optimization problem by exchanging information via pheromone trails deposited on artificial paths. ACO algorithms are composed of three major phases, namely, the initialization phase, the solution construction phase, and the pheromone updating phase; there are other optional phases, such as a phase that locally updates the pheromone trails [36].

Generally, ACO is suitable for discrete optimization problems because it can easily deal with constraints [37]. We refer to Max-Min Ant System (MMAS) to develop an ACO algorithm to solve the WTA problem, the implementation scheme of which will be described in Section 3.1. To adapt to the characteristics of the WTA problem and improve the algorithm performance, an elitist strategy and a specifically designed pheromone trail updating rule are embedded into the algorithm.

PSO was developed in 1995 based on bird swarming and fish schooling [19], for which each agent or particle exchanges previous experiences. In PSO, each particle exploits two types of information to modify its position and velocity: the current known global best position, gbest, which is found by the entire group, and the local best position, pbest, which a particle has reached so far. PSO is composed of three major steps [38]:

(1)

Generating the initial condition of each particle, including the initial position in solution space and the initial velocity;

(2)

Evaluating the searching point for each particle and updating the global best-so-far position gbest and the local best-so-far position pbest;

(3)

Modifying the position and velocity of each particle to obtain a new searching point.

Steps (2) and (3) are executed repeatedly until one of the exit conditions is met. PSO was originally aimed at addressing nonlinear optimization problems with continuous variables. However, many practical management and engineering problems are often formulated as combinatorial optimization problems. To enable PSO to tackle the combinatorial optimization problems, a discrete version of PSO (DPSO) has emerged [39]. One advantage of PSO is the efficient treatment of nonlinear optimization problems with only a small program. In general, PSO is highly suitable for continuous optimization problems, but it does not handle constraints well. We design two types of DPSO to solve the WTA problem, including BPSO and IPSO, which will be described in Section 3.2 and Section 3.3, respectively.

SCA is a newly developed optimization algorithm that is inspired by a trigonometric function. SCA has two phases: exploration and exploitation [40]. In the exploration phase, the algorithm combines the random solutions in the set of solutions with a high rate of randomness to find the promising regions in the search space. In the exploitation phase, however, there are gradual changes in the random solutions. We will describe the implementation scheme of SCA for the WTA problem in Section 3.4.

3.1. ACO Algorithm

3.1.1. Coding Scheme

We adopt an integer coding scheme when implementing ACO. A complete solution consists of D × S × A variables x_dsa, which is expressed by a row vector:

$$X=[x_{1,1,1},x_{1,1,2},\cdots ,x_{1,1,A},\cdots ,x_{d,s,a},\cdots ,x_{D,S,1},x_{D,S,2},\cdots ,x_{D,S,A}]$$

(6)

Each component of X can only take an integer value indicating the actual weapon number.

3.1.2. Definition of Search Space

The process of ant foraging is very similar to that of solving the traveling salesman problem (TSP); thus, the first ACO algorithm is successfully applied to solve TSP. To enable ACO to be applicable to non-TSP, the original problem must be converted to a TSP-like form. For the WTA problem, we divide the search space into L stages, as shown in Figure 2.

The number of stages is set to the number of variables, namely, L = D × S × A. Each variable is linked to a stage that is set in the order of the decision variables, i.e., the first stage is associated with decision variable x_1,1,1, stage 2 is associated with x_1,1,2, and the last stage L is associated with x_D,S,A. The ith stage has a total of U_i+1 nodes which are numbered from 0 to U_i. The number on a node represents the specific value being taken by the variable. U_i denotes the maximum possible of the variable at stage i. For the sake of simplicity, we set U_i to B_d, i.e., the number of available defensive weapons of type d. Alternatively, to narrow the search space of a large-scale WTA, while accounting for constraints (2)~(5), U_i is identified by:

$$U_i=(\mathrm{int})\min \left[B_d,\frac{G_s}{t_d}|{}_{s=1,2,\cdots ,S},\frac{C_{\max }}{c_d},\frac{M_d}{m_d}\right]$$

(7)

The symbol (int) represents the operation of taking an integer value. At each stage of the search space, an ant selects a node to step over. Then, all of the nodes that the ant has passed through from the first stage to the last stage are lined up sequentially to form a search path. Such a search path represents a solution to the problem. Compared with conventional ACO algorithm, the pheromone trails are deposited on nodes instead of paths. The more pheromone trails a node has, the more ants will select the node to pass through.

3.1.3. Transit Probability

At stage i and iteration t, the transit probability $p_{ij}^k\left(t\right)$ is defined as the probability of ant k selecting node j to step over:

$$p_{ij}^k(t)=\{\begin{array}{cc}\frac{{\tau }_{ij}(t-1)}{{\displaystyle \sum _{j\in allo{w}_i^k(t)}{\tau }_{ij}(t-1)}}& \mathrm{for}j\in allo{w}_i^k(t)\\ \hfill 0\hfill & \hfill \mathrm{otherwise}\end{array}\hspace{1em}i=1,2,\cdots ,L$$

(8)

where τ_ij(t−1) denotes node j’s pheromone trail at iteration t − 1, $allo{w}_i^t\left(t\right)$ is an allowable set of nodes for ant k, comprising those nodes of stage i that do not produce any constraint conflict if the decision variable of stage i takes the values on those nodes. Of course, $allo{w}_i^t\left(t\right)$ will depend on the particular values of the decision variables linked to the previous i − 1 stages. We define $allo{w}_i^t\left(t\right)$ through a feasibility check, which is conducted in the following way: Given the values for the variables at the previous i − 1 stages, the value of all variables after stage i is set to 0; only the variable x_d,s,a of stage i can change. Then, x_d,s,a is set to 0, 1, 2, …, in turn. For each value taken by x_d,s,a, check whether any constraint is violated. Once a value, say l, leads to some constraint unmet, then the feasibility check is terminated and set $allo{w}_i^t\left(t\right)=\left\{0,1,2,\dots ,l-1\right\}$. Obviously, the introduction of $allo{w}_i^t\left(t\right)$ makes the solutions constructed by ants always feasible. In this way, we have managed to manipulate the constraints and drastically reduce the search space.

3.1.4. Pheromone Trail Updating

After all ants complete one round of searching iteration, the pheromone trails on nodes are updated. We adopt an elitist strategy to update the pheromone trails, namely, only the pheromone trails of the nodes on the current globally optimal path (the path with the largest objective function) are strengthened, while the pheromone trails on other nodes are evaporated. When iteration t is completed, the pheromone trail on node j of stage i is updated to τ_ij(t).

$${\tau }_{ij}(t)=\{\begin{array}{cc}(1-\rho ){\tau }_{ij}(t-1)+{\tau }_0\frac{f_{best\_so\_far}}{f_{average}\left(t\right)}\hfill & \hfill ,\mathrm{node}j\mathrm{of}\mathrm{stage}i\mathrm{on}\mathrm{the}\mathrm{global}\mathrm{optimal}\mathrm{path}\\ (1-\rho ){\tau }_{ij}(t-1)\hfill & \hfill \mathrm{otherwise}\end{array}$$

(9)

where ρ denotes the evaporation coefficient of pheromone trail, τ₀ denotes the initial value of pheromone trail, f_{best_so_far} and f_average(t) represents the current maximum objective function and average objective function, respectively. To prevent prematurity, referring to the practice in MMAS, the pheromone trail is limited within a predefined interval [τ_min, τ_max].

3.2. BPSO Algorithm

WTA is an optimization problem with constraints. One weakness of PSO is the difficulty in addressing constraints; as a result, we exploit the widely used penalty function method to transform the constrained WTA problem into a non-constrained form. The penalty function is constructed as:

$$\begin{array}{ll}\phi (X)=& f(X)/{\displaystyle \sum _{s=1}^{S}v(s)}-\alpha \{{\displaystyle \sum _{d=1}^D\max \left[0,{\displaystyle \sum _{s=1}^S{\displaystyle \sum _{a=1}^A{x}_{dsa}}}/B_d-1\right]}+{\displaystyle \sum _{s=1}^S\max \left[0,{\displaystyle \sum _{d=1}^D{\displaystyle \sum _{a=1}^A{t}_d{x}_{dsa}}}/G_s-1\right]}\\ & \hspace{1em}+\max \left[0,{\displaystyle \sum _{d=1}^D{\displaystyle \sum _{s=1}^S{\displaystyle \sum _{a=1}^A{c}_d{x}_{dsa}}}}/C_{\max }-1\right]+{\displaystyle \sum _{d=1}^D\max \left[0,{\displaystyle \sum _{s=1}^S{\displaystyle \sum _{a=1}^A{m}_d{x}_{dsa}}}/M_d-1\right]}\}\end{array}$$

(10)

In Equation (10), α is a penalty factor. To eliminate the effect of inconsistent dimensions, all items at the RHS of Equation (10) are normalized. The subsequent algorithm design for BPSO and IPSO is based on this non-constrained form.

3.2.1. Coding Scheme

In BPSO, D × S × A decision variables x_dsa are also arranged in a row vector X that is expressed by (6). Then, each component of X is decoded into a binary substring. In this way, one solution to the problem, which can be thought of as one particle, is represented by one binary string, which consists of D × S × A binary substrings. The length of the total binary string is jointly determined by the length of the integer interval associated with each decision variable and the number of decision variables.

Suppose that the maximum value possible for decision variable x_dsa is U_d,s,a. U_d,s,a can be determined by an approach similar to that used in ACO described by Equation (7). Then, the integer interval within which x_dsa can take the value of [0, U_d,s,a]. The encoding length of x_dsa is set to l_d,s,a = [log₂U_d,s,a] + 1 (the expression [log₂U_d,s,a] means the maximum integer that does not exceed log₂U_d,s,a). For example, if U_d,s,a = 50, then l_d,s,a = 6. Therefore, the length (or the number of bits) of a binary string representing one solution (particle) is ${\displaystyle \sum }_d{\displaystyle \sum }_s{\displaystyle \sum }_a{l}_{d,s,a}$.

3.2.2. Initialization of Particle Population

The initial positions of the particle population are generated randomly, while the initial velocity vectors are simply set to 0. In general, a particle’s position is initialized by setting each bit in the binary string to 0 or 1 with an equal probability of 0.5. However, for a constrained optimization problem, unfortunately, this initialization approach will produce a large number of infeasible solutions. Because the subsequent position of a particle changes constantly in the iteration process, even if the initial position of a particle (or more precisely, the initial solution) is feasible, the feasibility of subsequent positions cannot be guaranteed. For this reason, it is not necessary to emphasize that the initial particle population should be feasible. On the other hand, of course, if the initial particle population can attempt to meet the feasibility requirement, then this arrangement can undoubtedly facilitate the solution quality and the algorithm convergence resulting from a better iteration starting point. Based on this understanding, we exert an additional control on the random initialization process of the particle population, which is illustrated as follows.

Because weapon availability is often considered to be a primary constraint in real life, particle initialization should account for weapon availability meeting the constraint as much as possible, if not completely. The encoding length of x_dsa in a binary system is l_d.s.a. Let each bit of x_dsa’s binary string take 1 with a probability of p_d rather than the usual 0.5 and take 0 with a probability of (1 − p_d). It is not difficult to deduce that the expected value of x_dsa is $p_d=\left(2^{l_{d,s,a}}-1\right)$. For a given weapon type d, the weapon availability constraint is ${\displaystyle \sum }_s{\displaystyle \sum }_a{x}_{dsa}\le B_d$. Replacing x_dsa in this constraint by its expected value, we have ${\displaystyle \sum }_s{\displaystyle \sum }_a{p}_d\left(2^{l_{d,s,a}}-1\right)\le B_d$. This means $p_d\le \frac{B_d}{{\displaystyle \sum _s{\displaystyle \sum _a(2^{l_{d,s,a}}-1)}}}$.

For the sake of simplifying the calculations, we set:

$$p_d=\frac{B_d}{{\displaystyle \sum _s{\displaystyle \sum _a{2}^{l_{d,s,a}}}}},d=1,2,\cdots ,D$$

(11)

By exerting such a control on the particle population initialization, it can be expected that nearly half of the population would meet the weapon availability constraint. This outcome not only maintains the diversification of the initial population but also provides a better iteration starting point.

3.2.3. Fitness Measure

The particle’s fitness is measured solely by the penalty function itself (ϕ(X)). For a feasible particle, its fitness function is identical to the normalized objective function defined by the first term at the RHS of Equation (10).

3.2.4. Particle Velocity and Position Updating

The formula for particle velocity updating is:

$$V_{ij}^{k+1}=w{V}_{ij}^k+c_1{r}_1(pbes{t}_{ij}-X_{ij}^k)+c_2{r}_2(gbes{t}_j-X_{ij}^k)$$

(12)

where $V_{ij}^k$ and $V_{ij}^{k+1}$ denote the jth component of particle i’s velocity vector at iteration k and at iteration k+1, respectively; $X_{ij}^k$ denotes the j-th component of particle i’s position vector at iteration k; pbest_ij denotes the jth component of the best position that particle i has achieved so far; gbest_j denotes the j-th component of the global best position that the population has achieved so far; r₁ and r₂ are random numbers between 0 and 1 with uniform distribution; c₁ and c₂ are accelerating coefficients; and w is an inertial coefficient.

The formula for particle position updating is:

$$X_{ij}^{k+1}=\{\begin{array}{cc}1\hfill & \hfill \hspace{1em}\hspace{1em}\mathrm{if}{\rho }_{ij}<sig(V_{ij}^k)\\ 0\hfill & \hfill \hspace{1em}\hspace{1em}\mathrm{otherwise}\end{array}$$

(13)

where $X_{ij}^{k+1}$ denotes the j-th component of particle i’s position vector at iteration k+1. Here, ρ_ij is a random number between [0, 1] with a uniform distribution, and $sig\left(V_{ij}^k\right)=1/(1+\exp \left(-V_{ij}^k\right))$ is the sigmoid function. To avoid $sig\left(V_{ij}^k\right)$ approaching too closely to 0 or 1, we set $V_{ij}^k$ within the range of [−6, +6].

Specifically, to prevent premature convergence, we set a re-initialization probability c₀ (0 < c₀ < 1). For each particle, when updating its velocity and position, a re-initialization check is conducted. To do so, first, a random number r between [0, 1] with uniform distribution is generated. Then, r and c₀ are compared. If r > c₀, then formula Equations (12) and (13) are used to update the particle’s velocity and position; otherwise, its position is reinitialized using the method described above, and the velocity is reset to 0.

3.3. IPSO Algorithm

In IPSO, the decision variables are represented as their actual values. However, based on the velocity and position updating rules used in the basic PSO for continuous optimization problems, we make slight modifications to accommodate the integer programming situation.

3.3.1. Coding Scheme

The decision vector X is expressed by Equation (6). Each component x_dsa takes its actual integer value within the interval [0,U_d,s,a]. One vector is a particle representing one solution to the problem. Obviously, the encoding length of one complete solution is the same as the number of components in X.

3.3.2. Initialization of Particle Population

The initial positions of the particle population are generated randomly, and the initial velocity vectors are simply set to 0. Similar to BPSO, if a particle is initialized by randomly generating an integer in the range of [0,U_d,s,a] with uniform distribution for component x_dsa, a large number of infeasible solutions will be produced. Hence, it is necessary to exert additional control on the particle population initialization. Most likely, the simplest control method is to compress the initial position vector. Note that the expected value of x_dsa randomly generated within the interval [0,U_d,s,a] is U_d,s,a/2. For a given weapon type d, assume the compression factor for component x_dsa is η_d. Once a specific value for x_dsa is produced, then compress it to η_dx_dsa. The expected value for this compressed variable is reduced to η_dU_d,s,a/2 with the same proportion. Next, replace x_dsa in the weapon availability constraint (Equation (2)) by this compressed expected value, and we have ${\displaystyle \sum }_s{\displaystyle \sum }_a{\eta }_d{U}_{d,s,a}/2\le B_d$. Hence, ${\eta }_d\le \frac{2B_d}{{{\displaystyle \sum }}_s{{\displaystyle \sum }}_a{U}_{d,s,a}}$. For the sake of simplifying the calculations, we set:

$${\eta }_d=\frac{2B_d}{{\displaystyle \sum _s{\displaystyle \sum _a{U}_{d,s,a}}}},d=1,2,\cdots ,D.$$

(14)

Once a value is assigned to x_dsa, we multiply x_dsa by the associated compression factor η_d. Then, the product η_dX_dsa is rounded off and is used as a substitute for x_dsa. Nearly half of the population will meet the weapon availability constraint. In this way, a balance can be obtained between the diversification of the initial population and a better iteration starting point.

3.3.3. Fitness Measure

In IPSO, a particle’s fitness is measured by the penalty function ϕ(X) (Equation (10)), which is the same as that used in BPSO.

3.3.4. Particle Velocity and Position Updating

The formula for particle velocity updating is

$$V_{ij}^{k+1}=(roundoff)[w{V}_{ij}^k+c_1{r}_1(pbes{t}_{ij}-X_{ij}^k)+c_2{r}_2(gbes{t}_j-X_{ij}^k)]$$

(15)

where $V_{ij}^k$ and $V_{ij}^{k+1}$ denote the j-th component of particle i’s velocity vector at iteration k and at iteration k+1, respectively; $X_{ij}^k$ denotes the j-th component of particle i’s position vector at iteration k; pbest_ij denotes the j-th component of the best position that particle i has achieved so far; gbest_j denotes the j-th component of the global best position that the population has achieved so far; r₁ and r₂ are random numbers between 0 and 1 with uniform distribution; c₁ and c₂ are accelerating coefficients; and $w$ is an inertial coefficient. The symbol (roundoff) denotes taking an integer number that is the closest to a given real number.

The formula for particle position updating is:

$$X_{ij}^{k+1}=X_{ij}^k+V_{ij}^{k+1}$$

(16)

where $X_{ij}^{k+1}$ and $X_{ij}^k$ denote the j-th component of particle i’s position vector at iteration k+1 and at iteration k, respectively. To deal with the case where a particle oversteps the boundary, we set the following rule:

(a)

If $X_{ij}^k<0$, then set $X_{ij}^k=0$ and $V_{ij}^k=0$;

(b)

If $X_{ij}^k>U_j$, then set $X_{ij}^k=U_j$ and $V_{ij}^k=0$.

where U_j represents the maximum possible for the decision variable associated with the j-th component of the position vector.

Again, to prevent prematurity, a re-initialization factor c₀ (0 < c₀ < 1) is set. When updating a particle, a random number r between [0, 1] with uniform distribution is generated. If r ≤ c₀, then the particle position to be updated is reinitialized, and the velocity is reset to 0; otherwise, formula Equations (15) and (16) are used to update the velocity and position.

3.4. SCA Algorithm

The implementation scheme and procedure of SCA are similar to IPSO. The difference is that the updating of decision variable x_dsa in SCA does not address velocity updating. The updating rule in SCA is:

$$X_i^{t+1}=\{{}_{X_i^t+r_1\times \cos (r_2)\times \left|r_3{P}_i^t-X_i^t\right|,\hspace{1em}\hspace{1em}{r}_4\ge 0.5}^{X_i^t+r_1\times \sin (r_2)\times \left|r_3{P}_i^t-X_i^t\right|,\hspace{1em}\hspace{1em}{r}_4<0.5}$$

(17)

where $X_i^t$ is the position of the current solution in the i-th dimension at iteration t, r₁, r₂, r₃ and r₄ are random numbers, and $P_i^t$ is the position of the destination point in the i-th dimension at iteration t. $X_i^{t+1}$ is updated by Equation (17). r₁ is calculated by:

$$r_1=a-t\frac{a}{T}$$

(18)

where t is the number of the current iteration, T is the total number of preset iterations, and a is a constant. We set a = 5. Specifically, we improve the original SCA algorithm to fit the WTA model. First, to reduce the randomness of decision variables, we change r₃ from a random value to a fixed value of 0.9. Second, the original SCA only exploits the current optimal solution, while we change $X_i^t$ in the second formula of Equation (17) to the global optimal position of particles in the i-th dimension.

4. Performance Evaluation Based on a Benchmark Problem

4.1. Solving Results

The ACO, BPSO, IPSO and SCA algorithms described above are implemented to solve the benchmark problem. Generally, the recommended schemes in the literature can be used to set the parameters of various heuristic algorithms. Better yet, in order to optimize the performance of the algorithm for a specific problem, one can choose a set of optimal parameter settings by experimental comparison. Through many trials and errors on the settings for various parameters, including varying population size, pheromone trail and evaporation coefficient, inertial and accelerating coefficients, stopping criterion, etc., we filter out the ideal parameter settings in these four algorithms.

The major parameter settings of ACO: size of ant colony m = 40; initial pheromone trail τ₀ = 1; evaporation coefficient of pheromone trail ρ = 0.01; maximum pheromone trail τ_max = 10τ₀ = 1; minimum pheromone trail τ_min = 0.1τ₀; maximum iteration number iter_max = 1000 (stopping criterion).

For the benchmark problem, there are a total of 12 decision variables, so the search space in ACO comprises 12 stages. The objective function is normalized by dividing the sum of the three assets’ values.

The main parameters in BPSO, IPSO and SCA are set as follows: size of particle population m = 40; inertial coefficient w = 1; accelerating coefficients c₁ = c₂ = 2; re-initialization probability c₀ = 0.1; penalty factor α = 100; maximum iteration number iter_max = 1000 (stopping criterion).

These algorithms are implemented using VC++6.0 programming on a computer with an Intel Core i7 2.4 GHz processor and 16 GB RAM.

Table 2. Result summary of the four algorithms.

	ACO		BPSO		IPSO		SCA
	Objective Function	Relative Deviation	Objective Function	Relative Deviation	Objective Function	Relative Deviation	Objective Function	Relative Deviation
1	0.59392	−0.556%	0.58407	−2.205%	0.59713	−0.018%	0.57176	−4.27%
2	0.59159	−0.946%	0.57480	−3.757%	0.58147	−2.640%	0.59194	−0.89%
3	0.59617	−0.179%	0.58557	−1.954%	0.59651	−0.122%	0.56355	−5.64%
4	0.59248	−0.797%	0.58064	−2.779%	0.59722	−0.003%	0.55336	−7.35%
5	0.59009	−1.197%	0.58761	−1.612%	0.58891	−1.395%	0.55544	−7.00%
6	0.59325	−0.668%	0.58910	−1.363%	0.57674	−3.432%	0.56413	−5.54%
7	0.59135	−0.986%	0.58917	−1.351%	0.59724	0	0.55186	−7.60%
8	0.59561	−0.273%	0.56630	−5.180%	0.59724	0	0.57834	−3.16%
9	0.59497	−0.380%	0.57925	−3.012%	0.59688	−0.060%	0.56639	−5.17%
10	0.59547	−0.296%	0.57915	−3.029%	0.57189	−4.245%	0.56320	−5.70%
Best	0.59617	−0.179%	0.58917	−1.351%	0.59724	0	0.59194	−0.89%
Worst	0.59009	−1.197%	0.56630	−5.180%	0.57189	−4.245%	0.55186	−7.60%
Average	0.59349	−0.628%	0.58157	−2.624%	0.59012	−1.192%	0.56600	−5.23%
standard deviation	0.00208		0.00718		0.00986		0.01223
coefficient of variation	0.350%		1.235%		1.671%		2.16%
average CPU time	1362 ms		456 ms		95 ms		120 ms

Note: CPU means the Central Processing Unit.

summarizes the results of 10 random runs.

Also, the relative deviations of the objective function from the theoretical optimum (0.59724) and the associated variation coefficients are presented in Table 2.

The variation coefficient, CV, indicates the robustness of an algorithm:

$$CV=\frac{\sigma }{\mu }$$

(19)

μ is the average objective function over 10 runs, and σ is the standard deviation. A smaller variation coefficient implies the algorithm has a higher robustness.

Table 3. Solution associated with the best objective function.

	Solution
ACO (0.59617)	$x_{111}$ = 0, $x_{112}$ = 43, $x_{121}$ = 2, $x_{122}$ = 0, $x_{131}$ = 25, $x_{132}$ = 0 $x_{211}$ = 6, $x_{212}$ = 0, $x_{221}$ = 28, $x_{222}$ = 0, $x_{231}$ = 0, $x_{232}$ = 16
BPSO (0.58917)	$x_{111}$ = 0, $x_{112}$ = 53, $x_{121}$ = 2, $x_{122}$ = 0, $x_{131}$ = 15, $x_{132}$ = 0 $x_{211}$ = 4, $x_{212}$ = 0, $x_{221}$ = 26, $x_{222}$ = 2, $x_{231}$ = 8, $x_{232}$ = 10
IPSO (0.59724)	identical to the theoretical optimal solution
SCA (0.59194)	$x_{111}$ = 0, $x_{112}$ = 44, $x_{121}$ = 0, $x_{122}$ = 0, $x_{131}$ = 26, $x_{132}$ = 0 $x_{211}$ = 11, $x_{212}$ = 0, $x_{221}$ = 28, $x_{222}$ = 0, $x_{231}$ = 0, $x_{232}$ = 11

Note: The data in parentheses is the best objective function attainable by the corresponding algorithm.

lists the solutions to the benchmark problem corresponding to the best objective function obtained by different algorithms. The best objective function obtained by IPSO is 0.59724, which is exactly the same as the theoretical optimum. Accordingly, the best solution is the same as the theoretical optimal solution. The best value of the objective function from ACO is 0.59617 and the associated solution is near to the theoretical optimal solution. At this solution, the availability constraint on weapons of type 2 and the manpower constraint on weapons of type 1 are active, while other constraints are all inactive.

This shows the properties that are completely consistent with the theoretical optimal solution. The best objective function from BPSO is 0.58917. Note that strictly speaking, this is the value of the penalty function. Because all of the constraints are met, the penalty function is identical to the normalized objective function. At the solution corresponding to the best objective, except the availability constraint on weapons of type 2 and the manpower constraint on weapons of the type 1 are active, all other constraints are inactive, which is also completely consistent with the properties at the theoretical optimal solution. The best objective function obtained by SCA is 0.59194, which also exhibits similar characteristics to ACO and BPSO.

Figure 3 depicts the iteration processes of ACO, BPSO, IPSO and SCA with respect to the objective function. It can be seen that BPSO and SCA fall into a local optimum early, and from that point, the objective function has no obvious improvement. In contrast, ACO and IPSO can achieve continuous improvement in the objective function and can produce higher-quality solutions.

4.2. Discussion

4.2.1. Algorithm Effectiveness

As shown in Table 2, the relative deviations of the best objective functions by ACO, BPSO, IPSO and SCA are −0.179%, −1.351%, 0 and −0.89%, respectively; the relative deviations of the worst objective functions obtained by ACO, BPSO, IPSO and SCA are −1.197%, −5.180%, −4.245% and −7.60%, respectively, and the relative deviations of the average objective functions obtained by ACO, BPSO, IPSO and SCA are −0.628%, −2.624%, −1.192% and −5.23%, respectively. Among these figures, the largest one (in absolute value) is approximately 8%, which means that regardless of whether the best, average or worst objective function is used, the solving results by these algorithms are very close to the theoretical optimum. Considering such a small magnitude of relative deviations, we can conclude that all these algorithms are capable of finding satisfactory approximate solutions to the benchmark problem.

4.2.2. Comparison of Algorithms

The performance of the four algorithms in solving the benchmark problem is compared from three aspects, including quality of solution, robustness of algorithm and efficiency of computation.

(1) Quality of Solution

The solution quality is compared based on two indices, i.e., the best and average objective function over 10 random runs. As seen from Table 2, the best objective function from IPSO is the largest, followed by ACO, SCA, and BPSO. The average objective function, from large to small, comes from ACO, IPSO, BPSO and SCA. Considering these two indices comprehensively and observing that for IPSO, 2 out of 10 random runs obtain the theoretical optimal solution, we can conclude that the solution quality of IPSO is the highest, the next highest is ACO, and the last two are BPSO and SCA.

(2) Robustness of Algorithm

The robustness of an algorithm is indicated by the coefficient of variation. The coefficients of variation for ACO, BPSO, IPSO and SCA are 0.350%, 1.235%, 1.671% and 2.16%, respectively, all of which do not exceed 3%. This implies that all four algorithms have high robustness and have an unremarkable distinction in robustness. Even so, we can still rank order the robustness of the four algorithms according to the coefficient of variation. ACO has the highest robustness, followed by BPSO and IPSO, and the last is SCA.

(3) Efficiency of Computation

Usually, the computational efficiency of an algorithm is measured by the CPU time required. Note that the population sizes and maximum iteration times for the four algorithms are the same; it is thus convincing to compare their computational efficiencies according to the CPU time needed by them. The average CPU times per run for ACO, BPSO, IPSO and SCA are 1362 milliseconds, 456 milliseconds, 95 milliseconds and 120 milliseconds, respectively. This indicates that the computational efficiency of IPSO is the highest; the second is SCA, the third is BPSO, and the last is ACO. Notably, the computational efficiency of IPSO is significantly higher than that of ACO. Furthermore, as seen from Figure 3, IPSO can find a solution that is closest to the theoretical optimal solution more quickly than ACO, BPSO and SCA. This observation also implies that the computational efficiency of IPSO is higher than that of other algorithms.

It is worth mentioning that, in addition to the benchmark problem, we construct more than a dozen numerical examples of the WTA problem with various dimensions, such as 3 × 20 × 3 and 4 × 30 × 4. We also set different population sizes and maximum iteration times to examine the CPU time required by these four algorithms to solve these problems. It is found that when keeping the same population size and maximum iteration times, the CPU time needed by IPSO is only approximately proportional to the number of decision variables. For example, the CPU time needed for the 2 × 3 × 2 benchmark problem with 40 particles and 1000 iterations is 95 ms; then, the CPU time needed for the 3 × 20 × 3 problem, also with 40 particles and 1000 iterations, is approximately 1204 ms. Of course, if the population size increases to 80 or the iteration number increases to 2000, the CPU time will almost double to 2378 ms.

According to the three dimensions of performance evaluation discussed above, we conclude that the comprehensive performance of IPSO is the best among these four algorithms. Furthermore, from the viewpoint of computer programming, IPSO also has a significant advantage, because it has a relatively short amount of programming code and is easy to implement.

5. Solving a Large-Scale WTA Problem Using IPSO

In [11], an instantiated WTA problem with dimensions of 3 × 20 × 3 was constructed. Compared to the benchmark problem, this instance can be thought of as a large-scale WTA, described as follows.

The defender is to construct a defense system with three layers, i.e., D = 3. In the defense system, three types of weapons are deployed from the first to the third layer. There are 20 strategic assets to be guarded, namely, S = 20. The available weapons of types 1, 2 and 3 are B₁ = 560, B₂ = 300 and B₃ = 140. The manpower needed per defensive weapon of types 1, 2 and 3 are m₁ = 6, m₂ = 5 and m₃ = 4. The total available manpower for the three types of weapons is M₁ = 3500, M₂ = 1600 and M₃ = 500. The costs of operation and maintenance are c₁ = 20, c₂ = 30 and c₃ = 40. The available budget is C_max = 25,000. The ground area occupied by individual defensive weapons is t₁ = 32, t₂ = 48 and t₃ = 72. Other data, including the asset values, space available and intercept probabilities can be found in [35].

The attacker has three types of offensive weapons, i.e., A = 3. The available offensive weapons of types 1, 2 and 3, R₁ = 275, R₂ = 170 and R₃ = 95. The attacking plan and destruction probabilities of various offensive weapons can be found in [35]. Assume that the information about enemy’s attacking plan and destruction probabilities is symmetric to the defender.

5.1. Solving Results

IPSO is used to solve the above large-scale WTA containing 180 decision variables. The implementation scheme and parameter settings are the same as in Section 4.1, except the size of the particle population is m = 200. The algorithm is implemented using VC++6.0 programming on a computer with an Intel Core i7, 2.4 GHz and 16 GB RAM. Figure 4 summarizes the results of 10 random runs.

For the 10 random runs, the best objective function is 0.63048, the worst is 0.62133, and the average is 0.62572 with a standard deviation of 0.00268. The average CPU time is 5905 ms. The very small coefficient of variation (0.428%) implies that even for a large-scale WTA problem, IPSO can give robust results. At the same time, the CPU time of approximately 6 s is also acceptable. The CPU time consumed may be negligible if an advanced computer with a higher operation speed is utilized. This result again shows that IPSO has good prospects for solving applications, such as in practical large-scale WTA problems.

Table 4. Solution to the large-scale WTA.

Defending Weapon d	Asset s	$\mathbf{Variable}{\mathit{x}}_{\mathit{d}\mathit{s}\mathit{a}}$			Defending Weapon d	Asset s	$\mathbf{Variable}{\mathit{x}}_{\mathit{d}\mathit{s}\mathit{a}}$			Defending Weapon d	Asset s	$\mathbf{Variable}{\mathit{x}}_{\mathit{d}\mathit{s}\mathit{a}}$
		Attacking Weapon a					Attacking Weapon a					Attacking Weapon a
		1	2	3			1	2	3			1	2	3
1	1	2	16	6	2	1	13	8	13	3	1	5	3	3
1	2	21	17	11	2	2	13	1	4	3	2	1	0	3
1	3	10	2	8	2	3	6	5	7	3	3	4	2	5
1	4	6	17	19	2	4	0	16	9	3	4	1	0	1
1	5	2	5	8	2	5	3	11	3	3	5	2	3	4
1	6	20	6	17	2	6	0	9	0	3	6	0	4	2
1	7	12	8	1	2	7	7	6	5	3	7	2	6	0
1	8	12	4	5	2	8	9	7	0	3	8	2	2	2
1	9	12	7	10	2	9	7	5	1	3	9	0	6	2
1	10	5	5	12	2	10	9	6	15	3	10	3	3	1
1	11	9	9	9	2	11	7	3	6	3	11	2	0	2
1	12	11	4	11	2	12	0	1	3	3	12	5	0	1
1	13	9	18	18	2	13	10	15	0	3	13	0	1	1
1	14	17	0	6	2	14	8	0	7	3	14	6	3	0
1	15	11	12	6	2	15	0	0	4	3	15	2	4	2
1	16	0	9	17	2	16	9	4	0	3	16	0	3	0
1	17	17	21	3	2	17	1	1	0	3	17	0	1	5
1	18	0	0	4	2	18	0	6	0	3	18	1	0	1
1	19	7	10	8	2	19	7	1	4	3	19	3	3	1
1	20	0	12	5	2	20	1	4	0	3	20	1	0	5

shows the optimal solution associated with the maximum objective function of 0.63048. With respect to this solution, the actual operation and maintenance cost is 24,980.

Table 5. Weapon number deployed and manpower required.

$\mathbf{Defensive}\mathbf{Weapon}\mathit{d}$	Number Deployed	Manpower Required
1	549	3294
2	300	1500
3	125	500

lists the number of weapons deployed actually and the manpower required, and

Table 6. Ground area occupied.

Asset s	Space Occupied	Asset s	Space Occupied
1	3192	11	1920
2	2720	12	1456
3	2296	13	2784
4	2688	14	2104
5	1944	15	1696
6	2240	16	1672
7	2112	17	1840
8	1872	18	560
9	2128	19	1880
10	2648	20	1216

lists the space occupied actually. Table 5 and Table 6 show that the availability constraint on defensive weapons of type 2 and the manpower constraint on defensive weapons of type 3 are tight. On the other hand, although the budget constraint is loose, the budget will soon be exhausted. Other constraints, including all of the space constraints, are inactive.

The primary limitation on the survival value of assets lies in the available number of defensive weapons of type 2 and the available manpower for defensive weapons of type 3 as well as the available budget.

5.2. Discussion

To further assess the performance of IPSO on the large-scale WTA problem, we solve the relaxed version of the 3 × 20 × 3 WTA problem by using Lingo 11.0. In the relaxed problem, all decision variables are allowed to take continuous nonnegative values. Through 359 iterations, Lingo gives an optimal objective function of 0.68306 for the relaxed problem. Although 0.68306 is not the theoretical optimum of the original discrete problem, it can be thought of as an upper bound on the discrete problem. The objective functions from IPSO are very close to this upper bound. The best objective function for the discrete problem obtained by IPSO is 0.63048, and the average objective function is 0.62572. Compared to the upper bound, the deviation is only 7% and 9%, respectively. This fact again demonstrates that IPSO can provide a high-quality solution to a large-scale WTA problem.

This same large-scale instance is also solved by a distributed MMAS algorithm based on the distributed computing framework Spark [11], in which the size of ant colony m is set to 1000, much larger than the size in IPSO, and the maximum iteration is set to 2000. The best objective function by the distributed MMAS is 0.65540, being only 4% higher than that by IPSO, but the algorithm consumes much more time than IPSO. Compared with IPSO, the distributed MMAS consumes too much computing resources, but the solution quality is not significantly improved.

Our research shows that IPSO, as an efficient heuristic algorithm with short programming code, is very suitable for solving constrained integer programming problems like WTA. In addition to the logic of IPSO algorithm is simple and easy to understand, the implementation scheme designed by us has good universality and portability. This is mainly due to our handling of constraints. First, we embed constraints in the objective function in the form of the most common penalty terms. Second, by adding a set of feasibility detection operation based on the primary constraint of the problem, the invalid exploration effort of the algorithm in the infeasible space is greatly eliminated. Hence, we think although the solving results are partly dependent on specific WTA problem parameters, the performance of the IPSO algorithm proposed by us will not vary greatly with the WTA model.

Although we would not recommend using ACO to solve large-scale WTA problems because of its low computational efficiency, we are still interested in examining its performance. The same ACO algorithm as that described in Section 3.1 and Section 4.1 but with 200 ants is implemented on a computer with an Intel Core i7 processor (2.4 GHz) and 16 GB RAM. We find that the average objective function over 10 random runs by ACO is 0.62501, which is almost the same as the average objective function by IPSO. However, the average CPU time consumed by ACO is near 14 min, which is much longer than IPSO. This shows that for practical large-scale WTA problems, ACO will have an unsatisfactory computational efficiency.

6. Conclusions

As a classic problem in military operations research, the WTA problem has a concern of scholars ever since it was first proposed. The quick solution of WTA problems is very important for real-time battlefield decision-making. Developing effective heuristic algorithms to quickly solve NP-complete problems such as WTA is a feasible approach and a research hotspot at present. In this paper, considering the multi-constraint WTA problem in the context of multilayer defense, three types of heuristic algorithms inspired by swarm intelligence, ACO, PSO and SCA, are developed, where PSO has two discrete versions of BPSO and IPSO. The implementation schemes of the four algorithms customized for the multilayer defense WTA problem with multiple constraints are proposed.

By using a benchmark problem with small scale, the performance of different algorithms is evaluated and compared. Our study shows that all four of the algorithms are valid for the WTA problem and are capable of obtaining satisfactory solutions with high quality and high robustness. The comprehensive performance of IPSO is the best among these four algorithms with respect to the three dimensions of performance evaluation, including the solution quality, algorithm robustness and computational efficiency. In addition, IPSO has other significant advantages, namely that the computer programming code is very short and easy to implement on a computer. Hence, IPSO is adopted to solve a large-scale WTA instance along with further performance evaluation. Results show that IPSO can quickly find an approximate solution to the large-scale WTA instance, and the optimal objective function reached by IPSO is very close to the upper bound of the relaxed problem. We conclude that IPSO can find satisfactory solutions to large-scale WTA problems with high efficiency, high quality and high robustness, which is critical to real-time decision-making in modern warfare. We demonstrate that IPSO has good prospects for solving such applications as large-scale WTA problems. Future research will further improve IPSO to solve larger-scale WTA problems more effectively. Furthermore, we will extend our work from static WTA problems to dynamic situations.