Trees with Minimum Weighted Szeged Index Are of a Large Diameter

Abstract

The weighted Szeged index ($wSz$) has gained considerable attention recently because of its unusual mathematical properties. Searching for a tree (or trees) that minimizes the $wSz$ is still going on. Several structural details of a minimal tree were described. Here, it is shown a surprising property that these trees have maximum degree at most 16, and as a consequence, we promptly conclude that these trees are of large diameter.

1. Introduction

Molecular descriptors are playing a crucial role in the QSPR/QSAR researches. As a side-effect of the vigorous development of this area of science, a rise in the number of molecular descriptors has occurred. This is especially noticed among the class of the so-called topological indices. Nowadays, there are thousands of molecular descriptors. A vague idea on their number could be imagined by reading the book [1].

A number of topological descriptors have been devised as extensions or modifications of the previously known and well-performed indices (see [2,3,4,5,6,7] for the latest research on some of these descriptors). The Szeged index (1) may be regarded as a descendant of the oldest and heavily used Wiener index [8]. It is defined in the following manner:

$$Sz\left(G\right)=\sum _{e=\left\{uv\right\}\in E\left(G\right)}{n}_u\left(e\right)·n_v\left(e\right),$$

(1)

where $n_u\left(e\right)$ is cardinality of the set $N_u(e=\left\{uv\right\})=\{x\in V\left(G\right):d(x,u)<d(x,v)\}$.

The right-hand side of the Equation (1) was firstly appeared in the seminal paper on the Wiener index [8], used for its calculation in the case of trees. More than four decades later, the researchers have started to investigate properties of this formula in the case of connected graphs other than trees, where obtained values do not coincide with those of the Wiener index. Gutman named this invariant in [9]. The Szeged index has been extensively researched both in mathematical and in chemical community, which resulted in a vast literature and several modifications (see [9,10,11,12,13,14,15] and references cited therein).

One such modification of the Szeged index was done by the Ilić and Milosavljević in [16]. This quantity is named as the weighted Szeged index ($wSz$), and defined as follows:

$$wSz\left(G\right)=\sum _{e=\left\{uv\right\}\in E\left(G\right)}[deg\left(u\right)+deg\left(v\right)]·n_u\left(e\right)·n_v\left(e\right)$$

(2)

where $deg\left(u\right)$ is degree of the vertex u.

Several papers, dealing with $wSz$ on graph operations, have appeared [17,18,19]. In [20] the authors proved that the star is a tree having the maximal weighted Szeged index. They also gave examples of trees of order up to 25 with minimal weighted Szeged index and described the regularities which retain in them. However, the characterization of a tree (or trees) having the minimal weighted Szeged index remains an open problem.

The impression we get from the examples of trees of minimal weighted Szeged index in [20] is that they are having one “central” vertex and branches around it with subtrees of similar shape and small diameter. That would imply that these trees have a vertex whose degree increases as the order of the trees increases. Further, the examples in [20] give an impression that the diameter of the trees of minimal weighted Szeged index is bounded. However, in the next section we show that the degree of any vertex of a tree with minimum weighted Szeged index is at most 16. Consequently, this implies that the diameter of these trees is unbounded. In the last section of the paper we provide two properties of trees having minimal weighted Szeged index, which give an idea how these trees may grow as their order increases.

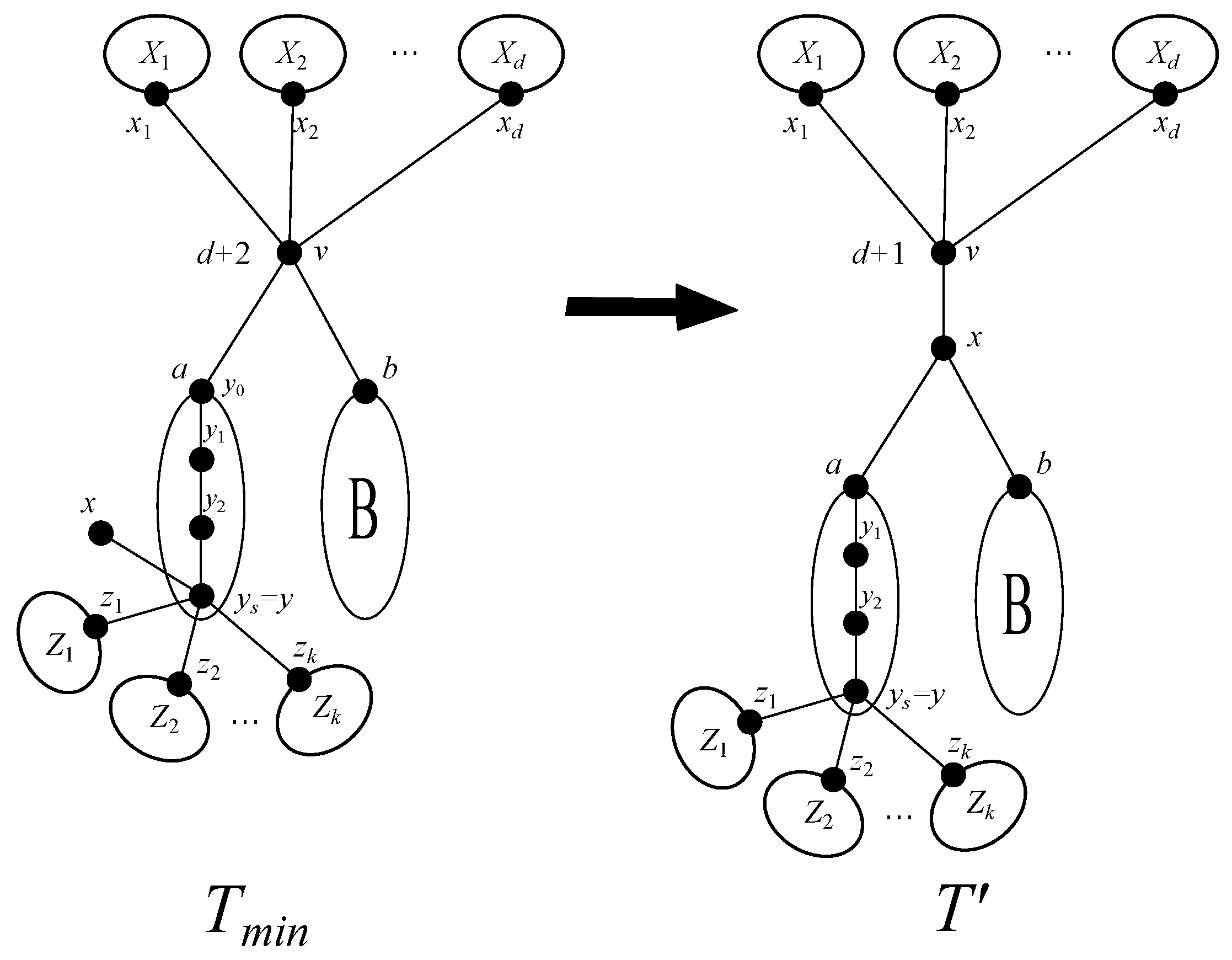
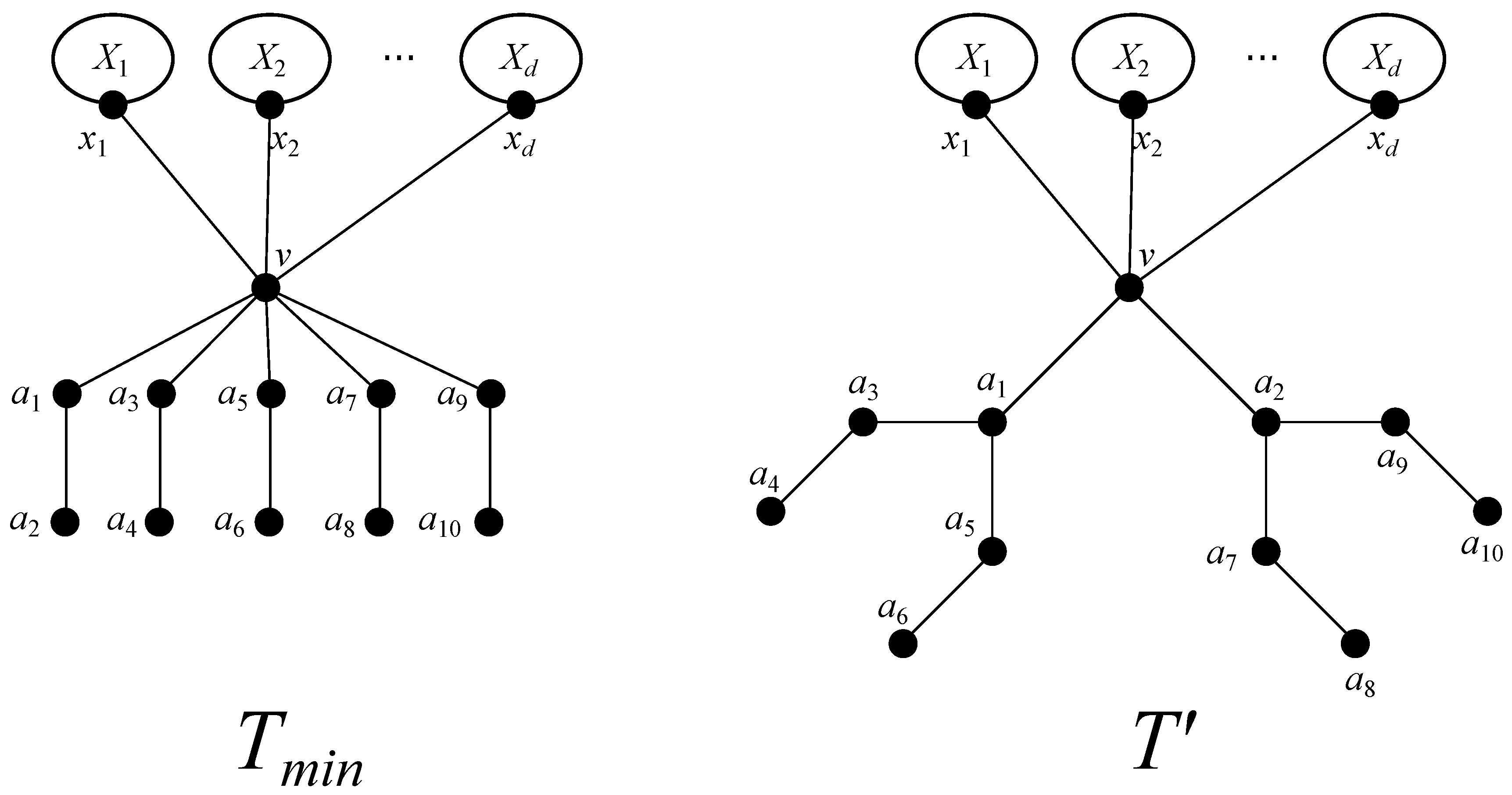
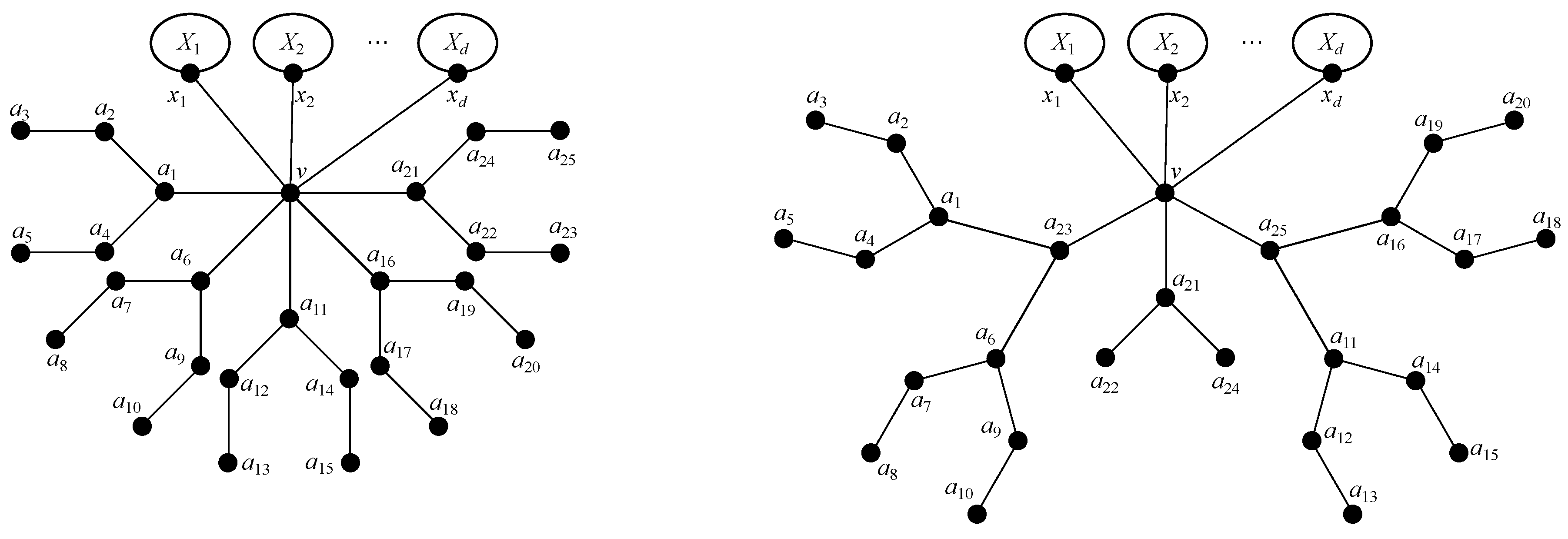
2. About the Diameter of Trees with Minimum Weighted Szeged Index

In this section, by $T_{min}$ we denote a tree with the minimum possible weighted Szeged index on n vertices. As we mentioned in the previous section, we will first show that $T_{min}$ cannot have a vertex of degree greater than 16.

Theorem 1.

The degree of any vertex in $T_{min}$ is at most 16.

Proof. 

Suppose that the claim of the theorem does not hold and suppose that $T_{min}$ is a counterexample, i.e., it has a vertex v of degree at least 17. Let a, b, $x_1,x_2,\dots ,x_d$ be the adjacent vertices of v ($d\ge 15$). We denote by A, B, $X_1,X_2,\dots ,X_d$ the set of vertices of the components of $T_{min}-v$ that contain a, b, $x_1,x_2,\dots ,x_d$ respectively. Without loss of generality, we may assume $\left|A\right|\le \left|B\right|\le |X_1|\le \cdots \le |X_d|$.

Let $a=y_0,y_1,\dots ,y_s=y,x$ be a path in $T_{min}$ such that x is a leaf and $a,y_1,y_2,\dots ,y_{s-1},y,x\in A$. We define the tree $T^{\prime }$ from $T_{min}$ as follows. We remove the vertex x, we add a new vertex, denoted again by x and three edges $vx$, $xa$ and $xb$ as on the Figure 1.

Thus

$$V\left(T^{\prime }\right)=V\left(T_{min}\right)\mathrm{and}E\left(T^{\prime }\right)=E\left(T_{min}\right)-\{yx,va,vb\}\cup \{vx,xa,xb\}.$$

Let $\mathsf{\Delta }=wSz\left(T_{min}\right)-wSz\left(T^{\prime }\right)$. We want to show that $\mathsf{\Delta }>0$. In order to do so, we first analyze the contribution of the edges of $T_{min}$ and $T^{\prime }$ to $\mathsf{\Delta }$.

The contribution of the edges with vertices in $B,X_1,X_2,\dots ,X_d$ in both $wSz\left(T_{min}\right)$ and $wSz\left(T^{\prime }\right)$ is equal. So, they will cancel out in $\mathsf{\Delta }$.

The contribution of the edges $v{x}_1,v{x}_2,\dots ,v{x}_d$ to $\mathsf{\Delta }$ is

$$\sum _{i=1}^d(d+2+\mathrm{deg}\left(x_i\right))|X_i\left|\right(n-|X_i\left|\right)-\sum _{i=1}^d(d+1+\mathrm{deg}\left(x_i\right))|X_i\left|\right(n-|X_i\left|\right)=\sum _{i=1}^d|X_i\left|\right(n-|X_i\left|\right).$$

We consider two cases regarding the size of A. We will first consider the case $\left|A\right|\ge 2$ and address the case $\left|A\right|=1$ later, at the end of the proof.

Case 1:$\left|A\right|\ge 2$. Here, we consider first the edges $y_0{y}_1,y_1{y}_2,\dots ,y_{s-2}{y}_{s-1}$. As $\left|A\right|\ge 2$ this list is non-empty. We will introduce additional notation. By $A_i$ we will denote the set of the vertices of the component of $A-y_{i-1}{y}_i$ that contains $y_i$.

The contribution of the edge $y_{i-1}{y}_i$ with $i\ne s$ to $\mathsf{\Delta }$ is

$$\begin{array}{cc}\hfill (\mathrm{deg}\left(y_{i-1}\right)+\mathrm{deg}\left(y_i\right))|A_i\left|\right(n-|A_i\left|\right)-(\mathrm{deg}\left(y_{i-1}\right)+\mathrm{deg}\left(y_i\right))\left(\right|A_i|-1)(n-|A_i|+1)& =\hfill \\ \hfill (\mathrm{deg}\left(y_{i-1}\right)+\mathrm{deg}\left(y_i\right))(n-2|A_i|+1)& >0.\hfill \end{array}$$

The last inequality holds because of the assumptions $\left|A\right|\le \left|B\right|\le |X_1|\le \cdots \le |X_d|$.

If $i=s$, we consider the edge $y_{s-1}{y}_s$ ($y_s=y$). The contribution of this edge to the difference $\mathsf{\Delta }$ is positive

$$\begin{array}{cc}\hfill (\mathrm{deg}\left(y_{s-1}\right)+\mathrm{deg}\left(y_s\right))|A_s\left|\right(n-|A_s\left|\right)-(\mathrm{deg}\left(y_{s-1}\right)+\mathrm{deg}\left(y_s\right)-1)\left(\right|A_s|-1)(n-|A_s|+1)& >\hfill \\ \hfill (\mathrm{deg}\left(y_{s-1}\right)+\mathrm{deg}\left(y_s\right))|A_s\left|\right(n-|A_s\left|\right)-(\mathrm{deg}\left(y_{s-1}\right)+\mathrm{deg}\left(y_s\right))\left(\right|A_s|-1)(n-|A_i|+1)& >\hfill & \hfill 0.\end{array}$$

As the degree of $y(=y_s)$ decreases by 1 in $T^{\prime }$, it affects the contribution of all edges incident with y. Denote by $z_1,z_2,\dots ,z_k$ all neighbors of y distinct from $x,y_{s-1},v$. Denote by $Z_i$ the set of vertices of the component of $T_{min}-y$ that contains $z_i$. Observe that the contribution of these edges to $\mathsf{\Delta }$ is positive

$$\sum _{i=1}^k(deg\left(z_i\right)+deg\left(y\right))|Z_i\left|\right(n-|Z_i\left|\right)-\sum _{i=1}^k(deg\left(z_i\right)+deg\left(y\right)-1)|Z_i\left|\right(n-|Z_i\left|\right)=\sum _{i=1}^k|Z_i\left|\right(n-|Z_i\left|\right)\ge 0.$$

Next, we consider the contribution of the edges $av$ and $ax$ to $\mathsf{\Delta }$, and also of the edges $bv$ and $bx$ to $\mathsf{\Delta }$. Let

$$\delta =\left\{\begin{array}{cc}1,\hfill & \mathrm{if}a=y\hfill \\ 0,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

Then

$$\begin{array}{cc}\hfill & \left(\mathrm{deg}\right(a)+d+2)\left|A\right|(n-|A\left|\right)-\left(\mathrm{deg}\right(a)+3-\delta )\left(\right|A|-1)(n-|A|+1)\ge \hfill \\ \hfill & \left(\mathrm{deg}\right(a)+d+2)\left|A\right|(n-|A\left|\right)-\left(\mathrm{deg}\right(a)+3)\left(\right|A|-1)(n-|A|+1)\ge \hfill \\ \hfill & \left(\mathrm{deg}\right(a)+d+2)\left|A\right|(n-|A\left|\right)-\left(\mathrm{deg}\right(a)+3)\left|A\right|(n-|A\left|\right)=\hfill \\ \hfill & \left(\mathrm{deg}\right(a)+d+2-\mathrm{deg}(a)-3)\left|A\right|(n-|A\left|\right)=(d-1)\left|A\right|(n-|A\left|\right).\hfill \end{array}$$

Thus the contribution of the edges $av$ and $ax$ to $\mathsf{\Delta }$ is at least $(d-1)\left|A\right|(n-|A\left|\right)$. Similarly, the contribution of $bv$ and $bx$ to $\mathsf{\Delta }$ equals to $(d-1)\left|B\right|(n-|B\left|\right)$.

At the edges $yx$ and $vx$, we have the following contribution. The edge $yx$ contributes $\left(\mathrm{deg}\right(y)+1)(n-1)>0$ and the edge $vx$,

$$-(d+1+3)\left(\right|A|+|B\left|\right)(n-|A|-|B\left|\right)=-(d+4)\left(\right|A|+|B\left|\right)(n-|A|-|B\left|\right).$$

Summing up all of the contributions listed above, except of some contributions that are clearly positive but possibly small, we have

$$\mathsf{\Delta }>\sum _{i=1}^d|X_i\left|\right(n-|X_i\left|\right)+(d-1)\left|A\right|(n-\left|A\right|)+(d-1)\left|B\right|(n-\left|B\right|)-(d+4)\left(\right|A|+\left|B\right|\left)\right(n-\left|A\right|-\left|B\right|)$$

which simplifies to

$$\mathsf{\Delta }>\sum _{i=1}^d|X_i\left|\right(n-|X_i\left|\right)+2\left|A\right|\left|B\right|d+{5\left|A\right|}^2+{5\left|B\right|}^2+8\left|A\right|\left|B\right|-5\left|A\right|n-5\left|B\right|n.$$

It is enough to show that

$$\sum _{i=1}^d|X_i\left|\right(n-|X_i\left|\right)\ge 5\left|A\right|n+5\left|B\right|n.$$

The last inequality is equivalent to

$$\sum _{i=1}^d|X_i|n-\sum _{i=1}^d|X_i{|}^2\ge 5\left|A\right|n+5\left|B\right|n.$$

Since ${\sum }_{i=1}^d|X_i|=n-|A|-|B|-1$, it is enough to show

$$n^2\ge 6\left|A\right|n+6\left|B\right|n+\sum _{i=1}^d{\left|X_i\right|}^2+n.$$

Using the well-known fact that ${(u+1)}^2+{(v-1)}^2>u^2+v^2$ for $u>v$ and $u,v\in \mathbb{N}$, we conclude that ${\sum }_{i=1}^d{\left|X_i\right|}^2$ attains its maximum value when $|X_1|=|X_2|=\cdots =|X_{d-1}|=|B|$ and $|X_d|=n-1-d|B|-|A|$. For simplicity, we will increase $|X_d|$ by 1, i.e., $|X_d|=n-d|B|-|A|$.

Thus it is enough to show

$$n^2\ge 6\left|A\right|n+6\left|B\right|n+{d\left|B\right|}^2+{(n-d|B|-|A\left|\right)}^2+n.$$

Notice that

$$\begin{array}{cc}\hfill 6\left|A\right|n+6\left|B\right|n+{d\left|B\right|}^2+{(n-d|B|-|A\left|\right)}^2& =\hfill \\ \hfill 4\left|A\right|n+n^2+{\left|A\right|}^2+\left|B\right|(6n+d\left|B\right|+d^2\left|B\right|+2d\left|A\right|-2dn).\end{array}$$

Since $d\left|B\right|<n$, $2d\left|A\right|<2n$, and $d^2\left|B\right|<dn$, we get that

$$\left|B\right|(6n+d|B|+d^2|B|+2d|A|-2dn)<\left|B\right|(9n+dn-2dn)=-\left|B\right|n(d-9).$$

Hence it is enough to show

$$n^2\ge 4\left|A\right|n+n^2+{\left|A\right|}^2-\left|B\right|n(d-9)+n.$$

As $\left|B\right|\ge \left|A\right|$ it suffices to have

$$n(d-10)\ge 4n+\left|A\right|,$$

or equivalently

$$n(d-14)\ge \left|A\right|.$$

Since $n\ge d\left|A\right|$, we want $d(d-14)\ge 1$ to hold, and this holds whenever $d\ge 15$. Since $deg\left(v\right)=d+2$, we conclude that whenever the degree of v is at least 17, we can obtain a tree with smaller weighted Szeged index than $T_{min}$. Therefore the degree of every vertex of $T_{min}$ is at most 16. This establishes Case 1.

Case 2:$\left|A\right|=1$. In this case, the tree $T_{min}$ has only the vertex a in the set A and, in this case, $x=a$ and $deg\left(a\right)=1$. Then the degree of x in $T^{\prime }$ is 2. The contribution of the edges $av$ and $vb$ in $wSz\left(T_{min}\right)$ is

$$(d+3)(n-1)+(d+2+\mathrm{deg}(b\left)\right)\left|B\right|(n-|B\left|\right).$$

The contribution of the edges $xv$ and $xb$ in $wSz\left(T^{\prime }\right)$ is

$$(d+3)\left(\right|B|+1)(n-|B|-1)+(2+\mathrm{deg}(b\left)\right)\left|B\right|(n-|B\left|\right).$$

Thus, the contribution of these four edges is $\mathsf{\Delta }$ is the difference of the previous two expressions, which is

$$2\left|B\right|d+6\left|B\right|+{3\left|B\right|}^2-3\left|B\right|n.$$

The contribution of the edges $v{x}_1,v{x}_2,\dots ,v{x}_d$ to $\mathsf{\Delta }$ is the same as in the previous case, i.e.

$$\sum _{i=1}^d|X_i\left|\right(n-|X_i\left|\right).$$

The contribution of the edges with both end-vertices in B is equal in both $wSz\left(T_{min}\right)$ and $wSz\left(T^{\prime }\right)$, so it will be 0 in $\mathsf{\Delta }$. Similarly holds for the sets $X_1,X_2,\dots ,X_d$. Therefore,

$$\mathsf{\Delta }=\sum _{i=1}^d|X_i\left|\right(n-|X_i\left|\right)+2d\left|B\right|+6\left|B\right|+{3\left|B\right|}^2-3\left|B\right|n.$$

In the case $\left|A\right|\ge 2$ we proved ${\sum }_{i=1}^d|X_i\left|\right(n-|X_i\left|\right)\ge 5\left|A\right|n+5\left|B\right|n$. Here, in case $\left|A\right|=1$, we argue similarly but simpler. As $1=\left|A\right|\le \left|B\right|\le |X_1|\le |X_2|\le |X_2|\le \cdots \le |X_d|$, we have $1+(d+1)\left|B\right|\le n$, and hence $\left|B\right|\le n/d$. Since $\left|B\right|\le |X_i|\le n-|B|$, we have $|X_i\left|\right(n-|X_i\left|\right)\ge \left|B\right|(n-\left|B\right|)$ for each i. Thus, we infer

$$\mathsf{\Delta }\ge d\left|B\right|(n-\left|B\right|)+2d\left|B\right|+6\left|B\right|+{3\left|B\right|}^2-3\left|B\right|n>d\left|B\right|(n-\frac{n}{d})-3\left|B\right|n=(d-4)\left|B\right|n>0.$$

This establishes the case $\left|A\right|=1$, and the proof of the theorem is completed.  □

Now, we deduce the following interesting property of optimal trees.

Corollary 1.

As the order n of the tree with minimum weighted Szeged index increases, its diameter increases as well.

3. Two Properties of Trees Having Minimum Weighted Szeged Index

Analyzing the examples of trees of order between seven and 25 with minimal weighted Szeged index in [20], we notice that there are vertices incident to 2-rays ($P_2$ attached to a vertex is called 2-ray (see Figure 2)). We also notice that the maximum number of 2-rays that a vertex is incident to is 4. As the order of the trees in those examples is at most 25, the natural question one may ask is if it is possible a tree with minimum weighted Szeged index to have a vertex incident to more that four 2-rays. The following proposition gives the answer to this question.

Proposition 1.

No vertex in $T_{min}$ is simultaneously incident to five 2-rays.

Proof. 

Suppose the claim of the statement is false. Let v be a vertex of degree at least $d+5$, $d\ge 0$ and incident to five 2-rays. Denote the vertices of the five 2-rays incident to v by $a_1,a_2,\dots ,a_{10}$ as on the figure. Denote by $x_1,x_2,\dots ,x_d$ the vertices incident to v in $T_{min}-v{a}_1-v{a}_3-v{a}_5-v{a}_7-v{a}_9$. We denote by $X_1,X_2,\dots ,X_d$ the set of vertices of the components of $T_{min}-v$ that contain $x_1,x_2,\dots ,x_d$ respectively. Without loss of generality, we may assume $|X_1|\le \cdots \le |X_d|$.

We define the tree $T^{\prime }$ from $T_{min}$ as follows

$$V\left(T^{\prime }\right)=V\left(T_{min}\right)$$

$$E\left(T^{\prime }\right)=E\left(T_{min}\right)-\{a_1{a}_2,v{a}_3,v{a}_5,v{a}_7,v{a}_9\}\cup \{v{a}_2,a_1{a}_3,a_1{a}_5,a_2{a}_7,a_2{a}_9\}.$$

Let $\mathsf{\Delta }=wSz\left(T_{min}\right)-wSz\left(T^{\prime }\right)$. We want to show that $\mathsf{\Delta }>0$. In order to do so, we first analyze the contribution of the edges of $T_{min}$ and $T^{\prime }$ to $\mathsf{\Delta }$.

All edges with vertices in $X_1,X_2,\dots ,X_d$ contribute the same values in both $wSz\left(T_{min}\right)$ and $wSz\left(T^{\prime }\right)$. Hence they will cancel out in $\mathsf{\Delta }$.

The contribution of the edges $v{x}_1,v{x}_2,\dots ,v{x}_d$ to $\mathsf{\Delta }$ is

$$\sum _{i=1}^d(d+5+\mathrm{deg}\left(x_i\right))|X_i\left|\right(n-|X_i\left|\right)-\sum _{i=1}^d(d+2+\mathrm{deg}\left(x_i\right))|X_i\left|\right(n-|X_i\left|\right)=3\sum _{i=1}^d|X_i\left|\right(n-|X_i\left|\right).$$

The contribution of the five 2-rays of $T_{min}$ in $wSz\left(T_{min}\right)$ is

$$5\left(3(n-1)+2(d+7)(n-2)\right),$$

while the contribution of the edges in $T^{\prime }-{\bigcup }_{i=1}^d{X}_i$ in $wSz\left(T^{\prime }\right)$ is

$$2\left(\right(d+5)·5(n-5\left)\right)+4(5·2(n-2)+3(n-1\left)\right).$$

The difference of the last two expressions is $30d-17n+187$. Thus

$$\mathsf{\Delta }=3\sum _{i=1}^d|X_i\left|\right(n-|X_i\left|\right)+30d-17n+187=3n\sum _{i=1}^d|X_i|-3\sum _{i=1}^d{|X_i|}^2+30d-17n+187.$$

Notice that ${\sum }_{i=1}^d\left|X_i\right|=n-11$. Similarly as in the proof of Theorem 1 we conclude that ${\sum }_{i=1}^d{\left|X_i\right|}^2$ attains the maximum value when $|X_1|=|X_2|=\cdots =|X_{d-1}|=1$ and $|X_d|=n-d-10$. Thus

$$\mathsf{\Delta }=3n\sum _{i=1}^d|X_i|-3\sum _{i=1}^d{\left|X_i\right|}^2+30d-17n+187\ge 3n(n-11)-(d-1)-{(n-d-10)}^2+30d-17n+187.$$

Hence $\mathsf{\Delta }\ge -d^2+2dn+9d+2n^2-30n+88$. Since $dn>d^2$, we have

$$\mathsf{\Delta }\ge -d^2+2dn+9d+2n^2-30n+88>-dn+2dn+2n^2-30n>n(2n-30).$$

Clearly $\mathsf{\Delta }>0$ for $n\ge 15$. For $n<15$, the examples generated in [20] verify the statement.  □

We call a branch in a tree Y-subtree, if it is isomorphic to the tree on Figure 3. We call a root the leaf of the Y-subtree incident to the vertex of degree 3, as it is attached as a branch to the tree of consideration.

We see Y-subtrees of $T^{\prime }$ in the proof of the previous proposition. We also see this type of subtrees in the examples of trees of minimal weighted Sezged index in [20]. Hence it is natural to ask if the number of Y-subtrees with a common root is bounded.

Proposition 2.

If $n\ge 54$, a tree with minimum weighted Szeged index cannot have a vertex that is a root of five Y-subtrees.

Proof. 

Let $\mathsf{\Delta }=wSz\left(T_{min}\right)-wSz\left(T^{\prime }\right)$. Suppose the claim of the statement is false. Let v be a vertex of degree at least $d+5$, $d\ge 0$ and a root to the five Y-subtrees. Denote the vertices of the five Y-subtrees by $a_1,a_2,\dots ,a_{25}$ as on the Figure 4. Denote by $x_1,x_2,\dots ,x_d$ the vertices incident to v in $T_{min}-v{a}_1-v{a}_6-v{a}_{11}-v{a}_{16}-v{a}_{21}$. We denote by $X_1,X_2,\dots ,X_d$ the set of vertices of the components of $T_{min}-v$ that contain $x_1,x_2,\dots ,x_d$ respectively. Without loss of generality, we may assume $|X_1|\le \cdots \le |X_d|$.

We define the tree $T^{\prime }$ from $T_{min}$ as follows

$$V\left(T^{\prime }\right)=V\left(T_{min}\right)$$

$$E\left(T^{\prime }\right)=E\left(T_{min}\right)-\{a_{22}{a}_{23},a_{24}{a}_{25},v{a}_1,v{a}_6,v{a}_{11},v{a}_{16}\}\cup \{v{a}_{23},v{a}_{25},a_1{a}_{23},a_6{a}_{23},a_{11}{a}_{25},a_{16}{a}_{25}\}.$$

All edges with vertices in $X_1,X_2,\dots ,X_d$ contribute the same values in both $wSz\left(T_{min}\right)$ and $wSz\left(T^{\prime }\right)$. Hence they will cancel out in $\mathsf{\Delta }$.

The contribution of the edges $v{x}_1,v{x}_2,\dots v{x}_d$ to $\mathsf{\Delta }$ is

$$\sum _{i=1}^d(d+5+\mathrm{deg}\left(x_i\right))|X_i\left|\right(n-|X_i\left|\right)-\sum _{i=1}^d(d+3+\mathrm{deg}\left(x_i\right))|X_i\left|\right(n-|X_i\left|\right)=2\sum _{i=1}^d|X_i\left|\right(n-|X_i\left|\right).$$

We consider the edges in $T_{min}-X_1-X_2-\cdots -X_d$. Their contribution to $wSz\left(T_{min}\right)$ is

$$5\left(\right(d+8)·5(n-5\left)\right)+10·5·2(n-2)+10·3(n-1)=25dn-125d+330n-1230.$$

Next we consider the edges in $T^{\prime }-X_1-X_2-\cdots -X_d$. Their contribution to $wSz\left(T^{\prime }\right)$ is

$$2(d+6)·11(n-11)+(d+6)·3(n-3)+4·6·5(n-5)+8·5·2(n-2)+8·3(n-1)+2·4(n-1)$$

which is equal to

$$25dn-251d+382n-2298.$$

Hence

$$\begin{array}{cc}\hfill \mathsf{\Delta }& =2\sum _{i=1}^d|X_i\left|\right(n-|X_i\left|\right)+25dn-125d+330n-1230-(25dn-251d+382n-2298)\hfill \\ \hfill & =2n\sum _{i=1}^d|X_i|-2\sum _{i=1}^d{\left|X_i\right|}^2+126d-52n+1068.\hfill \end{array}$$

Notice that ${\sum }_{i=1}^d\left|X_i\right|=n-26$. Similarly as in the proof of Theorem 1, we conclude that ${\sum }_{i=1}^d{\left|X_i\right|}^2$ attains the maximum value when $|X_1|=|X_2|=\cdots =|X_{d-1}|=1$ and $|X_d|=n-d-25$. Thus

$$\mathsf{\Delta }\ge 2n(n-26)-{(n-d-25)}^2+126d-52n+1068.$$

Hence

$$\mathsf{\Delta }\ge -d^2+2dn+76d+n^2-54n+443.$$

Similarly like in the proof of Proposition 1, since $\mathsf{\Delta }>dn+n^2-54n>n(n-54)$, it is valid for $n\ge 54$.  □

4. Conclusions

Characterization of trees that minimize or maximize the value of a topological invariant is one of the crucial problems that need to be solved in order to better understand its behavior and to find its possible applications. For the majority of topological indices, the path and the star are extremal trees. However, there are topological invariants that are violating this pattern. One of them is the weighted Szeged index. Computer screening, reported in [20], shows complex structures of trees that minimize it. Nevertheless, some details are keeping constant with varying the order of trees. All trees with a minimum $wSz$ have a vertex with a significantly greater degree than others. It was assumed that this vertex is a single root to which all other subtrees (with some specific structural details) are attached. However, here it is proved that such vertex cannot have a degree greater than 16. This implies the large diameter of the minimum trees and the existence of more than one root vertex.