Abstract
If is a simple connected graph with the vertex set and the edge set , S is a subset of , and let be the set of neighbors of S in . Then, the differential of S is defined as . The differential of G, denoted by , is the maximum value of for all subsets . The graph operator is defined as the graph that results by subdividing every edge of G once and joining pairs of these new vertices iff their corresponding edges are incident in G. In this paper, we study the relations between and . Besides, we exhibit some results relating the differential and well-known graph invariants, such as the domination number, the independence number, and the vertex-cover number.
1. Introduction
Some social networks arising from technologies such as Whatsapp, Facebook, Twitter, etc., have served as useful tools for communication and dissemination of information. Due to the high popularity of these technologies, they now have a wide variety of applications in the marketing of many products. With these facts in mind, several authors [1,2] have established some influential maximization problems, which share an algorithmic problem for information diffusion in social networks: the problem of determining the best set of nodes to influence the rest. For example, in [1], the authors attacked this problem by means of submodular functions and provided an algorithm that produced a solution that was provably within 63% of optimal for certain instances. Two years later, the same group of researchers [2] developed a more general framework and showed that the mentioned maximization problem can be approximated in a more general model known as the decreasing cascade model. In [3], it was explained how the differential of a graph G could be motivated by these scenarios.
The study of the differential together with several other variants started in [4]. In particular, in [4], some bounds were established for . In that paper, the differential of G was related to the following maximization problem:
“You are allowed to buy as many tokens as you like, say k tokens, at cost of $1 each. You then place the tokens on some subset of k vertices of G. For each vertex of G which has no token on it, but is adjacent to a vertex with a token on it, you receive $1. Your objective is to maximize your profit, that is, the total value received minus the cost of the tokens bought.“
The differential of a graph was also analyzed in [3,5,6,7,8,9,10,11,12,13]. In [10], it was established that , where n denotes the order of G and denotes the Roman domination number of G. These graph parameters lead to two natural algorithmic decision problems:
- DIF: If G is a graph and k is an integer, decide if ;
- ROM: If G is a graph and l is an integer, decide if .
Due to the relation that these parameters satisfy, an algorithm for DIF can be used to decide the ROM and vice versa. In [8], it was proven that DIF is NP-complete by a reduction from the three-dimensional matching problem.
Most of the contributions reported in [3,5,6,7,8,9,10,11,12,13] lied on at least one of the following issues of the differential of a graph:
- To obtain inequalities relating the differential of G with other graph invariants of G.
- To study the differential for the most important graph families (complete graphs, trees, star graphs, etc.).
- To study the variation of the differential under certain transformations (graph operators, products of graphs, etc.).
- To determine the computational complexity of the DIF problem.
We remark that, until now, the understanding of the differential of a graph has been relatively modest, and hence, the study of each of these four issues can lead to deep and fascinating problems for future research.
The differential of was also analyzed in [14], and the minimum differential of an independent set was studied in [15]. The B-differential or enclaveless number of G is and was treated in [16,17].
In this paper, G denotes a simple graph with vertex set , edge set , and . Let be two vertices of G, and let . As usual, is the set of neighbors that v has in , and denotes the closed neighborhood of v, i.e., . We denote by the degree of v in G and by and the minimum and the maximum degree of G, respectively. The subgraph of G induced by S is denoted by , and . Then, consists precisely of the neighbors that v has in . Let and . For , an external private neighbor of v with respect to S is a vertex , which satisfies that for any . The set of external private neighbors of v with respect to S is denoted by epn. Let be the set of elements of that have a neighbor in S, and let . Note that is a partition of . The differential of is defined as , and the differential of G is defined as . We will say that S is a differential set if . A differential set is a minimum (maximum) differential set if it has minimum (maximum) cardinality among all differential sets.
As long as no confusion can arise from the context, we often omit the reference to G in etc.
Notice that if G is disconnected and are its connected components, then . Then, we shall assume that any graph under consideration is connected.
A graph operator is a function , where and are two families of graphs. The study of how a graph invariant changes when a graph operator is applied is a classical problem in graph theory. We recall that the line graph of the graph G is the graph with vertex set on in which are adjacent in iff e and f are incident in G.
In [18], the subdivision graph of G as the graph constructed from G by subdividing every edge of G once was defined. The graph (following the notations [18]) is obtained from G by subdividing each edge of G once and joining pairs of these new vertices iff their corresponding edges have a common endvertex in G (see Figure 1). Then, contains both and as proper induced subgraphs.
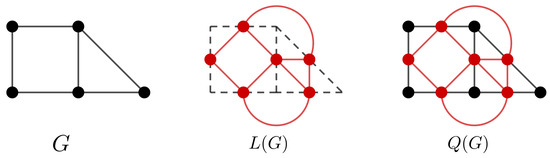
Figure 1.
Example of , and graphs.
For , let . Now, let us define:
and:
Then,
Remark 1.
From the last equality, it is clear that is the disjoint union of and . For brevity, we shall use and . Then, trivially, , . We also note that all vertices have exactly two neighbors in . See Figure 1.
From now on, we assume that V and L are the proper subsets of described in Remark 1.
The graphs provide a formal and natural language for modeling and studying several molecular phenomena in chemistry. A “topological index” is a graph invariant applicable in this kind of phenomena. Perhaps the best known topological indices are the Zagreb indices. They have been used to study molecular complexity, chirality, -isomerism, hetero-systems, etc. As can be seen in [19,20,21,22], , and other related graph operators have been widely studied in the context of the topological indices. On the other hand, the theory of graph operators is a classical and active area of research in graph theory, which has the following general question as the prime motivation: Given a graph G, a graph parameter , and a graph operator , what can we say about when certain information on G or on is known? As can be seen in [23,24] and the references therein, at least one of or has been studied from this second point of view.
2. Results
We start by listing some basic properties of , which can be deduced easily from the definition of . We use to denote the graph of order with no edges.
Proposition 1.
If G is a graph of order n, then:
- (i)
- (ii)
- (iii)
- is an induced subgraph of
- (iv)
- if and only if .
- (v)
- If , then .
- (vi)
- If , then .
- (vii)
- If and , then .
- (viii)
- If , then there exist vertices such that and .
- (ix)
- If G is a regular graph, then is a biregular graph.
We recall that a vertex cover of G is a subset such that each edge of G has at least one endvertex in S. The vertex-covering number of G is the size of any smallest vertex cover in G. A subset is a dominating set of G if each vertex in G belongs to S or has a neighbor in S. The domination number of G is the minimum cardinality of a dominating set of G. Similarly, a subset is independent if any two vertices in S are not adjacent in G. The independence number of G is the maximum cardinality of an independent set of G.
Proposition 2.
If G is a graph and S is a differential set of , then .
Proof.
Let be as in Proposition 2. Suppose that there is . If there exist , then , a contradiction. Let and with . Let us show that . If , then , a contradiction. If , then , again a contradiction. Therefore, ; hence, there exists such that ; according to this and by the definition of , we know that , and since u is arbitrary, we conclude , a contradiction. Therefore, . □
Proposition 3.
If G is a graph of order , then .
Proof.
Let S be a differential set of , and notice that ; even more, there exist , then . □
For the n star graph, equality holds in the above proposition. For an example, see Figure 2.
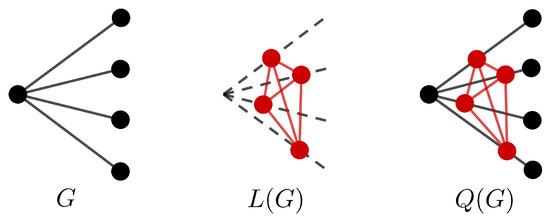
Figure 2.
Here, Gis the star graph . Note that and = 2.
Proposition 4.
If G is a graph, then L contains a dominating set S of such that .
Proof.
Let D be a minimum dominating set of . If , there is nothing to show, so we may assume that has at least one vertex v. We know that for any by Proposition 1. Then, is a minimum dominating set of with . Continuing in this way, we can construct the desired S. □
Proposition 5.
If G is a graph and S is a differential set of , then S is a dominating set of .
Proof.
Suppose that S is a differential set of . By Proposition 2, we know that . We recall that is a partition of . If S is a dominating set for , there is nothing to show, so we may assume that there exists a vertex . Proposition 1 (viii) implies that for some . If for some , then , a contradiction. If for some , then there exists such that for some , and therefore, . This implies , a contradiction. We conclude that , and so, , which is a contradiction. □
Corollary 1.
If G is a graph and S is a differential set of , then .
Corollary 2.
If G is a graph and S is a differential set of , then .
Proposition 6.
If G is a graph of order n, then .
Proof.
Suppose that D is a minimum dominating set of and that . By Proposition 2, we can assume that . This and Proposition 1 imply that D has at most adjacent vertices in V. If n is even, then ; therefore, D is not a dominating set of , which is a contradiction. If with , then ; therefore, D is not a dominating set in , a contradiction. □
Observation 1.
Note that for the cycle, complete, and path graphs, equality holds in the above proposition.
Proposition 7.
If G is a graph of order n, then G has a perfect matching iff .
Proof.
According to Proposition 6, it suffices to show that . Let be a perfect matching of G and the vertex set in corresponding to the edges of M. Let us prove that is a dominating set of . Let ; since M is a perfect matching, there is and such that . Hence, . Let ; by Proposition 1 (), there are y . Since M is a perfect matching, there is and such that , then is incident to , and hence, for some . This shows that is a dominating set of , and so, .
Conversely, assume that . Then, there is a minimum dominating set D of contained in L, by Proposition 4. Let be the set of edges of G, corresponding to the vertices of D. If , then there exist such that , and then, v is an endvertex of some edge in . Let us prove that is an independent edge set. Assume that there are () and such that y with , then , and by Proposition 1, we have that the maximum number of vertices in V adjacent to D is , a contradiction. Therefore, G has a perfect matching. □
Let us define . It is well known that . Now, we will determine what G is, when . For this, we need to recall three known facts.
Proposition 8
([5]). If D is a differential set of a graph G, then .
Proposition 9
([11]). If G is a graph of order and maximum degree Δ, then:
- (a)
- iff .
- (b)
- iff .
- (c)
- If , then .
Proposition 10.
If G is a simple graph of order n, then:
- (a)
- iff .
- (b)
- iff .
Proof.
(a) Suppose that . By Proposition 9 (a), we have that , and so, . Then, Proposition 6 implies , and consequently, . If , then and , a contradiction; therefore . The backward implication is easy to check. (b) Now, we suppose that . By Proposition 9 (b), we have that , and so, . Then, Proposition 6 implies that . It is not hard to derive a contradiction for each of the cases and . Then, we can assume . If , by Proposition 1 vi), we conclude , a contradiction. If , then . Since does not satisfy the hypothesis, we are done. Again, the backward implication is easy to see. □
Theorem 1.
If G is a graph of order , then .
Proof.
Since for all , then V is an independent set of . Let be a maximum independent set of . We will show that . Seeking a contradiction, suppose that there is . From Proposition 1, we know that there exist such that . From this and the independence of D, it follows that . Even more, for all and , otherwise ; this contradicts the independence of D. Therefore, is independent in , contradicting the maximality of D. Therefore, , and by the maximality of D, we conclude that . □
Observation 2.
[25] For any graph G, .
Corollary 3.
If G is a graph, then .
Corollary 4.
If G is a graph, then .
Observation 3.
If S is a differential set of , , and , then and .
Proposition 11.
If G is a graph and S is a minimum differential set of , then .
Proof.
Suppose that S is a minimum differential set of . By Proposition 2, we know that . If , by the definition of , the equality holds. Thus, we can assume that S has at least two vertices, say and .
Now, suppose that and are adjacent in . Then, there exist such that and . Since S is a minimum differential set, then |epn for all . This and the fact for all imply the existence of an epn. Since , then has exactly two neighbors in V, say and .
If is adjacent to some of or , then , contradicting that is a private neighbor of . Then, we conclude that and that for some . Without loss of generality, we can assume . Therefore, for all . Since epn, then . If , then there exists such that , and so, , contradicting that is a private neighbor of . Thus, we can assume that . From the latter, we get , a contradiction. This last contradiction implies that S is independent in . The latter and imply that , as required. □
Corollary 5.
If G is a graph of order n and S is a minimum differential set in , then .
Theorem 2.
If G is a graph of order n, then .
Proof.
Suppose that S is a minimum differential set of . Then:
□
Corollary 6.
Let be the complete, star, double star, complete bipartite, path, cycle, wheel, and tree graphs, respectively, then the following hold:
- (i)
- .
- (ii)
- .
- (iii)
- .
- (iv)
- .
- (v)
- .
- (vi)
- .
- (vii)
- .
- (viii)
- .
Proof.
Theorem 2 implies , and Corollary 3 implies . On the other hand, note that the expression on the right side of each equation is precisely the number of edges of the corresponding graph . Clearly, each of the claimed equalities follows directly from these three facts. □
3. Concluding Remarks
If G is a simple graph, then denotes the graph on in which two distinct elements of are adjacent as vertices of iff they are adjacent or incident in G. The graph operator belongs to an extensive collection of graph operators that have been widely studied in graph theory for a long time. Perhaps the better known member of that collection is the line graph of G. A simple inspection of graphs and reveals that is contained in as the induced subgraph.
In this work, we determined the exact value of three graph theoretical parameters for , namely the differential , the vertex-covering number , and the independence number . We also provided a tight lower bound for the domination number of .
Surprisingly, we discovered that is equal to and that the latter is exactly the number of edges of G. As a consequence, we managed to give explicit expressions for , when G belongs to some fundamental graphs, such as complete graphs, trees, etc.
The graph parameters , and are of quite independent interest in graph theory. For instance, it is well known that the exact determination of each of them is computationally hard for most of the graphs. However, as can be seen throughout this work, it seems that the structure of and the concept of the differential of a graph have enabled establishing some interesting relationships between these parameters and some of the invariants of .
In the Introduction, we already mentioned several interesting general problems involving the differential of a graph. In particular, we mentioned that the decision problem DIF is NP-complete. On the other hand, here, we showed that , and so, given a graph G and an integer k, we can decide whether in polynomial time. Motivated by this fact, we propose the following question: Which graph operators maintain the decision problem DIF in the NP-complete class?
Author Contributions
The authors contributed equally to this work. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Acknowledgments
The authors would like to thank the Editor and the anonymous referees, whose comments and suggestions greatly improved the presentation of this paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Kempe, D.; Kleinberg, J.; Tardos, E. Maximizing the spread of influence through a social network. In Proceedings of the 9th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, New York, NY, USA, 24–27 August 2003; pp. 137–146. [Google Scholar]
- Kempe, D.; Kleinberg, J.; Tardos, E. Influential nodes in a diffusion model for social networks. In International Colloquium on Automata, Languages, and Programming; Springer: Berlin/Heidelberg, Germany, 2005; pp. 1127–1138. [Google Scholar]
- Bermudo, S.; Fernau, H. Lower bound on the differential of a graph. Discret. Math. 2012, 312, 3236–3250. [Google Scholar] [CrossRef]
- Mashburn, J.L.; Haynes, T.W.; Hedetniemi, S.M.; Hedetniemi, S.T.; Slater, P.J. Differentials in graphs. Util. Math. 2006, 69, 43–54. [Google Scholar]
- Basilio, L.A.; Bermudo, S.; Sigarreta, J.M. Bounds on the differential of a graph. Util. Math. 2017, 103, 319–334. [Google Scholar]
- Bermudo, S. On the Differential and Roman domination number of a graph with minimum degree two. Discret. Appl. Math. 2017, 232, 64–72. [Google Scholar] [CrossRef]
- Bermudo, S.; De la Torre, L.; Martín-Caraballo, A.M.; Sigarreta, J.M. The differential of the strong product graphs. Int. J. Comput. Math. 2015, 92, 1124–1134. [Google Scholar] [CrossRef]
- Bermudo, S.; Fernau, H. Computing the differential of a graph: hardness, approximability and exact algorithms. Discret. Appl. Math. 2014, 165, 69–82. [Google Scholar] [CrossRef]
- Bermudo, S.; Fernau, H. Combinatorics for smaller kernels: the differential of a graph. Theor. Comput. Sci. 2015, 562, 330–345. [Google Scholar] [CrossRef]
- Bermudo, S.; Fernau, H.; Sigarreta, J.M. The differential and the Roman domination number of a graph. Appl. Anal. Discret. Math. 2014, 8, 155–171. [Google Scholar] [CrossRef]
- Bermudo, S.; Rodríguez, J.M.; Sigarreta, J.M. On the differential in graphs. Util. Math. 2015, 97, 257–270. [Google Scholar]
- Pushpam, P.R.L.; Yokesh, D. Differential in certain classes of graphs. Tamkang J. Math. 2010, 41, 129–138. [Google Scholar] [CrossRef]
- Sigarreta, J.M. Differential in Cartesian Product Graphs. Ars Comb. 2016, 26, 259–267. [Google Scholar]
- Goddard, W.; Henning, M.A. Generalised domination and independence in graphs. Congr. Numer. 1997, 123, 161–171. [Google Scholar]
- Zhang, C.Q. Finding critical independent sets and critical vertex subsets are polynomial problems. SIAM J. Discrete Math. 1990, 3, 431–438. [Google Scholar] [CrossRef]
- Basilio, L.A.; Bermudo, S.; Leaños, J.; Sigarreta, J.M. β-Differential of a Graph. Symmetry 2017, 9, 205. [Google Scholar] [CrossRef]
- Slater, P.J. Enclaveless sets and MK-systems. J. Res. Natl. Bur. Stand. 1977, 82, 197–202. [Google Scholar] [CrossRef]
- Cvetkocić, D.M.; Doob, M.; Sachs, H. Spectra of Graphs: Theory and Application; Academic Press: New York, NY, USA, 1980. [Google Scholar]
- Bindusree, A.R.; Cangul, I.N.; Lokesha, V.; Cevik, A.S. Zagreb polynomials of three graph operators. Filomat 2016, 30, 1979–1986. [Google Scholar] [CrossRef]
- Prisner, E. Graph Dynamics; CRC Press: Boca Raton, FL, USA, 1995; Volume 338. [Google Scholar]
- Ranjini, P.S.; Lokesha, V. Smarandache-Zagreb index on three graph operators. Int. J. Math. Comb. 2010, 3, 1. [Google Scholar]
- Yan, W.; Yang, B.Y.; Yeh, Y.N. The behavior of Wiener indices and polynomials of graphs under five graph decorations. Appl. Math. Lett. 2007, 20, 290–295. [Google Scholar] [CrossRef]
- Harary, F.; Norman, R.Z. Some properties of line digraphs. Rend. Circ. Mat. Palermo 1960, 9, 161–168. [Google Scholar] [CrossRef]
- Méndez-Bermúdez, J.A.; Reyes, R.; Rodríguez, J.M.; Sigarreta, J.M. Hyperbolicity on Graph Operators. Symmetry 2018, 10, 360. [Google Scholar] [CrossRef]
- Gallai, T. Über extreme Punkt-und Kantenmengen. Ann. Univ. Sci. Budapest Eötvös Sect. Math. 1959, 2, 133–138. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).