Fast Convergence Methods for Hyperbolic Systems of Balance Laws with Riemann Conditions
Abstract
1. Introduction
2. Sinc-Approximation Formula
3. The Sinc–Galerkin Method: Balance Laws
Treatment of Non-Zero Boundary Conditions
4. The Adomian Decomposition Method (ADM)
Convergence of the ADM Approximation
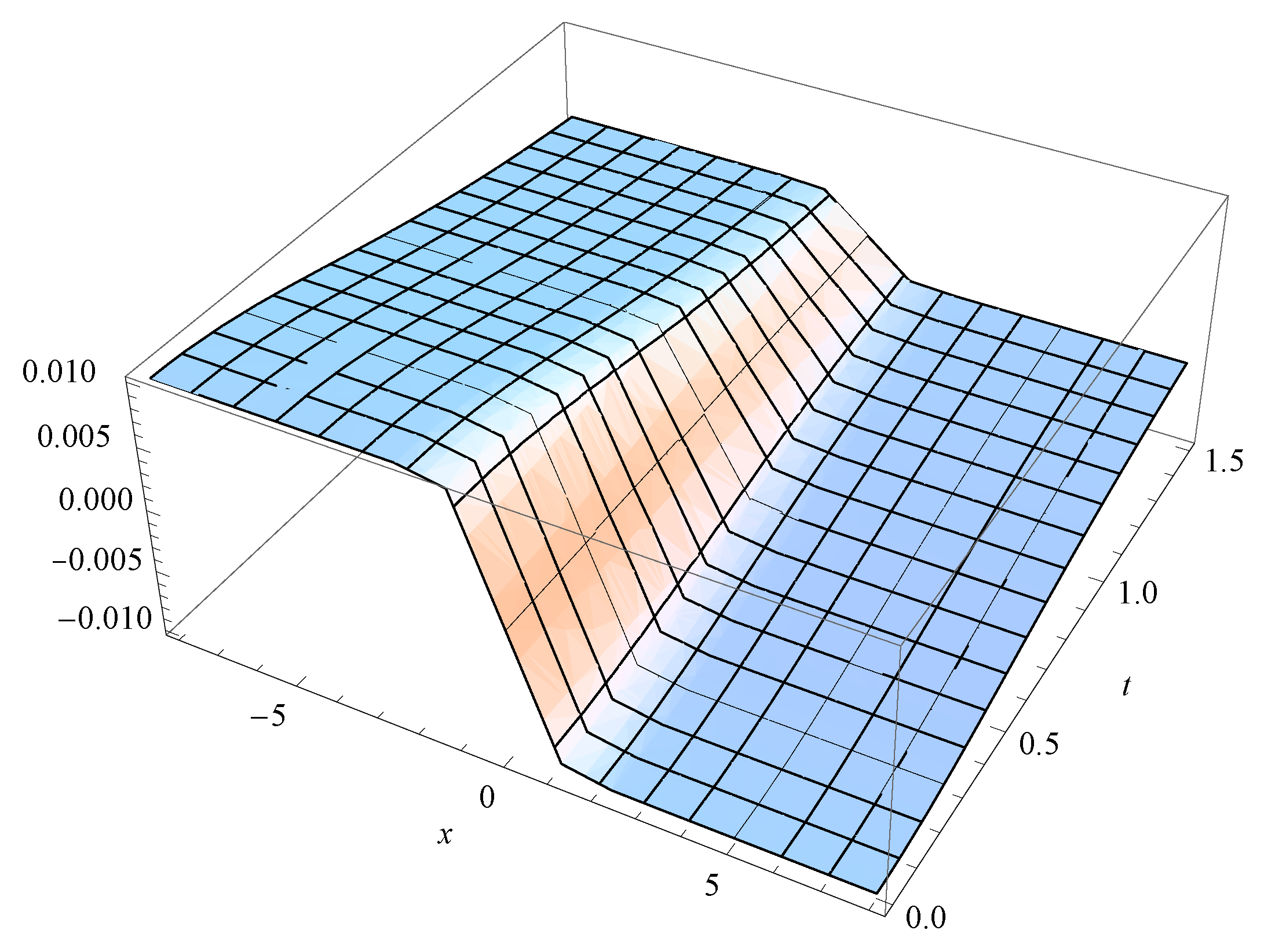
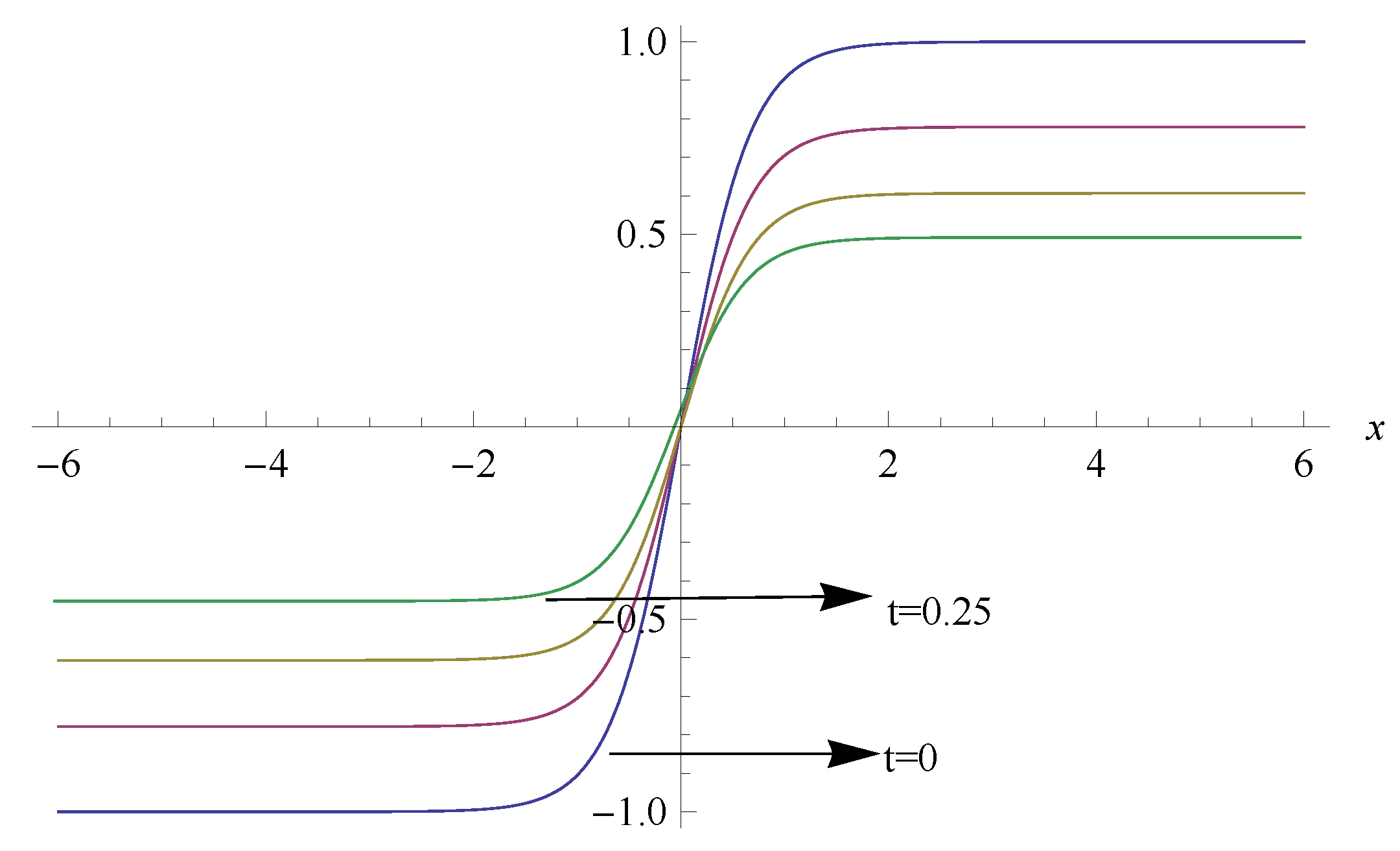
5. Applications: Riemann Type
Author Contributions
Funding
Conflicts of Interest
References
- Pirkhedri, A.; Javdi, H.H.S.; Navidi, H.R. Numerical algorithm based on Haar-Sinc collocation method for solving the hyperbolic PDEs. Sci. World J. 2014, 2014, 340752. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Kalisch, H.; Mitrovic, D.; Teyekpiti, V. Existence and uniqueness of singular solutions for a conservation law arising in magnetohydrodynamics. Nonlinearity 2018, 31, 5463–5483. [Google Scholar] [CrossRef]
- Fitt, A.D. The numerical and analytical systems of conservation laws. Appl. Math. Model. 1989, 13, 618–631. [Google Scholar] [CrossRef]
- Az-Zo’bi, E.A. Construction of solutions for mixed hyperbolic elliptic Riemann initial value system of conservation laws. Appl. Math. Model. 2013, 37, 6018–6024. [Google Scholar] [CrossRef]
- Sod, G.A. A survey of several finite difference methods for systems of nonlinear hyperbolic conservation laws. J. Comput. Phys. 1978, 27, 1–31. [Google Scholar] [CrossRef]
- Rashidinia, J.; Barati, A. Numerical solutions of one-dimensional non-linear parabolic equation using Sinc collocation method. Ain Shams Eng. J. 2015, 6, 381–389. [Google Scholar] [CrossRef][Green Version]
- Al-Khaled, K.; Allan, F. Decomposition method for solving nonlinear integro-differential equations. J. Appl. Math. Comput. 2005, 19, 415. [Google Scholar] [CrossRef]
- Al-Khaled, K. Cardinal-type approximations for conservation laws of mixed type. Nonlinear Stud. 2014, 21, 423–433. [Google Scholar]
- Alquran, M.; Ali, M.; Al-Khaled, K. Solitary wave solutions to shallow water waves arising in fluid dynamics. Nonlinear Stud. 2012, 19, 555–562. [Google Scholar]
- Al-Khaled, K. Numerical solutions of time-fractional partial differential equation using Sumudu decomposition method. Rom. J. Phys. 2015, 60, 99–110. [Google Scholar]
- Az-Zo’bi, E.A.; Al-Khaled, K. A new convergence proof of the Adomian decomposition method for a mixed hyperbolic elliptic system of conservation laws. Appl. Math. Comput. 2010, 217, 4248–4256. [Google Scholar] [CrossRef]
- Fjordholm, U.S.; Lye, K.; Mishra, S.; Weber, F. Statistical solutions of hyperbolic systems of conservation laws: Numerical approximation. arXiv 2019, arXiv:1906.02536. [Google Scholar] [CrossRef]
- Hussain, A.; Bano, S.; Khan, I.; Baleanu, D.; Sooppy Nisar, K. Lie Symmetry Analysis, Explicit Solutions and Conservation Laws of a Spatially Two-Dimensional Burgers-Huxley Equation. Symmetry 2020, 12, 170. [Google Scholar] [CrossRef]
- Randall, J.L. Numerical Methods for Conservation Laws, Lectures in Mathematics, 2nd ed.; ETH Zürich: Zürich, Switzerland; Birkhäuser: Basel, Switzerland, 1992. [Google Scholar]
- Stenger, F. Numerical Methods Based on Sinc and Analytical Functions; Springer: New York, NY, USA, 1993. [Google Scholar]
- Al-Khaled, K. Theory and Computation in Hyperbolic Model Problems. Ph.D Thesis, University of Nebraska, Lincoln, NE, USA, 1996. [Google Scholar]
- Lund, J.; Rowers, K.L. Sinc Methods for Quadrature and Differential Equations; SIAM: Philadelphia, PA, USA, 1992. [Google Scholar]
- Al-Khaled, K. Kamel Al-Khaled; A Sinc-Galerkin approach to the p-system. Saitama Math. J. 1998, 16, 1–13. [Google Scholar]
- Adomian, G. A review of the decomposition method in applied Mathematics. J. Math. Anal. Appl. 1988, 135, 501–544. [Google Scholar] [CrossRef]
- Adomian, G. Solving Frontier Problems of Physics: The Decomposition Method; Kluwer: Boston, UK, 1994. [Google Scholar]
- Cherrualt, Y.; Adomian, G. Decomposition methods: A new proof of convergence. Math. Comput. Model. 1993, 18, 103–106. [Google Scholar] [CrossRef]
- Alquran, M.T.; Al-Khaled, K.M. Numerical Comparison of Methods for Solving Systems of Conservation Laws of Mixed Type. Int. J. Math. Anal. 2011, 5, 35–47. [Google Scholar]
- El-Sayed, A.M.A.; Hashem, H.H.G.; Ziada, E.A.A. Picard and Adomian decomposition methods for a quadratic integral equation of fractional order. Comput. Appl. Math. 2014, 33, 95–109. [Google Scholar] [CrossRef]
- Rach, R. On the Adomian (decomposition) method and comparisons with Picard’s method. J. Math. Anal. Appl. 1987, 128, 480–483. [Google Scholar] [CrossRef]
- Holden, H.; Holden, L.; Risebro, N.H. Some qualitative properties of 2 × 2 systems of conservation laws of mixed type. In Nonlinear Evolution Equations That Change Type; Springer: New York, NY, USA, 1990. [Google Scholar]
| 4 | ||
| 8 | ||
| 16 | ||
| 32 | ||
| 64 |
| Iteration No. | ||
|---|---|---|
| First | ||
| Second | ||
| Third | ||
| Fourth |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al-Khaled, K.; Rababah, N.M. Fast Convergence Methods for Hyperbolic Systems of Balance Laws with Riemann Conditions. Symmetry 2020, 12, 757. https://doi.org/10.3390/sym12050757
Al-Khaled K, Rababah NM. Fast Convergence Methods for Hyperbolic Systems of Balance Laws with Riemann Conditions. Symmetry. 2020; 12(5):757. https://doi.org/10.3390/sym12050757
Chicago/Turabian StyleAl-Khaled, Kamel, and Nid’a M. Rababah. 2020. "Fast Convergence Methods for Hyperbolic Systems of Balance Laws with Riemann Conditions" Symmetry 12, no. 5: 757. https://doi.org/10.3390/sym12050757
APA StyleAl-Khaled, K., & Rababah, N. M. (2020). Fast Convergence Methods for Hyperbolic Systems of Balance Laws with Riemann Conditions. Symmetry, 12(5), 757. https://doi.org/10.3390/sym12050757





