Abstract
In this paper, we develop an accurate technique via the use of the Adomian decomposition method (ADM) to solve analytically a systems of partial differential equation that represent balance laws of hyperbolic-elliptic type. We prove that the sequence of iteration obtained by ADM converges strongly to the exact solution by establishing a construction of fixed points. For comparison purposes, we also use the Sinc function methodology to establish a new procedure to solve numerically the same system. It is shown that approximation by Sinc function converges to the exact solution exponentially, also handles changes in type. A numerical example is presented to demonstrate the theoretical results. It is noted that the two methods show the symmetry in the approximate solution. The results obtained by both methods reveal that they are reliable and convenient for solving balance laws where the initial conditions are of the Riemann type.
1. Introduction
Many mathematical and practical problems in physics can be modeled by balance laws, which are systems of nonlinear partial differential equations, usually of hyperbolic type. Balance laws describe very large branches of scientific fields, specifically in fluid and gas dynamics, quantum mechanics, and astrophysics.
In this paper, we present the mathematical formulation for finding numerical solution using Sinc basis functions for systems of balance laws, while for comparison purposes, we also use the Adomian series technique to find approximate analytical solutions for the same model system that which can be written as
The solution U, which is a vector of two components that might represent the length of a wave, and another component, say which is the velocity of that wave. i.e., . On the other hand the flux function can be represented as , and finally, the source term has the form . where F is a smooth function on of U, and the derivative of F possesses strictly nonlinear or linearly degenerate eigenfunctions and eigenvalues. The system (1) is of mixed type, it is of elliptic type, for all values of that satisfy and of hyperbolic type for data that lying in . We consider in Equation (1) the simplest piece-wise constant initial data, i.e., for certain dispositions of the Riemann initial data
We solve Equation (1) subject to the initial conditions
that turn (1) and (3) into a system that is of mixed type (hyperbolic-elliptic). In recent years, the numerical (approximate) solutions for (1) was considered by many authors. In [] they investigates the Haar-Sinc collocation method for the solution of hyperbolic systems of partial differential equations with applications to the telegraph equation. Existence and uniqueness for a system of conservation laws, called Brio system, that arising as a model used in magnetohydrodynamics is developed in []. In [] two mixed systems of conservation laws are considered, where numerical and analytical solutions for these two of ill-posed systems are presented. The Adomian decomposition method was used in [] to develop a fast and accurate algorithm for systems of conservation laws of mixed hyperbolic elliptic type. A survey of several numerical methods for solving nonlinear systems of conservation laws are presented in []. A numerical method based on the use of Sinc-collocation method for solving parabolic problems was proposed in []. For the construction of numerical solutions; see [,,]. In [], the Sumudu decomposition method was developed to solve general form of fractional partial differential equations. A new convergence proof for the solution conservation laws of mixed type using the ADM was proposed in []. This is with the knowledge that there are many previous studies dealing with this topic, and some of them gave examples from physics and other sciences, to demonstrate the importance of system appeared in (1), and how it is used in practical life, for example we refer to [,,,].
In this paper, we change the given partial differential equation into a Volterra integral equation, where we discretized in space direction by means of Sinc methodology. After that we apply the indefinite integral formula in time direction which is based on Sinc basis functions. As a result, we are replacing integrals and derivatives with their discrete Sinc approximations, to produce a discrete system of matrices. There are several reasons to approximate by Sinc functions, we mentioned, that they are easily performed and give good accuracy for mixed type problems, also approximation by Sinc are typified by errors of the form where is a constant and h is a step size.
This research is written in the following order. Initially, in Section 2, we review the important theories and definitions that were mentioned in Sinc theory that would be helpful in writing and building the approximate solution to the issue under study, while Section 3 is devoted to employing what was mentioned in the second section to write the solution using the Sinc method and converting differential equations into a system of algebraic equations, for which solutions can be found in traditional methods such as iterative techniques. As for the Section 4, it is devoted to finding the approximate solution by using the Adomian series, in adding to that, we state and proof a theorem that related to the convergence of the solution. In addition, some relationships related to the order of convergence of the approximate solution are also mentioned. In Section 5, the two methods under discussion are discussed in one example, and all the observations resulting from the solution of the example were mentioned as benefits of the two methods and summarized in tables and graphs. Finally, we will introduce a new issue called the Telegraph system, which is still new and has not been solved by Sinc methodology, and we hope to refer to it in upcoming research.
2. Sinc-Approximation Formula
The Sinc Galerkin method was developed by Stenger []. For the equation given in (1), together with the initial condition in (3), the Sinc–Galerkin scheme can be developed in both space and time directions as follows: Since our space domain is and time is , we define conformal maps which mapping from , the eye-shaped domain in the plane onto the infinite strip, , where
For the sinc method, the basis functions on the interval for , and for the time interval are derived from the composite translated sinc functions
where
and,
Let f be a function defined on , then for we define the Whittaker cardinal series
The properties of (6) were studied and surveyed in depth in Stenger and in Lund [,,]. They are based on the infinite strip defined in as
To approximate by the Sinc method, we will refer to an important class of functions, see [] called Play-Wiener class, denoted by which is the family of all analytic functions that are in , and satisfy some decaying conditions. For a function f and its derivative to be in the class , the derivative of the function f can be approximated by
where denotes the derivative of the cardinal function. Now we present a fundamental definition that has an important role in the development of Sinc methods on arc in . For the simply connected domain D, let be a map that take D onto with and . If the inverse map of is denoted by , define
When we evaluate a function and its derivative with respect to , we obtain
Since we will replace the first derivative by it matrix approximations, here we define the matrix whose entry is given by . An important class of functions denoted by play crucial rule in approximating derivatives will be needed in next formula (see, []). Let , is a positive constant, then for we have
An application to the above formula, and in order to approximate the first derivative with respect to x for the function in the domain leads to the approximation
where and . With and the skew-symmetric matrix is defined by (9). Finally, we shall indicate a general formula for approximating the integral . If , then for all ,
To simplify the situation, we define the new matrix , as, for N positive integer, define the matrix by
3. The Sinc–Galerkin Method: Balance Laws
Among the benefits of the Sinc method, is that the approximate solution is approaching the exact solution exponentially, as well as the Sinc method, it carefully handles systems in which the state changes from elliptic to hyperbolic and vis versa, as this depends on the change of the eigen-values of the system. To find an approximate solution for the balance law appeared in (1), without loss of generality, we begin with a 1-dimensional balance law defined in the domain
where the initial condition is taken to be
Suppose , and for the step-size .
Integrate Equation (12) with respect to time, and collocation with respect to the variable x will produce a system of Volterra integral equations of the form
where the column vector represent , here we use the notation , and , while the square matrix represents the discrete Sinc approximation for the first derivative. Subsequently an application of the use of the indefinite integration formula with respect to time variable t, and since our , then the domain is conformally mapped onto via . Define , to be the basis function for the interval . Now, we define a matrix with the nodes , where
, and as defined in (11), with . Then the solution of Equation (12) is in matrix form is given by the rectangular matrix :
we use ∘ to represents the Hadamard multiplication. For convergence purposes for the obtained solution we state two Theorems, in which the proof can be done by just resemble the theorems in [].
Theorem 1
([]). Let the matrix U be as defined in (15). Then for the number of points in both space and time to be bigger than some constant that depends on , we have
where
To guarantee that our approximate solution as obtained in the discrete system (15) converges uniquely to the true solution, we state the following theorem.
Theorem 2
([,]). For any positive constant R, we can find another positive constant so that whenever , then the solution of (15) is unique. Also, the iteration system
leads to a solution that converges to the unique solution.
Next, we state and prove a fact regarding the behavior of the solution, whenever the initial condition satisfies a decay condition. Consider the initial value problem for a balance law of the form
with initial condition . We need to assume some decaying conditions on the right hand side of Equation (16).
Definition 1.
We say a function decays exponentially in x and uniformly for if for some positive constants independent of t.
Theorem 3.
Suppose , and can be written as , where the function is analytic in the strip and grows no more than a polynomial in the strip , and suppose the source term and its derivatives with respect to are all exponentially decaying in x and uniformly for small t. Then the solution of (16) is in the class .
Proof.
However, and its derivatives with respect to the variables and t are all exponentially decaying in x and uniformly for small t. This implies that
is Lipschitz in the two variables . In addition, so, by the Picard theorem, the solution is unique. □
Treatment of Non-Zero Boundary Conditions
The obtained solution in (15) was valid if the initial condition satisfy some certain decaying conditions, i.e, the initial condition has to belong to the class . In Section 5, we will discuss problems which have non-zero boundary conditions with the Riemann-type initial condition, which means that the initial condition is no longer in . To illustrate the situation, we consider the problem in (1) with the initial condition (3), and since the Sinc functions composed with the various conformal maps, , are zero at the end-points of the domain of the problem, and since the boundary conditions are non-homogeneous Dirichlet conditions, then the change of variables
(similarly for ), will convert system (1) to another one with homogeneous Dirichlet conditions, with smooth initial condition. We substitute the transformation (19) into Equation (1) that leads to a new balance law for the new unknown with an initial condition that is in the class for large. Therefore, to find the solution for we can proceed as mentioned above.
4. The Adomian Decomposition Method (ADM)
A lot of published research papers talked about the method of Adomian, and presented it in a detailed way. Here, for the sake of non-repetition, we will suffice to mention the references that contributed to the development of the method. In addition, because of its abundance and where we cannot limit it, we mention the following [,,,]. We start by rewriting the system in (1) as follows:
or, we may express Equations (20) using linear differential operators as
In the above, the operators are defined to be and . Performing the inverse operator PDE system in (21) yields
where , , and . The ADM [,] suggests that our approximate solution for unknown functions and are given by the infinite series
while the four nonlinear operators can be expressed as an infinite series of Adomian polynomials as , where are what is called Adomian’s polynomials that can be computed according to specific formula set in []. Here, the general formulas for Adomian’s polynomials , has the form
These formulas are smoothly found using coding programs to get as many terms as we want. Plug the nonlinear system (23) into Equation (22) and we arrive at the recursive relation
The construction of the solutions of and are given by
Regarding the convergence of the above two series, there are previous studies that dealt with the topic in detail and in general, we mention [].
Convergence of the ADM Approximation
Here we give a proof to show that our obtained solution using ADM converges to the exacts solution via the use of the fixed-point theory. The partial differential equation that we are encountered to solve is
which can be written as
where H is the Hilbert space, and is the nonlinear operator and the source term is that is also in H. For the solution using ADM, we assume the solution u and the nonlinear functions are decomposed into an infinite series of the form
Substituting these series back into Equation (26) yields
Comparing terms, we end up with the algorithm . Then the approximate solution is given by a finite sum of the series . If If the limit exist, then is the solution of the fixed-point functional equation . Need to show that the sequence is Cauchy. The distance between two consecutive iterations and is a ball of radius r is given by
To prove that is Cauchy sequence, then for all positive integers where , we have
Choose such that, can be made arbitrarily small provided n is large enough for all . With this choice of r and we see that all iterations will remain in the ball
There is an integer N such that , for any m. So the sequence is Cauchy in the Hilbert space. Hence converges to some , i.e., , where . Solving Equation (26) is the same as solving the functional equation , by assuming that N is a continuous operator, we get
So S is the solution of Equation (26).
When viewing numerical calculations in the last section, and for purposes of comparison we will calculate what is called the order of convergence, we will provide the following definition
Definition 2.
A sequence is said to converge to S of order , if there is a positive constant α such that
Let us examine the order of convergence for the Cauchy sequence . We write Taylor’s series for about as
However, it is known that and , we may rewrite the above equation as
Assume our operator with the property that for all , while it satisfy , therefore we have
divide by and take limit as , we obtain
Using the fact that is Cauchy that converges to S, the above equation reduces to
Therefore, the order of convergence of is p.
For the purposes of calculating the order of convergence, we assume that the first four iterations of the computed solution are given by and so the following formula will be used to calculate the order of convergence
As mentioned in [], the first study comparing ADM and Picard’s method was in 1987 by Rach []. The study was done by reviewing several examples. Rach showed that solving differential equations of linear type using ADM was equivalent to the classical method of successive approximations, which is known as Picard iteration. Also it was shown that the Picard method gives more accurate solutions, but it needs more time than ADM; this happens because the main advantage of Adomian’s method over the Picard method is the ease of computation of successive terms.
5. Applications: Riemann Type
To investigate the accuracy of the ADM compared with the Sinc method, we choose examples with known solutions that allows for a more complete error analysis. So a system of balance laws with Riemann type conditions is tested numerically by using the Sinc function methodology, and for comparison purposes, we also solve the same model by ADM. The example reported here is selected to show the convergence of the two schemes. Consider the system
where T is some small constant. In addition,
with flux function , such that
with the approximations to Riemann type condition
given by
The left and right boundary conditions are
Here the true solution given by
Thus, we can calculate the appropriate source term by applying the differential operator to the solution. The source term in (28) turns out to be
and,
In Section 3 when we construct the approximate solution by means of the Sinc methodology, it was necessary that the initial condition belonged to the class of functions previously mentioned in Section 3, but we know that the Riemann condition does not belong to this family, so a transformation had to be made to make the primitive condition belong to the family. Since the boundary conditions are non-homogeneous, then the transformation
where , and will convert the given boundary conditions to homogeneous conditions, provided that . Now, after substituting the transformation (29) into Equation (28), we get a new system with the unknown given by
with initial condition
where . Equation (30) can be solved for , and then, using the transformation in (29), for . To proceed, since the space and the time domains are and , respectively, choose the conformal maps and . We solve the above system using ADM subject to the initial conditions . Integrate the system in (28) with respect to t and using the initial conditions , we arrive at
and,
In the above two integrals, set and for the nonlinear terms, we find Adomian polynomials as
The first few terms of Adomian polynomials are given by
Substitute the above infinite sum for Adomian polynomials, together with the approximate solutions into Equations (32) and (33), exactly as mentioned in Section 5. Balancing terms in Equations we obtain an approximate solution of the form
Table 1 shows that the method converges for using Sinc methodology, where the second column reports the supremum norm of the error between the exact solution and the Sinc approximate solution, while the third column reports the error between the exact solution and the Sinc approximate solution. The error in the approximate u-solution using ADM is reported in Figure 1. Figure 2 reported the -solution using ADM for different values of time t. The error in approximating show that most of the error concentrates at origin, which caused by approximating Riemann type condition by a smooth function. Through our study, and upon consulting the Table 1 and Table 2, we are able to find the values for the order of convergence using Equation (27), it was found that the order of convergence for the ADM is , while it is approximately using the Sinc method. This is in accordance with the theories formulated in Section 4, which show that the Sinc methodology is faster, better, and more comprehensive in finding an approximate solution. Because of the nature of the issues under discussion, it is noted that the two methods show the symmetry of the approximate solution. A quick look at in calculated approximate solutions for both and shows the symmetry of the solutions where the error value at the point is the same as at . The main goal of this research paper is to compare the two methods together, but if the reader wants more ways to solve systems from the same context, we cite the following []. It was shown in [] that traditional methods, like finite difference method is unstable when the system is of mixed-type when Riemann conditions are involved, which means that the two methods used in this research are an improvement over the previous traditional methods. To present a physical and engineering application for the purposes of explaining the importance of the topic, please review the research paper [] where the system was solved. Finally, what we intend to refer to in a future research in the hope of discussing it from all sides is the importance of the Telegraph system. As an illustration, we shall consider conductors (such as telephone wires or submarine cables) in which the current may leak to ground. The resultant decrease in current is governed by , where is voltage, is the conductance to ground, and is the capacitance with the ground. The change in voltage is governed by , where is the resistance and is the inductance of the cable.

Table 1.
The absolute error using Sinc method for different values of .
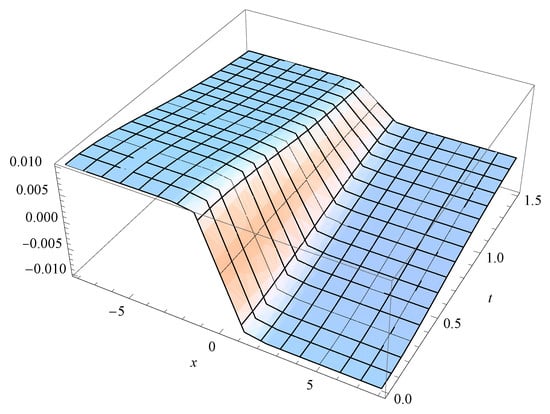
Figure 1.
The error for the solution using ADM.
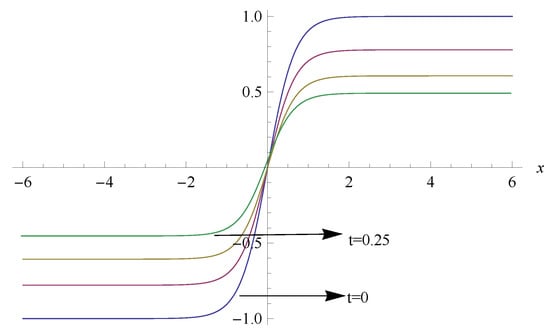
Figure 2.
The approximate solution using ADM for different values of time t.

Table 2.
The iterations that use ADM for at .
Author Contributions
Formal analysis, investigation, and writing-original draft preparation K.A.-K. and N.M.R. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare that there is no conflict of interests regarding the publication of this manuscript. The authors declare that they have no competing interests.
References
- Pirkhedri, A.; Javdi, H.H.S.; Navidi, H.R. Numerical algorithm based on Haar-Sinc collocation method for solving the hyperbolic PDEs. Sci. World J. 2014, 2014, 340752. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Kalisch, H.; Mitrovic, D.; Teyekpiti, V. Existence and uniqueness of singular solutions for a conservation law arising in magnetohydrodynamics. Nonlinearity 2018, 31, 5463–5483. [Google Scholar] [CrossRef]
- Fitt, A.D. The numerical and analytical systems of conservation laws. Appl. Math. Model. 1989, 13, 618–631. [Google Scholar] [CrossRef]
- Az-Zo’bi, E.A. Construction of solutions for mixed hyperbolic elliptic Riemann initial value system of conservation laws. Appl. Math. Model. 2013, 37, 6018–6024. [Google Scholar] [CrossRef]
- Sod, G.A. A survey of several finite difference methods for systems of nonlinear hyperbolic conservation laws. J. Comput. Phys. 1978, 27, 1–31. [Google Scholar] [CrossRef]
- Rashidinia, J.; Barati, A. Numerical solutions of one-dimensional non-linear parabolic equation using Sinc collocation method. Ain Shams Eng. J. 2015, 6, 381–389. [Google Scholar] [CrossRef][Green Version]
- Al-Khaled, K.; Allan, F. Decomposition method for solving nonlinear integro-differential equations. J. Appl. Math. Comput. 2005, 19, 415. [Google Scholar] [CrossRef]
- Al-Khaled, K. Cardinal-type approximations for conservation laws of mixed type. Nonlinear Stud. 2014, 21, 423–433. [Google Scholar]
- Alquran, M.; Ali, M.; Al-Khaled, K. Solitary wave solutions to shallow water waves arising in fluid dynamics. Nonlinear Stud. 2012, 19, 555–562. [Google Scholar]
- Al-Khaled, K. Numerical solutions of time-fractional partial differential equation using Sumudu decomposition method. Rom. J. Phys. 2015, 60, 99–110. [Google Scholar]
- Az-Zo’bi, E.A.; Al-Khaled, K. A new convergence proof of the Adomian decomposition method for a mixed hyperbolic elliptic system of conservation laws. Appl. Math. Comput. 2010, 217, 4248–4256. [Google Scholar] [CrossRef]
- Fjordholm, U.S.; Lye, K.; Mishra, S.; Weber, F. Statistical solutions of hyperbolic systems of conservation laws: Numerical approximation. arXiv 2019, arXiv:1906.02536. [Google Scholar] [CrossRef]
- Hussain, A.; Bano, S.; Khan, I.; Baleanu, D.; Sooppy Nisar, K. Lie Symmetry Analysis, Explicit Solutions and Conservation Laws of a Spatially Two-Dimensional Burgers-Huxley Equation. Symmetry 2020, 12, 170. [Google Scholar] [CrossRef]
- Randall, J.L. Numerical Methods for Conservation Laws, Lectures in Mathematics, 2nd ed.; ETH Zürich: Zürich, Switzerland; Birkhäuser: Basel, Switzerland, 1992. [Google Scholar]
- Stenger, F. Numerical Methods Based on Sinc and Analytical Functions; Springer: New York, NY, USA, 1993. [Google Scholar]
- Al-Khaled, K. Theory and Computation in Hyperbolic Model Problems. Ph.D Thesis, University of Nebraska, Lincoln, NE, USA, 1996. [Google Scholar]
- Lund, J.; Rowers, K.L. Sinc Methods for Quadrature and Differential Equations; SIAM: Philadelphia, PA, USA, 1992. [Google Scholar]
- Al-Khaled, K. Kamel Al-Khaled; A Sinc-Galerkin approach to the p-system. Saitama Math. J. 1998, 16, 1–13. [Google Scholar]
- Adomian, G. A review of the decomposition method in applied Mathematics. J. Math. Anal. Appl. 1988, 135, 501–544. [Google Scholar] [CrossRef]
- Adomian, G. Solving Frontier Problems of Physics: The Decomposition Method; Kluwer: Boston, UK, 1994. [Google Scholar]
- Cherrualt, Y.; Adomian, G. Decomposition methods: A new proof of convergence. Math. Comput. Model. 1993, 18, 103–106. [Google Scholar] [CrossRef]
- Alquran, M.T.; Al-Khaled, K.M. Numerical Comparison of Methods for Solving Systems of Conservation Laws of Mixed Type. Int. J. Math. Anal. 2011, 5, 35–47. [Google Scholar]
- El-Sayed, A.M.A.; Hashem, H.H.G.; Ziada, E.A.A. Picard and Adomian decomposition methods for a quadratic integral equation of fractional order. Comput. Appl. Math. 2014, 33, 95–109. [Google Scholar] [CrossRef]
- Rach, R. On the Adomian (decomposition) method and comparisons with Picard’s method. J. Math. Anal. Appl. 1987, 128, 480–483. [Google Scholar] [CrossRef]
- Holden, H.; Holden, L.; Risebro, N.H. Some qualitative properties of 2 × 2 systems of conservation laws of mixed type. In Nonlinear Evolution Equations That Change Type; Springer: New York, NY, USA, 1990. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).