Inertial Mann-Type Algorithm for a Nonexpansive Mapping to Solve Monotone Inclusion and Image Restoration Problems
Abstract
1. Introduction
2. Preliminaries
- 1.
- for all ,
- 2.
- for all ,
- 3.
- for all and
- 1.
- If (where ), then is bounded.
- 2.
- If and , then the sequence converges to 0.
- 1.
- and ,
- 2.
- , and ,
- 3.
3. Main Results
4. Applications
- 1.
- If we set for all in Lemma 5, where with
- 2.
- If we set for all in Lemma 5, where with
- 1.
- strongly converges to , wherefor some .
- 2.
- and strongly converge to .
- 1.
- strongly converges to for some .
- 2.
- and strongly converge to .
5. Numerical Experiments
5.1. Convex Minimization Problems
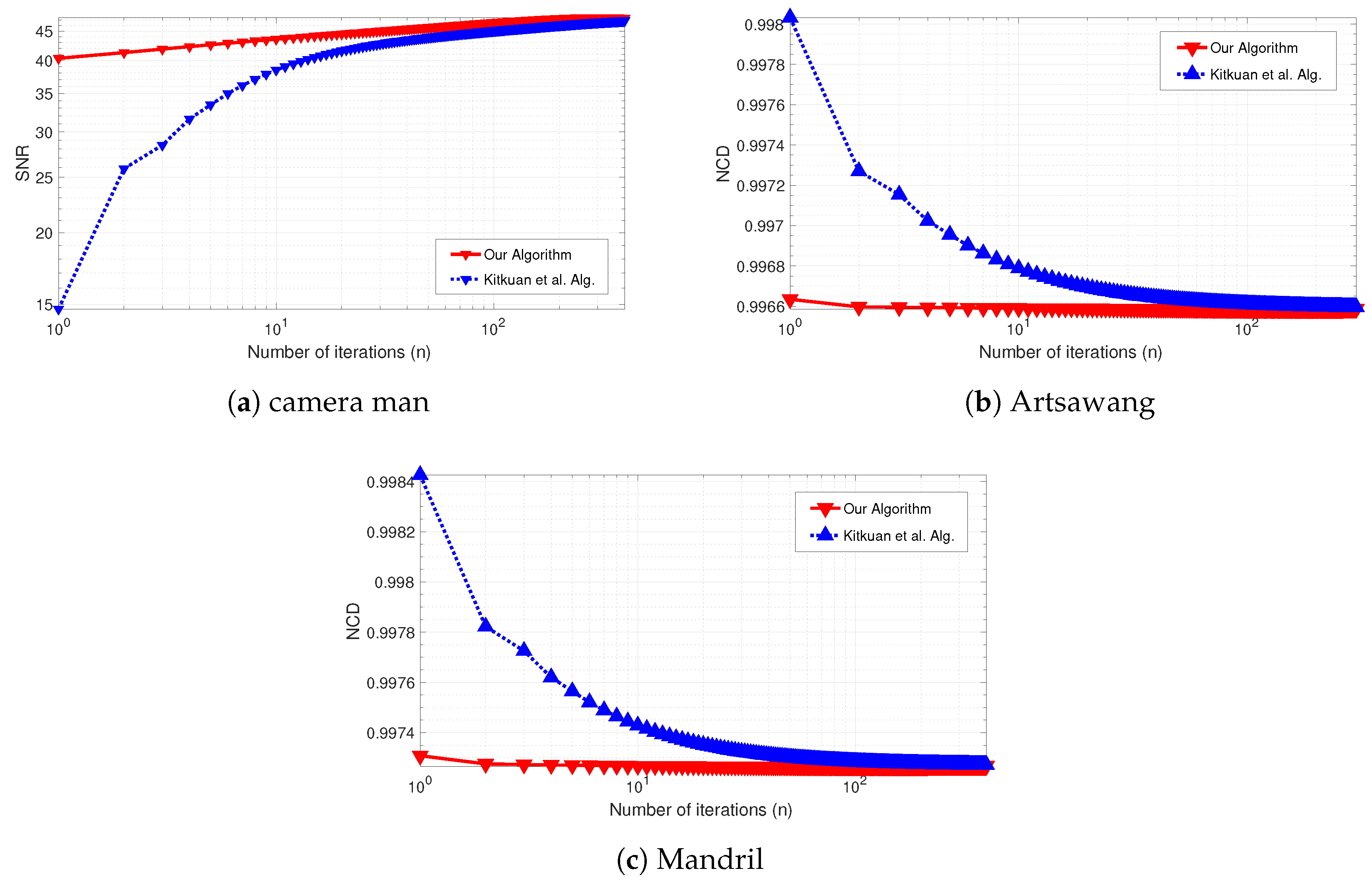
5.2. Image Restoration Problems
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bauschke, H.H.; Combettes, P.L. Convex Analysis and Monotone Operator Theory in Hilbert Spaces; CMS Books in Mathematics; Springer: New York, NY, USA, 2011. [Google Scholar]
- Bagiror, A.; Karmitsa, N.; Mäkelä, M.M. Introduction to Nonsmooth Optimization: Theory, Practice and Software; Springer: New York, NY, USA, 2014. [Google Scholar]
- Mann, W.R. Mean value methods in iteration. Proc. Am. Math. Soc. 1953, 4, 506–510. [Google Scholar] [CrossRef]
- Bauschke, H.H.; Combettes, P.L. A weak-to-strong convergence principle for fejer-monotone methods in Hilbert spaces. Math. Oper. Res. 2001, 26, 248–264. [Google Scholar] [CrossRef]
- Reich, S. Weak convergence theorems for nonexpansive mappings in Banach spaces. J. Math. Anal. Appl. 1979, 67, 274–276. [Google Scholar] [CrossRef]
- Halpern, B. Fixed points of nonexpansive maps. Bull. Am. Math. Soc. 1967, 73, 957–961. [Google Scholar] [CrossRef]
- Shioji, N.; Takahashi, W. Strong convergence of approximated sequences for nonexpansive mapping in Banach spaces. Proc. Am. Math. Soc. 1997, 125, 3641–3645. [Google Scholar] [CrossRef]
- Chidume, C.E.; Chidume, C.O. Iterative approximation of fixed points of nonexpansive mappings. J. Math. Anal. Appl. 2006, 318, 288–295. [Google Scholar] [CrossRef]
- Cholamjiak, P. A generalized forward-backward splitting method for solving quasi inclusion problems in Banach spaces. Numer. Algorithms 2016, 71, 915–932. [Google Scholar] [CrossRef]
- Lions, P.-L. Approximation de points fixes de contractions. CR Acad. Sci. Paris Sér. 1977, 284, A1357–A1359. [Google Scholar]
- Reich, S. Strong convergence theorems for resolvents of accretive operators in Banach spaces. J. Math. Anal. Appl. 1980, 75, 287–292. [Google Scholar] [CrossRef]
- Reich, S. Some problems and results in fixed point theory. Contemp. Math. 1983, 21, 179–187. [Google Scholar]
- Wittmann, R. Approximation of fixed points of nonexpansive mappings. Arch. Math. 1992, 58, 486–491. [Google Scholar] [CrossRef]
- Xu, H.-K. Iterative algorithms for nonlinear operators. J. Lond. Math. Soc. 2002, 66, 240–256. [Google Scholar] [CrossRef]
- Moudafi, A. Viscosity approximation methods for fixed points problems. J. Math. Anal. Appl. 2000, 241, 46–55. [Google Scholar] [CrossRef]
- Dong, Q.L.; Lu, Y.Y. A new hybrid algorithm for a nonexpansive mapping. Fixed Point Theroy Appl. 2015, 2015, 37. [Google Scholar] [CrossRef]
- Dong, Q.L.; Yuan, H.B. Accelerated Mann and CQ algorithms for finding a fixed point of a nonexpansive mapping. Fixed Point Theroy Appl. 2015, 2015, 125. [Google Scholar] [CrossRef]
- Kanzow, C.; Shehu, Y. Generalized Krasnoselskii-Mann-type iterations for nonexpansive mappings in Hilbert spaces. Comput. Optim. Appl. 2017, 67, 595–620. [Google Scholar] [CrossRef]
- Kim, T.H.; Xu, H.K. Strong convergence of modified Mann iterations. Non-Linear Anal. 2005, 61, 51–60. [Google Scholar] [CrossRef]
- Takahashi, W. Nonlinear Functional Analysis; Yokohama Publishers: Yokohama, Japan, 2000. [Google Scholar]
- Boţ, R.I.; Csetnek, E.R.; Meier, D. Inducing strong convergence into the asymptotic behaviour of proximal splitting algorithms in Hilbert spaces. Optim. Methods Softw. 2019. [Google Scholar] [CrossRef]
- Polyak, B.T. Some methods of speeding up the convergence of iterative methods. Zh. Vychisl. Mat. Mat. Fiz. 1964, 4, 1–17. [Google Scholar]
- Boţ, R.I.; Csetnek, E.R.; Hendrich, C. Inertial Douglas-Rachford splitting for monotone inclusion problems. Appl. Math. Comput. 2015, 256, 472–487. [Google Scholar] [CrossRef]
- Boţ, R.I.; Csetnek, E.R.; László, S. An inertial forward-backward algorithm for the minimization of the sum of two nonconvex functions. EURO J. Comput. Optim. 2016, 4, 3–25. [Google Scholar] [CrossRef]
- Boţ, R.I.; Csetnek, E.R.; Nimana, N. Gradient-type penalty method with inertial effects for solving constrained convex optimization problems with smooth data. Optim. Lett. 2017. [Google Scholar] [CrossRef] [PubMed]
- Boţ, R.I.; Csetnek, E.R.; Nimana, N. An Inertial Proximal-Gradient Penalization Scheme for Constrained Convex Optimization Problems. Vietnam J. Math. 2017, 46, 53–71. [Google Scholar] [CrossRef]
- Cholamjiak, W.; Cholamjiak, P.; Suantai, S. An inertial forward-backward splitting method for solving inclusion problems in Hilbert spaces. J. Fixed Point Theory Appl. 2018, 2018. [Google Scholar] [CrossRef]
- Cholamjiak, P.; Shehu, Y. Inertial forward-backward splitting method in Banach spaces with application to compressed sensing. Appl. Math. 2019, 64, 409–435. [Google Scholar] [CrossRef]
- Kitkuan, D.; Kumam, P.; Martínez-Moreno, J. Generalized Halpern-type forward-backward splitting methods for convex minimization problems with application to image restoration problems. Optimization 2019. [Google Scholar] [CrossRef]
- Kitkuan, D.; Kumam, P.; Martínez-Moreno, J.; Sitthithakerngkiet, K. Inertial viscosity forward–backward splitting algorithm for monotone inclusions and its application to image restoration problems. Int. J. Comput. Math. 2020, 97, 1–19. [Google Scholar] [CrossRef]
- Mainge, P.E. Convergence theorems for inertial KM-type algorithms. J. Comput. Appl. Math. 2008, 219, 223–236. [Google Scholar] [CrossRef]
- Combettes, P.L.; Yamada, I. Compositions and convex combinations of averaged nonexpansive operators. J. Math. Anal. Appl. 2015, 425, 55–70. [Google Scholar] [CrossRef]
- Shehu, Y.; Iyiola, O.S.; Ogbuisi, F.U. Iterative method with inertial terms for nonexpansive mappings: Applications to compressed sensing. Numer. Algorithms 2019. [Google Scholar] [CrossRef]
- Davis, D.; Yin, W. A Three-Operator Splitting Scheme and its Optimization Applications. Set-Valued Var. Anal. 2017, 25, 829–858. [Google Scholar] [CrossRef]
- Mainge, P.E. Approximation methods for common fixed points of nonexpansive mappings in Hilbert spaces. J. Math. Anal. Appl. 2007, 325, 469–479. [Google Scholar] [CrossRef]
- Tikhonov, A.N.; Arsenin, V.Y. Solutions of Ill—Posed Problems. SIAM Rev. 1979, 21, 266–267. [Google Scholar]
- Ma, Z.; Wu, H.R. Partition based vector filtering technique for color suppression of noise in digital color images. IEEE Trans. Image Process. 2006, 15, 2324–2342. [Google Scholar]
- Lim, J.S. Two-Dimensional Signal Processing; Prentice-Hall: Englewood Cliffs, NJ, USA, 1990. [Google Scholar]
- Gonzalez, R.C.; Woods, R.E. Digital Image Processing, 4th ed.; Prentice-Hall: Englewood Cliffs, NJ, USA, 2017. [Google Scholar]





| Algorithm 2 | MTA | Shehu et al.’s Algorithm Equation (3) | ||||
|---|---|---|---|---|---|---|
| CPU Time (s) | Iterations | CPU Time (s) | Iterations | CPU Time (s) | Iterations | |
| (20,700) | 0.0218 | 7 | 0.0428 | 278 | 0.0756 | 626 |
| (20,800) | 0.0189 | 7 | 0.0914 | 350 | 0.1745 | 796 |
| (20,7000) | 0.0302 | 7 | 1.7751 | 1273 | 0.0977 | 53 |
| (20,8000) | 0.0308 | 6 | 1.2419 | 1290 | 0.0671 | 54 |
| (200,7000) | 0.0365 | 8 | 1.9452 | 858 | 4.6538 | 2028 |
| (200,8000) | 0.0406 | 7 | 2.5115 | 977 | 0.1425 | 53 |
| (500,7000) | 0.0403 | 7 | 4.1647 | 892 | 8.3620 | 1956 |
| (500,8000) | 0.0548 | 8 | 4.3239 | 813 | 9.0929 | 1835 |
| (1000,7000) | 0.0703 | 7 | 6.7954 | 786 | 14.1693 | 1751 |
| (1000,8000) | 0.0728 | 7 | 7.8302 | 825 | 16.3752 | 1784 |
| (3000,7000) | 0.1597 | 7 | 18.0559 | 779 | 44.8129 | 1940 |
| (3000,8000) | 0.1763 | 7 | 22.3514 | 841 | 49.6872 | 1891 |
| (100,80,000) | 0.1376 | 8 | 26.6863 | 1489 | 1.5926 | 94 |
| (1000,80,000) | 0.6949 | 8 | 344.7048 | 3289 | 9.4181 | 93 |
| The Normalized Color Difference (NCD). | ||||
|---|---|---|---|---|
| Kitkuan et al.’s Algorithm | Our Algorithm in Equation (19) | |||
| Artsawang Image | Mandril Image | Artsawang Image | Mandril Image | |
| 1 | 0.99803 | 0.99842 | 0.99663 | 0.99731 |
| 50 | 0.99660 | 0.99730 | 0.99659 | 0.99727 |
| 100 | 0.99661 | 0.99729 | 0.99658 | 0.99726 |
| 200 | 0.99660 | 0.99728 | 0.99658 | 0.99726 |
| 300 | 0.99659 | 0.99727 | 0.99658 | 0.99726 |
| 400 | 0.99659 | 0.99727 | 0.99658 | 0.99726 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Artsawang, N.; Ungchittrakool, K. Inertial Mann-Type Algorithm for a Nonexpansive Mapping to Solve Monotone Inclusion and Image Restoration Problems. Symmetry 2020, 12, 750. https://doi.org/10.3390/sym12050750
Artsawang N, Ungchittrakool K. Inertial Mann-Type Algorithm for a Nonexpansive Mapping to Solve Monotone Inclusion and Image Restoration Problems. Symmetry. 2020; 12(5):750. https://doi.org/10.3390/sym12050750
Chicago/Turabian StyleArtsawang, Natthaphon, and Kasamsuk Ungchittrakool. 2020. "Inertial Mann-Type Algorithm for a Nonexpansive Mapping to Solve Monotone Inclusion and Image Restoration Problems" Symmetry 12, no. 5: 750. https://doi.org/10.3390/sym12050750
APA StyleArtsawang, N., & Ungchittrakool, K. (2020). Inertial Mann-Type Algorithm for a Nonexpansive Mapping to Solve Monotone Inclusion and Image Restoration Problems. Symmetry, 12(5), 750. https://doi.org/10.3390/sym12050750





