The Role of the Pauli Exclusion Principle in Nuclear Physics Models
Abstract
1. Introduction
2. Nuclear Cluster Physics and Algebraic Models
2.1. The Nuclear Vibron Model
2.2. The Semimicroscopic Algebraic Cluster Model
2.3. The Algebraic Cluster Model
2.4. Applications to Multi- Cluster Systems
2.4.1. C
- Each -cluster is assumed to be in a (0,0) irrep of the shell model.
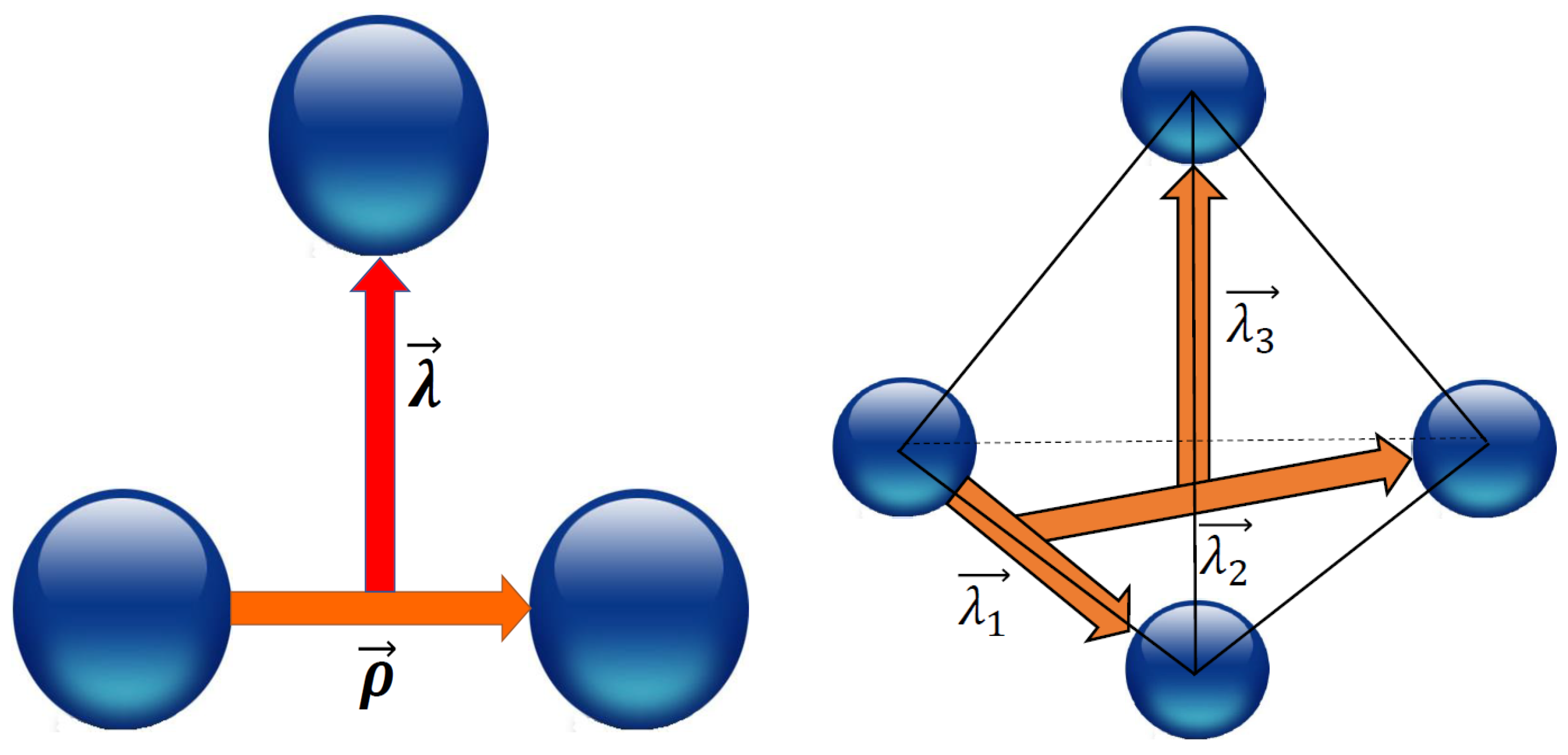
- Between the first two ’s the Wildermuth condition requires a minimal number of four oscillation quanta. (Be has 4 oscillation quanta within the shell model and each contributes zero, thus, 4 oscillation quanta have to be in the relative motion). The same is the case for the relative motion of the third particle with respect to the first two. C has 8 oscillation quanta and the 2- subsystem already 4, thus, 4 more oscillation quanta have to be added in the relative motion of the second Jacobi-coordinate.
- The symmetric states of the three -system is obtained using the procedure as exposes in [30].
- The obtained list of possible irreps is compared to the shell model space (programs are available for that), resulting in the final model space.
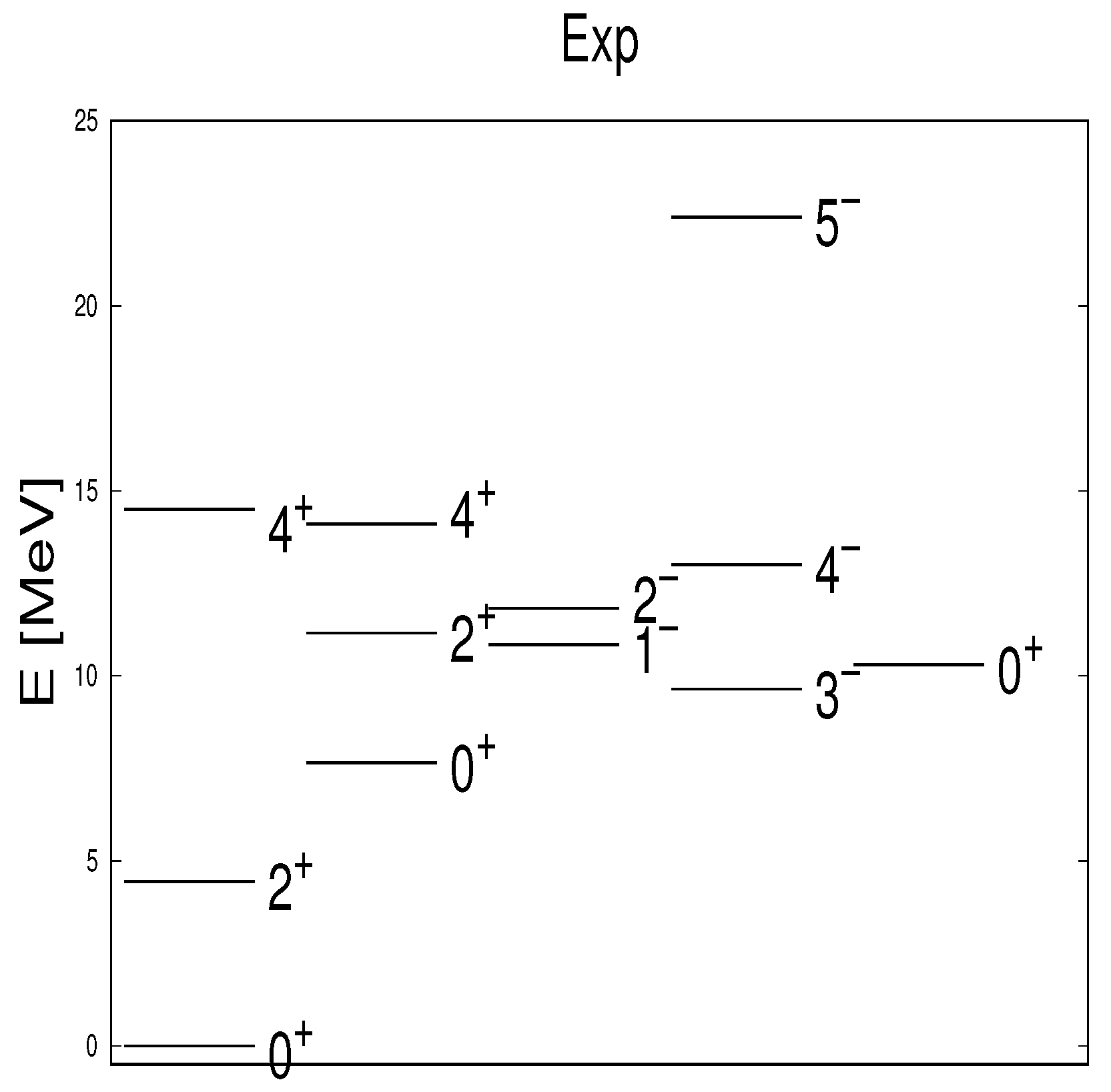
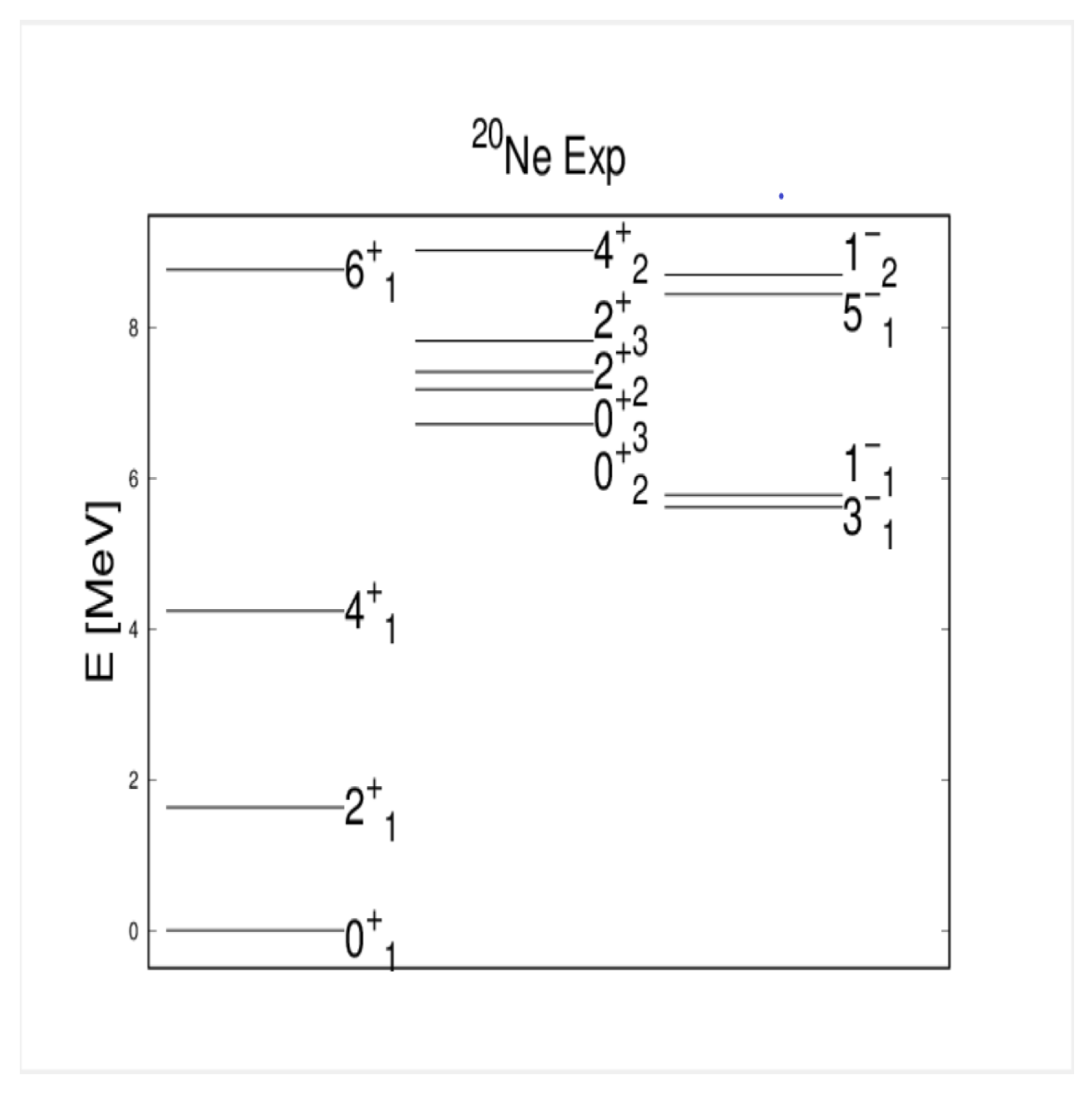
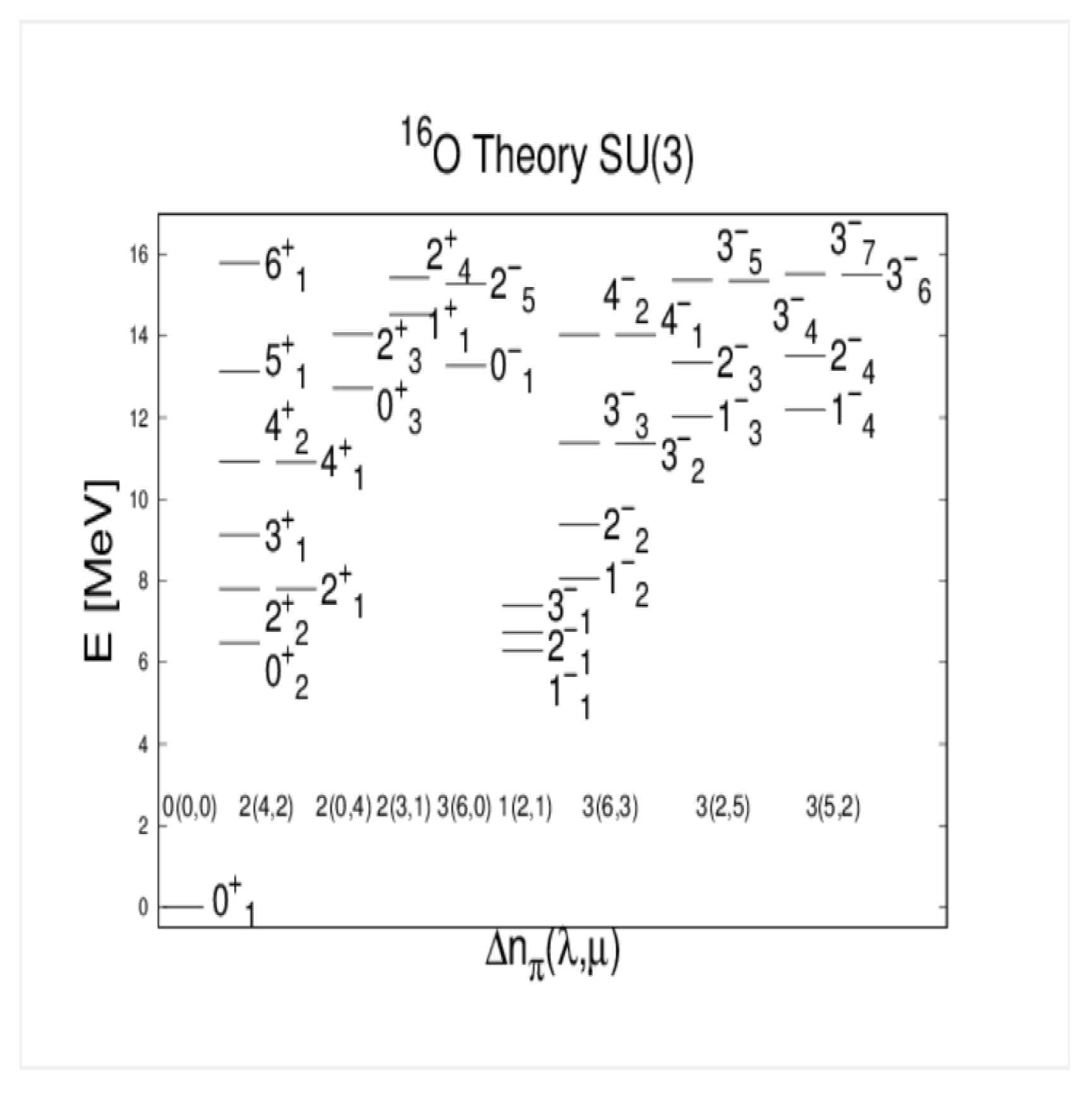
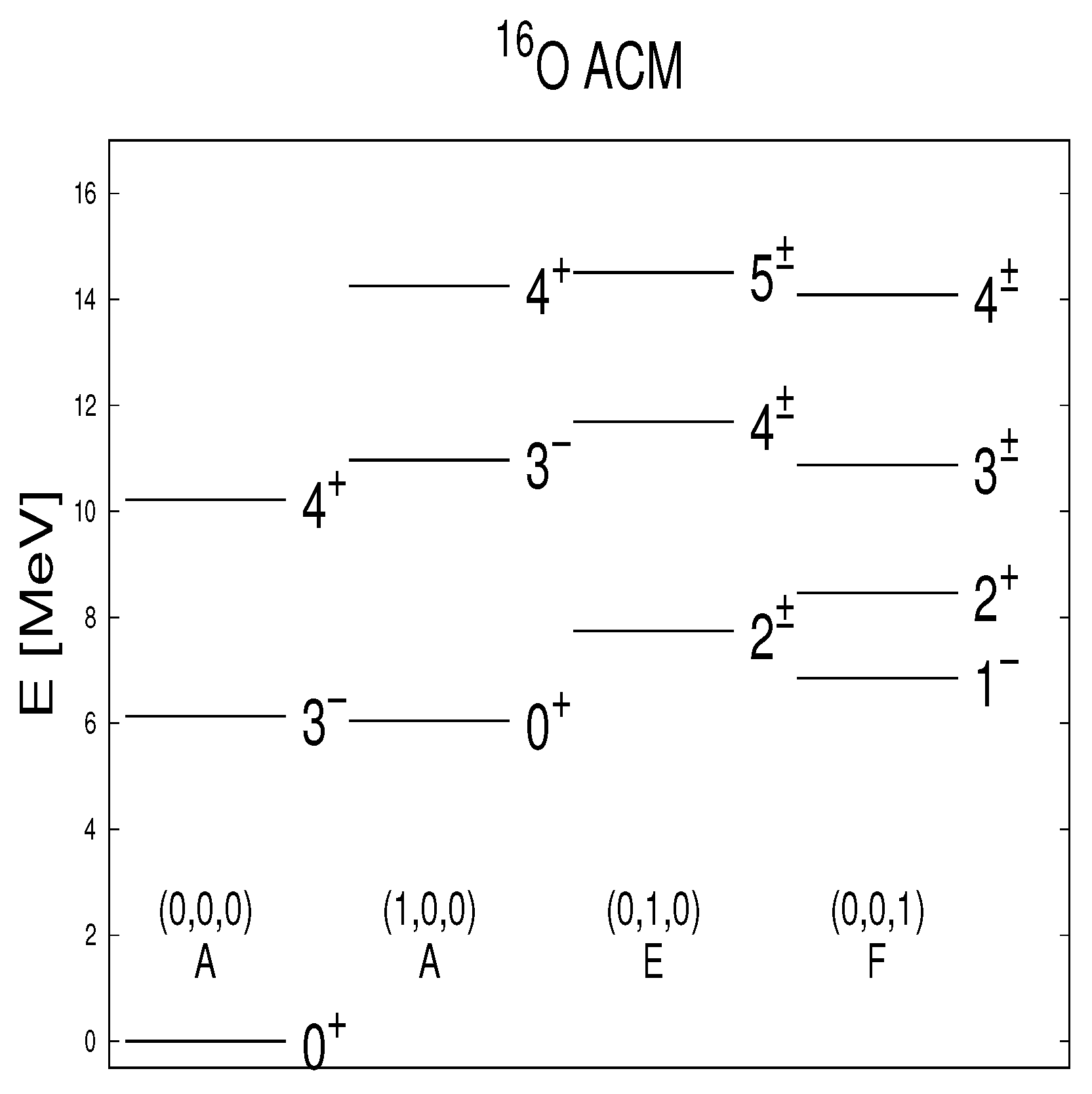
- At low energy there is only one state in the SACM, while in the ACM there are 2, a consequence of ignoring the PEP.
- The spectrum in the ACM is denser at low energy than in the SACM. For example, several predicted parity doublets vanish when the PEP is taken into account.
- Within the ACM, the maximal number of bosons was used as a parameter, which is not allowed. The number N is a cut-off and convergence should be checked with increasing N. This is also a problem in the SACM: we used finite N, otherwise the space becomes too large. One conforms with a renormalization of the parameters when N increases.
2.4.2. O
3. Algebraic Models in Nuclear Structure Physics
The Interacting Boson Model
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Wildermuth, K.; Tang, Y.C. A Unified Theory of the Nucleus; Academic Press: New York, NY, USA, 1977. [Google Scholar]
- Greiner, W.; Park, J.Y.; Scheid, W. Nuclear Moledcules; World Scientific: Singapore, 1995. [Google Scholar]
- Tohsaki, A.; Horiuchi, H.; Schuck, P.; Röpke, G. Alpha Cluster Condensation in 12C and 16O. Phys. Rev. Lett. 2001, 87, 192501. [Google Scholar] [CrossRef]
- Dreyfuss, A.C.; Launey, K.D.; Dytrych, T.; Draayer, J.P.; Bahri, C. Hoyle state and rotational features in Carbon-12 within a no-core shell-model framework. Phys. Lett. B 2013, 727, 511. [Google Scholar] [CrossRef]
- Horiuchi, H. Three-Alpha Model of 12C. Prog. Theor. Phys. 1974, 51, 1266. [Google Scholar] [CrossRef]
- Katō, K.; Fukatsu, K.; Tanaka, H. Systematic Construction Method of Multi-Cluster Pauli-Allowed States. Prog. Theor. Phys. 1988, 80, 663. [Google Scholar] [CrossRef]
- Cseh, J. Semimicroscopic algebraic description of nuclear cluster states. Vibron model coupled to the SU(3) shell model. Phys. Lett. B 1992, 281, 173. [Google Scholar] [CrossRef]
- Cseh, J.; Lévai, G. Semimicroscopic Algebraic Cluster Model of Light Nuclei. I. Two-Cluster-Systems with Spin-Isospin-Free Interactions. Ann. Phys. (N. Y.) 1994, 230, 165. [Google Scholar] [CrossRef]
- Marin-Lambarri, D.J.; Bijker, R.; Freer, M.; Gai, M.; Kokalova, T.; Parker, D.J.; Wheldon, C. Evidence for Triangular D3h Symmetry in 12C. Phys. Rev. lett. 2014, 113, 012502. [Google Scholar] [CrossRef]
- Bijker, R.; Iachello, F. The algebraic cluster model: Structure of 16O. Nucl. Phys. A 2017, 957, 154. [Google Scholar] [CrossRef]
- Herzberg, G. Molecular Spectra and Molecular Structure; D. Van Nostrand Company INC.: New York, NY, USA, 1963. [Google Scholar]
- Hess, P.O. 12C within the Semimicroscopic Algebraic Cluster Model. Eur. Phys. J. A 2018, 54, 32. [Google Scholar] [CrossRef]
- Hess, P.O.; Berriel-Aguayo, J.R.; Chávez-Nuñez, L.J. 16O within the Semimicroscopic Algebraic Cluster Model and the importance of the Pauli Exclusion Principle. Eur. Phys. J. A 2019, 55, 71. [Google Scholar] [CrossRef]
- Arima, A.; Iachello, F. The Interacting Boson Model; Cambridge University Press: Cambridge, UK, 1987. [Google Scholar]
- Daley, H.J.; Iachello, F. Nuclear vibron model. I. The SU(3) limit. Ann. Phys. 1986, 167, 73. [Google Scholar] [CrossRef]
- López-Moreno, E.; Castaños, O. Shapes and stability within the interacting boson model: Dynamical symmetries. Phys. Rev. C 1996, 54, 2374. [Google Scholar] [CrossRef] [PubMed]
- Bromley, D.A.; Kuehner, J.A.; Almqvist, E. Resonant Elastic Scattering of C12 by Carbon. Phys. Rev. Lett. 1960, 4, 365. [Google Scholar] [CrossRef]
- Yépez-Martínez, H.; Cseh, J.; Hess, P.O. Phase transitions in algebraic cluster models. Phys. Rev. C 2006, 74, 024319. [Google Scholar] [CrossRef]
- Elliott, J.P. Collective motion in the nuclear shell model. I. Classification schemes for states of mixed configurations. Proc. R. Soc. Lond. A 1958, 245, 128. [Google Scholar]
- Elliott, J.P. Collective motion in the nuclear shell model II. The introduction of intrinsic wave-functions. Proc. R. Soc. London A 1958, 245, 562. [Google Scholar]
- Available online: www.nndc.bnl.gov/ensdf (accessed on 12 April 2020).
- Hess, P.O.; Lévai, G.; Cseh, J. Geometrical interpretation of the semimicroscopic algebraic cluster model. Phys. Rev. C 1996, 54, 2345. [Google Scholar] [CrossRef]
- Smirnov, Y.F.; Tchuvil’sky, Y.M. The structural forbiddenness of the heavy fragmentation of the atomic nucleus. Phys. Lett. B 1984, 134, 25. [Google Scholar] [CrossRef]
- Yépez-Martínez, H.; Hess, P.O. The concept of nuclear cluster forbiddenness. J. Phys. G 2015, 42, 095109. [Google Scholar]
- Yépez-Martínez, H.; Ermamatov, M.J.; Fraser, P.R.; Hess, P.O. Application of the semimicroscopic algebraic cluster model to core+α nuclei in the p and sd shells. Phys. Rev. C 2012, 86, 034309. [Google Scholar]
- Cseh, J. Multichannel dynamical symmetry and heavy ion resonances J. Cseh. Phys. Rev. C 1994, 50, 2240. [Google Scholar] [CrossRef]
- Bijker, R.; Iachello, F. The Algebraic Cluster Model: Three-Body Clusters. Ann. Phys. (N. Y.) 2002, 298, 334. [Google Scholar] [CrossRef]
- Hoyle, F. On Nuclear Reactions Occuring in Very Hot STARS.I. the Synthesis of Elements from Carbon to Nickel. Astrophys. J. Suppl. 1954, 1, 121. [Google Scholar] [CrossRef]
- Schuck, P.; Funaki, Y.; Horiuchi, H.; Röpke, G.R.; Tohsaki, A.; Yamadas, T. Alpha particle clusters and their condensation in nuclear systems. Phys. Scr. 2016, 91, 123001. [Google Scholar] [CrossRef]
- Moshinsky, M.; Smirnov, Y.F. The Harmonic Oscillator in Modern Physics; Harwood Academic Publishers: New York, NY, USA, 1996. [Google Scholar]
- Kanada-En’yo, Y. The Structure of Ground and Excited States of 12C. Prog. Theor. Phys. 2007, 117, 655. [Google Scholar] [CrossRef]
- Chernykh, M.; Feldmeier, H.; Neff, T. Structure of the Hoyle State in 12C. Phys. Rev. Lett. 2007, 98, 032501. [Google Scholar] [CrossRef]
- Cseh, J.; Trencsényi, R. On the symmetries of the 12C nucleus. Int. J. Mod. Phys. E 2018, 27, 1850013. [Google Scholar] [CrossRef]
- Castaños, O.; Draayer, J.P.; Leschber, Y. Shape variables and the sehll model. Zeitschr. f. Physik A 1988, 329, 33. [Google Scholar]
- Rowe, D.J. Microscopic theory of the nuclear collective model. Rep. Prog. Phys. 1985, 48, 1419. [Google Scholar] [CrossRef]
- Eisenberg, J.M.; Greiner, W. Nuclear Theory I: Nuclear Models; North-Holland: Amsterdam, The Netherlands, 1987. [Google Scholar]
- Blomqvist, J.; Molinari, A. Collective 0− vibrations in even spherical nuclei with tensor forces. Nucl. Phys. A 1968, 106, 545. [Google Scholar] [CrossRef]
- Castaños, O.; Hess, P.O.; Rocheford, P.; Draayer, J.P. Pseudo-symplectoc model for strongly deformed nuclei. Nucl. Phys. A 1991, 524, 469. [Google Scholar] [CrossRef]
- Aguilera-Navarro, V.C.; Moshinsky, M.; Kramer, P. Harmonic-Oscillator States and the a Particle II. Configuration-Space States of Arbitrary Symmetry. Ann. Phys. 1969, 54, 379. [Google Scholar] [CrossRef]
- Iachello, F.; Arima, A. The Interacting Boson Model; Cambrige University Press: Cambridge, UK, 2011. [Google Scholar]
- Frank, A.; Isacker, P.; Jolie, J.; Jolie, J.; Van Isacker, P. Symmetries in Atomic Nuclei; Springer: Heidelberg, Germany, 2009. [Google Scholar]
- Iachello, F.; Talmi, I. Shell-model foundations of the interacting boson model. Rev. Mod. Phys. 1987, 59, 339. [Google Scholar] [CrossRef]
- Frank, A.; Van Isacker, P. Algebraic Methods in Molecular and Nuclear Structure Physics; Wiley: New York, NY, USA, 1994. [Google Scholar]
- Van Roosmalen, O.S. Algebraic Descriptions of Nuclear and Molecular Rotation-Vibration Spectra. Ph.D. Thesis, University of Groningen, Groningen, The Netherlands, 1982. [Google Scholar]
- Klein, A.; Marshalek, E.R. Boson realizations of Lie algebras with applications to nuclear physics. Rev. Mod. Phys. 1991, 63, 375. [Google Scholar] [CrossRef]
- Draayer, J.P. Contemporary Concepts in Physics. In Algebraic Approaches to Nuclear Structure: Interacting Boson and Fermion Models; Casten, R.F., Ed.; Harwood Academic Press: New York, NY, USA, 1993; Volume 6. [Google Scholar]
- Paar, V. Interacting Bosons in Nuclear Phsyics; Iachello, F., Ed.; Plenum Press: New York, NY, USA, 1979; p. 163. [Google Scholar]
- Castaños, O.; Frank, A.; Hess, P.O.; Moshinsky, M. Confrontations between the interacting boson approximation and the Bohr-Mottelson model. Phys. Rev. C 1981, 24, 1364. [Google Scholar] [CrossRef]
- Hecht, K.T. sp(6) & u(3) algebra of the fermion dynamical symmetry model. Notas Fisica 1985, 8, 165. [Google Scholar]
- Swaminathan, S.S.; Hecht, K.T. sp(6)⊃u(3) algebra of the fermion dynamical symmetry model for actinide nuclei. Phys. Rev. C 1994, 50, 1471. [Google Scholar] [CrossRef]
- Isacker, P.V.; Heyde, K.; Waroquier, M.; Wenes, G. The hexadecapole degree of freedom in rotational nuclei. Phys. Lett B 1981, 104, 5. [Google Scholar] [CrossRef]
- Mauthofer, A.; Stelzer, K.; Idzko, J.; Elze, T.W.; Wollersheim, H.J.; Emling, H.; Fuchs, P.; Grosse, E.; Schwalm, D. Triaxiality and γ-softness in 196Pt. Z. Phys. A 1990, 336, 263. [Google Scholar]
- Hess, P.O.; Maruhn, J.; Greiner, W. The general collective model applied to the chains of Pt, Os and W isotopes. J. Phys. G 1981, 7, 737. [Google Scholar] [CrossRef]
- Wood, J.L.; Heyde, K.; Nazarewicz, W.; Huyse, M.; van Duppen, P. Coexistence in even-mass nuclei. Phys. Rep. 1992, 215, 101. [Google Scholar] [CrossRef]
- Warner, D.D.; Casten, R.F.; Davidson, W.F. Interacting boson approximation description of the collective states of 168Er and a comparison with geometrical models. Phys. Rev. C 1981, 24, 1713. [Google Scholar] [CrossRef]
- Seiwert, M.; Maruhn, J.A.; Hess, P.O. Comparison of different collective models describing the low spin structure of 168Er. Phys. Rev. C 1984, 30, 1779. [Google Scholar] [CrossRef]
- Hess, P.O.; Seiwert, M.; Maruhn, J.A.; Greiner, W. General Collective Model and its Application to . Zeit. Phys. 1980, 296, 147. [Google Scholar] [CrossRef]
- Iachello, F. Microscopic Aspects of the Interacting Boson Model. Suppl Prog. Theor. Phys. 1983, 74, 296. [Google Scholar] [CrossRef]
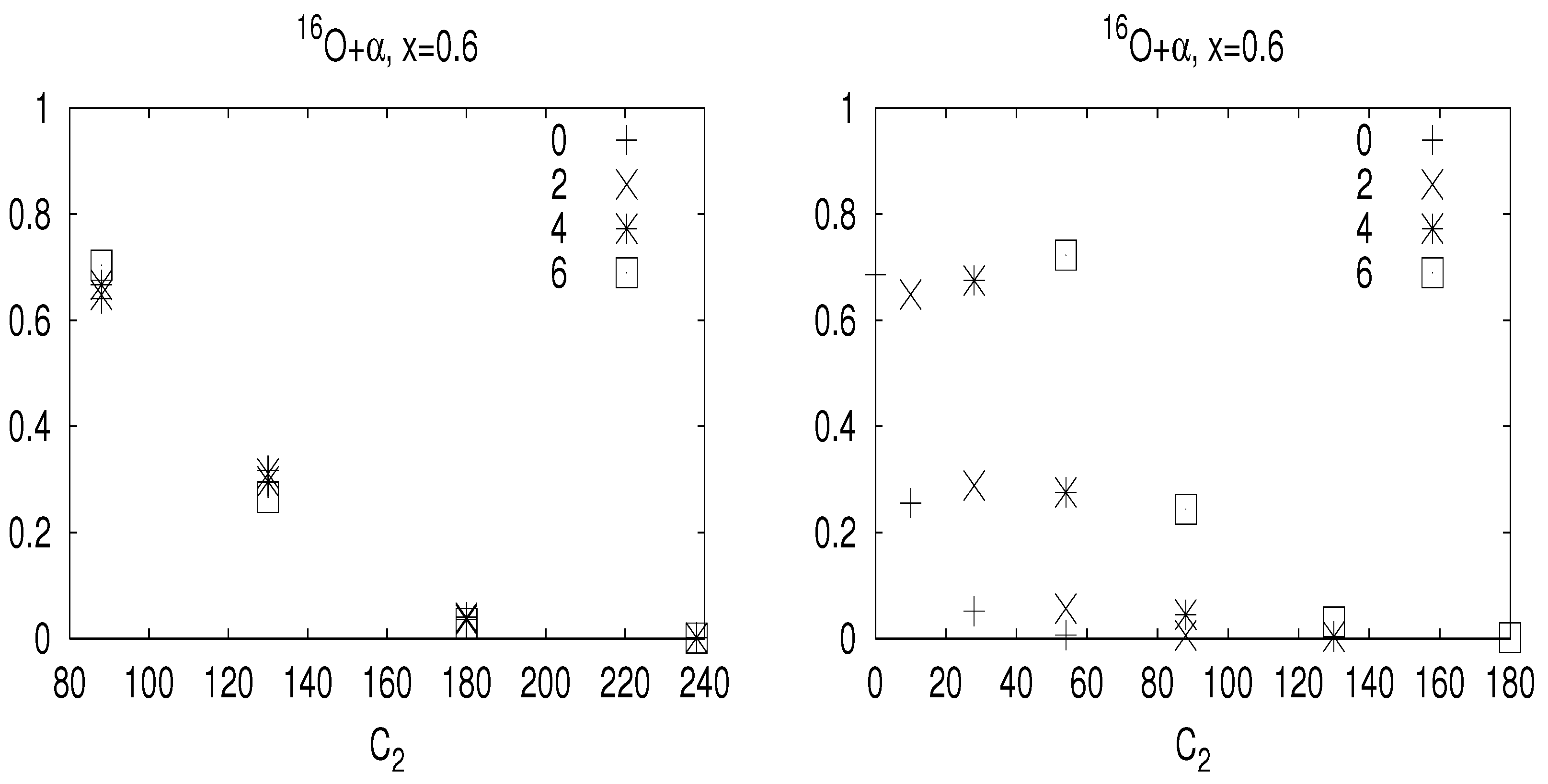

| 0 | (0,4) |
| 1 | (3,3) |
| 2 | (2,4), (6,2) |
| 3 | (3,4), (5,3), (9,1) |
| 4 | (0,6), (4,4), (6,3), (8,2), (12,0) |
| 5 | (3,5), (5,4), (7,3), (9,2), (11,1) |
| 6 | (2,6), (6,4), (8,3), (10,2), (12,1), (14,0) |
| EXP.[WU] | [WU] | SACM [WU] | ACM | |
|---|---|---|---|---|
| 4.65 | 5.37 | 5.15 | ||
| 0.0 | 7.73 | 0.8 | ||
| 6.32 | 24.28 | 5.14 |
| Kato | SACM | |
|---|---|---|
| 0 | ||
| 1 | ||
| 2 | ||
| 3 | ||
| 4 | ||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Berriel-Aguayo, J.R.M.; Hess, P.O. The Role of the Pauli Exclusion Principle in Nuclear Physics Models. Symmetry 2020, 12, 738. https://doi.org/10.3390/sym12050738
Berriel-Aguayo JRM, Hess PO. The Role of the Pauli Exclusion Principle in Nuclear Physics Models. Symmetry. 2020; 12(5):738. https://doi.org/10.3390/sym12050738
Chicago/Turabian StyleBerriel-Aguayo, Josué R. M., and Peter O. Hess. 2020. "The Role of the Pauli Exclusion Principle in Nuclear Physics Models" Symmetry 12, no. 5: 738. https://doi.org/10.3390/sym12050738
APA StyleBerriel-Aguayo, J. R. M., & Hess, P. O. (2020). The Role of the Pauli Exclusion Principle in Nuclear Physics Models. Symmetry, 12(5), 738. https://doi.org/10.3390/sym12050738