Abstract
In this paper, first, an evolutionary game model for Bayes-based strategy updating rules was constructed, in which players can only observe a signal that reveals a strategy type instead of the strategy type directly, which deviates from the strategy type of players. Then, the equilibrium selection of populations in the case of the asymmetric game, the Battle of the Sexes (BoS), and the case of a symmetric coordination game was studied where individuals make decisions based on the signals released by each player. Finally, it was concluded that in the BoS game, when the accuracy of the signal is low, the population eventually reaches an incompatible state. If the accuracy of the signal is improved, the population finally reaches a coordinated state. In a coordination game, when the accuracy of the signal is low, the population will eventually choose a payoff-dominated equilibrium. With the improvement of signal accuracy, the equilibrium of the final selection of the population depends on its initial state.
1. Introduction
Because there are many Nash equilibria in a coordination game, it is difficult to predict the final game equilibrium. Individuals constantly change their strategies in the process of the game, which, as a dynamic adjustment, is a process of equilibrium selection. In evolutionary game theory, individuals with bounded rationality adjust their strategies in the process of natural selection [1,2,3,4,5,6] and finally reach equilibrium.
In a uniformly mixed infinite population [5,7], the evolutionary stability of game equilibrium was studied by constructing a deterministic evolutionary dynamic process of replicator dynamics [1,4]. Then, a stochastic replicator dynamic model [8,9,10,11,12,13,14,15] was constructed based on the determined evolutionary dynamic model and considered the impact of external random shocks to study the impact of external random disturbances on population equilibrium selection. For uniformly mixed finite populations [6], a Markov chain-based stochastic evolutionary dynamic model was constructed [16,17,18,19,20,21,22,23] to study the evolution of population strategies. For ergodic Markov processes, the stationary distribution of the population state space was calculated [17]. For non-ergodic Markov processes, the rooting probability of the absorption state of the process was calculated [16,24].
In the above studies, it is assumed that players can directly observe the strategies adopted by other players and the payoffs obtained. Players update their strategies based on the payoffs that determine the probability of choosing one of the strategies. However, in the real world, it is often difficult to directly observe the strategies adopted by opponents, which need to be considered based on the signals released by them. Therefore, some researchers have begun to use the Bayes Theorem to construct learning and updating rules based on Bayesian inference to study the mechanism of collective behavior formation [25,26,27,28,29,30] and to analyze the equilibrium selection of the population in the long-term evolution process.
Fudenberg and Imhof (2006) [17] studied a symmetric game with a rare mutation rate in a finite population. They construct a Markov chain where the transition probabilities were related to their payoff. Their research shows that the evolutionary process simplifies significantly and approximates a simpler process over the pure states, which dramatically reduces the state space and the calculation of the stationary distribution. Based on the research of Fudenberg and Imhof (2006), Veller and Hayward (2016) [18] further studied an asymmetric game with a rare mutation rate in a finite population and presented the analytic results of the stationary distribution of the evolutionary process. However, recent studies have identified Bayesian inference as a mechanism behind collective behavior in nature and human society [26,27]. Therefore, it is necessary to analyze the equilibrium selection from the perspective of Bayesian inference.
In this paper, strategy updating rules based on Bayesian inference were constructed, in which players cannot directly observe the payoffs and strategies of their opponents, but only receive the related signals and then analyze their strategy evolution under the updating rules. For the problem of multiple equilibrium selection in a coordinated game, these rules were used to analyze the equilibrium selection in the long-term evolution process. The equilibrium choice in an asymmetric game represented by the Battle of the Sexes game (BOS) [17,18] and a symmetric game were studied, respectively. In the asymmetric Battle of the Sexes game [31,32,33,34], players with different roles use different strategies. The male player prefers a football match, while the female player prefers a ballet performance. They have to convince each other, otherwise they will get nothing. For the collective payoff, it is optimal for them to choose the same strategy. Players hold different preferences but hope to adopt the same strategy. Contrary to the Battle of the Sexes game, in a symmetric coordination game, players hold the same preferences and hope to adopt the same strategy. We constructed the evolutionary game model with strategy updating rules based on Bayesian inference and studied the evolutionary equilibrium selection in these games.
2. Model in the BoS Game
Suppose a Battle of the Sexes game has two populations, men (m) and women (w), with the size of . At each time t, a population is randomly selected from two populations to update the strategy, and all players in the population update the strategy at the same time. For each individual in the two populations, there is the same strategy space, and the strategy type is . The payoff matrix of the game is as follows in Table 1:

Table 1.
The payoff matrix of the Battle of the Sexes game.
In this matrix, . There are two pure-strategy Nash equilibria and in this game. Both populations want to choose the same strategy. At each time t, each player cannot directly observe the strategy type of the players in the other population, but can only receive a signal , about their strategy type. The signal of each player’s strategy type is public knowledge; that is, all the players’ strategy types in each population will be observed by all the players in the opposite population, the received signals of all the players’ strategy types are the same. There is a deviation between the type of strategy and the signal sent by player i and j in m and w. The conditional probability of the signal accurately reflecting the type of strategy of players i and j is as follows:
where . Meanwhile, because every player updates their strategy according to public signal information at the same time, all players in a population will adopt the same strategy at every time t. and represent the probability that all players in m and w adopt strategy A at time t, respectively. The strategy type of the population is inferred according to Bayesian rules updating. The posteriori probability of strategy A being selected by the opposite population considered by the population is as follows:
where , ; and represent the number of signals of strategy A sent by the two populations w and m at time t, respectively; and represent the difference between the signals of strategy A and strategy B sent by the two populations at time t. As with the previous model, it is assumed in this paper that the prior probabilities of strategies A and B are equal for two populations at each time t, i.e.,, ; the probability of choosing strategies A and B is 1/2 at the initial time.
In the BoS game, there is a mixed Nash equilibrium . For population m, if the posterior probability of population w in the state of strategy A at time t meets , then population m will adopt strategy A; otherwise, population m will adopt strategy B. Similarly, for population w, if the posterior probability of the population m in the state of strategy A at time t meets , then population w will adopt strategy A; otherwise, population w will adopt strategy B. From and , we derive the following:
Thus, . Then, population m will adopt strategy A, while population w will adopt strategy A when .
Because players only update the posterior probability of each other’s strategy type according to the currently received signal and its prior probability at time t. At the same time, it is assumed in this paper that, at every time t, players will not be affected by the posterior probability of the previous period; that is, the prior probability of players to the other party’s strategy type in each period is always equiprobable . and will only affect the current decision-making, not future ones. At this time, the strategy update of the two populations only depends on the current signal state, and the strategy update process is a Markov process with a state space of , and the transition probabilities are given by the following:
where , . Meanwhile, let , . Similarly, the transition probability matrix of Markov process is as follows:
Proposition 1.
When, the Markov process is ergodic with a stable distribution as follows:
According to Proposition 1, when t →∞, the population is in a coordinated state; that is, the probability of and states is equal. At the same time, it is derived from that . When the population is in an incompatible state, strategy A will bring higher payoffs to m, while strategy B will bring higher payoffs to population w. Compared with the incompatible state (B, A), the population will choose the incompatible state with higher probability.
Proposition 2.
When, population m and population w will eventually be in an incompatible state.
It is proven that when , and . At this time, the matrix of transition probability of the Markov process becomes:
In the Markov process, states are transient, and state is the absorbing state of the process.
Proposition 2 shows that in this asymmetric game, if there is a big difference in payoff between the two kinds of coordinated equilibria, the population will choose the strategy that brings higher payoffs to itself, which makes the two populations always in an incompatible state, unable to reach the Nash equilibrium.
In Figure 1, (a) shows the probability that the population is in coordination or under the combination of different parameters and . Figure 1b shows the final evolutionarily stable state of the strategy updating process in the region with different parameter combinations.
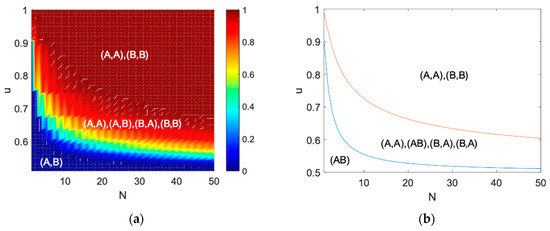
Figure 1.
The probability that the population reaches the coordination states or in the Battle of the Sexes game.
In Figure 1, (b) also shows that when the population size is smaller or the signal reliability is smaller, the population will be more inclined to choose the strategy that brings higher payoffs to itself. Because the two populations have different incomes under different equilibrium tendencies, population m is more inclined to choose equilibrium, while population w is more inclined to choose equilibrium, which makes the two populations always in an incompatible state . With the improvement of signal accuracy, four states coexist. When the signal accuracy is further improved, the population must be in an or equilibrium state after a long-time evolution. It is thus concluded that the increase of signal accuracy and population size is more conducive to population coordination.
Proposition 3.
When, there is a, so that when, the population m and the population w will finally be in a coordinated stateor.
It is proven that when , , from the law of large numbers, . Meanwhile, let , when , , and , . At this time, there must be a point that makes, when,. When , , and then . Similarly, according to the law of large numbers, when , .
It is derived from Proposition 3 that when the population size area is infinite, there are two absorbing states and in the Markov process. After a long time of evolution, the population will finally reach the absorbing state; that is, the population will be in an equilibrium state. Based on the theoretical model of replicator dynamics of infinite population, as shown in Figure 2, show the evolutionary stable equilibrium of the replicator dynamic system. After a long series of games between populations, the evolutionary stable equilibrium will be achieved, and the final evolutionary stable state of the population depends on its initial state. Replicator dynamics is a deterministic imitation process. However, under the Bayes-based strategy updating rules, when the infinite population meets the assumption that the signal accuracy is , that is, the signal has a higher probability to reflect its real strategy type, even if the players cannot directly observe the strategy type of the opponent, they can still accurately guess and update the strategy according to a large number of signals sent by the opponent’s population. At this time, the population will still reach the equilibrium state.
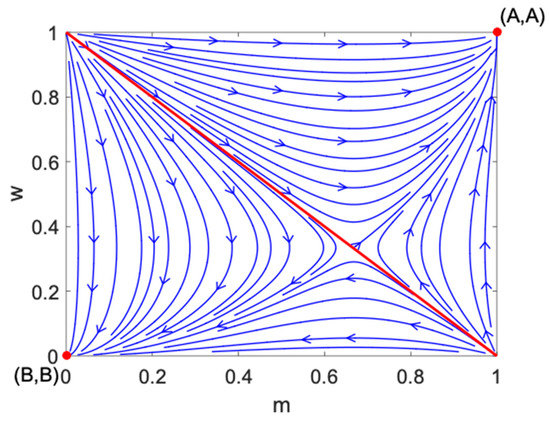
Figure 2.
Evolutionary stable equilibrium of the BoS game under replicator dynamics.
3. Model for Coordination Game
As showed in Table 2, suppose a coordination game has two populations, 1 and 2 with the size of . At each time t, a population is randomly selected from two populations to update the strategy, and all players in the population update the strategy at the same time. For each individual in the two populations, there is the same strategy space, and the strategy type is . The payoff matrix of the game is as follows:

Table 2.
The payoff matrix of the coordination game.
In this matrix, a > b. There are two pure-strategy Nash equilibria and in this game. Both populations want to choose the same strategy. Same as the previous model, at each time t, each player cannot directly observe the strategy type of the players in the other population, but can only receive the signal about the their strategy type. The signal of each player’s strategy type is public knowledge; that is, all the players’ strategy types in each population will be observed by all the players in the opposite population, and the received signals of all the players’ strategy types are the same. There is a deviation between the type of strategy and the signal sent by player i in each population. The conditional probability of the signal accurately reflecting the type of strategy of player i is as follows:
In the coordination game, there is a mixed Nash equilibrium . At this time, if the posterior probability of the other population in the state of strategy A at t time meets , then population w will adopt strategy A; otherwise, population w will adopt strategy B. It is derived from that when , the population will choose strategy A. , . At the same time, let , . Similarly, the matrix of transition probability of Markov process is as follows:
Proposition 4.
When, the Markov process is ergodic with a stable distribution as follows:
It is derived from that , because the equilibrium point will bring higher payoffs than , the population will be in the equilibrium state with a higher probability. Strategy A will bring higher payoffs to population 1, while strategy B will bring higher payoffs to population 2; thus, the population will choose the incompatible state with higher probability compared with the incompatible state (B, A).
Proposition 5.
When, the two populations will eventually choose the payoff-dominant equilibrium.
It is proved that when , and . At this time, the matrix of transition probability of the Markov process becomes the following:
In the Markov process, state are transient, and state is the absorbing state of the process.
Proposition 5 shows that in this coordination game, if there is a big difference in payoff between the two kinds of coordinated equilibria, the population will choose the equilibrium that brings higher payoffs to itself, which results in the two populations always being in a coordinated state, finally reaching the Nash equilibrium.
Figure 3 shows the probability that the population is in coordination or under the combination of different parameters and . It shows the final evolutionarily stable state of the strategy updating process in the region with different parameter combinations.
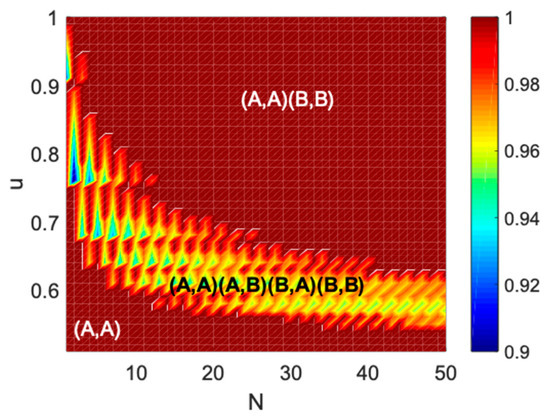
Figure 3.
The probability that the population reaches the coordination state
or in the coordination game.
Figure 3 shows that when the accuracy of the signal is low and the population size is small, it will be difficult for the population to determine the strategy type of the opponent through signals, and the population will prefer to choose the payoff-dominant equilibrium . With the improvement of signal accuracy and the increase of population size, people can infer the strategy type of opponents to a certain extent. At this time, there will be the coexistence of four strategies. When the signal accuracy is very high or the population size is very large, the population can accurately determine the strategy type of the opponent and be in equilibrium. Compared with the BoS game, there is a very small chance for the probability of players in the coordination game to be in a non-equilibrium state.
Proposition 6.
When, there is a, so that when, the two populations will finally be in a coordinated stateor.
The proof is same as that of Proposition 3. When , , the matrix of transition probability at this time of this process is the following:
At this time, there are two absorbing states and , and the final state of the process depends on its initial state.
It is derived from Proposition 6 that when the population size area is infinite, there are two absorbing states and in the Markov process. After a long time of evolution, the population will finally reach the absorbing state; that is, the population will be in an equilibrium state. Based on the theoretical model of replicator dynamics of infinite population, as shown in Figure 4, show the evolutionary stable equilibrium of the replicator dynamic system. After a long period of games between populations, the evolutionary stable equilibrium will be achieved, and the final evolutionary stable state of the population depends on its initial state. Replicator dynamics is a deterministic imitation process. However, under the Bayes-based strategy updating rules, when the infinite population meets the assumption that the signal accuracy is , that is, the signal has a higher probability to reflect its real strategy type, even if the players cannot directly observe the strategy type of the opponent, they can still accurately guess and update the strategy according to a large number of signals sent by the opponent’s population. At this time, the population will still reach the equilibrium state.
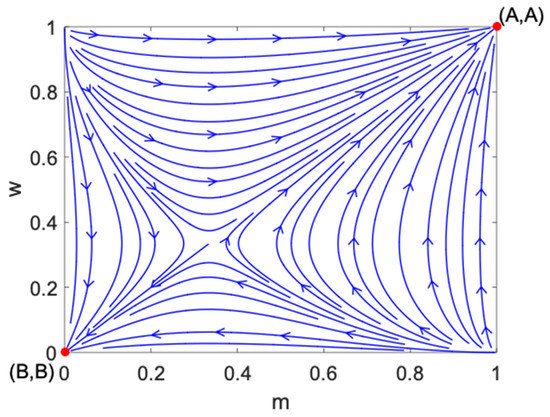
Figure 4.
Evolutionary stable equilibrium of the coordination game under replicator dynamics.
4. Conclusions
In this paper, we analyzed the equilibrium selection from the perspective of Bayesian inference. In the study of Veller and Hayward (2016) [18], the state of population switches among different pure states but tends to lead towards the coordination state. However, our research shows that the finite population finally reaches the incompatible state when the accuracy of the signal is low in the BoS game. With the improvement of signal accuracy, the Markov process has a stable distribution, and the population transfers between the coordinated and incompatible states. When the signal accuracy is very high, the population will eventually reach a coordinated state. Because the state of the population is closely related to the accuracy of the signal, populations always tend towards uncoordinated states because of inaccurate signal, which is different from the results of Veller and Hayward (2016) [18]. In the infinite populations, as long as the accuracy of the signal is more than one half, the population will eventually reach a coordinated state. In the coordination game, when the accuracy of the signal is low, the population will reach the coordinated state and finally choose the payoff-dominant equilibrium, which is different from the case of the BoS game. With the improvement of signal accuracy, the population transfers between the coordinated and incompatible states and will eventually reach a coordinated state when the signal accuracy is very high, which is similar to the case of the BoS game. In the infinite populations, the population will always reach a coordinated state, and the finally selected equilibrium of the population depends on its initial state.
Author Contributions
C.Z. contributed to the conception of the study, J.L. performed the data analyses and wrote the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Research Foundation from Ministry of Education of China (Grant No.15JZD024) 2020 MOE Layout Foundation of Humanities and Social Sciences (Grant No.932).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Maynard, S.J. Evolution and the Theory of Games; USA Cambridge University Press: New York, NY, USA, 1982. [Google Scholar]
- Axelrod, R. The Evolution of Cooperation; Basic Books: New York, NY, USA, 1981. [Google Scholar]
- Weibull, J.W. Evolutionary Game Theory; MIT press: Cambridge, MA, USA.
- Hofbauer, J.; Sigmund, K. Evolutionary Games and Population Dynamics; Cambridge university press: Cambridge, UK, 1998. [Google Scholar]
- Hauert, C.; De, M.S.; Hofbauer, J.; Sigmund, K. Replicator Dynamics for Optional Public Good Games. J. Theor. Biol. 2002, 218, 187–194. [Google Scholar] [CrossRef] [PubMed]
- Nowak, M.A. Evolutionary Dynamics; MIT press: Cambridge, MA, USA, 2006. [Google Scholar]
- Hauert, C.; Traulsen, A.; Brandt, H.; Nowak, M.A.; Sigmund, K. Public Goods with Punishment and Abstaining in Finite and Infinite Populations. Biol. Theory 2008, 3, 114–122. [Google Scholar] [CrossRef] [PubMed]
- Foster, D.; Young, P. Stochastic evolutionary game dynamics. Theor. Popul. Biol. 1990, 38, 219–232. [Google Scholar] [CrossRef]
- Fudenberg, D.; Harris, C. Evolutionary dynamics with aggregate shocks. J. Econ. Theory 1992, 57, 420–441. [Google Scholar] [CrossRef]
- Cabrales, A. Stochastic Replicator Dynamics. Int. Econ. Rev. 2000, 41, 451–481. [Google Scholar] [CrossRef]
- Imhof, L.A. The Long-Run Behavior of the Stochastic Replicator Dynamics. Ann. Appl. Probab. 2005, 15, 1019–1045. [Google Scholar] [CrossRef]
- Hofbauer, J.; Imhof, L.A. Time averages, recurrence and transience in the stochastic replicator dynamics. Ann. Appl. Probab. 2009, 19, 1347–1368. [Google Scholar] [CrossRef]
- Citil, H.G. Important Notes for a Fuzzy Boundary Value Problem. Appl. Math. Nonlinear Sci. 2019, 4, 305–314. [Google Scholar] [CrossRef]
- Josheski, D.; Karamazova, E.; Apostolov, M. Shapley-Folkman-Lyapunov theorem and Asymmetric First price auctions. Appl. Math. Nonlinear Sci. 2019, 4, 331–350. [Google Scholar] [CrossRef]
- Dewasurendra, M.; Vajravelu, K. On the Method of Inverse Mapping for Solutions of Coupled Systems of Nonlinear Differential Equations Arising in Nanofluid Flow, Heat and Mass Transfer. Appl. Math. Nonlinear Sci. 2018, 3, 1–14. [Google Scholar] [CrossRef]
- Lessard, S. Long-term stability from fixation probabilities in finite populations: New perspectives for ESS theory. Theor. Popul. Biol. 2005, 68, 19–27. [Google Scholar] [CrossRef] [PubMed]
- Fudenberg, D.; Imhof, L.A. Imitation processes with small mutations. J. Econ. Theory 2006, 131, 251–262. [Google Scholar] [CrossRef]
- Veller, C.; Hayward, L.K. Finite-population evolution with rare mutations in asymmetric games. J. Econ. Theory 2016, 162, 93–113. [Google Scholar] [CrossRef]
- Imhof, L.A.; Nowak, M.A. Evolutionary game dynamics in a Wright–Fisher process. J. Math. Biol. 2006, 52, 667–681. [Google Scholar] [CrossRef]
- Wu, B.; Gokhale, C.S.; Wang, L.; Traulsen, A. How small are small mutation rates? J. Math. Biol. 2012, 64, 803–827. [Google Scholar] [CrossRef]
- Sekiguchi, T.; Ohtsuki, H. Fixation probabilities of strategies for bimatrix games in finite populations. Dyn. Games Appl. 2017, 7, 93–111. [Google Scholar] [CrossRef]
- Du, J.; Wu, B.; Altrock, P.M.; Wang, L. Aspiration dynamics of multi-player games in finite populations. J. R. Soc. Interface 2014, 11, 20140077. [Google Scholar] [CrossRef]
- Nowak, M.A.; Sasaki, A.; Taylor, C.; Fudenberg, D. Emergence of cooperation and evolutionary stability in finite populations. Nature 2004, 428, 646–650. [Google Scholar] [CrossRef]
- Altrock, P.M.; Traulsen, A.; Nowak, M.A. Evolutionary games on cycles with strong selection. Phys. Rev. E 2017, 95, 022407. [Google Scholar] [CrossRef]
- McNamara, J.M.; Houston, A.I. The application of statistical decision theory to animal behavior. J. Theor. Biol. 1980, 85, 673–690. [Google Scholar] [CrossRef]
- McNamara, J.M.; Green, R.F.; Olsson, O. Bayes’ theorem and its applications in animal behaviour. Oikos 2006, 112, 243–251. [Google Scholar] [CrossRef]
- André, O. Bayesian interactions and collective dynamics of opinion: Herd behavior and mimetic contagion. J. Econ. Behav. Organ. 1995, 28, 257–274. [Google Scholar]
- Nishi, R.; Masuda, N. Collective opinion formation model under bayesian updating and confirmation bias. Phys. Rev. E 2013, 87, 062123. [Google Scholar] [CrossRef] [PubMed]
- Chen, H.C.; Chow, Y.Y. Equilibrium Selection in Evolutionary Games with Imperfect Monitoring. J. Appl. Prob. 2008, 45, 388–402. [Google Scholar] [CrossRef][Green Version]
- Chen, H.C.; Chow, Y.Y.; Hsieh, J. Boundedly Rational Quasi-Bayesian Learning in Coordination Games with Imperfect Monitoring. J. Appl. Prob. 2006, 43, 335–350. [Google Scholar] [CrossRef][Green Version]
- Lang, G.; Li, X. Mixed evolutionary strategies imply coexisting opinions on networks. Phys. Rev. E 2008, 77, 016108. [Google Scholar]
- Alonso-Sanz, R. Self-organization in the spatial battle of the sexes with probabilistic updating. Phys. A Stat. Mech. Appl. 2011, 390, 2956–2967. [Google Scholar] [CrossRef]
- Zhao, J.; Szilagyi, M.N.; Szidarovszky, F. n-person Battle of sexes games—A simulation study. Phys. A Stat. Mech. Appl. 2008, 387, 3678–3688. [Google Scholar] [CrossRef]
- Mylius, S.D. What pair formation can do to the battle of the sexes: Towards more realistic game dynamics. J. Theor. Biol. 1999, 197, 469–485. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).