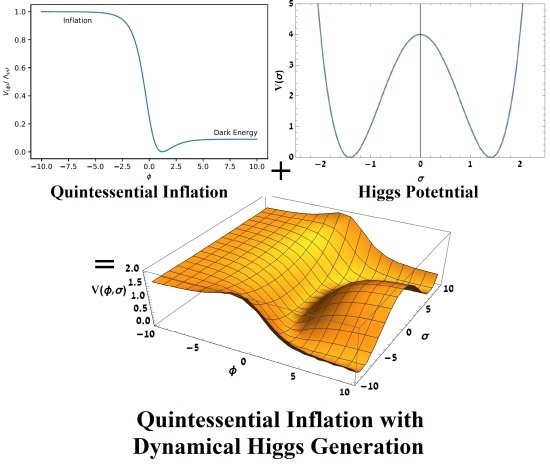
Quintessential Inflation with Dynamical Higgs Generation as an Affine Gravity

Abstract

First, we propose a scale-invariant modified gravity interacting with a neutral scalar inflaton and a Higgs-like $SU\left(2\right)\times U\left(1\right)$ iso-doublet scalar field based on the formalism of non-Riemannian (metric-independent) spacetime volume-elements. This model describes, in the physical Einstein frame, a quintessential inflationary scenario driven by the “inflaton” together with the gravity-“inflaton” assisted dynamical spontaneous $SU\left(2\right)\times U\left(1\right)$ symmetry breaking in the post-inflationary universe, whereas the $SU\left(2\right)\times U\left(1\right)$ symmetry remains intact in the inflationary epoch. Next, we find the explicit representation of the latter quintessential inflationary model with a dynamical Higgs effect as an Eddington-type purely affine gravity.

1. Introduction

Studies in cosmology are dominated by the fundamental concept of “inflation”—a period of exponential expansion, which provides a plausible solution for the “puzzles” of the Big-Bang cosmology (the horizon problem, the flatness problem, the magnetic monopole problem, etc.) [1,2,3,4,5,6,7,8]. For more extensive accounts, see the books [9,10,11,12,13,14,15,16,17,18,19,20,21]. The most widely discussed mechanism for generating a period of accelerated expansion is through the presence of some vacuum energy. In the context of models with scalar field(s)-driven inflation, vacuum energy density appears naturally when the scalar field(s) acquire an effective potential $U_{\mathrm{eff}}$ which has flat regions so that the scalar field(s) can “slowly roll” [5,6,22,23,24] and their kinetic energy can be neglected resulting in an energy-momentum tensor of the form $T_{\mu \nu }\simeq -g_{\mu \nu }{U}_{\mathrm{eff}}$.

With the discovery of the accelerating expansion of the present universe [25,26,27,28,29,30,31,32,33], it appears plausible that a small vacuum energy density, usually referred in this case as “dark energy”, is also present even today. The two vacuum energy densities, the one of inflation and the other of the dark energy dominated universe nowadays, have however a totally different scale which demands a plausible explanation of how cosmological evolution may naturally interpolate between two apparently quite distinctive physical situations.

The possibility of continuously connecting an inflationary phase of the “early” universe to a slowly accelerating universe of nowadays through the evolution of a single scalar field—the quintessential inflation scenario—has been first studied in [34]. Subsequently, a multitude of different quintessential inflationary models have been proposed: (a) based on modified $f\left(R\right)$ gravity [35,36,37]; (b) based on the k-essence concept [38,39,40,41,42]; based on the “variable gravity” model [43]. For an extensive list of references to earlier work on the topic of quintessential inflation, see the References [44,45,46,47,48,49,50,51,52,53] (some of them focusing on Higgs inflation) and [54,55,56,57,58,59], In particular, see the recent Reference [60] for quintessential inflation in the context of Einstein-Gauss-Bonnet gravity and Reference [61] for warm quintessential inflation.

Another parallel groundbreaking development alongside the quintessential inflationary cosmology is the advent of extended modified gravitational theories. The main motivation aims to overcome the limitations of the canonical Einstein’s general relativity manifesting themselves in: (i) Cosmology, for solving the problems of dark energy and dark matter and explaining the large scale structure of the Universe [26,62,63]; (ii) Quantum field theory in curved spacetime, due to the non-renormalizabilty of ultraviolet divergences in higher loops [64,65,66,67,68,69]; and (iii) Modern string theory, given the natural appearance of higher-order curvature invariants and scalar-tensor couplings in low-energy effective field theories [70,71,72,73,74].

Various classes of modified gravity theories have been employed to construct plausible inflationary models: $f\left(R\right)$-gravity, scalar-tensor gravity, Gauss-Bonnet gravity (see [75,76] for an extensive review); also recent proposals based on non-local gravity ([77] and references therein) or based on brane-world scenarios ([78] and references therein). Let us recall the first early successful cosmological model based on the extended $f\left(R\right)=R+R^2$-gravity producing the classical Starobinsky inflationary scalar field potential [2].

For a recent detailed work on quintessential inflation based on $f\left(R\right)$-gravity, where the role of dark matter is being played by axions, see Refernece [79].

A broad class of actively developed modified/extended gravitational theories is based on employing (one or more) alternative non-Riemannian spacetime volume-forms, i.e., metric-independent generally covariant volume-elements in the pertinent Lagrangian actions on spacetime manifolds with an ordinary Riemannian geometry, instead of (or alongside with) the canonical Riemannian volume-element $\sqrt{-g}{d}^{4}x$, whose density is given by the square-root of the determinant of the Riemannian metric $\sqrt{-g}\equiv \sqrt{-det\parallel g_{\mu \nu }\parallel }$.

Originally the formalism employing non-Riemannian volume-elements in generally-covariant Lagrangian actions as in Equation (7) below was proposed in [80,81,82,83,84]. The concise geometric formulation was presented in [85,86]. A brief outline of the basics of the formalism of non-Riemannian volume-elements is given in Section 2 below.

This formalism was used as a basis for constructing a series of modified gravity-matter models describing unified dark energy and dark matter scenario [87,88], quintessential cosmological models with gravity-assisted and inflaton-assisted dynamical suppression (in the “early” universe) or dynamical generation (in the post-inflationary universe) of electroweak spontaneous symmetry breaking and charge confinement [89,90,91], as well as a novel mechanism for the supersymmetric Brout-Englert-Higgs effect (dynamical spontaneous supersymmetry breaking) in supergravity [85].

In the present paper our first principal goal is to analyze (Section 3 below) the close interplay between cosmological dynamics and the patterns of (spontaneous) symmetry breaking along the history of universe, which itself is one of the most important paradigms at the interface of particle physics and cosmology. We will extend our construction, started in [89], of a modified gravity model coupled to (the Higgs part) of the standard electroweak matter content (see, for example, [92,93]) besides the scalar “inflaton” field. The main aim here is to provide an explicit realization from first (Lagrangian action) principles of the remarkable proposal of Bekenstein [94] about the so called gravity-assisted dynamical generation of the Higgs effect—dynamical symmetry breaking of the electroweak $SU\left(2\right)\times U\left(1\right)$ symmetry—without introducing unnatural (according to Bekenstein’s opinion) ingredients such as negative (“ghost”-like) mass squared and quartic self-interaction for the Higgs field. Here we study the interrelation between the presence or absence of dynamical spontaneous electroweak symmetry breaking and the different stages of universe’s evolution driven by the “inflaton”—triggering inflation in the “early” universe as well as representing quintessential variable dark-energy in the “late” universe.

It is shown that during inflation there is no spontaneous electroweak symmetry breaking and the Higgs field resides in its “wrong” vacuum state (“wrong” from the point of view of standard high-energy particle physics). The non-trivial symmetry-breaking Higgs vacuum is dynamically generated in the post-inflationary epoch.

Let us specifically stress that this mechanism is different from the widely discussed scenario of Higgs inflation, where the Higgs field triggers the inflation in the “early” universe through a non-minimal coupling to gravity [95,96,97,98,99,100,101,102,103,104,105,106,107,108,109,110]. In our scenario the impact of the Higgs field dynamics starts after end of inflation.

Another ground-laying branch of gravitational theories is the purely affine gravity formalism, first proposed in [111,112,113,114,115]. It has attracted since then a significant interest primarily due to the established dynamical equivalence [116] of the three principal formulations of standard Einstein’s gravity: purely metric (second-order formalism), metric-affine (Palatini or first-order formalism) and purely affine formalism. For more recent developments and list of references, see [117,118,119,120,121,122,123,124,125,126,127,128,129,130,131,132,133,134], in particular about incorporating torsion and explaining dark energy as an instrinsic property of space-time.

To establish the connection of our non-Riemannian volume-element formalism and the purely affine formalism, our next task (Section 4) will be to represent the above quintessential inflationary model with a dynamical Higgs effect in the form of a no-metric purely affine (Eddington-type) gravity.

2. The Essence of the Non-Riemannian Volume-Form Formalism

Volume-forms define volume-elements (generally covariant integration measures) over differentiable manifolds $\mathcal{M}$, not necessarily Riemannian ones, so no metric is a priori needed [135]. They are given by nonsingular maximal-rank differential forms $\omega$ on $\mathcal{M}$ (for definiteness we will consider the case of $D=4$ dimensional $\mathcal{M}$):

$${\int }_{\mathcal{M}}\omega \left(\dots \right)={\int }_{\mathcal{M}}{d}^{4}x\Omega \left(\dots \right)$$

(1)

where:

$$\omega =\frac{1}{4!}{\omega }_{\mu \nu \kappa \lambda }d{x}^{\mu }\wedge d{x}^{\nu }\wedge d{x}^{\kappa }\wedge d{x}^{\lambda },{\omega }_{\mu \nu \kappa \lambda }=-{\epsilon }_{\mu \nu \kappa \lambda }\Omega ,\Omega =\frac{1}{4!}{\epsilon }^{\mu \nu \kappa \lambda }{\omega }_{\mu \nu \kappa \lambda }.$$

(2)

The conventions for the alternating symbols ${\epsilon }^{\mu \nu \kappa \lambda }$ and ${\epsilon }_{\mu \nu \kappa \lambda }$ are: ${\epsilon }^{0123}=1$ and ${\epsilon }_{0123}=-1$.

The volume-element density (integration measure density) $\Omega$ transforms as scalar density under general coordinate reparametrizations.

In standard general-relativistic theories the Riemannian spacetime volume-form is defined through the tetrad canonical one-forms $e^A=e_{\mu }^{A}d{x}^{\mu }$ ($A=0,1,2,3$):

$$\omega =e^0\wedge e^1\wedge e^2\wedge e^3=det\parallel e_{\mu }^A\parallel d{x}^0\wedge d{x}^1\wedge d{x}^2\wedge d{x}^3,$$

(3)

which yields:

$$\Omega =det\parallel e_{\mu }^A\parallel =\sqrt{-det\parallel g_{\mu \nu }\parallel }\equiv \sqrt{-g}.$$

(4)

Instead of $\sqrt{-g}{d}^{4}x$ we can employ another alternative non-Riemannian volume-element as in (1) and (2) given by a non-singular exact 4-form $\omega =dA$ where:

$$\begin{array}{c}\hfill A=\frac{1}{3!}{A}_{\mu \nu \kappa }d{x}^{\mu }\wedge d{x}^{\nu }\wedge d{x}^{\kappa }⟶\omega =\frac{1}{4!}{\partial }_{[\mu }{A}_{\nu \kappa \lambda ]}d{x}^{\mu }\wedge d{x}^{\nu }\wedge d{x}^{\kappa }\wedge d{x}^{\lambda }.\end{array}$$

(5)

Therefore, the corresponding non-Riemannian volume-element density

$$\Omega \equiv \Phi \left(A\right)=\frac{1}{3!}{\epsilon }^{\mu \nu \kappa \lambda }{\partial }_{\mu }{A}_{\nu \kappa \lambda }.$$

(6)

is defined in terms of the dual field-strength scalar density of an auxiliary rank 3 tensor gauge field $A_{\mu \nu \kappa }$.

In the next Section we will discuss in some detail the properties of a quintessential inflationary model coupled to a truncated version of the electro-weak particle content carrying the standard electro-weak $SU\left(2\right)\times U\left(1\right)$ symmetry. Namely, for simplicity we retain only a Higgs-like scalar field and discard the electro-weak gauge fields and fermions.

Before proceeding let us note the following important property of Lagrangian action terms involving (one or more) non-Riemannian volume-elements:

$$S=\int d^{4}x\sum _j\Phi \left(A^{\left(j\right)}\right){\mathcal{L}}^{\left(j\right)}\left(\mathrm{other}\mathrm{fields}\right)+\dots .$$

(7)

The equations of motion of (7) with respect to the auxiliary tensor gauge fields $A_{\mu \nu \kappa }^{\left(j\right)}$ according to (6) imply:

$${\partial }_{\mu }{\mathcal{L}}^{\left(j\right)}\left(\mathrm{other}\mathrm{fields}\right)=0⟶{\mathcal{L}}^{\left(j\right)}\left(\mathrm{other}\mathrm{fields}\right)=M_j,$$

(8)

where $M_j$ are free integration constants not present in the original action (7). This illustrates the significant advantage of the non-Riemannian volume-element formalism over the “Lagrange-multiplier gravity” method [136], which appeared a decade later and which requires picking a priori some ad hoc constant as opposed to the dynamical appearance of the arbitrary integration constants (8). For further advantages of the non-Riemannian volume-element formalism, see the above remarks.

A characteristic feature of the modified gravitational theories (7) is that when starting in the first-order (Palatini) formalism, all non-Riemannian volume-elements $\Phi \left(A^{\left(j\right)}\right)$ yield almost pure-gauge degrees of freedom, i.e., they do not introduce any additional physical (field-propagating) gravitational degrees of freedom except for few discrete degrees of freedom with conserved canonical momenta appearing as arbitrary integration constants $M_j$. The reason is that the modified gravity action (7) in Palatini formalism is linear with respect to the velocities of some of the components of the auxiliary gauge fields $A_{\mu \nu \kappa }^{\left(j\right)}$ defining the non-Riemannian volume-element densities, and does not depend on the velocities of the rest of auxiliary gauge field components. The (almost) pure-gauge nature of the latter is explicitly shown in [86,89] (Appendix A) employing the standard canonical Hamiltonian treatment of systems with gauge symmetries, i.e., systems with first-class Hamiltonian constraints according to the classification of Dirac [137,138].

3. Quintessential Inflationary Model with Dynamical Higgs Effect

Our starting point is the following specific example of the general class of modified gravity models [85,86,89,90,91,139,140]) involving several non-Riemannian volume-elements (using units with $16\pi G_{\mathrm{Newton}}=1$):

$$S=\int d^{4}x{\Phi }_1\left(A\right)\left[R(g,\Gamma )-2{\mathsf{\Lambda }}_0\frac{{\Phi }_1\left(A\right)}{\sqrt{-g}}+X_{\varphi }+f_1{e}^{\alpha \varphi }+X_{\sigma }-V_0\left(\sigma \right)e^{\alpha \varphi }\right]+\int d^{4}x{\Phi }_2\left(B\right)\left[f_2{e}^{2\alpha \varphi }-\frac{{\Phi }_0\left(C\right)}{\sqrt{-g}}\right].$$

(9)

Here the following notations are used:

• The scalar curvature $R(g,\Gamma )=g^{\mu \nu }{R}_{\mu \nu }(\Gamma )$ is given in terms of the Ricci tensor $R_{\mu \nu }(\Gamma )$ in the first-order (Palatini) formalism:

  $$R_{\mu \nu }(\Gamma )={\partial }_{\alpha }{\Gamma }_{\mu \nu }^{\alpha }-{\partial }_{\nu }{\Gamma }_{\mu \alpha }^{\alpha }+{\Gamma }_{\alpha \beta }^{\alpha }{\Gamma }_{\mu \nu }^{\beta }-{\Gamma }_{\beta \nu }^{\alpha }{\Gamma }_{\mu \alpha }^{\beta }$$

  (10)

  defined by the affine connection ${\Gamma }_{\mu \nu }^{\lambda }$ a priori independent of the metric $g_{\mu \nu }$.
• The non-Riemannian volume-element densities ${\Phi }_1\left(A\right),{\Phi }_2\left(B\right),{\Phi }_0\left(C\right)$ are defined as in (6):

  $${\Phi }_1\left(A\right)=\frac{1}{3!}{\epsilon }^{\mu \nu \kappa \lambda }{\partial }_{\mu }{A}_{\nu \kappa \lambda },{\Phi }_2\left(B\right)=\frac{1}{3!}{\epsilon }^{\mu \nu \kappa \lambda }{\partial }_{\mu }{B}_{\nu \kappa \lambda },{\Phi }_0\left(C\right)=\frac{1}{3!}{\epsilon }^{\mu \nu \kappa \lambda }{\partial }_{\mu }{C}_{\nu \kappa \lambda }.$$

  (11)
• $\varphi$ is a neutral scalar “inflaton” and $\sigma \equiv \left({\sigma }_a\right)$ is a complex $SU\left(2\right)\times U\left(1\right)$ iso-doublet Higgs-like scalar field with the isospinor index $a=+,0$ indicating the corresponding $U\left(1\right)$ charge. The corresponding kinetic energy terms in (9) read:

  $$X_{\varphi }\equiv -\frac{1}{2}{g}^{\mu \nu }{\partial }_{\mu }\varphi {\partial }_{\nu }\varphi ,X_{\sigma }\equiv -g^{\mu \nu }{\partial }_{\mu }{\sigma }_a^{*}{\partial }_{\nu }{\sigma }_a,$$

  (12)

  and

  $$V_0\left(\sigma \right)\equiv m_0^2{\sigma }_a^{*}{\sigma }_a,$$

  (13)

  is a canonical mass term for the Higgs-like field, i.e., neither negative (“ghost-like”) mass-squared term nor quartic self-interaction are introduced unlike the case in the standard electro-weak model [92,93].
• $f_{1,2}$ and $\alpha$ are dimensionful coupling constants in the “inflaton” potential. The ${\mathsf{\Lambda }}_0$ is a small dimensional constant which will be identified in the sequel with the “late” universe cosmological constant in the dark energy dominated accelerated expansion’s epoch.

The specific form of the action (9) is fixed by the requirement of global Weyl-scale invariance under:

$$\begin{array}{c}\hfill g_{\mu \nu }\to \lambda g_{\mu \nu },A_{\mu \nu \kappa }\to \lambda A_{\mu \nu \kappa },B_{\mu \nu \kappa }\to {\lambda }^2{B}_{\mu \nu \kappa },C_{\mu \nu \kappa }\to C_{\mu \nu \kappa },\end{array}$$

(14)

$$\begin{array}{c}\hfill \varphi \to \varphi -\frac{1}{\alpha }ln\lambda ,{\sigma }_a\to {\sigma }_a,\end{array}$$

(15)

where the scaling parameter is $\lambda =\mathrm{const}$. The importance of global scale symmetry within the context of non-Riemannian volume-element formalism has been already stressed in the first original papers (see [82]), where in particular models with spontaneously broken dilatation symmetry have been constructed along these lines, which are free of the Fifth Force Problem [84].

Varying the action (9) with respect to $g^{\mu \nu }$, ${\Gamma }_{\mu \nu }^{\lambda }$, $A_{\mu \nu \lambda }$, $B_{\mu \nu \lambda }$, $C_{\mu \nu \lambda }$, $\varphi$ and ${\sigma }^a$ , yield the following equations of motion, respectively:

$$\begin{array}{c}\hfill R_{\mu \nu }(\Gamma )-{\mathsf{\Lambda }}_0\frac{{\Phi }_1\left(A\right)}{\sqrt{-g}}{g}_{\mu \nu }-\frac{1}{2}{\partial }_{\mu }\varphi {\partial }_{\nu }\varphi -{\partial }_{\mu }{\sigma }_a^{*}{\partial }_{\nu }{\sigma }_a-\frac{1}{2}{g}_{\mu \nu }\frac{{\Phi }_2\left(B\right){\Phi }_0\left(C\right)}{{\Phi }_1\left(A\right)\sqrt{-g}}=0,\end{array}$$

(16)

$$\begin{array}{c}\hfill {\Phi }_1\left(A\right)g^{\mu \nu }\left({\nabla }_{\lambda }\delta {\Gamma }_{\mu \nu }^{\lambda }-{\nabla }_{\mu }\delta {\Gamma }_{\lambda \nu }^{\lambda }\right)=0,\end{array}$$

(17)

$$\begin{array}{c}\hfill g^{\mu \nu }\left(R_{\mu \nu }(\Gamma )-\frac{1}{2}{\partial }_{\mu }\varphi {\partial }_{\nu }\varphi -{\partial }_{\mu }{\sigma }_a^{*}{\partial }_{\nu }{\sigma }_a\right)-4{\mathsf{\Lambda }}_0\frac{{\Phi }_1\left(A\right)}{\sqrt{-g}}+\left(f_1-m_0^2{\sigma }_a^{*}{\sigma }_a\right)e^{\alpha \varphi }=M_1\equiv \mathrm{const},\end{array}$$

(18)

$$\begin{array}{c}\hfill f_2{e}^{-2\alpha \varphi }-\frac{{\Phi }_0\left(C\right)}{\sqrt{-g}}=-M_2\equiv \mathrm{const},\frac{{\Phi }_2\left(B\right)}{\sqrt{-g}}={\chi }_2\equiv \mathrm{const},\end{array}$$

(19)

$$\begin{array}{c}\hfill {\partial }_{\mu }\left({\Phi }_1\left(A\right)g^{\mu \nu }{\partial }_{\nu }\varphi \right)+\alpha {\Phi }_1\left(A\right)\left(f_1-m_0^2{\sigma }_a^{*}{\sigma }_a\right)e^{\alpha \varphi }+2\alpha {\Phi }_2\left(B\right)f_2{e}^{2\alpha \varphi }=0,\end{array}$$

(20)

$$\begin{array}{c}\hfill {\partial }_{\mu }\left({\Phi }_1\left(A\right)g^{\mu \nu }{\partial }_{\nu }{\sigma }_a\right)-{\Phi }_1\left(A\right)m_0^2{e}^{\alpha \varphi }{\sigma }_a=0.\end{array}$$

(21)

Equations (18) and (19) are special cases of the general Equation (8) discussed above. Here $M_{1,2}$ and ${\chi }_2$ are arbitrary (dimensional and dimensionless, respectively) integration constants, with $M_{1,2}$ triggering a spontaneous breaking of the global Weyl-scale symmetry (15).

Taking the trace of Equation (16) and comparing with Equations (18) and (19), we find for the ratio of volume-element densities:

$${\chi }_1\equiv \frac{{\Phi }_1\left(A\right)}{\sqrt{-g}}=\frac{2{\chi }_2\left(f_2{e}^{2\alpha \varphi }+M_2\right)}{M_1+\left(m_0^2{\sigma }_a^{*}{\sigma }_a-f_1\right)e^{\alpha \varphi }}\equiv {\chi }_1(\varphi ,\sigma ).$$

(22)

On the other hand, following analogous derivation in [82], Equation (17) yields a solution for ${\Gamma }_{\nu \lambda }^{\mu }$ as a Levi-Civita connection:

$${\Gamma }_{\nu \lambda }^{\mu }={\Gamma }_{\nu \lambda }^{\mu }\left(\overline{g}\right)=\frac{1}{2}{\overline{g}}^{\mu \kappa }\left({\partial }_{\nu }{\overline{g}}_{\lambda \kappa }+{\partial }_{\lambda }{\overline{g}}_{\nu \kappa }-{\partial }_{\kappa }{\overline{g}}_{\nu \lambda }\right)$$

(23)

with respect to a Weyl-conformally rescaled metric:

$${\overline{g}}_{\mu \nu }={\chi }_1(\varphi ,\sigma )g_{\mu \nu }$$

(24)

with ${\chi }_1(\varphi ,\sigma )$ as in (22).

Conformal transformation $g_{\mu \nu }\to {\overline{g}}_{\mu \nu }$ via (24) convert the modified gravity action (9) into the physical Einstein-frame action (objects in the Einstein-frame indicated by a bar):

$$S_{\mathrm{EF}}=\int d^{4}x\sqrt{-\overline{g}}\left[R\left(\overline{g}\right)-\frac{1}{2}{\overline{g}}^{\mu \nu }{\partial }_{\mu }\varphi {\partial }_{\nu }\varphi -{\overline{g}}^{\mu \nu }{\partial }_{\mu }{\sigma }_a^{*}{\partial }_{\nu }{\sigma }_a-U_{\mathrm{eff}}(\varphi ,\sigma )\right],$$

(25)

with an effective Einstein-frame scalar field potential:

$$\begin{array}{c}\hfill U_{\mathrm{eff}}(\varphi ,\sigma )\equiv \frac{M_1+e^{\alpha \varphi }\left(m_0^2{\sigma }_a^{*}{\sigma }_a-f_1\right)}{{\chi }_1(\varphi ,\sigma )}-\frac{{\chi }_2\left(f_2{e}^{2\alpha \varphi }+M_2\right)}{{\left({\chi }_1(\varphi ,\sigma )\right)}^2}+2{\mathsf{\Lambda }}_0\\ \hfill =\frac{{\left[M_1+e^{\alpha \varphi }\left(m_0^2{\sigma }_a^{*}{\sigma }_a-f_1\right)\right]}^2}{4{\chi }_2\left(f_2{e}^{2\alpha \varphi }+M_2\right)}+2{\mathsf{\Lambda }}_0,\end{array}$$

(26)

which is entirely dynamically generated due to the appearance of the free integration constants $M_{1,2}$ and ${\chi }_2$ (18) and (19).

As discussed in [86,90,91,141] the scalar potential $U_{\mathrm{eff}}(\varphi ,\sigma )$ (26) has a remarkable feature: it possesses two (infinitely) large flat regions as a function of $\varphi$ at ${\sigma }_a=\mathrm{fixed}$ (see the graphical representation on Figure 1) with the following properties:

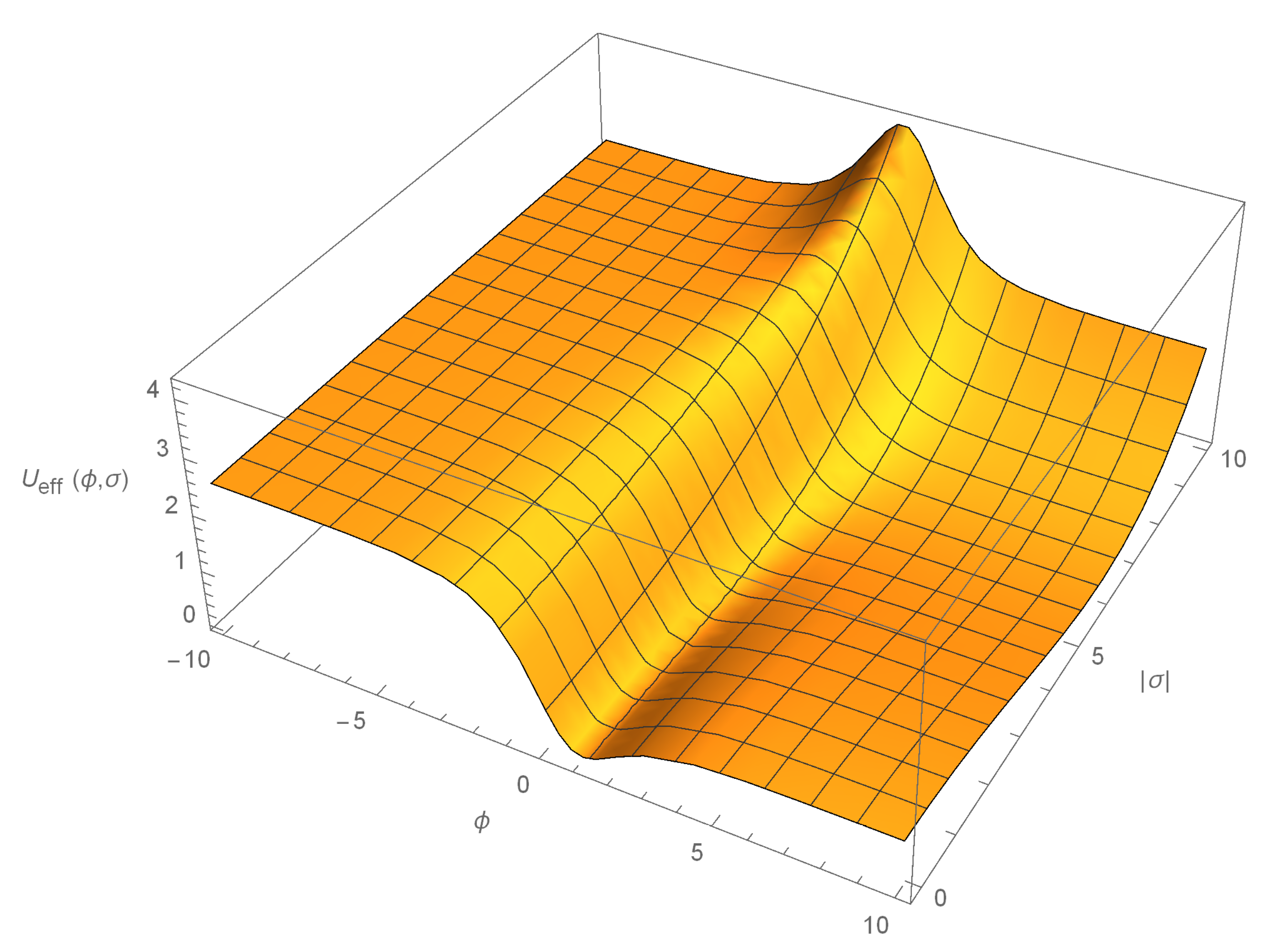
• (a) (−) flat “inflaton” region for large negative values of $\varphi$ (and ${\sigma }_a$ is finite) corresponding to the “slow-roll” inflationary evolution of the “early” universe driven by $\varphi$. Here the effective potential (26) reduces to (an almost) constant value independent of the finite value of ${\sigma }_a$—this is energy scale of the inflationary epoch:

  $$U_{\mathrm{eff}}\left(\varphi ,\sigma \right)\simeq U_{(-)}=\frac{M_1^2}{4{\chi }_2{M}_2}+2{\mathsf{\Lambda }}_0.$$

  (27)
  Thus, in the “early” universe the Higgs-like field ${\sigma }_a$ must be (approximately) either massless or constant with no non-zero vacuum expectation value, therefore there is no spontaneous breaking of $SU\left(2\right)\times U\left(1\right)$ symmetry. Moreover, in fact as shown in the Remark below, ${\sigma }_a$ does not participate in the “slow-roll” inflationary evolution, so $\sigma$ stays constant there equal to the “false”vacuum value $\sigma =0$.
• (b) (+) flat “inflaton” region for large positive values of $\varphi$ (and ${\sigma }_a$—finite) corresponding to the evolution of the post-inflationary (“late”) universe, where:

  $$U_{\mathrm{eff}}\left(\varphi ,\sigma \right)\simeq U_{(+)}\left(\sigma \right)=\frac{{\left(m_0^2{\sigma }_a^{*}{\sigma }_a-f_1\right)}^2}{4{\chi }_2{f}_2}+2{\mathsf{\Lambda }}_0$$

  (28)

  acquires the form of a dynamically induced $SU\left(2\right)\times U\left(1\right)$ spontaneous symmetry breaking Higgs potential with a Higgs “vacuum” at:

  $$|{\sigma }_{\mathrm{vac}}|=\frac{1}{m_0}\sqrt{f_1},$$

  (29)

  where the parameters are naturally identified as:

  $$f_1\sim M_{EW}^4,m_0\sim M_{EW}$$

  (30)

  in terms of the electro-weak energy scale $M_{EW}\sim {10}^{-16}{M}_{Pl}$.
• Thus, the residual cosmological constant ${\mathsf{\Lambda }}_0$ in (28) has to be identified with the current epoch observable cosmological constant ($\sim {10}^{-122}{M}_{Pl}^4$) and, therefore, according to (27) the integration constants $M_{1,2}$ are naturally identified by orders of magnitude as

  $$M_1\sim M_2\sim {10}^{-8}{M}_{Pl}^4,$$

  (31)

  since in the latter case the order of magnitude of the vacuum energy density in the (−) flat region (27) becomes:

  $$U_{(-)}\sim M_1^2/M_2\sim {10}^{-8}{M}_{Pl}^4,$$

  (32)

  which conforms to the Planck Collaboration data [142,143] for the “early” universe’s energy scale of inflation being of order ${10}^{-2}{M}_{Pl}$.
• Here the order of magnitude for $f_2$ is determined from the mass term of the Higgs-like field $\sigma$ in the $(+)$ flat region resulting from (28) upon expansion around the Higgs vacuum ($\sigma ={\sigma }_{\mathrm{vac}}+\tilde{\sigma }$):

  $$\frac{f_1{m}_0^2}{{\chi }_2{f}_2}{\left({\tilde{\sigma }}_a\right)}^{*}\left({\tilde{\sigma }}_a\right),$$

  (33)

  which implies that:

  $$f_2\sim f_1\sim M_{EW}^4.$$

  (34)
• Let us specifically note that the viability of the present model (in a slightly simplified form without the Higgs scalar) concerning confrontation with the observational data has already been analyzed and confirmed numerically in Reference [141]. In particular, a graphical plot of the evolution of r (tensor-to-scalar ratio) vs. $n_s$ (scalar spectral index) has been provided there.

Remark 1.

Assuming that in the (−) flat “inflaton” region (for large negative values of ϕ and ${\sigma }_a$—finite) both the “inflaton” ϕ and the Higgs-like field ${\sigma }_a$ evolve in a “slow-role” regime, their “slow-role” equations of motion in the standard FLRW (Friedmann-Lemaitre-Robertson-Walker) reduction of the Einstein-frame metric (${\overline{g}}_{\mu \nu }d{x}^{\mu }d{x}^{\nu }\equiv -N^2\left(t\right)d{t}^2+a^2\left(t\right)d\overrightarrow{x}.d\overrightarrow{x}$) read accordingly (see, for example, [5,6,22,23]):

$$\begin{array}{c}\hfill \stackrel{.}{\varphi }\simeq -\frac{1}{3H}\frac{\partial U_{\mathrm{eff}}(\varphi ,\sigma )}{\partial \varphi },\frac{\partial U_{\mathrm{eff}}(\varphi ,\sigma )}{\partial \varphi }=\frac{\alpha e^{\alpha \varphi }\left[M_1+e^{\alpha \varphi }\left(m_0^2{\left|\sigma \right|}^2-f_1\right)\right]\left[M_2\left(m_0^2{\left|\sigma \right|}^2-f_1\right)-M_1{f}_2{e}^{\alpha \varphi }\right]}{2{\chi }_2{\left(M_2+f_2{e}^{2\alpha \varphi }\right)}^2}\end{array}$$

(35)

$$\begin{array}{c}\hfill \stackrel{.}{\sigma }\simeq -\frac{1}{3H}\frac{\partial U_{\mathrm{eff}}(\varphi ,\sigma )}{\partial \sigma }⟶\frac{d\left|\sigma \right|}{dt}\simeq -\frac{1}{3H}\frac{m_0^2\left|\sigma \right|e^{\alpha \varphi }\left[M_1+e^{\alpha \varphi }\left(m_0^2{\left|\sigma \right|}^2-f_1\right)\right]}{2{\chi }_2\left(M_2+f_2{e}^{2\alpha \varphi }\right)},\end{array}$$

(36)

where ${\left|\sigma \right|}^2\equiv {\sigma }_a^{*}{\sigma }_a$ and $H=\frac{\stackrel{.}{a}}{a}$ denotes the Hubble parameter. Equations (35) and (36) define parametrically a curve $\left|\sigma \right|=\left|\sigma \right|\left(\varphi \right)$ in the two-field $(\varphi ,|\sigma \left|\right)$ target space. Equivalently, this curve is defined through the differential equation:

$$\frac{d\left|\sigma \right|}{dz}\simeq \frac{m_0^2\left|\sigma \left(z\right)\right|\left(M_2+f_2{z}^2\right)}{{\alpha }^{2}z\left[M_2\left(m_0^2{\left|\sigma \left(z\right)\right|}^2-f_1\right)-M_1{f}_{2}z\right]},z\equiv e^{\alpha \varphi }.$$

(37)

In the (−) flat “inflaton” region (ϕ – large negative) z is very small, so in this case Equation(37) can be rewritten as:

$$\alpha \left(\left|\sigma \right|-\frac{f_1}{m_0^2\left|\sigma \right|}\right)d\left|\sigma \right|\simeq \frac{dz}{z}⟶\alpha \left(\frac{1}{2}{\left|\sigma \left(z\right)\right|}^2-\frac{f_1}{m_0^2}ln\left|\sigma \left(z\right)\right|\right)\simeq lnz.$$

(38)

Obviously, a consistent solution $\left|\sigma \right(z\left)\right|$ of (38)does not exist for $z=e^{\alpha \varphi }\to 0$, therefore, the assumption for the “slow-roll” evolution (36) of the Higgs-like field ${\sigma }_a$ in the inflationary region (large negative values of ϕ) is invalid. Thus $\left|\sigma \right|$ must be constant and Equation (36) implies $\left|\sigma \right|=0$ in the (−) flat “inflaton” region.

To conclude this section, we see that thanks to the remarkable dynamically generated scalar potential (26) the “inflaton” $\varphi$ plays the role both of driving “slow-roll” inflationary dynamics in the “early” universe, as well as it plays the role of a quintessential variable dark-energy field triggering slowly accelerating de Sitter expansion in the “late” universe.

Accordingly, gravity-inflaton dynamics generates dynamically spontaneous $SU\left(2\right)\times U\left(1\right)$ symmetry breaking – Higgs effect – in the post-inflationary epoch, whereas it dynamically suppresses spontaneous symmetry breaking during inflation in the “early” universe. Namely, the dynamical transition from the “false” Higgs vacuum to the genuine electroweak spontaneously broken vacuum is driven by the inflaton evolving from (large) negative values (on the “(−)” flat region (27) of the scalar potential (26)) to (large) positive values (on the “(+)” flat region (28) of the scalar potential (26)).

Thus, our scale invariant modified gravity model (9) in its Einstein-frame representation (25) and (26) turns out to be an explicit implementation of Bekenstein’s idea [94] about a gravity-assisted spontaneous symmetry breaking of electro-weak (Higgs) type without invoking negative mass squared and a quartic Higgs field self-interaction unlike the canonical case in the standard particle model [92,93].

4. Eddinton-Type No-Metric Gravity and Quintessential Inflation

Let us now consider a generic model of gravity, with some Riemannian metric ${\overline{g}}_{\mu \nu }$ and with the ordinary Riemannian volume-element $\sqrt{-\overline{g}}$ within the first-order (Palatini) formalism, interacting with a multi-component scalar field ${\varphi }^A$, $A=1,\dots ,N$ (using again units with $16\pi G_{\mathrm{Newton}}=1$):

$$S=\int d^{4}x\sqrt{-\overline{g}}\left[{\overline{g}}^{\mu \nu }{R}_{\mu \nu }(\Gamma )-\frac{1}{2}{\overline{g}}^{\mu \nu }{h}_{AB}{\partial }_{\mu }{\varphi }^A{\partial }_{\nu }{\varphi }^B-U\left(\varphi \right)\right],$$

(39)

where the Ricci tensor $R_{\mu \nu }(\Gamma )$ is the same as in (10), and $h_{AB}\left(\varphi \right)$ indicates some “metric” in the scalar field target space (in the present case it will be just a unit matrix).

The equations of motion with respect to $g^{\mu \nu }$, ${\varphi }^A$ and ${\Gamma }_{\mu \nu }^{\lambda }$ read accordingly:

$$\begin{array}{c}\hfill R_{\mu \nu }(\Gamma )=\frac{1}{2}\left(T_{\mu \nu }-\frac{1}{2}{\overline{g}}_{\mu \nu }{T}_{\lambda }^{\lambda }\right),\end{array}$$

(40)

$$\begin{array}{c}\hfill T_{\mu \nu }=h_{AB}\left(\varphi \right){\partial }_{\mu }{\varphi }^A{\partial }_{\nu }{\varphi }^B-{\overline{g}}_{\mu \nu }\left[\frac{1}{2}{\overline{g}}^{\kappa \lambda }{h}_{AB}\left(\varphi \right){\partial }_{\kappa }{\varphi }^A{\partial }_{\lambda }{\varphi }^B+U\left(\varphi \right)\right],\end{array}$$

(41)

$$\begin{array}{c}\hfill \frac{1}{\sqrt{-\overline{g}}}{\partial }_{\mu }\left(\sqrt{-\overline{g}}{g}^{\mu \nu }{h}_{AB}{\partial }_{\nu }{\varphi }^B\right)-\frac{1}{2}{\overline{g}}^{\mu \nu }\frac{\partial h_{CD}}{\partial {\varphi }^A}{\partial }_{\mu }{\varphi }^C{\partial }_{\nu }{\varphi }^D-\frac{\partial U\left(\varphi \right)}{\partial {\varphi }^a}=0,\end{array}$$

(42)

$$\begin{array}{c}\hfill \int d^{4}x\sqrt{-\overline{g}}{\overline{g}}^{\mu \nu }\left({\nabla }_{\lambda }\delta {\Gamma }_{\mu \nu }^{\lambda }-{\nabla }_{\mu }\delta {\Gamma }_{\lambda \nu }^{\lambda }\right)=0\end{array}$$

(43)

Following again the analogous derivation in [82], the solution of Equation (43) is that ${\Gamma }_{\mu \nu }^{\lambda }$ becomes the canonical Levi-Civita connection w.r.t. ${\overline{g}}_{\mu \nu }$:

$${\Gamma }_{\nu \lambda }^{\mu }={\Gamma }_{\nu \lambda }^{\mu }\left(\overline{g}\right)=\frac{1}{2}{\overline{g}}^{\mu \kappa }\left({\partial }_{\nu }{\overline{g}}_{\lambda \kappa }+{\partial }_{\lambda }{\overline{g}}_{\nu \kappa }-{\partial }_{\kappa }{\overline{g}}_{\nu \lambda }\right).$$

(44)

Equations (40) and (41) can be equivalently written as:

$${\overline{g}}_{\mu \nu }=\frac{2}{U\left(\varphi \right)}\left(R_{\mu \nu }(\Gamma )-\frac{1}{2}{h}_{AB}\left(\varphi \right){\partial }_{\mu }{\varphi }^A{\partial }_{\nu }{\varphi }^B\right),$$

(45)

that is, the metric ${\overline{g}}_{\mu \nu }$ in (39) is expressed entirely in terms of the affine connection and the matter field.

Now, we will show that the gravity-matter theory (39) is equivalent, in a sense of producing the same equations of motion (41)–(44), to the following Eddington-type purely affine gravity theory:

$$S_{Edd}=\int d^{4}x\frac{2}{U\left(\varphi \right)}\sqrt{det\parallel R_{\mu \nu }(\Gamma )-\frac{1}{2}{h}_{AB}\left(\varphi \right){\partial }_{\mu }{\varphi }^A{\partial }_{\nu }{\varphi }^B\parallel },$$

(46)

i.e., (46) does not involve at all a Riemannian metric.

Indeed, varying the action (46) w.r.t. ${\Gamma }_{\mu \nu }^{\lambda }$ and ${\varphi }^a$ we get:

$$\frac{2}{U\left(\varphi \right)}\sqrt{det\parallel H_{\alpha \beta }(\Gamma ,\varphi ,\sigma )\parallel }{\left(H^{-1}((\Gamma ,\varphi ,\sigma )\right)}^{\mu \nu }\left({\nabla }_{\lambda }\delta {\Gamma }_{\mu \nu }^{\lambda }-{\nabla }_{\mu }\delta {\Gamma }_{\lambda \nu }^{\lambda }\right)=0,$$

(47)

with the short-hand notation:

$$H_{\mu \nu }(\Gamma ,\varphi )\equiv R_{\mu \nu }(\Gamma )-\frac{1}{2}{h}_{AB}\left(\varphi \right){\partial }_{\mu }{\varphi }^A{\partial }_{\nu }{\varphi }^B,$$

(48)

and

$$\begin{array}{c}\hfill {\partial }_{\mu }\left(\frac{1}{U\left(\varphi \right)}\sqrt{det\parallel H_{\alpha \beta }(\Gamma ,\varphi )\parallel }{\left(H^{-1}(\Gamma ,\varphi )\right)}^{\mu \nu }{h}_{AB}\left(\varphi \right){\partial }_{\nu }{\varphi }^B\right)\\ \hfill -\frac{1}{2U\left(\varphi \right)}\sqrt{det\parallel H_{\alpha \beta }(\Gamma ,\varphi )\parallel }{\left(H^{-1}(\Gamma ,\varphi )\right)}^{\mu \nu }\frac{\partial h_{CD}}{\partial {\varphi }^A}{\partial }_{\mu }{\varphi }^C{\partial }_{\nu }{\varphi }^D+2\frac{\partial }{\partial \varphi }\left(\frac{1}{U\left(\varphi \right)}\right)\sqrt{det\parallel H_{\alpha \beta }(\Gamma ,\varphi )\parallel }=0.\end{array}$$

(49)

Now, using the identification Equation (45) for the Riemannian metric ${\overline{g}}_{\mu \nu }=\frac{2}{U\left(\varphi \right)}{H}_{\mu \nu }(\Gamma ,\varphi )$ with $H_{\mu \nu }(\Gamma ,\varphi )$ as in (48), Equations (47)–(49) become identical to Equations (42) and (43), respectively.

The above derivation of purely affine gravity interacting with multi-component scalar fields appeared previously in [144]. Historically, this formulation was proposed for the first time in [115] in the special case of a single Klein-Gordon field with $U\left(\varphi \right)=\frac{1}{2}{m}^2{\varphi }^2$, see also [145].

Applying the above established equivalence between the models (39) and (46) to the initial modified gravity action (9) and its Einstein-frame representation (25) with $U_{\mathrm{eff}}(\varphi ,\sigma )$ as in (26), analyzed in Section 3 above, we find that the following specific Eddington-type purely affine no-metric gravity model:

$$\begin{array}{c}\hfill S_{Edd}=\int d^{4}x\frac{8{\chi }_2\left(f_2{e}^{-2\alpha \varphi }+M_2\right)}{{\left[M_1+\left(m_0^2{\sigma }_a^{*}{\sigma }_a-f_1{e}^{-\alpha \varphi }\right)\right]}^2+8{\mathsf{\Lambda }}_0{\chi }_2\left(f_2{e}^{-2\alpha \varphi }+M_2\right)}\\ \hfill \times \sqrt{det\parallel R_{\mu \nu }(\Gamma )-\frac{1}{2}{\partial }_{\mu }\varphi {\partial }_{\nu }\varphi -{\partial }_{\mu }{\sigma }_a^{*}{\partial }_{\nu }{\sigma }_a\parallel },\end{array}$$

(50)

actually describes a quintessential inflationary dynamics with dynamically generated Higgs effect in the post-iflationary epoch with all the properties discussed in Section 3. The metric $g_{\mu \nu }$ in the initial modified scale-invariant gravity action (9) with non-Riemannian volume-elements, taking into account relation (45) applied for the Einstein-frame metric (24) where $U\left(\varphi \right)=U_{\mathrm{eff}}(\varphi ,\sigma )$ (26) and using the on-shell relations (19) and (22), is identified as:

$$g_{\mu \nu }=\frac{2}{{\chi }_1(\varphi ,\sigma )U_{\mathrm{eff}}(\varphi ,\sigma )}\left[R_{\mu \nu }(\Gamma )-\frac{1}{2}{\partial }_{\mu }\varphi {\partial }_{\nu }\varphi -{\partial }_{\mu }{\sigma }_a^{*}{\partial }_{\nu }{\sigma }_a\right],$$

(51)

with $R_{\mu \nu }(\Gamma )$ as in (10), and ${\chi }_1(\varphi ,\sigma )$ and $U_{\mathrm{eff}}(\varphi ,\sigma )$ explicitly given in (22) and (26), respectively:

$$\frac{1}{{\chi }_1(\varphi ,\sigma )U_{\mathrm{eff}}(\varphi ,\sigma )}=\frac{2\left[M_1+e^{\alpha \varphi }\left(m_0^2{\sigma }_a^{*}{\sigma }_a-f_1\right)\right]}{{\left[M_1+e^{\alpha \varphi }\left(m_0^2{\sigma }_a^{*}{\sigma }_a-f_1\right)\right]}^2+8{\mathsf{\Lambda }}_0{\chi }_2\left(f_2{e}^{2\alpha \varphi }+M_2\right)}.$$

(52)

5. Conclusions

In the present paper we have employed two fundamental concepts, namely, non-Riemannian metric-independent spacetime volume-elements and (global) scale invariance, to construct a self-consistent model of modified gravity coupled to a neutral scalar “inflaton” and to a Higgs-like $SU\left(2\right)\times U\left(1\right)$ iso-boublet scalar possessing the following extraordinary features:

(a) In the physical Einstein frame, thanks to a dynamical generation of a remarkable scalar potential with two long flat “inflaton” regions with vastly different heights, the model describes a plausible quintessential inflationary scenario, driven by the “inflaton”, with a “slow-roll” inflationary stage in the “early” universe and a slow accelerating de Sitter expansion in the “late” universe;

(b) This model provides an explanation of the interplay between cosmological dynamics and the patterns of symmetry breaking during the evolution of the universe. Namely, we find an explicit realization from first (Lagrangian-action) principles of the noteworthy proposal of Bekenstein from 1986 about “gravity-assisted” dynamical Higgs-like spontaneous symmetry breakdown (Higgs effect). We exhibit gravity-“inflaton” suppression of the Higgs effect during inflation, i.e., no electroweak spontaneous breakdown there), whereas in the post-inflationary epoch a Higgs-type symmetry breaking potential is dynamically created.

(c) The coupling constants in the initial modified gravity action are naturally identified as powers of the standard electroweak mass scale.

(d) It is shown how to represent the above quintessential inflationary model with a dynamical Higgs effect in the form of a no-metric purely affine (Eddington-type) gravity.

A next important task is to study in some detail, within the present quintessential inflationary scenario with a dynamical Higgs effect, the numerical solutions for the basic inflationary observables (scalar power spectral index, tensor-to-scalar ratio, etc.) extending the numerical analysis from Reference [141] (where the Higgs field was absent). Since in the present scenario the Higgs field during (most of the) inflation resides in its “false” vacuum, the significant impact of Higgs field dynamics will occur after end of inflation when the “inflaton” starts to generate the non-trivial Higgs symmetry breaking potential.