Abstract
In the present era, nanofluids are one of the most important and hot issue for scientists, physicists, and mathematicians. Nanofluids have many important and updated characteristics compared to conventional fluids. The thermal conductivity, thermal expansion, and the heat transfer rate of conventional fluids are not up to the mark for industrial and experimental uses. To overcome these deficiencies, nanoparticles have been dispersed into base fluids to make them more efficient. The heat transfer characteristics through symmetry trapezoidal-corrugated channels can be enhanced using nanofluids. In the present article, a literature survey has been presented for different models of nanofluids and their solutions—particularly, exact solutions. The models for hybrid nanofluids were also mentioned in the present study. Furthermore, some important and most used models for the viscosity, density, coefficient of thermal expansion, coefficient of mass expansion, heat capacitance, electrical conductivity, and thermal conductivity are also presented in tabular form. Moreover, some future suggestions are also provided in this article.
1. Introduction
In many industrial fields, heat transfer is not only a technical issue where it is important but also a challenge for engineers and businesspeople. To overcome this challenge, one of the common methods is to increase the available surface area for heat exchange. In thermal management systems, this method leads to undesirable and unrealistic increases in heat transport. Businesspeople and engineers are faced with the poor thermal properties of traditional fluids such as water, alcohol, ethylene glycol, or oil. Therefore, there is an urgent need to improve the thermal conductivity of these fluids to overcome such problems in heat transport [1]. Nanofluids are the best solution to this problem with the fact that it is a suspension of nanometer-sized metal oxides, metals (Figure 1), polymers, carbon nanotubes or silica particles dispersed in the ordinary fluid [2]. This idea was proposed in 1995 by Choi [3]. In recent years, many researchers have studied the effects of nanofluids to improve heat transfer in thermal engineering devices, both experimentally and theoretically. Researchers also applied various preparation methods, properties, and different models used to calculate the thermophysical properties of nanofluids (i.e., thermal conductivity, viscosity, density, specific heat capacity) [4,5,6,7,8,9,10,11]. Some scientists have also studied the effects of nanoflares on the flow and heat transfer in natural and forced heating in different systems [12,13,14,15]. Different schemes and approaches have been reported in the literature for the solutions of mathematical problems regarding nanofluid flow [16,17,18,19,20,21,22,23].
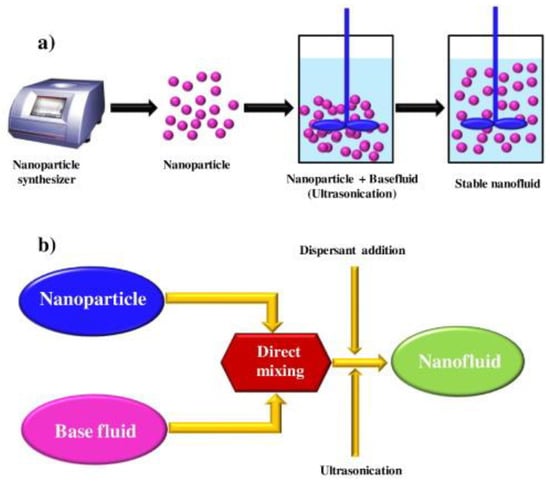
Figure 1.
(a) Nanoparticles and (b) nanofluids.
2. Models for Nanofluids
In the literature, two different models are used for the description of nanofluids, namely, single-phase flow models and two-phase flow models. In a single flow model, the effects of slip and other related forces are neglected, and in the two-phase flow, these effects have been considered [24].
3. Properties of Nanofluids
The nanofluids have different properties than conventional fluids. Some properties of the nanofluids are discussed in the following sub-sections.
3.1. Density
The density of the nanofluid, according to the existing literature is give by the following formula [24]:
3.2. Specific Heat Capacity
According to the published literature, the specific heat capacity of nanofluid is defined as [25]
In another way, specific heat capacity is given by [26]
3.3. Electrical Conductivity
Electrical conductivity is the important feature of the fluid. For the nanofluid the electrical conductivity is defined as [27]
3.4. Coefficient of Thermal Expansion
The thermal expansion for the nanofluid is calculated as [28]
3.5. Coefficient of Mass Expansion
The coefficient of mass expansion for the nanofluid is calculated as [28]
3.6. Dynamic Viscosity
In the literature, different models have been used for the dynamics viscosity of the nanofluids. The dynamic viscosity is very important property while studying nanofluid; this is evident form Figure 2 [29].
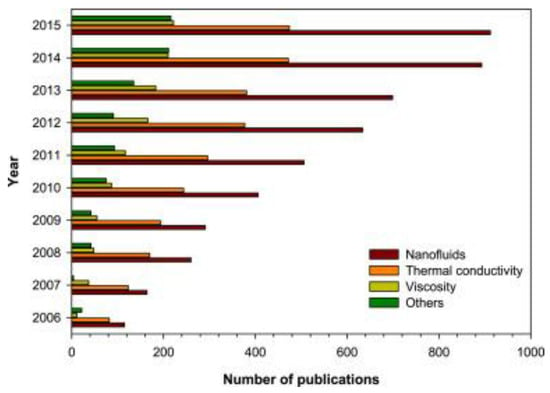
Figure 2.
Year-wise publications records on different areas of nanofluids from Web of Science.
In this review article, we have tried to mention most of these models in Table 1.

Table 1.
Different models for dynamics viscosity of nanofluids.
3.7. Thermal Conductivity
The thermal conductivity of nanofluid is the most important property. Many researchers have conducted many studies on this property of nanofluid and have proposed different models for this. Some important and useful models are given in Table 2.

Table 2.
Different expressions for thermal conductivity of nanofluids.
4. Exact Solutions
In physics and mathematics, the term exact solutions refers to the solutions that capture the entire physical and mathematical aspects of the problem. Theoretical solvers and experimentalists use exact solutions for the validation of their studies and results [57,58,59,60] (See Figure 3).In the literature, several studies have been reported on the exact solutions of fluid flow problems (see Table 3).
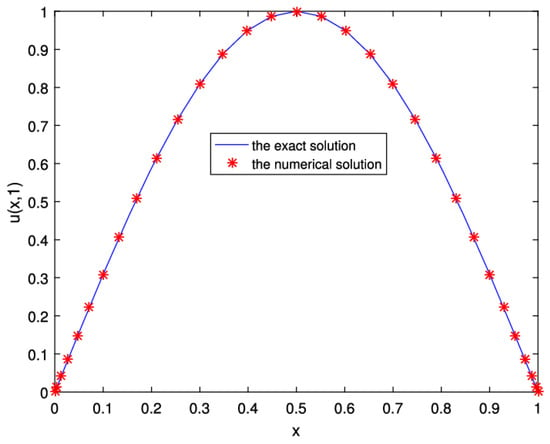
Figure 3.
Comparison of the numerical and exact solution.

Table 3.
Exact solutions for fluids flow problems.
In the above papers, exact solutions are obtaibed under certain limitations as it is not possible to solve such problems completely for exact solutions. There are some limitations to find the exact solutions; for example, the flow is laminar, unidirectional, and one dimensional. After these assomputions, the problem becomes linear and can be solved by a suitable analytical technique, such as Laplace and/or Fourier transform. However, in some problems, two-directional and one-dimensional or uni-directional and two-dimensional problems such as channel flow (the flow is taken along x-axis, while, y-axis is perpendicular to the flow direction) or rotating flow can also be solved under the above assumptions.
5. Exact Solutions for the Flow of Nanofluids
Many researchers have proposed exact solutions for the flow of a nanofluid in different geometries and with different techniques. Integral transforms have been used for such solutions. The flow of nanofluid over a vertical plate with heat and mass transfer is considered by Turkyilmazoglu and Pop [89], who obtained the exact solutions by the Laplace transform technique. In their paper [89], the radiation effect for two different boundary conditions is considered. Copper, silver, copper oxide, aluminum oxide, and titanium oxides nanoparticles have been considered in this research article. In the concluding remarks of this research paper, it is mentioned that the nanofluid with copper nanoparticles has the highest heat transfer and the nanofluid with titanium oxide has the least one (Figure 4).
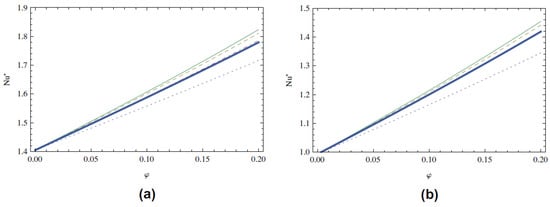
Figure 4.
Values of Nusselt number against volume fraction for five different water-based nanofluids; dotted curve for TiO2, the dot-dashed curve for Al2O3, the dashed curve for CuO, the thin curve for Cu, and thick curve for Ag. (a) Nr = 0 and (b) Nr = 1 [89].
The flow of water-based nanofluid with silver and titanium oxide nanoparticles was analyzed by Nandkeolyar et al. [90] for the exact solutions. The authors considered the heat transfer. and the fluid was electrically conducted. The engineering applications of nanofluids are discussed in this research article. The key finding of this paper is that skin friction is decreasing with higher values of volume fraction for titanium oxide nanoparticles in the base fluid, while it is of oscillatory form in case silver nanoparticles. Stokes’ second problem for the unsteady free convection flow of nanofluid is discussed by Khalid et al. [91]. Exact solutions have been obtained using integral transform—namely, the Laplace transform technique. The solutions are presented for both ramped wall temperature and isothermal temperature. Also, the corresponding skin friction and heat transfer rate are calculated and presented in tabular form (please see Tables 2–5 in Khalid et al. [91]). The following model has been used to describe the flow situation.
where the corresponding initial and boundary conditions are
Four different nanoparticles were considered in the base fluid, and the authors concluded that silver nanoparticles have high efficiency in the nanofluid as compared to the other three (Figure 5).
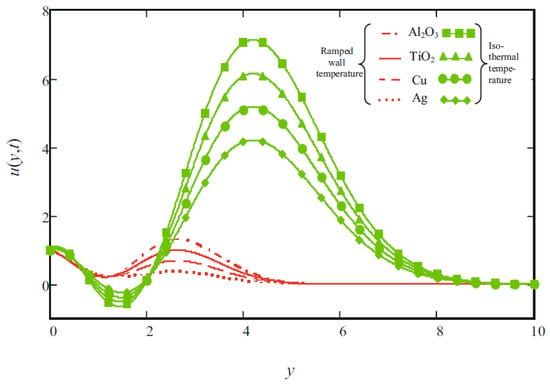
Figure 5.
Velocity profile for different nanoparticles [91].
Ahmad and Pop [92] studied the steady mixed convection flow of nanofluid taking in to account three different nanoparticles—i.e., copper, aluminum oxide, and titanium oxide nanoparticles—in the base fluid. They have considered the boundary layer flow over an infinite vertical pale and obtained the solutions. Mixed convection MHD flow of ferrofluid is analyzed by Gul et al. [93] in their article by taking into account the ferric oxide nanoparticles along with the non-magnetic nanoparticles aluminum oxide. In their study, the variable wall temperature on the vertical wall is considered. The bottom line drawn from this research work is that the velocity of the ferrofluid is strongly dependent on the viscosity and thermal conductivity along with the Lorentz’s forces. Das et al. [94] considered the fully developed convective flow in the channel filled with the water-based nanofluid with three different nanoparticles. The influence of physical parameters is shown on the velocity and temperature profiles of the flow graphically. Furthermore, the shear stress and Nusselt number are shown in tables and graphs. The conclusion drawn from this research paper was that the critical Rayleigh number is dependent on the volume fraction and MHD parameters. The unsteady flow of ferrofluid with cylindrical shaped nanoparticles is studied by Khalid et al. [95]. The flow past a porous media is taken into consideration in their analysis. The effective thermal and electrical conductivities are taken from the Maxwell model in this research. The ramped wall and isothermal wall temperatures are taken into consideration in this research work. They have mentioned that the Nusselt number increases with the increasing values of the Prandtl number. Stoke’s second problem for the flow of nanofluid is considered by Shafie et al. [96], where the effects of four different shapes of molybdenum disulfide nanoparticles on the fluid flow and temperature profiles were discussed. Furthermore, a comparison is presented for the different shapes of nanoparticles. Their results show that the platelet and the cylindrical-shaped nanoparticles have the highest thermal conductivity and viscosity as compared to the other shapes of nanoparticles. Moreover, the temperature increases with the increase in the volume fraction of the molybdenum disulfide nanoparticles. Ali et al. [97] discussed the unsteady MHD free convection flow of an engine-oil-based nanofluid past a vertical plate. Molybdenum disulfide powder with each particle of nanosized is dissolved in the base fluid. Heat and mass transfer are also considered in their study. The following model has been chosen to analyze the flow of second-grade nanofluids.
where the corresponding initial and boundary conditions are
The idea of Caputo Fabrizio fractional derivatives [98] is utilized to generalize the classical model. Furthermore, Nusselt number, Sherwood number, and skin friction have been calculated. The results reveal that the lubrication of the engine oil increased with the increasing values of the volume fraction of the nanoparticles. In another paper, Ali et al. [28] studied the flow of Brinkman-type nano liquid embedded in a porous media. Four different types of nanoparticles of spherical shape—silver, copper, titanium oxide, and aluminum oxide—are taken in this research work. Moreover, the variable velocity, variable temperature, and concentration were considered on the boundary. Furthermore, three cases—impulsive velocity on the wall, constantly accelerated wall, and variable accelerated wall were analyzed. They concluded that the skin friction enhances with the enhancement in the material parameter of Brinkman type fluid and Prandtl number (Table 4).

Table 4.
Variations in skin friction for different parameters [28].
Exact solutions are found for the flow of Jeffrey nanofluid embedded in a Darcian porous media with heat transfer by Zin et al. [99]. They discussed copper and silver nanoparticles in a base fluid kerosene oil. Moreover, the local skin friction and heat transfer rate at the boundary were also calculated and presented in tabular form. The key finding mentioned in their paper was that both the velocity and temperature are the increasing functions of the volume fraction of the nanoparticles. The flow of a nanofluid in a rotating frame (Figure 6) with Hall Effect and MHD was considered by Ali et al. [100].
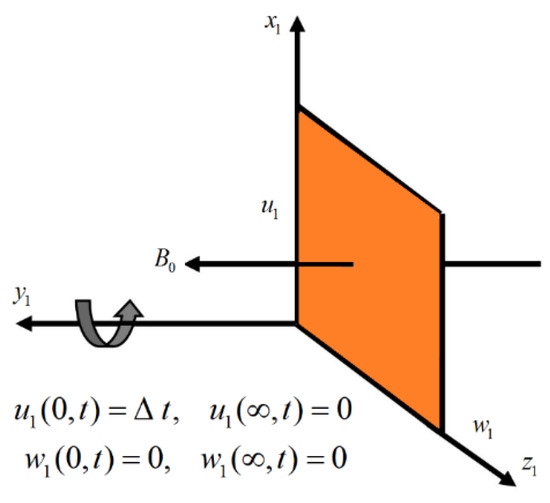
Figure 6.
The illustrative diagram of the problem [100].
In their research article, they chose engine oil as a base fluid with molybdenum disulfide nanoparticles. The modeled partial differential equations are solved using the Laplace transform technique. Furthermore, important physical quantities like skin friction and Nusselt number are also calculated. A very useful conclusion has been drawn in this article that the rate of heat transfer is increased by 6.35% by adding Molybdenum disulfide nanoparticles in the engine oil, which will lead to improving the efficiency of the engine oil (Table 5).

Table 5.
Impact of volume fraction on Nusselt number and percent enhancement [100].
The unsteady mixed convection Poiseuille flow of Casson nanofluid is studied by Aman et al. [101]. They obtained the semi-exact solutions by the Light–Hill technique. The single-walled carbon nanotubes and multi-walled carbon nanotubes are chosen as nanoparticles in the base fluid. The effects of various parameters on the fluid flow, temperature profile, skin friction, and Nusselt number were discussed in detail. The bottom line is that the velocity of the nanofluid decreases with the increasing values of the volume fraction of carbon nanotubes which means that the nanofluid will become denser when the fraction of the carbon nanotubes is increased. Kataria and Mittal [102] have taken into consideration the flow of nanofluid with heat and mass transfer. In this article, they considered the ramped wall temperature and ramped wall concentration on the wall. Besides, they calculated the Nusselt number, Sherwood number, and skin friction on the boundary. They mentioned in their conclusion that the heat transfer increases with increasing values of the volume fraction when ramped wall temperature is taken and decreases in the case of isothermal wall temperature on the boundary. Heat transfer enhancement in the free convection flow of Maxwell nanofluid is considered by Aman et al. [103]. The exact solutions are obtained for the velocity and temperature profile via the Laplace transform method. The behavior of velocity and temperature profiles of the nanofluid with single-walled carbon nanotubes and multi-walled carbon nanotubes in four different base fluids i.e., Kerosene oil, Engine oil, water, and ethylene glycol have been studied in their paper. Their study has concluded that the velocity increases with the increase in the Grashof number, and the shear stress is decreasing, while there is no motion in the absence of Grashof number. The MHD flow of nanofluid inside a channel is studied by Khan [104]. He considered the slip condition on the lower boundary of the channel. The analysis of the flow and heat transfer provided for four different shapes of molybdenum disulfide nanoparticles in the base fluid. The fluid was taken to be electrically conducted and passing through porous media. The bottom-line of this research work [104] is that the blade and platelet-shaped nanoparticles showed the highest heat transfer rate as compared to the cylinder and brick shapes. The comparative analysis of two different fractional models for nanofluid flow was presented by Sheikh et al. [105] in their study. For the generalization of the classical model of nanofluid the concepts of Caputo Fabrizio [98] and Atangana Balaenu [106], fractional derivatives were used. In their article, the applications of nanofluids in solar collectors were provided (Figure 7).
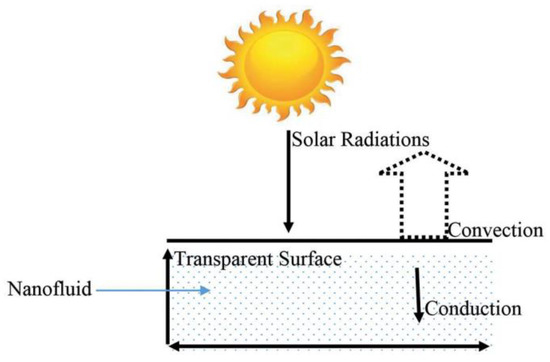
Figure 7.
Nanofluid-Based DAC [105].
Their results show that, by adding the aluminum nanoparticles to the working fluid (water), the efficiency of the solar collector may be enhanced by 5.2% (Figure 8).
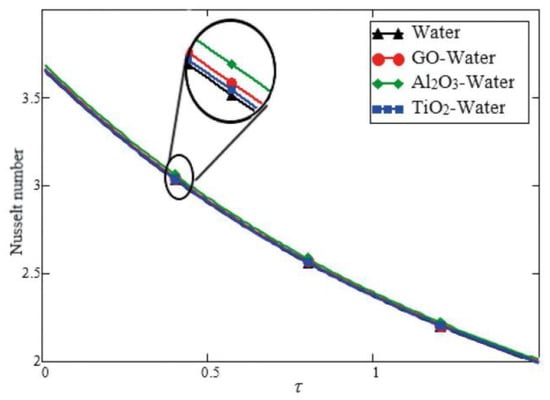
Figure 8.
Variation in Nusselt number for different nanoparticles [105].
The combined effects of thermal radiation and the magnetic effect on the unsteady flow of Brinkman-type nanofluid is studied by Gohar et al. [107]. Water, kerosene oil, and engine oil were considered as the base fluids and carbon nanotubes as the nanoparticles. The key finding from this research article is that the velocity of the nanofluid with multi-walled carbon nanotubes is higher as compared to the velocity of the nanofluid with single-walled carbon nanotubes. Moreover, the velocity decreases with the increasing values of the Brinkman-type fluid parameter. The microrotation and microinertia characteristics of nanofluids are discussed by Hussanan et al. [108]. Like the paper presented by Gohar et al. [107], this research article [108] also includes water, kerosene oil, and engine oil as the base fluid, and five different nanoparticles (copper oxide, titanium oxide, alumina oxide, iron oxide, and graphene oxide) were considered. The main outcome of this research is that the temperature of micropolar fluid with suspended nanoparticles of graphene oxide is higher than the nanofluid with other nanoparticles. The mixed convection Poiseuille flow of a Casson nanofluid is studied by Aman et al. [101]. Three different base fluids with carbon nanotubes as suspended nanoparticles were chosen to analyze the flow. The finding of their research work is that the temperature is higher for single-walled carbon nanotubes as compared to the multi-walled carbon nanotubes. Moreover, the velocity of the nanofluid decreases with the increase in the volume fraction of the nanoparticles. The convective flow of a carboxy–methyl–cellulose fluid with carbon nanotubes is studied by Saqib et al. [109] in their research article. The fluid is considered electrically conducted and passing through a porous media. They transformed the classical model of the nanofluid to the Atangana–Baleanu fractional model and then solved it by using the Laplace transform technique. The results show that multi-walled carbon nanotubes are more efficient in the base fluid as compared to the single-walled carbon nanotubes. The unsteady free convection flow of polyethylene glycol–based nanofluid was carried out by Ali et al. [110]. They considered polyethylene glycol as a base fluid and molybdenum disulfide as the suspended nanoparticles. Moreover, they considered the ramped wall temperature and isothermal temperature on the wall. The problem was modeled in terms of partial differential equations and then solved by the Laplace transform technique. From the results, the velocity, temperature, and concentration were higher for the isothermal wall temperature and lower for the ramped wall temperature. The effects of thermal radiation, thermal diffusion, and chemical reaction on the MHD mixed convection Poiseuille flow of nanofluid passing through a porous medium was taken into consideration by Aman et al. [111]. Five different types of nanoparticles were suspended in the base fluid, and their comparison was presented in graphs. In their paper, they concluded that nanofluids with metal nanoparticles have a high heat transfer rate as compared to the nanofluids with metal oxide nanoparticles. The applications of gold nanoparticles were discussed for cancer therapy (Figure 9).
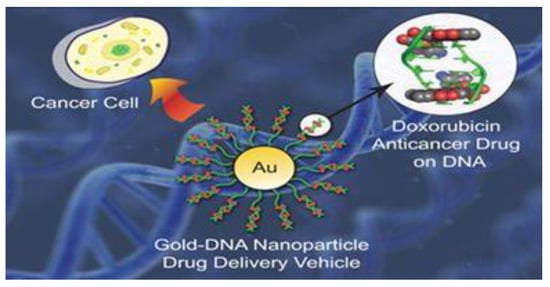
Figure 9.
Applications of gold nanoparticles in cancer therapy [111].
Moreover, it is mentioned that heat transfer is higher for gold nanoparticles followed by aluminum and magnetite. Entropy generation is an important property of nanofluid [112,113,114]. Gul et al. [115] analyzed the entropy generation in Jeffrey nanofluid. The problem is modeled in terms of the partial differential equation and the solutions are obtained. The entropy generation as a function of the velocity and temperature of the nanofluid is calculated. Moreover, the results show that an increase in temperature leads to the reduction of the entropy generation in the nanofluids, while entropy generation increases with the increasing values of the Brinkman number. The unsteady flow of Casson nanofluid over an isothermal vertical plate is discussed by Khan et al. [116]. Sodium alginate is chosen as base fluid with three different nanoparticles (Silver, Titanium oxide, Copper and Aluminum oxide). The Newtonian heating is also considered at the boundary and the effect of porous medium on the fluid flow is taken. The partial differential equations are solved with the help of the Laplace transform technique. The results show that the increasing values of volume fraction of the nanoparticles increases the velocity and temperature of the nanofluid. Sheikh et al. [117] theoretically discussed the applications of cerium oxide and aluminum oxide nanoparticles on the performance of the solar collector.
The flow of the Newtonian fluid over an inclined plate (Figure 10) is taken into account. The problem is modeled in terms of partial differential equations and is then generalized using the Atangana–Baleanu fractional derivatives [106]. The fractional model is solved for exact solutions by using the Laplace transform technique. The key findings of this research work are that the efficiency of the solar collector may be enhanced using the cerium oxide nanoparticles in the working fluid of the solar collector (Figure 11).
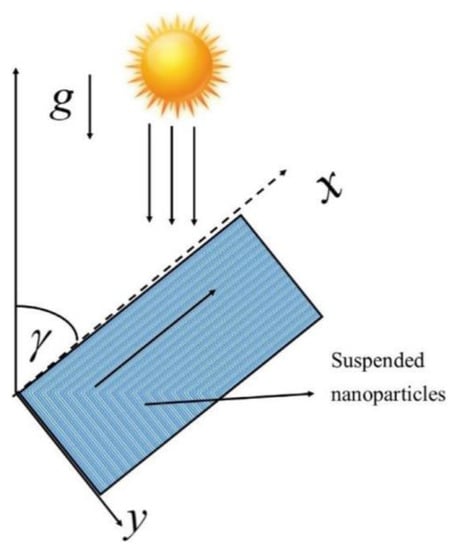
Figure 10.
Direct absorption solar collector [117].
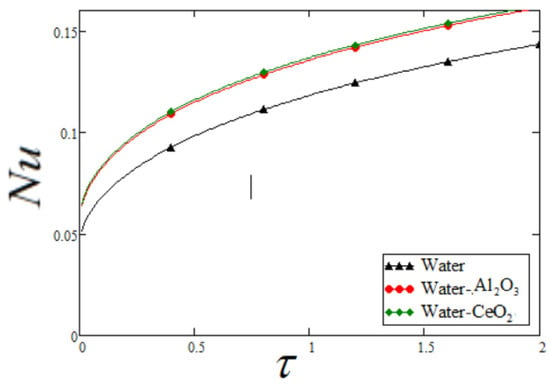
Figure 11.
Variations in Nusselt number [117].
Aman et al. studied the heat and mass transfer effects on the MHD flow of nanofluid with graphene oxide nanoparticles [118]. They considered the base fluid as a working fluid in the solar collectors. The model was generalized by using the Caputo fractional derivative approach and then solved by the Laplace transform technique. The solutions are presented in terms of the Wright function [82]. They noted that the heat transfer rate of the nanofluid increased with the increasing values of the volume fraction of the nanoparticles and the Caputo fractional parameter. In another paper, Aman et al. [119] presented the idea of hybrid nanofluid. They considered the Casson nanofluid with hybrid nanoparticles, i.e., alumina and copper nanoparticles. The problem is modeled in terms of the fractional differential equations using the definition of Caputo fractional derivatives. The fractional model is then solved by the Laplace transform technique, and the exact solutions are obtained. In this paper, they missed the plot for the velocity profile, which would show the effect of the volume fraction of the nanoparticles on the fluid velocity. The unsteady flow of water-based nanofluid with carbon nanotubes as suspended nanoparticles is discussed by Khan et al. [120]. Newtonian heating on the wall of the channel is taken into account, and the model is generalized using the modern concept of Atangana–Baleanu fractional derivatives [106]. The fractional model is solved by using the Laplace transform technique and the Laplace inversion is presented using Tzou’s and Stehfest’s algorithms [121]. It is concluded that the temperature distribution is increased by increasing the volume fraction of the nanoparticles. The unsteady MHD flow of diathermic oils with heat transfer is studied by Ali et al. [122]. The Brinkman-type fluid model is considered in their research article. Engine oil and kerosene oils were chosen as base fluids and molybdenum disulfide nanoparticles were taken in different shapes (Table 6 and Figure 12).

Table 6.
Constants a and b empirical shape factors [122].
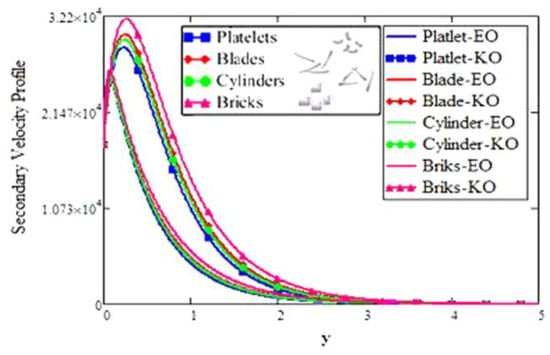
Figure 12.
Different shapes of nanoparticles [122].
The classical model is generalized using the fractional derivatives with non-singular kernel and solved by the Laplace transform technique. The results show that, as compare to bricks and cylinder-shaped nanoparticles, the platelet and blade-shaped nanoparticles of molybdenum disulfide have more tendency to improve the heat transfer rate in the oil. Moreover, they mentioned that the heat transfer rate in the fluid is enhanced by 13.51% when Molybdenum disulfide nanoparticles are added in the base fluid oil as shown in Table 7.

Table 7.
Impact of volume fraction on heat transfer rate and percent enhancement [122].
Hussain et al. [123] attempted to find the exact solutions for the MHD flow of the viscous nanofluid. They considered the inclined magnetic field and the ramped wall temperature in their study. Aluminum oxide, copper, and titanium oxide nanoparticles were dispersed in the base fluid water. The results show that both the velocity and the temperature of the nanofluids are smaller for ramped wall temperature and higher for the isothermal wall temperature. Jan et al. [124] studied the flow of Brinkman-type nanofluid in a porous media with heat transfer and magnetic field. Engine oil was taken as a base fluid and molybdenum disulfide nanoparticles have been dispersed in the base fluid. The classical model of the Brinkman-type fluid is generalized to the fractional model using the Atangana–Baleanu fractional derivative approach and then solved using the Laplace transform technique. A table is presented for the heat transfer rate in the engine oil, and the results show that the heat transfer increased with the increasing values of the Prandtl number. Saqib et al. [125] discussed the flow and entropy production of different types of fractionalized nanofluids that have different electrical conductivities through infinite vertical plates embedded in porous media. The governing equation is transformed into a dimensionless form, and then the time-fractional model is generated using the Caputo method. Two different nanoparticles (molybdenum disulfide and graphene oxide) are dispersed in three different base fluids (water, kerosene, and methanol). This problem is solved using the Laplace transform technique. The results reveal that the velocity, temperature and entropy generation is higher for the water-based nanofluid with graphene oxide nanoparticles. In another paper, Saqib et al. [126] discussed the MHD flow of ethylene glycol-based nanofluid with molybdenum disulfide nanoparticles. The flow is considered over an infinite isothermal vertical plate. The classical model of the fluid is generalized using the modern approach Atangana-Baleanu fractional derivatives. Using the concept of the Laplace transform method they have obtained the exact solutions to the problem. The obtained solutions for Cassin nanofluid is reduced to the corresponding solutions of the Newtonian nanofluid. The bottom line drawn from this research article is that the heat transfer rate is improved with the increasing values of volume fraction parameter of the nanoparticles which will enhance the efficiency of the base fluid. Abro et al. [85] studied the magnetohydrodynamic flow of the nanofluid through a porous medium. The model is transformed into generalized models by using the concept of Caputo–Fabrizio and Atangana–Baleanu fractional derivatives. The models are solved by using the Laplace transform technique and the exact solutions are presented in terms of Fox-H and Mittag–Leffler functions. They mentioned that the velocity of the ethylene-glycol with copper nanoparticles is higher than the velocity of a fluid with titanium oxide and aluminum oxide nanoparticles. The applications of the nanofluid in solar collectors are studied by Ali et al. [127] in their research article. The generalized model of Brinkman-type fluid with nanoparticles is considered in their analysis. The flow is taken in a rotating frame with heat transfer and MHD effect. The generalized model is solved for the exact solutions with the help of the Laplace transform technique. This article concludes that the performance of the solar collector is enhanced by 36.61% by adding single walled nanoparticles in the working fluid.
6. Hybrid Nanofluid
For a specific purpose, an angle material does not have all the important properties, either it will have excellent thermal characteristics or some good rheological specifications. It is of immense importance in many industrial and real-world problems to deal with the several properties of materials, and here, the idea of hybrid nanofluids emerges. When two different nanoparticles are efficiently dispersed in a liquid medium it forms a hybrid nanofluid (Figure 13).
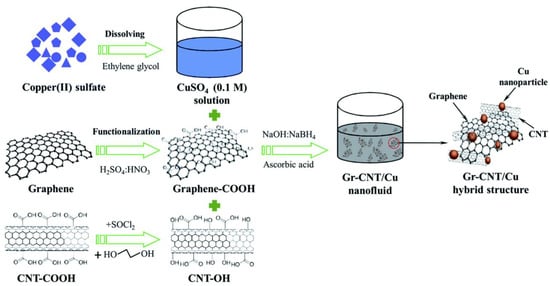
Figure 13.
Hybrid nanofluid [128].
This technology is used to improve the thermal properties of basic heat transfer fluid for important purposes. Due to its synergy effects, it produces a better thermal conductivity as expected from the individual nanoparticles. The industries that deal with electronic cooling, heat management of automobiles, welding of iron and steel, cooling systems of nuclear reactors, indoor heating, and cooling systems, heating of solar collectors, bioengineering, reduction of drugs, etc. have applications for hybrid nanofluids. Because of the above-mentioned characteristics, many researchers have worked on the hybrid nanofluids. The generalized model using the concept of Caputo–Fabrizio fractional derivative for the flow of hybrid nanofluid is discussed by Gohar et al. [41]. They have specified their study to the applications of hybrid nanofluid in the cement. The problem is modeled in terms of the partial differential equation and then solved by the integral transform technique. They have used two nanoparticles—aluminum oxide nanoparticles and multi-walled carbon nanofluid—in their analysis. The main finding of this research work is that, by adding these two nanoparticles together in the base fluid cement, the binding strength may be enhanced. The idea of MWCNT-Fe3O4 is discussed by Sheikholislami et al. [129]. In this analysis, they considered the variable magnetic field in electric wires. By adding these hybrid nanoparticles, the heat transmission rate of the base fluid in the cavity is enhanced. Khan et al. studied the flow of a hybrid nanofluid in a channel with the analysis of entropy generation [130]. The flow is taken in a rotating system.
7. Conclusions
In this article, the literature regarding nanofluids is summarized in detail, and the exact solutions for the flow problems of nanofluids are discussed. From the survey of the literature, it is clear that the exact solutions are reliable and more important for the flow problems of the nanofluids. Many useful applications are discussed by different researchers. For example, there are applications for nanofluids in engine oil, kerosene oil, solar collectors, blood flow, the cement industry, etc. Some important models for various characteristics of nanofluids are presented in this article. From this survey of the literature, it is noted that nanoparticles are good agents to enhance the thermal performance of working fluids. Metallic and non-metallic nanoparticles show different performance in this regard but many of the researches prefer to use metallic nanoparticles. Besides, nanoparticles in the base fluids are also used for other performances of the working fluid, in the engine oil, for instance, to improve the lubrication. Carbon nanotubes are also used by researches and represent an emerging field of study.
8. Future Suggestions
This literature review shows that much work has been done on the exact solutions for the flow problems of nanofluid in different geometries (i.e., flow infinite plate, in a channel and cylindrical domain). Also, different nanoparticles have been used with various applications.
Less work has reported on the flow problems of nanofluid in the rotating system. The researchers may model different problems in the rotating system and their exact solutions may be obtained. The exact solutions for the flow problems of nanofluid with carbon nanotubes are rare in the literature. More focus may be given to these types of flows. The existing flow models may be extended for other complex fluids [82,131,132,133].
In the future, the exact solvers are suggested to work closer with the experimenters to give more accurate and applied solutions. Hybrid nanofluids are newly developed fluids. Exact solvers are suggested to focus more on hybrid nanofluids. Form the literature servery, it is found that less attention is given to some nanoparticles like clay nanoparticles [134], cerium oxide nanoparticles [135], graphene oxide nanoparticles [136], zirconia nanoparticles [137], and greigite nanoparticles [103,138]. In the future, interesting and useful results can be obtained using these nanoparticles. The models can be transformed into generalized models using different fractional operators to have a deep insight into the flow and heat transfer regime [58,59,139,140,141].
Author Contributions
Conceptualization, I.K., D.L.C.C. and N.A.S.; methodology, I.K.; validation, D.L.C.C. and N.A.S.; formal analysis, N.A.S.; investigation, I.K. and D.L.C.C.; resources, I.K. and D.L.C.C.; writing—original draft preparation, N.A.S.; writing—review and editing, D.L.C.C. and I.K.; visualization, N.A.S.; supervision, D.L.C.C. and I.K.; project administration, I.K.; funding acquisition, D.L.C.C. All authors have read and agreed to the published version of the manuscript.
Funding
The APC was funded by CRG 015MC0 -011.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| MHD | Magnetohydrodynamics |
| DAC | Direct Absorption Collector |
| DNA | Deoxyribonucleic acid |
| GO | Graphene oxide |
| TiO2 | Titanium Oxide |
| Al2O3 | Aluminum Oxide |
| CuO | Coper Oxide |
| Cu | Copper |
| CeO2 | Cerium Oxide |
| Ag | Silver |
| Nr | Radiation Parameter |
| u | dimensional velocity |
| dimensional time | |
| coordinate axis normal to the plate | |
| acceleration due to gravity | |
| electrical conductivity | |
| thermal conductivity of the fluid | |
| amplitude of the plate oscillations | |
| specific heat at constant pressure | |
| the temperature of the fluid | |
| ambient temperature | |
| wall temperature | |
| concentration | |
| ambient concentration | |
| wall concentration | |
| H(t) | Unit step function |
| ω | frequency of the plate oscillation |
| ρ | density of the fluid |
| viscosity | |
| Thermal Expansion | |
| Mass Expansion | |
| D | Mass Diffusivity |
| Brinkman parameter | |
| Re | Reynold’s number |
| M | Hartmann number |
| Grashof number | |
| Pr | Prandtl number |
| Mass Grashof number | |
| Porosity Parameter | |
| Schmidt number | |
| Nusselt number | |
| Chemical reaction parameter | |
| the volume fraction of nanoparticles | |
| diameter of particle | |
| diameter of the tube | |
| and | empirical coefficients of nanoparticles |
| diameter of the nanotube | |
| length of the nanotube | |
| Kiptza’s Constant | |
| is the sphericity factor | |
| subscript for nanofluid | |
| subscript for hybrid nanofluid | |
| subscript for fluid | |
| subscript for base fluid | |
| subscript for carbon nanotube | |
| subscript for solid | |
| subscript for particle |
References
- Yu, W.; Xie, H.; Bao, D. Enhanced thermal conductivities of nanofluids containing graphene oxide nanosheets. Nanotechnology 2009, 21, 055705. [Google Scholar] [CrossRef]
- Reddy, J.R.; Sugunamma, V.; Sandeep, N. Impact of nonlinear radiation on 3D magnetohydrodynamic flow of methanol and kerosene based ferrofluids with temperature dependent viscosity. J. Mol. Liq. 2017, 236, 93–100. [Google Scholar] [CrossRef]
- Choi, S.U.; Eastman, J.A. Enhancing thermal conductivity of fluids with nanoparticles. In Proceedings of the International Mechanical Engineering Congress and Exhibition, San Francisco, CA, USA, 1 October 1995. [Google Scholar]
- Li, Y.; Tung, S.; Schneider, E.; Xi, S. A review on development of nanofluid preparation and characterization. Powder Technol. 2009, 196, 89–101. [Google Scholar] [CrossRef]
- Lee, J.H.; Lee, S.H.; Choi, C.J.; Jang, S.P.; Choi, S.U. A review of thermal conductivity data, mechanisms and models for nanofluids. Int. J. Micro-Nano Scale Transp. 2010, 1, 269–322. [Google Scholar] [CrossRef]
- Ghadimi, A.; Saidur, R.; Metselaar, H. A review of nanofluid stability properties and characterization in stationary conditions. Int. J. Heat Mass Transf. 2011, 54, 4051–4068. [Google Scholar] [CrossRef]
- Ramesh, G.; Prabhu, N.K. Review of thermo-physical properties, wetting and heat transfer characteristics of nanofluids and their applicability in industrial quench heat treatment. Nanoscale Res. Lett. 2011, 6, 334. [Google Scholar] [CrossRef]
- Khanafer, K.; Vafai, K. A critical synthesis of thermophysical characteristics of nanofluids. Int. J. Heat Mass Transf. 2011, 54, 4410–4428. [Google Scholar] [CrossRef]
- Fan, J.; Wang, L. Review of heat conduction in nanofluids. J. Heat Transf. 2011, 133, 040801. [Google Scholar] [CrossRef]
- Vajjha, R.S.; Das, D.K. A review and analysis on influence of temperature and concentration of nanofluids on thermophysical properties, heat transfer and pumping power. Int. J. Heat Mass Transf. 2012, 55, 4063–4078. [Google Scholar] [CrossRef]
- Trisaksri, V.; Wongwises, S. Critical review of heat transfer characteristics of nanofluids. Renew. Sustain. Energy Rev. 2007, 11, 512–523. [Google Scholar] [CrossRef]
- Daungthongsuk, W.; Wongwises, S. A critical review of convective heat transfer of nanofluids. Renew. Sustain. Energy Rev. 2007, 11, 797–817. [Google Scholar] [CrossRef]
- Kakaç, S.; Pramuanjaroenkij, A. Review of convective heat transfer enhancement with nanofluids. Int. J. Heat Mass Transf. 2009, 52, 3187–3196. [Google Scholar] [CrossRef]
- Godson, L.; Raja, B.; Lal, D.M.; Wongwises, S. Enhancement of heat transfer using nanofluids—An overview. Renew. Sustain. Energy Rev. 2010, 14, 629–641. [Google Scholar] [CrossRef]
- Sarkar, J. A critical review on convective heat transfer correlations of nanofluids. Renew. Sustain. Energy Rev. 2011, 15, 3271–3277. [Google Scholar] [CrossRef]
- Sheikholeslami, M. Magnetic field influence on nanofluid thermal radiation in a cavity with tilted elliptic inner cylinder. J. Mol. Liq. 2017, 229, 137–147. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Ellahi, R. Three dimensional mesoscopic simulation of magnetic field effect on natural convection of nanofluid. Int. J. Heat Mass Transf. 2015, 89, 799–808. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Ganji, D. Nanofluid convective heat transfer using semi analytical and numerical approaches: A review. J. Taiwan Inst. Chem. Eng. 2016, 65, 43–77. [Google Scholar] [CrossRef]
- Khan, W.; Pop, I. Boundary-layer flow of a nanofluid past a stretching sheet. Int. J. Heat Mass Transf. 2010, 53, 2477–2483. [Google Scholar] [CrossRef]
- Mebarek-Oudina, F. Convective heat transfer of Titania nanofluids of different base fluids in cylindrical annulus with discrete heat source. Heat Transf. Asian Res. 2019, 48, 135–147. [Google Scholar] [CrossRef]
- Raza, J.; Mebarek-Oudina, F.; Chamkha, A. Magnetohydrodynamic flow of molybdenum disulfide nanofluid in a channel with shape effects. Multidiscip. Modeling Mater. Struct. 2019, 15, 737–757. [Google Scholar] [CrossRef]
- Reza, J.; Mebarek-Oudina, F.; Makinde, O.D. MHD slip flow of Cu-Kerosene nanofluid in a channel with stretching walls using 3-stage Lobatto IIIA formula. Defect Diffus. Forum 2018, 387, 51–62. [Google Scholar] [CrossRef]
- Angayarkanni, S.A.; Philip, J. Review on thermal properties of nanofluids: Recent developments. Adv. Colloid Interface Sci. 2015, 225, 146–176. [Google Scholar] [CrossRef] [PubMed]
- Sheikholeslami, M.; Rokni, H.B. Simulation of nanofluid heat transfer in presence of magnetic field: A review. Int. J. Heat Mass Transf. 2017, 115, 1203–1233. [Google Scholar] [CrossRef]
- Pak, B.C.; Cho, Y.I. Hydrodynamic and heat transfer study of dispersed fluids with submicron metallic oxide particles. Exp. Heat Transf. Int. J. 1998, 11, 151–170. [Google Scholar] [CrossRef]
- Eastman, J. Novel Thermal Properties of Nanostructured Materials; Argonne National Lab: Lemont, IL, USA, 1999. [Google Scholar]
- Sheikholeslami, M.; Mustafa, M.; Ganji, D.D. Nanofluid flow and heat transfer over a stretching porous cylinder considering thermal radiation. Iran. J. Sci. Technol. Trans. Sci. 2015, 39, 433–440. [Google Scholar]
- Ali, F.; Gohar, M.; Khan, I. MHD flow of water-based Brinkman type nanofluid over a vertical plate embedded in a porous medium with variable surface velocity, temperature and concentration. J. Mol. Liq. 2016, 223, 412–419. [Google Scholar] [CrossRef]
- Murshed, S.M.S.; Estellé, P. A state of the art review on viscosity of nanofluids. Renew. Sustain. Energy Rev. 2017, 76, 1134–1152. [Google Scholar] [CrossRef]
- Einstein, A. Investigations on the Theory of the Brownian Movement; Courier Corporation: North Chelmsford, MA, USA, 1956. [Google Scholar]
- Batchelor, G.K. The effect of Brownian motion on the bulk stress in a suspension of spherical particles. J. Fluid Mech. 1977, 83, 97–117. [Google Scholar] [CrossRef]
- Dávalos-Orozco, L.A.; Del Castillo, L.F. Hydrodynamic Behavior of Suspensions of Polar Particles; CRC Press: New York, NY, USA, 2005. [Google Scholar]
- Brinkman, H. The viscosity of concentrated suspensions and solutions. J. Chem. Phys. 1952, 20, 571. [Google Scholar] [CrossRef]
- Nguyen, C.; Desgranges, F.; Roy, G.; Galanis, N.; Maré, T.; Boucher, S.; Mintsa, H.A. Temperature and particle-size dependent viscosity data for water-based nanofluids–hysteresis phenomenon. Int. J. Heat Fluid Flow 2007, 28, 1492–1506. [Google Scholar] [CrossRef]
- Abu-Nada, E. Effects of variable viscosity and thermal conductivity of Al2O3–water nanofluid on heat transfer enhancement in natural convection. Int. J. Heat Fluid Flow 2009, 30, 679–690. [Google Scholar] [CrossRef]
- Jang, S.P.; Lee, J.-H.; Hwang, K.S.; Choi, S.U. Particle concentration and tube size dependence of viscosities of Al2O3-water nanofluids flowing through micro-and minitubes. Appl. Phys. Lett. 2007, 91, 243112. [Google Scholar] [CrossRef]
- Koo, J.; Kleinstreuer, C. A new thermal conductivity model for nanofluids. J. Nanopart. Res. 2004, 6, 577–588. [Google Scholar] [CrossRef]
- Maiga, S.E.B.; Palm, S.J.; Nguyen, C.T.; Roy, G.; Galanis, N. Heat transfer enhancement by using nanofluids in forced convection flows. Int. J. Heat Fluid Flow 2005, 26, 530–546. [Google Scholar] [CrossRef]
- Nguyen, C.; Desgranges, F.; Galanis, N.; Roy, G.; Maré, T.; Boucher, S.; Mintsa, H.A. Viscosity data for Al2O3–water nanofluid—hysteresis: Is heat transfer enhancement using nanofluids reliable? Int. J. Therm. Sci. 2008, 47, 103–111. [Google Scholar] [CrossRef]
- Masoumi, N.; Sohrabi, N.; Behzadmehr, A. A new model for calculating the effective viscosity of nanofluids. J. Phys. D Appl. Phys. 2009, 42, 055501. [Google Scholar] [CrossRef]
- Gherasim, I.; Roy, G.; Nguyen, C.T.; Vo-Ngoc, D. Experimental investigation of nanofluids in confined laminar radial flows. Int. J. Therm. Sci. 2009, 48, 1486–1493. [Google Scholar] [CrossRef]
- Gohar, M.; Ali, F.; Khan, I.; Sheikh, N.A.; Shah, A. The unsteady flow of generalized hybrid nanofluids: Applications in cementitious materials. J. Aust. Ceram. Soc. 2018, 55, 657–666. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Ganji, D.; Ashorynejad, H. Investigation of squeezing unsteady nanofluid flow using ADM. Powder Technol. 2013, 239, 259–265. [Google Scholar] [CrossRef]
- Hamilton, R.L.; Crosser, O. Thermal conductivity of heterogeneous two-component systems. Ind. Eng. Chem. Fundam. 1962, 1, 187–191. [Google Scholar] [CrossRef]
- Jang, S.P.; Choi, S.U. Role of Brownian motion in the enhanced thermal conductivity of nanofluids. Appl. Phys. Lett. 2004, 84, 4316–4318. [Google Scholar] [CrossRef]
- Wang, B.X.; Zhou, L.P.; Peng, X.F. A fractal model for predicting the effective thermal conductivity of liquid with suspension of nanoparticles. Int. J. Heat Mass Transf. 2003, 46, 2665–2672. [Google Scholar] [CrossRef]
- Chon, C.H.; Kihm, K.D.; Lee, S.P.; Choi, S.U. Empirical correlation finding the role of temperature and particle size for nanofluid (Al2O3) thermal conductivity enhancement. Appl. Phys. Lett. 2005, 87, 153107. [Google Scholar] [CrossRef]
- Xuan, Y.; Li, Q.; Hu, W. Aggregation structure and thermal conductivity of nanofluids. AIChE J. 2003, 49, 1038–1043. [Google Scholar] [CrossRef]
- Charunyakorn, P.; Sengupta, S.; Roy, S. Forced convection heat transfer in microencapsulated phase change material slurries: Flow in circular ducts. Int. J. Heat Mass Transf. 1991, 34, 819–833. [Google Scholar] [CrossRef]
- Eastman, J.A.; Phillpot, S.; Choi, S.; Keblinski, P. Thermal transport in nanofluids. Annu. Rev. Mater. Res. 2004, 34, 219–246. [Google Scholar] [CrossRef]
- Yu, W.; Choi, S. The role of interfacial layers in the enhanced thermal conductivity of nanofluids: A renovated Maxwell model. J. Nanopart. Res. 2003, 5, 167–171. [Google Scholar] [CrossRef]
- Patel, H.E.; Anoop, K.; Sundararajan, T.; Das, S.K. A micro-convection model for thermal conductivity of nanofluids. In Proceedings of the International Heat Transfer Conference 13, Sydney, Australia, 13–18 August 2006. [Google Scholar]
- Mintsa, H.A.; Roy, G.; Nguyen, C.T.; Doucet, D. New temperature dependent thermal conductivity data for water-based nanofluids. Int. J. Therm. Sci. 2009, 48, 363–371. [Google Scholar] [CrossRef]
- Firkowska, I.; Boden, A.; Vogt, A.M.; Reich, S. Effect of carbon nanotube surface modification on thermal properties of copper–CNT composites. J. Mater. Chem. 2011, 21, 17541–17546. [Google Scholar] [CrossRef]
- Deng, F.; Zheng, Q.S.; Wang, L.F.; Nan, C.W. Effects of anisotropy, aspect ratio, and nonstraightness of carbon nanotubes on thermal conductivity of carbon nanotube composites. Appl. Phys. Lett. 2007, 90, 021914. [Google Scholar] [CrossRef]
- Xue, Q.Z. Model for thermal conductivity of carbon nanotube-based composites. Phys. B Condens. Matter 2005, 368, 302–307. [Google Scholar] [CrossRef]
- Vieru, D.; Fetecau, C.; Fetecau, C. Flow of a generalized Oldroyd-B fluid due to a constantly accelerating plate. Appl. Math. Comput. 2008, 201, 834–842. [Google Scholar] [CrossRef]
- Yang, X.; Jiang, X.; Zhang, H. A time–space spectral tau method for the time fractional cable equation and its inverse problem. Appl. Numer. Math. 2018, 130, 95–111. [Google Scholar] [CrossRef]
- Sheikh, N.A.; Ali, F.; Saqib, M.; Khan, I.; Jan, S.A.A.; Alshomrani, A.S.; Alghamdi, M.S. Comparison and analysis of the Atangana–Baleanu and Caputo–Fabrizio fractional derivatives for generalized Casson fluid model with heat generation and chemical reaction. Results Phys. 2017, 7, 789–800. [Google Scholar] [CrossRef]
- Ali, F.; Sheikh, N.A.; Khan, I.; Saqib, M. Magnetic field effect on blood flow of Casson fluid in axisymmetric cylindrical tube: A fractional model. J. Magn. Magn. Mater. 2017, 423, 327–336. [Google Scholar] [CrossRef]
- El-Shehawey, E.; Elbarbary, E.M.; Afifi, N.; Mostafa, E. MHD flow of an elastico-viscous fluid under periodic body acceleration. Int. J. Math. Math. Sci. 2000, 23, 795–799. [Google Scholar] [CrossRef]
- Tan, W.; Masuoka, T. Stokes’ first problem for a second grade fluid in a porous half-space with heated boundary. Int. J. Non-Linear Mech. 2005, 40, 515–522. [Google Scholar] [CrossRef]
- Tan, W.; Masuoka, T. Stokes’ first problem for an Oldroyd-B fluid in a porous half space. Phys. Fluids 2005, 17, 023101. [Google Scholar] [CrossRef]
- Jordan, P.; Puri, A.; Boros, G. On a new exact solution to Stokes’ first problem for Maxwell fluids. Int. J. Non-Linear Mech. 2004, 39, 1371–1377. [Google Scholar] [CrossRef]
- Fetecau, C.; Fetecau, C. A new exact solution for the flow of a Maxwell fluid past an infinite plate. Int. J. Non-Linear Mech. 2003, 38, 423–427. [Google Scholar] [CrossRef]
- Khan, M.; Malik, R.; Fetecau, C.; Fetecau, C. Exact Solutions for the Unsteady Flow of a Burgers’ Fluid between Two Sidewalls Perpendicular to the Plate. Chem. Eng. Commun. 2010, 197, 1367–1386. [Google Scholar] [CrossRef]
- Nazar, M.; Fetecau, C.; Vieru, D.; Fetecau, C. New exact solutions corresponding to the second problem of Stokes for second grade fluids. Nonlinear Anal. Real World Appl. 2010, 11, 584–591. [Google Scholar] [CrossRef]
- Salah, F.; Aziz, Z.A.; Ching, D.L.C. New exact solution for Rayleigh–Stokes problem of Maxwell fluid in a porous medium and rotating frame. Results Phys. 2011, 1, 9–12. [Google Scholar] [CrossRef]
- Fetecau, C.; Mahmood, A.; Fetecau, C.; Vieru, D. Some exact solutions for the helical flow of a generalized Oldroyd-B fluid in a circular cylinder. Comput. Math. Appl. 2008, 56, 3096–3108. [Google Scholar] [CrossRef][Green Version]
- Khan, M.; Anjum, A.; Fetecau, C.; Qi, H. Exact solutions for some oscillating motions of a fractional Burgers’ fluid. Math. Comput. Model. 2010, 51, 682–692. [Google Scholar] [CrossRef]
- Siddique, I.; Vieru, D. Exact solution for the rotational flow of a generalized second grade fluid in a circular cylinder. Acta Mech. Sin. 2009, 25, 777–785. [Google Scholar] [CrossRef]
- Vieru, D.; Akhtar, W.; Fetecau, C.; Fetecau, C. Starting solutions for the oscillating motion of a Maxwell fluid in cylindrical domains. Meccanica 2007, 42, 573–583. [Google Scholar] [CrossRef]
- Vieru, D.; Fetecau, C.; Fetecau, C. Flow of a viscoelastic fluid with the fractional Maxwell model between two side walls perpendicular to a plate. Appl. Math. Comput. 2008, 200, 459–464. [Google Scholar] [CrossRef]
- Fetecau, C.; Zafar, A.A.; Vieru, D.; Awrejcewicz, J. Hydromagnetic flow over a moving plate of second grade fluids with time fractional derivatives having non-singular kernel. Chaos Solitons Fractals 2020, 130, 109454. [Google Scholar] [CrossRef]
- Shakeel, A.; Ahmad, S.; Khan, H.; Vieru, D. Solutions with Wright functions for time fractional convection flow near a heated vertical plate. Adv. Differ. Equ. 2016, 2016, 51. [Google Scholar] [CrossRef][Green Version]
- Asif, M.; Haq, S.U.; Islam, S.; Khan, I.; Tlili, I. Exact solution of non-Newtonian fluid motion between side walls. Results Phys. 2018, 11, 534–539. [Google Scholar] [CrossRef]
- Saqib, M.; Ali, F.; Khan, I.; Sheikh, N.A.; Jan, S.A.A. Exact solutions for free convection flow of generalized Jeffrey fluid: A Caputo-Fabrizio fractional model. Alex. Eng. J. 2018, 57, 1849–1858. [Google Scholar] [CrossRef]
- Ali, F.; Jan, S.A.A.; Khan, I.; Gohar, M.; Sheikh, N.A. Solutions with special functions for time fractional free convection flow of Brinkman-type fluid. Eur. Phys. J. Plus 2016, 131, 310. [Google Scholar] [CrossRef]
- Ali, F.; Khan, I.; Shafie, S. Closed form solutions for unsteady free convection flow of a second grade fluid over an oscillating vertical plate. PLoS ONE 2014, 9, e85099. [Google Scholar] [CrossRef] [PubMed]
- Khan, I.; Ali, F.; Shafie, S. Exact Solutions for Unsteady Magnetohydrodynamic oscillatory flow of a maxwell fluid in a porous medium. Z. Nat. A 2013, 68, 635–645. [Google Scholar] [CrossRef]
- Ali, F.; Khan, I.; Shafie, S.J.Z.f.N.A. A note on new exact solutions for some unsteady flows of Brinkman-type fluids over a plane wall. Z. Nat. A 2012, 67, 377–380. [Google Scholar] [CrossRef]
- Ali, F.; Sheikh, N.A.; Khan, I.; Saqib, M. Solutions with Wright function for time fractional free convection flow of Casson fluid. Arab. J. Sci. Eng. 2017, 42, 2565–2572. [Google Scholar] [CrossRef]
- Sheikh, N.A.; Ali, F.; Khan, I.; Saqib, M. A modern approach of Caputo–Fabrizio time-fractional derivative to MHD free convection flow of generalized second-grade fluid in a porous medium. Neural Comput. Appl. 2018, 30, 1865–1875. [Google Scholar] [CrossRef]
- Abro, K.A.; Memon, A.A.; Uqaili, M.A. A comparative mathematical analysis of RL and RC electrical circuits via Atangana-Baleanu and Caputo-Fabrizio fractional derivatives. Eur. Phys. J. Plus 2018, 133, 113. [Google Scholar] [CrossRef]
- Ali, M.; ul Haq, S.; ur Rahman, A. Solutions of Stokes Second Problem for Casson Fluid over an Infinite Plate: A Comparison of the Laplace and Fourier Transforms. City Univ. Int. J. Comput. Anal. 2018, 2, 18–25. [Google Scholar]
- Abro, K.A.; Chandio, A.D.; Abro, I.A.; Khan, I. Dual thermal analysis of magnetohydrodynamic flow of nanofluids via modern approaches of Caputo–Fabrizio and Atangana–Baleanu fractional derivatives embedded in porous medium. J. Therm. Anal. Calorim. 2018, 135, 2197–2207. [Google Scholar] [CrossRef]
- Sheikh, N.A.; Ching, D.L.C.; Khan, I.; Kumar, D.; Nisar, K.S. A new model of fractional Casson fluid based on generalized Fick’s and Fourier’s laws together with heat and mass transfer. Alex. Eng. J. 2019. [Google Scholar] [CrossRef]
- Abro, K.A.; Khan, I.; Tassaddiq, A. Application of Atangana-Baleanu fractional derivative to convection flow of MHD Maxwell fluid in a porous medium over a vertical plate. Math. Model. Nat. Phenom. 2018, 13, 1. [Google Scholar] [CrossRef]
- Turkyilmazoglu, M.; Pop, I. Heat and mass transfer of unsteady natural convection flow of some nanofluids past a vertical infinite flat plate with radiation effect. Int. J. Heat Mass Transf. 2013, 59, 167–171. [Google Scholar] [CrossRef]
- Nandkeolyar, R.; Das, M.; Pattnayak, H. Unsteady hydromagnetic radiative flow of a nanofluid past a flat plate with ramped temperature. J. Orissa Math. Soc. 2013, 975, 2323. [Google Scholar]
- Khalid, A.; Khan, I.; Shafie, S. Exact solutions for free convection flow of nanofluids with ramped wall temperature. Eur. Phys. J. Plus 2015, 130. [Google Scholar] [CrossRef]
- Ahmad, S.; Pop, I. Mixed convection boundary layer flow from a vertical flat plate embedded in a porous medium filled with nanofluids. Int. Commun. Heat Mass Transf. 2010, 37, 987–991. [Google Scholar] [CrossRef]
- Gul, A.; Khan, I.; Shafie, S.; Khalid, A.; Khan, A. Heat Transfer in MHD Mixed Convection Flow of a Ferrofluid along a Vertical Channel. PLoS ONE 2015, 10, e0141213. [Google Scholar] [CrossRef]
- Das, S.; Jana, R.N.; Makinde, O.D. Mixed convective magnetohydrodynamic flow in a vertical channel filled with nanofluids. Eng. Sci. Technol. Int. J. 2015, 18, 244–255. [Google Scholar] [CrossRef]
- Khalid, A.; Khan, I.; Shafie, S. Heat transfer in ferrofluid with cylindrical shape nanoparticles past a vertical plate with ramped wall temperature embedded in a porous medium. J. Mol. Liq. 2016, 221, 1175–1183. [Google Scholar] [CrossRef]
- Shafie, S.; Gul, A.; Khan, I. Molybdenum disulfide nanoparticles suspended in water-based nanofluids with mixed convection and flow inside a channel filled with saturated porous medium. AIP Conf. Proc. 2016, 1775, 1–8. [Google Scholar] [CrossRef]
- Ali, F.; Gohar, M.; Khan, I.; Sheikh, N.A.; Jan, S.A.A.; Saqib, M. Magnetite Molybdenum Disulphide Nanofluid of Grade Two: A Generalized Model with Caputo-Fabrizio Derivative. Microfluid. Nanofluidics 2018. [Google Scholar] [CrossRef]
- Caputo, M.; Fabrizio, M. A new definition of fractional derivative without singular kernel. Progr. Fract. Differ. Appl. 2015, 1, 1–13. [Google Scholar]
- Mohd Zin, N.A.; Khan, I.; Shafie, S. The impact silver nanoparticles on MHD free convection flow of Jeffrey fluid over an oscillating vertical plate embedded in a porous medium. J. Mol. Liq. 2016, 222, 138–150. [Google Scholar] [CrossRef]
- Ali, F.; Aamina, B.; Khan, I.; Sheikh, N.A.; Saqib, M. Magnetohydrodynamic flow of brinkman-type engine oil based MoS2-nanofluid in a rotating disk with hall effect. Int. J. Heat Technol. 2017, 4, 893–902. [Google Scholar]
- Aman, S.; Khan, I.; Ismail, Z.; Salleh, M.Z.; Alshomrani, A.S.; Alghamdi, M.S. Magnetic field effect on Poiseuille flow and heat transfer of carbon nanotubes along a vertical channel filled with Casson fluid. AIP Adv. 2017, 7. [Google Scholar] [CrossRef]
- Kataria, H.R.; Mittal, A.S. Velocity, mass and temperature analysis of gravity-driven convection nanofluid flow past an oscillating vertical plate in the presence of magnetic field in a porous medium. Appl. Therm. Eng. 2017, 110, 864–874. [Google Scholar] [CrossRef]
- Aman, S.; Khan, I.; Ismail, Z.; Salleh, M.Z.; Al-Mdallal, Q.M. Heat transfer enhancement in free convection flow of CNTs Maxwell nanofluids with four different types of molecular liquids. Sci. Rep. 2017, 7, 2445. [Google Scholar] [CrossRef]
- Khan, I. Shape effects of MoS 2 nanoparticles on MHD slip flow of molybdenum disulphide nanofluid in a porous medium. J. Mol. Liq. 2017, 233, 442–451. [Google Scholar] [CrossRef]
- Sheikh, N.A.; Ali, F.; Khan, I.; Gohar, M.; Saqib, M. On the applications of nanofluids to enhance the performance of solar collectors: A comparative analysis of Atangana-Baleanu and Caputo-Fabrizio fractional models. Eur. Phys. J. Plus 2017, 132. [Google Scholar] [CrossRef]
- Atangana, A.; Gómez-Aguilar, J.F. Numerical approximation of Riemann-Liouville definition of fractional derivative: From Riemann-Liouville to Atangana-Baleanu. Numer. Methods Partial Differ. Equ. 2018, 34, 1502–1523. [Google Scholar] [CrossRef]
- Ali, F.; Gohar, M.; Khan, I.; Sheikh, N.A.; Jan, S.A.A. Thermal Radiation and Magnetic Field Effects on Different Channel Flows of CNTs Brinkman-Type Nanofluids with Water, Kerosene and Engine-oil. City Univ. Int. J. Comput. Anal. 2018, 2. [Google Scholar] [CrossRef]
- Hussanan, A.; Salleh, M.Z.; Khan, I.; Shafie, S. Convection heat transfer in micropolar nanofluids with oxide nanoparticles in water, kerosene and engine oil. J. Mol. Liq. 2017, 229, 482–488. [Google Scholar] [CrossRef]
- Saqib, M.; Khan, I.; Shafie, S. Application of Atangana–Baleanu fractional derivative to MHD channel flow of CMC-based-CNT’s nanofluid through a porous medium. Chaos Solitons Fractals 2018, 116, 79–85. [Google Scholar] [CrossRef]
- Ali, F.; Arif, M.; Khan, I.; Sheikh, N.; Saqib, M. Natural convection in polyethylene glycol based molybdenum disulfide nanofluid with thermal radiation, chemical reaction and ramped wall temperature. Int. J. Heat Technol. 2018, 36, 619–631. [Google Scholar] [CrossRef]
- Aman, S.; Khan, I.; Ismail, Z.; Salleh, M.Z. Impacts of gold nanoparticles on MHD mixed convection Poiseuille flow of nanofluid passing through a porous medium in the presence of thermal radiation, thermal diffusion and chemical reaction. Neural. Comput. Appl. 2018, 30, 789–797. [Google Scholar] [CrossRef] [PubMed]
- Rashidi, M.; Abelman, S.; Mehr, N.F. Entropy generation in steady MHD flow due to a rotating porous disk in a nanofluid. Int. J. Heat Mass Transf. 2013, 62, 515–525. [Google Scholar] [CrossRef]
- Mahian, O.; Kianifar, A.; Kleinstreuer, C.; Moh’d, A.A.-N.; Pop, I.; Sahin, A.Z.; Wongwises, S. A review of entropy generation in nanofluid flow. Int. J. Heat Mass Transf. 2013, 65, 514–532. [Google Scholar] [CrossRef]
- Khan, M.I.; Kumar, A.; Hayat, T.; Waqas, M.; Singh, R. Entropy generation in flow of Carreau nanofluid. J. Mol. Liq. 2019, 278, 677–687. [Google Scholar] [CrossRef]
- Gul, A.; Khan, I.; Makhanov, S.S. Entropy generation in a mixed convection Poiseulle flow of molybdenum disulphide Jeffrey nanofluid. Results Phys. 2018, 9, 947–954. [Google Scholar] [CrossRef]
- Khan, A.; Khan, D.; Khan, I.; Ali, F.; Karim, F.U.; Imran, M. MHD Flow of Sodium Alginate-Based Casson Type Nanofluid Passing Through A Porous Medium With Newtonian Heating. Sci. Rep. 2018, 8, 8645. [Google Scholar] [CrossRef] [PubMed]
- Sheikh, N.A.; Ali, F.; Khan, I.; Gohar, M. A theoretical study on the performance of a solar collector using CeO2 and Al2O3 water based nanofluids with inclined plate: Atangana–Baleanu fractional model. Chaos Solitons Fractals 2018, 115, 135–142. [Google Scholar] [CrossRef]
- Aman, S.; Khan, I.; Ismail, Z.; Salleh, M.Z.; Tlili, I. A new Caputo time fractional model for heat transfer enhancement of water based graphene nanofluid: An application to solar energy. Results Phys. 2018, 9, 1352–1362. [Google Scholar] [CrossRef]
- Aman, S.; Zokri, S.M.; Ismail, Z.; Salleh, M.Z.; Khan, I. Effect of MHD and porosity on exact solutions and flow of a hybrid Casson-nanofluid. J. Adv. Res. Fluid Mech. Therm. Sci. 2018, 44, 131–139. [Google Scholar]
- Khan, I.; Saqib, M.; Alqahtani, A.M. Channel flow of fractionalized H2O-based CNTs nanofluids with Newtonian heating. Discret. Contin. Dyn. Syst. S 2018, 13, 769–779. [Google Scholar] [CrossRef]
- Tzou, D.Y. Macro-to Microscale Heat Transfer: The Lagging Behavior; John Wiley & Sons: Hoboken, NJ, USA, 2014. [Google Scholar]
- Ali, F.; Aamina; Khan, I.; Sheikh, N.A.; Gohar, M.; Tlili, I. Effects of Different Shaped Nanoparticles on the Performance of Engine-Oil and Kerosene-Oil: A generalized Brinkman-Type Fluid model with Non-Singular Kernel. Sci. Rep. 2018, 8, 15285. [Google Scholar] [CrossRef]
- Hussain, S.M.; Jain, J.; Seth, G.S.; Rashidi, M.M. Effect of thermal radiation on magneto-nanofluids free convective flow over an ac-celerated moving ramped temperature plate. Sci. Iran. 2017, 25, 1243–1257. [Google Scholar] [CrossRef]
- Jan, S.A.A.; Ali, F.; Sheikh, N.A.; Khan, I.; Saqib, M.; Gohar, M. Engine oil based generalized brinkman-type nano-liquid with molybdenum disulphide nanoparticles of spherical shape: Atangana-Baleanu fractional model. Numer. Methods Partial Differ. Equ. 2018, 34, 1472–1488. [Google Scholar] [CrossRef]
- Saqib, M.; Ali, F.; Khan, I.; Sheikh, N.A.; Khan, A. Entropy Generation in Different Types of Fractionalized Nanofluids. Arab. J. Sci. Eng. 2018, 44, 531–540. [Google Scholar] [CrossRef]
- Saqib, M.; Ali, F.; Khan, I.; Sheikh, N.A.; Shafie, S.B. Convection in ethylene glycol-based molybdenum disulfide nanofluid. J. Therm. Anal. Calorim. 2018, 135, 523–532. [Google Scholar] [CrossRef]
- Aamina; Ali, F.; Khan, I.; Sheikh, N.A.; Gohar, M. Exact solutions for the Atangana-Baleanu time-fractional model of a Brinkman-type nanofluid in a rotating frame: Applications in solar collectors. Eur. Phys. J. Plus 2019, 134. [Google Scholar] [CrossRef]
- Van Trinh, P.; Anh, N.N.; Thang, B.H.; Hong, N.T.; Hong, N.M.; Khoi, P.H.; Minh, P.N.; Hong, P.N. Enhanced thermal conductivity of nanofluid-based ethylene glycol containing Cu nanoparticles decorated on a Gr–MWCNT hybrid material. RSC Adv. 2017, 7, 318–326. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Mehryan, S.A.M.; Shafee, A.; Sheremet, M.A. Variable magnetic forces impact on magnetizable hybrid nanofluid heat transfer through a circular cavity. J. Mol. Liq. 2019, 277, 388–396. [Google Scholar] [CrossRef]
- Khan, M.I.; Hafeez, M.U.; Hayat, T.; Khan, M.I.; Alsaedi, A. Magneto rotating flow of hybrid nanofluid with entropy generation. Comput. Methods Programs Biomed. 2019, 183, 105093. [Google Scholar] [CrossRef]
- Ali, F.; Sheikh, N.A.; Saqib, M.; Khan, I. Unsteady MHD flow of second-grade fluid over an oscillating vertical plate with isothermal temperature in a porous medium with heat and mass transfer by using the Laplace transform technique. J. Porous Media 2017, 20, 671–690. [Google Scholar] [CrossRef]
- Gul, T.; Shayan, W.; Ali, F.; Khan, I.; Shafie, S.; Sheikh, N.A. Analysis of time dependent third grade fluid in wire coating. J. Nonlinear Sci. Lett. A 2017, 8, 374–388. [Google Scholar]
- Sheikh, N.A.; Ali, F.; Khan, I.; Saqib, M.; Khan, A. MHD flow of micropolar fluid over an oscillating vertical plate embedded in porous media with constant temperature and concentration. Math. Probl. Eng. 2017, 2017. [Google Scholar] [CrossRef]
- Lei, C.; Wollenberger, U.; Bistolas, N.; Guiseppi-Elie, A.; Scheller, F.W. Electron transfer of hemoglobin at electrodes modified with colloidal clay nanoparticles. Anal. Bioanal. Chem. 2002, 372, 235–239. [Google Scholar] [CrossRef]
- Xia, T.; Kovochich, M.; Liong, M.; Madler, L.; Gilbert, B.; Shi, H.; Yeh, J.I.; Zink, J.I.; Nel, A.E. Comparison of the mechanism of toxicity of zinc oxide and cerium oxide nanoparticles based on dissolution and oxidative stress properties. ACS Nano 2008, 2, 2121–2134. [Google Scholar] [CrossRef]
- Marcano, D.C.; Kosynkin, D.V.; Berlin, J.M.; Sinitskii, A.; Sun, Z.; Slesarev, A.; Alemany, L.B.; Lu, W.; Tour, J.M. Improved synthesis of graphene oxide. ACS Nano 2010, 4, 4806–4814. [Google Scholar] [CrossRef]
- Bansal, V.; Rautaray, D.; Ahmad, A.; Sastry, M. Biosynthesis of zirconia nanoparticles using the fungus Fusarium oxysporum. J. Mater. Chem. 2004, 14, 3303–3305. [Google Scholar] [CrossRef]
- Chang, Y.S.; Savitha, S.; Sadhasivam, S.; Hsu, C.K.; Lin, F.H. Fabrication, characterization, and application of greigite nanoparticles for cancer hyperthermia. J. Colloid Interface Sci. 2011, 363, 314–319. [Google Scholar] [CrossRef]
- Yang, X.J.; Srivastava, H.M.; Machado, J. A new fractional derivative without singular kernel: Application to the modelling of the steady heat flow. arXiv 2015, arXiv:1601.01623. [Google Scholar] [CrossRef]
- Cattani, C. Sinc-fractional operator on Shannon wavelet space. Front. Phys. 2018, 6, 118. [Google Scholar] [CrossRef]
- Yang, X.J.; Gao, F.; Machado, J.T.; Baleanu, D. A new fractional derivative involving the normalized sinc function without singular kernel. Eur. Phys. J. Spec. Top. 2017, 226, 3567–3575. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).