A Vector Field Texture Generation Method without Convolution Calculation
Abstract
1. Introduction
2. Related Work
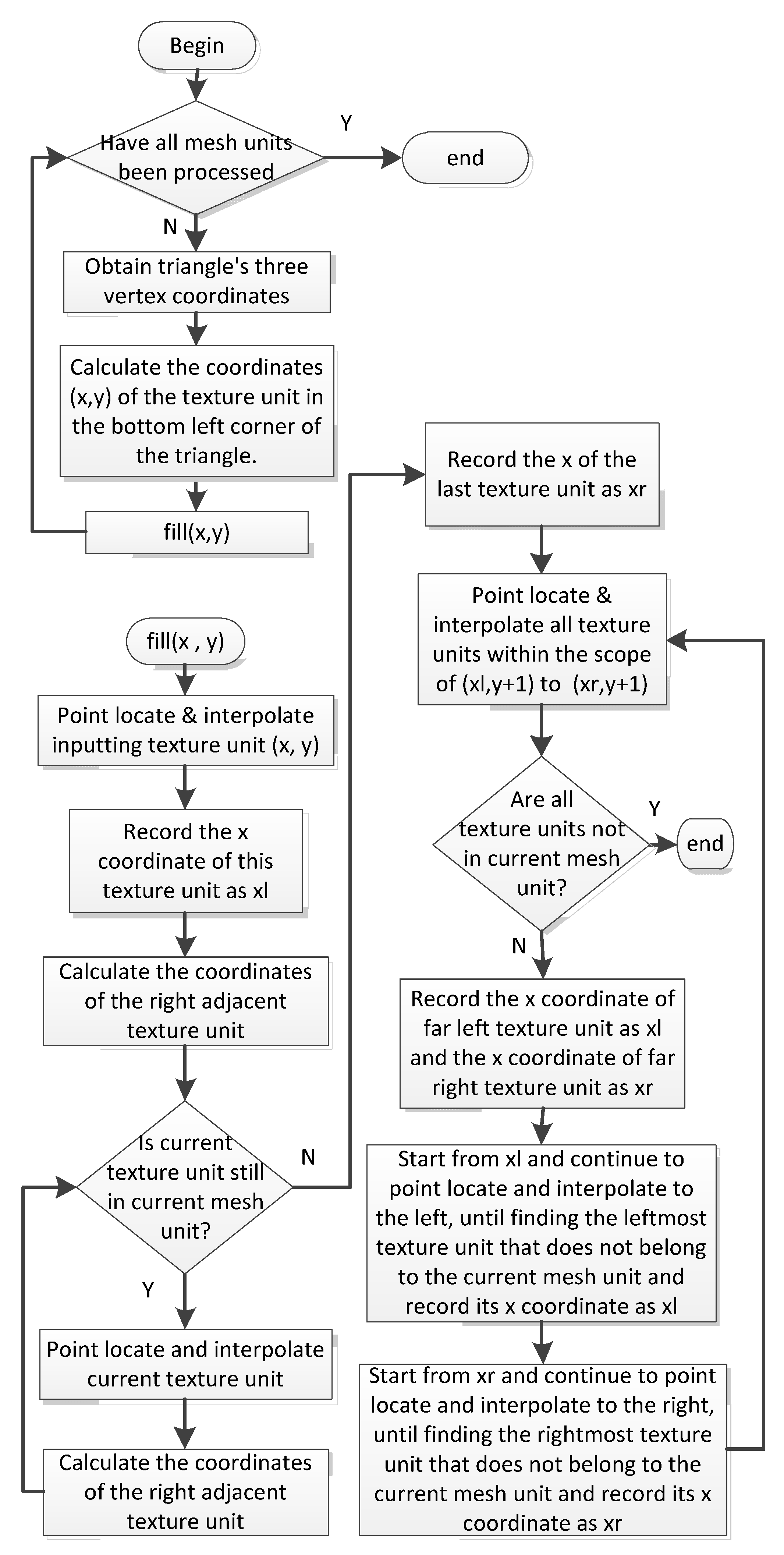
3. Mesh Unit Filling Preprocessing Method
3.1. Texture Pixel
3.2. Mesh Unit Filling Preprocessing Method
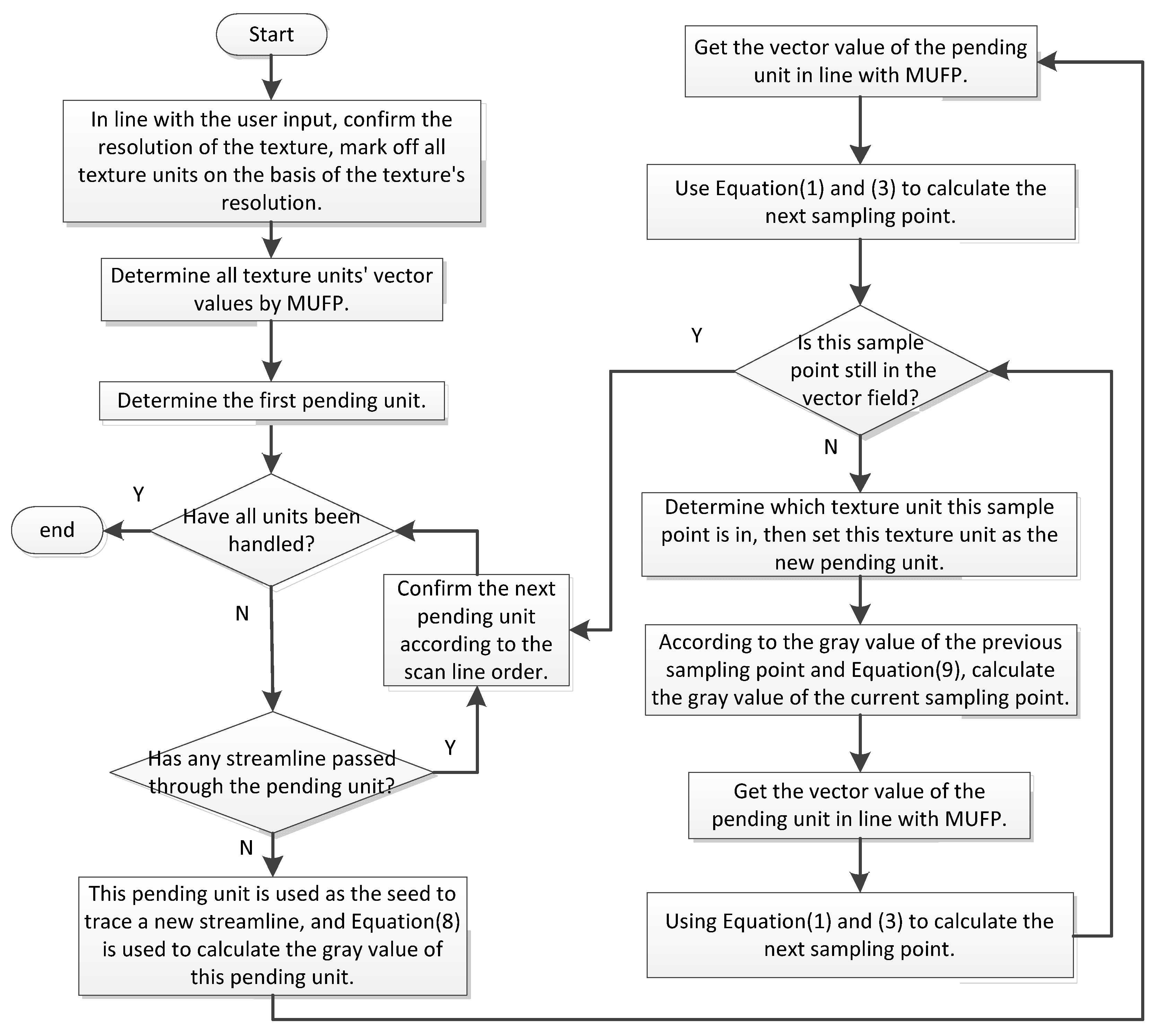
4. Random Increment Streamline Method
4.1. Basic Idea
4.2. Periodic Circulating Animation
5. Simplified RIS Algorithm
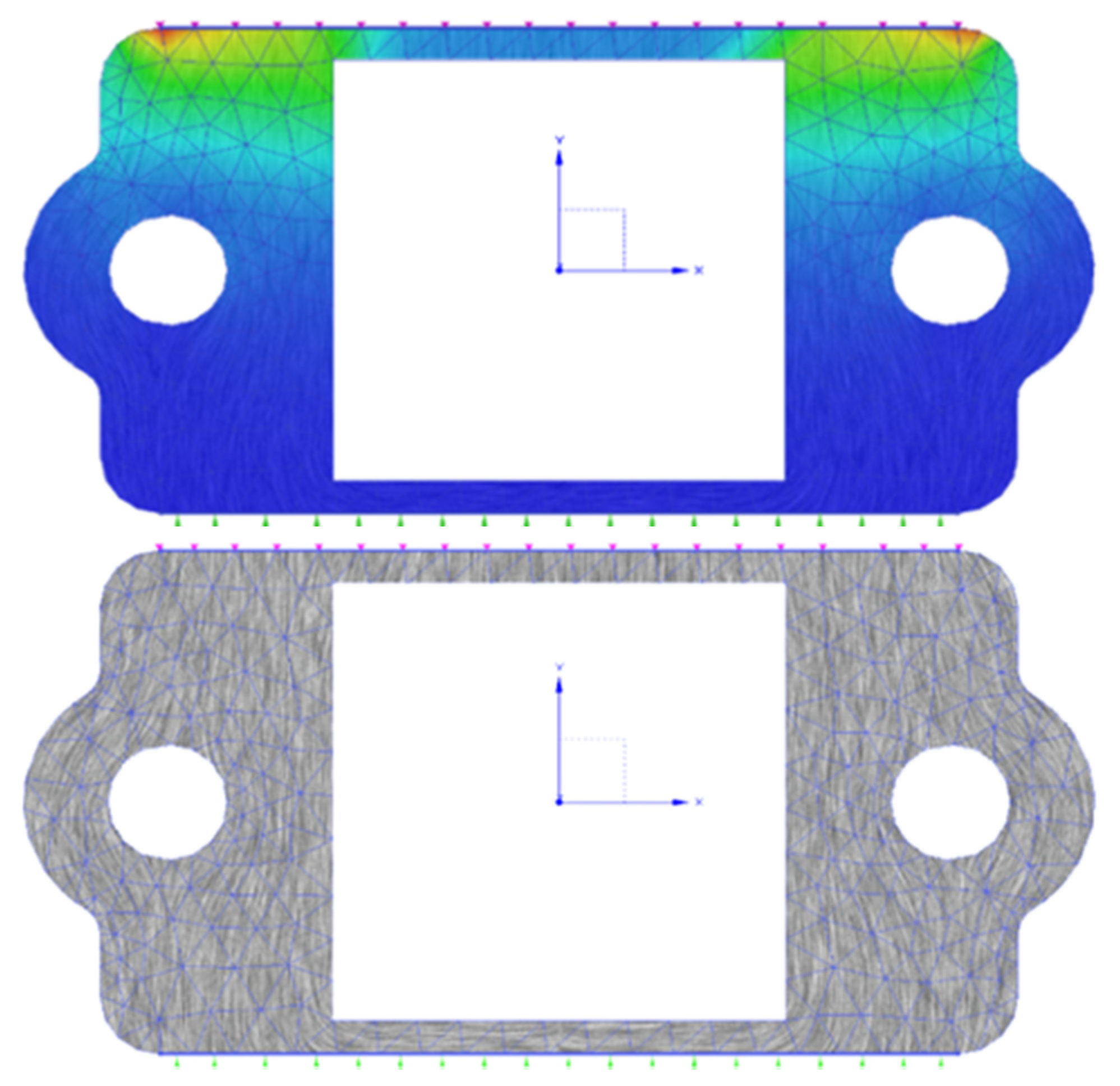
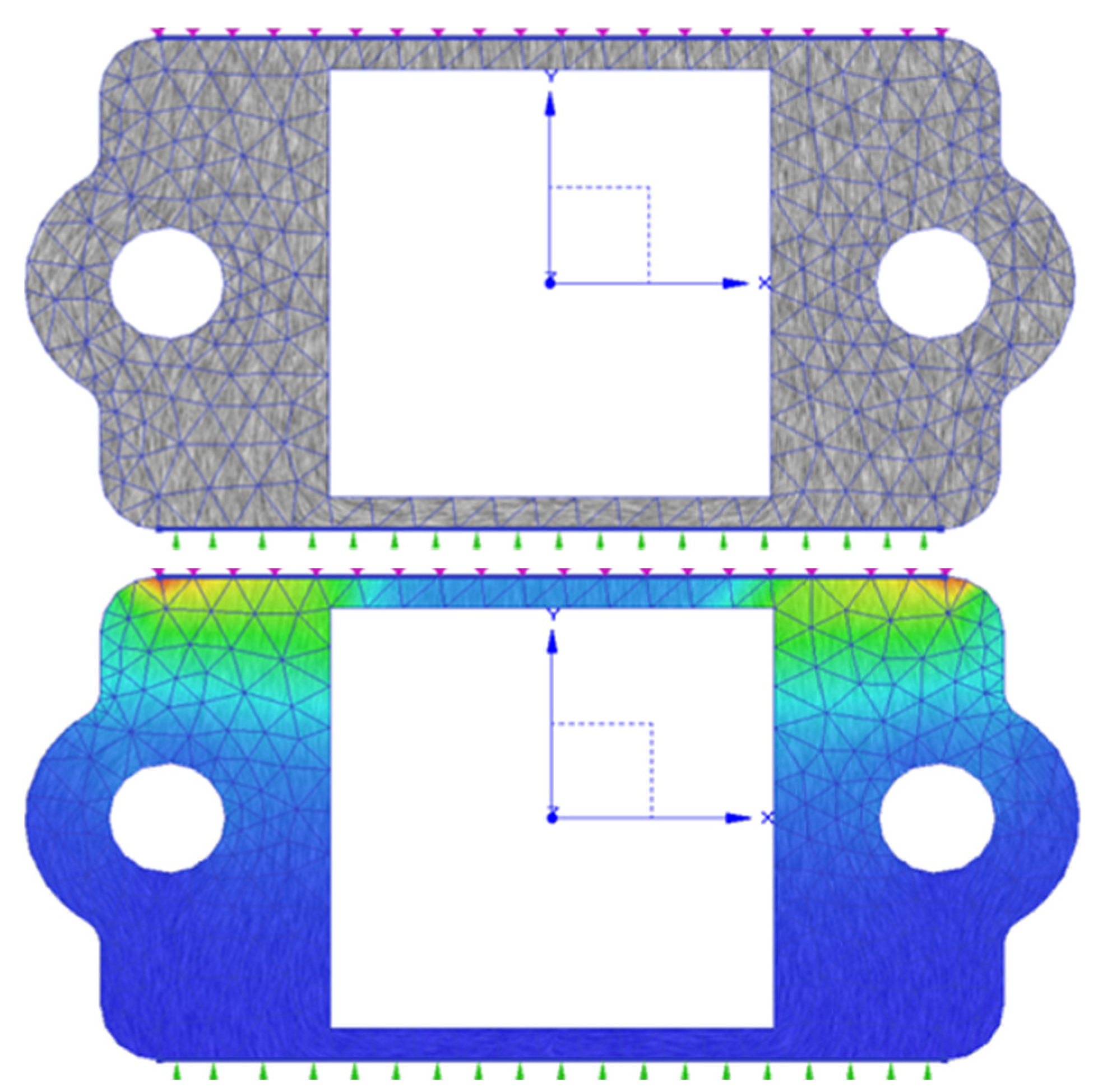
6. Results and Discussion
Author Contributions
Funding
Conflicts of Interest
References
- David, H.L.; Robert, M.K.; Cullen, D.J.; Davidson, J.S.; Timothy, S.M.; Marco, D.S.; William, H.W.; Michael, J.T. Comparing 2D Vector Field Visualization Methods: A User Study. IEEE Trans. Vis. Comput. Graph. 2005, 11, 59–70. [Google Scholar]
- Van, W.; Jarke, J. Spot noise: Texture synthesis for data visualization. In Proceedings of the ACM Siggraph, New York, NY, USA, 3 July 1991; pp. 309–318. [Google Scholar]
- Vivek, V.; David, K.; Alex, P. PLIC: Bridging the Gap between Streamlines and LIC. In Proceedings of the IEEE Visualization, San Francisco, CA, USA, 24–29 October 1999; pp. 341–348. [Google Scholar]
- Van, W.; Jarke, J. Image based flow visualization. ACM Trans. Graph. 2002, 3, 745–754. [Google Scholar]
- Brian, C.; Leith, L. Imaging vector fields using line integral convolution. In Proceedings of the ACM Siggraph, Anaheim, CA, USA, 2–6 August 1993; pp. 263–270. [Google Scholar]
- Detlev, S.; Hege, H.C. Fast and resolution independent line integral convolution. In Proceedings of the ACM Siggraph, Los Angeles, CA, USA, 6–11 August 1995; pp. 249–256. [Google Scholar]
- Bruno, J.; Wilfrid, L. The Motion Map: Efficient Computation of Steady Flow Animations. In Proceedings of the IEEE Visualization’97, Phoenix, AZ, USA, 19–24 October 1997; pp. 323–328. [Google Scholar]
- Arthur, O.; David, K. Enhanced line integral convolution with flow feature detection. In Proceedings of the IS&T/SPIE Electronic Imaging, San Jose, CA, USA, 9–13 June 1997; pp. 206–217. [Google Scholar]
- Du, X.F.; Liu, H.L. Seed Filling Preprocessing: A universal visualization preprocessing method in irregular grids. In Proceedings of the 30th Chinese Control and Decision Conference (CCDC2018), Shenyang, China, 9–11 June 2018; pp. 4378–4382. [Google Scholar]
- Du, X.F. A New Texture Generating Algorithm: Random Increment Streamline Method. In Proceedings of the 37th Chinese Control Conference (CCC2018), Wuhan, China, 25–27 July 2018; pp. 1679–1684. [Google Scholar]
- De, L.; Willem, C.; Van, W.; Jarke, J. Enhanced spot noise for vector field visualization. In Proceedings of the IEEE Visualization, Atlanta, GA, USA, 29 October–3 November 1995; pp. 233–239. [Google Scholar]
- Wang, B.; Wang, W.P.; Yong, J.H.; Sun, J.G. Flow Visualization by Near-Regular Texture Synthesis. J. Comput. Aided Des. Comput. Graph. 2005, 8, 1678–1685. [Google Scholar]
- Lin, L.L.; Yang, G.; Huang, H.D.; Liu, X.H.; Wu, E.H. Vector Field Visualization Based on Texture Synthesis. J. Comput. Aided Des. Comput. Graph. 2006, 11, 1677–1682. [Google Scholar]
- Jarke, J.; Van, W. Image Based Flow Visualization for Curved Surfaces. In Proceedings of the IEEE VIS 2003, Seattle, WA, USA, 19–24 October 2003; pp. 123–130. [Google Scholar]
- Sun, C.H.; Fan, Y.; Li, Q.; Huang, W. Enhanced IBFV 2D vector field visualization. J. Image Graph. 2011, 6, 1064–1069. [Google Scholar]
- Rainer, W.; Eduard, G. Animating flow fields: Rendering of oriented line integral convolution. In Proceedings of the IEEE Computer Animation, Geneva, Switzerland, 5–6 June 1997; pp. 15–21. [Google Scholar]
- Rainer, W.; Eduard, G. Fast Oriented Line Integral Convolution for Vector Field Visualization via the Internet. In Proceedings of the IEEE Visualization, Phoenix, AZ, USA, 19–24 October 1997; pp. 309–316. [Google Scholar]
- Qin, X.J.; Fang, X.; Chen, L.H.; Zheng, H.B.; Ma, J.; Zhang, M.Y. A Line Integral Convolution Method with Dynamically Determining Step Size and Interpolation Mode for Vector Field Visualization. IEEE Access 2019, 7, 19414–19422. [Google Scholar] [CrossRef]
- Shen, H.-W.; David, L.; Kao, A. New Line Integral Convolution Algorithm for Visualizing Time-Varying Flow Fields. IEEE Trans. Vis. Comput. Graph. 1998, 4, 98–108. [Google Scholar] [CrossRef]
- Interrante, V.; Grosch, C. Strategies for effectively visualizing 3D flow with volume LIC. In Proceedings of the IEEE Visualization, Phoenix, AZ, USA, 19–24 October 1997; pp. 421–424. [Google Scholar]
- Dibin, Z.; Lijun, X.; Yao, Z. Enhanced Texture-Based 3D Flow Visualization. J. Comput. Aided Des. Comput. Graph. 2009, 21, 406–411. [Google Scholar]
- Lu, D.; Zhu, D.; Wang, Z.; Gao, Z.; Ni, J. Enhanced Texture Advection Algorithm. J. Comput. Aided Des. Comput. Graph. 2017, 29, 670–679. [Google Scholar]
- Jia, Q.; Li, L.; Hou, L.; Hao, S.; Fan, Z.; Lu, D. A Texture Advection Method for Vector Field. Electron. Technol. 2018, 47, 6–8. [Google Scholar]
- Wang, H.; Wang, S.; Wu, Y.; Han, Y.; Wu, B. Sparse Noise Based Volume LIC Rendering Method Accelerated by GPU. J. Southwest Univ. Sci. Technol. 2016, 31, 72–80. [Google Scholar]
- Shi, H. Research on Enhanced Vector Field Visualization Based on Line Integral Convolution; Harbin Engineering University: Harbin, China, 2018. [Google Scholar]
- Ma, Y.; Li, H.; Guo, Y. Visualization of Wind Vectors Using Line Integral Convolution with Visual Perception. Comput. Sci. 2019, 46, 242–245. [Google Scholar]
- Xu, Q.; Zhang, J. Visualization of flow field motion direction based on multi-frequency sparse noise. Appl. Res. Comput. 2017, 37. [Google Scholar] [CrossRef]
- Gao, M.; Dong, H.; Zhou, F. Improved LIC algorithm based on nonlinear gradual-changing color mapping. Appl. Res. Comput. 2019, 36, 2834–2839. [Google Scholar]
- Liu, T. Research of Parallel Visualization for Vector Field Based on Fast-LIC; Harbin Engineering University: Harbin, China, 2017. [Google Scholar]
- Zahra, M. Unstructured grid adaptation for multiscale finite volume method. Comput. Geosci. 2019, 6, 1293–1316. [Google Scholar]
- Hoshiko, R.; Kawahara, M. 3-dimensional mesh generation using the Delaunay method. WIT Trans. Built Environ. 2008, 102, 91–97. [Google Scholar]
- Mazzolari, A.; da Costa Araújo, M.A.V.; Trigo-Teixeira, A. Improved advancing front mesh algorithm with pseudoislands as internal fronts. J. Waterw. PortCoast. Ocean Eng. 2014, 140, 04014013. [Google Scholar] [CrossRef]
- Wang, F.; Deng, L.; Zhao, D.; Li, S.K. An Efficient Preprocessing and Composition based Finite-time Lyapunov Exponent Visualization Algorithm for Unsteady Flow Field. In Proceedings of the 2016 International Conference on Virtual Reality and Visualization, Hangzhou, China, 23–25 September 2016; pp. 497–502. [Google Scholar]
- Qu, Z.Y.; Mao, X.J.; Deng, Z.A. Radar Signal Intra-Pulse Modulation Recognition Based on Convolutional Neural Network. IEEE Access 2018, 6, 43874–43884. [Google Scholar] [CrossRef]
- Shan, J.L.; Li, Y.M.; Guo, Y.Q.; Guan, Z.Q. A robust backward search method based on walk-through for point location on a 3D surface mesh. Int. J. Numer. Methods Eng. 2008, 73, 1061–1076. [Google Scholar] [CrossRef]
- Gao, W.J. Boundary character based declining scanning-line filling algorithm. In Proceedings of the SPIE—The International Society for Optical Engineering, San Diego, CA, USA, 1 August 2010. [Google Scholar]
- Eichelbaum, S.; Hlawitschka, M.; Hamann, B.; Scheuermann, G. Image-space tensor field visualization using a LIC-like method. Math. Vis. 2012, 202509, 191–208. [Google Scholar]


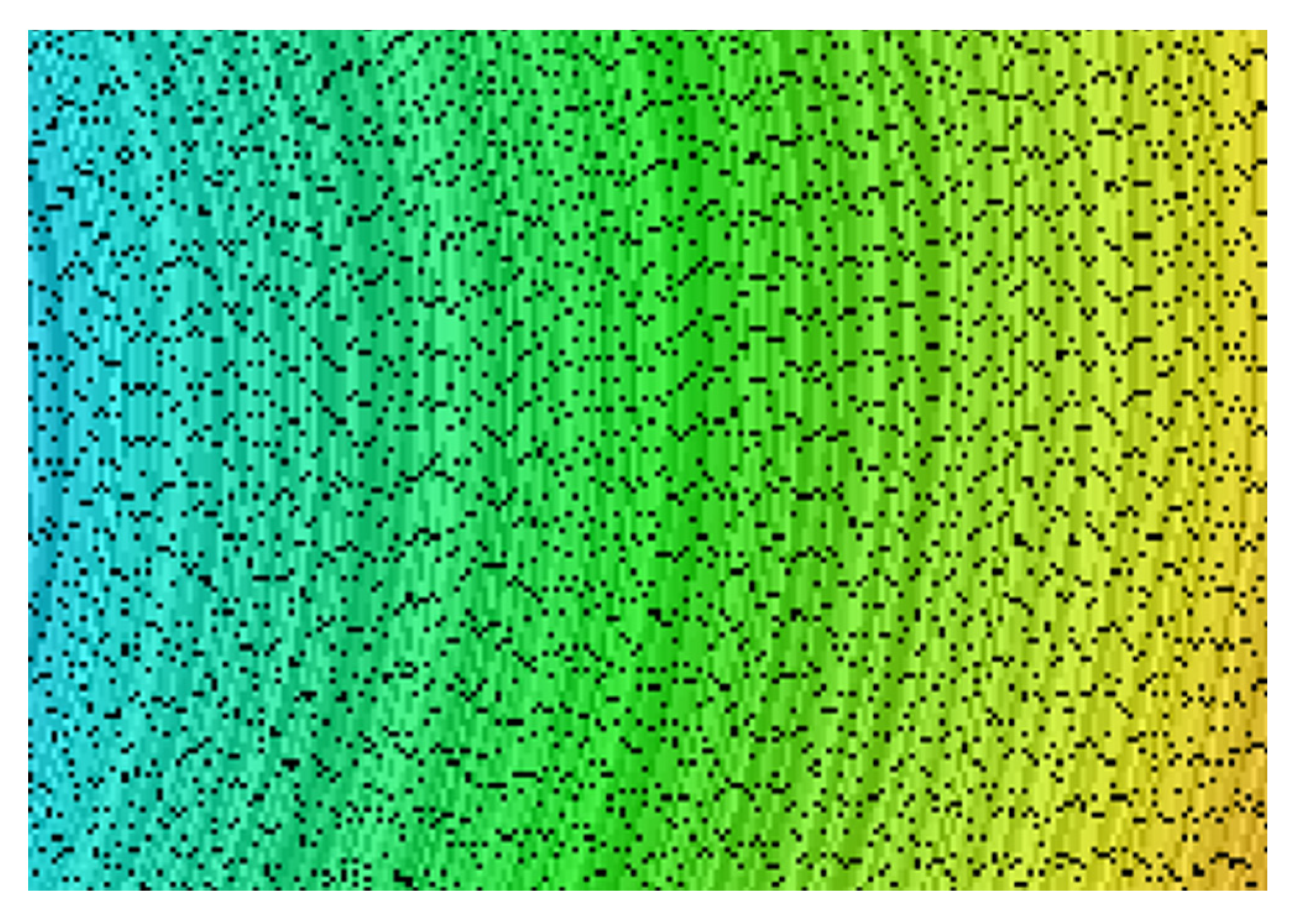

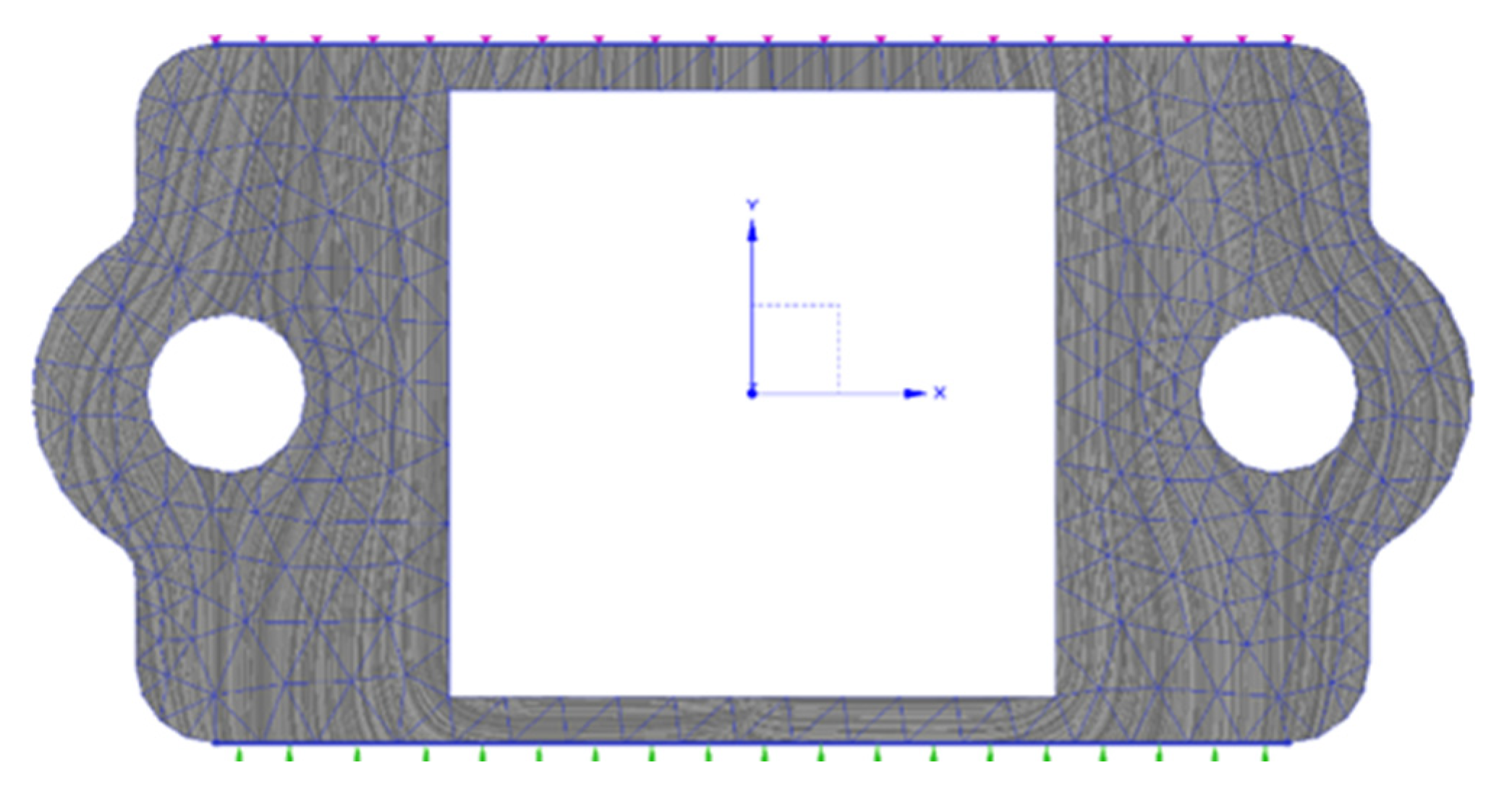
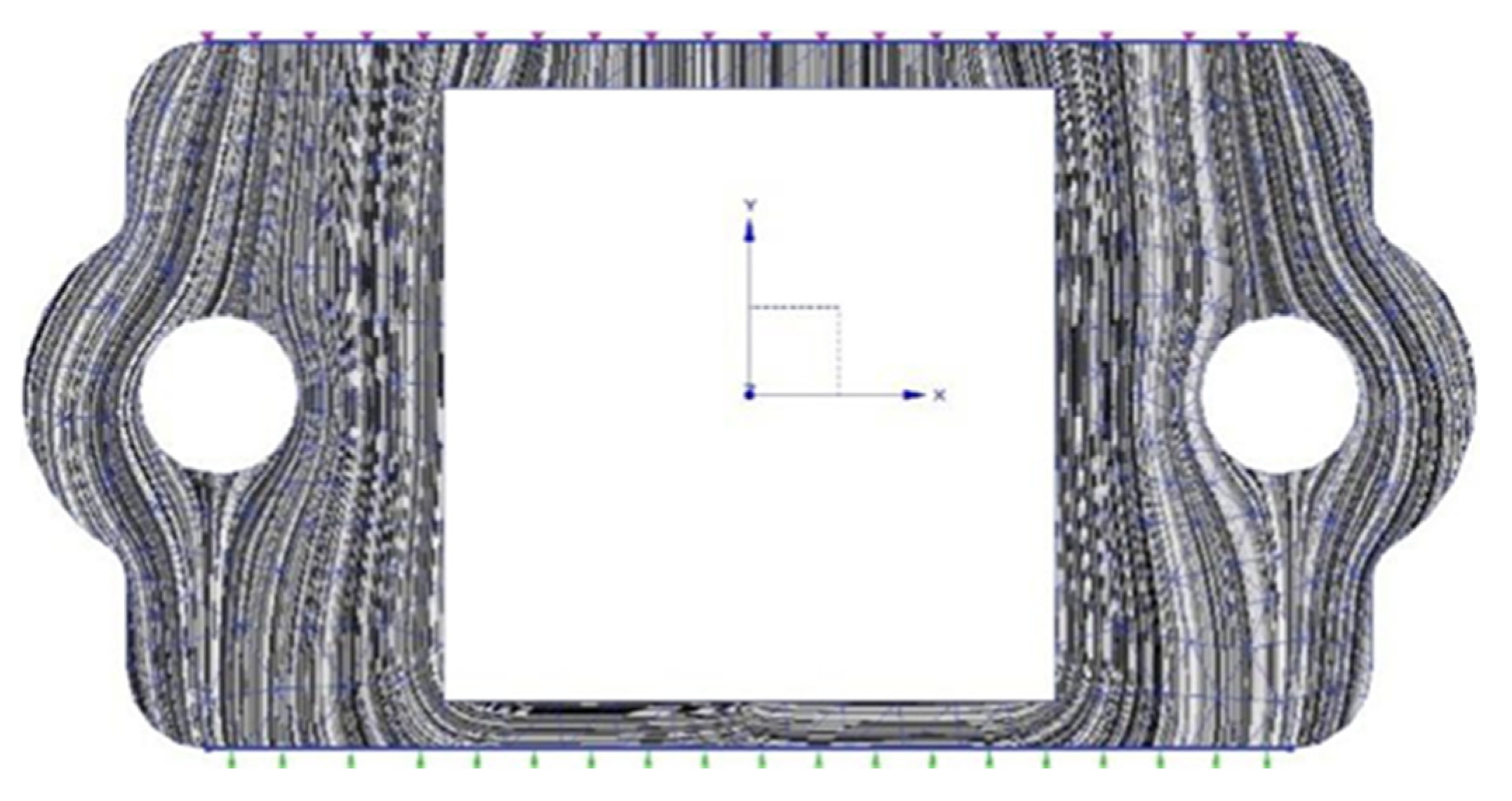

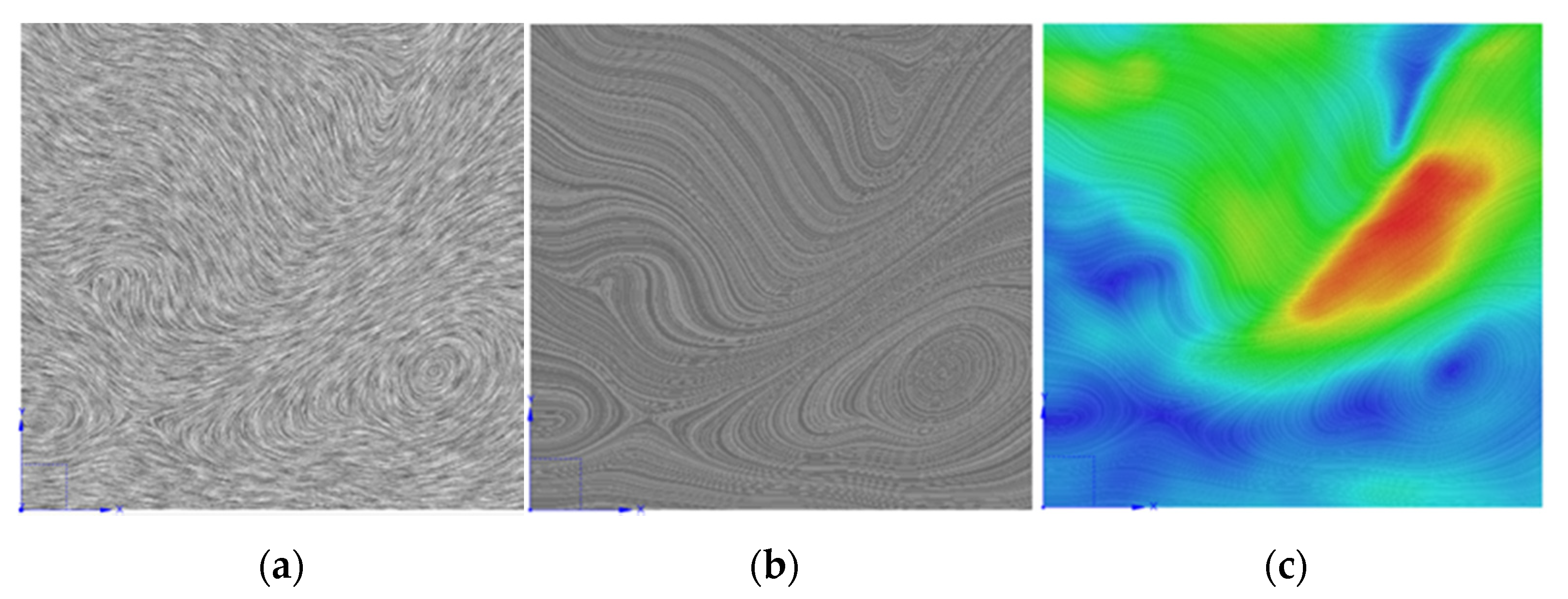
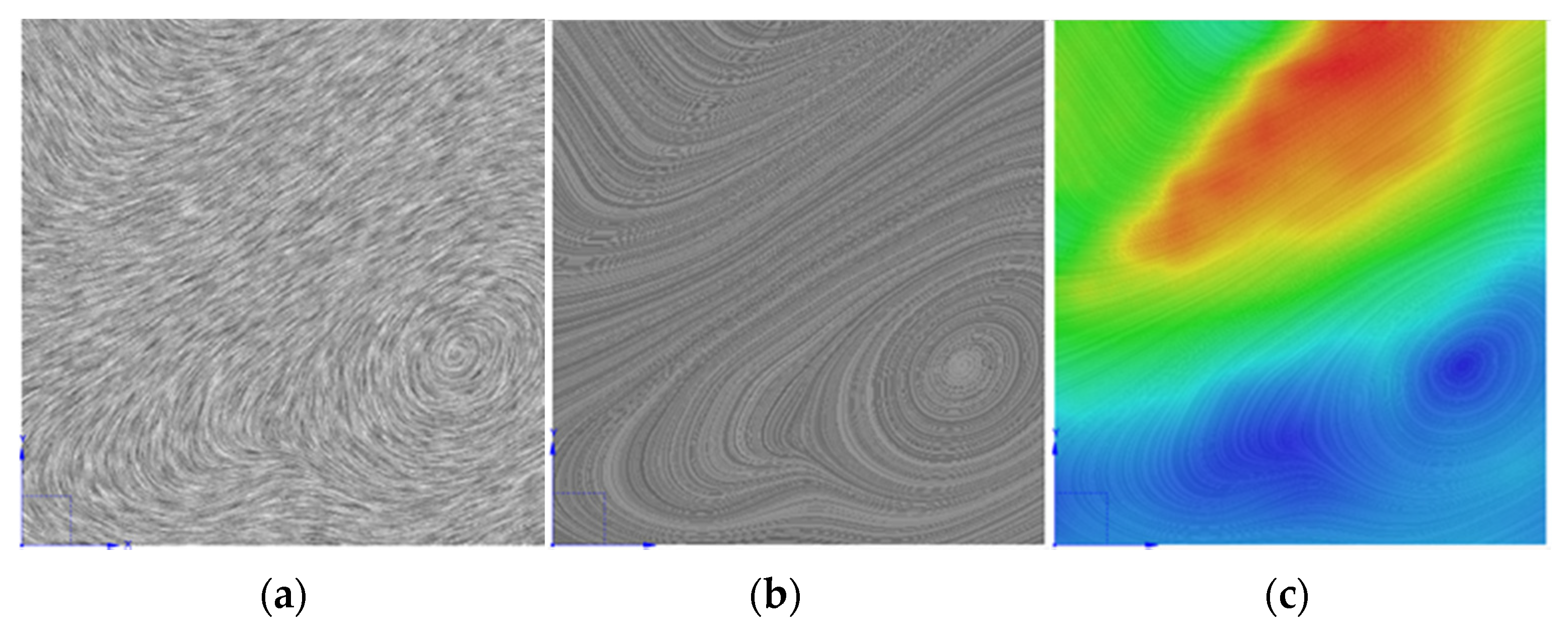
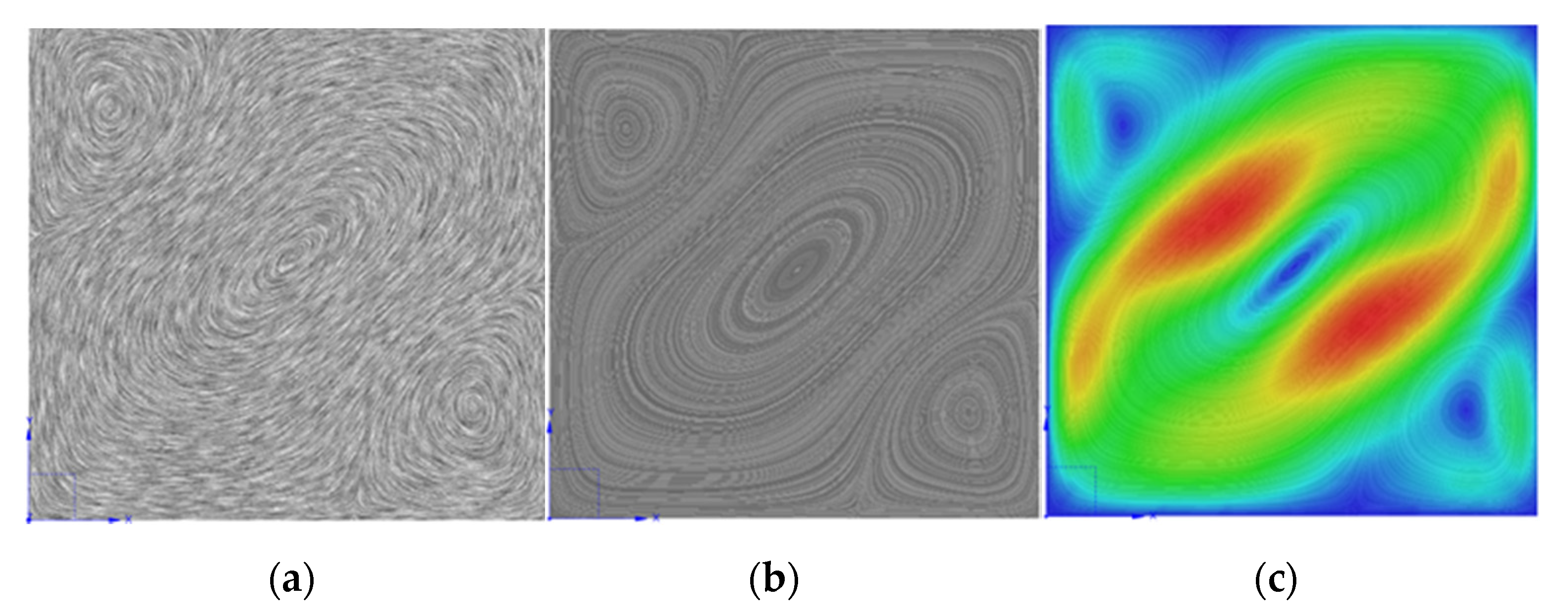
| Algorithms | Speed | Was the Cyclic Animation Provided? | Two Dimensions/Three Dimensions | With or Without Enhanced Contrast Function |
|---|---|---|---|---|
| Line Integral Convolution (LIC) [5] | Very slow | Yes | Two dimensions | Without |
| Fast Line Integral Convolution (FLIC) [6] | Much faster | Yes | Two dimensions | Without |
| Motion Map [7] | Slow | Yes | Two dimensions | Without |
| Enhanced Line Integral Convolution (ELIC) [8] | Slow | No | Two dimensions | With |
| Unsteady Flow Line Integral Convolution (UFLIC) [19] | Slow | Yes | Two dimensions | Without |
| Volume Line Integral Convolution [20] | Slow | No | Three dimensions | Without |
| Enhanced 3D Line Integral Convolution [21] | Slow | Yes | Three dimensions | With |
| Grid Unit Number | Texture Pixel Number | Walk-Through | Seed Filling Preprocessing (SFP) | Mesh Unit Filling Preprocessing (MUFP) |
|---|---|---|---|---|
| 11,056 | 1,705,600 | 6374.198 | 15.249 | 14.122 |
| 11,056 | 426,400 | 326.71 | 3.772 | 3.57 |
| 11,056 | 106,400 | 155.639 | 0.928 | 0.878 |
| 11,056 | 26,600 | 124.338 | 0.234 | 0.229 |
| 2740 | 1,705,600 | 322.923 | 16.743 | 14.108 |
| 2740 | 426,400 | 15.426 | 3.869 | 3.52 |
| 2740 | 106,400 | 7.271 | 0.952 | 0.872 |
| 2740 | 26,600 | 6.055 | 0.237 | 0.226 |
| 720 | 1,705,600 | 150.001 | 17.216 | 14.102 |
| 720 | 426,400 | 7.223 | 3.944 | 3.46 |
| 720 | 106,400 | 3.436 | 1.083 | 0.869 |
| 720 | 26,600 | 2.837 | 0.368 | 0.217 |
| 176 | 1,705,600 | 68.843 | 18.386 | 14.074 |
| 176 | 426,400 | 3.428 | 4.075 | 3.43 |
| 176 | 106,400 | 1.622 | 1.126 | 0.864 |
| 176 | 26,600 | 1.345 | 0.394 | 0.208 |
| Figure 9 | Figure 11 | Figure 12 | Figure 13 | Figure 14 | Figure 15 | |
|---|---|---|---|---|---|---|
| Grid units | 46 | 5000 | 5000 | 7440 | 45,552 | 7938 |
| Texture Pixels | 310,400 | 160,000 | 160,000 | 154,800 | 149,600 | 160,000 |
| Mesh Unit Filling Preprocessing | 2.516 | 1.201 | 1.202 | 1.292 | 1.259 | 1.318 |
| Line Integral Convolution | 4.915 | 3.526 | 3.527 | 3.523 | 3.474 | 3.528 |
| Fast Line Integral Convolution | 0.552 | 0.312 | 0.313 | 0.316 | 0.311 | 0.318 |
| Random Increment Streamline | 0.351 | 0.192 | 0.192 | 0.191 | 0.187 | 0.193 |
| Simplified Random Increment Streamline | 0.344 | 0.186 | 0.187 | 0.187 | 0.183 | 0.188 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Du, X.; Liu, H.; Tseng, H.-W.; Meen, T.-H. A Vector Field Texture Generation Method without Convolution Calculation. Symmetry 2020, 12, 724. https://doi.org/10.3390/sym12050724
Du X, Liu H, Tseng H-W, Meen T-H. A Vector Field Texture Generation Method without Convolution Calculation. Symmetry. 2020; 12(5):724. https://doi.org/10.3390/sym12050724
Chicago/Turabian StyleDu, Xiaofu, Huilin Liu, Hsien-Wei Tseng, and Teen-Hang Meen. 2020. "A Vector Field Texture Generation Method without Convolution Calculation" Symmetry 12, no. 5: 724. https://doi.org/10.3390/sym12050724
APA StyleDu, X., Liu, H., Tseng, H.-W., & Meen, T.-H. (2020). A Vector Field Texture Generation Method without Convolution Calculation. Symmetry, 12(5), 724. https://doi.org/10.3390/sym12050724






