The Exponentiated Truncated Inverse Weibull-Generated Family of Distributions with Applications
Abstract
1. Introduction
2. The ETIW-G Family
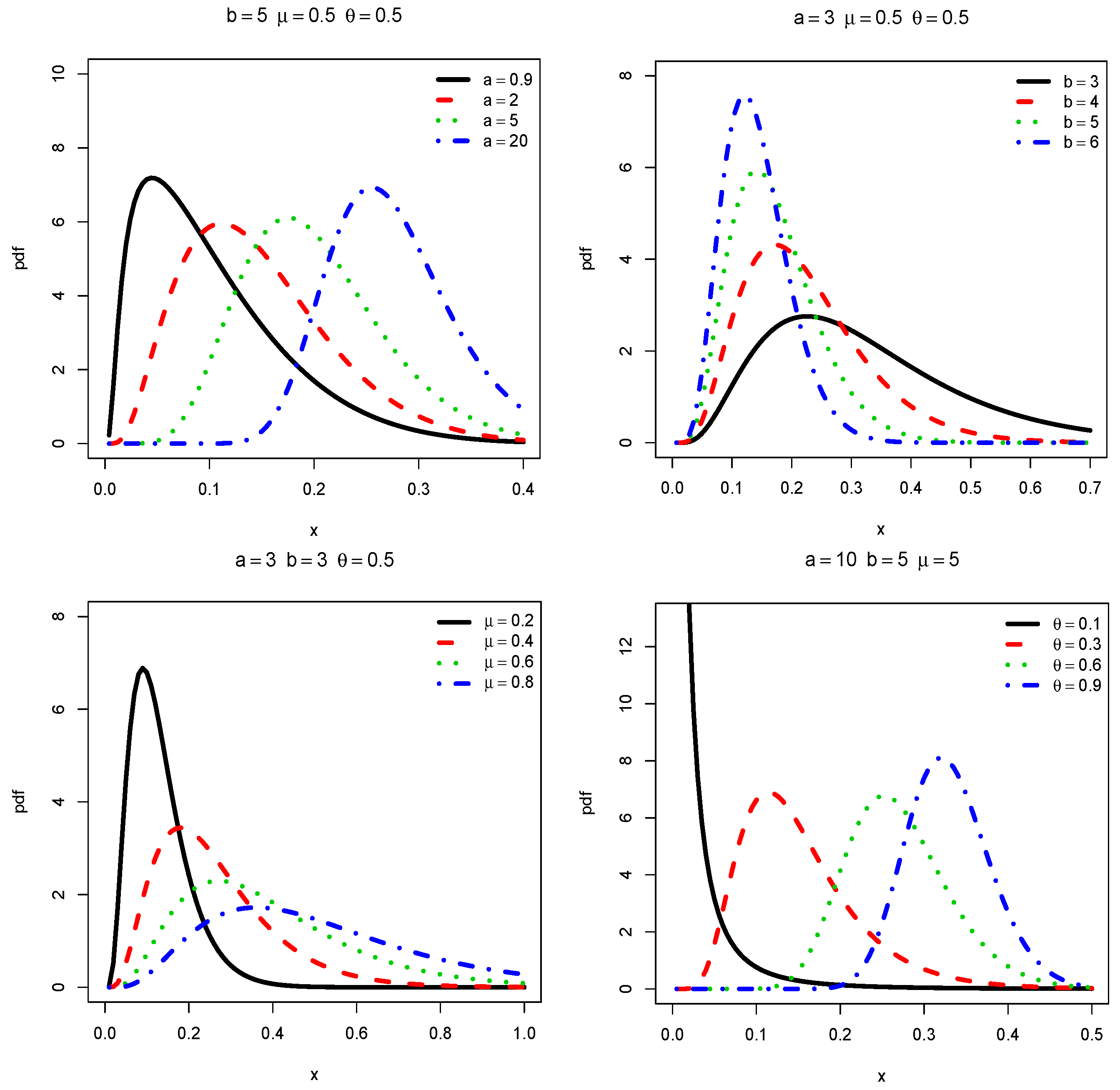
2.1. Probability Functions
2.2. Some Special Members of the ETIW-G Family
2.3. The ETIWIW Distribution
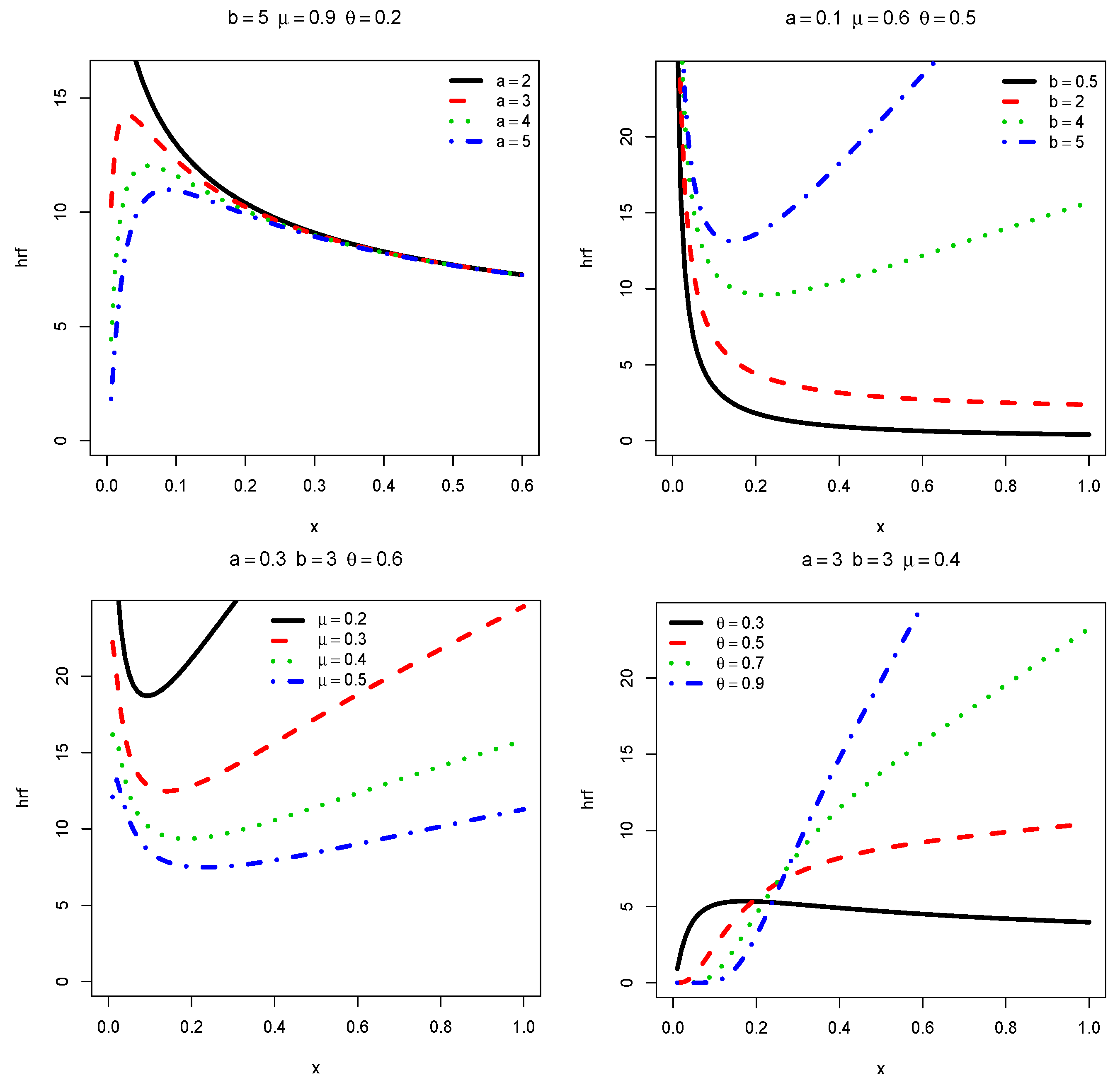
3. Mathematical Investigations
3.1. Stochastic Ordering Results
- For anyand, and any, we have
- The desired inequality follows from the fact that , where , , is an increasing function with respect to x (as the cdf of the exponentiated type II truncated inverse Weibull distribution over ).
- Since (excluding the limit cases), and , we have the following chain of equivalences:implying that .
3.2. Uni/multimodality Analysis
3.3. Tractable Series Expansions
3.4. Probability Weighted Moments
3.5. Raw and Central Moments, with Applications
3.6. Order Statistics
3.7. Maximum Likelihood Method
4. Numerical Studies
4.1. Simulation Work
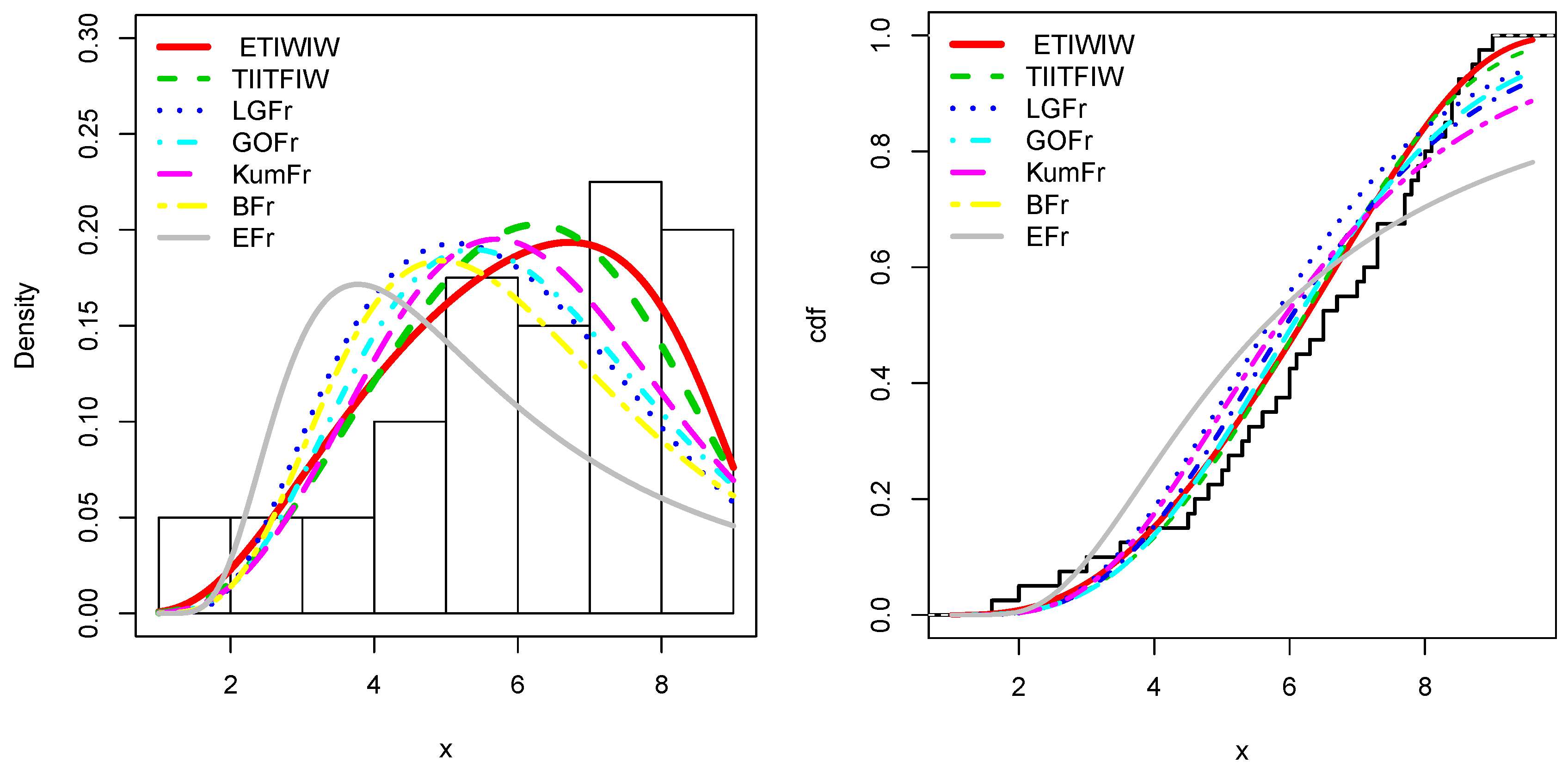
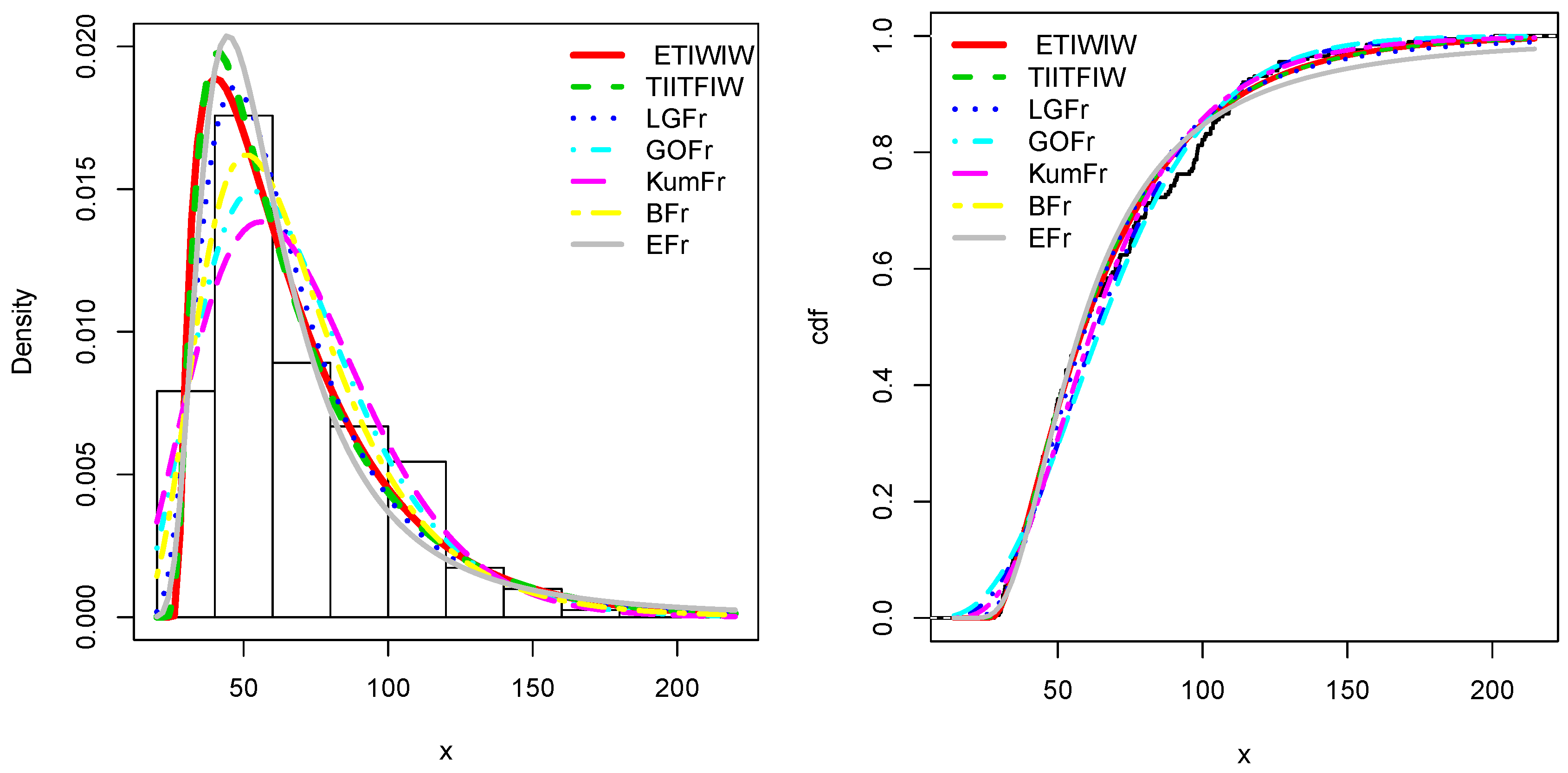
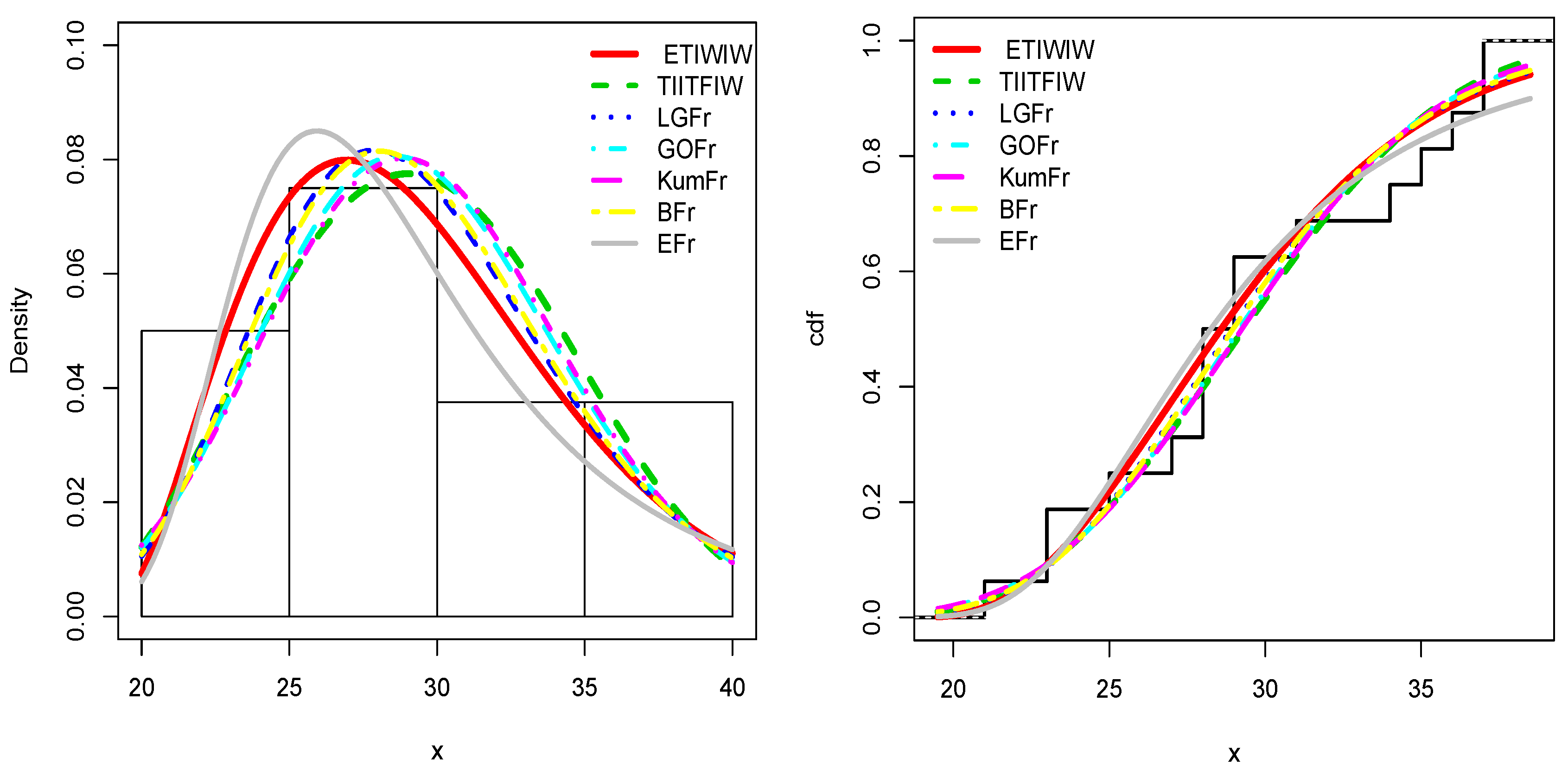
4.2. Application to the Rainfall Data Set
4.3. Application to the Sum of Skin Folds Data Set
4.4. Application to the Completed Passes of Drew Brees Data Set
5. Concluding Remarks and Perspectives
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Gupta, R.D.; Kundu, D. Exponentiated exponential family: An alternative to Gamma and Weibull distributions. Biom. J. 2001, 43, 117–130. [Google Scholar] [CrossRef]
- Cordeiro, G.M.; de Castro, M. A new family of generalized distributions. J. Stat. Comput. Simul. 2011, 81, 883–898. [Google Scholar] [CrossRef]
- Zografos, K.; Balakrishnan, N. On families of beta- and generalized gamma-generated distributions and associated inference. Stat. Methodol. 2009, 6, 344–362. [Google Scholar] [CrossRef]
- Marshall, A.; Olkin, I. A new method for adding a parameter to a family of distributions with applications to the exponential and Weibull families. Biometrika 1997, 84, 641–652. [Google Scholar] [CrossRef]
- Shaw, W.T.; Buckley, I.R. The alchemy of probability distributions: Beyond Gram-Charlier expansions, and a skew-kurtotic-normal distribution from a rank transmutation map. arXiv 2009, arXiv:0901.0434. [Google Scholar]
- Eugene, N.; Lee, C.; Famoye, F. Beta-normal distribution and its applications. Commun. Stat.-Theory Methods 2002, 31, 497–512. [Google Scholar] [CrossRef]
- Torabi, H.; Montazari, N.H. The logistic-uniform distribution and its application. Commun. Stat.-Simul. Comput. 2014, 43, 2551–2569. [Google Scholar] [CrossRef]
- Bourguignon, M.; Silva, R.B.; Cordeiro, G.M. The Weibull-G family of probability distributions. J. Data Sci. 2014, 12, 53–68. [Google Scholar]
- Brito, C.R.; Rêgo, L.C.; Oliveira, W.R.; Gomes-Silva, F. Method for generating distributions and classes of probability distributions: The univariate case. Hacet. J. Math. Stat. 2019, 48, 897–930. [Google Scholar]
- Ahmad, M. On the theory of inversion. Int. J. Stat. Sci. 2007, 6, 43–53. [Google Scholar]
- Lehmann, E.L.; Shaffer, J.P. Inverted distributions. Am. Stat. 1988, 42, 833–836. [Google Scholar]
- Sheikh, A.K.; Ahmad, M.; Ali, Z. Some remarks on the hazard functions of the inverted distributions. Reliab. Eng. 1987, 19, 255–261. [Google Scholar] [CrossRef]
- Hassan, A.; Nassr, G. The inverse Weibull-generator of distributions: Properties and applications. J. Data Sci. 2018, 16, 723–742. [Google Scholar]
- Jamal, F.; Chesneau, C.; Elgarhy, M. Type II general inverse exponential family of distributions. J. Stat. Manag. Syst. 2019. [Google Scholar] [CrossRef]
- Jamal, F.; Nasir, M.A.; Ozel, G.; Elgarhy, M.; Khan, N.M. Generalized inverted Kumaraswamy generated family of distributions: Theory and applications. J. Appl. Stat. 2019, 46, 2927–2944. [Google Scholar] [CrossRef]
- Abid, S.H.; Al-Noor, N.H.; Boshi, M.A.A. On the generalized inverse Weibull distribution. AIP Conf. Proc. 2019, 2086, 030002. [Google Scholar]
- Abid, A.H.; Abdulrazak, R.K. [0,1] truncated Fréchet-G generator of distributions. Appl. Math. 2017, 7, 51–66. [Google Scholar]
- Jamal, F.; Bakouch, H.S.; Nasir, M.A. A Truncated General-G Class of Distributions with Application to Truncated Burr-G Family. 2019. Available online: https://hal.archives-ouvertes.fr/hal-01956892/document (accessed on 15 March 2020).
- Aldahlan, M.A.; Jamal, F.; Chesneau, C.; Elgarhy, M.; Elbatal, I. The truncated Cauchy power family of distributions with inference and applications. Entropy 2019, 22, 346. [Google Scholar] [CrossRef]
- Bantan, R.A.R.; Jamal, F.; Chesneau, C.; Elgarhy, M. Truncated inverted Kumaraswamy generated family of distributions with applications. Entropy 2019, 21, 1089. [Google Scholar] [CrossRef]
- Aldahlan, M.A. Type II truncated Fréchet generated family of distributions. Int. J. Math. Appl. 2019, 7, 221–228. [Google Scholar]
- Murthy, D.P.; Xie, M.; Jiang, R. Weibull Models; John Wiley and Sons: New York, NY, USA, 2004. [Google Scholar]
- Lai, C.-D.; Murthy, D.N.; Xie, M. Weibull Distributions and Their Applications; Springer: Berlin, Germany, 2006; pp. 63–78. [Google Scholar]
- Shahzad, M.N.; Ullah, E.; Hussanan, A. Beta exponentiated modified Weibull distribution: Properties and application. Symmetry 2019, 11, 781. [Google Scholar] [CrossRef]
- De Gusmo, F.R.; Ortega, E.M.; Cordeiro, G.M. The generalized inverse Weibull distribution. Stat. Pap. 2011, 52, 591–619. [Google Scholar] [CrossRef]
- Zhang, T.; Xie, M. On the upper truncated Weibull distribution and its reliability implications. Reliab. Eng. Syst. Saf. 2011, 96, 194–200. [Google Scholar] [CrossRef]
- Aydin, D. The doubly-truncated exponentiated inverse Weibull distribution. Anadolu Univ. J. Sci. Technol. B-Theor. Sci. 2018, 6, 55–74. [Google Scholar] [CrossRef][Green Version]
- Lehmann, E.L. The power of rank tests. Ann. Math. Stat. 1953, 24, 23–43. [Google Scholar] [CrossRef]
- Tahir, M.H.; Cordeiro, G.M.; Alizadeh, M.; Mansoor, M.; Zubair, M.; Hamedani, G.G. The odd generalized exponential family of distributions with applications. J. Stat. Distrib. Appl. 2015, 2, 1–28. [Google Scholar] [CrossRef]
- Merovci, F.; Alizadeh, M.; Yousof, H.M.; Hamedani, G.G. The exponentiated transmuted-G family of distributions: Theory and applications. Commun. Stat.-Theory Methods 2017, 46, 10800–10822. [Google Scholar] [CrossRef]
- Bantan, R.A.R.; Jamal, F.; Chesneau, C.; Elgarhy, M. Type II Power Topp-Leone Generated Family of Distributions with Statistical Inference and Applications. Symmetry 2020, 12, 75. [Google Scholar] [CrossRef]
- Aldahlan, M.A.; Jamal, F.; Chesneau, C.; Elbatal, I.; Elgarhy, M. Exponentiated power generalized Weibull power series family of distributions: Properties, estimation and applications. PLoS ONE 2020, 15, e0230004. [Google Scholar] [CrossRef]
- Gómez-Déniz, E.; Iriarte, Y.A.; Calderín-Ojeda, E.; Gómez, H.W. Modified power-symmetric distribution. Symmetry 2019, 11, 1410. [Google Scholar] [CrossRef]
- Prasetyo, R.B.; Kuswanto, H.; Iriawan, N.; Ulama, B.S.S. Binomial regression models with a flexible generalized logit link function. Symmetry 2020, 12, 221. [Google Scholar] [CrossRef]
- Klein, J.P.; Moeschberger, M.L. Survival Analysis: Techniques for Censored and Truncated Data, 2nd ed.; Springer: Berlin, Germany, 2003. [Google Scholar]
- Kenney, J.F.; Keeping, E.S. Mathematics of Statistics, 3rd ed.; Pt. 1; Van Nostrand: Princeton, NJ, USA, 1962. [Google Scholar]
- Moors, J.J.A. A quantile alternative for kurtosis. J. R. Stat. Soc. Ser. 1988, 37, 25–32. [Google Scholar] [CrossRef]
- Green Wood, J.A.; Landwehr, J.M.; Matalas, N.C.; Walti, J.R. Probability weighted moments; Definition and relation to parameters of distribution expressible in inverse form. Water Resour. Res. 1979, 3, 281–292. [Google Scholar]
- Furrer, R.; Naveau, P. Probability weighted moments properties for small samples. Stat. Probab. Lett. 2007, 70, 190–195. [Google Scholar] [CrossRef]
- Arnold, B.C.; Balakrishnan, N.; Nagaraja, H.N. A First Course in Order Statistics; John Wiley and Sons: New York, NY, USA, 1992. [Google Scholar]
- Khaleel, M.; Ibrahim, N.; Shitan, M.; Merovci, F.; Rehman, E. Beta Burr type-x with application to rainfall data. Malays. J. Math. Sci. 2017, 11, 73–86. [Google Scholar]
- Hosseini, B.; Afshari, M.; Alizadeh, M. The generalized odd gamma-G family of distributions: Properties and applications. Austrian J. Stat. 2018, 47, 69–89. [Google Scholar] [CrossRef]
- Amini, M.; MirMostafaee, S.M.T.K.; Ahmadi, J. Log-gamma-generated families of distributions. Statistics 2014, 48, 913–932. [Google Scholar] [CrossRef]
- Mead, M.E.; Abd-Eltawab, A.R. A note on Kumaraswamy Fréchet distribution. Aust. J. Basic Appl. Sci. 2014, 8, 294–300. [Google Scholar]
- Nadarajah, S.; Gupta, A.K. The beta Fréchet distribution. Far East J. Theor. Stat. 2004, 14, 15–24. [Google Scholar]
- Nadarajah, S.; Kotz, S. The Exponentiated Fréchet Distribution, InterStat. Available online: http://interstat.statjournals.net/YEAR/2003/articles/0312002.pdf (accessed on 15 March 2020).
- Weisberg, S. Applied Linear Regression; John Wiley and Sons: New York, NY, USA, 2005; Volume 528. [Google Scholar]
| ETIW-G | Baseline Distribution | Support | |||
|---|---|---|---|---|---|
| ETIWU | Uniform | ||||
| ETIWP | Power | ||||
| ETIWD | Dagum | ||||
| ETIWLi | Lindley | ||||
| ETIWHC | Half Cauchy | ||||
| ETIWG | Gamma | ||||
| ETIWLo | Logistic | ||||
| ETIWN | Normal |
| n | Set1 | Set2 | Set3 | |||
|---|---|---|---|---|---|---|
| MLE | MSE | MLE | MSE | MLE | MSE | |
| 50 | 0.747 | 0.159 | 1.028 | 0.734 | 1.377 | 1.031 |
| 0.507 | 0.065 | 1.729 | 1.568 | 1.704 | 1.279 | |
| 0.729 | 0.436 | 0.768 | 0.128 | 0.678 | 0.059 | |
| 0.707 | 0.093 | 2.711 | 2.992 | 3.322 | 2.939 | |
| 100 | 0.737 | 0.153 | 1.318 | 0.599 | 1.463 | 0.825 |
| 0.502 | 0.027 | 1.522 | 0.631 | 1.393 | 0.449 | |
| 0.662 | 0.227 | 0.698 | 0.073 | 0.641 | 0.034 | |
| 0.662 | 0.046 | 2.227 | 0.896 | 3.204 | 2.127 | |
| 200 | 0.718 | 0.124 | 1.31 | 0.29 | 1.6 | 0.501 |
| 0.487 | 0.014 | 1.241 | 0.361 | 1.229 | 0.268 | |
| 0.66 | 0.22 | 0.636 | 0.036 | 0.605 | 0.019 | |
| 0.662 | 0.036 | 2.204 | 0.827 | 3.075 | 1.481 | |
| 500 | 0.786 | 0.12 | 1.394 | 0.208 | 1.644 | 0.344 |
| 0.475 | 0.0063 | 1.184 | 0.185 | 1.209 | 0.149 | |
| 0.475 | 0.09 | 0.611 | 0.02 | 0.598 | 0.013 | |
| 0.645 | 0.026 | 2.168 | 0.55 | 2.943 | 1.037 | |
| 1000 | 0.761 | 0.087 | 1.394 | 0.125 | 1.673 | 0.241 |
| 0.464 | 0.0042 | 1.15 | 0.165 | 1.335 | 0.125 | |
| 0.449 | 0.03 | 0.601 | 0.015 | 0.584 | 0.0084 | |
| 0.651 | 0.025 | 2.152 | 0.499 | 2.948 | 0.975 | |
| n | Set4 | Set5 | Set6 | |||
|---|---|---|---|---|---|---|
| MLE | MSE | MLE | MSE | MLE | MSE | |
| 50 | 1.016 | 0.934 | 1.138 | 0.087 | 1.272 | 1.642 |
| 1.299 | 2.379 | 0.438 | 0.054 | 1.76 | 3.227 | |
| 1.604 | 4.595 | 0.926 | 0.279 | 1.461 | 2.553 | |
| 1.2 | 0.391 | 0.93 | 0.413 | 1.309 | 0.637 | |
| 100 | 0.968 | 0.48 | 1.152 | 0.06 | 1.304 | 1.152 |
| 1.034 | 0.574 | 0.445 | 0.03 | 1.359 | 0.719 | |
| 1.146 | 1.367 | 0.927 | 0.244 | 1.097 | 0.919 | |
| 1.05 | 0.175 | 0.813 | 0.173 | 1.183 | 0.29 | |
| 200 | 0.985 | 0.398 | 1.249 | 0.042 | 1.477 | 1.021 |
| 0.908 | 0.184 | 0.455 | 0.019 | 1.221 | 0.45 | |
| 0.905 | 0.611 | 0.862 | 0.18 | 0.88 | 0.498 | |
| 1.01 | 0.108 | 0.756 | 0.1 | 1.102 | 0.196 | |
| 500 | 0.978 | 0.309 | 1.238 | 0.018 | 1.485 | 0.352 |
| 0.734 | 0.035 | 0.463 | 0.0075 | 0.994 | 0.136 | |
| 0.65 | 0.119 | 0.852 | 0.162 | 0.672 | 0.092 | |
| 0.937 | 0.074 | 0.713 | 0.054 | 1.096 | 0.131 | |
| 1000 | 0.907 | 0.158 | 1.229 | 0.011 | 1.511 | 0.109 |
| 0.686 | 0.024 | 0.465 | 0.0061 | 0.985 | 0.103 | |
| 0.57 | 0.033 | 0.815 | 0.13 | 0.617 | 0.046 | |
| 0.854 | 0.065 | 0.711 | 0.053 | 1.049 | 0.093 | |
| Model | a | b | ||||
|---|---|---|---|---|---|---|
| ETIWIW | 0.4443 | 477.2912 | 118.7575 | 0.6907 | - | - |
| (0.1084) | (8.6456) | (5.4174) | (0.0392) | - | - | |
| TIITFIW | - | 40.7759 | 62.1370 | 0.6356 | - | - |
| - | (7.9297) | (1.14315) | (0.0982) | - | - | |
| LGFr | 0.2832 | 23.0128 | 21.4924 | 1.3365 | - | - |
| (0.0413) | (7.8511) | (2.2458) | (1.1915) | - | - | |
| GOFr | - | - | 13.0778 | 4.6917 | 0.1739 | 1.1748 |
| - | - | (9.1451) | (3.4160) | (0.8502) | (0.3630) | |
| KwFr | 5.2239 | 554.6118 | 9.8825 | 0.5019 | - | - |
| (36.8518) | (22.0773) | (38.8463) | (0.0927) | - | - | |
| BFr | - | - | 71.1502 | 259.1749 | 74.9748 | 0.1685 |
| - | - | (12.1141) | (30.5647) | (1.0465) | (3.1490) | |
| EFr | - | - | 1.6108 | 1.9444 | 7.9293 | - |
| - | - | (67.4174) | (1.0673) | (1.0274) | - |
| Model | AIC | W* | A* | K-S | p-Value | |
|---|---|---|---|---|---|---|
| ETIWIW | 80.8218 | 169.6438 | 0.0540 | 0.4239 | 0.1185 | 0.6276 |
| TIITFIW | 82.9131 | 171.8263 | 0.0905 | 0.6681 | 0.1274 | 0.5340 |
| LGFr | 88.9168 | 185.8337 | 0.2372 | 1.5496 | 0.1820 | 0.1412 |
| GOFr | 87.8787 | 183.7575 | 0.2201 | 1.4468 | 0.1353 | 0.4562 |
| KwFr | 86.1506 | 180.3014 | 0.1710 | 1.1615 | 0.1218 | 0.5928 |
| BFr | 91.2658 | 190.5317 | 0.3161 | 1.9815 | 0.1523 | 0.3109 |
| EFr | 101.5918 | 209.1836 | 0.6067 | 3.4796 | 0.2438 | 0.0172 |
| Model | a | b | ||||
|---|---|---|---|---|---|---|
| ETIWIW | 1.5665 | 0.0580 | 28.7074 | 16.2632 | - | - |
| (0.1228) | (0.0024) | (0.0290) | (0.0292) | - | - | |
| TIITFIW | - | 0.1709 | 34.8247 | 5.9024 | - | - |
| - | (0.0755) | (2.5283) | (2.2193) | - | - | |
| LGFr | 6.6285 | 2.9542 | 21.9999 | 2.0724 | - | - |
| (2.0456) | (2.0521) | (1.2151) | (0.1112) | - | - | |
| GOFr | - | - | 4.8711 | 12.9533 | 0.0626 | 0.6005 |
| - | - | (2.9411) | (1.1160) | (0.2531) | (0.0680) | |
| KwFr | 16.8895 | 486.2870 | 5.3100 | 0.3782 | - | - |
| (4.0633) | (2.0475) | (2.1463) | (0.0058) | - | - | |
| BFr | - | - | 122.7997 | 230.4647 | 88.7582 | 0.1570 |
| - | - | (2.1441) | (30.1642) | (7.0361) | (0.1290) | |
| EFr | - | - | 11.0292 | 2.6174 | 53.4457 | - |
| - | - | (6.0124) | (0.1432) | (5.0211) | - |
| Model | AIC | W* | A* | K-S | p-Value | |
|---|---|---|---|---|---|---|
| ETIWIW | 946.3521 | 1900.7040 | 0.0838 | 0.6006 | 0.0645 | 0.3646 |
| TIITFIW | 947.5516 | 1901.1030 | 0.0905 | 0.6789 | 0.0663 | 0.3366 |
| LGFr | 953.4254 | 1914.8510 | 0.1722 | 1.1660 | 0.0722 | 0.2419 |
| GOFr | 959.3028 | 1926.6060 | 0.3388 | 1.9968 | 0.0836 | 0.1181 |
| KwFr | 963.5626 | 1935.120 | 0.4373 | 2.5605 | 0.0921 | 0.0645 |
| BFr | 955.9227 | 1919.8450 | 0.2539 | 1.5299 | 0.0714 | 0.2542 |
| EFr | 955.8263 | 1917.6530 | 0.1998 | 1.4661 | 0.0706 | 0.2660 |
| Model | a | b | ||||
|---|---|---|---|---|---|---|
| ETIWIW | 2.5869 | 0.1048 | 19.1715 | 21.3741 | - | - |
| (0.16813) | (0.4131) | (4.5844) | (3.7627) | - | - | |
| TIITFIW | - | 0.4384 | 24.7133 | 7.0868 | - | - |
| - | (0.7951) | (6.0332) | (8.6529) | - | - | |
| LGFr | 30.2455 | 58.6674 | 26.2278 | 0.8824 | - | - |
| (6.9793) | (5.6592) | (1.4252) | (0.1689) | - | - | |
| GOFr | - | - | 11.3884 | 26.4729 | 0.1791 | 1.1221 |
| - | - | (0.2455) | (2.6733) | (0.0022) | (0.1192) | |
| KwFr | 23.4933 | 47.1455 | 9.9122 | 1.5850 | - | - |
| (2.2203) | (1.1471) | (2.1669) | (0.2254) | - | - | |
| BFr | - | - | 16.4844 | 92.6404 | 72.7783 | 0.6991 |
| - | - | (5.9942) | (23.1349) | (8.9369) | (0.0223) | |
| EFr | - | - | 18.7691 | 6.0666 | 8.2824 | - |
| - | - | (864.5581) | (1.1360) | (4.45652) | - |
| Model | AIC | W* | A* | K-S | p-Value | |
|---|---|---|---|---|---|---|
| ETIWIW | 48.3270 | 104.6542 | 0.0516 | 0.3559 | 0.1219 | 0.9438 |
| TIITFIW | 49.6099 | 105.2198 | 0.0532 | 0.3646 | 0.1433 | 0.8974 |
| LGFr | 48.4793 | 104.9587 | 0.0523 | 0.3652 | 0.1337 | 0.9369 |
| GOFr | 48.3591 | 104.7184 | 0.0545 | 0.3694 | 0.1382 | 0.9199 |
| KwFr | 48.3594 | 104.7189 | 0.0559 | 0.3751 | 0.1451 | 0.8891 |
| BFr | 48.4446 | 104.8893 | 0.0524 | 0.3639 | 0.1345 | 0.9341 |
| EFr | 49.4775 | 104.9550 | 0.0753 | 0.5013 | 0.1686 | 0.7533 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Almarashi, A.M.; Elgarhy, M.; Jamal, F.; Chesneau, C. The Exponentiated Truncated Inverse Weibull-Generated Family of Distributions with Applications. Symmetry 2020, 12, 650. https://doi.org/10.3390/sym12040650
Almarashi AM, Elgarhy M, Jamal F, Chesneau C. The Exponentiated Truncated Inverse Weibull-Generated Family of Distributions with Applications. Symmetry. 2020; 12(4):650. https://doi.org/10.3390/sym12040650
Chicago/Turabian StyleAlmarashi, Abdullah M., Mohammed Elgarhy, Farrukh Jamal, and Christophe Chesneau. 2020. "The Exponentiated Truncated Inverse Weibull-Generated Family of Distributions with Applications" Symmetry 12, no. 4: 650. https://doi.org/10.3390/sym12040650
APA StyleAlmarashi, A. M., Elgarhy, M., Jamal, F., & Chesneau, C. (2020). The Exponentiated Truncated Inverse Weibull-Generated Family of Distributions with Applications. Symmetry, 12(4), 650. https://doi.org/10.3390/sym12040650







