Relaxation of the Radio-Frequency Linewidth for Coherent-Optical Orthogonal Frequency-Division Multiplexing Schemes by Employing the Improved Extreme Learning Machine
Abstract
1. Introduction
- We propose a modified ELM under supervised learning for maximizing the system performance (the BER minimization) of a phase-uncorrelated OFDM signal in the optical domain based on the adoption of the pilot subcarriers as training samples, as well as the consideration of the regularization parameter in the learning stage.
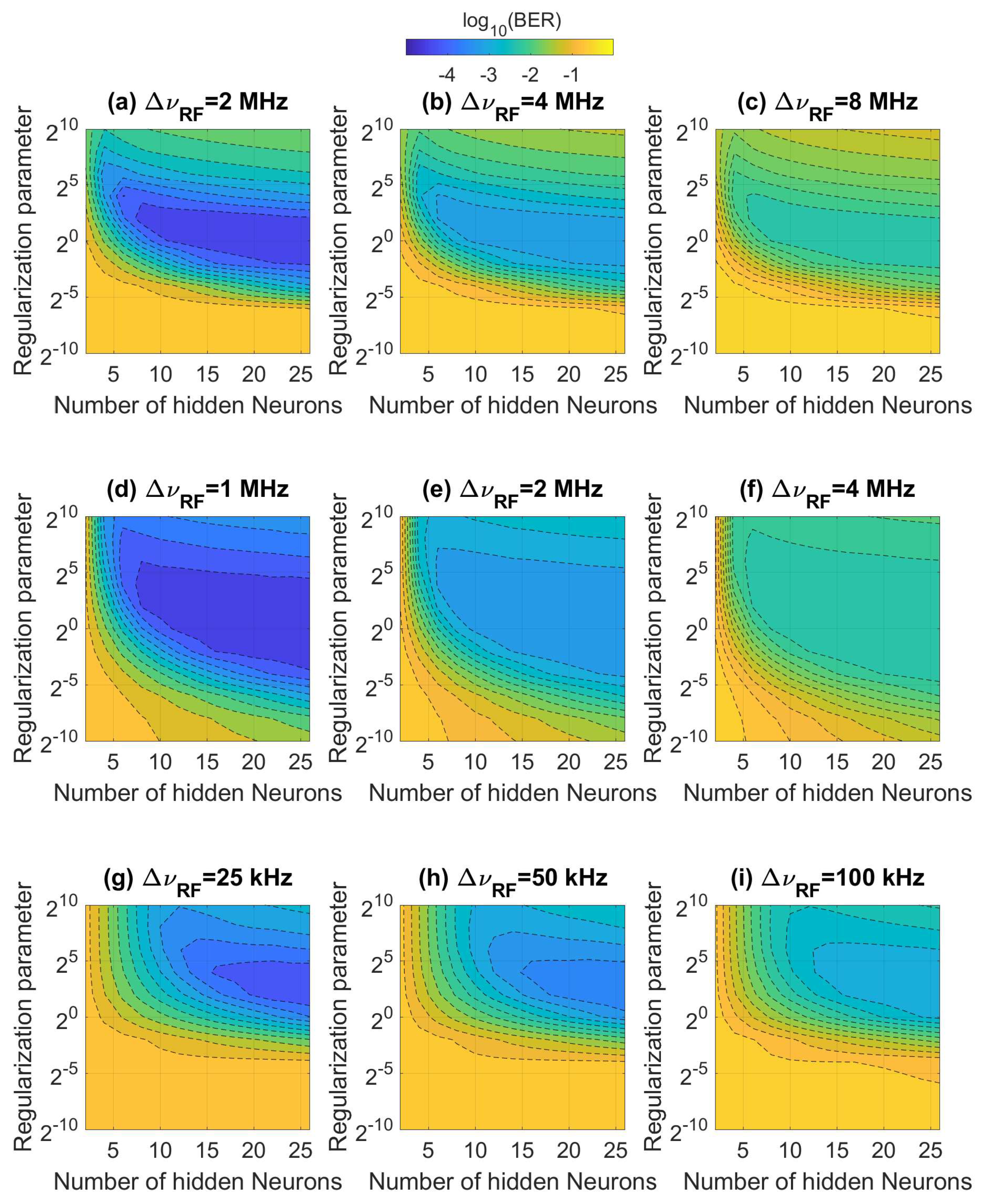
- Taking into account the RF phase error as well as the subcarrier modulation format, we find the sub-optimal ELM parameters (the number of hidden nodes, penalty coefficient, and activation function) that yield the best BER via extensive simulations. This result is explained by the evaluation of the error vector magnitude (EVM) metric in the training as well as testing steps, which can properly quantify the root mean square error for complex numbers in the telecommunication industry.
- We verify that when the Moore–Penrose generalized inverse of the hidden layer output matrix takes into account the regularization parameter, the ELM significantly improves in terms of stability and precision. As a result, the distortion induced by the laser oscillators is less within the constellation symbols.
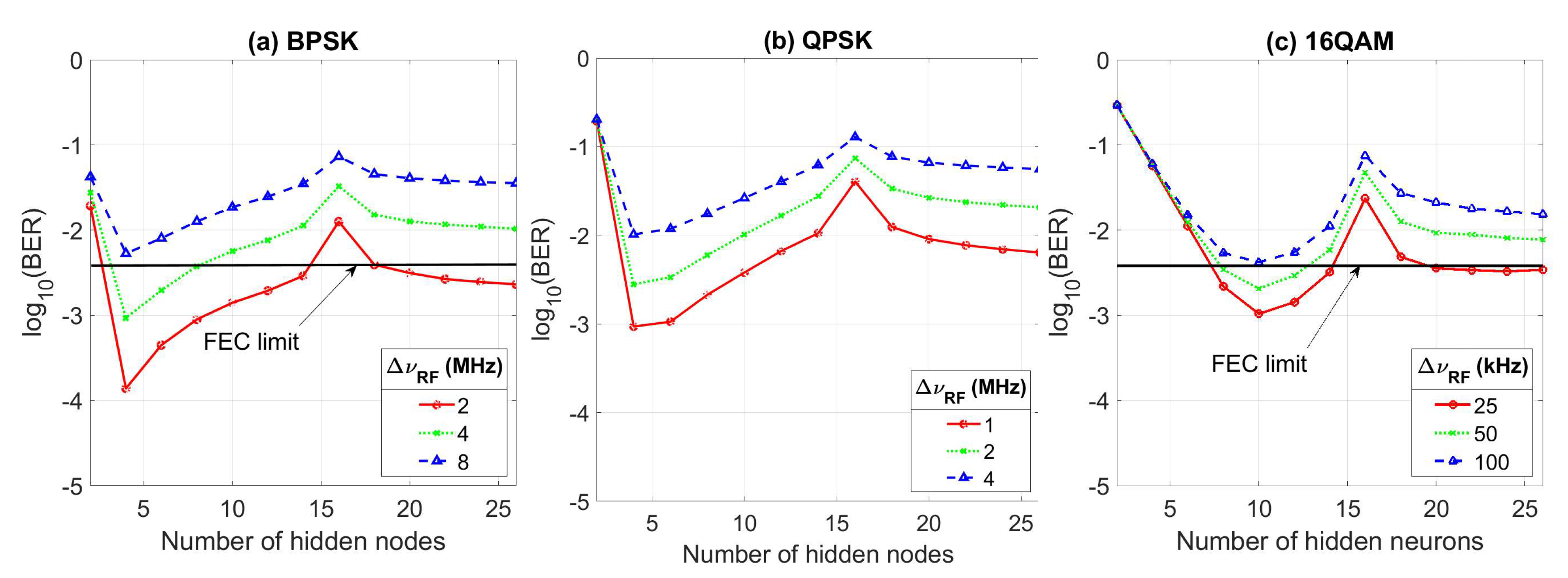
- For several signal to noise ratio (SNR) levels and RF-linewidth values, we respectively observe the superiority, and competitiveness of the novel ELM algorithm in terms of the BER metric among the benchmark PAE and a fully-real ELM, and the sophisticated ELM defined in the complex plane and non-effective bandwidth CPE compensator for binary phase-shift keying (BPSK) and QPSK modes.
2. Background
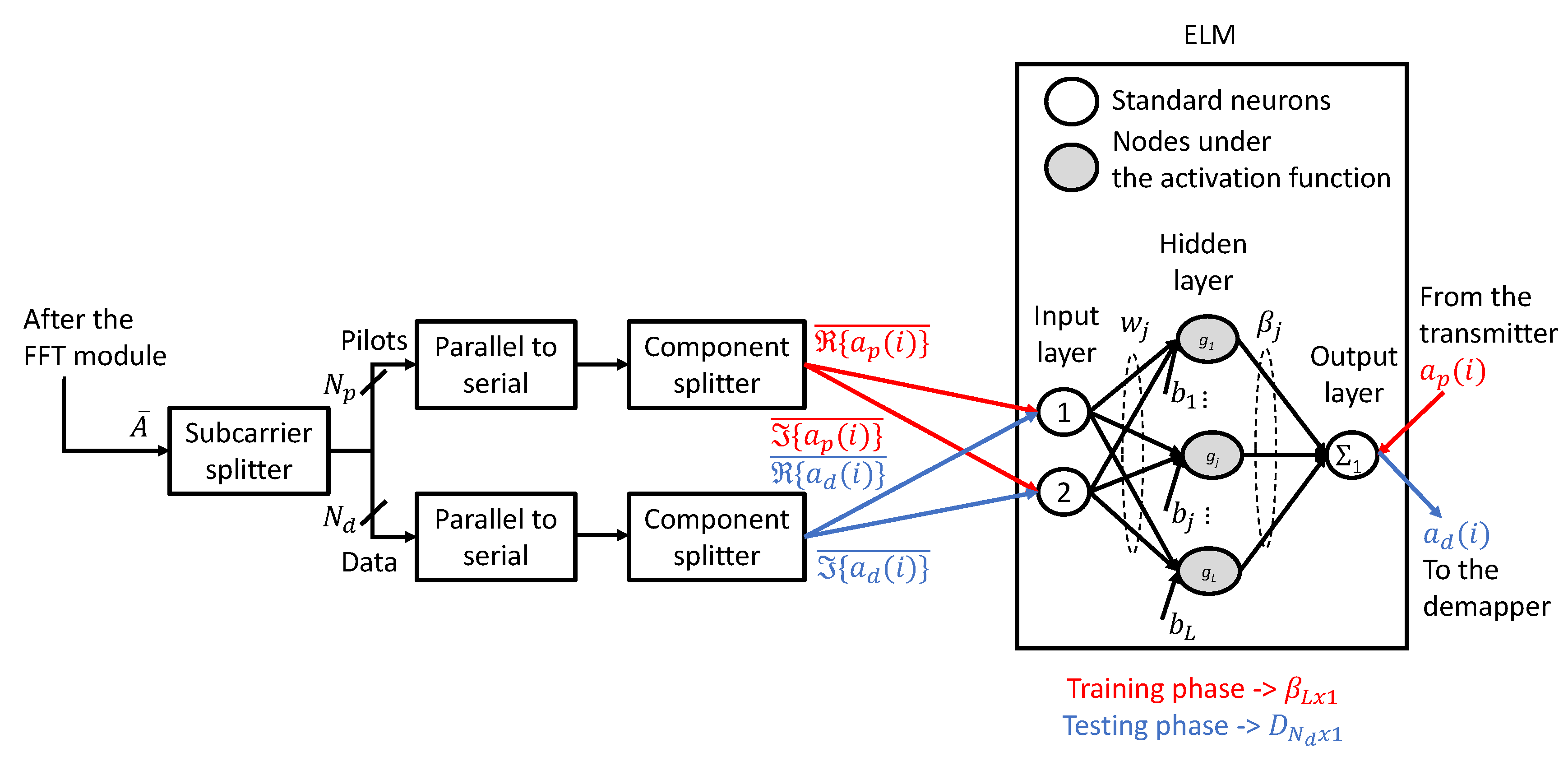
2.1. Extreme Learning Machine
- Setting the hidden neurons L, the activation function , and the regularization parameter C.
- Randomly choosing the input weights as well as biases .
- Finding the output layer weights via Equation (2), where N samples are known.
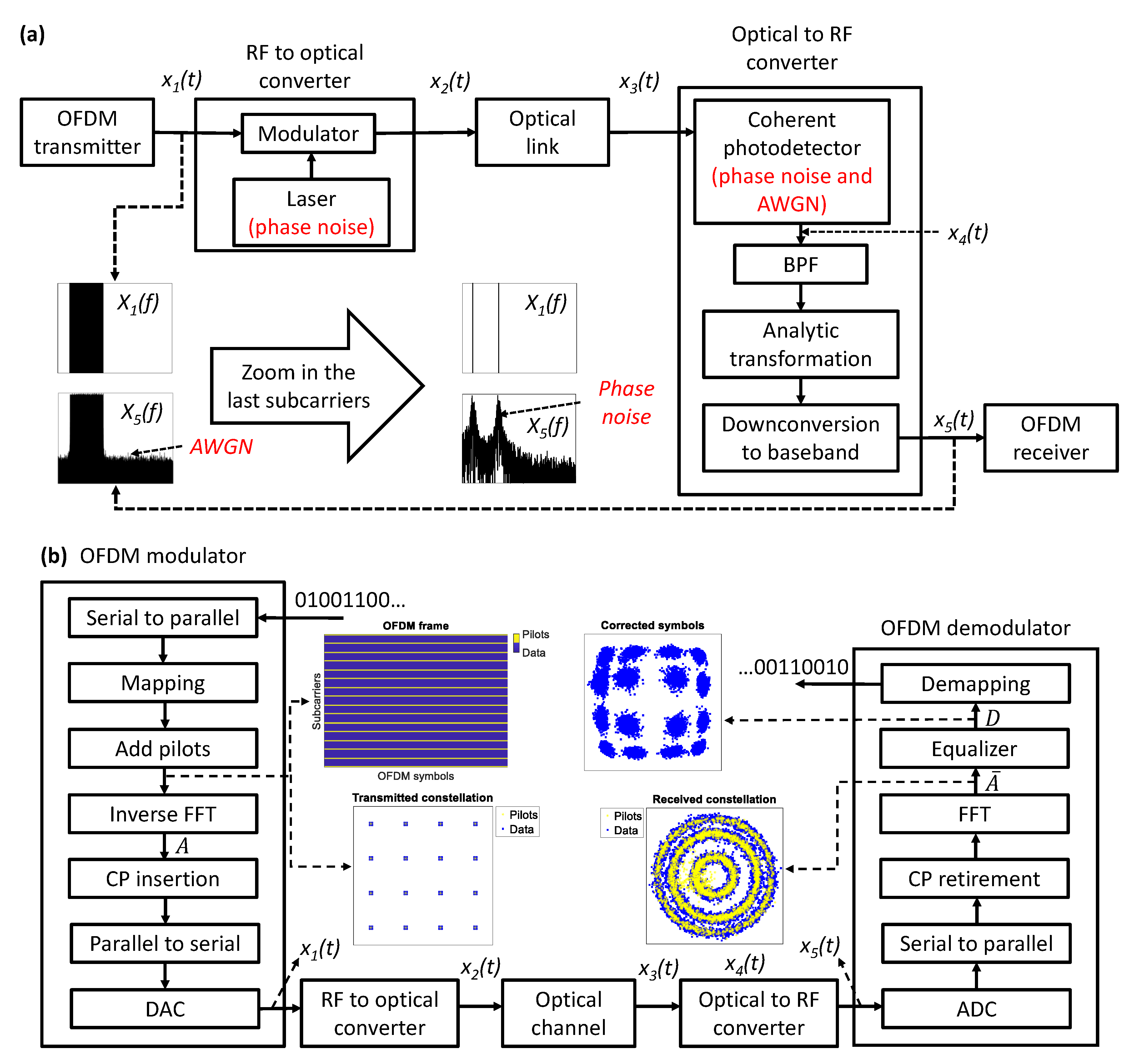
2.2. Coherent Optical OFDM Network
3. Proposed Extreme Learning Machine Algorithm for Laser Phase-Noise Reduction Purposes
4. Results and Discussion
4.1. Parameters’ Optimization of the Extreme Learning Machine
4.2. Performance Evaluation
4.3. Complexity Analysis
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| ADC | Analog-to-digital converter |
| AWGN | Additive white Gaussian noise |
| BER | Bit error rate |
| BPF | Band pass filter |
| BPSK | Binary phase shift keying |
| C-ELM | Extreme learning machine in the complex plane |
| CO | Coherent optical |
| COS | Cosine |
| CP | Cyclic prefix |
| CPE | Common phase error |
| DAC | Digital-to-analog converter |
| ELMs | Extreme learning machines |
| EVM | Error vector magnitude |
| FEC | Forward error correction |
| FFT | Fast Fourier transform |
| HL | Hard limit |
| HT | Hyperbolic tangent |
| ICI | Inter-carrier interference |
| OFDM | Orthogonal frequency division multiplexing |
| PAE | Pilot-assisted equalization |
| QAM | Quadrature amplitude modulation |
| QPSK | Quadrature phase-shift keying |
| RC | Real-complex |
| RF | Radio frequency |
| SIG | Sigmoid |
| SLFNs | Single-hidden layer feedforward networks |
| SNR | Signal to noise ratio |
| RB | Radial basis |
| R-ELM | Fully-real extreme learning machine |
| TB | Triangular basis |
References
- Wang, Y.; Wang, D.; Ma, J. On the Performance of coherent OFDM Systems in free-space optical communications. IEEE Photonics J. 2015, 7, 1–10. [Google Scholar] [CrossRef]
- Gonzalez-Guerrero, L.; Shams, H.; Fatadin, I.; Fice, M.J.; Naftaly, M.; Seeds, A.J.; Renaud, C.C. Single sideband signals for phase noise mitigation in wireless THz-over-fibre systems. J. Lightw. Technol. 2018, 36, 4527–4534. [Google Scholar] [CrossRef]
- Mathecken, P.; Riihonen, T.; Werner, S.; Wichman, R. Performance analysis of OFDM with Wiener phase noise and frequency selective fading channel. IEEE Trans. Commun. 2011, 59, 1321–1331. [Google Scholar] [CrossRef]
- Zabala-Blanco, D.; Campuzano, G.; Aldaya, I.; Castanon, G.; Vargas-Rosales, C. Impact of partial phase decorrelation on the performance of pilot-assisted millimeter-wave RoF-OFDM systems. Phys. Commun. 2018, 26, 106–115. [Google Scholar] [CrossRef]
- Garcia Armada, A.; Calvo Ramon, M. Rapid prototyping of a test modem for terrestrial broadcasting of digital television. IEEE Trans. Consum. Electron. 1997, 43, 1100–1109. [Google Scholar] [CrossRef]
- Ferreira, A.; Dias, B.; de Oliveira, J.A.; Alves, A.; Marconi, J.D.; Campuzano, G.; Pita, J.; Aldaya, I. Optimization of OFDM parameters for 10-Gbps long reach coherent PONs. In Proceedings of the 2019 21st International Conference on Transparent Optical Networks (ICTON), Angers, France, 9–13 July 2019; pp. 1–4. [Google Scholar] [CrossRef]
- Zabala-Blanco, D.; Azurdia-Meza, C.A.; Montejo-Sánchez, S.; Dehghan Firoozabadi, A. OFDM tolerance to additive white Gaussian and laser phase noises in optical heterodyning systems accompanied by the feasible pilot-assisted equalization. Opt. Rev. 2020. [Google Scholar] [CrossRef]
- Yi, X.; Shieh, W.; Ma, Y. Phase noise effects on high spectral efficiency coherent optical OFDM transmission. J. Lightw. Technol. 2008, 26, 1309–1316. [Google Scholar] [CrossRef]
- Randel, S.; Adhikari, S.; Jansen, S.L. Analysis of RF-pilot-based phase noise compensation for coherent optical OFDM systems. IEEE Photonics Technol. Lett. 2010, 22, 1288–1290. [Google Scholar] [CrossRef]
- Huang, G.B.; Zhu, Q.Y.; Siew, C.K. Extreme learning machine: Theory and applications. Neurocomputing 2006, 70, 489–501. [Google Scholar] [CrossRef]
- Chen, Z.X.; Zhu, H.Y.; Wang, Y.G. A modified extreme learning machine with sigmoidal activation functions. Neural Comput. Appl. 2013, 22, 541–550. [Google Scholar] [CrossRef]
- Luo, J.; Vong, C.; Wong, P. Sparse Bayesian extreme learning machine for multi-classification. IEEE Trans. Neural Netw. Learn. Syst. 2014, 25, 836–843. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Mei, K.; Zhang, X.; Ma, D.; Wei, J. Online extreme learning machine-based channel estimation and equalization for OFDM systems. IEEE Commun. Lett. 2019, 23, 1276–1279. [Google Scholar] [CrossRef]
- Luo, X.; Jiang, C.; Wang, W.; Xu, Y.; Wang, J.H.; Zhao, W. User behavior prediction in social networks using weighted extreme learning machine with distribution optimization. Future Gener. Comput. Syst. 2019, 93, 1023–1035. [Google Scholar] [CrossRef]
- Zhong, J.; Zhang, J.; Liang, J.; Wang, H. Multi-fault rapid diagnosis for wind turbine gearbox using sparse Bayesian extreme learning machine. IEEE Access 2019, 7, 773–781. [Google Scholar] [CrossRef]
- Kale, A.P.; Sonavane, S. PF-FELM: A robust PCA feature selection for fuzzy extreme learning machine. IEEE J. Sel. Top. Signal Process. 2018, 12, 1303–1312. [Google Scholar] [CrossRef]
- Shafiullah, M.; Abido, M.A.; Al-Hamouz, Z. Wavelet-based extreme learning machine for distribution grid fault location. IET Gener. Transm. Distrib. 2017, 11, 4256–4263. [Google Scholar] [CrossRef]
- Li, M.B.; Huang, G.B.; Saratchandran, P.; Sundararajan, N. Fully complex extreme learning machine. Neurocomputing 2005, 68, 306–314. [Google Scholar] [CrossRef]
- Huang, G.B.; Li, M.B.; Chen, L.; Siew, C.K. Incremental extreme learning machine with fully complex hidden nodes. Neurocomputing 2008, 71, 576–583. [Google Scholar] [CrossRef]
- Huang, G.; Huang, G.B.; Song, S.; You, K. Trends in extreme learning machines: A review. Neural Netw. 2015, 61, 32–48. [Google Scholar] [CrossRef]
- Muhammad, I.G.; Tepe, K.E.; Abdel-Raheem, E. QAM equalization and symbol detection in OFDM systems using extreme learning machine. Neural Comput. Appl. 2013, 22, 491–500. [Google Scholar] [CrossRef]
- Yang, L.; Zhao, Q.; Jing, Y. Channel equalization and detection with ELM-based regressors for OFDM systems. IEEE Commun. Lett. 2020, 24, 86–89. [Google Scholar] [CrossRef]
- Kaur, G.; Kaur, G. Performance analysis of Wilcoxon-based machine learning nonlinear equalizers for coherent optical OFDM. Opt. Quantum Electron. 2018, 50, 256. [Google Scholar] [CrossRef]
- Zabala-Blanco, D.; Mora, M.; Azurdia-Meza, C.A.; Dehghan Firoozabadi, A. Extreme learning machines to combat phase noise in RoF-OFDM schemes. Electronics 2019, 8, 921. [Google Scholar] [CrossRef]
- Michell, T. Machine Learning; McGraw-Hill: New York, NY, USA, 1997. [Google Scholar]
- Moustafa, M.M.A.; El-Ramly, S.H.A. Channel estimation and equalization using backpropagation neural networks in OFDM systems. In Proceedings of the IFIP International Conference on Wireless and Optical Communications Networks, Cairo, Egypt, 28–30 April 2009; pp. 1–4. [Google Scholar] [CrossRef]
- Friedman, J.H. Stochastic gradient boosting. Comput. Stat. Data Anal. 2002, 38, 367–378. [Google Scholar] [CrossRef]
- Shieh, W.; Bao, H.; Tang, Y. Coherent optical OFDM: Theory and design. Opt. Express 2008, 16, 841–859. [Google Scholar] [CrossRef] [PubMed]
- Mun, K.; Jung, S.; Kang, S.; Han, S. Channel equalization and phase noise compensation free DAPSK-OFDM transmission for Coherent PON System. IEEE Photonics J. 2017, 9, 1–9. [Google Scholar] [CrossRef]
- Peng, W. Analysis of laser phase noise effect in direct- detection optical OFDM transmission. J. Lightw. Technol. 2010, 28, 2526–2536. [Google Scholar] [CrossRef]
- Gallion, P.; Mendieta, F.J.; Leconte, R. Single-frequency laser phase-noise limitation in single-mode optical-fiber coherent-detection systems with correlated fields. J. Opt. Soc. Am. 1982, 72, 1167–1170. [Google Scholar] [CrossRef]
- Agrawal, G.P. Fiber-Optic Communication Systems; John Wiley & Sons: Hoboken, NJ, USA, 2012; Volume 222. [Google Scholar]
- Yi, X.; Shieh, W.; Tang, Y. Phase estimation for coherent optical OFDM. IEEE Photonics Technol. Lett. 2007, 19, 919–921. [Google Scholar] [CrossRef]
- Lowery, A.J.; Du, L.B. Optical orthogonal division multiplexing for long haul optical communications: A review of the first five years. Opt. Fiber Technol. 2011, 17, 421–438. [Google Scholar] [CrossRef]
- Jansen, S.L.; Morita, I.; Schenk, T.C.; Tanaka, H. Long-haul transmission of 16 × 52.5 Gbits/s polarization-division- multiplexed OFDM enabled by MIMO processing (Invited). J. Opt. Netw. 2008, 7, 173–182. [Google Scholar] [CrossRef]
- Agrawal, G.P. Nonlinear Fiber Optics; Elsevier: Amsterdam, The Netherlands, 2015; Volume 648. [Google Scholar]
- Zhang, L.; Ming, Y.; Li, J. Suppression of laser phase noise in direct-detection optical OFDM transmission using phase-conjugated pilots. Opt. Commun. 2017, 403, 197–204. [Google Scholar] [CrossRef]
- Mandelli, S.; Gatto, A.; Magarini, M.; Boffi, P.; Martelli, P.; Pecorino, S.; Spalvieri, A. Phase noise impact on directly detected optical OFDM transmission in uncompensated links. In Proceedings of the 18th International Conference on Transparent Optical Networks (ICTON), Trento, Italy, 10–14 July 2016; pp. 1–4. [Google Scholar] [CrossRef]
- Hanzo, L.; Munster, M.; Choi, B.; Keller, T. OFDM and MC-CDMA for Broadband Multi-User Communications, WLANs and Broadcasting; John Wiley & Sons: Hoboken, NJ, USA, 2005. [Google Scholar] [CrossRef]
- Zhu, J.; Omomukuyo, O.; Venkatesan, R.; Li, C.; Dobre, O.A. RF-pilot phase noise compensation for long-haul coherent optical OFDM systems. In Proceedings of the IEEE 14th Canadian Workshop on Information Theory (CWIT), St. John’s, NL, Canada, 14 September 2015; pp. 127–130. [Google Scholar] [CrossRef]
- Huang, G.; Song, S.; Gupta, J.N.D.; Wu, C. Semi-supervised and unsupervised extreme learning machines. IEEE Trans. Cybern. 2014, 44, 2405–2417. [Google Scholar] [CrossRef] [PubMed]
- Ma, J.; Wen, Y.; Yang, L. Lagrangian supervised and semi-supervised extreme learning machine. Appl. Intell. 2019, 49, 303–318. [Google Scholar] [CrossRef]
- Wei, C.; Lin, C.; Huang, H.; Liang, W.; Chi, S. Estimation and suppression of dispersion-induced phase noise in W-band direct-detection OFDM radio-over-fiber systems. J. Lightw. Technol. 2014, 32, 3874–3884. [Google Scholar] [CrossRef]
- Guimaraes, D.A. Digital Transmission: A Simulation-Aided Introduction With VISSIM/COMM; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar] [CrossRef]
- Freiberger, K.; Enzinger, H.; Vogel, C. A noise power ratio measurement method for accurate estimation of the error vector magnitude. IEEE Trans. Microw. Theory Tech. 2017, 65, 1632–1645. [Google Scholar] [CrossRef]
- Wu, K.; Ren, G.; Wang, Q. Error vector magnitude analysis of uplink multiuser OFDMA and SC-OFDMA systems in the presence of nonlinear distortion. IEEE Commun. Lett. 2017, 21, 172–175. [Google Scholar] [CrossRef]
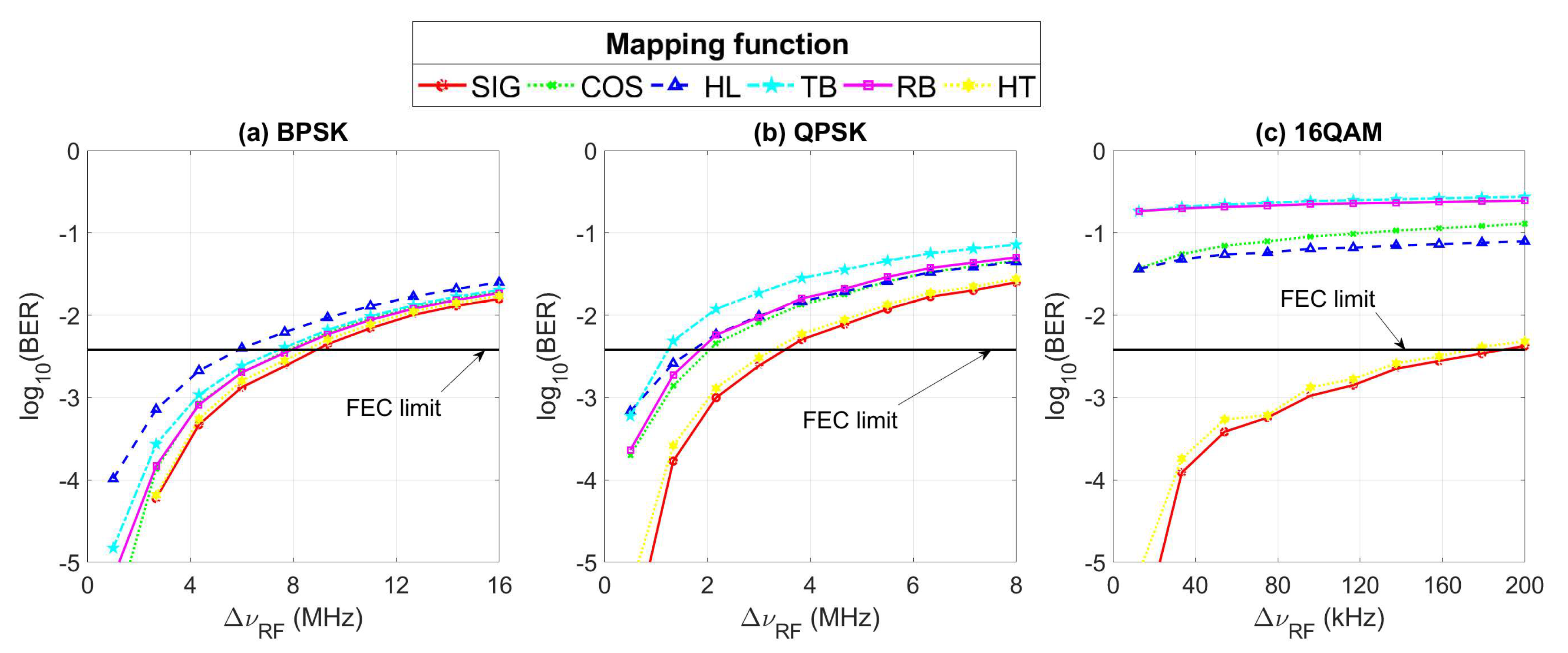

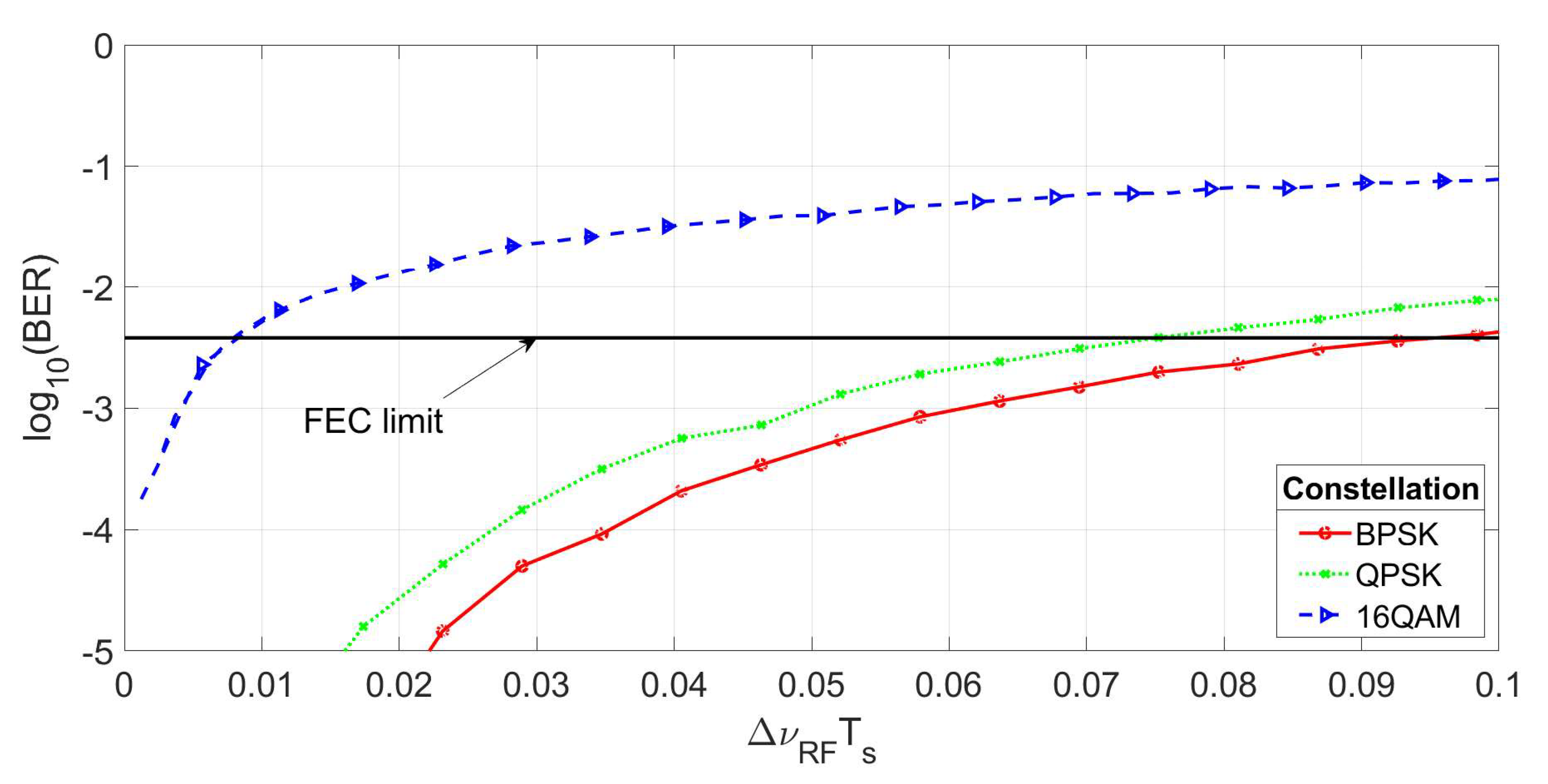
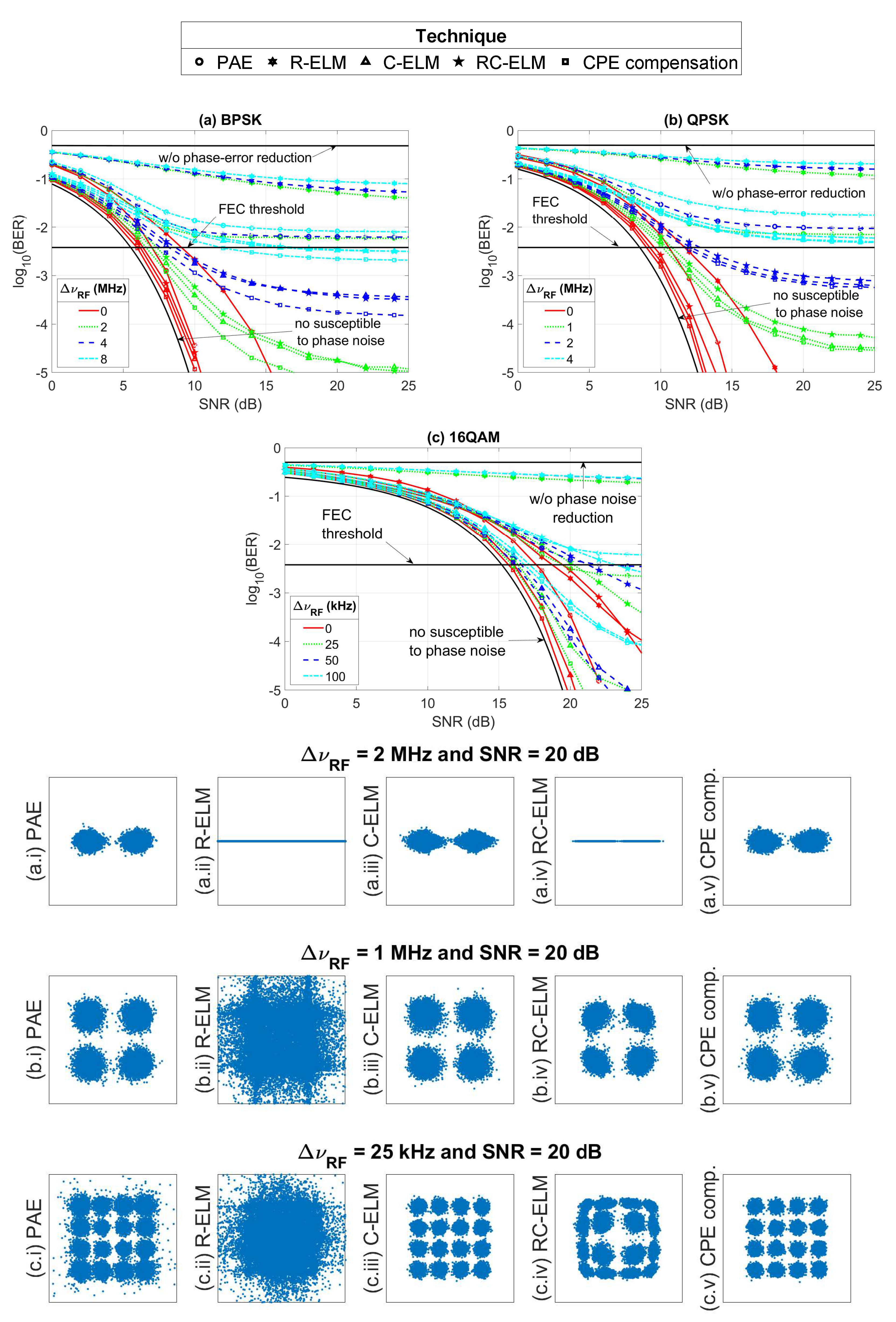
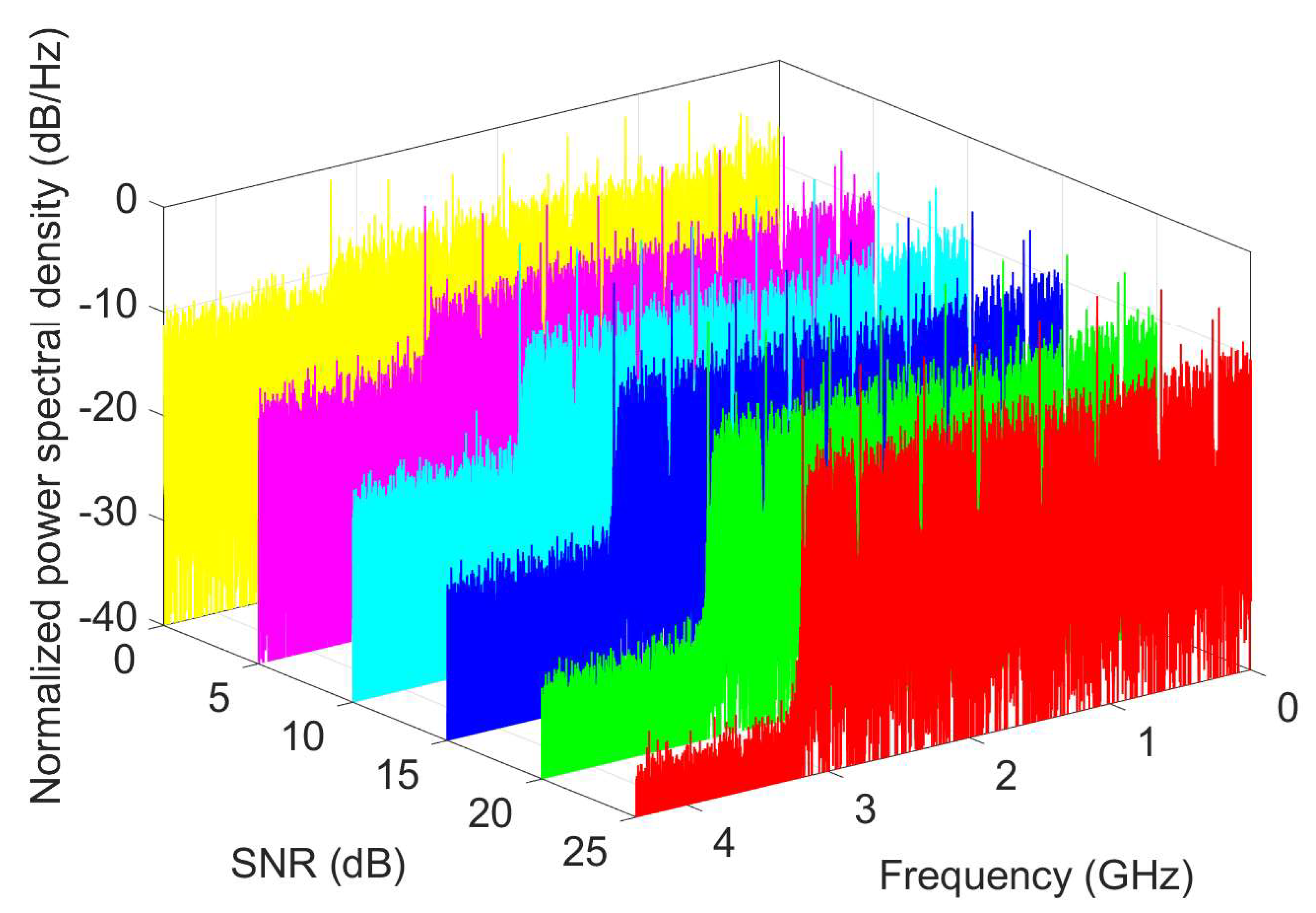
| Function | |
| Sigmoid (SIG) | |
| Cosine (COS) | |
| Hard limit (HL) | |
| Triangular basis (TB) | max |
| Radial basis (RB) | |
| Hyperbolic tangent (HT) |
| Parameter | Value |
|---|---|
| Subcarrier modulation format | BPSK, QPSK, and 16QAM |
| Bit rate | 10 Gbps |
| Number of data | 112 |
| Number of pilots | 16 |
| FFT size | 128 |
| CP length | 1/10 |
| Sample rate | 100 Gsps |
| Number of bits |
| Technique | Training Time | Testing Time | Total Time |
|---|---|---|---|
| PAE | - | - | |
| R-ELM | |||
| C-ELM | |||
| RC-ELCM | |||
| CPE compensation | - | - |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zabala-Blanco, D.; Mora, M.; Azurdia-Meza, C.A.; Dehghan Firoozabadi, A.; Palacios Játiva, P.; Soto, I. Relaxation of the Radio-Frequency Linewidth for Coherent-Optical Orthogonal Frequency-Division Multiplexing Schemes by Employing the Improved Extreme Learning Machine. Symmetry 2020, 12, 632. https://doi.org/10.3390/sym12040632
Zabala-Blanco D, Mora M, Azurdia-Meza CA, Dehghan Firoozabadi A, Palacios Játiva P, Soto I. Relaxation of the Radio-Frequency Linewidth for Coherent-Optical Orthogonal Frequency-Division Multiplexing Schemes by Employing the Improved Extreme Learning Machine. Symmetry. 2020; 12(4):632. https://doi.org/10.3390/sym12040632
Chicago/Turabian StyleZabala-Blanco, David, Marco Mora, Cesar A. Azurdia-Meza, Ali Dehghan Firoozabadi, Pablo Palacios Játiva, and Ismael Soto. 2020. "Relaxation of the Radio-Frequency Linewidth for Coherent-Optical Orthogonal Frequency-Division Multiplexing Schemes by Employing the Improved Extreme Learning Machine" Symmetry 12, no. 4: 632. https://doi.org/10.3390/sym12040632
APA StyleZabala-Blanco, D., Mora, M., Azurdia-Meza, C. A., Dehghan Firoozabadi, A., Palacios Játiva, P., & Soto, I. (2020). Relaxation of the Radio-Frequency Linewidth for Coherent-Optical Orthogonal Frequency-Division Multiplexing Schemes by Employing the Improved Extreme Learning Machine. Symmetry, 12(4), 632. https://doi.org/10.3390/sym12040632








