Abstract
In this paper, we study such combinatorial objects as labeled binary trees of size n with m ascents on the left branch and labeled Dyck n-paths with m ascents on return steps. For these combinatorial objects, we present the relation of the generated number triangle to Catalan’s and Euler’s triangles. On the basis of properties of Catalan’s and Euler’s triangles, we obtain an explicit formula that counts the total number of such combinatorial objects and a bivariate generating function. Combining the properties of these two number triangles allows us to obtain different combinatorial objects that may have a symmetry, for example, in their form or in their formulas.
Keywords:
number triangle; labeled binary tree; labeled Dyck path; Euler–Catalan’s triangle; generating function MSC:
11Y55; 05A15; 05C05
1. Introduction
Combinatorial objects such as permutations, combinations, partitions, graphs, trees, paths, etc. play an important role in mathematics and computer science and also have many applications in practice. Knuth [1] gave an overview of the formation and development of the direction related to designing combinatorial algorithms. In this field of mathematics, the following tasks are distinguished: enumerating, listing, and generating combinatorial objects.
Sometimes combinatorial sets can be described by using number triangles, for example, for their enumerating (in this case, an element of a number triangle shows the total number of objects in the corresponding combinatorial set , i.e., where is the cardinality of the combinatorial set ). A number triangle is a doubly-indexed sequence in which the length of each row corresponds to the index of the row. There are many well-known number triangles such as Pascal’s triangle, Catalan’s triangle, Euler’s triangles, Stirling’s triangles, Narayana’s triangle, etc., whose elements have a whole set of combinatorial interpretations [2].
To define a number triangle, it is necessary to specify the rules for generating elements of this triangle. For example, it can be some expression for in the form of an explicit formula or a recurrence relation. It can also be an expression of a bivariate generating function:
Generating functions are a powerful tool for solving problems in many fields of mathematics and they can also be applied for studying combinatorial sets, especially for their enumeration. Some examples of using generating functions for solving this problem can be found in [3,4,5,6,7]. In addition, describing the properties of combinatorial objects with the help of generating functions, it is often possible to find a relationship with special numbers [8,9,10,11,12].
In this paper, we study labeled binary trees with ascents on the left branch and labeled Dyck paths with ascents on return steps. For these combinatorial objects, we obtain an explicit formula that counts the total number of such objects and a bivariate generating function. In addition, we present the relation of the obtained number triangle to Catalan’s and Euler’s triangles and call the obtained number triangle as Euler–Catalan’s triangle and the elements of this triangle as the Euler–Catalan numbers.
2. Combinatorial Objects
Binary trees are widely used in many different topics of discrete mathematics. They allow us to represent objects with a hierarchical structure in a convenient form for their storage and processing. Depending on the set of parameters and characteristics that describe the structural features of the binary tree, the class of binary trees is divided into many subclasses. Therefore, a large number of different combinatorial sets can be distinguished. There are also many different kinds of problems related to trees, for example, their enumeration or algorithmic problems that are discoursed in [13].
Let us consider the following combinatorial object: a labeled binary tree of size n with m ascents on the left branch. In such a tree structure, a tree consists of n nodes, each node has at most two children (the left child and the right child), and each node has its own label (a unique value from 1 to n) [14]. By the left branch of a tree, we mean the tree obtained by removing all right children (the identifier St000061 in [15]). If we consider the sequence of labels of the left branch of a tree starting from the root, then it has exactly m ascents (that is, there are exactly m labels that are greater than the previous).
Figure 1 shows all possible variants of such labeled trees for and . For the left branch of a tree, every pair of labels that form an ascent is marked with a green edge and every pair of labels that form a descent is marked with a red edge.
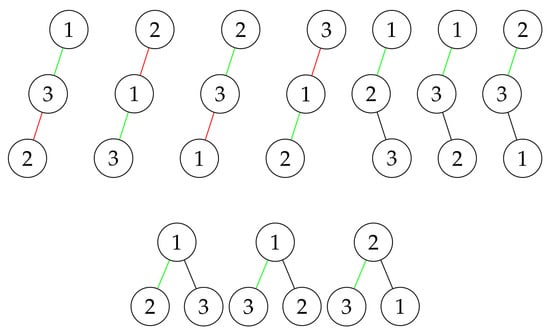
Figure 1.
All labeled binary trees of size 3 with 1 ascent on the left branch.
The following combinatorial object has the same properties: a labeled Dyck n-path with m ascents on return steps. In such a Dyck n-path, each down-step has its own label (a unique value from 1 to n). If we consider the sequence of labels of down-steps of a Dyck n-path starting from , then it has exactly m ascents (that is, there are exactly m labels that are greater than the previous).
A Dyck n-path is a lattice path in the plane which begins at , ends at , and consists of steps called rises or up-steps and called falls or down-steps. A return step is a down-step at level 1 (a return to the ground level 0) [16]. There are many research papers dedicated to studying Dyck paths. For example, it can be: the enumeration of Dyck paths and the study of their statistics [16,17,18], the study of different generalizations [19,20,21,22], the generation of Dyck paths, their ranking and unranking [23,24], and many other tasks.
Figure 2 shows all possible variants of the considered labeled Dyck paths for and .
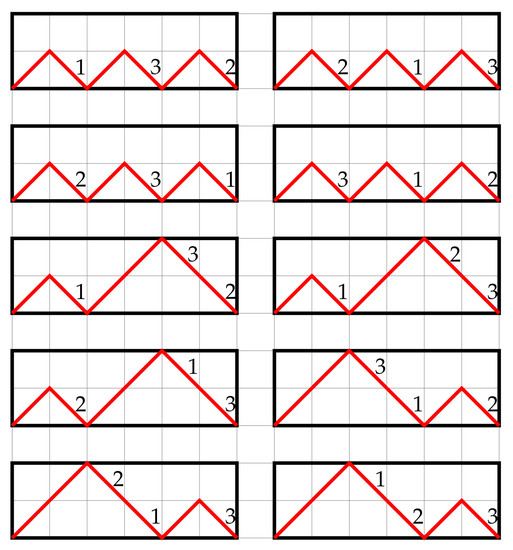
Figure 2.
All labeled Dyck paths of size 3 with 1 ascent on return steps.
The presented combinatorial objects have similar properties related to their structure and it is possible to define a bijection between them. We can also define other combinatorial objects that have similar properties. To do this, we need to consider such unlabeled combinatorial objects for which the number of objects is defined by the elements of the transposed Catalan triangle (the sequence in OEIS [25]).Then, we need to get the labeled version of such objects.
The connection of the transposed Catalan triangle with the Catalan numbers allows us to obtain a variety of combinatorial interpretations for the elements of this number triangle. It is possible because Catalan numbers are used in many combinatorial problems and there are more than 200 known combinatorial interpretations for them [26,27].
The Catalan numbers form the following sequence of positive integers (the sequence in OEIS [25]):
The Catalan numbers are denoted as . According to Graham et al. [2], an explicit formula for is
and an ordinary generating function is
The Catalan numbers also satisfy the following recurrence relation:
In addition, there are many different generalizations of the Catalan numbers that associate them with other special numbers. For example, it could be numbers such as the Catalan–Mersenne numbers [28], the Eulerian–Catalan numbers [29], the Catalan–Daehee numbers [30,31,32], etc.
3. Main Results
For the presented combinatorial objects, we have obtained an explicit formula for their enumerating. However, to state the theorem, it is necessary to consider the description of the following number triangles: the transposed Catalan triangle, Euler’s triangle, and the number of m-permutations of n.
The elements of the transposed Catalan triangle (the sequence in OEIS [25]) are denoted as . According to Deutsch [16], an explicit formula for is
Table 1 presents several first values of the transposed Catalan triangle.

Table 1.
Several first values of the transposed Catalan triangle.
The elements of Euler’s triangle (the sequence in OEIS [25]) are denoted as . The elements of Euler’s triangle are also called the Eulerian numbers of the first kind [33]. According to Graham et al. [2], an explicit formula for is
Table 2 presents several first values of Euler’s triangle.

Table 2.
Several first values of Euler’s triangle.
The numbers of the m-permutations of n [34] form the number triangle (the sequence in OEIS [25]) that elements are denoted as . According to Graham et al. [2], an explicit formula for is
Table 3 presents several first values of this number triangle.

Table 3.
Several first values of .
Theorem 1.
The number of labeled binary trees of size n with m ascents on the left branch is
where is the transposed Catalan triangle, is Euler’s triangle, and is the number of m-permutations of n.
Proof.
The number of binary trees of size n with m nodes on the left branch is defined by the elements of the transposed Catalan triangle (the sequence in OEIS [25]). Then, we consider a labeled version of these binary trees (for each node, there is an associated unique value from 1 to n). We need to count the number of ways to label the given binary tree of size n with k nodes on the left branch such that it has exactly m ascents on the left branch. For this, it is necessary that the labels of k nodes on the left branch form a permutation of k elements with m ascents and the remaining labels of nodes form all possible permutations.
An ascent of a permutation of is a place where [2,35]. The number of permutations of n elements with m ascents is defined by the elements of Euler’s triangle (the sequence in OEIS [25]). The number of permutations of m elements given from a set of n elements is defined by (the sequence in OEIS [25]). Hence, combining Equations (1) and (2), we get the number of ways to label the given binary tree of size n with k nodes on the left branch such that it has exactly m ascents on the left branch
If we consider all variants of binary trees of size n with k nodes on the left branch for k from to n (since for ) and get the number of ways to label them using Equation (4), we obtain the total number of labeled binary trees of size n with m ascents on the left branch
We also need to consider a special case for when . This means that there is only one variant to get a labeled binary tree of size 0 without ascents on the left branch (an empty labeled binary tree).
Hence, we obtain the desired result in Equation (3). □
It is known that the number of Dyck n-paths with m return steps is also defined by the elements of the transposed Catalan triangle [16]. If we consider labeled version of Dyck n-paths with k return steps (for each down-step there is an associated unique value from 1 to n) with m ascents on return steps, then we can get the same result:
Corollary 1.
The number of labeled Dyck n-paths with m ascents on return steps is
where is the transposed Catalan triangle, is Euler’s triangle, and is the number of m-permutations of n.
Proof.
The proof of Corollary 1 is the same as for Theorem 1: we need to count the number of ways to label the given Dyck n-path with k return steps such that the labels of k return steps form a permutation of k elements with m ascents and the remaining labels of return steps form all possible permutations. □
The sequence of forms a number triangle (see Table 4). Due to the connection with Catalan’s and Euler’s triangles, let us call it Euler–Catalan’s triangle. The elements of Euler–Catalan’s triangle are here called the Euler–Catalan numbers.

Table 4.
Several first values of Euler–Catalan’s triangle.
The next step in studying the introduced number triangle is to obtain an expression for the generating function of the Euler–Catalan numbers.
Theorem 2.
The Euler–Catalan numbers are defined by the following bivariate generating function:
where is the generating function of the Catalan numbers.
Proof.
Let us consider as the composition of generating functions
where
is the bivariate generating function of Euler’s triangle [2].
According to Kruchinin and Kruchinin [36], if we have the composition
of generating functions and , then we can obtain the values of the coefficient function
where is the composita of the generating function :
The composita of is [37]
Using Equation (6) for the composition , we get
Hence, we obtain the desired result in Equation (5). □
4. Conclusions
In this paper, we study labeled binary trees of size n with m ascents on the left branch and labeled Dyck n-paths with m ascents on return steps. Using properties of Catalan’s and Euler’s number triangles, we obtain the explicit formula that counts the total number of such combinatorial objects. The obtained results can be generalized for enumerating many other combinatorial sets that are also related to labeled versions of combinatorial interpretations for the transposed Catalan triangle.
In addition, for these combinatorial objects, we derive the bivariate generating function. Information about the generating function that describes a combinatorial set can be applied for a more detailed study of the properties of the combinatorial set.
Author Contributions
Investigation, Y.S. and D.K.; writing—original draft preparation, Y.S.; and writing—review and editing, D.K. All authors have read and agreed to the published version of the manuscript.
Funding
Obtaining the explicit formula was funded by the Russian Foundation for Basic Research (the research project No. 18-31-00201). Obtaining the bivariate generating function was supported by the Russian Science Foundation (the research project No. 18-71-00059).
Acknowledgments
The authors would like to thank the referees for their helpful comments and suggestions.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Knuth, D.E. The Art of Computer Programming, Volume 4A: Combinatorial Algorithms; Addison-Wesley: Boston, MA, USA, 2011. [Google Scholar]
- Graham, R.L.; Knuth, D.E.; Patashnik, O. Concrete Mathematics; Addison-Wesley: Boston, MA, USA, 1994. [Google Scholar]
- Banderier, C.; Bousquet-Melou, M.; Denise, A.; Flajolet, P.; Gardy, D.; Gouyou-Beauchamps, D. Generating functions for generating trees. Discret. Math. 2002, 246, 29–55. [Google Scholar] [CrossRef]
- Mansour, T.; Shattuck, M.; Wagner, S. Enumerating set partitions by the number of positions between adjacent occurrences of a letter. Appl. Anal. Discret. Math. 2010, 4, 284–308. [Google Scholar]
- Drmota, M. Embedded trees and the support of the ISE. Eur. J. Combin. 2013, 34, 123–137. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Srivastava, H.M.; Chaudhary, M.P. Some relationships between g-product identities, combinatorial partition identities and continued-fraction identities. Adv. Stud. Contemp. Math. 2015, 25, 265–272. [Google Scholar]
- Mansour, T.; Shattuck, M. New refined enumerations of set partitions related to sorting. J. Differ. Equ. Appl. 2018, 24, 1588–1603. [Google Scholar] [CrossRef]
- Bayad, A.; Simsek, Y.; Srivastava, H.M. Some array type polynomials associated with special numbers and polynomials. Appl. Math. Comput. 2014, 244, 149–157. [Google Scholar] [CrossRef]
- Cakic, N.P.; El-Desouky, B.S.; Milovanovic, G.V. Explicit formulas and combinatorial identities for generalized Stirling numbers. Mediterr. J. Math. 2013, 10, 57–72. [Google Scholar] [CrossRef]
- Gould, H.W. A new symmetrical combinatorial ldentity. J. Combin. Theory Ser. A 1972, 13, 278–286. [Google Scholar] [CrossRef]
- Mansour, T.; Shattuck, M. A generalized class of restricted Stirling and Lah numbers. Math. Slovaca 2018, 68, 727–740. [Google Scholar] [CrossRef]
- Simsek, Y. New families of special numbers for computing negative order Euler numbers and related numbers and polynomials. Appl. Anal. Discret. Math. 2018, 12, 1–35. [Google Scholar] [CrossRef]
- Belov, A.Y. Linear recurrence equations on a tree. Math. Notes 2005, 78, 603–609. [Google Scholar] [CrossRef]
- Gessel, I.M.; Griffin, S.T.; Tewari, V. Labeled binary trees, subarrangements of the Catalan arrangements, and Schur positivity. Adv. Math. 2019, 356, 1–67. [Google Scholar] [CrossRef]
- Rubey, M.; Stump, C. FindStat—The combinatorial statistics database. Available online: http://www.findstat.org (accessed on 1 March 2020).
- Deutsch, E. Dyck path enumeration. Discret. Math. 1999, 204, 167–202. [Google Scholar] [CrossRef]
- Banderier, C.; Krattenthaler, C.; Krinik, A.; Kruchinin, D.; Kruchinin, V.; Nguyen, D.; Wallner, M. Explicit formulas for enumeration of lattice paths: Basketball and the kernel method. In Lattice Path Combinatorics and Applications; Springer: Cham, Switzerland, 2019; Volume 58, pp. 78–118. [Google Scholar]
- Sapounakis, A.; Tasoulas, I.; Tsikouras, P. Dyck path statistics. WSEAS Trans. Math. 2006, 5, 459–464. [Google Scholar]
- Labelle, J.; Yeh, Y.N. Generalized Dyck paths. Discret. Math. 1990, 82, 1–6. [Google Scholar] [CrossRef]
- Rukavicka, J. On generalized Dyck paths. Electron. J. Combin. 2011, 18, 1–3. [Google Scholar] [CrossRef]
- Cameron, N.T.; McLeod, J.E. Returns and hills on generalized Dyck paths. J. Integer Seq. 2016, 19, 1–28. [Google Scholar]
- Xu, R.; Yeh, Y.N.; Zhu, X. List colouring of graphs and generalized Dyck paths. Discret. Math. 2018, 341, 810–819. [Google Scholar] [CrossRef]
- Penaud, J.G.; Roques, O. Génération de chemins de Dyck à pics croissants. Discret. Math. 2002, 246, 255–267. [Google Scholar] [CrossRef]
- Manes, K.; Sapounakis, A.; Tasoulas, I.; Tsikouras, P. Recursive generation of k-ary trees. J. Integer Seq 2009, 12, 1–18. [Google Scholar]
- Sloane, N.J.A. The on-line encyclopedia of integer sequences. Available online: http://oeis.org (accessed on 1 March 2020).
- Stanley, R.P. Catalan Numbers; Cambridge University Press: New York, NY, USA, 2015. [Google Scholar]
- Kim, D.S.; Kim, T. A new approach to Catalan numbers using differential equations. Russ. J. Math. Phys. 2017, 24, 465–475. [Google Scholar] [CrossRef]
- Eum, I.S. A congruence relation of the Catalan–Mersenne numbers. Indian J. Pure Appl. Math. 2018, 49, 521–526. [Google Scholar] [CrossRef]
- Bidkhori, H.; Sullivant, S. Eulerian–Catalan numbers. Electron. J. Combin. 2011, 18, 1–10. [Google Scholar] [CrossRef]
- Kim, T.; Kim, D.S. Some identities of Catalan-Daehee polynomials arising from umbral calculus. Appl. Comput. Math. 2017, 16, 177–189. [Google Scholar]
- Kim, T.; Kim, D.S. Differential equations associated with Catalan-Daehee numbers and their applications. Rev. R. Acad. Cienc. Exactas Fis. Nat. Ser. A Mat. RACSAM 2017, 111, 1071–1081. [Google Scholar] [CrossRef]
- Dolgy, D.V.; Jang, G.W.; Kim, D.S.; Kim, T. Explicit expressions for Catalan-Daehee numbers. Proc. Jangjeon Math. Soc. 2017, 20, 1–9. [Google Scholar]
- Mariconda, C.; Tonolo, A. Stirling numbers and Eulerian numbers. In Discrete Calculus; Springer: Cham, Switzerland, 2016; pp. 105–151. [Google Scholar]
- Chen, B.F.; Ghorbani, E.; Wong, K.B. Cyclic decomposition of k-permutations and eigenvalues of the arrangement graphs. Electron. J. Combin. 2013, 20, 1–18. [Google Scholar] [CrossRef]
- Tanimoto, S. An operator on permutations and its application to Eulerian numbers. Eur. J. Combin. 2001, 22, 569–576. [Google Scholar] [CrossRef]
- Kruchinin, V.V.; Kruchinin, D.V. Composita and its properties. J. Anal. Number Theory 2014, 2, 37–44. [Google Scholar]
- Kruchinin, D.V.; Kruchinin, V.V. A method for obtaining generating functions for central coefficients of triangles. J. Integer Seq. 2012, 15, 1–10. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).