Change Point Detection with Mean Shift Based on AUC from Symmetric Sliding Windows
Abstract
1. Introduction
- (1)
- We do not need to know the exact distribution of the data. We only assume that the data follows some indpendent and identically distributed (i.i.d.) continuous distribution. In other words, our method is a completely distributed free method.
- (2)
- The strategy of reducing false alarm change points can enhance the robustness of the algorithm.
- (3)
- We design the optimal window size ratio and size, so as to optimize the algorithm.
2. Data Model of Abrupt Change with Mean Shift
3. AUC Statistics for Change Point with Abrupt Mean Shift
3.1. AUC Statistics from Symmetric Sliding Windows
- (i)
- (ii)
- For all of the Δ, the variance of based on X and Y reaches its minimum when .
- (i).
- Denote by and the probability density functions (pdfs) of X and Y, respectively. Since , it follows that , which is equivalent to . Therefore is equivalent to . Hence,
- (ii).
- Given the assumption that is fixed, it follows from (4) thatwhich, along with the result of the above equation, leads toTherefore, we havewhich shows that the variance of depends only on the length segmentation factor . It thus follows readily that is minimized when , or equivalently, . ☐
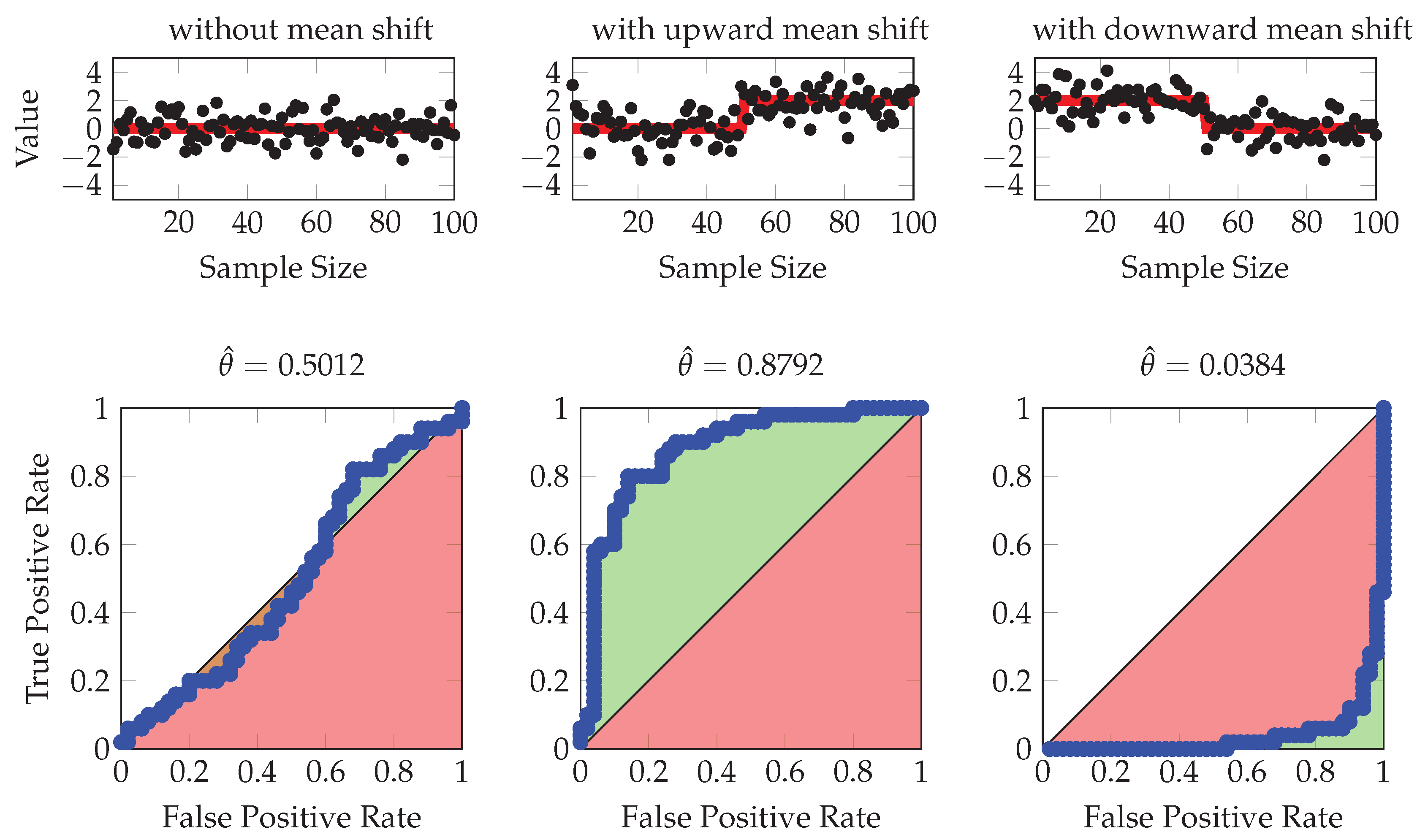
3.2. Change Point Detection with AUC Statistics
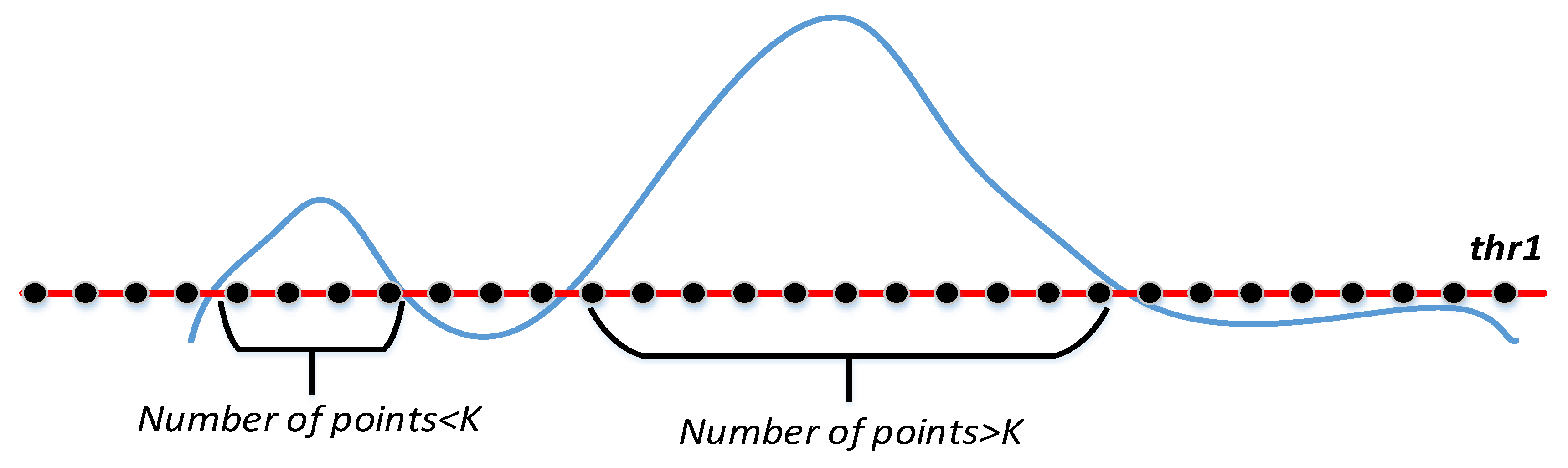
3.3. The Window Size and K
4. Comparative Studies and Analysis
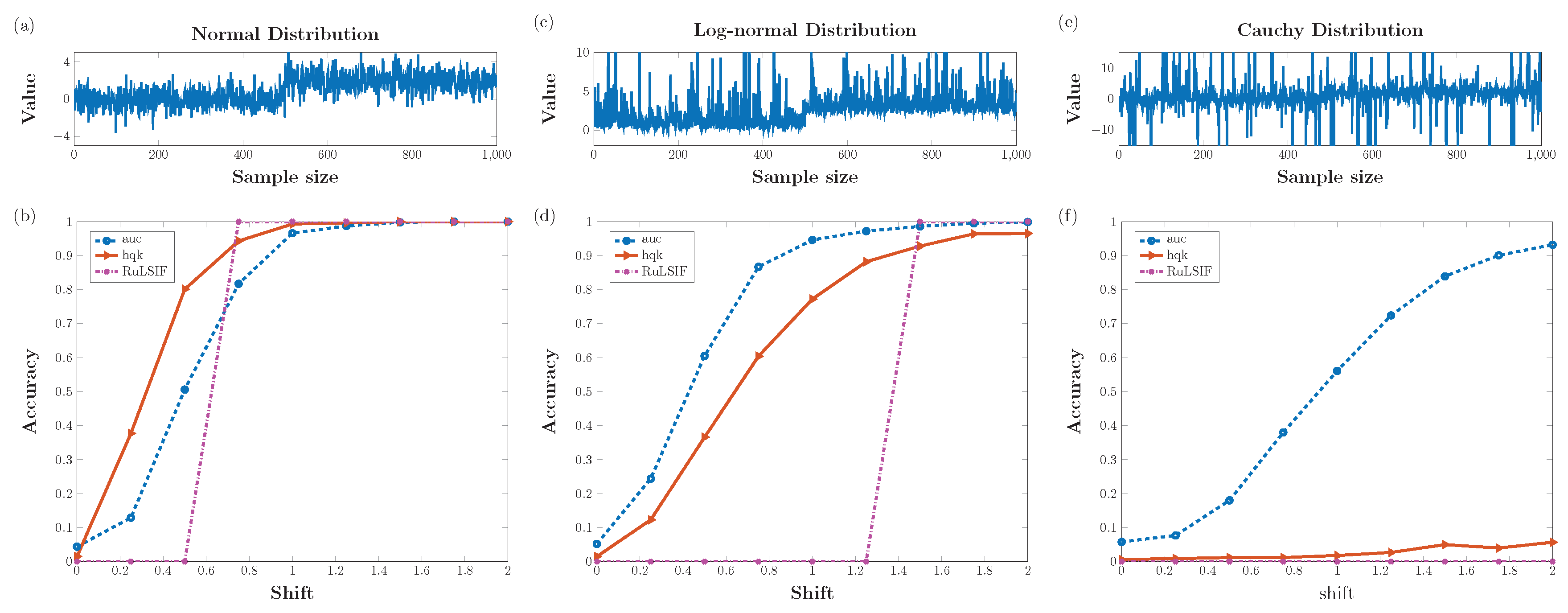
4.1. Comparative Results for Single Change Point Detection
- Model 1: Normal distribution
- Model 2: Log normal distribution
- Model 3: Standard Cauchy distribution
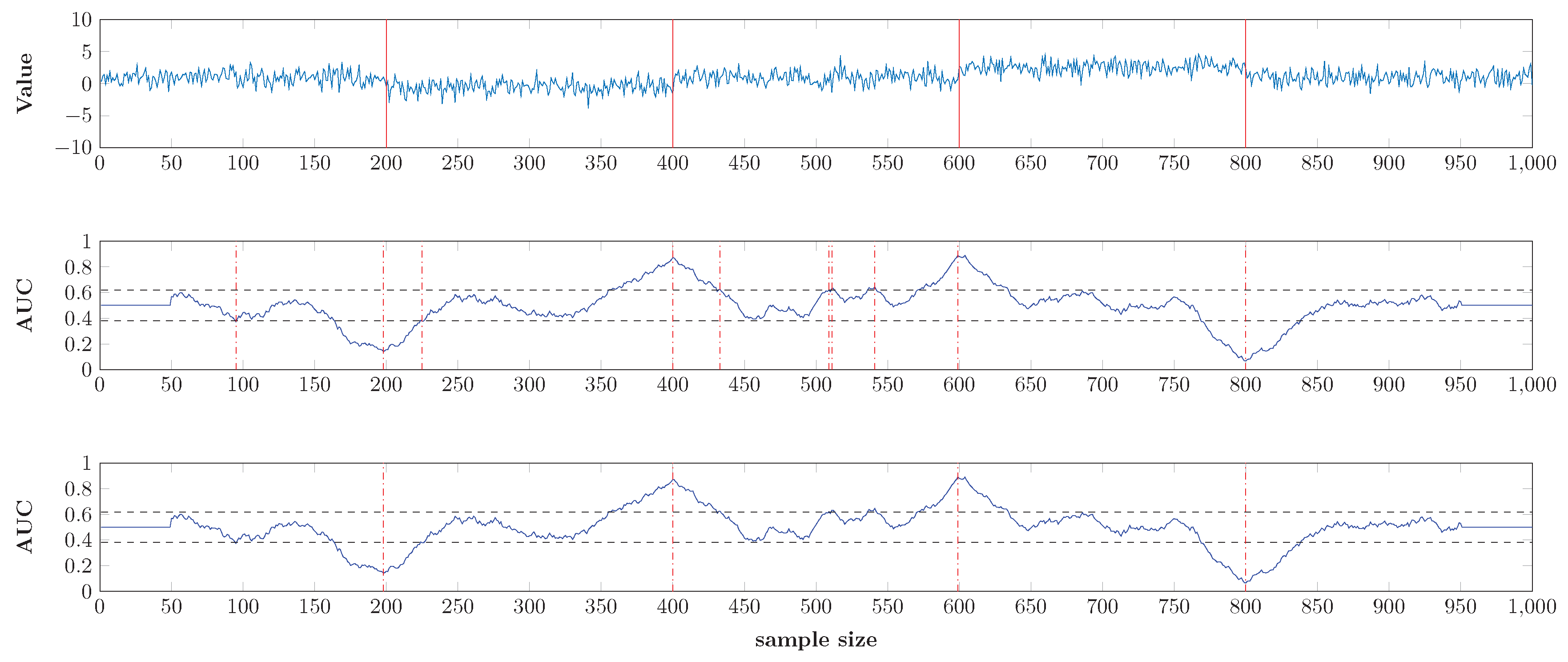
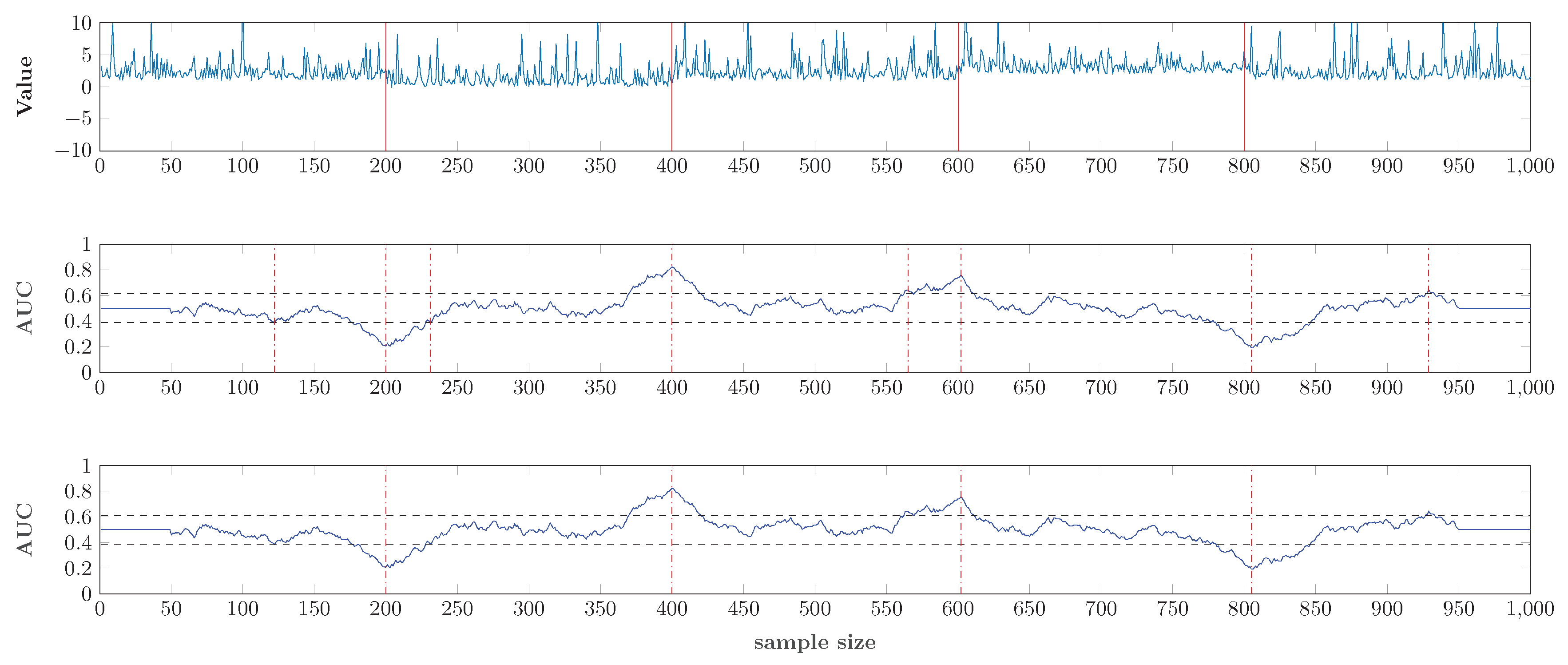
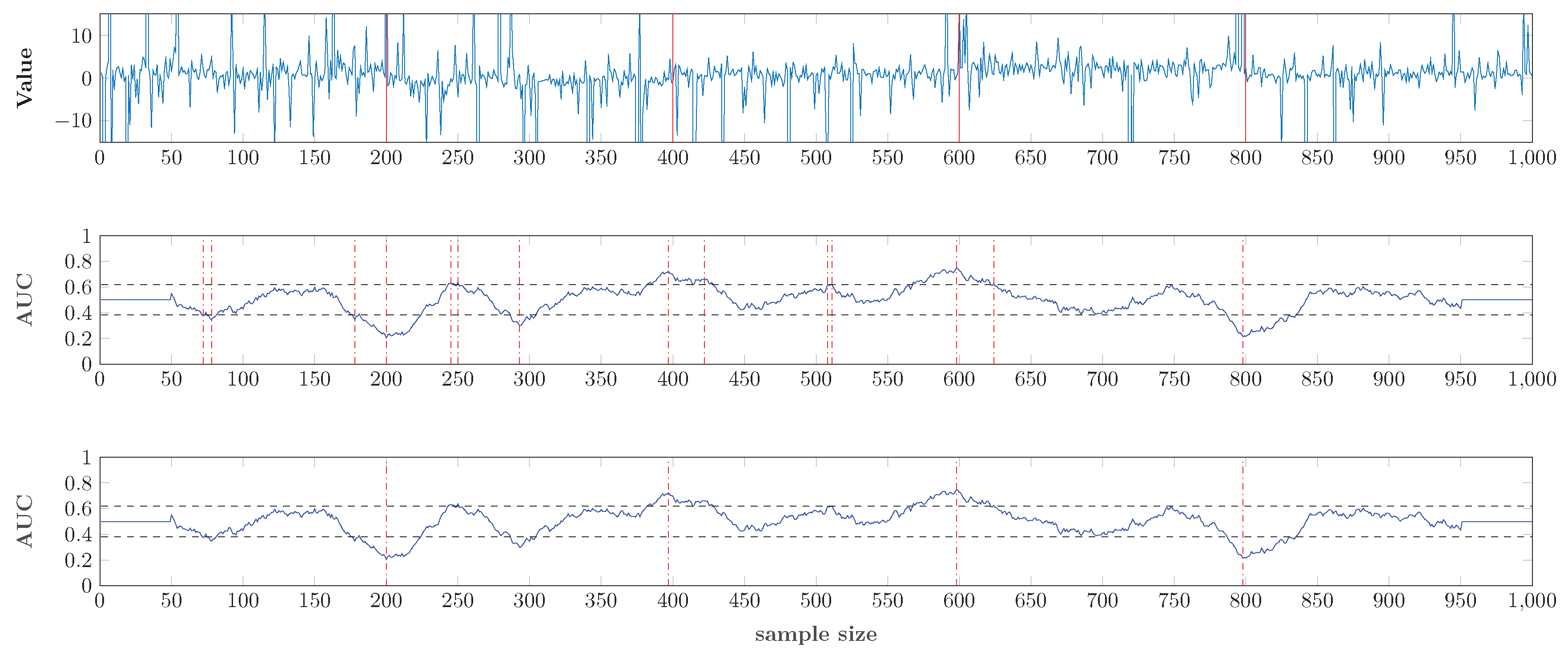
4.2. Multiple Change Points Detection
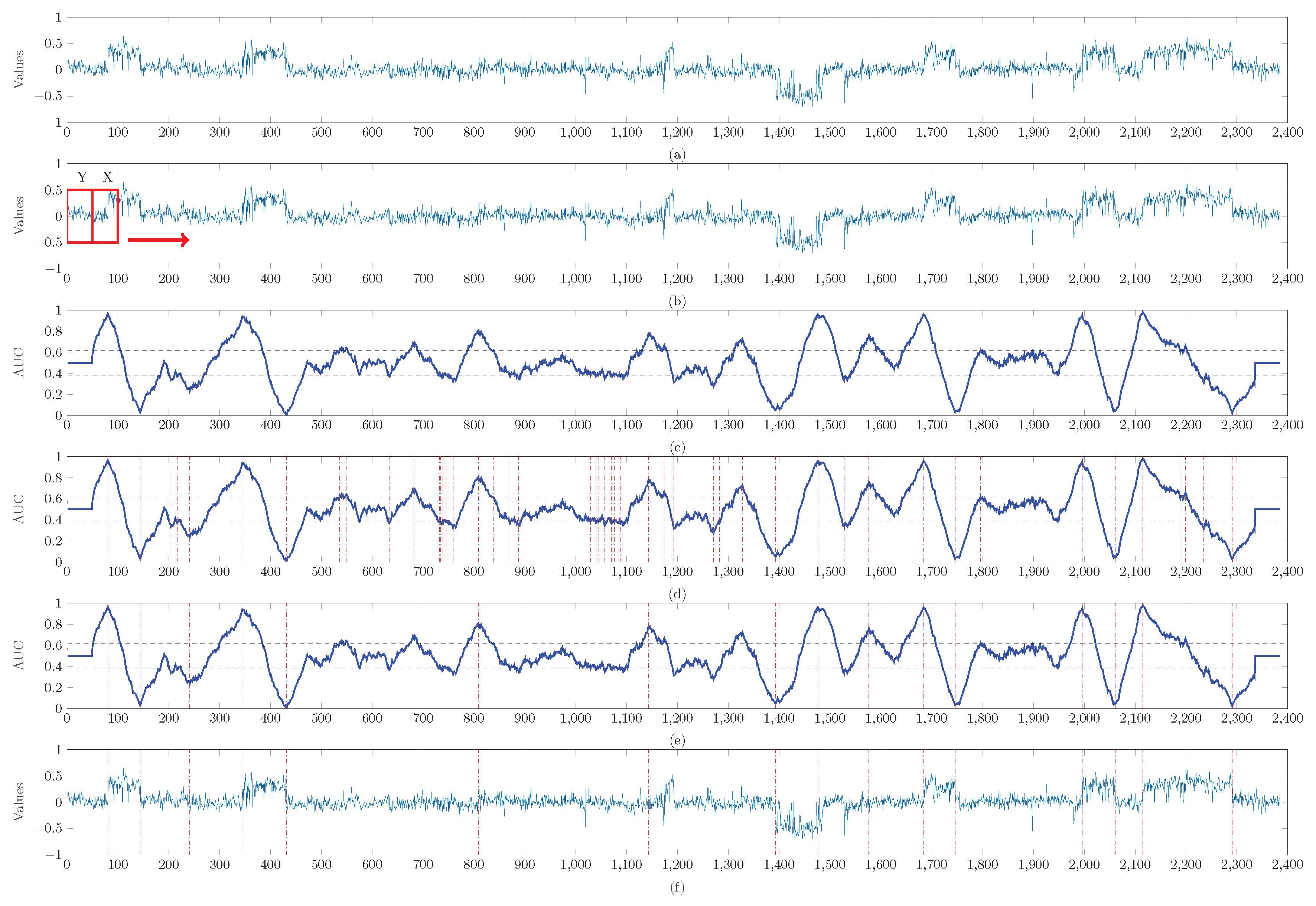
4.3. An Application to Real Data Set
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| ROC | Receiver Operating Characteristic |
| AUC | Area Under the receiver operating characteristic Curve |
| MWUS | Mann Whitney U statistic |
| HQK | Hawkins, Qiu, and Kang |
| DoS | Denial of Service |
| RuLSIF | Relative unconstrained Least-Squares Importance Fitting |
| ARL | Average Run Length |
| ANN | Artificial Neural Network |
| EWMA | Exponentially Weighted Moving Average |
| CUSUM | Cumulative Sum Control Chart |
| i.i.d. | independent and identically distributed |
| cdf | cumulative distribution functions |
Appendix A. Data of Figure 7
| Shift () | Normal Distribution | Log Normal Distribution | Cauchy Distribution | ||||||
|---|---|---|---|---|---|---|---|---|---|
| AUC | RuLSIF | HQK | AUC | RuLSIF | HQk | AUC | RuLSIF | HQK | |
| 0 | 0.047 | 0.0 | 0.014 | 0.052 | 0.0 | 0.015 | 0.058 | 0.0 | 0.006 |
| 0.25 | 0.188 | 0.0 | 0.391 | 0.244 | 0.0 | 0.123 | 0.077 | 0.0 | 0.009 |
| 0.5 | 0.496 | 0.0 | 0.808 | 0.605 | 0.0 | 0.366 | 0.180 | 0.0 | 0.012 |
| 0.75 | 0.778 | 1 | 0.939 | 0.867 | 0.0 | 0.604 | 0.380 | 0.0 | 0.012 |
| 1 | 0.954 | 1 | 0.988 | 0.946 | 0.0 | 0.772 | 0.561 | 0.0 | 0.018 |
| 1.25 | 0.989 | 1 | 0.998 | 0.972 | 1 | 0.882 | 0.724 | 0.0 | 0.027 |
| 1.50 | 0.998 | 1 | 1 | 0.986 | 1 | 0.928 | 0.839 | 0.0 | 0.050 |
| 1.75 | 1 | 1 | 1 | 0.995 | 1 | 0.964 | 0.901 | 0.0 | 0.040 |
| 2.00 | 1 | 1 | 1 | 0.999 | 1 | 0.965 | 0.932 | 0.0 | 0.057 |
References
- Nikovski, D.; Jain, A. Memory-based algorithms for abrupt change detection in sensor data streams. In Proceedings of the 2007 5th IEEE International Conference on Industrial Informatics, Vienna, Austria, 23–27 July 2007; Volume 1, pp. 547–552. [Google Scholar]
- Nikovski, D.; Jain, A. Fast adaptive algorithms for abrupt change detection. Mach. Learn. 2010, 79, 283–306. [Google Scholar] [CrossRef][Green Version]
- Goswami, B.; Boers, N.; Rheinwalt, A.; Marwan, N.; Heitzig, J.; Breitenbach, S.F.; Kurths, J. Abrupt transitions in time series with uncertainties. Nat. Commun. 2018, 9, 48. [Google Scholar] [CrossRef] [PubMed]
- Staniszewski, M.; Skorupa, A.; Boguszewicz, Ł.; Sokół, M.; Polański, A. Quality Control Procedure Based on Partitioning of NMR Time Series. Sensors 2018, 18, 792. [Google Scholar] [CrossRef] [PubMed]
- Xie, Y.; Siegmund, D. Sequential multi-sensor change-point detection. Ann. Stat. 2013, 41, 670–692. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, D.; Shin, K.G. Change-point monitoring for the detection of DoS attacks. IEEE Trans. Dependable Secur. Comput. 2004, 1, 193–208. [Google Scholar] [CrossRef]
- Oudre, L.; Lung-Yut-Fong, A.; Bianchi, P. Segmentation of accelerometer signals recorded during continuous treadmill walking. In Proceedings of the IEEE 2011 19th European Signal Processing Conference, Barcelona, Spain, 29 August–2 September 2011; pp. 1564–1568. [Google Scholar]
- Gan, F. An optimal design of CUSUM control charts for binomial counts. J. Appl. Stat. 1993, 20, 445–460. [Google Scholar] [CrossRef]
- Jiang, W.; Shu, L.; Tsui, K.L. Weighted CUSUM control charts for monitoring Poisson processes with varying sample sizes. J. Qual. Technol. 2011, 43, 346–362. [Google Scholar] [CrossRef]
- Steiner, S.H.; Mackay, R.J. Monitoring processes with highly censored data. J. Qual. Technol. 2000, 32, 199–208. [Google Scholar] [CrossRef][Green Version]
- Noura, A.; Read, K. Proportional hazards changepoint models in survival analysis. J. R. Stat. Soc. Ser. C Appl. Stat. 1990, 39, 241–253. [Google Scholar] [CrossRef]
- Gijbels, I.; Goderniaux, A.C. Bandwidth selection for changepoint estimation in nonparametric regression. Technometrics 2004, 46, 76–86. [Google Scholar] [CrossRef]
- Oh, K.J.; Moon, M.S.; Kim, T.Y. Variance change point detection via artificial neural networks for data separation. Neurocomputing 2005, 68, 239–250. [Google Scholar] [CrossRef]
- Goldenshluger, A.; Tsybakov, A.; Zeevi, A. Optimal change-point estimation from indirect observations. Ann. Stat. 2006, 34, 350–372. [Google Scholar] [CrossRef]
- Wang, Z.F.; Wu, Y.H.; Zhao, L.C. Change-point estimation for censored regression model. Sci. China Ser. A Math. 2007, 50, 63–72. [Google Scholar] [CrossRef]
- Pettitt, A. A non-parametric approach to the change-point problem. J. R. Stat. Soc. Ser. C Appl. Stat. 1979, 28, 126–135. [Google Scholar] [CrossRef]
- Hawkins, D.M.; Deng, Q. A nonparametric change-point control chart. J. Qual. Technol. 2010, 42, 165–173. [Google Scholar] [CrossRef]
- Ross, G.J.; Tasoulis, D.K.; Adams, N.M. Nonparametric monitoring of data streams for changes in location and scale. Technometrics 2011, 53, 379–389. [Google Scholar] [CrossRef]
- Zou, C.; Tsung, F.; Wang, Z. Monitoring profiles based on nonparametric regression methods. Technometrics 2008, 50, 512–526. [Google Scholar] [CrossRef]
- Qiu, P.; Zou, C.; Wang, Z. Nonparametric profile monitoring by mixed effects modeling. Technometrics 2010, 52, 265–277. [Google Scholar] [CrossRef]
- Keriven, N.; Garreau, D.; Poli, I. NEWMA: A new method for scalable model-free online change-point detection. arXiv 2018, arXiv:1805.08061. [Google Scholar]
- Hawkins, D.M.; Qiu, P.; Kang, C.W. The changepoint model for statistical process control. J. Qual. Technol. 2003, 35, 355–366. [Google Scholar] [CrossRef]
- Liu, S.; Yamada, M.; Collier, N.; Sugiyama, M. Change-point detection in time-series data by relative density-ratio estimation. Neural Netw. 2013, 43, 72–83. [Google Scholar] [CrossRef] [PubMed]
- Kanamori, T.; Hido, S.; Sugiyama, M. A least-squares approach to direct importance estimation. J. Mach. Learn. Res. 2009, 10, 1391–1445. [Google Scholar]
- Hanley, J.A.; McNeil, B.J. The meaning and use of the area under a receiver operating characteristic (ROC) curve. Radiology 1982, 143, 29–36. [Google Scholar] [CrossRef] [PubMed]
- Xu, W.; Dai, J.; Hung, Y.; Wang, Q. Estimating the area under a receiver operating characteristic (ROC) curve: Parametric and nonparametric ways. Signal Process. 2013, 93, 3111–3123. [Google Scholar] [CrossRef]
- Hettmansperger, T.P.; McKean, J.W. Robust Nonparametric Statistical Methods; CRC Press: Boca Raton, FL, USA, 2010. [Google Scholar]
- Mason, S.J.; Graham, N.E. Areas beneath the relative operating characteristics (ROC) and relative operating levels (ROL) curves: Statistical significance and interpretation. Q. J. R. Meteorol. Soc. A J. Atmos. Sci. Appl. Meteorol. Phys. Oceanogr. 2002, 128, 2145–2166. [Google Scholar] [CrossRef]
- Lehmann, E.L. Elements of Large-Sample Theory; Springer: New York, NY, USA, 1999. [Google Scholar]
- Schweder, T. Window estimation of the asymptotic variance of rank estimators of location. Scand. J. Stat. 1975, 113–126. [Google Scholar]
- Cunen, C.; Hermansen, G.; Hjort, N.L. Confidence distributions for change-points and regime shifts. J. Stat. Plan. Inference 2018, 195, 14–34. [Google Scholar] [CrossRef]
- Nicolas, S.; Céline, V.; Fabien, R.; Isabelle, B.P.; Medina Sixtina Gil Diez, D.; Rick, S.; Yann, D.R.; Paul, E.; Andrew, C.; Carolyn, S. Regional copy number-independent deregulation of transcription in cancer. Nat. Genet. 2006, 38, 1386–1396. [Google Scholar]
- Matteson, D.S.; James, N.A. A nonparametric approach for multiple change point analysis of multivariate data. J. Am. Stat. Assoc. 2014, 109, 334–345. [Google Scholar] [CrossRef]




© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Y.; Huang, G.; Yang, J.; Lai, H.; Liu, S.; Chen, C.; Xu, W. Change Point Detection with Mean Shift Based on AUC from Symmetric Sliding Windows. Symmetry 2020, 12, 599. https://doi.org/10.3390/sym12040599
Wang Y, Huang G, Yang J, Lai H, Liu S, Chen C, Xu W. Change Point Detection with Mean Shift Based on AUC from Symmetric Sliding Windows. Symmetry. 2020; 12(4):599. https://doi.org/10.3390/sym12040599
Chicago/Turabian StyleWang, Yanguang, Guanna Huang, Junjie Yang, Huadong Lai, Shun Liu, Changrun Chen, and Weichao Xu. 2020. "Change Point Detection with Mean Shift Based on AUC from Symmetric Sliding Windows" Symmetry 12, no. 4: 599. https://doi.org/10.3390/sym12040599
APA StyleWang, Y., Huang, G., Yang, J., Lai, H., Liu, S., Chen, C., & Xu, W. (2020). Change Point Detection with Mean Shift Based on AUC from Symmetric Sliding Windows. Symmetry, 12(4), 599. https://doi.org/10.3390/sym12040599





