The Effect of Fractional Time Derivative of Bioheat Model in Skin Tissue Induced to Laser Irradiation
Abstract
1. Introduction
2. Mathematical Model
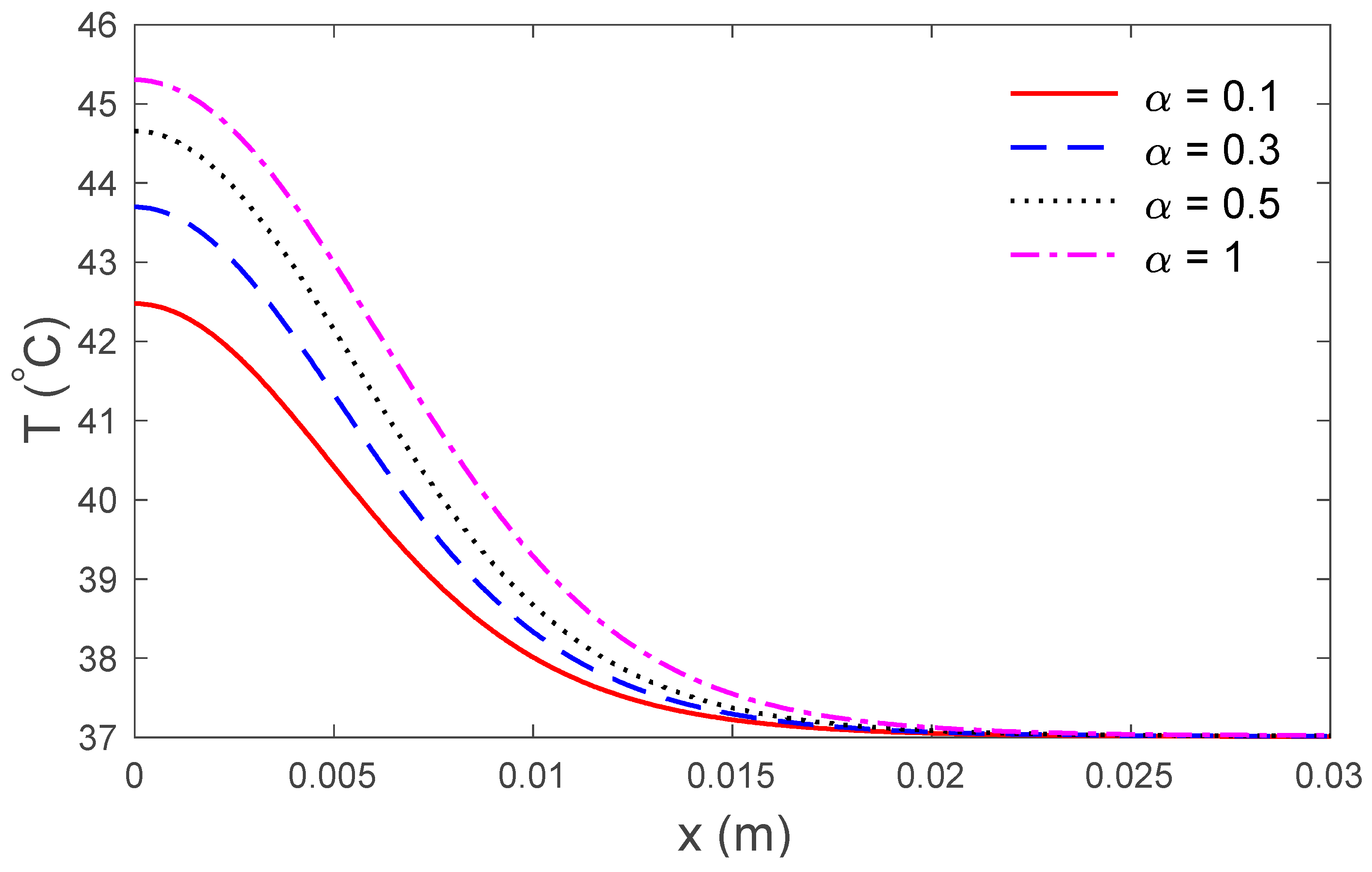
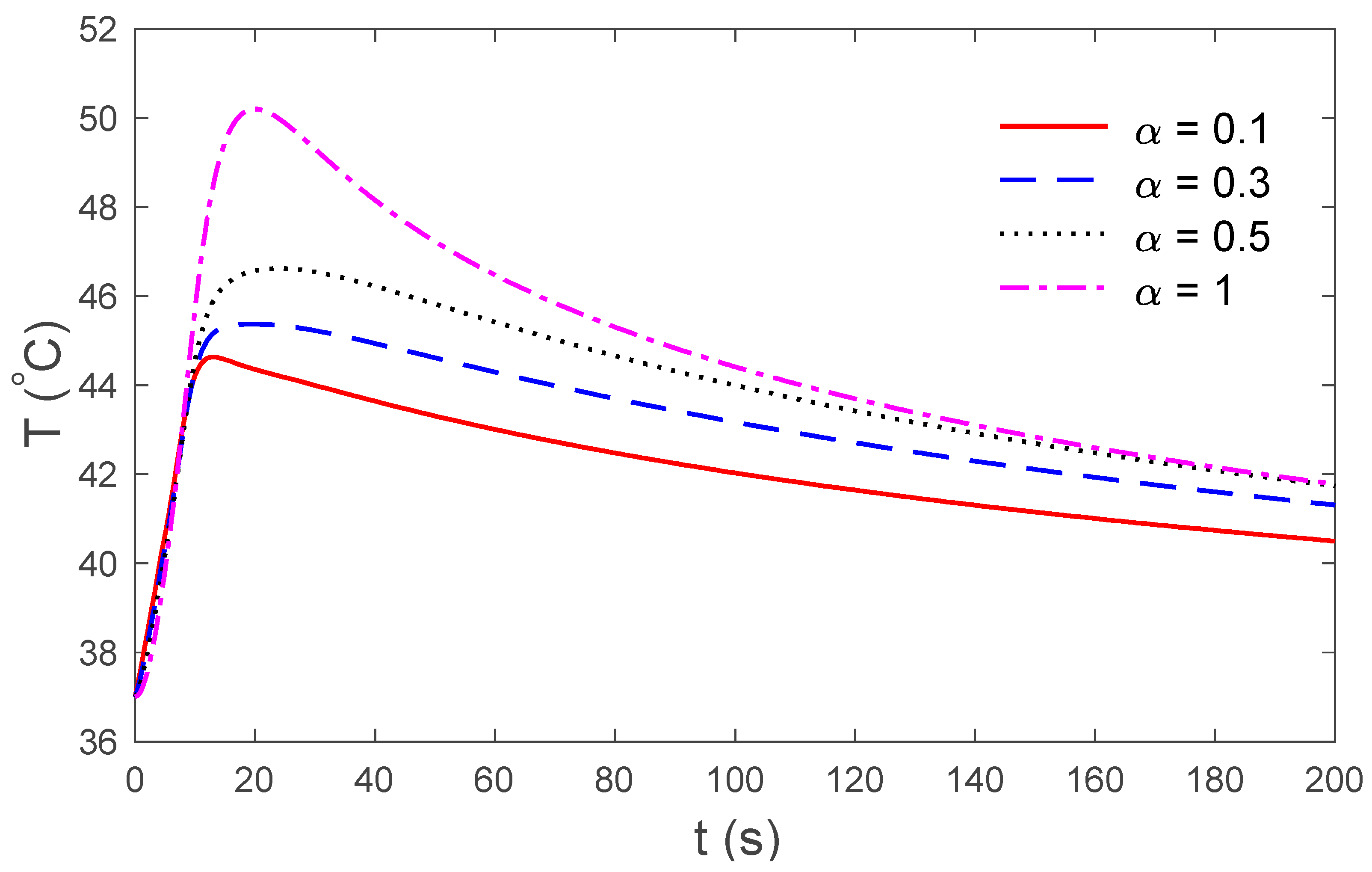
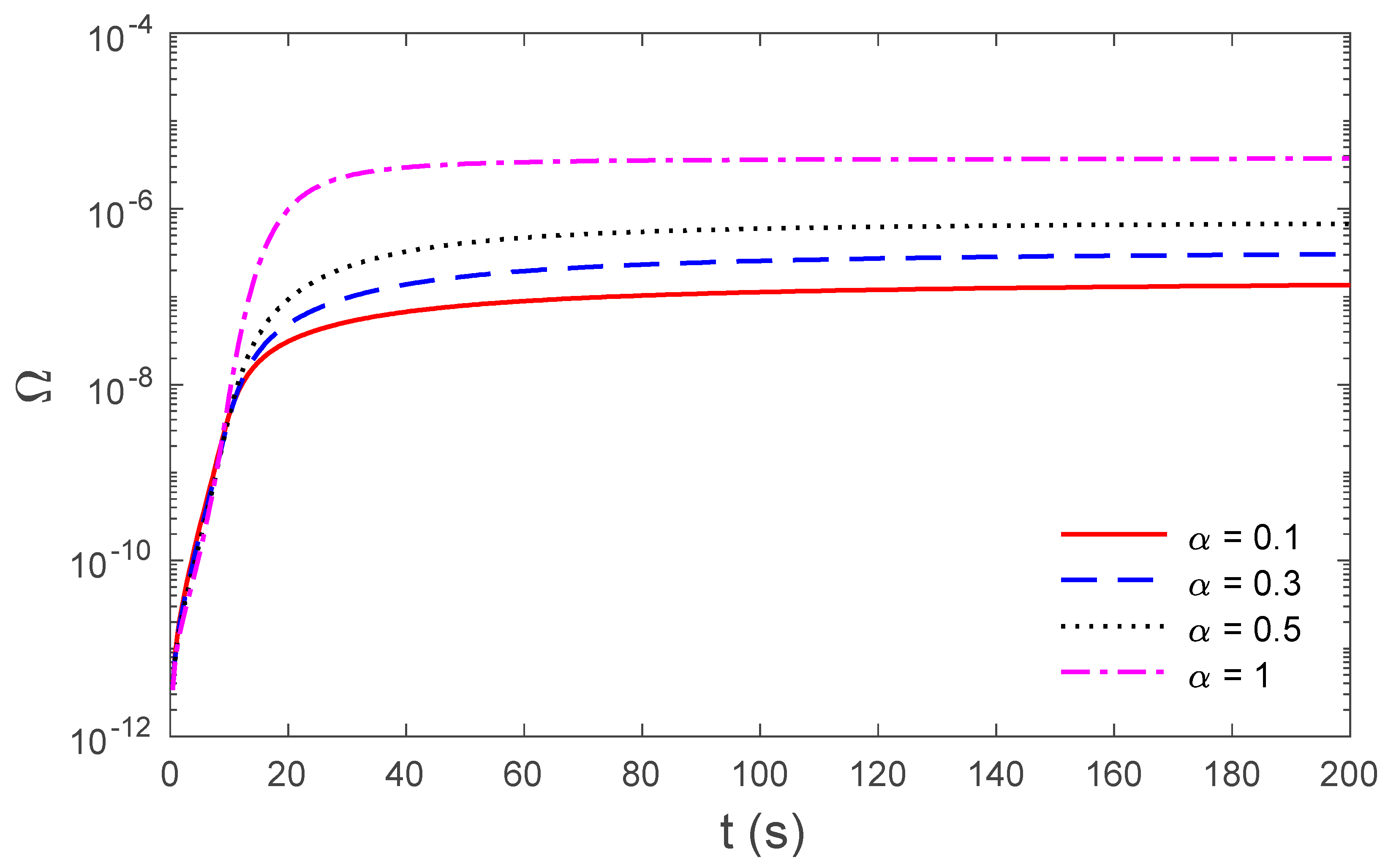
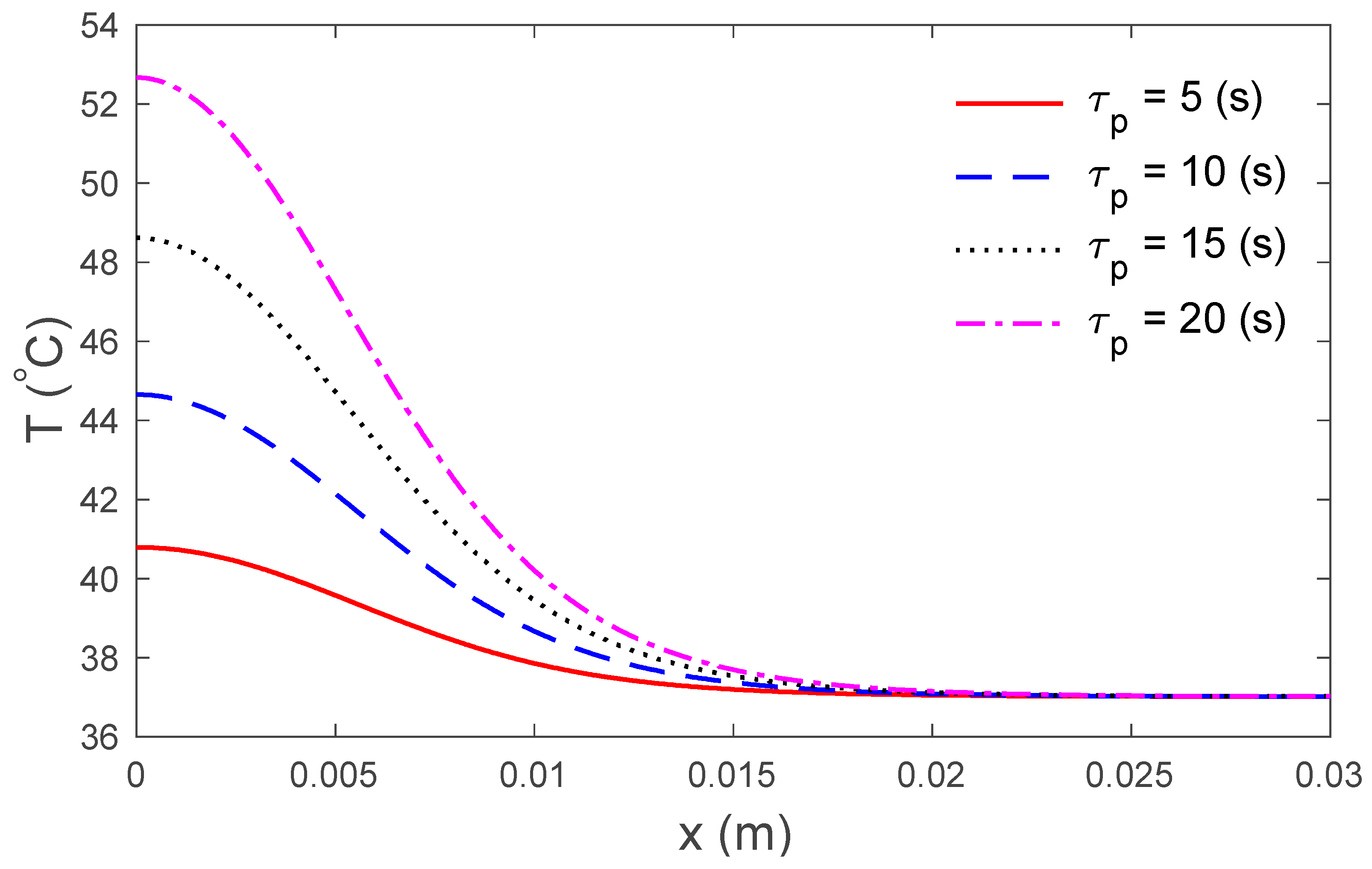
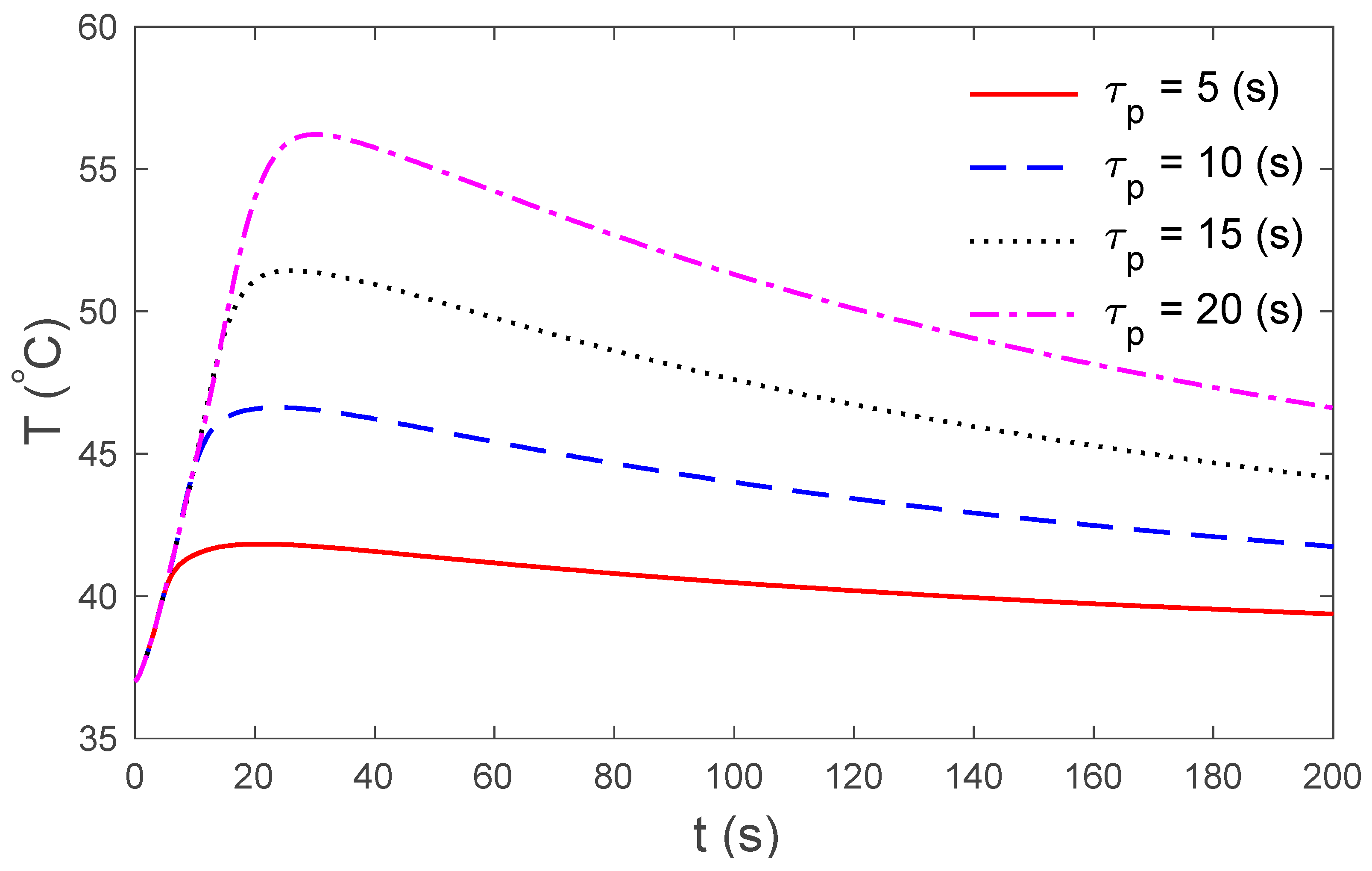
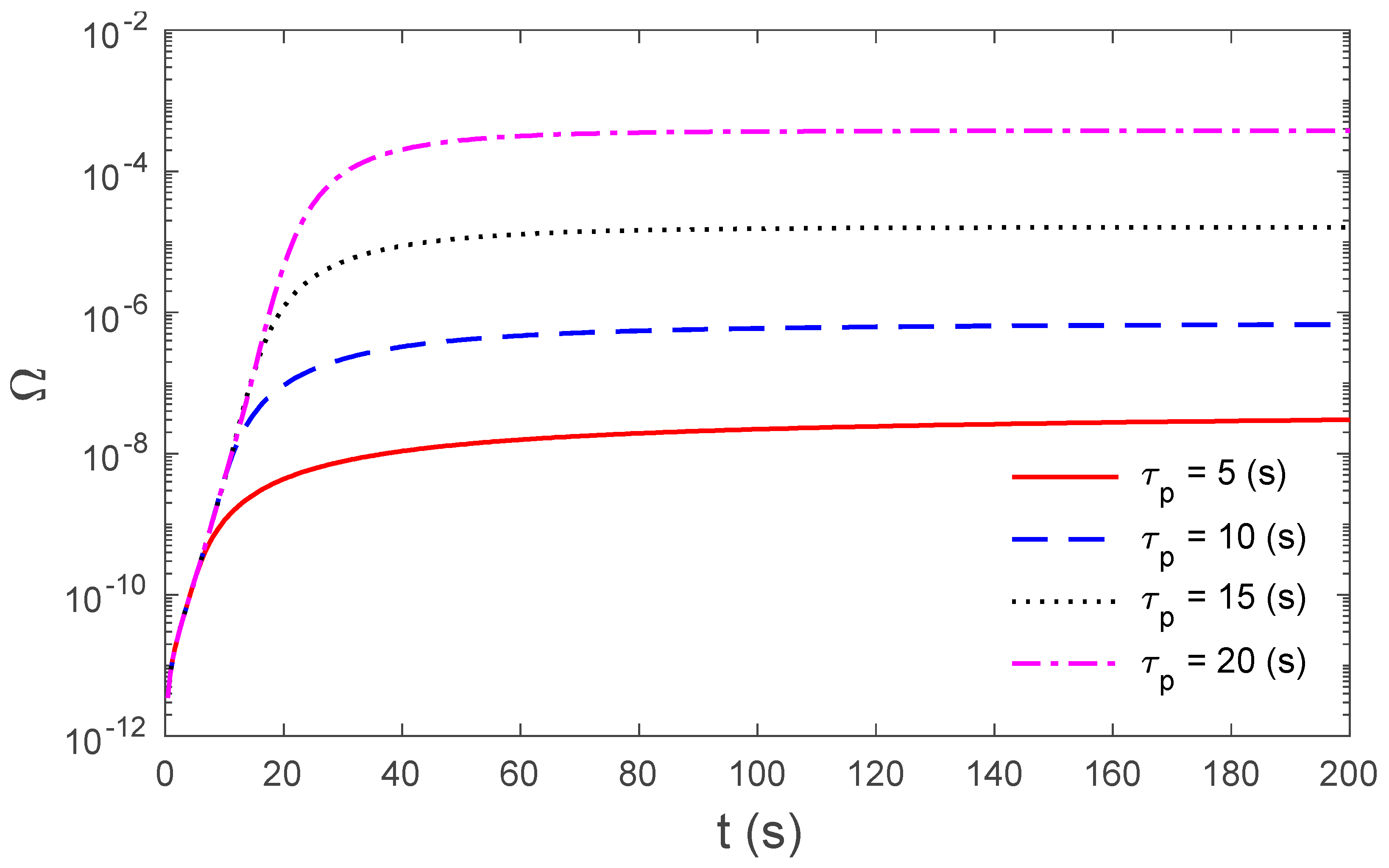
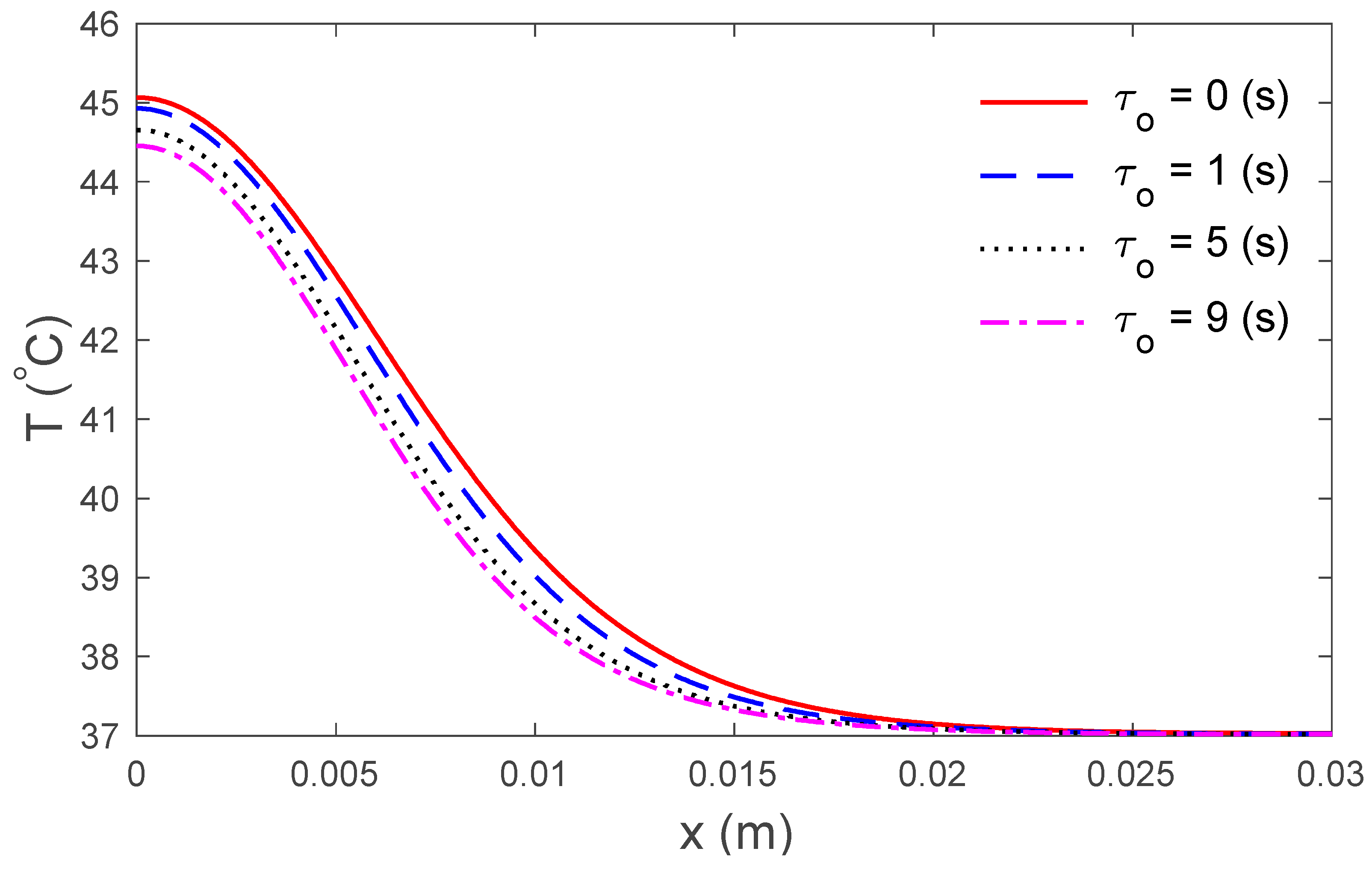
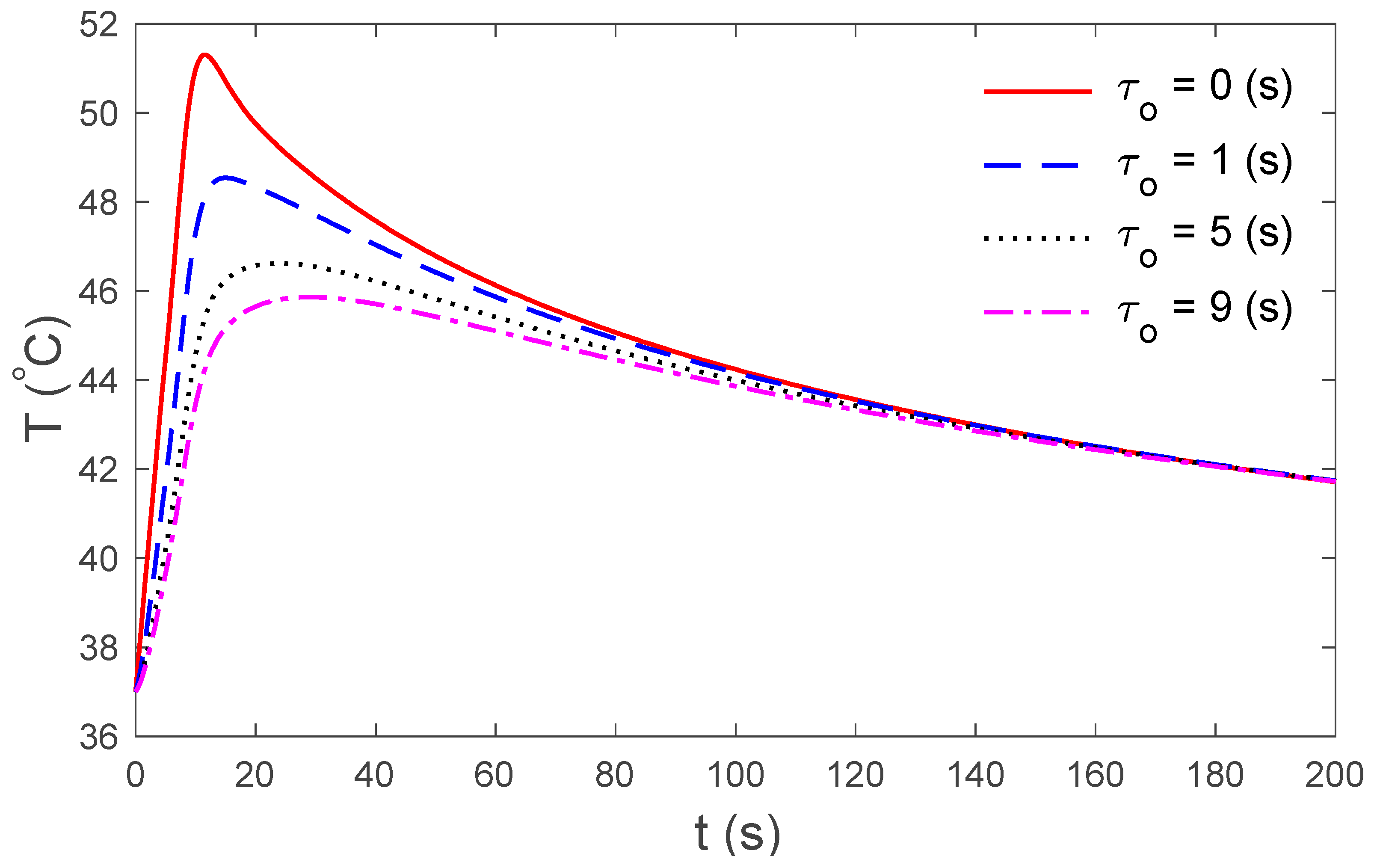
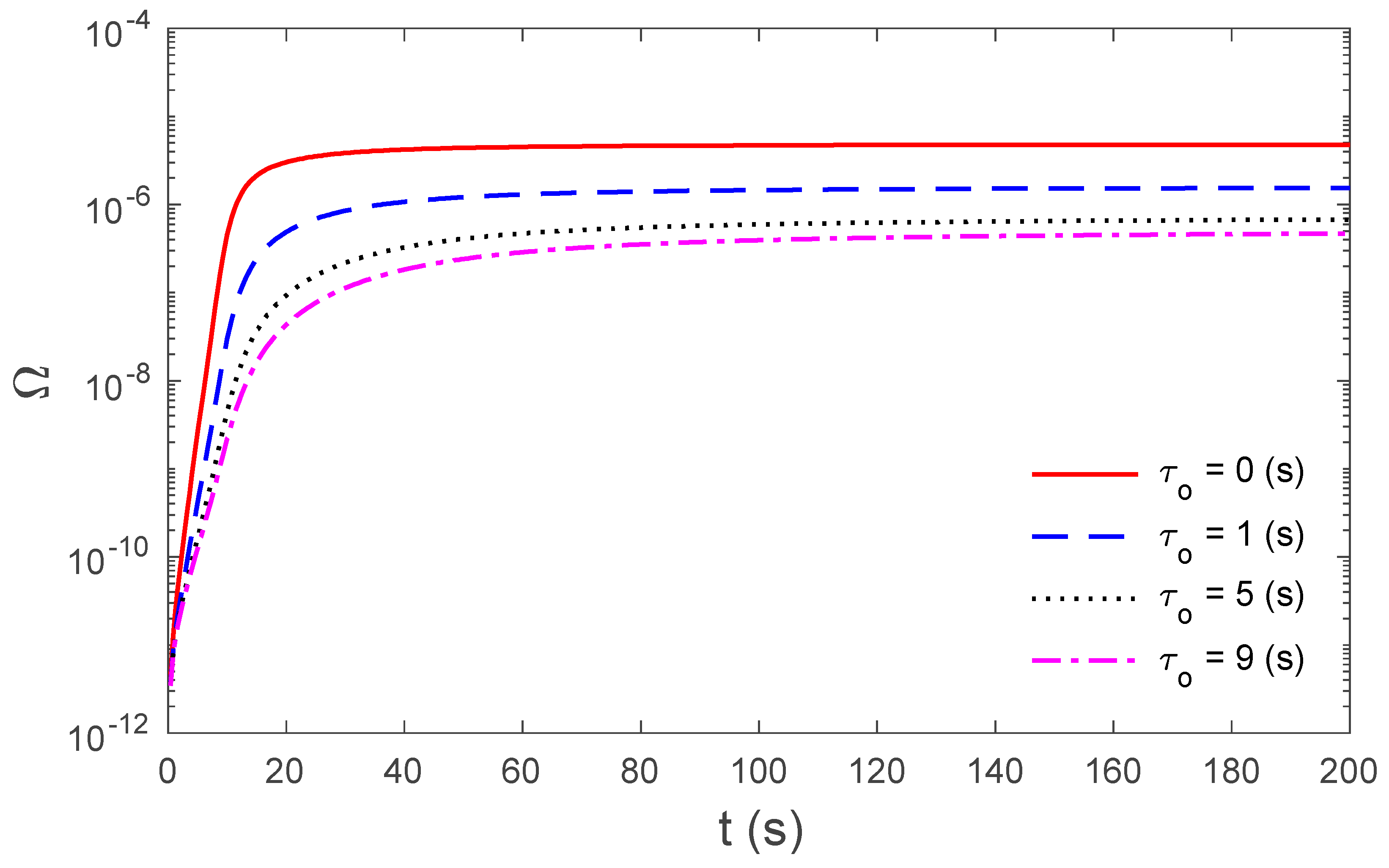
3. Results and Discussions
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Mahjoob, S.; Vafai, K. Analytical characterization of heat transport through biological media incorporating hyperthermia treatment. Int. J. Heat Mass Transf. 2009, 52, 1608–1618. [Google Scholar] [CrossRef]
- Gabay, I.; Abergel, A.; Vasilyev, T.; Rabi, Y.; Fliss, D.M.; Katzir, A. Temperature-controlled two-wavelength laser soldering of tissues. Lasers Surg. Med. 2011, 43, 907–913. [Google Scholar] [CrossRef] [PubMed]
- Zhou, J.; Chen, J.; Zhang, Y. Dual-phase lag effects on thermal damage to biological tissues caused by laser irradiation. Comput. Biol. Med. 2009, 39, 286–293. [Google Scholar] [CrossRef] [PubMed]
- Pennes, H.H. Analysis of tissue and arterial blood temperatures in the resting human forearm. J. Appl. Physiol. 1948, 1, 93–122. [Google Scholar] [CrossRef] [PubMed]
- Cattaneo, C. A form of heat conduction equation which eliminates the paradox of instantaneous propagation. Compt. Rendu 1958, 247, 431–433. [Google Scholar]
- Vernotte, P. Les paradoxes de la theorie continue de l’equation de la chaleur. Compt. Rendu 1958, 246, 3154–3155. [Google Scholar]
- Hobiny, A.D.; Abbas, I.A. Theoretical analysis of thermal damages in skin tissue induced by intense moving heat source. Int. J. Heat Mass Transf. 2018, 124, 1011–1014. [Google Scholar] [CrossRef]
- Gupta, P.K.; Singh, J.; Rai, K. Numerical simulation for heat transfer in tissues during thermal therapy. J. Therm. Biol. 2010, 35, 295–301. [Google Scholar] [CrossRef]
- Gupta, P.K.; Singh, J.; Rai, K.; Rai, S. Solution of the heat transfer problem in tissues during hyperthermia by finite difference–decomposition method. Appl. Math. Comput. 2013, 219, 6882–6892. [Google Scholar] [CrossRef]
- Dillenseger, J.-L.; Esneault, S. Fast FFT-based bioheat transfer equation computation. Comput. Biol. Med. 2010, 40, 119–123. [Google Scholar] [CrossRef]
- Zhu, D.; Luo, Q.; Zhu, G.; Liu, W. Kinetic thermal response and damage in laser coagulation of tissue. Lasers Surg. Med. 2002, 31, 313–321. [Google Scholar] [CrossRef] [PubMed]
- Ezzat, M.A.; AlSowayan, N.S.; Al-Muhiameed, Z.I.; Ezzat, S.M. Fractional modelling of Pennes’ bioheat transfer equation. Heat Mass Transf. 2014, 50, 907–914. [Google Scholar] [CrossRef]
- Ezzat, M.A.; El-bary, A.A.; Al-sowayan, N.S. Tissue responses to fractional transient heating with sinusoidal heat flux condition on skin surface. Anim. Sci. J. 2016, 87, 1304–1311. [Google Scholar] [CrossRef] [PubMed]
- Ghanmi, A.; Abbas, I.A. An analytical study on the fractional transient heating within the skin tissue during the thermal therapy. J. Therm. Biol. 2019, 82, 229–233. [Google Scholar] [CrossRef]
- Mondal, S.; Sur, A.; Kanoria, M. Transient heating within skin tissue due to time-dependent thermal therapy in the context of memory dependent heat transport law. Mech. Based Des. Struct. Mach. 2019, 1–15. [Google Scholar] [CrossRef]
- Díaz, S.H.; Nelson, J.S.; Wong, B.J. Rate process analysis of thermal damage in cartilage. Phys. Med. Biol. 2002, 48, 19. [Google Scholar] [CrossRef]
- Abbas, I.A.; Zenkour, A.M. The effect of rotation and initial stress on thermal shock problem for a fiber-reinforced anisotropic half-space using Green-Naghdi theory. J. Comput. Theor. Nanosci. 2014, 11, 331–338. [Google Scholar] [CrossRef]
- Abbas, I.A.; El-Amin, M.; Salama, A. Effect of thermal dispersion on free convection in a fluid saturated porous medium. Int. J. Heat Fluid Flow 2009, 30, 229–236. [Google Scholar] [CrossRef]
- Abbas, I.A. The effects of relaxation times and a moving heat source on a two-temperature generalized thermoelastic thin slim strip. Can. J. Phys. 2015, 93, 585–590. [Google Scholar] [CrossRef]
- El-Naggar, A.; Kishka, Z.; Abd-Alla, A.M.; Abbas, I.A.; Abo-Dahab, S.M.; Elsagheer, M. On the initial stress, magnetic field, voids and rotation effects on plane waves in generalized thermoelasticity. J. Comput. Theor. Nanosci. 2013, 10, 1408–1417. [Google Scholar] [CrossRef]
- Marin, M. Cesaro means in thermoelasticity of dipolar bodies. Acta Mech. 1997, 122, 155–168. [Google Scholar] [CrossRef]
- Marin, M.; Ellahi, R.; Chirilă, A. On solutions of Saint-Venant’s problem for elastic dipolar bodies with voids. Carpathian J. Math. 2017, 33, 219–232. [Google Scholar]
- Marin, M.; Nicaise, S. Existence and stability results for thermoelastic dipolar bodies with double porosity. Contin. Mech. Thermodyn. 2016, 28, 1645–1657. [Google Scholar] [CrossRef]
- Abbas, I.A. Nonlinear transient thermal stress analysis of thick-walled FGM cylinder with temperature-dependent material properties. Meccanica 2014, 49, 1697–1708. [Google Scholar] [CrossRef]
- Zenkour, A.M.; Abbas, I.A. Magneto-thermoelastic response of an infinite functionally graded cylinder using the finite element method. J. Vib. Control. 2014, 20, 1907–1919. [Google Scholar] [CrossRef]
- Gardner, C.M.; Jacques, S.L.; Welch, A. Light transport in tissue: Accurate expressions for one-dimensional fluence rate and escape function based upon Monte Carlo simulation. Lasers Surg. Med. 1996, 18, 129–138. [Google Scholar] [CrossRef]
- Stehfest, H. Algorithm 368: Numerical inversion of Laplace transforms [D5]. Commun. ACM 1970, 13, 47–49. [Google Scholar] [CrossRef]
- Henriques, F., Jr.; Moritz, A.R. Studies of thermal injury: I. The conduction of heat to and through skin and the temperatures attained therein. A theoretical and an experimental investigation. Am. J. Pathol. 1947, 23, 530. [Google Scholar]
- Moritz, A.R.; Henriques, F., Jr. Studies of thermal injury: II. The relative importance of time and surface temperature in the causation of cutaneous burns. Am. J. Pathol. 1947, 23, 695. [Google Scholar]
- Askarizadeh, H.; Ahmadikia, H. Analytical analysis of the dual-phase-lag model of bioheat transfer equation during transient heating of skin tissue. Heat Mass Transf. 2014, 50, 1673–1684. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hobiny, A.; Alzahrani, F.; Abbas, I.; Marin, M. The Effect of Fractional Time Derivative of Bioheat Model in Skin Tissue Induced to Laser Irradiation. Symmetry 2020, 12, 602. https://doi.org/10.3390/sym12040602
Hobiny A, Alzahrani F, Abbas I, Marin M. The Effect of Fractional Time Derivative of Bioheat Model in Skin Tissue Induced to Laser Irradiation. Symmetry. 2020; 12(4):602. https://doi.org/10.3390/sym12040602
Chicago/Turabian StyleHobiny, Aatef, Faris Alzahrani, Ibrahim Abbas, and Marin Marin. 2020. "The Effect of Fractional Time Derivative of Bioheat Model in Skin Tissue Induced to Laser Irradiation" Symmetry 12, no. 4: 602. https://doi.org/10.3390/sym12040602
APA StyleHobiny, A., Alzahrani, F., Abbas, I., & Marin, M. (2020). The Effect of Fractional Time Derivative of Bioheat Model in Skin Tissue Induced to Laser Irradiation. Symmetry, 12(4), 602. https://doi.org/10.3390/sym12040602





