1. Introduction
Metabolic Syndrome (MetS) encompasses a group of cardiovascular risk factors that increase the likelihood of suffering heart and other metabolic illnesses, such as cerebrovascular stroke and diabetes.
MetS was first described by Kylin in 1920 as the coexistence of hypertension, hyperglycemia, and gout [
1]. In 1940, the central obesity component was added [
2]; since then, several definitions have been used to describe it, even different names have been given, such as the X syndrome, the insulin resistance syndrome [
3] or the deadly quartet [
4].
Due to the controversy regarding a worldwide definition, in 1998, an international initiative gather-up in an attempt to achieve an agreement on this matter. The World Health Organization (WHO 1999) proposed a set of criteria [
5], then the National Cholesterol Education Program’s Adult Treatment Panel III (NCEP: ATP III-2004) [
6] and the European Group on the Study of Insulin Resistance (IDF) [
7] (
Table 1). Even though these definitions agree on the essential components (glucose intolerance, obesity, hypertension, and dyslipidemia), there is a disagreement in the cutoff points of some components as well as in the cluster of components that should be included, an example of this is the anthropometric indexes that have been used to define obesity and central obesity. Also, because the distribution of adipose tissue may vary concerning age, gender and ethnicity, these proposed definitions have failed to appropriately classify a specific population or ethnic group, such as Africans, Latin-Americans or Japanese, among others.
On the other hand, machine learning, a sub-discipline of artificial intelligence has had a high tendency in health research, providing methods and techniques that have been successfully applied in a variety of medical domains and the early diagnosis of several diseases such as hypertension [
8,
9] diabetes [
10,
11], and MetS [
12,
13].
One of the first medical research applying machine learning algorithms [
14], used the blood pressure data of 300 clinically healthy participants and 85 subjects with hypertension. An expert system applying neural networks was developed to diagnose and treat high blood pressure; the final system acieved 94% accuracy, this means that 94 out of every 100 participants were correctly diagnosed, either positives or negatives.
The use of machine learning to predict the MetS, applying algorithms such as decision tree [
15,
16], logistic regression [
17], Naïve Bayes [
18] and support vector machine (SVM) [
19] among others, have achieved high performance. Karimi-Alavijeh et al. [
20] used a decision tree and their results showed that SVM had a better performance, with an accuracy of 75%. Barakat et al. [
21] also used SVM and other algorithms, such as the rule-based RIPPER (JRip), Classification and Regression Trees (CART), and C5.0 tree (C5) for diagnosis of MetS; however, the SVM achieved the best performance with an accuracy of 97%.
Artificial Neural Networks (ANN) have as well obtained a high performance in the prediction of MetS. Hirose et al. [
13] predicted successfully the 6-year incidence of MetS using an ANN, with a sensitivity of 0.93 and a specificity of 0.91. Lin et al. [
17] used ANN and logistic regression models to identify MetS in patients with second-generation antipsychotics treatment; as a result, the ANN (88.3%) achieved the best performance in accuracy, though logistic regression (83.6%) does not differ much from the ANN. Sedehi et al. [
22] concluded that machine learning algorithms compared to logistic regression and discriminant analysis has better performance to predict MetS with higher accuracy.
Random Forest, another machine learning algorithm, has been applied in the prediction of MetS [
23,
24]. This algorithm performs a classification and regression process and the ranking of prognostic variables to support the early diagnosis or prediction of a specific disease. Apilak Worachartcheewan et al. [
25] determined the prevalence of MetS and achieved an accuracy above 98%. According to related research, the value obtained with Random Forest to predict MetS was higher than SVM and ANN.
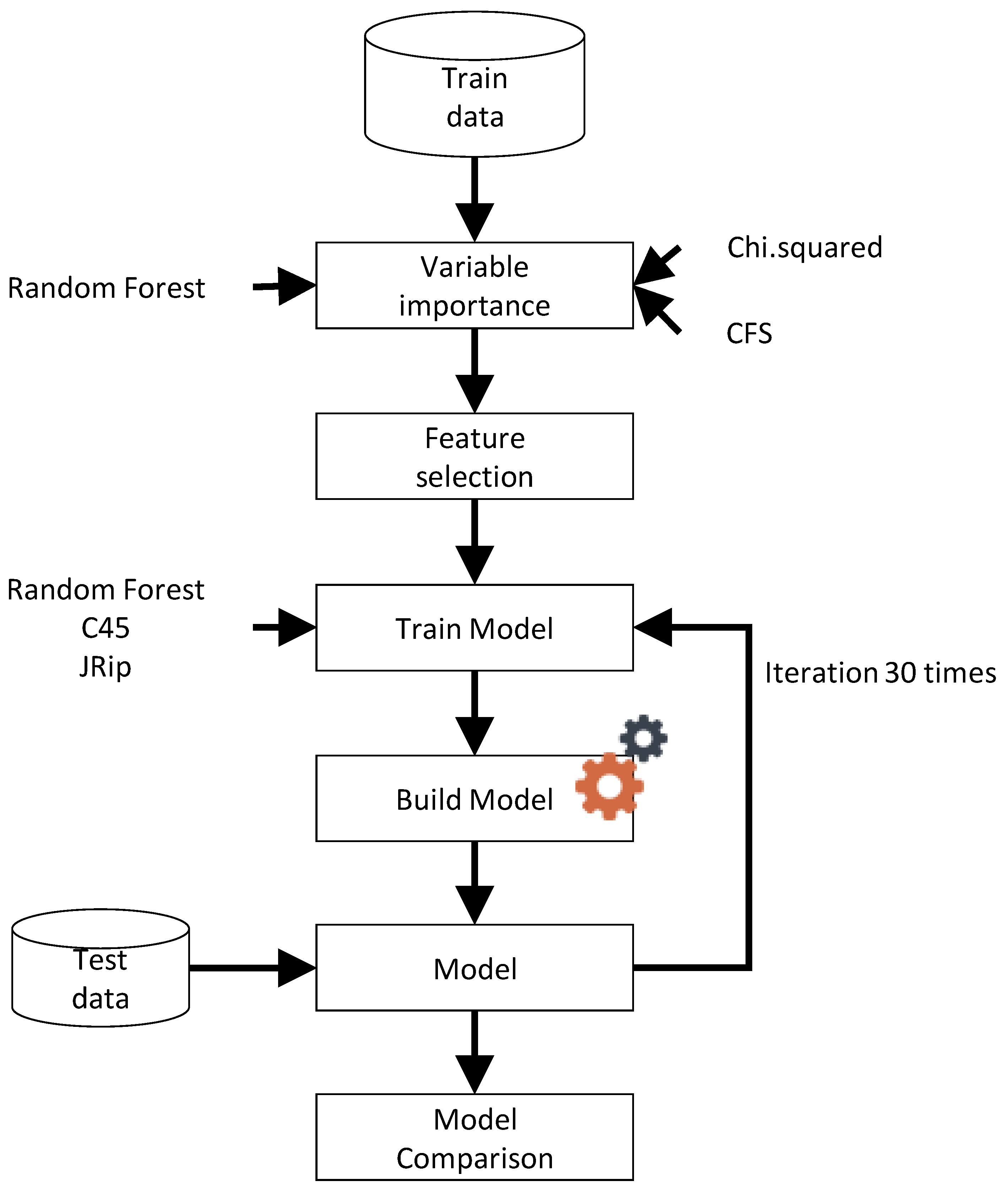
In this study, machine learning algorithms were used to rank the health parameters to determine the most appropriate variables for the classification of MetS in the Mexican population, using the Mexico City Tlalpan 2020 cohort [
26] data set. We look for some new information, although there are symmetric relationships between findings in the established literature. Correlation-based Feature Selection (CFS) was applied as well as, chi.squared filter methods to select relevant features in MetS diagnosis. Several experiments were performed to create the predictive models, applying JRip, C4.5 and Linear SVM classifiers. The performance among the different models was compared.
Filter methods help to identify those variables that were the most important for classification and discard those that were not important. Their advantages are simplicity, speed, and low computational cost. Filter methods used in this study were obtained from the FSelector R package [
27].
JRip, C4.5, and Linear SVM are known for getting good results in classification tasks [
28,
29,
30]. JRip and C4.5 also provide predictive models, understandable by humans. JRip and C4.5 were taken from the RWeka R Package [
31,
32].
This paper is structured as follows: in
Section 2, the materials and methods are introduced. In
Section 3, the experiment’s performance is presented. A discussion (
Section 4) and conclusion (
Section 5) complete this paper, as well as some ideas for future works.
3. Results
In this study, we used a data set from a cohort study called Tlalpan 2020 (the study protocol for this cohort was published elsewhere [
26]). The ATP III criteria were applied (see
Table 1) to identify influential cardiovascular risk factors and classify participants with or without MetS.
Figure 1 shows a general diagram of our proposed model, where the first step was to identify the variable importance of all data set applying Random Forest, chi-squared and CFS. The results obtained indicate the most important variables (features), which were used to train different models using Random Forest, C45, and JRip. Models were created using 30 independent iterations, as it is the typical number used in the literature for fair comparisons among experiments [
51,
52]. Then, their performance was compared considering balanced accuracy, sensitivity, and specificity.
The prevalence of MetS according to ATP III criteria was 20.5% (603 participants), and no significant differences were identified between sexes (with MetS: women 20.6% vs. men 20.4%, without MetS: women 79.4% vs. men 79.6%).
The median and interquartile range (IQR) of anthropometric, clinical, and biochemical parameters are shown in
Table 2. Participants with MetS were significantly older than those without MetS and showed higher values of all anthropometric and clinical parameters. Concerning biochemical parameters, MetS participants had substantially higher values than those without MetS.
Variable Importance and Prediction Model
As a first step, we identify the most important variables of the data set using Random Forest algorithm to construct the corresponding model, where the number of trees (ntree) varied between 100 to 1000 (ntree = 100, 200, 300, 500, 800, and 1000) and the mtry value varied between 1 to 10, applying the grid search method proposed by Hsu et al. [
53]. Also, 10-fold cross-validation with ten repeats to train the model was used to ensure all data. Once the training process was finished and the best parameters were found and applied, the variable importance was obtained.
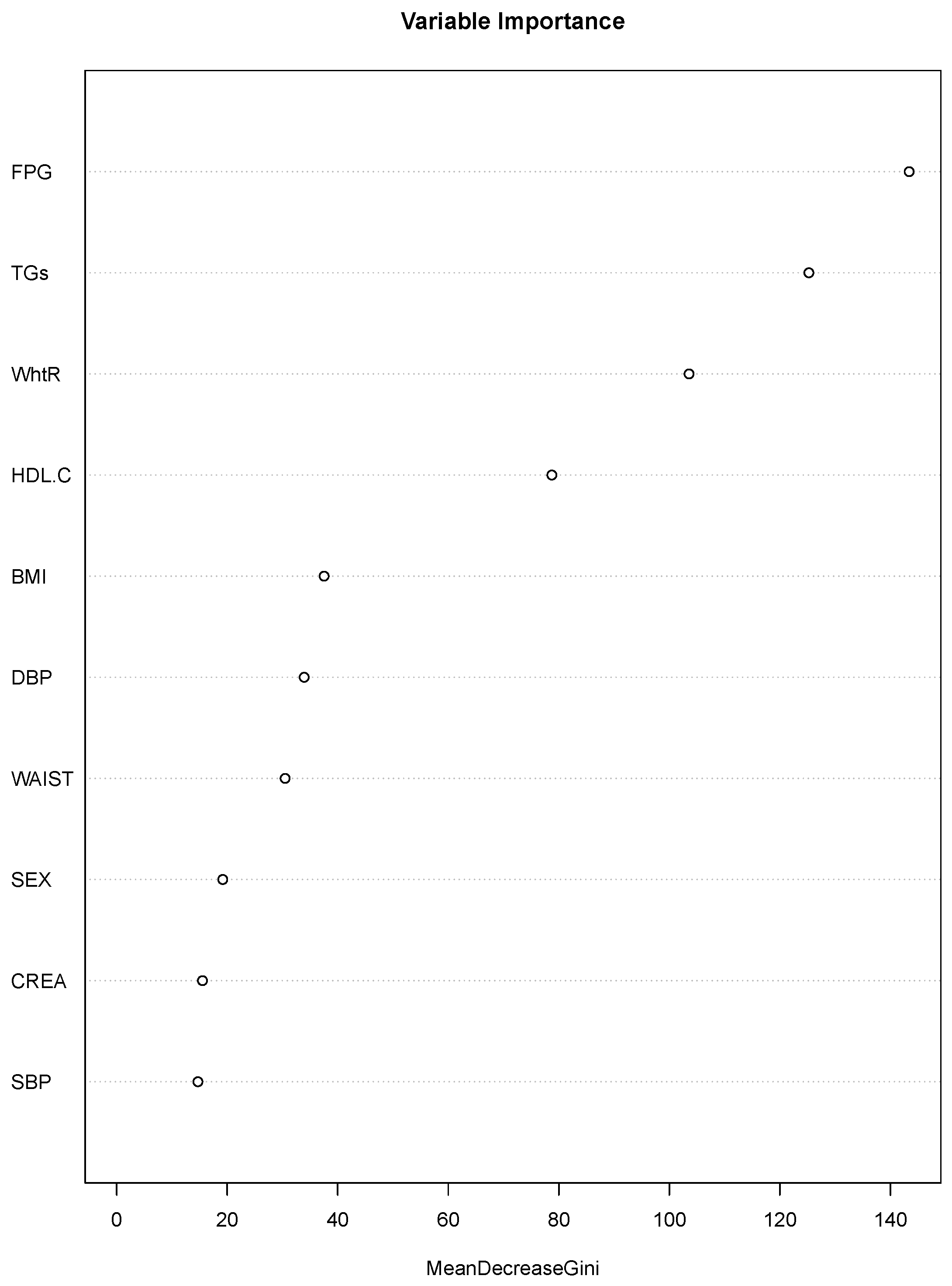
Figure 2 shows the features attained by the model, where the best value in mtry was 10 and in ntree was 1000, to achieve a balanced accuracy of 0.9675 and a standard deviation (SD) of 0.0006.
In
Figure 2, the variable importance is shown. FPG displayed the highest value of importance, followed by TGs, WHtR, and HDL.C; then there was a second group (BMI, DBP, and waist) and SEX, CREA and SBP showed the lowest values. Three of the four variables within the first group are considered to be indicators used by ATP III to identify MetS. However, the anthropometric index that ATP III uses to identify abdominal obesity is the waist. In our results, this index showed a lower value of importance than WHtR and even than BMI. Therefore, considering the role that abdominal obesity has as a cardiometabolic risk factor, the importance of each of the three anthropometric indexes (WHtR, BMI and waist) was tested. We performed experiments where WEIGHT, HEIGHT, and BMI, waist or WHtR were eliminated depending on the case, and a separate algorithm was built applying Random Forest and chi.squared.
Table 3 shows the variable importance of BMI, WHtR and WAIST using Random Forest. WHtR was placed in the second position with a value higher (146.4299) than BMI (118.7353) and WAIST (118.6575), which were placed in the third position.
Table 4, shows the variable importance of BMI, WHtR and WAIST, using chi.squared. Even though the three anthropometric indexes were placed in the third position, WHtR achieved a higher value (0.5118) than WAIST (0.5068) and BMI (0.4975). As for the last six variables for which the importance was 0, it means that they are not important for diagnosing MetS according to chi.squared filter, therefore they can be discarded from the models.
Once the importance of the variables was obtained with Random Forest (see
Table 3) and chi.squared (
Table 4), the models for each anthropometric index (WHtR, WAIST, and BMI) using Random Forest, C45 and JRIP as classifiers were developed.
In
Table 5, the performance of the 30 models developed for each anthropometric index (WHtR, WAIST, and BMI) using Random Forest, C45 and JRIP as classifiers are shown. The classifier that performed best was the Random Forest for the three anthropometric indexes; however, WAIST showed the highest importance. On the other hand, C45 and JRIP obtained lower importance for the three anthropometric indexes, and the highest importance was observed for the WHtR.
Since ATP III is one of the most used guidelines in Latin America to define the MetS, we constructed three models, one to measure the performance of variables used by ATP III (see
Table 6), another to measure the same ATP III variables, replacing WAIST for WHtR (see
Table 7) and the last one to measure the same ATP III variables using the BMI instead of WAIST.
Table 6,
Table 7 and
Table 8 show sensitivity, specificity, and the balanced accuracy, as well as their respective standard deviations of the average performance for the 30 models generated for each case. In the case of the model using ATP III variables (
Table 6), the best performance was attained by Random Forest with a Balanced Accuracy of 0.8754 and an SD of 0.0036, followed by JRip (0.8723, 0.0203). The worst average performance was attained by SVM linear with a cost = 100, where the Balanced Accuracy was 0.7561 and the SD was 0.0136. The model in which WAIST was replaced with WHtR achieved the best performance with JRip with a balanced accuracy of 0.8926 and an SD of 0.0142, followed by Random Forest (0.8905, 0.0022), the worst average performance was attained by SVM linear with a cost = 50 (0.7812, 0.0154).
Finally, the model using ATP III variables, replacing WAIST with BMI, achieved the best performance model with JRip with a balanced accuracy of 0.8691 and an SD of 0.0168, followed by Random Forest (0.8650, 0.0033), the worst average performance was attained by SVM linear with a cost = 50 (0.7694, 0.0153).
The executed experiments showed that the model using the ATP III variables with WHtR instead of WAIST achieved the best performance, whereby could be a useful index for the identification of MetS in a Mexican population, along with the variables already proposed by ATP III.
4. Discussion
In this study, a set of health parameters was ranked applying Random Forest and compared with chi.squared and CFS filter methods to obtain the variable importance. These results showed that the main prognostic variables of MetS in our cohort of the Mexico City population according to its importance were: FPG, TGs, WHtR, HDL-C, and BMI, four out of these five variables are among those proposed by the WHO, IDF and ATP III criteria for the classification of people with MetS; however, not taking into consideration its predictability importance. Other studies have also found these prognostic variables; however, using different classification methods [
15,
20,
54].
An interesting result was that WHtR was considered the third variable in order of importance, which is an important finding especially concerning the obesity epidemic in our country [
55], and its relationship with cardiovascular disease, which is the first cause of morbidity and mortality worldwide and in Mexico.
Abdominal obesity has become an indicator of cardiometabolic risk. Therefore, significant efforts have been made to find the proper anthropometric measurement that reflects the accumulation of fat tissue in the abdominal area and can be easily obtained without high technology equipment.
It is also true that anthropometric indexes are importantly influenced by age, gender, and ethnicity, among other factors, and therefore, finding the appropriate one could be an overwhelming task. BMI has been used as an indicator of body fatness; however, it does not reflect abdominal obesity. Furthermore, BMI might scale to height with other power than 2, and therefore erroneous conclusions might be made regarding the adipose composition in people with different heights [
56].
In recent years, abdominal obesity indexes such as BMI, WAIST, and recently the WHtR have been proposed as indicators of a high cardiometabolic risk [
57,
58].
A systematic review that included seventy-eight cross-sectional and prospective studies analyzed the predicting capability of WHtR, WAIST, and BMI to identify the risk of diabetes and CVD, and found that WHtR, WAIST, and BMI are useful predictors for this matter, furthermore, balance and adjusted data suggested that WHtR and WAIST are stronger predictors than BMI [
59]. Browning et al. [
59] suggest that “Keep your waist circumference to less than half your height”, could be a suitable cutoff point for all ethnic groups.
In a more recent systematic review and meta-analysis, Ashwell et al. [
57], aimed to differentiate the screening potential of WHtR and WAIST for adult cardiometabolic risk (hypertension, diabetes, dyslipidemia, MetS, and overall cardiovascular outcomes) and found that WHtR had significantly higher discriminatory power compared with BMI. However, most importantly, statistical analysis of the with-in study showed that WHtR was a better predictor than WAIST for hypertension, diabetes, cardiovascular disease, and all outcomes in both genders.
The predictive capability of WHtR has been tested in several populations [
58,
60,
61,
62,
63].
Comparing WHtR, WAIST, and BMI
To compare the importance value of WHtR, WAIST, and BMI separately in the complete data set we applied Random Forest and chi.squared. The results showed that WHtR is the most important variable since it obtained the highest values with Random Forest (see
Table 3) and chi.squared (
Table 4). Likewise, in the results shown in
Table 5, WHtR achieved the best performance in balanced accuracy, sensitivity, and specificity with C45 and JRip, using CFS as a feature selection method, even if WAIST achieves better performance with Random Forest.
The ATP III guidelines are the most used to diagnose MetS; however, ethnic and regional characteristics need to be recognized to adjust the parameters for the diagnosis of abdominal obesity. Thus, the performance of WHtR and BMI using the variables of ATP III except for the WAIST was proved. The results in
Table 6 show the performance of the model using only ATP III variables, where Random Forest achieves the highest value (0.8754). In
Table 7, BMI reached the best performance with JRip (0.8691); however, it fails to reach the value obtained by WAIST. The values attained by WHtR showed the best performance using all classifiers, highlighting Random Forest with the highest values. This shows that for our study, using data from the Mexico City Tlalpan 2020 cohort participants, the WHtR in combination with the variables of ATP III (except for the waist) achieves a better performance in classification than the WAIST and BMI.
5. Conclusions
Machine learning algorithms have become a useful prognostic tool in medicine [
64] to predict different medical outcomes such as treatment response to (chemo)radiotherapy [
65], study metabolomic [
66], and to identify the association between microbes, metabolites and abdominal pain in children with irritable bowel syndrome [
67]. In our case, we used Random Forest to rank health parameters evaluating the prediction performance of the algorithm by accuracy (97%), sensitivity (97%) and specificity (93%). Even though the results of Apilak Worachartcheewan et al. [
25] are similar to ours, they obtained an accuracy of 98% using Random Forest to determine MetS prevalence. However, when using other algorithms, such as SVM, results have shown an important variability, for instance, Karimi Alavijeh et al. [
20] achieved an accuracy of 75%, while Barakat et al. [
21] achieved an accuracy of 97%. Similar results were published using ANN; Hirose et al. [
13] reported a sensitivity of 93% and a specificity of 91%. Lin et al. [
17] achieved a lower accuracy (88.3%) using the same technique and 83.6% applying logistic regression. However, it is necessary to emphasize that an adequate feature selection and feature ranking significantly impacts the performance and computational burden of machine learning algorithms [
11].
In this study, we only included a population living in Mexico City. Nevertheless, MetS encompasses chronic degenerative diseases with a significant genetic burden. Also, Mexico is a country with a wide variety of ethnic groups. Therefore, it will be essential to include populations from other regions of Mexico to have these ethnicities, cultures, customs, lifestyles, diet, and anthropometric characteristics represented and to develop an algorithm that can be applied throughout Mexico to detect and predict the MetS.
Finally, machine learning algorithms have potential applicability in medicine for diagnosis, being Random Forest the most useful algorithm for prediction and ranking variables; in our Tlalpan 2020 cohort, FPG, TGs, WHtR, HDL-C, BMI, DBP, and WAIST were the most important variables to diagnose (or predict) MetS, these results were similar to those found in other cohorts [
15,
25,
54]. Likewise, results using JRip, C4.5, Knn, SVM and Random Forest, showed that WHtR could be a useful index for the identification of MetS, along with other variables proposed by ATP III.