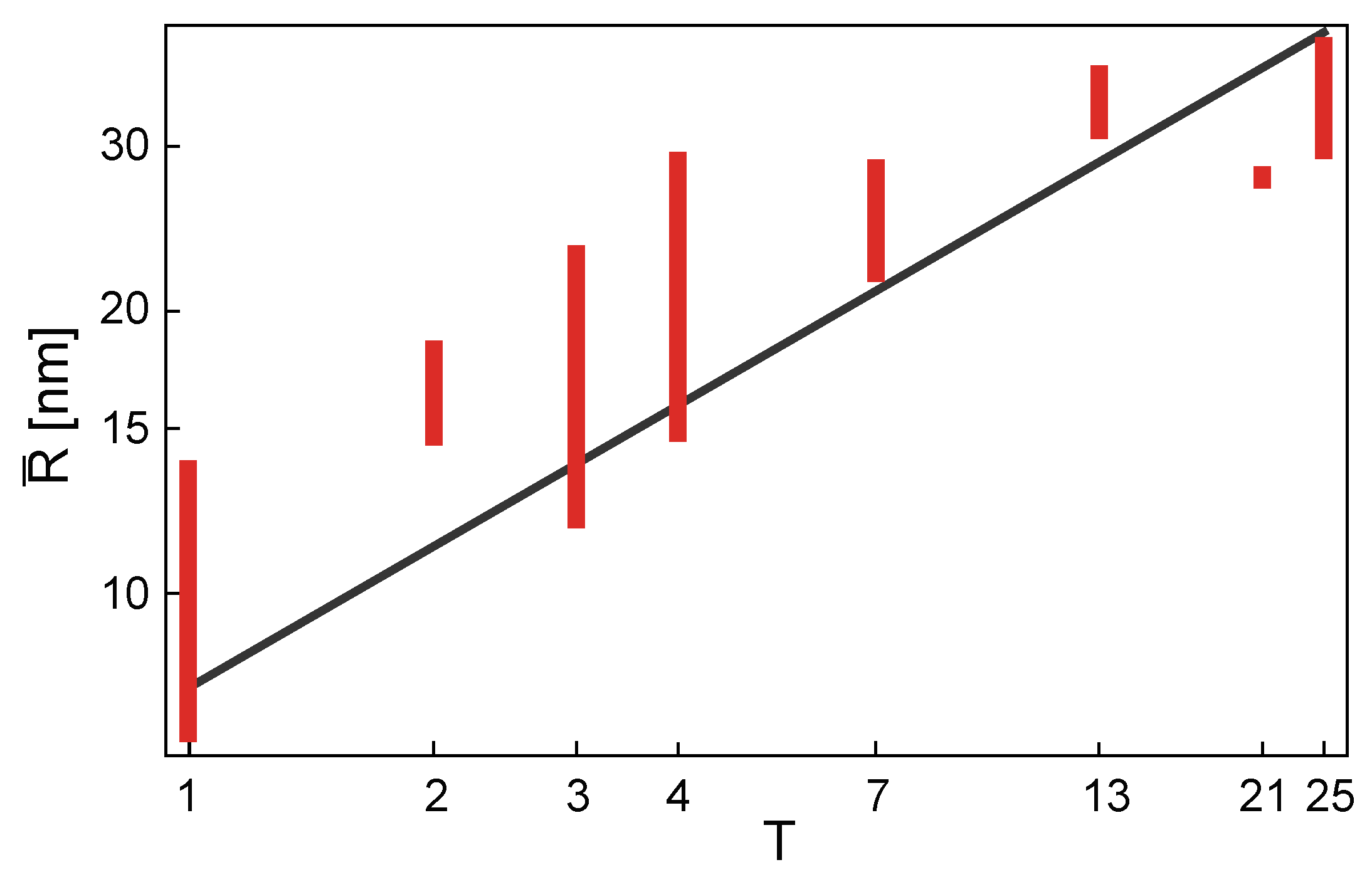Icosadeltahedral Geometry of Geodesic Domes, Fullerenes and Viruses: A Tutorial on the T-Number

Abstract

The Caspar–Klug (CK) classification of viruses is discussed by parallel examination of geometry of icosahedral geodesic domes, fullerenes, and viruses. The underlying symmetry of all structures is explained and thoroughly visually represented. Euler’s theorem on polyhedra is used to calculate the number of vertices, edges, and faces in domes, number of atoms, bonds, and pentagonal and hexagonal rings in fullerenes, and number of proteins and protein–protein contacts in viruses. The T-number, the characteristic for the CK classification, is defined and discussed. The superposition of fullerene and dome designs is used to obtain a representation of a CK virus with all the proteins indicated. Some modifications of the CK classifications are sketched, including elongation of the CK blueprint, fusion of two CK blueprints, dodecahedral view of the CK shapes, and generalized CK designs without a clearly visible geometry of the icosahedron. These are compared to cases of existing viruses.

1. Introduction

Although the fullerene molecules were theoretically predicted and discussed [1], it was nevertheless a surprise for the largest part of the scientific community when Kroto et al. published a paper announcing their experimental discovery [2]. Some of the surprise can be attributed to an impressive and amazingly symmetrical arrangement of carbon atoms in the most abundant of all the fullerene molecules—Buckminsterfullerene or C${}_{60}$. Kroto and colleagues named this molecule after Richard Buckminster Fuller, who was well known in his time for his far reaching ideas, envisioning new ways of living and working that are popular and perhaps more relevant today than they ever were. Still, he is perhaps [2] most recognized for popularizing geodesic domes—networks of interconnected struts forming a (hemi)spherical grid. Fuller constructed them as an alternative to typical 1960’s architecture in the USA [3]. Perhaps the most famous Fuller’s dome housed the American pavilion for the 1967 World Expo exhibition in Montreal. Yet, the basic geometry and symmetry behind such structures was known at least since 1937 when Goldberg discussed a class of polyhedra, now often called Goldberg polyhedra, with only pentagonal and hexagonal faces [4].

Fuller’s geodesic domes were not chiral [5] (i.e., they were equal to their mirror images), and even before the discovery of fullerenes, it was known that achiral domes that Fuller constructed belong to a larger class of mathematical structures, which also includes chiral (or skew) objects. It was already known that fullerian-like designs are not only artificial constructions but are realized in structures occurring in nature. Pollen grains were observed to sometimes have dome-like shapes, formed apparently by many similar elements or modules, or at least with their surface divided in such a way to exhibit similarity to geodesic domes [6,7]. From Haeckel’s beautiful and precise illustration [8,9], some Radiolaria were known to have geodesic-dome-like structures, although, in addition to hexagonal and pentagonal faces, they contained some heptagonal faces [9,10], which do not appear in Fuller’s design and are not a feature of icosadeltahedral constructions that will be discussed in the following. Perhaps it was then not so surprising that viruses were proposed to have a similar modular, dome-like structure. Extending Fuller’s design ideas [11,12], in the year 1962, Donald Caspar and Aaron Klug constructed the first theory that explained the features of most of the so-called ”spherical” (icosahedral) viruses known at the time [13].

It is intriguing that objects so different in size (fullerenes—1 nm, viruses—100 nm, and geodesic domes—100 m), in addition to history, also share the design and symmetry. A partial reason for this must have something to do with the fact that all these objects are built up of identical or nearly identical elements or modules—carbon atoms in fullerenes, proteins in viruses, and struts in geodesic domes—which arrange so to fully enclose the object interior, i.e., to form a cage-like structure. The nearly identical elements are in nearly identical surroundings, which is the essence of the concept used to rationalize the appearance of such shapes in viruses—the quasiequivalence concept. Caspar and Klug note that the appearance of a (nearly) symmetrical structure is a necessary outcome of the arrangement of (nearly) identical units in (nearly) identical environments [13].

The aim of this paper is to explain the design principles and symmetries of a large subset of these objects, which can be called icosadeltahedral. The term was used by Caspar and Klug in their seminal paper [13] and will be explained and often used in what follows. The language of the paper is, thus, perhaps most similar to the one used by Caspar and Klug [5,13]. The objects of interest are the icosahedral geodesic domes, fullerenes, and viruses, and a parallel examination of these objects will be used to illustrate the universality and versatility of CK blueprint and provide a wide view of the CK quasiequivalent construction.

There have been many reviews of virus structure in the past (see, e.g., [14]), and it would be impractical to count them all here—perhaps one of the best references to quickly grasp the basic ideas and forms is still the early paper by Caspar and Klug [13]. The parallels between the fullerenes, geodesic domes, and viruses have also been discussed [10,11,15,16], which leaves a restricted space for the originality of this work. Yet, the basic Fuller–Caspar–Klug [1,13] blueprint can be extended to account for more complicated structures, although the extension may be clumsy, especially when not resorting to the powerful group-theoretical methods [17]. It is intriguing that many structures based on the modified or, at least, slightly reformulated blueprints have been observed, some relatively recently. These include different types of viruses, which require at least a subtle reformulation of the blueprint. Perhaps the most famous and well known such case is the one which already bothered D. Caspar [18]—the case of the SV-40 polyoma virus, which required only a slight, yet important modification of the general construction put forth by Caspar and Klug (CK). In recent years, it was proposed that such and similar cases (e.g., bovine papilloma virus) could be better viewed as dodecahedral structures or dodecahedral tessellations of the sphere [19]. There are also elongated viruses, typically bacteriophages, which require a different sort of modification allowing for elongation of the CK design [20]; somewhat similarly, the carbon nanotubes can be obtained by formally “elongating” the fullerenes. And yet, there are structures that are difficult to think of in terms of the CK construction but still fulfill some of the universal features guaranteed for the class of Goldberg polyhedra [4,17]—such is the case of the HIV virus [21,22] and fullerenes with lower symmetry [17]. Why and how such structures arise is still not entirely clear, yet it is important to note them, especially in the context of violation of the CK construction. Some extensions and violations of the CK construction, which are manifested in real objects, will also be briefly discussed, without the ambition of fully classifying them.

The article is certainly not a novel research contribution to the field but is neither a typical research review. A mathematician may view it as inadequate in terms of rigor and application of the full-blown machinery of group-theoretical symmetry concepts. A theoretical chemist, especially one doing work in graph-theoretical fields, may think the same, while a chemist dealing with electron structure may find it lacking substance with respect to quantum theoretical considerations explaining the stability and activity of different fullerenes. A structural virologist may find the discussion of geodesic domes and fullerenes irrelevant in the context of virus structure and may also note that the article does not cover the intricacies of protein structure, which enable the formation of the dome-like virus protein coatings. She/he may also note that the article does not discuss the biological and evolutionary reasons for the CK design and its violations, in particular. A physicist may note that the article does not go sufficiently deep in explaining why the same motif appears in many different systems and that it must have to do something with the overarching thermodynamic concepts that favor the formation of such structures in quite different circumstances. All of these remarks would be true. However, to cover even a single of these fields would require several thorough and extensive reviews. Nevertheless, the paper was written with the hope to clarify the different languages and approaches of authors working in different fields, yet on the objects that have the same symmetry and share many important characteristics that are fixed by the symmetry. It is surely of interest to add here that the key formula derived for viruses by CK (Equation (2)) [13] was in fact a rediscovery of the expression published 25 years earlier by M. Goldberg in a completely abstract, mathematical context [12].

The language of this work is simple in mathematical terms. This level of mathematical language was adopted with the aim of making the paper readable to a wide audience of researchers and students. That is also why the visualizations of structures and concepts are often used in place of mathematical formulas and theorems. This article is a significantly extended and appropriately updated rewrite of my unpublished manuscript, deposited in the year 2007 in the ArXiv database [23]. In particular, the parallels between the dome, fullerene, and virus designs have been additionally interlinked in Section 4.1. The virus is, both visually and mathematically represented as a sort of union of a geodesic (sub)dome in which triangular faces correspond to individual proteins and fullerenes in which bonds indicate the borders between the pentameric and hexameric clusters in viruses. In Section 4.2, possible ambiguities of the CK designs are discussed, particularly in the view that a distribution of protein density in a capsid may visually look like a distribution of protein dimers or trimers, rather than pentamers and hexamers, which is typically observed in CK shapes. The dependence of the virus size on its T-number is discussed in Section 4.3. The aim of this section is to provide a rough link between the CK structures of various T-numbers and the size and shape of their material manifestations in the form of virus capsids. A long yet non-exhaustive discussion of some of the structures requiring a modification of the CK rules is presented in Section 5. These include elongated CK designs, the fusion of two incomplete CK designs, dodecahedral view of the CK designs, and generalized CK designs without a clearly visible geometry of the icosahedron. All of these are compared to cases of existing viruses. The discussion also briefly touches some more recent studies of virus geometry, for example, the alternative and the so-called quasi-crystal approaches to virus tilings [19,24,25]. These are, however, covered only partially and to the extent that is compatible with the concept of this article.

2. Icosa(delta)hedral Geodesic Domes

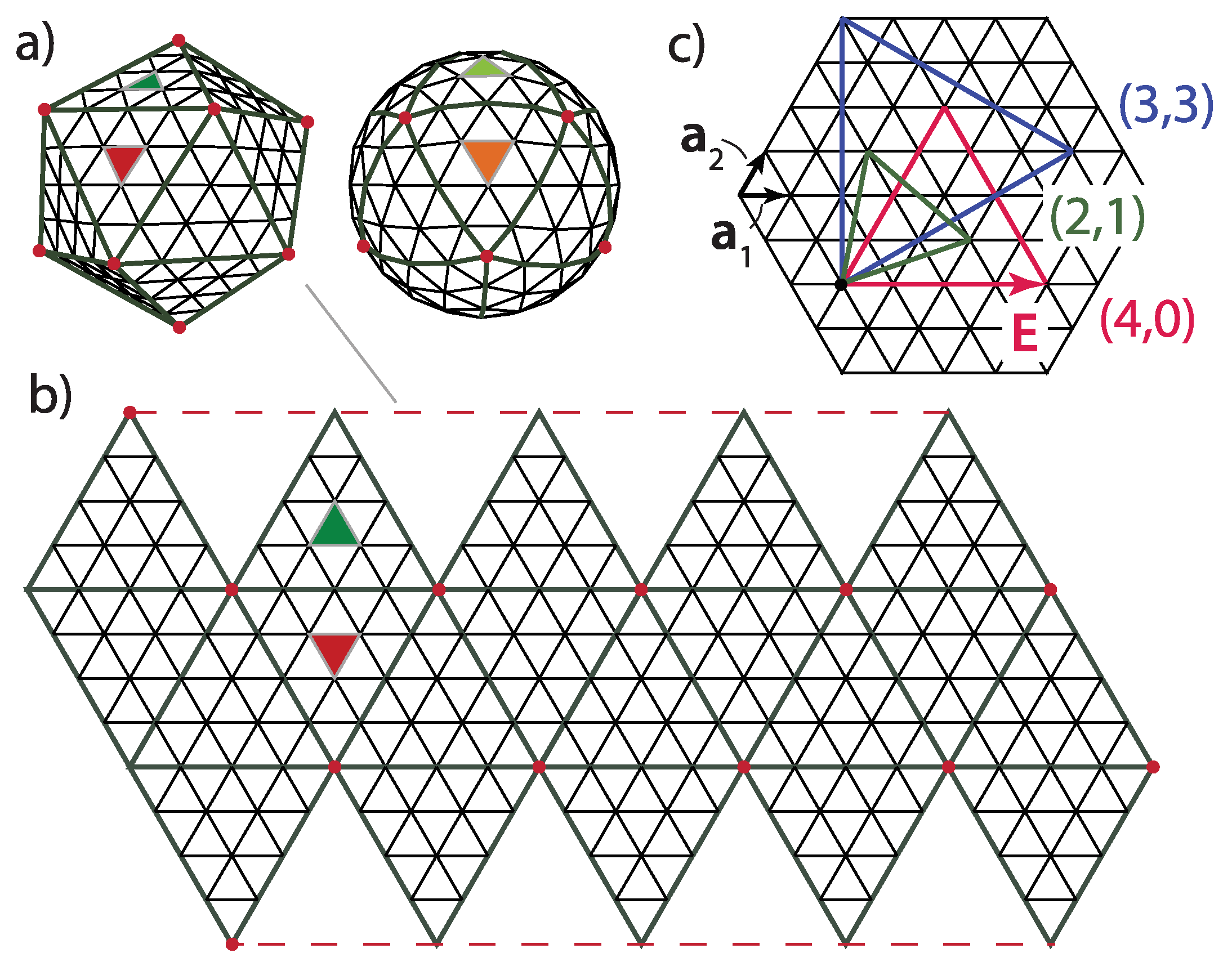
Geodesic domes, in general, are tessellations of a spherical surface (or a part of it). A perfect icosahedron can also be thought of as a simple geodesic dome, containing twenty triangular faces and twelve vertices, all on the same radial distance from the center, i.e., on a sphere. Each side of the (starting) icosahedron can be iteratively subdivided into equilateral triangles. The new vertices and faces obtained in such a way lie in planes of the original icosahedron faces, i.e., are not on a sphere. However, one can project them on a sphere containing the first twelve icosahedron vertices (Figure 1a). This procedure yields the geodesic domes of different iteration orders. All the faces of the thus obtained geodesic dome are triangles. The projection will change the areas of the faces obtained by the subdivision, depending on their position within the starting icosahedron face—the subdivided faces will not have the same edge lengths and areas once projected on a sphere. A typical (spherical) geodesic dome is thus not a deltahedron, i.e., a polyhedron in which all faces are equilateral triangles. This is a well known fact to real dome builders, and they know that they need several different strut lengths (edge lengths) in order to build a spherical or hemispherical dome [12]—the number of different strut length classes increases with the iteration order. If they were to build an icosahedron, all the required struts would have the same lengths because an icosahedron is a deltahedron.

The polyhedron can be unwrapped, i.e., cut along certain edges and flattened so that all of the polyhedron faces lie in the same plane—this is called a net (an unsolved mathematical problem is whether every (convex) polyhedron has a net, but this is not really important for our purposes). A net of a geodesic dome would contain triangles of different sizes, but it is easier to think of a net of an icosahedron whose faces have been subdivided/triangulated prior to projecting them on the sphere—such a polyhedron has a simple net, with the triangles/faces that are all equal and equilateral and which can be grouped within 20 larger triangles, the faces of the starting icosahedron (see Figure 1b). This is what is meant by the icosadeltahedral—the triangular subdivision of icosahedron faces that produces polyhedra with a larger number of triangular faces, which become unequal once the subdivided faces are projected on a sphere (Note here that the icosahedron with subdivided faces is not strictly convex and that there are neighboring triangular(sub)faces with a dihedral angle of $\pi$.). Such geodesic domes are thus triangulations of the sphere with the “icosahedral backbone”. The starting icosahedron can be detected in the subdivided polyhedra by exactly twelve vertices in which exactly five faces meet (these twelve vertices are called pentavalent)—these are the vertices of the starting icosahedron, and they have five nearest neighboring vertices (see Figure 1). Exactly six faces and edges meet in all other vertices (the remaining vertices are called hexavalent—they all have six nearest neighboring vertices). The “backbone” is, thus, a sort of the fixation of the subdivided structure in twelve points, i.e., the twelve vertices of the starting icosahedron. These twelve vertices can always be recognized in the subdivided structure, no matter how dense and fine the subdivision.

There are many ways to triangulate a sphere so that there are twelve points that make the vertices of an icosahedron and have five nearest neighbors, all other points having six nearest neighboring points. The different triangulation patterns can be obtained by overlapping the one face of the icosahedron—the equilateral triangle—with the triangular mesh, so that the three vertices of the icosahedron face coincide with the mesh points (see Figure 1c). This is also known as a Coxeter construction [17,26].

A three-dimensional illustration of the geometry discussed is shown in Figure 2. The neighboring points of the icosahedral vertices are outlined as thick pentagons. As already discussed, the icosadeltahedral geodesic domes are not (icosa)deltahedra since the triangles that they consist of are not equilateral. The requirement that all of the polyhedral faces be equilateral or nearly equilateral triangles necessarily produces aspherical (spiky) polyhedra (see Figure 2), quite different from the geodesic domes, which can also be considered as polyhedral approximates of a sphere. In the following, the word dome is used only for an icosadeltahedral geodesic dome, but one can obviously devise different polyhedral approximates, with non-icosahedral symmetries (e.g., octahedral or tetrahedral).

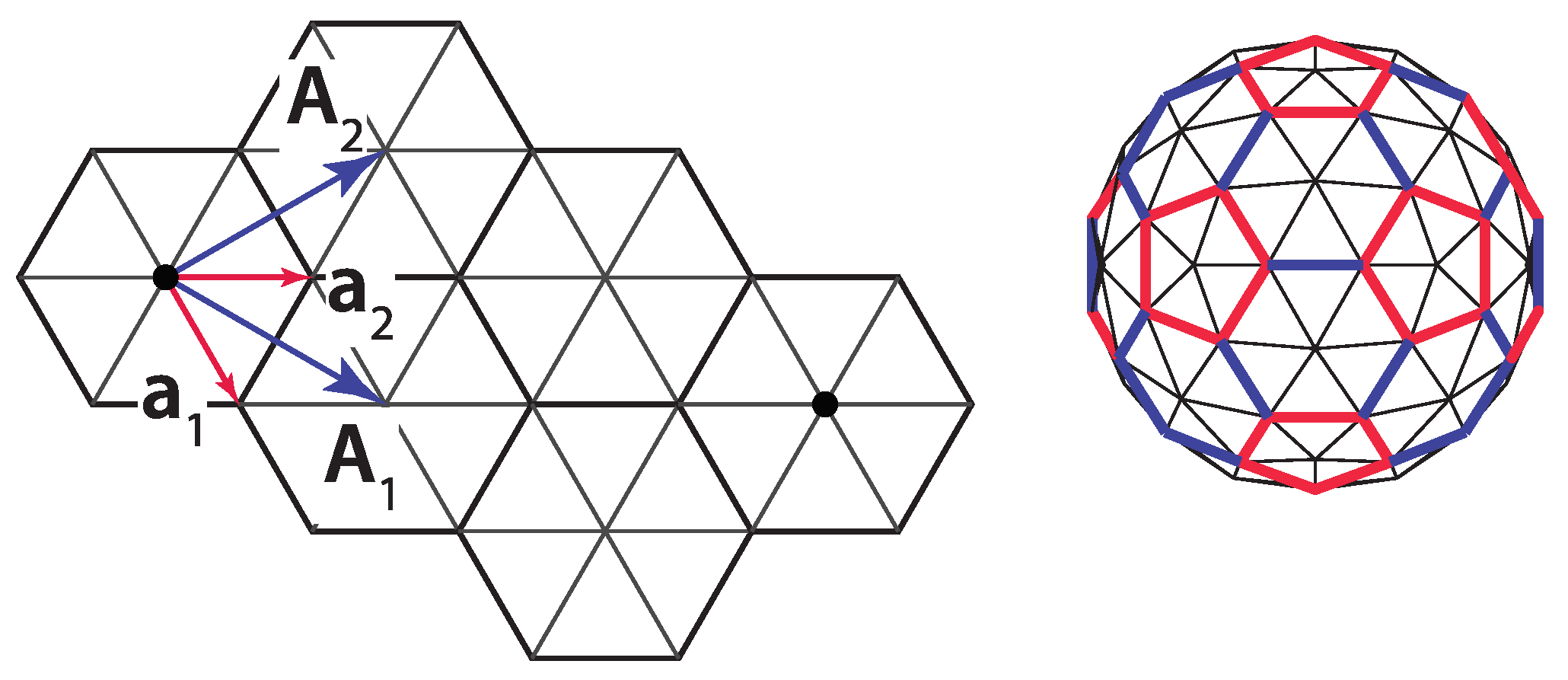
The icosadeltahedral triangulation can be defined in terms of the triangular mesh base vectors, ${\mathbf{a}}_1$ and ${\mathbf{a}}_2$ (Figure 1c). The oriented icosahedron edge, $\mathbf{E}$, in such a mesh can be written as

$$\mathbf{E}=m{\mathbf{a}}_1+n{\mathbf{a}}_2.$$

(1)

Each of the domes can be, thus, characterized by two nonnegative integers, m and n. These can also be thought of as numbers of ”jumps” through the vertices of a dome that need to be performed in order to reach a pentavalent vertex from its closest pentavalent vertex. Except for $(m,0)$ dome, the jumps need to be directed along two different spherical geodesics (the shortest lines between two points on a sphere)—m jumps along one of them, and n along another one. The two geodesics make an angle of 60 degrees in the unwrapped, flattened, and deltahedral projection of the dome. In order to be definite, we need to specify whether the ”jumper” needs to turn left or right after the m jumps along the first spherical geodesic. In what follows, the left turn shall be assumed and the type of the icosadeltahedral structures will be denoted by $(m,n)$. 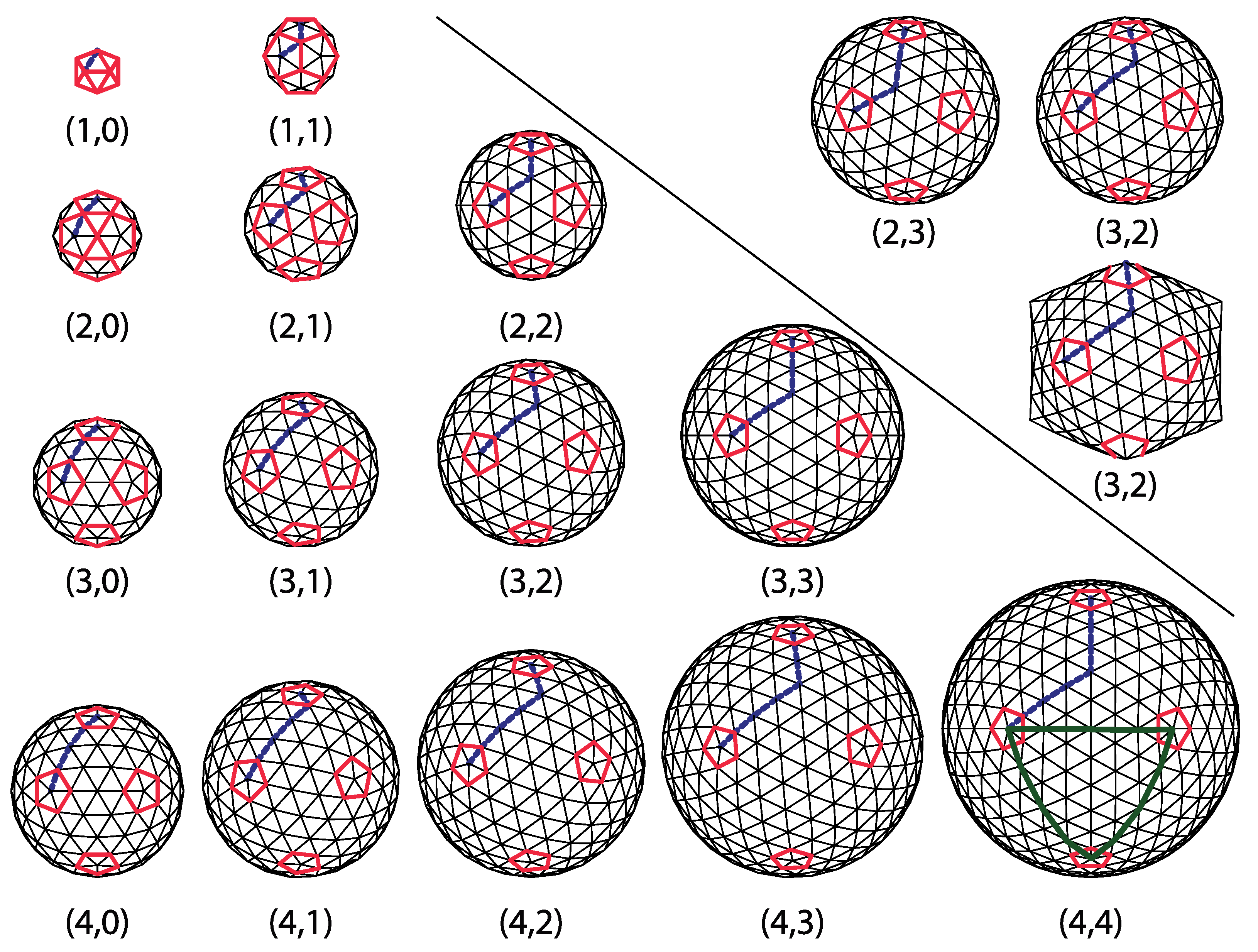Were the other convention chosen (turning right by 60 degrees after first set of jumps), the $(m,n)$ dome in our convention would correspond to $(n,m)$ dome in the alternative convention. The domes with $m\ne n$; $m,n>0$ are chiral (or skew). A mirror image of $(m,n)$ dome is $(n,m)$ dome. This is illustrated in the upper-right corner of Figure 2 for $(3,2)$ dome.

From m and n, one can calculate the number of triangles in a dome. The number of triangles, t, in one face of the icosahedron can be obtained by dividing the area of the face, $\sqrt{3}/4a^2(m^2+mn+n^2)$, with the area of a mesh triangle, $\sqrt{3}/4a^2$, where $a=|{\mathbf{a}}_1|=|{\mathbf{a}}_2|$. This gives [4,17,26]

$$\mathrm{t}=m^2+n^2+mn.$$

(2)

The total number of triangles (or faces) in an icosadeltahedron is

$$f=20\mathrm{t}.$$

(3)

Integer number t is called the triangulation number or simply the t-number. It adopts special integer values, $\mathrm{t}=1,3,4,7,9,12,13,16,19,\dots$. Instead of m and n integers, the t-number can be used to classify the icosadeltahedral order. The problem with this choice is that it doesn’t discriminate between $(m,n)$ and $(n,m)$ domes. That is why the t-number is sometimes used in combination with words laevo (left) and dextro (right) to resolve this ambiguity. For example, $(2,1)$ structure in our convention would be, in this case, denoted as $\mathrm{t}=7_{laevo}$ or $\mathrm{t}=7_l$ or simply $\mathrm{t}=7$, while $(1,2)$ structure would be denoted as $\mathrm{t}=7_{dextro}$ or $\mathrm{t}=7_d$ [14]. In our convention, when $m>n$ ($m<n$), the domes are laevo (dextro). There is an additional problem when using only the t-number to classify the dome and that is that different pairs, $(m,n)$ and $(p,q)$ may produce the same t [4]. In particular, Goldberg has shown that $\left(\right[3P+Q\left]\right[P-Q],4PQ)$ domes have the same t-number as $(3P^2+Q^2,0)$ domes. The lowest t-number for which a duplicity occurs is 133—the same t-number corresponds to (9,4) and (11,1) domes in this case. Although it may seem as a quite large triangulation order, larger t’s are realized in nature. For example, a recent study [27] reported on a virus that has $\mathrm{t}={169}_d$. Intriguingly, this is again the t-number that allows for duplicity of structures. The virus has a (7,8) [27] rather than (13,0) structure, which would not require dextro or laevo classification. Larger t-numbers may produce even higher multiplicities. For example, the $\mathrm{t}=8281$ class of domes contains five different dome types: $(91,0)$, $(85,11)$, $(80,19)$, $(65,39)$, and $(56,49)$ [4].

From the known number of the polyhedron faces (f) one can proceed to find the number of its vertices (v) and edges (e) by using Euler’s formula for polyhedra [17,28], which relates these nonzero integer quantities as

$$v-e+f=2.$$

(4)

This equation is valid for polyhedra, which are homeomorphic to the sphere [17], i.e., their topology is the same as that of a sphere, which means that they do not have holes like tori or coffee cups—this is the case of interest to us. In the icosadeltahedral domes, twelve vertices belong to five edges, and these are located at the vertices of an icosahedron. All the other vertices belong to six edges, i.e., six edges meet at those vertices. Each edge is bounded by two vertices, and all these facts together can be used to relate e and v as [17]

$$2e=5·12+6·(v-12)=60+6(v-12).$$

(5)

In combination with Euler’s formula, one obtains that

$$v=\frac{f}{2}+2=10\mathrm{t}+2,$$

(6)

and

$$e=\frac{3f}{2}=30\mathrm{t}.$$

(7)

3. Icosahedral Fullerenes

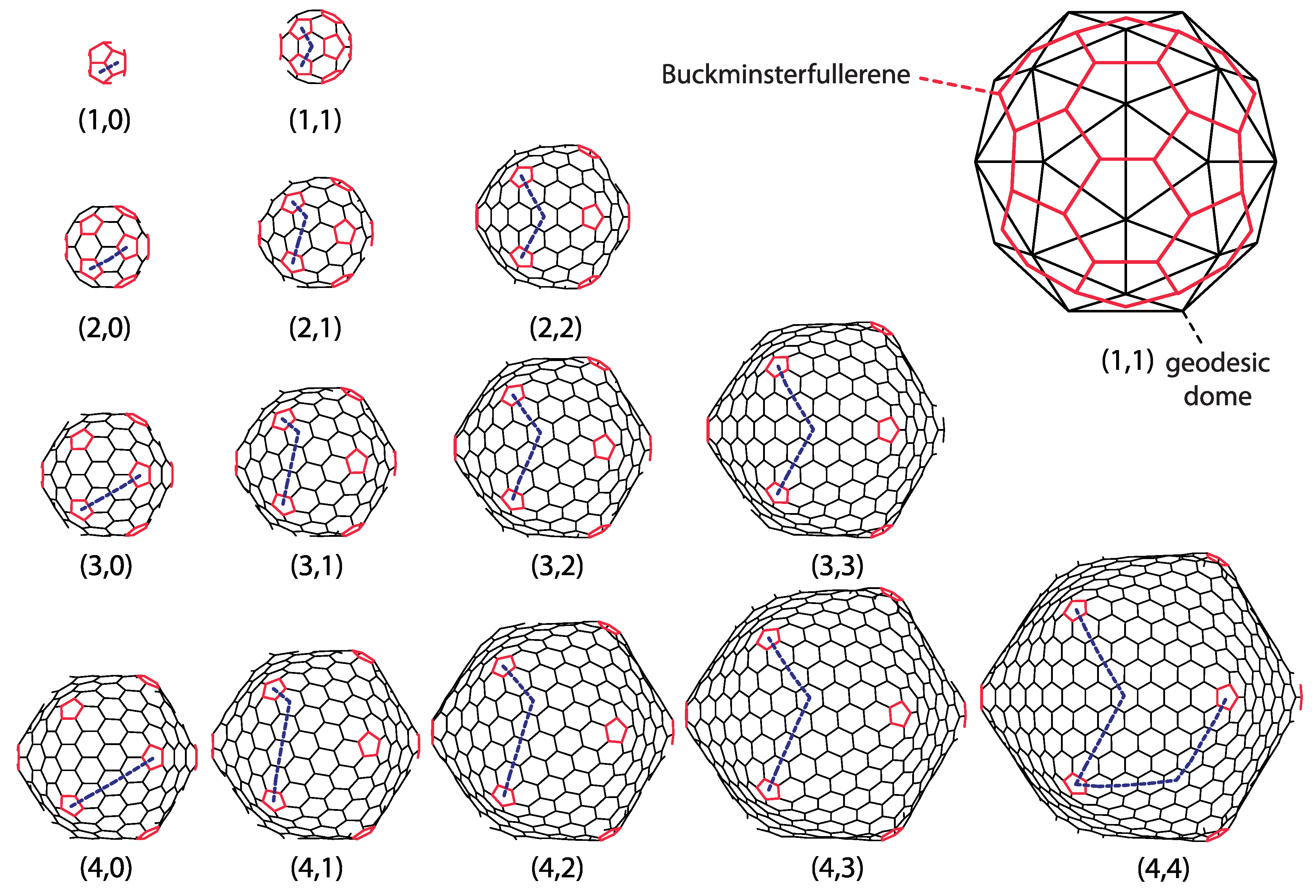
Fullerene molecules are carbon cages in which all carbon rings are either pentagonal or hexagonal, and all carbon atoms make three covalent bonds with their nearest neighbors (sp${}^2$ bonding). There are many different structures that can be made of carbon atoms connected with sp${}^2$ bonds, at least conceptually (see, for example [29,30,31,32]). Quite a different question is whether such structures can be experimentally obtained. The icosadeltahedral structure of geodesic domes is characteristic of a class of especially symmetric fullerene molecules, sometimes called icosahedral fullerenes, or giant icosahedral fullerenes in the case that molecules contain more than about 100 carbon atoms. Buckminsterfullerene belongs to this class. Its “companion” molecule C${}_{70}$ that was discovered simultaneously [2] does not, however. These carbon molecules, at least in their proper symmetry, if not an energy-minimizing state, can be obtained from icosadeltahedral domes by placing carbon atoms in the (bary)centers of every triangle in the dome. The newly obtained set of points (carbon atoms) is then interlinked so that each point becomes connected to its three nearest neighbors, i.e., the carbon–carbon bonds are established (this procedure is illustrated in the upper-right corner of Figure 3). The basic chemical requirement for carbon atoms in the sp${}^2$ bonding electronic configuration are obviously established, as each vertex in the new structure (i.e., the carbon atom) is three-valent, i.e., connected with three edges (sp${}^2$ bonds) to its neighbors—this is a simple consequence of the fact that every triangle in a dome has three neighboring dome triangles.

The construction produces a dual tessellation of the sphere—the centers of triangles in the geodesic dome become vertices of the dual structure. The geodesic domes and icosahedral fullerenes can thus be considered as dual polyhedra. Icosahedral fullerenes contain twelve pentagonal carbon rings (pentagons) and a certain number of hexagonal carbon rings (hexagons), depending on the t-number of the dome. The $(m,n)$ pair that was characteristic of the dome will also be characteristic of its dual fullerene-like polyhedron, but now the “jumping” that characterizes icosadeltahedral ordering is allowed only through the centers of pentagons and hexagons (not along the carbon–carbon bonds—see Figure 4). I used the term “fullerene-like polyhedron” to emphasize that the true fullerene molecules will in general be different from the polyhedron obtained by a simple mathematical dualization of the (spherical) dome. The shape of the fullerene molecule is governed by the energetics of carbon–carbon interactions. Carbon–carbon bonds are much easier to bend than to stretch [30], so the shape of the fullerene molecule will be such to keep the nearest-neighbor carbon–carbon distances as uniform as possible and as close to their equilibrium value as possible (the equilibrium length of carbon–carbon bonds in an infinite graphene plane is about 1.42 Å, but in fullerenes, the bonds in the pentagons are longer than the bonds fusing hexagons together [33]). This means that large enough fullerenes will necessarily be aspherical, looking more like an icosahedron with vertices slightly above the centers of carbon pentagons as the molecules get larger (One should be a bit careful when using the terms pentagon (hexagon) and pentagonal (hexagonal) carbon rings as synonyms. All of the carbon atoms in a pentagonal or hexagonal ring need not necessarily lie in a plane.). The pentagons can also be understood as effective sources of curvature in the fullerenes, and exactly twelve of them are required to completely close a flat piece of graphene and produce a cage-like carbon molecule [30,32,34].

Figure 3 displays a gallery of icosahedral fullerenes. Their shape is not merely a mathematical construction obtained by dualization of a dome, but a true minimum of energy, calculated by using the realistic model of energetics of carbon sp${}^2$ bonding [35], as described in [30]. Note that the buckminsterfullerene $(1,1)$ is almost perfectly spherical, i.e., all of its carbon atoms are almost equally distanced from the geometrical center of the molecule. A high degree of sphericity is also present in $(2,0)$ fullerene, but already in $(2,1)$ fullerene, a visible icosahedral shape of the molecule develops, and this becomes more prominent in larger molecules.

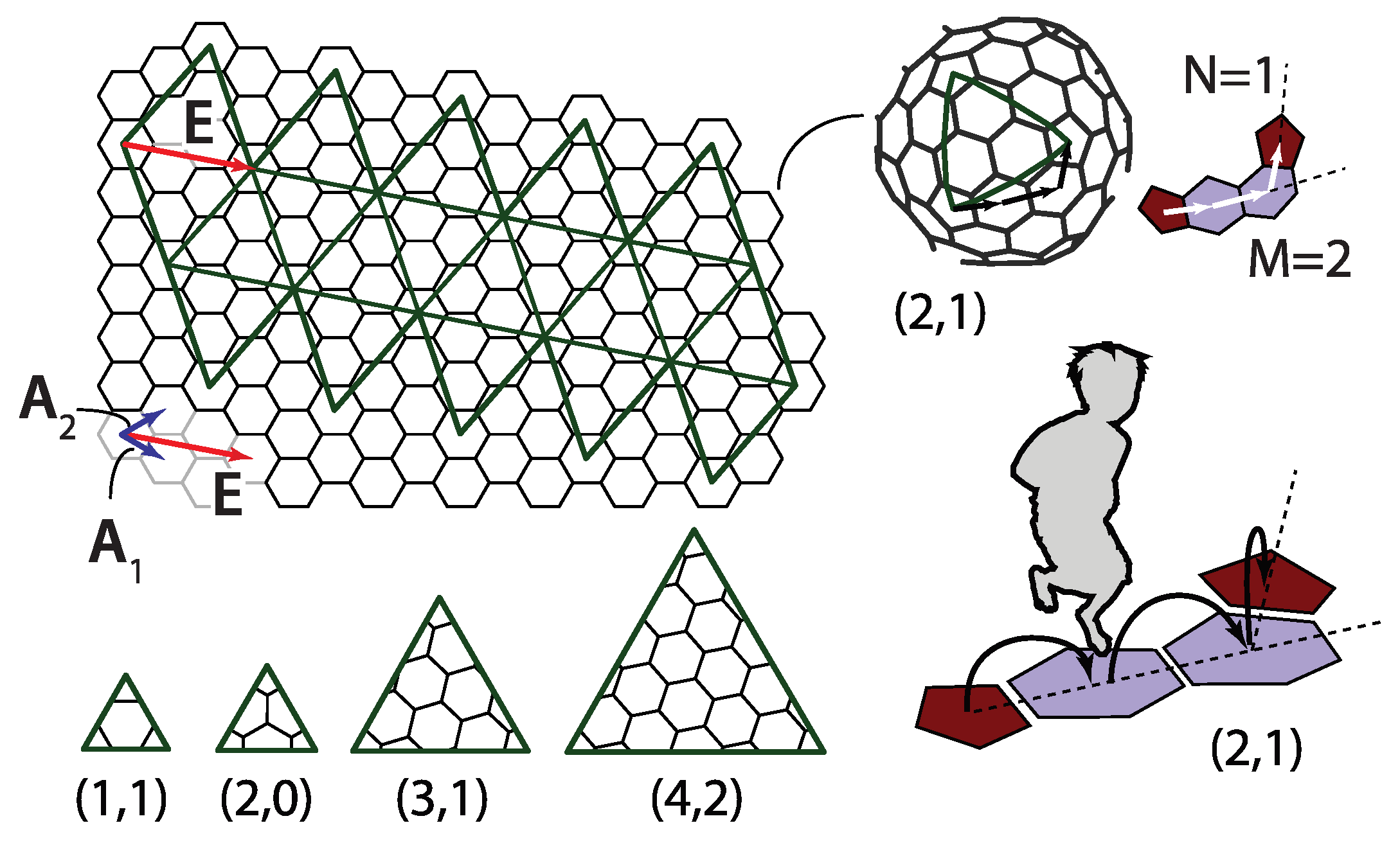
A way to better comprehend the symmetry of fullerenes is to unfold them so that they become polygonal pieces of graphene. Alternatively, and analogously to the case of geodesic domes, one can also think of this procedure, illustrated in Figure 4, as a way to construct these molecules. The polygonal shape consisting of 20 equilateral triangles outlined by thick lines is cut out from the graphene plane. The polygon is then creased along the edges shared by the triangles and folded into a perfect icosahedron. Thus, the obtained shape is not a physical fullerene since the details of its shape are wrong, but it has the same connectivity and number of carbon atoms as the icosahedral fullerene does. The shape of a physical fullerene can be obtained by a relaxation of the mathematically constructed entity towards the minimum of (chemical) energy [30]. The integers m and n that characterize the shape can now be interpreted as components of a two-dimensional vector $\mathbf{E}$ in a basis of graphene unit cell vectors ${\mathbf{A}}_1$ and ${\mathbf{A}}_2$ denoted in Figure 4,

$$\mathbf{E}=M{\mathbf{A}}_1+N{\mathbf{A}}_2,M,N>0.$$

(8)

The $\mathbf{E}$ vector is directed along the side of one of the twenty triangles making the icosahedron, as illustrated in Figure 4. In this convention, the unit cell vectors ${\mathbf{A}}_1$ and ${\mathbf{A}}_2$ need to be chosen so that their cross product $({\mathbf{A}}_1\times {\mathbf{A}}_2)$ points from the paper towards the reader. This reproduces the jumping-to-the-left convention discussed in the previous section.

An important piece of information on fullerene molecules can again be obtained from the Euler’s theorem on polyhedra [17,36]. Since exactly three bonds (or polyhedron edges) finish at each of the carbon atoms (polyhedron vertices) and the bond (edge) is shared by two atoms (vertices), it follows that

$$2e=3v.$$

(9)

By definition, the fullerenes contain only pentagonal and hexagonal faces (carbon rings). Let us denote the number of a pentagonal and hexagonal faces by $f_5$ and $f_6$, respectively. The total number of faces is obviously given by

$$f=f_5+f_6.$$

(10)

Pentagonal and hexagonal faces are bounded by five and six vertices (atoms), respectively, and each vertex (atom) belongs to exactly three faces. This means that

$$5f_5+6f_6=3v.$$

(11)

Combining these equations with Euler’s theorem in Equation (4), one obtains that [17]

$$f_5=12.$$

(12)

This is obviously true for the icosahedral fullerenes discussed so far, but the equation holds for general fullerenes as long as they are topologically equivalent to a sphere (including, e.g., C${}_{70}$). In other words, every network of pentagonal and hexagonal ring of carbon atoms with spherical topology necessarily has five pentagonal rings. A relation between the number of carbon atoms in fullerenes and the number of hexagonal faces can also be obtained from the above consideration,

$$v=2(f_6+10).$$

(13)

This means that the number of carbon atoms in the fullerene molecules is necessarily even (this can also be seen from the fact that $e=3v/2$, and since the number of edges must be an integer, the number of vertices must be even) [17]. This, at first puzzling, piece of information was observed already in the mass spectra of carbon clusters obtained by laser vaporization from the graphitic sample [37]. Only signatures of clusters containing an even number of carbon atoms were detected, which can be nicely explained by assuming that the clusters detected were, in fact, fullerenes. Specifying now the discussion to the case of icosahedral fullerenes, the total number of carbon atoms in these molecules is

$$v=20(M^2+MN+N^2)=20\mathrm{T},$$

(14)

and the number of carbon–carbon bonds is

$$e=30\mathrm{T}.$$

(15)

As shown earlier, there are exactly twelve pentagonal carbon rings and

$$f_6=10(\mathrm{T}-1)$$

(16)

hexagonal carbon rings.

4. Caspar–Klug Classification of Viruses: The  T-Number

The simplest viruses are particles made of DNA or RNA molecules (genome) protected by a coating made of proteins (capsid). Some viruses are additionally enveloped by parts of their host cell membranes decorated by virus (glyco)proteins. A typical diameter of a virus is about 50 nm. For example, the diameter of a herpes simplex virus is ∼125 nm, while polio virus is about 32 nm in diameter [14].

In 1956, Crick and Watson [38] proposed that the spherical protein coating probably has a platonic polyhedral symmetry, i.e., that it is built of identical proteins or protein subunits assembled in a polyhedral shell. They developed this notion by noting that the quantity of information contained in the viral genome is quite small, so that only a few different proteins can be produced from it. Thus, they reasoned that the capsid is most likely constructed from a single subunit, which is repeated many times to form a protein shell. Caspar and Klug considered different polyhedral shells made of identical proteins with tetrahedral, octahedral, and icosahedral symmetry and deduced that icosadeltahedral ordering provides a structure in which all of the proteins are in surroundings that are to the best approximation equal (quasiequivalent) of all the choices considered [13]. They called this the principle of quasiequivalence. Their proposition is based on the idea that the identical protein subunits have a certain degree of flexibility in their bonding to their neighbors but that only a certain degree of their deformation when packed can be tolerated in this respect. The idea can be explained by examining the subdivisions starting from different polyhedra. If the subdivision of sides is performed, for example, on an octahedron, all the vertices would be hexavalent, except for the six vertices of the starting octahedron, which would be four-valent. The combination of pentavalent and hexavalent vertices in the case of the icosadeltahedral arrangement is obviously more uniform, in fact, the most uniform of all deltahedral subdivisions of Platonic polyhedra—all the sides and vertices of such polyhedra are to the best approximation equivalent, i.e., quasiequivalent. In addition, the CK also emphasize the energy of the structure proposed—it enables formation of the maximum number of the most stable bonds between the units [13]. This is in part due to a dense packing of the proteins on a sphere and, in part, to small deviations of the different units from their ideal, minimum energy positions, so that the binding energy is still favorable.

The geometry behind the principle of quasiequivalence is the one already discussed in the cases of icosadeltahedral geodesic domes and fullerenes. A historical review focusing on the determination of the structure of viruses and their relation to geodesic domes can be found in [11].

In most of the “spherical” viruses (Not all viruses are “spherical”. For example, the coating of the tobacco mosaic virus has a shape of a cylinder with viral RNA in its interior [39]. Even in such cases, there are strong parallels between the viruses and similarly structured shapes of sp${}^2$ carbon—see, e.g., [32].), the proteins are typically grouped in clusters called capsomers. The capsomers consist of five (pentamers; pentons) and six (hexamers; hexons) proteins. 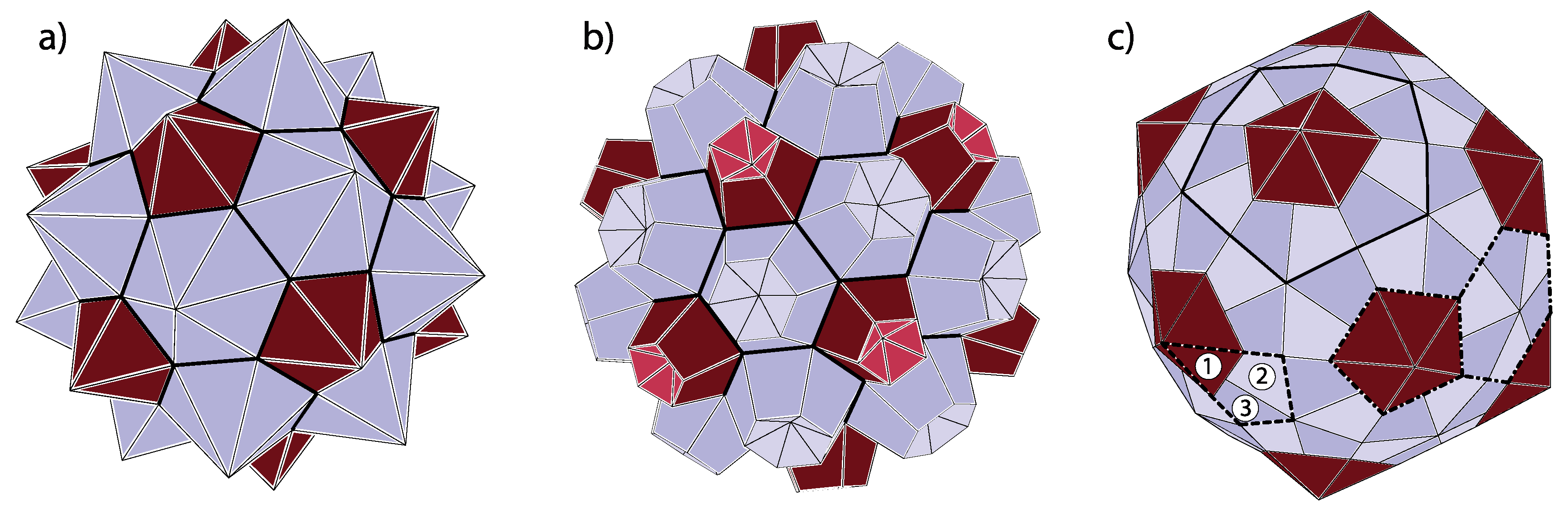This is very often the case even if not all proteins are equal, i.e., when the capsid consists of several types of proteins [14]. In the assembled spherical capsids, the twelve pentamers occupy the same spatial positions as carbon pentagons in fullerenes. The hexamers are analogous to hexagonal carbon rings in fullerenes. Viruses, thus, with all the individual proteins delineated, can be constructed by connecting each of the vertices in pentagonal and hexagonal rings of the fullerenes with the ring centers and interpreting the thus obtained divisions of the pentagons and hexagons as the dividing lines between the viral proteins in a capsomere. The (fullerene) vertices need not be connected necessarily to the centers of the rings but to points lying on approximate normals to the pentagonal and hexagonal faces and passing through centers of the faces. This corresponds to capping the pentagons and hexagons with pentagonal and hexagonal pyramids, respectively, but the capping (i.e., modeling of protein pentamers and hexamers) can also be performed in many other ways. The thus obtained polyhedron may be called omnicapped fullerene (all (omni) of the fullerene faces capped by pyramids or some other polyhedra). This procedure is illustrated in Figure 5a,b.

The viral proteins have a certain shape, which is of course three-dimensional [41]. Representation of protein capsomers by pyramids or any other polyhedron is, thus, approximate. Any three -dimensional shape erected above the hexagon (pentagon) and having a six-fold (five-fold) symmetry with respect to rotations around the hexagon (pentagon) normal may serve as a representation of a viral hexamer (pentamer). The classification of the symmetry of the capsid, however, does not depend on the shape of individual protein but only on the characteristics of the arrangement of all the proteins in the capsid (at least when all proteins are equal, see below). The symmetry of viruses is characterized in the same way as in the case of fullerenes: M and N integers are counted by “jumping” through the centers of the capsomers and using the convention of turning left after the first M jumps. If $M\ge N$, the virus is classified as a member of ${\mathrm{T}}_{laevo}=M^2+MN+N^2$ class (or simply T), and if otherwise ($M<N$), the virus is classified as a member of the ${\mathrm{T}}_{dextro}$ (or ${\mathrm{T}}_d$) class. The virus-like polyhedra depicted in panels (a) and (b) of Figure 4 both belong to $\mathrm{T}=3$ class, although the details of their shapes are quite different. The cut-and-fold constructions, shown in Figure 4 for fullerenes, can also be easily applied to viruses—each carbon hexagon (pentagon) is to be interpreted as protein hexamer (pentamer) [42].

4.1. Viruses as Overlapping Dome and Fullerene Designs

The total number of capsomers (c) in a T-class virus is the same as the number points in the icosadeltahedral dome with triangulation number T,

$$c=10T+2.$$

(17)

It is instructive to overlap the hexagonal net of fullerenes with a triangular net of a corresponding dome in which every triangle corresponds to an individual protein subunit, as in Figure 6. The fullerene bonds in this representation indicate the borders between the protein capsomers. The base vectors of a hexagonal mesh, ${\mathbf{A}}_1$ and ${\mathbf{A}}_2$ can be expressed using the base vectors of triangular (sub)mesh, ${\mathbf{a}}_1$ and ${\mathbf{a}}_2$,

$$\begin{array}{ccc}\hfill {\mathbf{A}}_1& =& {\mathbf{a}}_1+{\mathbf{a}}_2\hfill \\ \hfill {\mathbf{A}}_2& =& -{\mathbf{a}}_1+2{\mathbf{a}}_2,\hfill \end{array}$$

(18)

and the icosahedron edge vector E can then be expressed in both bases as

$$\begin{array}{c}\hfill \mathbf{E}=M{\mathbf{A}}_1+N{\mathbf{A}}_2=(M-N){\mathbf{a}}_1+(M+2N){\mathbf{a}}_2.\end{array}$$

(19)

The pair of integers characterizing the dome submesh is, thus, $(m,n)=(M-N,M+2N)$. The t-number of the (sub)dome is then

$$\mathrm{t}=m^2+mn+n^2=3(M^2+MN+N^2)=3\mathrm{T}.$$

(20)

The total number of proteins in a virus (p) is a sum of 60 proteins in 12 pentamers and $60(\mathrm{T}-1)$ proteins in $10(\mathrm{T}-1)$ hexamers [13]. Alternatively (see Figure 4), one can deduce that p for a virus in class T should be the same as the number of faces in a dome in class t = 3T, i.e.,

$$p=60\mathrm{T},$$

(21)

so that both approaches give the same answer. There are 3T proteins, analogous to dome triangles, per icosahedron side, but not all of them are in different settings on a sphere—only a third of these are indeed mutually different, so that there are T different classes of protein surroundings in a virus of T class. The individual proteins need to be sufficiently flexible to adopt all of these T slightly different (quasiequivalent) positions in a completed virus shell [43]. It is, in this respect, remarkable to note that CK construction applies even to huge viruses, with T numbers in the range of ${10}^3$—such are, for example, the mimiviruses [44] for which $\mathrm{T}\approx 1150$, i.e., there are more than 1000 different but quasiequivalent positions in such viruses.

It is of interest to count the number of protein–protein contacts in a viral capsid since this determines a large part of its energy [45]. It makes sense to separate the contacts to those that pertain to proteins belonging to the same capsomer (intra-capsomer; $e_1$) and those between the proteins in different capsomers (inter-capsomer; $e_2$). These contacts may be expected to have different association energies. Capsomers are typically more strongly bound and formation of capsomers from individual proteins is observed, at least in some viruses (see, for example [46]), to precede their assembly in the virus capsid. There are five (six) protein–protein contacts per pentamer (hexamer), so that

$$e_1=5·12+6·10(\mathrm{T}-1)=60\mathrm{T}.$$

(22)

The number of inter-capsomer protein–protein contacts is the same as the number of carbon–carbon bonds in a fullerene of the same T-number as the virus in question (see Figure 5), so that

$$e_2=30\mathrm{T}.$$

(23)

These are perhaps the simplest of the results, which can be easily obtained by employing the analogy between domes, fullerenes, and viruses.

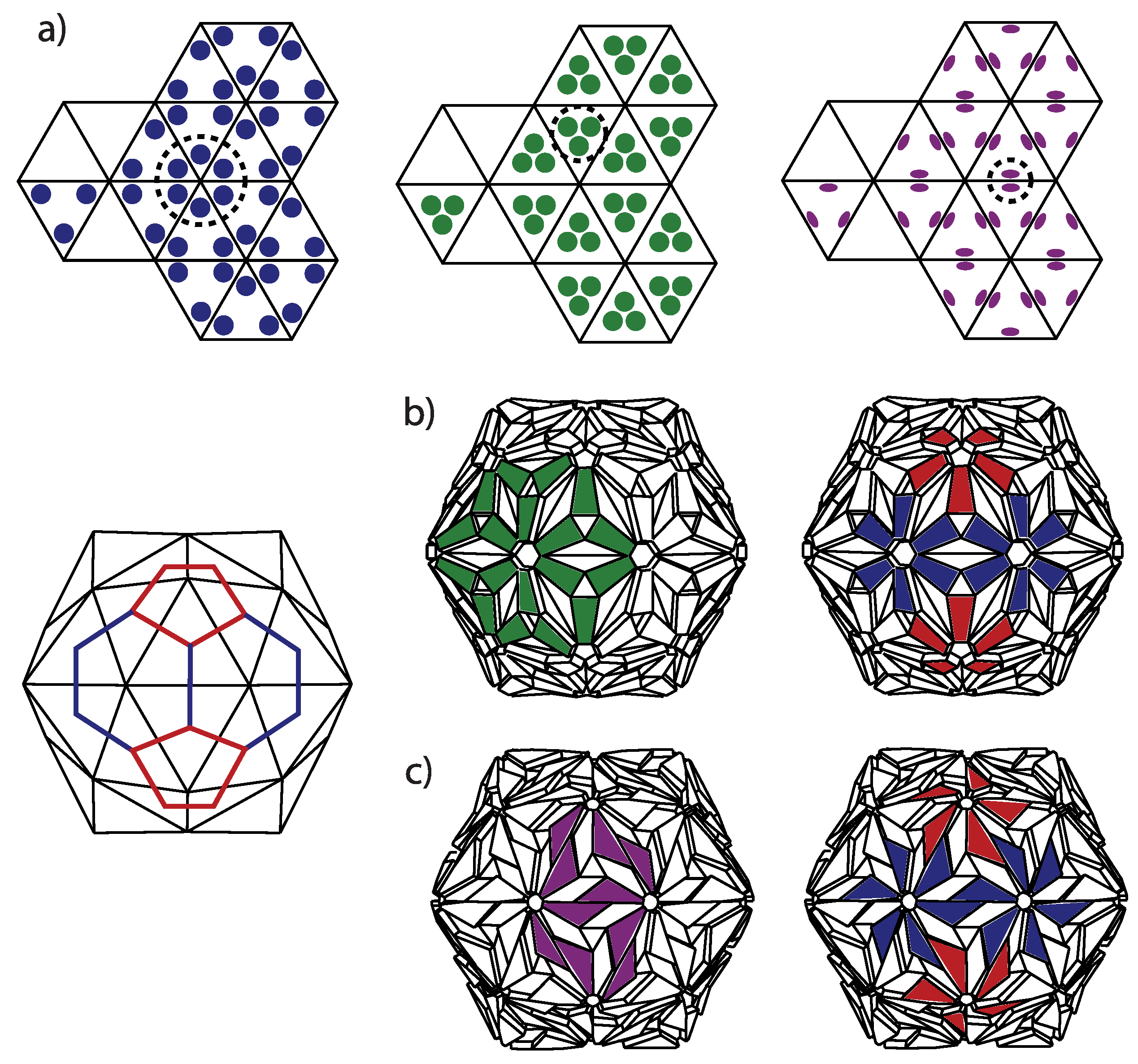
4.2. Possible Ambiguities of the CK Designs

Caspar and Fuller presented the quasiequivalent construction slightly differently [13]. They start from the dome and put three proteins in symmetric positions in each triangle of the dome, which is yet another and alternative way to think of correspondence between the domes and the viruses. In such a construction, if the proteins are situated near the triangle vertices, then they form clusters of five and six around the dome vertices, i.e., pentamers and hexamers (see Figure 7). However, if the proteins are clustered near the center of the dome triangles, then one can think of structure as consisting of trimeric clusters. When the proteins are near the midpoints of the edges, one most easily recognizes the dimeric clusters. Real proteins can be thought of as (atomic) density distributions, and they can, thus, not be represented as points in a triangle. In viruses, one can typically visually observe both pentameric-hexameric and trimeric or dimeric signatures of capsid protein density, depending on the point of view taken (see, for example [47] for the case of the Zika virus)—this is illustrated in Figure 7. It may happen that the morphological features that are most easily discerned are not the physical subunits but, for example, trimeric-like density signatures of a pentameric-hexameric arrangement.

There may also occur problems in identifying the capsid class when several different proteins form a capsid, for example, when building blocks of the capsid are not individual protein subunits but trimers (clusters of three proteins). A typical situation is illustrated by the shape in panel (c) of Figure 5. The building block of this shape is a protein trimer outlined by thick dashed lines. It consists of a darker triangular protein (denoted by 1) and two brighter kite-shaped proteins (denoted by 2 and 3). This structure could be identified as belonging to $\mathrm{T}=1$ class, with only twelve “pentons” (outlined by thick full lines in Figure 5c)) composed of five protein trimers (180 proteins in total). On the other hand, one could, at least conceptually, arrange the proteins in pentamers and hexamers as indicated by thick dash-dotted lines in Figure 5c). In this case, the hexamers would contain three pairs of 2- and 3-proteins from three different trimers, while pentamers would consist of five 1-proteins from five different trimers. If the proteins 1, 2, and 3 are reasonably similar, as they often are in viruses, the pentamers and hexamers would almost look as if they were made of the same protein repeated five and six times, respectively. This would implicate that the shape belongs to $\mathrm{T}=3$ class. Such viruses are called pseudo-T3 (or pT3) viruses. The problem with the ambiguity of identification could be resolved on physical grounds—if the binding energy between the proteins of the trimer is larger than between the proteins from different trimers, it makes sense to speak about the trimer as the basic building block and to identify the structure as belonging to $T=1$ class. However, the problem in the mathematical sense occurs when there are two $\mathrm{T}$ numbers that can be divided without remainder (e.g., $\mathrm{T}=21$ and $\mathrm{T}=7$). In the most trivial case, every capsid with T-number ${\mathrm{T}}_1$ could be interpreted as a $\mathrm{T}=1$ capsid consisting of ${\mathrm{T}}_1$-mers. In addition, every $(M,M)$ capsid could, in principle, be thought of as a $(M,0)$ capsid made of trimers. The important question is again whether the conceptually obtained protein multimers make any sense as the strongly bonded elementary units. A further complication can occur if the particularly stable protein cluster is a trimer that geometrically looks just like a hexamer (hexagon). Those quasi-hexamers can, thus, tile the sides of the icosadeltahedron as already described; the quasi-pentamers in such situations are typically special, i.e., formed differently (see, e.g., [48]).

4.3. The  T-Number and the Capsid Size and Shape

Viruses differ very much in size, depending on the type [14]. The variation in the mean radius of a virus capsid could, in general, arise from the variation in size of the proteins that make the capsid. This means that two capsids having the same T-number may be quite different in size due to the difference in the size of their coat (capsid) proteins. On the other hand, if the size of the capsid proteins were similar across different virus families, the variation in virus size would arise dominantly from the change in T-number of different viruses—the viruses with the same T-number would, in this case, have similar radii. As the total number of capsid proteins is proportional to T (see Equation (21)), the area of the capsid is also proportional to T, and the (mean) radius of the capsid should then be proportional to $\sqrt{\mathrm{T}}$, across the different virus families. To test whether this is indeed the case, a statistical analysis of 130 capsid entries deposited by the end of the year 2012 in VIPERdb database [49] was performed [50]. The mean capsid radius, $\overline{R}$, was calculated for each of the viruses analyzed, as explained in [50], and plotted against its T-number. The results of the study were reanalyzed and redrawn in Figure 8 so to emphasize the T-number dependence of the mean radii and the spread of radii within a particular T-number class.

A large spread of radii is, in general, observed within a T-number class, but an overall trend of mean radius increasing proportionally to $\sqrt{\mathrm{T}}$, $\overline{R}=r_0\sqrt{\mathrm{T}}$ is visible. An area in which a “typical” coat protein contributes to the overall mean capsid area, $a_p$, can be estimated from

$$a_p=r_0^2\frac{\pi }{15}\approx 13{\mathrm{nm}}^2.$$

(24)

The thicknesses of the virus capsid also differ quite a lot. This is in part due to the fact that the external morphology of the capsid, its grooves, and ridges play a part in the binding of the virus to cellular receptors and its subsequent entry. Some viruses have, thus, quite pronounced morphological features, including long spikes located often at pentamers [50]. Nevertheless, a mean capsid thickness, which could be considered as typical for many viruses, is about 3 nm [50].

The overall shape and the (a)sphericity of viruses have been a subject of several studies, and deliberately simplified theories representing the capsid as a thin elastic shell predict that smaller viruses should be spherical while larger should show pronounced faceting, i.e., should look more like an icosahedron than a sphere, similar to the case of fullerenes. This has indeed been observed to be the case, at least to a certain extent [50,51]. The interactions between the proteins in a virus are much more complicated than those characterizing carbon atoms in fullerenes, and the theoretical descriptions of shape depend on much more details, which also include the presence of ions in the solution, which modify and screen the protein–protein interaction [52,53]. Functional viruses also contain the genome molecule, RNA or DNA, and the interaction of the coat proteins with the nucleic acid may also influence the shape of the capsid. In particular, the packed DNA can be to some approximation often described as effective physical pressure acting outwards, to expand the capsid [54]. The internal pressure both increases the mean radius of the capsid, inducing a kind of swelling, and smooths out the polygonal nature of the capsid a bit [54,55]. The virus proteins can also have shapes and active binding regions which promote spontaneous curvatures of their assemblies. Such proteins will then prefer a certain radius [56], and a certain T-number will be effectively encoded in the details of the protein shape. This is a point in stark contrast when compared to the case fullerenes. All of these, physically and biologically relevant considerations go beyond the simplest description of a virus as a thin icosadeltahedral shell.

5. Some Modifications and Variations of the Icosadeltahedral Geometry in Viruses

Caspar and Klug quasiequivalence principle predicts that there are only twelve pentameric capsomers, all other being hexameric. In the year 1982, it became clear that there were viruses (e.g., SV-40 virus from polyomavirus genus) composed only of pentamers but still retaining the icosadeltahedral ordering of their arrangement [57]. The concept of T-number is still valid in that case, and the number of capsomers is still given by Equation (17), but the total number of proteins is no longer given by Equation (21) because there are no hexamers in the structure. For such viruses, the total number of proteins is

$$p=5c=5(10\mathrm{T}+2).$$

(25)

This is a seemingly innocent modification of the CK principle, yet it is important in the light of cut-and-fold constructions of the CK structures [13,43]. Namely, the missing material at the position of cuts where there are pentamers in the standard CK construction acts as a source of curvature around these positions [30,32,34]. If all the capsomers are the same, the source of curvature must be equally distributed in all of them, so that the formation of a spherical structure is not surprising [56]. It is, however, intriguing that even in this case, such a structure has an icosadeltahedral order and can be, to a large degree, described by CK construction. In such a structure, not all capsomers are in identical surroundings. All the capsomers have six nearest neighboring capsomers (these would be hexamers in standard CK construction, but are pentamers in SV-40 viruses [57]), except for the twelve of them at the position of icosahedron vertices (these would be pentamers in standard CK construction and are indeed pentamers in SV-40 viruses [57]).

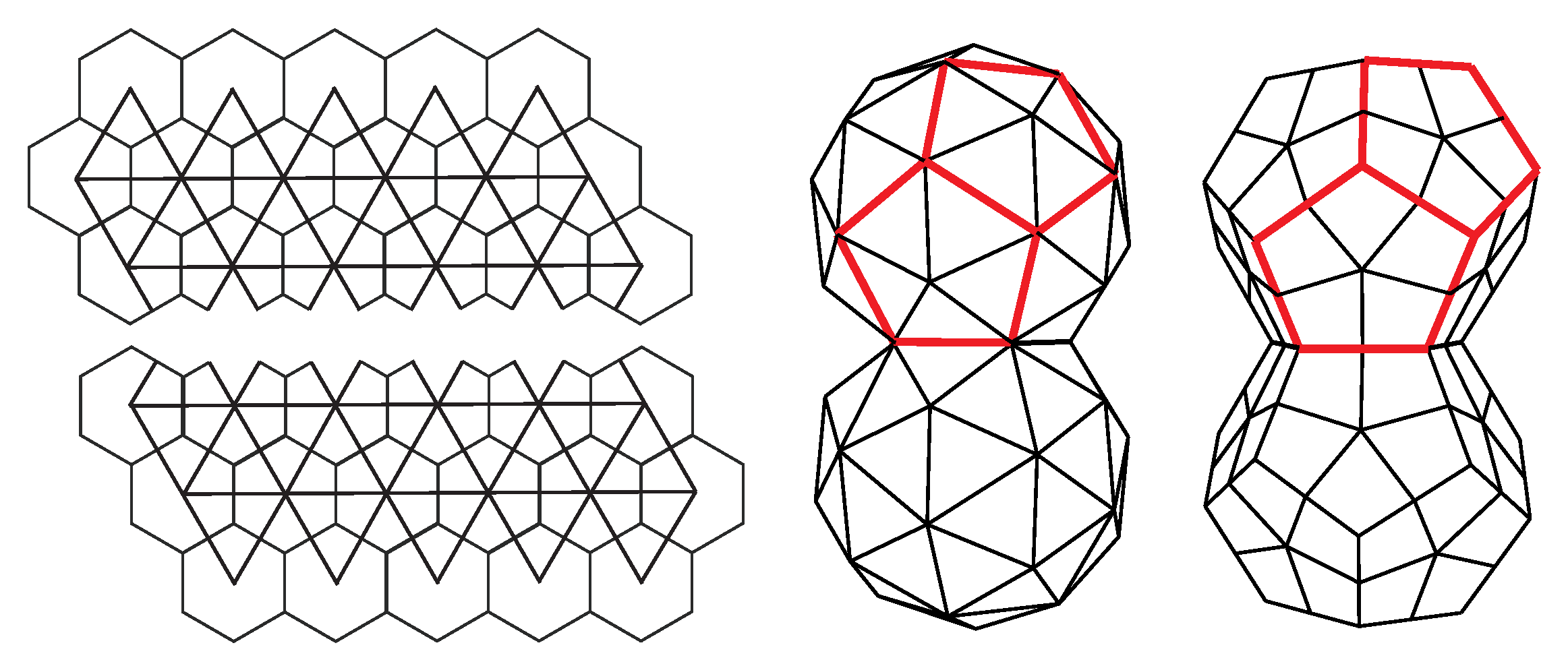
The correspondence between CK shapes and geodesic domes expressed in Equation (20) indicates that there are domes that cannot be represented by pentameric and hexameric clusters of proteins (or triangles). Such are all the domes for which it is not divisible by three, for example, (1,0), (2,0), (2,1), (2,2), and (4,1) domes. Yet, these domes can still be thought of as representing different clusters of virus proteins, as illustrated in Figure 9. Triangles are (2,0), and (2,1) domes can be organized in pentagons (pentamers) and individual triangles (protein monomers). The (2,2) domes can be reorganized and tiled by pentagons, rectangles, and triangles, which may, for example, represent different types of capsid proteins or protein clusters. The (4,1) domes can be thought of as being tiled by pentamers (pentagons) and hexamers (hexagons), with an additional layer of monomers (triangles) surrounding each pentamer and hexamer. The reorganization is not unique, and several different designs may be given for a particular dome. Such modifications of the CK approach are being studied and applied to real viruses [24,25,58].

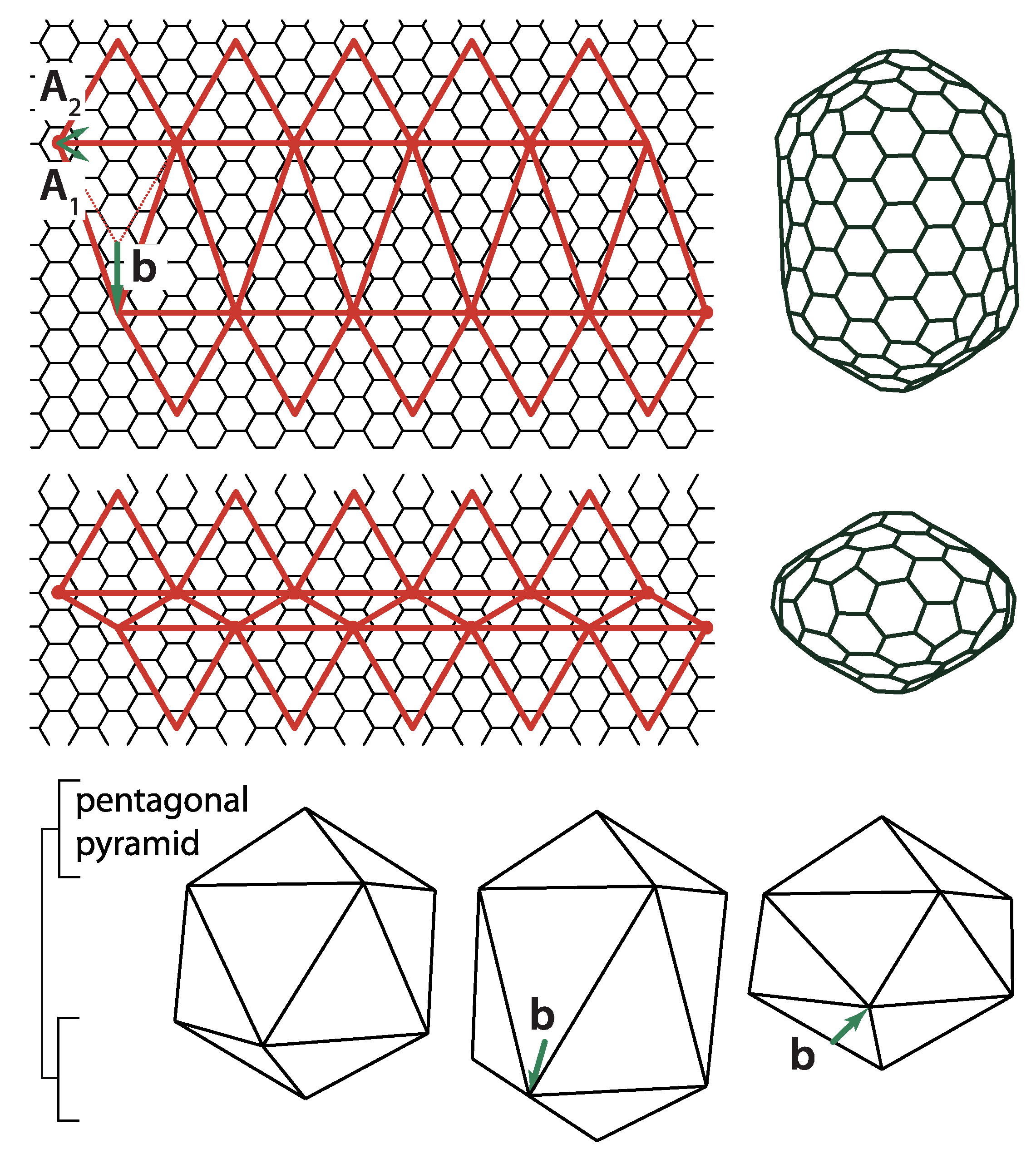
A simplest modification of the icosadeltahedral cut-and-fold blueprint is to elongate it or shorten it along a five-fold axis of symmetry by a distance b, which needs to conform to the lattice distances of the net, as illustrated in Figure 10 [30]. Very elongated icosadeltahedra can be thought of as cylinders capped by two pentagonal pyramids, i.e., capped tubes. This, of course, reminds one of (capped) carbon nanotubes [30]. It is intriguing that Buckminster Fuller also designed elongated forms of his domes; his design for the entrance pavilion of the Union Tank Car Company dome appears to be a dual of the capped carbon nanotube [59]. Elongated (prolate) viruses are well known, and such a geometry is fairly typical for bacteriophage viruses [60,61]. Oblate viruses, i.e., those shortened along the five-fold axis of symmetry do not appear to be the native shape of any virus. However, some of the aberrant capsids of mutant T4 bacteriophages have been proposed to have an oblate (also termed shortened) icosahedral shape [61]. Note that the vector $\mathbf{b}$ may be non-parallel to the five-fold axis of symmetry of the pentagonal pyramids that cap the shape. The phage T4 [60] has such a symmetry. The isometric icosadeltahedral shapes can also be thought of as two pentagonal pyramids capping the middle portion (midsection) of the icosahedron. This middle portion, of which two caps have been cut off, is called the uniform pentagonal antiprism. It consists of 10 triangular sides and two pentagonal bases rotated with respect to each other by 36 degrees ($2\pi /10$). The vector $\mathbf{b}$ defines the elongation (shortening) of the midsection as well as the angle of mutual rotation of the two capping pentagonal pyramids. The elongated structure is typically characterized in terms of two T-numbers, one specifying the triangulation of the caps, i.e., smaller triangular faces, ${\mathrm{T}}_{end}$ and the other specifying the triangulation of the middle portion, i.e., elongated triangular faces, ${\mathrm{T}}_{mid}$. For example, in phage $\varphi$29, T${}_{end}$ = 3, T${}_{mid}$ = 5, and many different cases can be found in [20]. The two numbers can be elegantly defined by specifying an additional coordinate system for the elongated faces, rotated by 60 degrees with respect to the one used to define the T-number for the caps [20,62]. If one decided to define $\mathbf{b}$ on the same basis as $\mathbf{E}$, $\mathbf{b}=P{\mathbf{A}}_1+Q{\mathbf{A}}_2$, ${\mathrm{T}}_{mid}$ could be expressed as ${\mathrm{T}}_{mid}={\mathrm{T}}_{end}+MP-NQ$. Such relations can be derived by calculating the area of the triangular faces, i.e., by performing the cross products of the vectors defining the edges of the faces. For example, for the elongated shape in Figure 10, the capping pyramid is a part of the (2,2) CK shape, so T = 12. Vector $\mathbf{b}$ can be expressed as $\mathbf{b}=2{\mathbf{A}}_1-2{\mathbf{A}}_2$, so $P=2$ and $Q=-2$, which gives ${\mathrm{T}}_{mid}=12+8=20$. The total number of proteins in the shape is now 30T${}_{end}$ in the two pentagonal pyramids and 30T${}_{mid}$ in the midsection [20], which means that it is increased with respect to isometric shape by $30(20-12)=240$. That this is indeed the case can, in this case, be easily checked by calculating the area of the strip of hexagonal mesh of height $\left|\mathbf{b}\right|$ inserted in the midsection of the isometric shape.

Quasiequivalence in elongated capsids is valid to a lesser degree than in isometric, CK capsids—this can also be seen from the fact that two T numbers are required to describe the construction. In particular, the two pentamers at the top and the bottom of the shape, i.e., at the apices of the pyramidal caps, are in different positions than the ten positioned on the two borderlines between the caps and the midsection. The curvature of the capsid may be quite different in these positions, the difference growing with $\left|\mathbf{b}\right|$ [20].

There is another type of elongated design in which the capsid can be thought of as consisting of two fused, incomplete icosahedral capsids. Such a capsid could be constructed as a modification of the cut-and-fold plan, as illustrated in Figure 11. The structure has $2\times 11=22$ pentavalent vertices, which may host twelve protein pentamers. This obviously contradicts the standard CK construction, which predicts only 12 of them. Note, however, that in addition to pentavalent and hexavalent vertices, the fused structure also contains octavalent (eightfold coordinated) vertices, five of them around the ring, which fuses the two incomplete capsids—these restore the validity of the Euler formula in Equation (4). Such design can be found in geminiviruses that consist of 22 pentamers, i.e, they can be thought of as two incomplete T = 1 capsids fused together. In these viruses, the two halves are slightly rotated with respect to each other around the five-fold axis of symmetry of the virus. Such details of architecture depend crucially on the flexibility of the proteins that make the capsid and the details of their conformations [63]. The gemini capsid has an obvious advantage in that it can pack more DNA than a single capsid. It also appears as if the DNA is essential for the assembly of the capsid as no empty geminivirus capsids have been reported [63]. The capsids could also be thought of as two fused dodecahedra (Figure 11)—the faces of dodecahedra are, in this case, tiled by protein pentamers. Erecting a pentagonal pyramid on each of the dodecahedron faces produces a T = 1 CK structure [13].

The duality between the icosahedra and dodecahedra, observed here for the case of geminivirus, has been employed in an alternative description of the virus architecture [19]. Some viruses, for example, bovine papilloma virus, can perhaps be better thought of as dodecahedra in which faces are tiled by protein pentamers. Protein density maxima in pentagonal faces exhibit patterns similar to those found in chiral pentagonal quasicrystals [19].

Another modification of the icosadeltahedral design is to form a structure similar to a truncated cone, which is capped by two pyramid-like shapes of different sizes [20]—the larger connected to the larger, bottom base of the cone, and the smaller to the smaller, top base of the cone (see Figure 12). This is approximately the structure of the HIV virus, although it seems that the HIV virus is quite polymorphic and that functional HIV viruses may have many different coat structures [64]. The coat structure does not, thus, appear to be strongly fixed, but varies in details, although there are obvious constraints that the structure must fulfill; it must, in the first place, be spacious enough to pack properly its own RNA molecule. There are obviously many different ways to form a closed polyhedral structure containing only hexagonal and pentagonal sides, but the number of pentagons must, in all cases, be 12, as the derivation leading to Equation (12) demonstrates. Any such polyhedron can be represented by a net on a lattice of hexagons. The net will necessarily consist of exactly twelve cuts, i.e., positions where the wedge of exactly 60 degrees has been removed by cutting. Pentagons will be formed at these positions once the net is folded in order to make the polyhedron. However, none of the faces of the polyhedron needs to be an equilateral triangle. This was already seen in the case of elongated icosahedral designs, where the mid-faces can be isosceles triangles, or their edge lengths can be even all different.

Twelve cuts of 60 degrees can be positioned in many different ways in a lattice, as Figure 12 suggests. All of these nets correspond in general to different polyhedra. All such polyhedra could, in principle, be thought of as modifications of the perfect icosa(delta)hedron, as they bear the signature of the twelve vertices of the icosahedron where the twelve pentagons reside. Furthermore, all such structures could be considered as if obeying a relaxed variant of the principle of quasiequivalence put forth by Caspar and Klug since all of the vertices and faces in such polyhedra are in nearly equivalent surroundings—a fact of essential importance in rationalizing the appearance of perfect icosadeltahedral geometry [13]. The reservations are in order when the two pentagons (pentamers) are very close to each other. In such cases, the effective interactions acting in the regions between the two pentagons may be quite different from the interactions far away, in large patches consisting exclusively of hexagons. Due to a loss of symmetry of the folding pattern, the number of different protein surroundings increases, and the concept of T-number loses its strength as the structures become more complex.

Caspar has noted the usefulness of icosadeltahedral cut-and-fold schemes in constructing different fullerenes and has proposed many different polyhedral nets of deltahedra dual to fullerenes [5]. Note here that one can conceptually construct an octahedral, fullerene-like shape by putting pairs of pentagons near the octahedron vertices—the necessary twelve pentagons are now distributed in pairs of six near the six octahedron vertices. Putting triples of pentagons near four tetrahedron vertices again produces a fullerene-like structure with a tetrahedral shape (see also [32]). The pairs and triples of pentagons in these shapes define the effective vertices of the fullerene-octahedron and fullerene-tetrahedron. The “vertices” are, in fact, the smooth, curved regions of the lattice of which curvature is determined by the number of pentagons (two or three)—the more pentagons, the larger the curvature of the effective vertex [32]. The pentagons in each pair or triple should be near each other if the effective octahedra and tetrahedra are to have fairly pointed effective vertices. In such situations, the notions of quasiequivalence may fail.

6. Conclusions

This completes a brief introduction to the geometry of icosadeltahedral structures, but many questions, of course, remain. In the case of structures made of carbon, one would like to know which factors govern the appearance of different shapes and can the process of production of these shapes be tuned to produce predominantly one type of myriad of possible closed structures. In the case of viruses, one is, of course, interested in the assembly processes that produce such large and complex objects. It is even more intriguing that some of them can be assembled spontaneously, even outside a living cell. This was first observed already in the year 1955 for a tubular tobacco mosaic virus [66]. Some large viruses use scaffolding proteins to guide the process of assembly, perhaps somewhat similar to what workers assembling a geodesic dome would do—build a scaffold to stand on [67]. Some viruses (e.g., adenovirus) produce proteins that are packed in their interior together with the DNA. It appears that these proteins reduce the pressure in the capsid due to electrostatic self-repulsion of the DNA, perhaps stabilizing the structure [68]. These mechanisms are actively researched and still not understood completely. As viruses are simple structures and yet subject to evolution, they seem to be ideal systems to better understand the evolutionary processes and mechanisms. It would certainly be of importance to construct some sort of the evolutionary narrative explaining the appearance of icosadeltahedral structures in the living world and their assembly. The field of virology is currently experiencing a sort of revival, as scientists from very different backgrounds show interest in viruses and approach the subject from their perspective [69,70]. There is also a somber aspect of this revival—new and potentially deadly viruses are constantly entering the human population. Powerful diagnostic and genome sequencing tools enable us to quickly detect them and assess their pandemic potential—just as I am writing this sentence, whole countries are put under quarantine due to the outbreaks of the coronavirus COVID-19 infection throughout the world [71]. New ideas and approaches to the monitoring and control of viruses are needed. A better understanding of virus stability and assembly may help in devising new anti-viral drugs. This paper is hoped to be of some use to the newcomers in this interesting interdisciplinary and quickly-developing field of research.