Abstract
The multi-symplectic integrator, as a numerical integration approach with symmetry, is known to have the characteristic of preserving the qualitative features and geometric properties of certain systems. Using the multi-symplectic integrator, the numerical simulation of the Gaussian solitary wave propagation of the logarithmic Korteweg–de Vries (logarithmic-KdV) equation was investigated. The multi-symplectic formulation of the logarithmic-KdV equation was explored by introducing some intermediate variables. A fully implicit version of the centered box scheme was used to discretize the multi-symplectic equations. In addition, numerical experiments were carried out to show the conservative properties of the proposed scheme.
1. Introduction
Since being proposed by Bridges [1] and Marsden et al. [2], multi-symplectic integrators have received huge attention in the past twenty years. As a kind of geometric integration method, the multi-symplectic method aims to construct numerical schemes which can preserve qualitative features and geometric properties of the solution of a partial differential equation (PDE) under discretization. In comparison with the well-known symplectic integrators used in Hamiltonian ordinary differential equations (ODEs), multi-symplectic integrators are able to overcome the limitation of symplectic geometry in dealing with PDEs [1,3]. The symplecticness in symplectic structures is a global property, while the symplecticness in multi-symplectic structures is a local property which varies both in time and space [4]. In recent years, many famous conservative nonlinear PDEs, including integrable and non-integrable models, have been solved by multi-symplectic integrators, such as the Korteweg–de Vries (KdV) equation [5,6], Schrödinger equation [7], Klein–Gordon equation [8] and Camassa–Holm equation [9,10]. The numerical results are non-dissipative and display excellent conservation properties. In order to overcome the limitation that the multi-symplectic method can only be used in conservative systems, some scholars have further developed this approach and applied it to non-conservation dynamic systems, including the generalized multi-symplectic method [11,12,13], stochastic multi-symplectic method [14,15] and conformal multi-symplectic method [16,17].
The studies on traveling wave solutions are of great importance because these models describe various applications in nonlinear engineering fields [18]. As effective approaches, multi-symplectic integrators have been successfully used to solve many traveling wave solutions that exist in nonlinear PDEs. These traveling wave solutions have common properties that spread at a constant velocity without changing their shape during propagation, such as solitary solutions, shock wave solutions and multiple-soliton solutions [18].
In this work, the multi-symplectic discretization method is used to investigate the strong nonlinear Gaussian solitary wave of the logarithmic-KdV equation numerically. Gaussian solitary waves are special solitons which have bell-shaped waveforms. Because they decay super-exponentially, the wings of Gaussian solitary waves decay in a short width [19].
The logarithmic-KdV equation, as a kind of generalized KdV equation that is derived as formal asymptotic limits of the nonlinear Fermi–Pasta–Ulam (FPU) lattices is defined by:
This equation describes the solitary wave propagation in harmonic chains with the nonlinear Hertzian interaction forces [20] that admit Gaussian solitary wave solutions. The Gaussian solitary wave solutions can be given as:
From Equation (2), it can be found that this type of solution has strong nonlinearity and decays super-exponentially [21].
The studies on Equation (1) have been reported in recent years: James and Pelinovsky analyzed the localized wave propagation in the nonlinear FPU lattices and derived asymptotic models as the logarithmic-KdV equation which possesses Gaussian solitary wave solutions [20]; Wazwaz studied the generalized logarithmic-KdV equation and obtained more Gaussian solitary waves [21]; Wang and Xu derived a complete description of Lie point symmetries for the logarithmic-KdV equation [22]; and Wazwaz investigated a variety of nonlinear evolution equations which have logarithmic nonlinearities, including logarithmic KdV-like, KP-like and Klein–Gordon equations [18].
Note that the works mentioned above mainly focus on the analytical solutions of the logarithmic-KdV equation. To the best of our knowledge, numerical experiments on the Gaussian solitary wave for this equation have not been reported. To do the numerical analysis, the challenge is that the Gaussian-type solitary wave has strong nonlinearity, which will affect the stability of the numerical solutions.
This work aims to extend the applications of the multi-symplectic integrator when dealing with the strong nonlinear traveling solitary wave. The numerical simulations of the logarithmic-KdV equation are studied under the theory of this structure-preserving method. The work is organized as follows. In Section 2, a multi-symplectic formulation of the logarithmic-KdV equation is obtained. In Section 3, a fully implicit centered box scheme is introduced to discretize the corresponding multi-symplectic equations. Numerical results are carried out and the error analyses are shown in Section 4. Finally, some concluding remarks are given in the last section.
2. A Multi-Symplectic Formulation for the Logarithmic-KdV Equation
As shown in Equation (1), the logarithmic-KdV equation is a kind of generalized KdV equation. Thus, the multi-symplectic structure of the KdV equation can be used for reference. The logarithmic-KdV equation (Equation (1)) has an absolute value term. The absolute value does not need any treatment during the numerical simulation process.
It can be found that the structure of the logarithmic-KdV equation (Equation (1)) is similar to the KdV equation:
The general procedure of deriving a multi-symplectic formulation includes introducing some appropriate canonical momenta to let a high-order PDE reduce to the first-order coupled PDEs’ symmetric form. The multi-symplectic form of the KdV equation (Equation (3)) has been reported in the literature. Here, similar to Reference [5], the canonical momenta can be given as:
According to the multi-symplectic theory [1], the corresponding multi-symplectic formulation of Equation (1) can be obtained as:
where the skew-symmetric matrices and and the Hamiltonian function are respectively expressed by:
There is an important consequence for the multi-symplectic structure: if the Hamiltonian function is independent of , the multi-symplectic equation adheres to the local energy conservation law, and when the Hamiltonian function is independent of , the equation adheres to the local momentum conservation law. These local conservation laws given by multi-symplectic symmetric form assure the conservation of the energy and momentum quantities during the numerical integration. The multi-symplectic discrete scheme can be constructed through the multi-symplectic formulation of the logarithmic-KdV equation shown in Equations (5) and (6).
3. A Multi-Symplectic Centered Box Scheme for the Logarithmic-KdV Equation
A multi-symplectic finite difference scheme can be obtained through integration of multi-symplectic equations, like Equation (5) over the domain, and choosing a suitable approximation to the integral terms for both the and directions.
The centered box scheme, which satisfies the concatenated midpoint rule, is used here. This scheme is fully implicit and is also called the Preissman box scheme, which is widely used in hydraulics.
Defining some discrete operators [4]:
and applying the implicit midpoint rule, the Preissman box discretization for Equation (5) takes form as:
Notice that the operators are linear and can be exchanged with one another [4]. For the majority of the grid point choices, the iterative method for scheme (8) will not converge without some other approaches. In our study, the variables were eliminated and the reduced box scheme only contained the variable , which was obtained as:
Equation (9) is a fully implicit scheme that includes twelve mesh points. The structure of this three-level implicit scheme is shown in Figure 1. The scheme (Equation (9)) is a closed form for the logarithmic-KdV equation involving logarithmic nonlinearity.
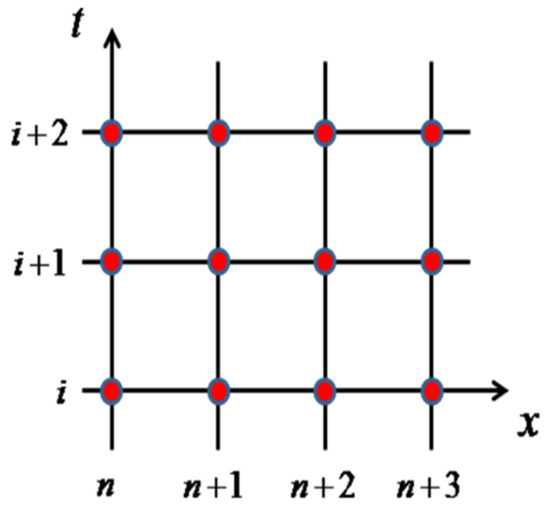
Figure 1.
Structure of the multi-symplectic centered box scheme for Equation (9).
The Newton iteration method is used to solve the nonlinear difference scheme (Equation (9)). It can be found that the third part of the scheme (Equation (9)) contains an absolute value term, while the absolute value term does not change the coefficients in the Jacobian matrix. Therefore, the scheme (Equation (9)) can be used directly.
4. Numerical Experiments on Gaussian Solitary Wave Propagation
In this section, the propagation of the Gaussian solitary wave is investigated using the above multi-symplectic implicit centered box scheme (Equation (9)).
Equation (9) is a three-level scheme, and the initial values of the first two levels should be given. We can consider the numerical simulation with the periodic boundary condition as:
where and are the left and right boundaries, respectively. The initial condition can be given as the Gaussian soliton solution. If one gives the schemes:
where is the first level initial value and represents the second level value, the discrete value of the second level can be obtained. From the third level, the multi-symplectic difference scheme (Equation (9)) can be used for the iterative computation.
We can consider the case of with the following initial condition:
where the speed takes . We can use the multi-symplectic centered box scheme (Equation (9)) to simulate the evolution of the Gaussian solitary wave in the domain . The time step length takes and the spatial resolution is .
Figure 2 shows the comparison of the numerical solution and analytical solution. It can be found that the Gaussian soliton is a kind of solitary wave and maintains the same shape during the traveling process. It is also clear that the numerical solution coincides with the analytical solution, which implies that the multi-symplectic centered box scheme (Equation (9)) can be used to capture the propagation process of the Gaussian solitary wave effectively.
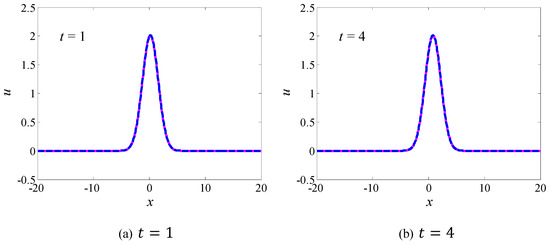
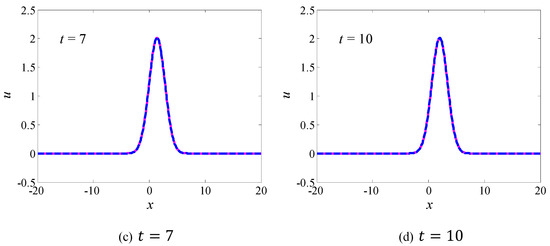
Figure 2.
The waveforms of the Gaussian soliton at (a) , (b) , (c) and (d) when (where the dashed line is the analytical solution and the solid line is the numerical solution).
Figure 3 shows the errors between the numerical and analytical solution at , 4, 7 and 10. It can be found from Figure 3 that the scheme (Equation (9)) can simulate the traveling Gaussian soliton with small errors. The maximum errors mainly appear at the locations near the soliton core.
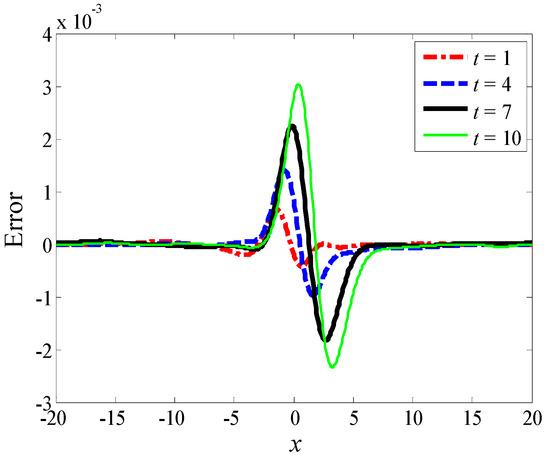
Figure 3.
The numerical errors at different times when .
The logarithmic-KdV equation satisfies the three conserved quantities, which are the mass, momentum and energy conservations as follows [21]:
Considering the case when the speed takes , we further investigate the conservative properties of the numerical results for the dynamic conserved quantities in Equation (13). The approximate discrete schemes for the conserved quantities in Equation (13) are expressed as:
Considering the integral values of the initial conditions as the initial values of the conserved quantities in Equation (13), the numerical absolute errors of the conserved quantities in each time step can be obtained, which are the difference between the numerical results and the initial values.
The initial results of the three conserved quantities are , and , respectively. The numerical errors of the three conserved quantities are shown in Figure 4. It can be seen from Figure 4 that the mass conserved quantity is very stable, and remains at the order. The momentum and energy quantities have larger errors, the order and order, respectively. It is clear that the errors of the conserved quantities are all relatively stable and do not increase obviously with time. Thus, Figure 4 reflects the conservative properties of the scheme (Equation (9)) well.
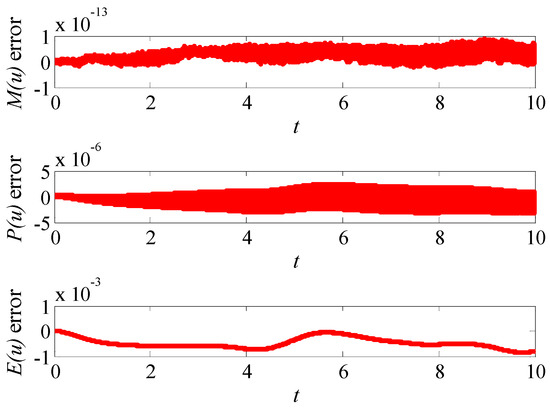
Figure 4.
The numerical errors of the conserved quantities when .
From the analysis above, it can be found that the multi-symplectic implicit centered box scheme (Equation (9)) can give relatively ideal results of the Gaussian solitary wave propagation. During the process of the soliton propagation, the three conserved quantities of the logarithmic-KdV equation can be preserved well. Hence, the multi-symplectic implicit centered box scheme has good numerical behaviors and can be used to simulate the Gaussian solitary wave propagation for the logarithmic-KdV equation.
.
5. Conclusions
A multi-symplectic formulation for the logarithmic-KdV equation was obtained and the implicit centered box scheme was developed to derive the multi-symplectic discretization scheme. The evolution process of the Gaussian type solitary wave was simulated. It was found that the numerical results had good conservative properties. It is worth mentioning that the proposed method is an attempt to explore the numerical simulation of the logarithmic-KdV equation, and may extend the range of the application of the multi-symplectic integrator.
However, the error control at the Gaussian soliton core position and for the quantity of energy conserved in this method are still not perfect. Therefore, improved numerical approaches for this strong nonlinear dynamic model deserve further exploration in future investigations.
Author Contributions
Y.Z. drafted the original manuscript, and S.L. helped to modify the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (Grant Numbers 11902206, 11972238).
Acknowledgments
The authors would like to thank the editors and reviewers for their help.
Conflicts of Interest
The authors declare that they have no competing interests.
References
- Bridges, T.J. Multi-symplectic structures and wave propagation. Math. Proc. Camb. Philos. Soc. 1997, 121, 147–190. [Google Scholar] [CrossRef]
- Marsden, J.E.; Patrick, G.P.; Shkoller, S. Multisymplectic geometry, variational integrators, and nonlinear PDEs. Commun. Math. Phys. 1998, 199, 351–395. [Google Scholar] [CrossRef]
- Bridges, T.J.; Reich, S. Multi-symplectic integrators: Numerical schemes for Hamiltonian PDEs that conserve symplecticity. Phys. Lett. A 2001, 284, 184–193. [Google Scholar] [CrossRef]
- Wlodarczyk, T.H. Stability and Preservation Properties of Multisymplectic Integrators. Ph.D. Thesis, University of Central Florida, Orlando, FL, USA, 2007. [Google Scholar]
- Zhao, P.F.; Qin, M.Z. Multisymplectic geometry and multisymplectic Preissman scheme for the KdV equation. J. Phys. A-Math. Gen. 2000, 33, 3613–3626. [Google Scholar] [CrossRef]
- Wang, Y.S.; Wang, B.; Chen, X. Multi-symplectic Euler box scheme for the KdV equation. Chin. Phys. Lett. 2007, 24, 312–314. [Google Scholar]
- Aydin, A.; Karasozen, B. Symplectic and multi-symplectic methods for coupled nonlinear Schrödinger equations with periodic solutions. Comput. Phys. Commun. 2007, 177, 566–583. [Google Scholar] [CrossRef]
- Hong, J.L.; Jiang, S.S.; Li, C. Explicit multi-symplectic methods for Klein-Gordon-Schrödinger equations. J. Comput. Phys. 2009, 228, 3517–3532. [Google Scholar] [CrossRef]
- Cohen, D.; Owren, B.; Raynaud, X. Multi-symplectic integration of the Camassa-Holm equation. J. Comput. Phys. 2008, 227, 5492–5512. [Google Scholar] [CrossRef]
- Zhang, Y.; Deng, Z.C.; Hu, W.P. Multisymplectic method for the Camassa-Holm equation. Adv. Diff. Equ. 2016, 7, 1–12. [Google Scholar] [CrossRef]
- Hu, W.P.; Deng, Z.C.; Han, S.M.; Zhang, W.R. Generalized multi-symplectic integrators for a class of Hamiltonian nonlinear wave PDEs. J. Comput. Phys. 2013, 235, 394–406. [Google Scholar] [CrossRef]
- Zhang, Y.; Deng, Z.C.; Hu, W.P. Generalized Multi-symplectic integrator for vibration of a damping string with the driving force. Int. J. Appl. Mech. 2017, 9, 1750004. [Google Scholar] [CrossRef]
- Hu, W.P.; Deng, Z.C. Competition between geometric dispersion and viscous dissipation in wave propagation of KdV-Burgers equation. J. Vib. Control 2015, 21, 2937–2945. [Google Scholar] [CrossRef]
- Hong, J.L.; Ji, L.H.; Zhang, L.Y. A stochastic multi-symplectic scheme for stochastic Maxwell equations with additive noise. J. Comput. Phys. 2014, 268, 255–268. [Google Scholar] [CrossRef]
- Chen, C.C.; Hong, J.L.; Zhang, L.Y. Preservation of physical properties of stochastic Maxwell equations with additive noise via stochastic multi-symplectic methods. J. Comput. Phys. 2016, 306, 500–519. [Google Scholar] [CrossRef]
- Bhatt, A.; Floyd, D.; Moore, B.E. Second order conformal symplectic schemes for damped Hamiltonian systems. J. Sci. Comput. 2016, 66, 1234–1259. [Google Scholar] [CrossRef]
- Bhatt, A.; Moore, B.E. Exponential integrators preserving local conservation laws of PDEs with time-dependent damping/driving forces. J. Comput. Appl. Math. 2019, 352, 341–351. [Google Scholar] [CrossRef]
- Wazwaz, A.M. Gaussian solitary wave solutions for nonlinear evolution equation with logarithmic nonlinearities. Nonlinear Dyn. 2016, 83, 591–596. [Google Scholar] [CrossRef]
- Darvishi, M.T.; Najafi, M. Some extensions of Zakharov-Kuznetsov equations and their Gaussian solitary wave solutions. Phys. Scr. 2018, 93, 085204. [Google Scholar] [CrossRef]
- James, G.; Pelinovsky, D. Gaussian solitary waves and compactons in Fermi-Pasta-Ulam lattices with Hertzian potentials. Proc. R. Soc. A-Math. Phys. 2014, 470, 20130462. [Google Scholar] [CrossRef]
- Wazwaz, A.M. Gaussian solitary waves for the logrithmic-KdV and the logarithmic-KP equations. Phys. Scr. 2014, 89, 095206. [Google Scholar] [CrossRef]
- Wang, G.W.; Xu, T.Z. Group analysis, explicit solutions and conservation laws of the Logarithmic-KdV equation. J. Korean Phys. Soc. 2015, 66, 1475–1481. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).