Selecting FFT Word Length for an OFDM Receiver That Supports Undersampling

Abstract

In this paper, we focus on Orthogonal Frequency Division Multiplexing (OFDM) transceivers where undersampling is employed by the receiver Analog/Digital Converter (ADC) when sparse information is exchanged. Several Fast Fourier Transform (FFT) symmetry properties are exploited to allow the substitution of specific input values by others that have already been sampled by the ADC. Several architectures have been proposed in the literature for efficient FFT implementations in terms of power, speed and hardware resources. The FFT input/output values, twiddle factors, etc., are complex numbers with their real and imaginary parts being represented using fixed point format. A tradeoff has to be made between rounding error and complexity. The optimal minimum FFT word length is investigated by combining the undersampling and the rounding error. A configurable new FFT architecture has been developed in hardware description language to test the error model with various FFT sizes, word lengths and Quadrature Amplitude Modulations (QAM). A system designer can take into account the sparseness of the input data and define the desired rounding and undersampling error relation. Τhe developed error model would then predict the required word length and ADC resolution with average Root Mean Square Error (RMSE) less than 1.

1. Introduction

Recovering information from fewer samples is possible if data are sparse or compressible. In this case, an ADC can operate in a sampling rate closer to the actual information rate rather than the Nyquist one [1]. The ADCs in this case are often called Analog to Information Converters (AIC) [2]. Compressive Sampling or Sensing (CS) methods employ iterative optimization techniques like Regressive Analysis or Orthogonal Matching Pursuit [3] to recover information from fewer measurements. The hardware implementation of a CS algorithm requires a large number of resources due to its increased complexity. CS techniques are applied in image processing applications such as radar, medical imaging (such as Magnetic Resonance Imaging (MRI), ultrasounds, X-ray imaging), surveillance systems, etc. For example, in [4], the acquisition time needed for MRI scans is significantly reduced. In [5], radar data are compressed and decompressed using CS techniques with Normalized Mean Square Error (NMSE) ranging between 1.5 and 2.5 under certain measurement conditions.

In OFDM environments channel estimation is achieved using CS techniques since it can be assumed that the OFDM channel is sparse. In this way, the number of pilots can be substantially reduced as described in [6], where 511 subcarriers and 20 pilots are used, and only a few of the 40 channels taps are assumed non-zero. The Bit Error Rate (BER) is approximately 0.003 if Signal/Noise Ratio (SNR) is 30dB and 5 of the 40 channel taps are non-zero. The efficient implementation of sparse FFT and Inverse FFT (IFFT) in OFDM environments is an important target since these modules are computationally intensive and power greedy. In [7] sub-sampling of the input signal is performed with O(k∙logk) complexity. For example, using a 280 × 280 pixel image in [7] with the number of non-zero pixels being 3509, the NMSE is 0.0085 when 35308 samples are used.

In the work presented in [8,9], the sparse IFFT input samples of an OFDM transmitter are ordered appropriately to allow the information recovery on the receiver side from fewer FFT input samples. In this way, the power consumption of the receiver ADC is reduced down to the half while the memory requirements, power dissipation and the speed of the IFFT and the FFT modules can also be reduced. More specifically, a wired OFDM architecture is studied in [8], where 1024-point FFT/IFFT is employed. The simulation results show that full information recovery can be achieved if 50% of the time the ADC operates in 7/8 of its normal rate and the sparseness s in input data is less than 2% i.e., less than 2% of the input bits are non-trivial. If a lower ADC sampling rate is employed, an error floor appears that may be acceptable in some applications. Full information recovery can also be achieved if lower ADC sampling rate is applied when sparseness level is higher. The only noise source taken into consideration in [8] is Additive White Gaussian Noise (AWGN). The effect of the ADC Quantization Errors (QE) and the Round-off Errors (RE) caused by the representation of the operands with limited number of bits is not studied in [8]. The proposed undersampling technique is extended in [9], to cover wireless OFDM transceivers with Space-Time Block Code (STBC) encoding. A general Signal to Interference, Distortion Noise Ratio (SIDNR) expression is derived taking into consideration the ADC quantization noise as modeled in [10] as well as wireless channel features like Inter-Symbol-Interference (ISI).

In the present work, we focus on the most critical part of the OFDM transceiver system that is the FFT on the receiver side. A precise error model has been developed by describing how the employed undersampling technique can affect the overall error in the received data. This Undersampling Error (UE) is combined with the RE/QE errors. The target is to optimally select the appropriate word length for the representation of the FFT input values and coefficients in order to avoid excessive additional error overhead beyond the error caused by the UE. For example, the end user may ask for an RE error that will not exceed 10% of the UE. Selecting the desired modulation scheme and FFT size the developed error model will estimate the minimum word length to achieve the specified relation between RE and UE for a particular sparseness level of the input data. The real numbers (or the real/imaginary parts of a complex number) can be represented in IEEE-754 standard 32-bit floating-point format [11]. In this format, a real number is described by one bit for the sign, a number of bits for the significand and a signed exponent. Although the IEEE-754 floating point format can cover a wide range of real numbers with a very high precision, the number of resources that it needs is excessively high. For this reason, fixed point format is employed in this work. In fixed point format (b,f), b bits are used for the description of a number and f of these b bits are used for the fraction: $B_{b-1}\dots B_{f+1}{B}_f{B}_{f-1}\dots B_1{B}_0=B_{b-1}{2}^{b-f-1}+\dots +B_0{2}^{-f}$. Several operations such as multiplications and divisions by 2 can be implemented with simpler circuits in fixed point format but the results of these operations have to be monitored for scaling and overflow errors.

A memory-based pipeline configurable FFT has been developed in synthesizable Very high speed IC Hardware Description Language (VHDL) to accurately assess the proposed error model. Two FFT sizes have been tested (256 and 1024 points) with different number of word lengths (ranging from 5 to 10 bits). The alternative modulations tested were 16-QAM and 4-QAM with various levels of data sparseness ranging between 0.5% and 10%. The OFDM configuration in terms of FFT size, modulation and word length cannot change dynamically in real time. They are statically defined in order to measure the error for various sparseness levels. The average RMSE error between the predicted word length and the experimental results is less than 1, for the various QE error targets that have been set. The predicted word length can also be used as the ADC resolution.

This paper is organized as follows: In Section 2, the undersampling method presented in [8] and [9] is briefly described as well as some indicative QE and RE error estimation methods presented in the literature. The combined UE, RE error model proposed in this paper is presented in Section 3. The synthesizable memory-based pipeline FFT architecture used to assess the error model is presented in Section 4. Finally, in Section 5 the simulation results are presented along with a discussion on how the error modeling followed can be useful for other non-OFDM telecommunication systems.

2. Background

2.1. Proposed Undersampling Method on OFDM Receiver Side

In an OFDM transmitter, the binary input data stream is encoded for the generation of a parity bit stream used for error correction on the receiver side. The data and parity bit streams are usually interleaved in order to avoid burst errors. Then, groups of log₂q bits are mapped to q-QAM constellation symbols X_k (0≤k<N) that form the parallel input to an N-point IFFT. The output of this IFFT are the symbols x_n (0≤n<N) that are serially transmitted over the channel. Pilot symbols with known value are placed on reserved subcarriers for channel estimation and equalization. A cyclic prefix is also appended to avoid Inter-Symbol Interference (ISI). Digital/Analog Conversion (DAC) is required for the transmission of the resulting symbols using an appropriate pulse shaping method [12,13]. In wired OFDM transceivers the channel noise is assumed to be Additive White Gaussian Noise (AWGN) and the y_n symbols received are y_n=x_n+z_n, (z_n is the noise with variance ${\sigma }_n^2$). A different model is used for wireless channels that takes into consideration the reflections, interference, Rayleigh fading, etc. In optical communications the fiber channels are affected by several sources of distortion including Kerr non-linearity, chromatic dispersion, optical filtering, double Rayleigh scattering, shot and thermal noise and especially Amplified Spontaneous Emission (ASE) [12]. The y_n symbols at the output of the receiver ADC, form the input of an FFT. The FFT output symbols Y_k (0≤k<N) are mapped to the closest QAM symbol and then QAM demodulation is performed (e.g., using hard or preferably soft decision demodulators). Forward Error Correction (FEC) decoding (Viterbi, Turbo codes, etc) exploits the available parity bits in order to correct as many errors as possible on the receiver side.

A Recursive Systematic Convolutional (RSC) FEC encoder can be used such as the one with feed forward and feedback polynomials: 1+D+D²+D³ and 1+D+D² respectively, where the D^p denotes a delay of p clock periods. In order to apply the proposed undersampling method, the Interleaver should generate q-QAM symbols derived from parity or data bits only. Thus, a pair of small buffers at the FEC encoder output can store temporarily log₂(q) bits from the systematic and the parity output of the RSC encoder before they are mapped to the corresponding q-QAM symbol. Most of the q-QAM symbols derived from sparse data bits will have a common value X_c. However, several parity q-QAM symbols derived from parity bits are likely to have identical values because the parity output of the employed RSC encoder described above remains ‘0’ until a first data ‘1’ appears. Then, the 7-bit pattern “0111010” is repeated as long as the data input remains ‘0’. A different 7-bit pattern is generated when another ‘1’ appears at the input and this is also repeated until a third ‘1’ appears. The distance between each ‘1’ at the FEC encoder input is expected to be high due to the sparseness in the input. Consequently, several identical consecutive 7-bit patterns are expected to appear at the parity output of the FEC encoder. These identical parity patterns can be treated as if they were X_c symbols as will be explained below.

The proposed undersampling method is taking advantage of the data sparseness in time domain in conjunction with some well-known properties of the Discrete Fourier Transform (DFT). Proper symbol arrangement is employed at the IFFT input, allowing the substitution of several symbols at the receiver FFT input, by others without significant loss of information. In this way, the receiver ADC can periodically relax (operate in lower rate) without sampling some y_n symbols since they can be substituted by others, that have already been received. The adopted symbol arrangement at the IFFT input, makes trivial several IFFT/FFT operations that can be omitted in order to achieve lower power and faster operation. This is similar to output pruning described in [14].

If $w_N^r=e^{i2\pi r/N}$ are the twiddle factors then DFT is defined as:

$$Y_k={\displaystyle \sum }_{n=0}^{N-1}{y}_n{w}_N^{-kn},$$

(1)

and the Inverse DFT (IDFT):

$$x_n=\frac{1}{N}{\displaystyle \sum }_{k=0}^{N-1}{X}_k{w}_N^{kn}$$

(2)

One of the IDFT symmetry properties used by the proposed undersampling method concerns the relationship between $x_n$ and $x_{n+N/2}$ when n is odd:

$$x_n=\frac{1}{N}\left({\displaystyle \sum }_{k=0,2,\dots }^{N-2}{X}_k{w}_N^{kn}+{\displaystyle \sum }_{k=1,3,\dots }^{\frac{N}{2}-1}(X_k-X_{k+\frac{N}{2}})w_N^{kn}\right),$$

(3)

$$x_{n+N/2}=\frac{1}{N}\left({\displaystyle \sum }_{k=0,2,\dots }^{N-2}{X}_k{w}_N^{kn}-{\displaystyle \sum }_{k=1,3,\dots }^{\frac{N}{2}-1}(X_k-X_{k+\frac{N}{2}})w_N^{kn}\right),$$

(4)

According to Equations (3) and (4), $x_n=x_{n+N/2}$. if $X_k=X_{k+N/2}$. As already mentioned, $X_k$ and $X_{k+N/2}$ with k being odd, are likely to have equal value if they are both sparse data q-QAM symbols or if they are parity q-QAM symbols generated in a relatively close distance. Consequently, if for example data q-QAM symbols are placed in the odd positions of the IFFT input, then up to half (N/4) of the odd y_n symbols at the FFT input can be replaced by their counterparts at distance N/2: y_n+N/2. It is obvious that no error would occur only if all the data q-QAM symbols placed the odd positions were equal to X_c, e.g., if the data input is constantly zero. An error occurs if some of the data q-QAM symbols at the odd positions are not trivial (not equal to X_c). To reduce the probability of errors, the number of samples R that can be substituted at the input of the receiver FFT can be lower than N/4, e.g., N/8 or N/16 [8].

Another DFT symmetry property had also been employed in [9] to extend the maximum number of samples that can be replaced from N/4 to 3N/8. It is based on the following properties: $w_N^{n\left(\frac{N}{2}-k\right)}=-w_N^{-nk}$, $w_N^{n\left(\frac{N}{2}+k\right)}=-w_N^{nk}$ and $w_N^{n\left(N-k\right)}=w_N^{-nk}$. The IFFT output x_n can be expressed as:

$$\begin{array}{c}{x}_n=({\displaystyle {\displaystyle \sum }_{k=1,3,\dots ,\frac{N}{4}}}(X_k{w}_N^{kn}-X_{\frac{N}{2}-k}{w}_N^{-kn})+{\displaystyle {\displaystyle \sum }_{k=1,3,\dots ,\frac{N}{4}}}(-X_{k+\frac{N}{2}}{w}_N^{kn}+X_{N-k}{w}_N^{-kn})\\ +{\displaystyle {\displaystyle \sum }_{k=2,\dots ,\frac{N}{2}-2}}(X_k{w}_N^{kn}+X_{N-k}{w}_N^{-kn})+X_0-X_{\frac{N}{2}})\frac{1}{N}=x_{\frac{N}{2}-n}\end{array}$$

(5)

From Equation (5) it can be deduced that x_n=x_N/2-n (n<N/4) if the following three conditions hold: a) $X_k=X_{\frac{N}{2}-k}$(with odd k and k≤N/4), b)$X_{N-k}=X_{\frac{N}{2}+k}$(with odd k and k≤N/4) and c) $X_k=X_{N-k}$ with even k and 0≤k<N/2. In a similar way, it can be shown that x_N/2+n=x_N-n (n<N/4). Consequently, the y_n samples with odd n≤N/4 can be substituted by the samples $y_{\frac{N}{2}-n}$ and the $y_{\frac{N}{2}+n}$ samples can be substituted by $y_{N-n}$.

If 16-QAM modulation is employed, the IFFT input packet structure shown in Figure 1 can be used in order to apply the proposed undersampling technique. The data QAM symbols have been placed at the even positions and most of them have identical value (X_c). If the RSC FEC encoder described earlier is employed then, the repeated 7-bit parity pattern can be padded with one more bit. The Most Significant 4-bits (Parity MSB) and the Least Significant 4-bits (Parity LSB) of the padded 8-bit parity patterns are placed in Figure 1 in appropriate positions in order to apply the proposed undersampling scheme with the lower possible error. In [9], the proposed undersampling method is extended to wireless OFDM systems with STBC encoding and several other IFFT input packet structures like the one shown in Figure 1 are described.

The representation of the real numbers is very important to computationally intensive operations like the FFT and IFFT module of an OFDM system. Due to the FFT’s high complexity, the real numbers have to be implemented using the minimum word length, otherwise severe rounding errors may occur. The selection of the minimum word length in the case of an OFDM system that supports undersampling is studied in conjunction with the UE error caused by the undersampling process. It would be redundant to use more bits for the representation of the real numbers since it would not improve the UE error.

2.2. Review of Quantization and Round-off Error Estimation Methods

One significant source of error is the communication channel that can be affected by AWGN, Rayleigh scattering, ASE, instant and thermal noise, etc., according to the physical media it consists of [12,13]. These sources of error are taken into account by the degradation they cause to the channel SNR. In this sense, the channel errors are not combined with the error sources at the receiver that are examined below.

The Quantization Error (QE) caused by ADCs and the Round-off Errors (RE) that stem from the use of finite word-length for the representation of real numbers have been extensively studied for several decades. Some of the popular old and newer methods are summarized here to combine with the specific requirements of the undersampling method described in Section 2.1.

Welch [15] studied the effect on the output of the rounding at each stage of a Radix-2 Decimation in Time (DIT) FFT. Block floating point format with the mantissa and exponent are stored with fixed bit length. The exponent is common for all numbers thus, only the mantissa is stored for each number. The biggest number at the input is downscaled until its absolute value is between 0.5 and 1. The rest of the numbers are downscaled in the same way in order to preserve a common exponent. The upper bound of the error expressed in RMSE is estimated as:

$$\frac{RMSE\left(error\right)}{RMSE\left(result\right)}\le \frac{2^{\left({\log }_{2}N+3\right)/2}\times 2^{-B}\times C}{RMSE\left(input\right)}$$

(6)

The parameter C is a constant between 0.4 and 0.9 depending on the signal shape. In a more recent paper, Pálfi and Kollár [16], showed experimentally that Welch’ s results [15] are not valid if the input is between −1–+1 instead of 0–+1.

A worst-case output Noise-to-Signal Ratio (NSR) is estimated in [17] taking into consideration the QE of the sin/cos coefficients of an FFT. If these coefficients are represented with b+1 bits then $NSR\le {\left|\mathit{\Delta }W\right|}^2\left(m_w-2\right)$ in radix-2 FFT, with $\left|\mathit{\Delta }W\right|=2^{-b}/\sqrt{2}$ and with windowed input signal. The parameter m_w depends on the window function (m values between 3 and 10 are tested in [17]). This limit is compared in [17] against older stochastic approximations presented in [18] ($NSR=2^{-2b}m/6$) and [19] ($NSR=2m^2{2}^{-2b}$).

If $\Delta$ is the minimum difference that can be discriminated between the quantized real numbers (or voltage levels) by a b_ADC-bit resolution ADC with reference voltage V_ref, then $\mathit{\Delta }=V_{ref}/2^{r_{ADC}}$ (see Figure 2). For normalization reasons we assume V_ref=1. The error caused by the quantization process is between $-\mathit{\Delta }/2$. and $+\mathit{\Delta }/2$. The error probability is assumed to be uniform ($1/\mathit{\Delta }$) in these limits. The variance of the error is then estimated as: ${\sigma }_{QE}^2={\mathit{\Delta }}^2/12$. The RE error caused by the use of finite word-length in an N-point FFT is also viewed as QE in [10]. The quantization noise power P_QE in all real and imaginary parts of the DFT outputs as defined in Equation (1) is estimated in [10] as:

$$P_{QE}=N\frac{{\mathit{\Delta }}^2}{12}$$

(7)

In FFT implementations, this P_QE noise is reduced as indicated by the relation (8) below [10]. The upper limit of the relation (8) corresponds to the classic FFT implementation by Cooley and Turkey [20].

$$P_{QE}\le \frac{{\mathit{\Delta }}^2}{6}\left({\log }_{2}N-2\right).$$

(8)

Swartzlander and Saleh [19], describe an FFT Implementation with fused floating-point operations and explain the worst-case error caused in Radix-2 and Radix-4 FFT implementations. Errors of ±1/2 Least Significant Bit (LSB) are caused by rounding and normalization at the output of the adder or the multiplier. Thus, one of the Radix-2 butterfly outputs may have a 1/2 LSB error, while the other may have a 2 LSB error. For the fused implementation the second error is reduced to 1 LSB. In Radix-4, all of the butterfly outputs may have 2 1/2 LSB errors. In the fused implementation presented in [21], rounding and normazation error is reduced to 1 1/2 LSB. Although Radix-2 butterfly error is smaller, the error in an FFT is expected to be smaller for a Radix-4 implementation due to fewer stages and this is confirmed in [21] by simulating 64K point FFT.

The effect of fixed-point format with limited precision for different FFT algorithms is studied in [22]. The error of a single quantization operation is modelled as above and then, the error of a complex multiplication is estimated as $4{\sigma }_{QE}^2$. A matrix representation of error propagation model is proposed to analyze the rounding effect in DIT and Decimation in Frequency (DIF) FFTs. A similar propagation model will be examined in the next subsection for the FFT of our case that supports undersampling [8,9]. The radix-2 DIT FFT algorithm has better accuracy in term of Signal-to-Quantization-Noise Ratio (SQNR) [22]. For this reason, we focus on the error modelling of DIT FFT in this paper. The overall output error $\mathit{\Delta }{\mathit{{\rm Y}}}_{\mathit{{\rm T}}}$ of a DIT FFT is estimated in [22] as:

$$\mathit{\Delta }{\mathit{{\rm Y}}}_{\mathit{{\rm T}}}={{\rm B}}_{d,d}{\displaystyle \sum }_{i=0}^{d-1}\left({\displaystyle \prod }_{j=i+1}^{d-1}{w}_{Tj}{B}_{d,j}\right)e_i$$

(9)

Where $w_{Tj}$ is the equivalent twiddle factor matrix at the i-th stage of DIT FFT algorithm. $B_{d,d-i}$ is the equivalent butterfly matrix at the i-th stage of $2^d$-point FFT and e_i (0≤i≤d) is the corresponding additive N×1 additive noise vector of $w_{Fi}$ (the equivalent twiddle factor matrix at the i-th stage of DIF FFT: $w_{F_i}=w_{T_{d-i-1}}$) with variance ${\sigma }_c^2$. The total quantization noise power P_nt of the DIT FFT algorithm is:

$$P_{nt}={\displaystyle \sum }_{i=0}^{d-1}{2}^{d-i}{n}_{T_i}{\sigma }_c^2$$

(10)

The parameter $n_{T_i}$ is the number of nontrivial twiddle factors at the i-th stage. In [23], the case where the twiddle factor word length is different from the register word length is studied. First, the statistical noise model for the prediction of the RE after a multiplication of two quantized signals u and a, of different precision, is presented: $\widehat{v}=\widehat{u}\ast \widehat{a}=\left(u+\epsilon 1\right)\left(\alpha +\epsilon 2\right)+\epsilon 3=au+noise$. The parameters ε1, ε2, ε3 are the errors caused by the rounding of u, a, and v, respectively. The total noise is $u\epsilon 2+\alpha \epsilon 1+\epsilon 1\epsilon 2+\epsilon 3$.The variance of noise ${\sigma }_n^2$ given u, a, is:

$${\sigma }_n^2=\frac{2^{-2b3}}{12}+u^2\frac{2^{-2b2}}{12}+a^2\frac{2^{-2b1}}{12}+\frac{2^{-2\left(b1+b2\right)}}{12}=\frac{2^{-2b}}{12}\left(1+u^2+a^2+2^{-2b}\right)$$

(11)

The parameters b1, b2, b3 are the word lengths of u, a and v, respectively. The last part of the Equation holds if all the word lengths were equal (b1 = b2 = b3 = b). The total variance of the RE error in the Radix-2 DIT FFT presented in [23] is simplified to $P_{RE}=8{\sigma }_n^2$ for large N values. This Radix-2 variance is compared with Radix-4 and Radix-8 variance (approximately 16${\sigma }_n^2$ and 24${\sigma }_n^2$, respectively). The approach presented in [23] will serve as the base for the development of our error model as will be described in the following section.

In [24] fast fixed-point algorithms are used to estimate the RE in the DFT. The RE variance depends on frequency index. Modelling RE as a random variable with uniform distribution holds only for the first FFT stage. RE probability density function is not uniform in the following stages. The discretization error variance at each stage p is estimated recursively as:

$${\sigma }_p^2\left(k\right)=\frac{1}{4}{\sigma }_{p-1}^2\left(k\right)+\frac{1}{4}{\sigma }_{p-1}^2\left(2^{p-1}+k\right)+{\delta }_{k,p}, with {\delta }_{k,p}=\{\begin{array}{c}4{\sigma }_h^2, if k=0 or 2^{p-2}\\ 2{\sigma }_h^2+4{\sigma }_{cs}^2,otherwise\end{array}$$

(12)

where k=0,…,2^p-1-1 and ${\sigma }_h^2=2^{-2b-4}$ if the operations are performed with b+1 precision. The parameter ${\sigma }_{cs}^2$ is the variance of the discretization error caused by the multiplication with the cos/sin coefficients. These theoretical models are statistically checked in [24] using DIT FFT with two rounding methods.

In [25], the authors optimize the FFT word length in a memory based architecture attempting to avoid a very pessimistic estimation. A butterfly operation is expressed as $Z=\frac{1}{2}{w}_N^{kn}\left(A+B\right)$ where A and B are the complex inputs. The Z norms are related to the norm of A and B by ${\parallel Z\parallel }^2\le ({\parallel A\parallel }^2+{\parallel B\parallel }^2)/2$. The covariance of the FFT error at stage p of an N-point FFT (with $p={\log }_{2}N$ stages) is estimated as:

$${\sigma }_p^2={\sum }_{k=0}^p{\left(\frac{1}{2}\right)}^{k}q\left(o-k\right), \mathit{with} q\left(o\right)=\frac{2^{-2b\left(p\right)}+2^{-2a\left(p\right)-2}}{3}>0$$

(13)

where a(p) and b(p) are the number of bits used to represent the butterfly inputs and sine/cosine coefficients at stage p, respectively. The upper bound of Signal to Noise and Quantization error Ratio (SNQR) is less than $-10{\log }_{10}{\sigma }_p^2$. The target of the optimization problem is to maximize the vector of q elements subject to ${\sigma }_p^2\le {10}^{-SNQR/10}$.

In our approach, the optimization target is to find the minimum number of bits b that can be used as the word length subject to $QE\le UE\times p_f$ where p_f is a fraction or a multiple of UE depending on the application specifications.

3. Proposed UE, RE Error Model

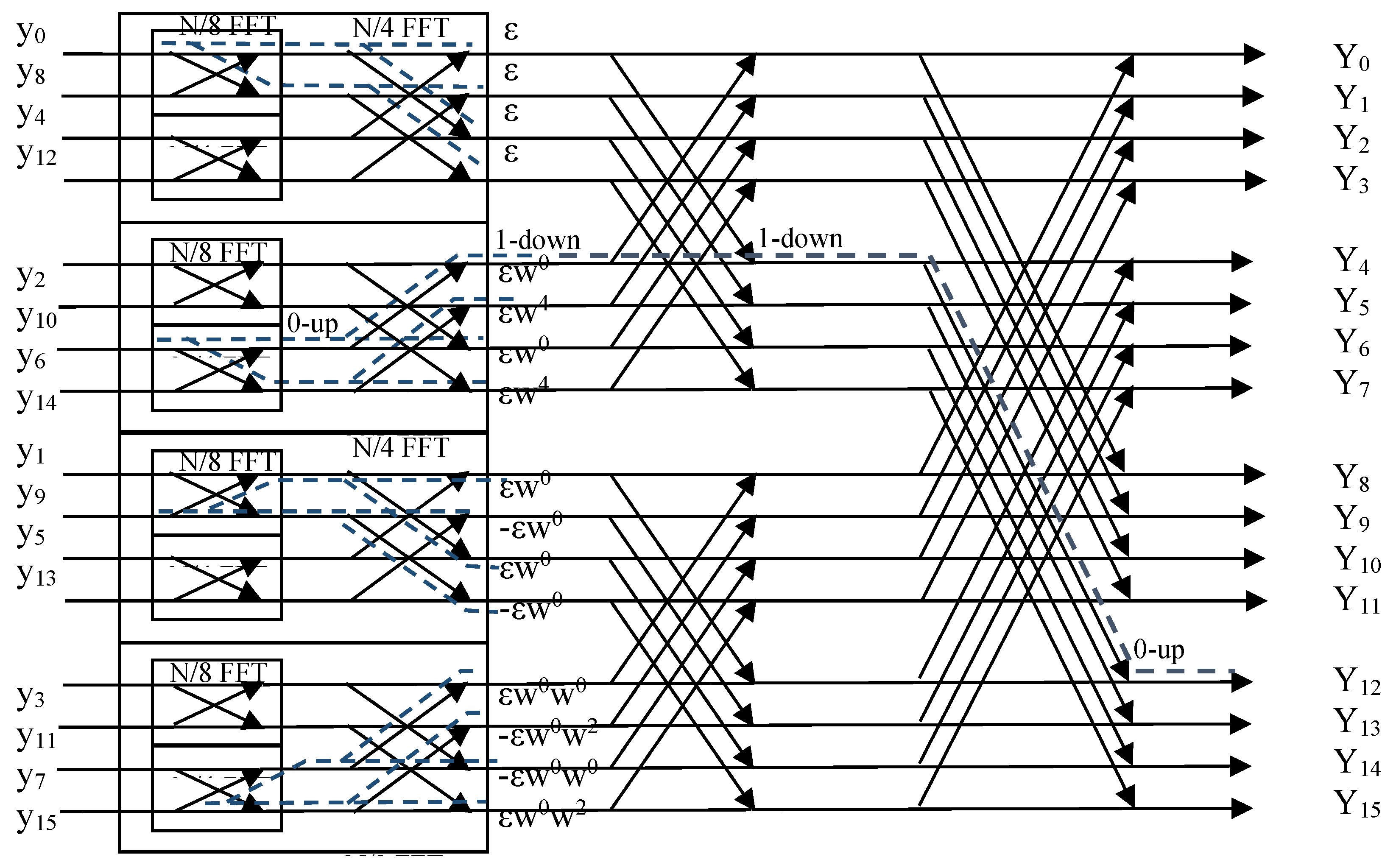
We focus on a 16-point FFT on the OFDM receiver side that is used as a case study and appears in Figure 2. It is attempted to estimate first, how the error, caused by the undersampling process described in Section 2.1, propagates and calculate the expected error on the FFT outputs. The FFT output error affects the Symbol Error Rate (SER) and the Bit Error Rate (BER) of the OFDM system. However, in this work the FFT output error caused by the undersampling process (P_UE) is compared to the QE error (P_QE) in order to find an acceptable word length for the FFT.

In the four propagation cases examined, a single error is caused by a QAM symbol $\widehat{y_i}$ that does not have the expected trivial value $y_i$(they differ by ε) in order to generate FFT outputs equal to zero (that can be pruned) or the expected trivial intermediate butterfly outputs. Instead, let us assume that: $\widehat{y_i}=y_i+\epsilon$. The propagation of the error in the first two levels of butterflies (a pair of 2-point and one 4-point FFT) is denoted with the dashed lines in Figure 2. In the first case, the error ε appears at the even input i of the 2-point FFT at the top. Τhe error at the outputs of the 4-point FFT is $e_{logN-1}^{\left(i\right)}=\left[\epsilon \epsilon \epsilon \epsilon \right]$. In the second case that appears from top to the bottom of Figure 2, the non-trivial y_i symbol appears at the even input i+2 of the four-point FFT. The error in this case is $e_{logN-1}^{\left(i+2\right)}=\left[\epsilon w^0 \epsilon w^{2^{logN-2}} \epsilon w^0 \epsilon w^{2^{logN-2}}\right]$. In the third case the error appears at the odd input i+1: $e_{logN-1}^{\left(i+1\right)}=\left[\epsilon w^0-\epsilon w^0 \epsilon w^0-\epsilon w^0\right]$. In the last case at the bottom of Figure 2, the error at the odd input i+3 is $e_{logN-1}^{\left(i+3\right)}=\left[\epsilon w^0{w}^0-\epsilon w^0{w}^{2^{logN-3}}-\epsilon w^0{w}^0 \epsilon w^0{w}^{2^{logN-3}}\right]$. In the previous expressions of e_logN-1 the twiddle factors $w_N^j$ are used without the index N for simplicity. The differences in the four e_logN-1 expressions are owed to the different twiddle factors that multiply the error ε as it propagates through different paths. Figure 3 shows how the e_logN-I error of stage logN-p propagates to the next butterfly stage logN-(p-1). The arrows in Figure 3 are buses and Figure 3a shows the propagation of the error from the top butterfly input, while Figure 3b shows the propagation of the error from the bottom input. In the first case $e_{logN-\left(p-1\right)}=\left[e_{logN-p} e_{logN-p}\right]$ while in the latter case $e_{logN-\left(p-1\right)}=\left[w.\ast e_{logN-p} –w.\ast e_{logN-p}\right]$. The symbol “.*” implies multiplication of the corresponding elements of the vectors and w is the vector of all the twiddles of a specific butterfly stage. If multiple errors exist in the FFT inputs, their effect is added at the FFT output. For example, if the errors ε₃ and ε₇ occur in the bit reversed 16-point DIT FFT inputs y₃ and y₇ (corresponding to Y₁₂ and Y₁₄ outputs), the individual output errors ($e_0^{y_3}$ and $e_0^{y_7}$, respectively) would be:

$$e_0^{y_3}\left[\begin{array}{c}\begin{array}{c}\begin{array}{c}\begin{array}{c}{w}^0{w}^0\\ w^2{w}^1\\ w^4{w}^2\\ w^6{w}^3\end{array}\\ -w^0{w}^4\\ -w^2{w}^5\\ -w^4{w}^6\end{array}\\ -w^6{w}^7\\ -w^0{w}^0\\ -w^2{w}^1\end{array}\\ -w^4{w}^2\\ -w^6{w}^3\\ \begin{array}{c}{w}^0{w}^4\\ w^2{w}^5\\ \begin{array}{c}{w}^4{w}^6\\ w^6{w}^7\end{array}\end{array}\end{array}\right]{\epsilon }_3,e_0^{y_7}=\left[\begin{array}{c}\begin{array}{c}\begin{array}{c}\begin{array}{c}{w}^0{w}^0{w}^0\\ w^4{w}^2{w}^1\\ -w^0{w}^4{w}^2\\ -w^4{w}^6{w}^3\end{array}\\ -w^0{w}^0{w}^4\\ -w^4{w}^2{w}^5\\ w^0{w}^4{w}^6\end{array}\\ w^4{w}^6{w}^7\\ -w^0{w}^0{w}^0\\ -w^4{w}^2{w}^1\end{array}\\ w^0{w}^4{w}^2\\ w^4{w}^6{w}^3\\ \begin{array}{c}{w}^0{w}^0{w}^4\\ w^4{w}^2{w}^5\\ \begin{array}{c}-w^0{w}^4{w}^6\\ -w^4{w}^6{w}^7\end{array}\end{array}\end{array}\right]{\epsilon }_7$$

(14)

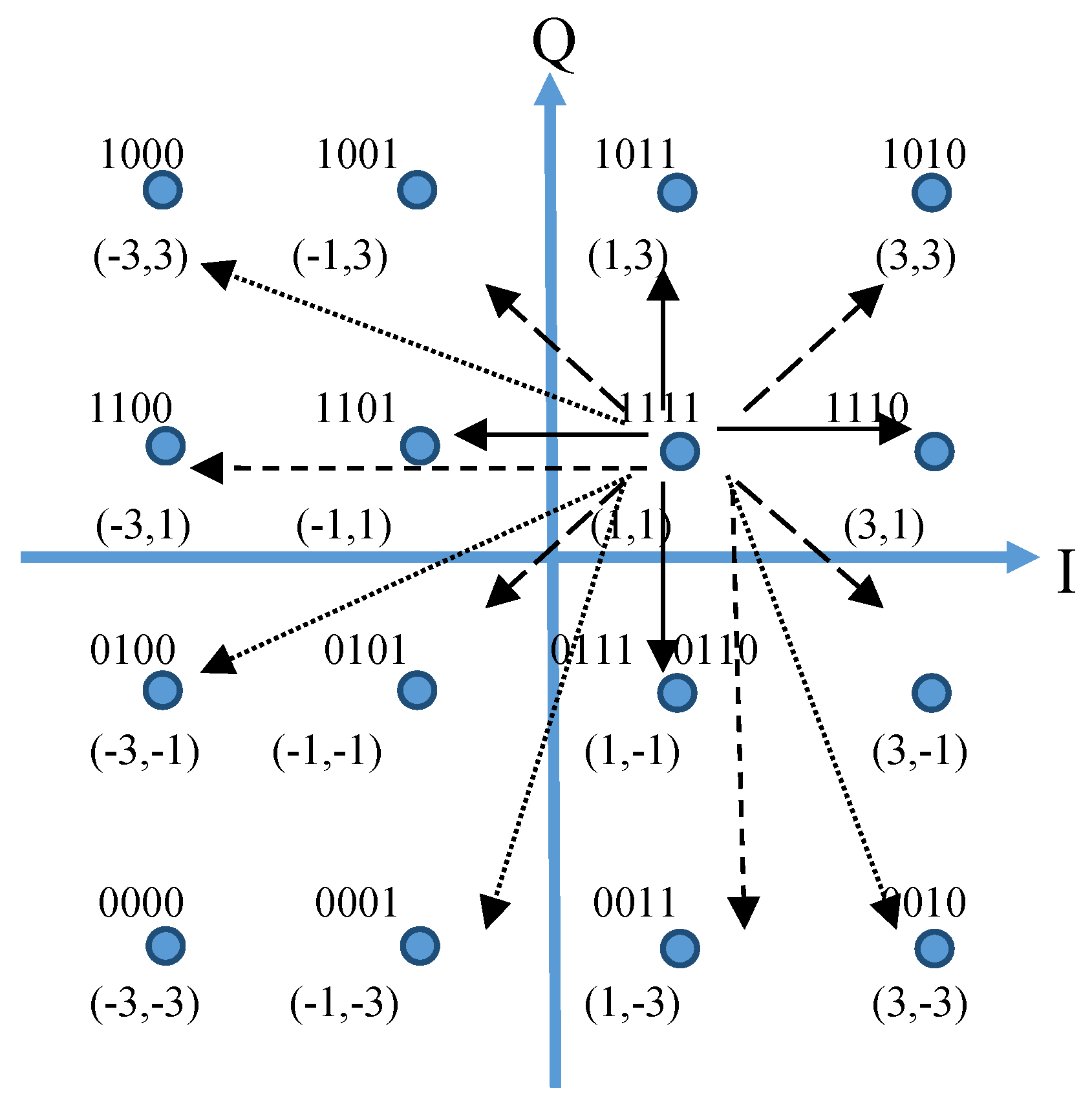
The combined output error if both ε₃ and ε₇ occur is $e_0^{y_3,y_7}=e_0^{y_3}+e_0^{y_7}$. Of course, the same error propagation model holds for the IFFT on the transmitter side. Moreover, the estimation of the error ε is easier on the transmitter side since, the IFFT inputs are QAM symbols with integer values. The 16-QAM constellation shown in Figure 4 is used as a case study, and we assume that X_c = ”1111”, i.e., the trivial input is ‘1’. We can see that there are: a) N₍₂₎ = 4 neighboring QAM symbols (X₍₂₎) that differ by 2 in the real or imaginary direction from X_c (the continuous arrows), b) N_(2,2) = 4 symbols (X_(2,2)) that differ by 2 in each direction from X_c (dashed arrows with big dashes), c) N_(2,4) = 4 symbols (X_(2,4)) that differ by 2 in one direction and by 4 in the other from X_c (dotted arrows), d) N₍₄₎ = 2 symbols (X₍₄₎) that differ by 4 in either the imaginary or real direction from X_c (dashed arrows with small dashes), and e) a single (N_(4,4) = 1) symbol (X_(4,4)) that differs from X_c by 4 in each direction. X₍₂₎ symbols correspond to 4 input bits with one ‘0’ while X_(2,2) and X₍₄₎ symbols are derived from 4 input bits with 2 zeros. Finally, the X_(2,4) symbols correspond to 4 input bits with 3 zeros and the QAM symbol (-3,-3) is derived by “0000”. The corresponding probability of each symbol is p_c, p₍₂₎, p_(2,2), p₍₄₎, p_(2,4), p_(4,4). The order of these probabilities is p_c > p₍₂₎ > p_(2,2) = p₍₄₎ > p_(2,4) > p_(4,4) due to data sparseness.

Since X_c = (1,1), the minimum error in 16-QAM modulation is ${\epsilon }_{min}=\sqrt{{\left(1-1\right)}^2+{\left(1-\left(-1\right)\right)}^2}=2={\epsilon }_{\left(2\right)}$. The rest of the errors are: ${\epsilon }_{\left(2,2\right)}=\sqrt{2\ast 2^2}=2\sqrt{2}$, ${\epsilon }_{\left(4\right)}=\sqrt{4^2}=4$, ${\epsilon }_{\left(2,4\right)}=\sqrt{2^2+4^2}=2\sqrt{5}$, ${\epsilon }_{\left(4,4\right)}=\sqrt{2\ast 4^2}=4\sqrt{2}$. The expected value of ε will be:

$$E[\epsilon ]={\displaystyle \sum }_k^{}{N}_{\left(k\right)}{p}_{\left(k\right)}{\epsilon }_k$$

(15)

For 16-QAM, E[ε]=3.37 if only the symbols that are different than X_c are taken into consideration and they have equal probability. In general, E[ε] depends on the sparseness level s<1 of the input and the QAM modulation. The sparseness level s means that a fraction s of the input data bits is non-trivial. If all the non-trivial symbols have equal probability to appear, then p_(k)=s/(N-1). In this case, Equation (15) can be rewritten as:

$$E[\epsilon ]=\frac{s}{N-1}{\displaystyle \sum }_k^{}{N}_{k}E\left[{\epsilon }_k\right]=\frac{sE\left[{\epsilon }_k\right]}{N-1}{\displaystyle \sum }_k^{}{N}_k=sE\left[{\epsilon }_k\right]$$

(16)

The effect of the employed modulation scheme to the BER/SER of a telecommunications’ system is explained in detail in Appendix C of [12]. The estimation of E[ε] for different modulation schemes can be assisted by the analysis performed in [12]. There are several alternative options to place the constellation symbols that correspond to a specific number of bits. The lower error is achieved when adjacent constellation symbols differ only in one digit (Gray mapping). In one-dimensional or ring constellations, the Gray mapping can be easily found while square QAM constellations can be Gray encoded hierarchically by examining smaller blocks. There are, however, constellations where there is no perfect Gray mapping. Each constellation X is surrounded by a decision region with minimum distance called Voronoi. When a received symbol Y resides within the Voronoi region of X it is decoded as X on the receiver. The higher the minimum distance of a modulation scheme, the lower the BER/SER that can be achieved. For example, if hard decoding is employed, i.e., if a received QAM symbol is first demodulated to its corresponding bits and then these bits are corrected by the supported FEC method, SER can be expressed as [12]:

$$SER=1-{\displaystyle \sum }_X^{}P\left(X\right){{\displaystyle \int }}_{Y\in R_x}^{}p\left(Y|X\right)dY$$

(17)

where Y is the received symbol, X is the constellations of a specific modulations scheme, p(Y|X) is the probability to get Y at the receiver given that the symbol transmitted is X and R_x is the decision region (Voronoi) of X. In the 16QAM modulation examined earlier, if one of the constellation bits is inverted, the effect on the BER of this error is 1/4 of the effect on the SER. It can be stated that SER represents the worst case effect of the error to the OFDM system. This is also confirmed by various simulations performed in the Appendix C of [12] where several modulations schemes are tested.

In order to estimate the variance of the UE in each one of the FFT outputs we have to define all the possible paths that the error can follow from the FFT input. The paths can be determined in a systematic way starting from a specific output. Let us assume that when a butterfly crossing is reached following the upper branch is denoted by ‘0’ while following the lower branch is denoted by ‘1’. All the paths can be determined in this way by the combination of log₂N bits. For example, in Figure 2, the dashed line that reaches output Y₁₂ shows a potential path that the error has followed from input y₆. The error propagation path in this case can be denoted by “0110” and the initial error ε can be multiplied in each branch by 1, a twiddle factor w or –w.

Table 1. Expected UE error in each output of an 8-point DIT FFT.

Path:	000 (×ε)	001 (×ε)	010 (×ε)	011 (×ε)	100 (×ε)	101 (×ε)	110 (×ε)	111 (×ε)	$\mathbf{Expected}\mathbf{Error}\left(\text{×}\mathbf{E}\right[\mathsf{\epsilon }\left]\right),\mathbf{Variance}{\mathit{\sigma }}_{\mathit{U}\mathit{S}}^2\left(\mathit{k}\right)(\times \mathbf{E}[\mathsf{\epsilon }{]}^2)$
Y0	1	$w_8^0$	$w_8^0$	$w_8^0{w}_8^0$	$w_8^0$	$w_8^0{w}_8^0$	$w_8^0{w}_8^0$	$w_8^0{w}_8^0{w}_8^0$	1, 0
Y1	1	$w_8^1$	$w_8^2$	$w_8^2{w}_8^3$	$-w_8^0$	$-w_8^0{w}_8^1$	$-w_8^0{w}_8^2$	$-w_8^0{w}_8^2{w}_8^3$	0, 1
Y2	1	$w_8^2$	-$w_8^0$	-$w_8^0{w}_8^2$	$w_8^0$	$w_8^0{w}_8^2$	$-w_8^0{w}_8^0$	$-w_8^0{w}_8^0{w}_8^2$	0, 1
Y3	1	$w_8^3$	$-w_8^2$	$-w_8^2{w}_8^3$	$-w_8^0$	$-w_8^0{w}_8^3$	$w_8^0{w}_8^2$	$w_8^0{w}_8^2{w}_8^3$	0, 1
Y4	1	$-w_8^0$	$w_8^0$	$-w_8^0{w}_8^0$	$w_8^0$	$-w_8^0{w}_8^0$	$w_8^0{w}_8^0$	$-w_8^0{w}_8^0{w}_8^0$	0, 1
Y5	1	$-w_8^1$	$w_8^2$	$-w_8^2{w}_8^1$	$-w_8^0$	$w_8^0{w}_8^1$	$-w_8^0{w}_8^2$	$w_8^0{w}_8^2{w}_8^1$	0, 1
Y6	1	$-w_8^2$	$-w_8^0$	$w_8^0{w}_8^2$	$w_8^0$	$-w_8^0{w}_8^2$	$-w_8^0{w}_8^0$	$w_8^0{w}_8^0{w}_8^2$	0, 1
Y7	1	$-w_8^3$	$-w_8^2$	$w_8^2{w}_8^3$	$-w_8^0$	$w_8^0{w}_8^3$	$w_8^0{w}_8^2$	$-w_8^0{w}_8^2{w}_8^3$	0, 1

, lists for example, all the potential errors that can occur at each output of an 8-point FFT as well as the expected output error values (in all cases they are 0 except from Y0 due to orthogonality) and its complex variance. Since the complex variance is the sum of the variances of the real and imaginary parts and the expected values of the error at each output is 0 (except Y0), the complex variance is actually the sum of the squares of the sine and cosine of the same number (the power of the corresponding twiddle factor) which results in 1. Thus, the complex variance is equal to 1×ε² in all cases but Y0. This fact holds for any N-point FFT. If R is the number of samples substituted by the undersampling procedure (e.g., R=1/16 means that N/16 of the FFT inputs have been substituted by others), the total power of the UE error (P_UE) can be estimated as a function of N, R, s, E[ε]:

$$P_{UE}={\displaystyle \sum }_{k=0}^{N-1}{\sigma }_{US}^2\left(k\right)=f\left(N,R,s,E[\epsilon ]\right)$$

(18)

The selection of an appropriate FFT word length and ADC resolution should target to the restriction of QE and RE errors within a fraction or a multiple p_f (e.g., P_QE, P_RE ≤ 10% of the P_UE) of the UE error estimated in the way described above. More specifically, using $P_{RE}=8{\sigma }_n^2$ from Equation (11) and defining $c=1+u^2+a^2$, P_RE can be expressed as:

$$P_{RE}=\frac{8}{12}{2}^{-2b}\left(c+2^{-2b}\right)$$

(19)

If $g=2^{-2b+1}$, Equation (20) can be expressed as a 2^nd degree equation as follows:

$$P_{RE}=\frac{g}{3}\left(c+\frac{g}{2}\right)=>g^2+2cg-6P_{RE}=0$$

(20)

The determinant Det in Equation (20) above is $Det=4c^2+24P_{RE}=4c^2\left(1+6P_{RE}\right)$. Solving (21) and keeping only the positive square root of the determinant (the negative square root is not applicable) we get:

$$g=\frac{-2c+\sqrt{Det}}{2}=\frac{-2c+2c\sqrt{1+\frac{6P_{RE}}{4c^2}}}{2}=c\left(-1+1+\frac{1}{2}·\frac{6P_{RE}}{4c^2}-\frac{1}{8}·\frac{36P_{RE}^2}{16c^4}+\dots \right)\approx \frac{3P_{RE}}{4c}$$

(21)

The first two terms of the Taylor series approximation of the square root were preserved in Equation (20). Since the variables α and u in the definition of c change in the various operations of the FFT, it is attempted to estimate only c and not α and u separately. Replacing g in Equation (20), the required word length b can be estimated as follows:

$$2^{-2b+1}=\frac{3P_{RE}}{4c}=>2^b=\sqrt{\frac{8c}{3P_{RE}}}=>b=\frac{1}{2}{\log }_2\left(8c\right)-\frac{1}{2}{\log }_2\left(3P_{RE}\right)$$

(22)

If $c_1=\frac{1}{2}{\log }_2\left(8c\right)$, and Equation (18) is written in a general form in order to adjust the weight of the parameters s, N, p_f, R, the word length b can be expressed as:

$$b=c_1-\frac{1}{2}{\log }_2\left(3s^{c_2}{p}_f^{c_3}{R}^{c_4}{N}^{c_5}E[\epsilon ]\right)$$

(23)

In order to select appropriate values for the unknown c_i values, the Octave fsolve function for non-linear equations is used with a small number of instances of Equation (23) i.e., with a small number of b, p_f, s, R, N, combinations. The experimental results show that Equation (23) can be used then to accurately estimate the required word length b for other p_f values given a specific OFDM configuration (s, R, N, ε). The physical meaning of the estimated c_i parameters will be explained in Section 5.

4. The Employed FFT Architecture

A DFT requires O(N²) operations that are reduced to O(N∙logN) if the original FFT architecture is employed [18]. The number of points used by the FFT can be expressed as a product of numbers that are powers of 2. Thus, a 1024-point FFT can be implemented by 10 Radix-2 stages, or 5 Radix-4 stages. If the number of points of the FFT is not a power of 2, then Radix-3 or Radix-5 butterflies can also be employed. For example, a 100-point FFT can be implemented with one stage of Radix-4 and two stages of Radix-5 butterflies [26]. The round-off errors depend on the architecture of the FFT (serial/parallel, Decimation in Time or Frequency, etc.) and the number of stages. An FFT can be implemented either in software if slower operation is acceptable or in hardware for faster response. Modern telecommunication systems require high speed hardware FFTs. Hardware FFTs can either consist of a large number of hardware resources working in parallel or reusable components for more compact, low power implementations with a slightly higher latency overhead.

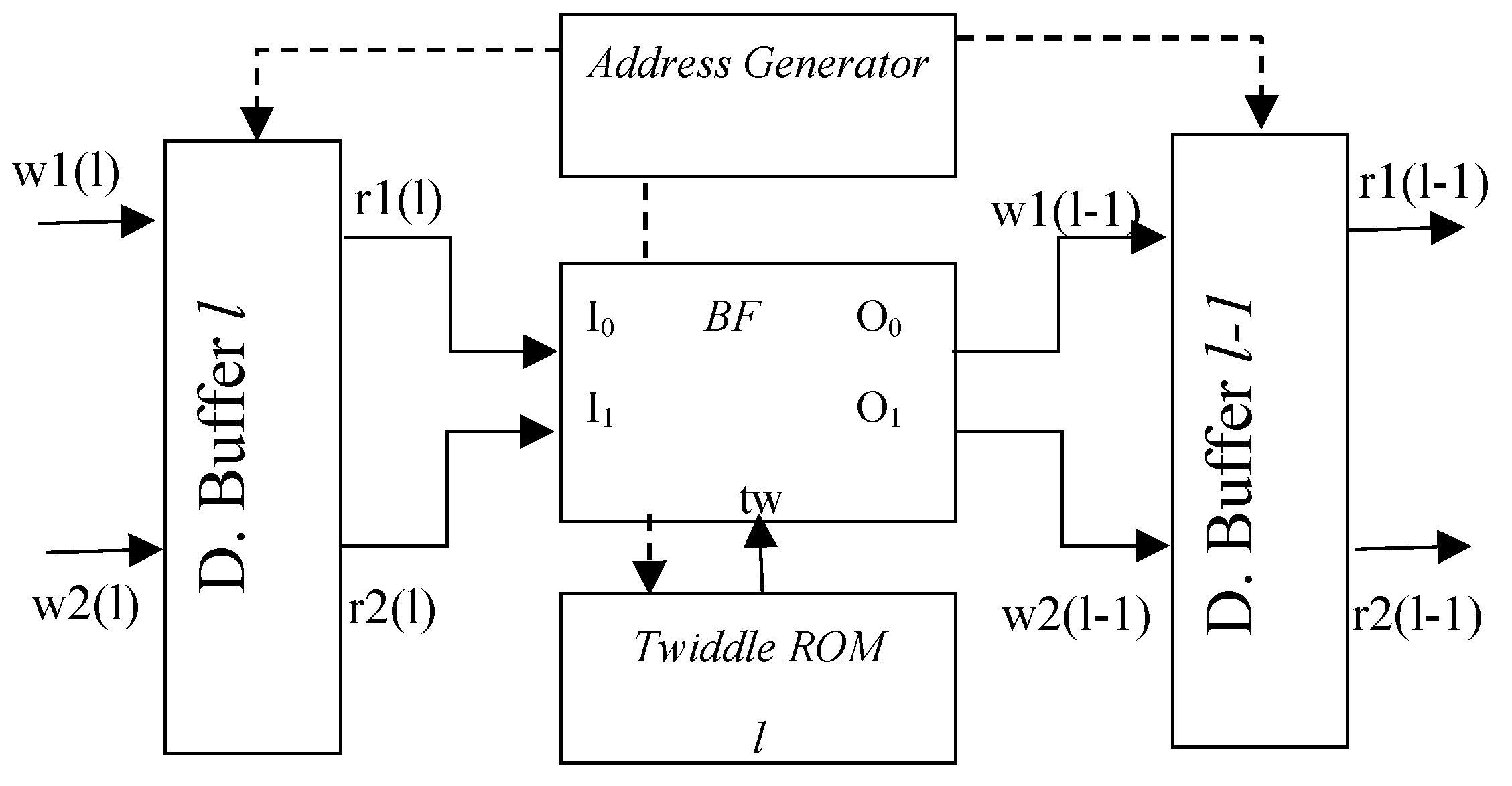
In this paper, a robust memory-based pipeline FFT has been developed to test the effect of round-off errors in conjunction with the undersampling scheme described in Section 2. It consists of log₂N stages (one of them appears in Figure 5). The inputs of stage l are stored in the double buffer l (its size is 2×N×b bits). The word length of a butterfly output can be larger by one bit compared to its inputs for optimal resource utilization. However, we use a constant size of b-bits for the inputs/outputs and twiddles of all stages in order to get similar results with the case where a single reusable pipeline stage was used iteratively. One buffer l of the pair is used to store the real and the other for the imaginary part of the FFT inputs/outputs. Buffer l is accessed for write through the buses w1(l) and w2(l), and for read through the buses r1(l) and r2(l). Each one of these buses consists of a log₂N bits, address bus (ra(l) or wa(l)) and a pair of b-bits data buses (Re{rd(l)} and Im{rd(l)}, or Re{rd(l)} and Im{rd(l)}). Each data bus carries real numbers in fixed point format with a size of b bits. The inputs of each Radix-2 butterfly are the rd1(l) and rd2(l) while its outputs are wd1(l) and wd2(l). The real and imaginary parts of the twiddle factors w are retrieved from the twiddle Read Only Memory (ROM). The size of the twiddle ROM of stage l is 2×N/2^l+1.

The operations performed at a Butterfly block are:

$$Re\left\{O_0\right\}=Re\left\{I_0\right\}+Re\left\{I_1\right\}·Re\left\{tw\right\}-Im\left\{I_1\right\}·Im\left\{tw\right\}$$

(24)

$$Im\left\{O_0\right\}=Im\left\{I_0\right\}+Re\left\{I_1\right\}·Im\left\{tw\right\}+Im\left\{I_1\right\}·Re\left\{tw\right\}$$

(25)

$$Re\left\{O_1\right\}=Re\left\{I_0\right\}-Re\left\{I_1\right\}·Re\left\{tw\right\}+Im\left\{I_1\right\}·Im\left\{tw\right\}$$

(26)

$$Im\left\{O_1\right\}=Im\left\{I_0\right\}-Re\left\{I_1\right\}·Im\left\{tw\right\}-Im\left\{I_1\right\}·Im\left\{tw\right\}$$

(27)

The address buses ra(l) and wa(l) are driven by the Address Generator module that is based on an up counter with log₂(N)-1 resolution. In each stage l the pair of addresses used for the retrieval of the butterfly inputs/outputs (Addr0 for I₀ and O₀, Addr1 for I₁, O₁) and AddrT for the corresponding twiddle factor are the following:

$$AddrT=Cnt\%\frac{N}{2^{l+1}}$$

(28)

$$Addr0=AddrT+(\lfloor Cnt/\left(\frac{N}{2^{l+1}}\right)\rfloor \%2^l)\frac{N}{2^l}$$

(29)

$$Addr1=Addr0+\frac{N}{2^{l+1}}$$

(30)

In Equations (28)–(30), % is the modulo operator, $\lfloor Cnt/\left(\frac{N}{2^{l+1}}\right)\rfloor$ is the floor function, and Cnt is the current value of the counter in the Address Generator. The stages of the developed FFT operate in a ping-pong manner. For example, in the first N/2 clock cycles the FFT inputs are loaded on the input Buffer at stage l=logN-1. In the next N/2 cycles, the butterfly of stage l is driving its outputs to Buffer l-1. Then in the next N/2 cycles, the stage l-1 is reading inputs from Buffer l-1 and driving the outputs to the Buffer l -2. At the same time the input Buffer l can be loaded with the next set of FFT inputs. The FFT latency is $\frac{N}{2}logN$ cycles and the throughput is an FFT output completed every N cycles.

The FFT architecture described in this section can be used to evaluate the complexity of the system in relation with the word length. Focus is given on the main FFT blocks: adders/subtractors and multipliers in the butterflies, counter in the address generator, input/output buffers and twiddle factor ROM. The silicon area or gate count of a ripple carry adder/subtractor is proportional to the word length of the operands. However, if the word length of an b-bit adder with carry look-ahead is increased by 1 (b+1) the required gate count will be increased by more than 1/b since the carry look-ahead logic needed to generate the additional carry is more complicated than the logic needed to generate the carry of the least significant bits. The gate count required by a multiplier depends on its architecture. For example, an b-bit Scaling Accumulator Multiplier (SAM) consists of b AND gates, a b-bit adder, a b-bit shift register and the b-bit output register. Thus, the SAM multiplier gate count is proportional to the word length b. The same holds for Serial by Parallel Booth Multipliers i.e., the gate count is proportional to the word length. In these kind of multiplier architectures one of the operands has to be inserted serially bit by bit. Ripple Carry Multipliers (RCM) require all the operand bits in parallel but the area needed is proportional to the square of the word length. Other multiplier architectures like row adder tree and carry-save multipliers require approximately the same gate count as RCM but can achieve faster operation. The storage area needed by the twiddle ROMs and the input/output buffers is proportional to the word length but the area needed by the corresponding address decoders is proportional to the logarithm of the word length. In general, it can be stated that the complexity of the FFT/IFFT modules in an OFDM transceiver is approximately proportional to the employed word length.

The proposed FFT architecture has been described in synthesizable VHDL and has been tested in Modelsim. The description of this module in VHDL is sufficient for the assessment of the effect of the finite word length in the overall error in the OFDM receiver. Implementation on a Field Programmable Gate Array (FPGA) would also be useful to estimate the speed and the power consumption of this module and this will be part of our future work.

5. Simulation Results and Discussion

In this section, the word length estimation based on Equation (23) is evaluated. The combinations examined are the following: 16QAM or Quadrature Phase Shift Keying (QPSK) modulation, N=256 or 1024, R=1/4 or 1/16, s=0.5%, 1%, 2% or 10%. When 16QAM is used E[ε]=3.37 as estimated in Section 3. In a similar way E[ε]=2.276 is estimated for QPSK. The number of bits estimated as the required word length b were between 5 and 10. The total number of configurations simulated are 116. A number of these configurations (four sets including between 5 and 16 non-linear equations) have been used in Octave in order to solve the non-linear Equation (23) for the unknown values of the c_i parameters. Then, the rest of the L=116 configurations were tested and the RMSE between the real value of b and the estimated b_est for a specific p_f value is extracted as shown in Equation (31). In this way, the minimum number of non-linear equations that have to be solved in order to determine the c_i parameters precisely is found.

$$RMSE=\sqrt{\frac{1}{L}{\displaystyle \sum }_{j=1}^L{\left(b_{est}-b\right)}^2}$$

(31)

The sets of non-linear equations described in

Table 2. Using a set of 16 non-linear Equations (23) to determine the c_i parameters.

RMSE: 0.816 (16QAM), 1.132 (QPSK), c1 = −5.6315, c2 = −2.0292, c3 = 2.0669, c4 = 1.1994, c5 = −2.3163
Equation	Word Length (b)	pf=PQE/PUE	QAM Modula-tion	FFT Size N	Number of Substituted Samples R	Sparseness s
1	5	0.0046	16QAM	1024	1/4	0.5%
2	8	0.000344	16QAM	1024	1/4	0.5%
3	5	0.046	16QAM	256	1/4	10%
4	8	0.002624	16QAM	256	1/4	10%
5	5	0.12	16QAM	1024	1/16	10%
6	10	0.00773	16QAM	1024	1/16	10%
7	5	0.002625	16QAM	256	1/16	0.5%
8	8	0.00026	16QAM	256	1/16	0.5%
9	5	0.00377	QPSK	1024	1/4	0.5%
10	10	0.001	QPSK	1024	1/4	0.5%
11	5	0.0245	QPSK	256	1/4	10%
12	10	0.000519	QPSK	256	1/4	10%
13	5	0.15	QPSK	1024	1/16	10%
14	10	0.036	QPSK	1024	1/16	10%
15	5	0.0016	QPSK	256	1/16	0.5%
16	10	0.000273	QPSK	256	1/16	0.5%

,

Table 3. Using a set of 12 non-linear equations (23) to determine the c_i parameters.

RMSE: 0.736 (16QAM), 1.09 (QPSK), c1 = −4.3811, c2 = −1.8297, c3 = 1.9560, c4 = 1.2176, c5 = −2.0358
Equation	Word Length (b)	pf=PQE/PUE	QAM Modula-tion	FFT Size N	Number of Substituted Samples R	Sparseness s
1	8	0.000344	16QAM	1024	1/4	0.5%
2	5	0.046	16QAM	256	1/4	10%
3	8	0.002624	16QAM	256	1/4	10%
4	5	0.12	16QAM	1024	1/16	10%
5	5	0.002625	16QAM	256	1/16	0.5%
6	8	0.00026	16QAM	256	1/16	0.5%
7	5	0.00377	QPSK	1024	1/4	0.5%
8	10	0.001	QPSK	1024	1/4	0.5%
9	10	0.000519	QPSK	256	1/4	10%
10	5	0.15	QPSK	1024	1/16	10%
11	10	0.036	QPSK	1024	1/16	10%
12	10	0.000273	QPSK	256	1/16	0.5%

,

Table 4. Using a set of 8 non-linear equations (23) to determine the c_i parameters.

RMSE: 1.118 (16QAM), 1.62 (QPSK), c1 = 4.00823, c2 = −1.29494, c3 = 1.55213, c4 = 1.04125,c5 = −0.16769
Equation	Word Length (b)	pf=PQE/PUE	QAM Modulation	FFT Size N	Number of Substituted Samples R	Sparseness s
1	8	0.000344	16QAM	1024	1/4	0.5%
2	5	0.046	16QAM	256	1/4	10%
3	5	0.12	16QAM	1024	1/16	10%
4	8	0.00026	16QAM	256	1/16	0.5%
5	5	0.00377	QPSK	1024	1/4	0.5%
6	10	0.000519	QPSK	256	1/4	10%
7	5	0.15	QPSK	1024	1/16	10%
8	10	0.000273	QPSK	256	1/16	0.5%

and

Table 5. Using a set of 5 non-linear Equation (23) to determine the c_i parameters.

RMSE: 3.694 (16QAM), 2.622 (QPSK), c1 = −33.2488, c2=−3.6799, c3 = 4.8570, c4 = 4.9535, c5 = −5.9386
Equation	Word Length (b)	pf=PQE/PUE	QAM Modulation	FFT Size N	Number of Substituted Samples R	Sparseness s
1	8	0.002624	16QAM	256	1/4	10%
2	5	0.002625	16QAM	256	1/16	0.5%
3	5	0.00377	QPSK	1024	1/4	0.5%
4	5	0.15	QPSK	1024	1/16	10%
5	10	0.036	QPSK	1024	1/16	10%

have been used to estimate the values of the c_i parameters. The average RMSE achieved in the word length estimation of all the 116 configurations is also listed in the 1^st row of these tables along with the estimated c_i values for each case. As can be seen from Table 3, determining the c_i values from 12 instances of Equation (23) leads to the lowest RMSE (0.736 for 16QAM and 1.09 for QPSK modulation). A relatively low RMSE is also estimated if 16 equations are used as shown in Table 2. The c_i parameters estimated in Table 2 and Table 3 are rounded to c₁ = −5, c₂ = −2, c₃ = 2, c₄ = 1, c₅ = 2 in order to explain the physical meaning of these values and how they lead to an accurate word length estimation.

Using the specific c_i values, Equation (23) can be written as:

$$b=c_1-\frac{1}{2}{\log }_2\left(3s^{-2}{p}_f^2{R}^1{N}^{-2}E[\epsilon ]\right)=\frac{1}{2}{\log }_2\left(8c\right)-\frac{1}{2}{\log }_2\left(3RE[\epsilon ]\right)-\frac{1}{2}{\log }_2\left(s^{-2}{p}_f^2\right)+{\log }_{2}N$$

(32)

From $c_1=\frac{1}{2}{\log }_2\left(8c\right)=\frac{1}{2}{\log }_2\left(8\left(1+u^2+a^2\right)\right)=-5$ we get that $1+u^2+a^2=0.000122$ or $u^2+a^2=-0.99988$ which is impossible unless u and a are assumed complex numbers. When the set of equations listed in Table 4 is used $c_1=+4$ and $u^2+a^2=31$ which is more consistent with the model presented in [22] and Equation (11). However, the initial definition of c₁ will be ignored in an attempt to define the overall error model that matches the experimental results more accurately. In this perspective, the rest of the terms in the right side of Equation (23) are interpreted as follows: $\frac{1}{2}{\log }_{2}3RE[\epsilon ]$ takes its minimum value (−0.185) for the experiments conducted in this paper when R=1/16 and E[ε]=2.276 with QPSK modulation and its maximum value (0.2) with R=1/4 and E[ε]=3.37 when 16QAM modulation is employed. The term $s^{-2}{p}_f^2$ is close to a constant since p_f is proportional to the sparse level s: if only non-sparse FFT inputs were present, there would be errors in all the FFT outputs and $p_{ns}=P_{QE}/P_{UE}$. The higher value measured for p_ns is 0.3. If the input is sparse, the ratio p_f of the quantization error to the undersampling error is proportional to the sparseness level s: $p_f=\propto p_{ns}s$. When the input is too sparse, the UE and QE errors are both low. When the input is less sparse (s value is higher), UE raises but the raise of QE is even higher. This is owed to the fact that although UE gets worse, there may be still FFT outputs unaffected by the undersampling process if some samples are replaced by the others with identical value. However, if s is higher, more operations with numbers that are not zero will be performed and the QE will increase respectively since all the results of these non-trivial operations will have QE error. In this sense, $s^2$ counterbalances $p_f^2$ and the maximum value for the 3rd term of Equation (23) will be $\frac{1}{2}{\log }_2{s}^{-2}{p}^2=\frac{1}{2}{\log }_2{p}_{ns}=\frac{1}{2}{\log }_{2}0.3=-0.87$. If p_ns is lower, a higher positive offset in Equation (23) occurs.

The last term of Equation (23) can have two values in the results presented in this paper: either ${\log }_{2}1024=10$ or ${\log }_{2}256=8$. This is the larger positive offset that counterbalances the negative value of the constant value c₁. The specific c_i parameters have been approximated for these two FFT sizes. Should different FFT sizes be covered, the set of nonlinear equations that have to be used for the approximation of c_i parameters must also include configurations with these FFT sizes. If we try to use the approximated c_i parameters of Table 3 for the case of a 64-point FFT size, $c_1+{\log }_{2}N$ would be 0. The term $-\frac{1}{2}{\log }_2\left(3·R·E[\epsilon ]\right)$ results in small signed offsets between −0.185 and 0.2 as explained above and thus, the word length would be actually determined by the factor $-\frac{1}{2}{\log }_2{s}^{-2}{p}_f^2=-\frac{1}{2}{\log }_2{p}_{ns}$. In order to get a realistic estimation of at least 5 bits as a word length, p_ns should be 10^-3, or, in other words, UE error should be 1000 times larger than QE error. Such a relation between UE and QE errors is not always guaranteed.

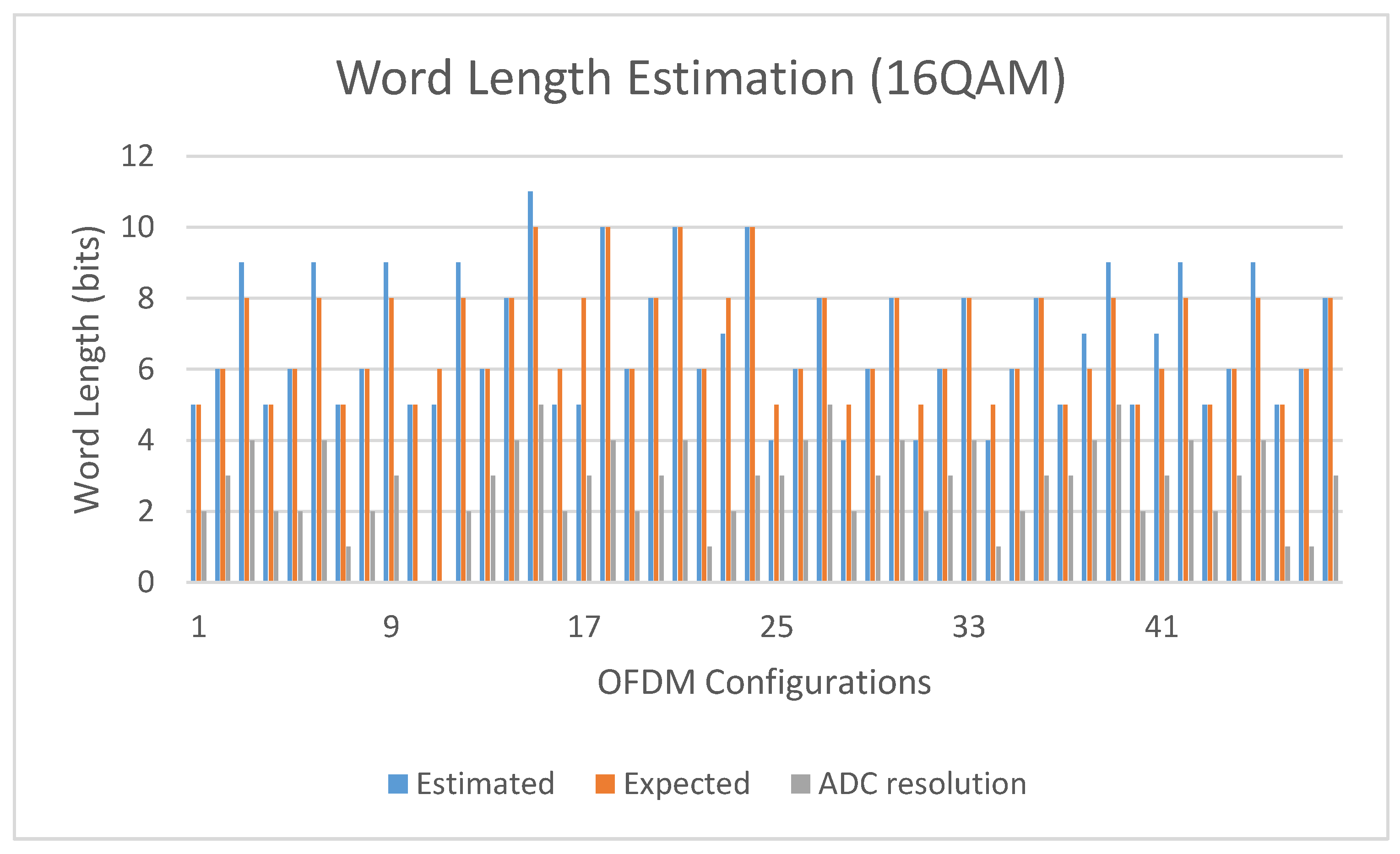
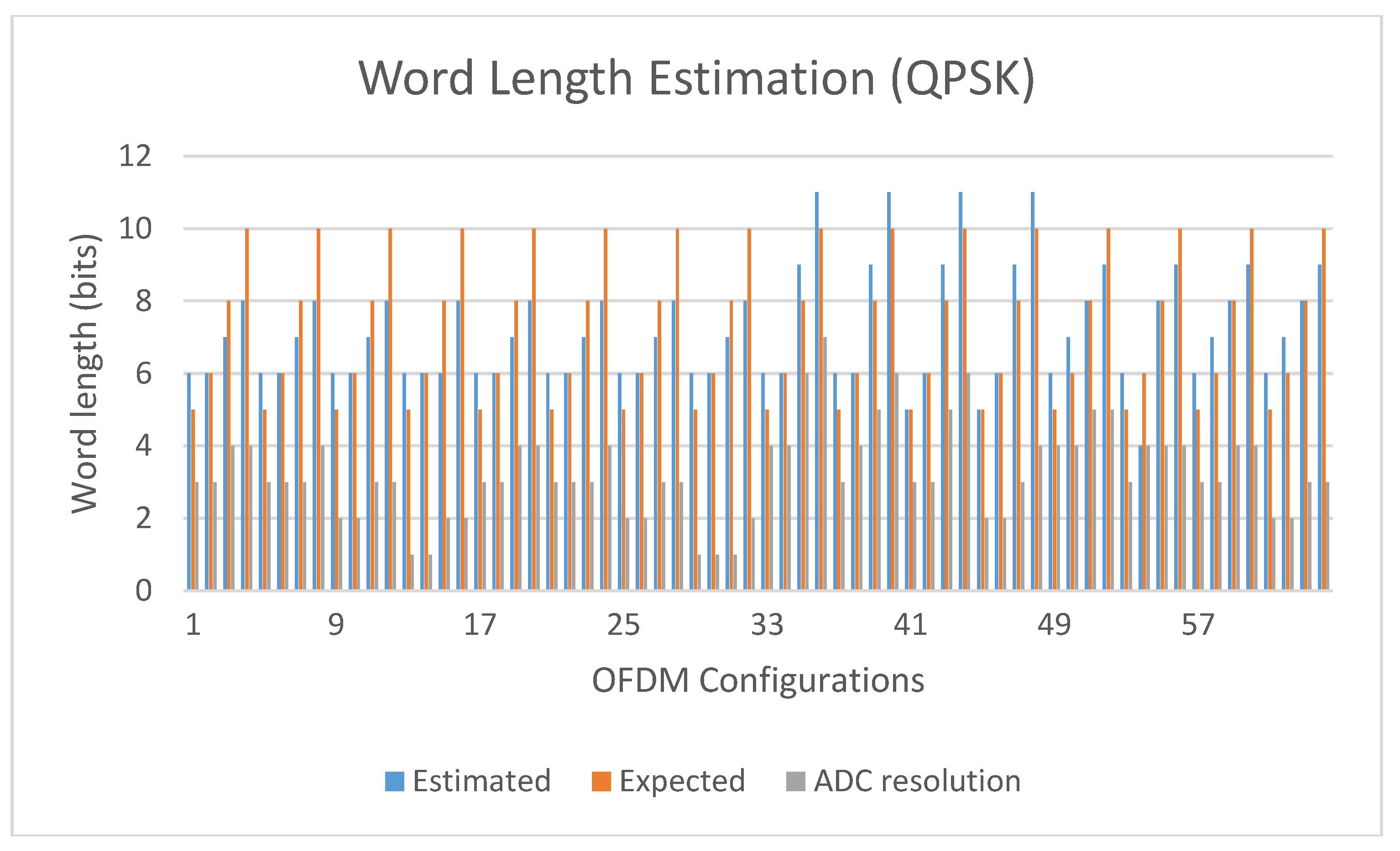
The estimated and expected word lengths for all the 16QAM and QPSK OFDM configurations tested when the c_i parameters listed in Table 3 are used, are compared in Figure 6 and Figure 7, respectively. In these figures, the required minimum ADC resolution is also included. This ADC resolution b_ADC has been estimated in Equation (33) that has been derived from Equation (8), the definition $\mathit{\Delta }=V_{ref}/2^{b_{ADC}}$ and the specification that P_QE should be equal to P_RE. V_ref was selected equal to 1V but approximately the same results would have been achieved if a different voltage reference had been selected, such as 3V. The ADC resolution b_ADC should match the FFT word length b thus, b_ADC should be selected equal to b since $b_{ADC}<b$ in all cases as shown in Figure 6 and Figure 7.

$$b_{ADC}=\frac{1}{2}{\log }_2\frac{{\log }_{2}N-2}{6P_{QE}}$$

(33)

The procedure followed in this paper to define a model that optimizes the word length subject to error restrictions and a predetermined relation between undersampling error and quantization/rounding error can be followed in other non-OFDM telecommunication systems. For example, in optical networks, a model can be created that selects the appropriate modulation (number of bits/symbol: R_s) in order to achieve a desired capacity, given a specific power budget P_o. Based on the analysis presented in [12], the capacity C_o can be expressed as:

$$C_o=R_s{\log }_2(1+\frac{P_o}{N_o{R}_s})$$

(34)

The noise term N_oR_s can be expressed as a weighted combination of the various noise sources in an optical channel [12]: the beat noise ${\sigma }_{beat}^2=4S_b^2{N}_o{P}_{LO}{B}_e$, the shot noise ${\sigma }_{shot}^2=2e{S}_b^{}{P}_{LO}{B}_e$ and the thermal/electronic noise ${\sigma }_{elec}^2$. Concerning the constants (we assume that their values are known) used in these noise variance expressions, S_b is the photodetector responsivity, N_o is the noise spectral density, P_LO the optical power, B_e the power equivalent bandwidth of the entire receiver and e the elementary charge. The most important optical noise is Amplified Spontaneous Emission (ASE) which actually describes the attenuation of the optical signal by a factor $a_{ASE}=0.2dB/Km$. The distortion posed by the required N_A repeater/amplifiers placed at distance $L_a$ can be described by the noise spectral density $N_{ASE}^{EDRA}=N_A\left(e^{a_{ASE}{L}_a}-1\right)h{v}_s{n}_{sp}$ or $N_{ASE}^{IDRA}=a_{ASE}{L}_{a}h{v}_s{K}_T$ if Erbium-doped fiber amplifiers (EDFAs) or Ideal Distributed Raman Amplification (IDRA) is used, respectively. The parameters used in these noise spectral densities are also assumed to have known values: h is the Plank constant, v_s is the optical frequency, K_T is the photon occupancy factor and $n_{sp}<1$ the spontaneous emission factor. The model can be trained by a number of non-linear equations that combine the channel error sources with various capacity and power requirements for specific predefined modulations schemes. The target of this training would be to estimate the weights of the channel error sources. After updating the error model with these weights, it can be used to select an appropriate modulation scheme for different capacity and power specifications or channel conditions.

6. Conclusions

An error model has been developed for an OFDM transceiver architecture that supports undersampling when sparse information is exchanged. The error model combines undersampling and round-off noise and determines the word length that should be employed by the FFT/IFFT modules. The desired round-off error can be defined as a fraction or a multiple of the undersampling error and an appropriate word length is estimated to achieve this goal. A new FFT pipeline module has been developed in synthesizable VHDL in order to evaluate the correctness of the predicted word length. Simulation for all the combinations of QPSK or 16QAM modulation, FFT sizes of N=256 or N=1024 points, sparseness levels 0.5%, 1%, 2% and 10%, and FFT input replacement of either N/4 or N/16 samples have been tested. The simulation results show that the appropriate word length can be determined with RMSE less than 1 and the ADC resolution should match the estimated word length.

Future work will focus on extending the developed error model for pipeline FFTs with different word length in each stage. A different range of FFT sizes and QAM modulations will also be tested. Finally, the FFT/IFFT as well as other OFDM modules will be implemented in real hardware (FPGA) to measure their power consumption and speed.

7. Patents

The undersampling method described in Section 2 is protected by the patents 1008130 and 1008564, Greek Patent Office, published November 2014 and September 2015 respectively.