Abstract
This work represents a method for investigating the energy efficiency of fan systems used to transport fluids. Applying the methods of dimensional analysis (DA) enables establishing five dimensionless complexes ( criteria), including some basic parameters having impacts on the consumed energy used for the transportation of a unit quantity of air. The proposed criterion includes the specific energy consumption (specific fan power SFP), and is used for the quantitative evaluation of the energy effectiveness of the fluid transportation. This criterion also includes the main geometric size of the pipe system (network) and the gas properties. The criterion indicates the impact of the applied method of flow rate regulation on the effective energy use of fan systems. This criterion includes parameters characterizing the selected method of flow rate regulation: speed () for using the frequency method and the referred length () of the pipe system for using the throttle method. The established (proposed) dimensionless parameters are used to study a concrete fan system. The obtained results concerning the evaluation of the impact of the two most used methods of flow rate regulation (frequency and throttle), as well as the density variation as a result of the temperature change, on the effective energy use are graphically presented: .
1. Introduction
The increasing of the energy efficiency of fan systems is a key priority emanating from the European Union (EU) directives, as well as the decreasing emissions of gases and reducing the continuously rising prices of energy and energy supplying.
The systems (fan and pump), used to transport fluids, are widely used in practice. The energy consumption of such systems, used to drive the pumps or fans, represents a significant part of the global energy use. According to [1], 22% of the global energy consumption of the installed motors is used to drive pumps and 16% for driving fans. It is well-known that the key elements of a system transporting fluids respectively are the fan (or pump) aggregate and the pipe system. The energy efficiency of a pipe system can be improved by using the proper elements (pipes, valves, etc.). However, to improve the efficiency of an electro-hydraulic aggregate it is necessary to involve high-efficiency machines combined with the relevant control systems.
To decrease the energy consumption of the existing fan (pump) systems is considered to be a topical problem. One of the main tasks in solving this problem is to ensure effective work regimes for a current system, as well as to select properly the method of its flow rate regulation. The most commonly used methods of flow rate regulation are well-known to the specialists and researchers. Mostly the energy effectiveness of these methods is determined qualitatively, while there is lack of information for the existing of any reliable methods for accomplishing a quantitative analysis.
It is well-known that the theory of similarity and dimensional analysis (DA), used to obtain dimensionless complexes, including the analyzed parameters, are widely use in generalizing the results found. The energy efficiency of a fan system is influenced by the type and quality of the installed fan aggregate (the energetic characteristics of its key elements), as well as the pipe system (its characteristic of resistance) and the features of the transported air. The energy efficiency of a current fan system depends significantly by the method used to perform the required work regime (point), i.e. the selected method of flow rate regulation. To analyze the impact of the mentioned parameters on the energy efficiency of a fan system, it is necessary to select appropriately the equations to be used. This paper represents a methodology, based on dimensional analysis, for establishing criteria equations, including dimensionless complexes containing the main parameters having impact on the effective energy use in fan systems.
2. Literature Review
In [2], the author reviews different methods for determining the energy consumption in regulating the flow rate of fluid-transporting systems, analyzing problems concerning their energy efficiency. Another study [3] provides analysis of the results found after the effectiveness of the most common methods of flow rate regulation is studied. The authors in [4] provide an analysis of energy efficiency in the case of parallel (in series) working centrifugal pumps. The impact of temperature variation on the energy efficiency of pump systems with variable demand is analyzed in [5], while [6] studies the impact of the air density variation on the energy consumption of fan systems. Popov et al. [7] present an analysis of the impact of a pump system technical state on the consumed energy.
In [8], the energy effectiveness of the well-known methods—frequency, throttle, or by using an inlet guide vane (IVC)—of a fan system flow rate regulation is analyzed. The objective of a pump system energy assessment is to determine the current energy consumption of an existing system and identify ways to improve system efficiency [9].
The applied method used in accomplishing this current work is based on the proposed in [10] methodology, where to evaluate the energy efficiency of the analyzed pump systems the specific energy consumption is used. For a given fan system represents:
where is the consumed power by the fan, measured in [kW]; Q is the fan volumetric flow rate, measured in [m3/s]; is the total pressure of the fan, measured in [Pa]; η is the total coefficient of efficiency of the fan system.
The parameter is analogous to the basic criteria of effectiveness—specific fan power (SFP)—used for ventilation systems, which can be determined by using the European standard EN 13,779 [11]. It represents the consumed energy, used to transport a unit volume of gas, and can be estimated by providing information about the current work regime of the analyzed fan system.
For the estimation of STF, in accordance to the aforementioned European standard, the following equation is used:
For the estimation of the parameter SFP, by using basic measuring units, the following equation is used:
The performed pump system energy efficiency assessment in [12] is accomplished by using the equations describing the pump work characteristics, while for assessing the energy efficiency of a fan system [8] uses the dimensionless coefficient characteristics of the analyzed fans.
Dimensional analysis is considered to be an appropriate method for summarizing the results found [13,14,15]. The authors in [16] recommend using this method in establishing of dimensionless criteria obtained by the basic equations in fluid mechanics (Cauchy and Navier–Stokes equations, continuity equation; energy equation). This work illustrates the applying of the obtained criterion groups in analyzing environmental and engineering processes.
In [17,18] it is shown how the head loss in microirrigation systems may be modeled. The proposed method can also be used in analyzing systems working with two-phase (air-water) flows. The obtaining of a criteria, used in analyzing an air–water flow with free surface, is given in [19].
Dimensional analysis (DA) also finds a wide range of application in analyzing the work performance of hydraulic machines.
Based on this method, some dimensionless complexes—including basic indicators concerning the current analyzed machine (for example, pressure p, flow rate Q; geometric and exploitation parameters–impeller diameter D, speed n; and fluid properties–density and viscosity ()—are found. In analyzing fan systems, the main fan indicators are used to be presented by using the relevant coefficients of pressure and flow rate , determined as described in [20]:
and
where u is the transitional velocity at the impeller outlet.
In other studies, for example [21], the authors estimate the flow rate coefficient by using the angular velocity and this can be determined as it follows:
In his PhD thesis [21], the author analyzes the impact of the relative roughness and Reynolds number on the processes of modeling centrifugal fans by using the equations of similarity. The resistance characteristic for the analyzed fan system is presented as it follows— [21]:
and
where (7) and (8) represent the equations used to estimate the Euler and Reynolds numbers by using the flow rate Q. In [21]—for the estimation of the Reynolds number—by using the angular velocity, the following equation is used:
No matter if the speed of rotation n or the angular velocity is taken into account in accomplishing the calculations, the pressure (head) and flow rate of a turbo machine are always set to be dimensionless parameters being proportional to and [22,23,24,25,26,27].
The authors in [28] suggest newly established equations for determining the coefficients of flow rate and pressure of multistage helico-axial pumps, working with two-phase mixtures of air and water, as a function of the gas void fraction.
An overview of the reviewed studies suggests that the equations of similarity and the relevant dimensionless coefficients are used to analyze the effective work of machines—turbo pumps, fans, pipe systems—but separately. However, it is also clear that there is a lack of information about using generalized parameters ( -criteria) in analyzing the energy efficiency of systems used to transport fluids, including the hydraulic machines (pumps and fans), as well as the relevant pipe system. The main reason for this may be the late appearance of increased interest in investigating the energy efficiency of such systems. In this regard, the current work aims to fill this gap. More specifically, this paper presents a newly proposed methodology for analyzing the collaboration between system’s key elements, in terms of energy efficiency, by applying the DA.
3. Research Methodology
As it is given in [22,29], the first step in using dimensional analysis is to clarify the physical relations concerning the analyzed process and create a list of parameters having impacts on it. In this regard, the following parameters are selected as having impact on the energy efficiency of a current fan system:
Fan characteristics:
- fan pressure—;
- fan flow rate—;
- speed—;
- fan system coefficient of efficiency—.
Fluid properties:
- fluid density—;
- gas viscosity—.
Pipe system characteristic of resistance:
- —pipe conventional diameter (in case of a pipe with not-round cross-section area, a hydraulic diameter is used). At first admission for the calculations, it can be used the size of the fan suction inlet or discharge outlet.
- —referred length of the pipe system (network), including its geometric sizes, as well as the hydraulic resistance in the pipes.
In accordance with SI, the dimensions of these parameters can be described by using three different measurements: unit-length L in meters [m], time T in seconds [s], and mass M in kilograms [kg]. The equations describing their dimensions are given in Table 1.

Table 1.
Dimension equations.
The total number of parameters used in this research is equal to eight (N = 8), and includes three basic measuring units—[kg], [m], and [s]. Therefore, the number of the new dimensionless complexes will be equal to five (k = 8 − 3 = 5).
The selection of new basic measuring units contains the following parameters:
- density: ρ = [M1L3T0];
- speed: n = [M0L0T−1];
- equivalent pipe diameter: D = [M0L1T0].
The determination of the rest of the dimension parameters is accomplished by using the new (basic) measuring units—ρ, n and, D—and applying the well-known methods of dimensional analysis. For this aim, the following equations are used:
The using of the above equations in combination with the new basic dimensions, presented in the system [MTL], makes it possible to achieve the following relations:
For the estimation of the superscript exponents: aj, bj, and cj (j = 1…5), the following system of equations is used:
| M | L | T | |
The final solution of this system of equations represents:
By replacing the superscript exponents with their values the determination of the dimensions of the parameters: p, Q, μ, LTP, and η, given in the system [D] [n] [ρ], is accomplished:
| or given as dimensionless parameters | ||
The analysis of these dimensionless complexes indicates that a part of them correspond in their structure to well-known criteria describing the hydrodynamic similarity of fluid flows. The component has the same dimension like velocity and therefore: . Indicating the previous statement, it can be concluded that the parameter has the same structure as Euler’s criterion—, and the parameter has the structure of Reynold’s criterion: . The other two complexes are also well known. The parameter corresponds to the dimensionless flow rate, which is widely used in analyzing turbo machines—including fans (in this case, is the outer diameter of the machine impeller). The ratio represents the geometric simplex, applied for the hydrodynamic criteria equation in case of studying the transportation of fluid flows through pipes and canals.
Combining the presented in this research work, dimensionless complexes ensure the possibility of establishing new criteria which may be applied adequately for a given analysis.
The mathematical transformation of the first parameter is as it follows:
Indicating that the ratio represents the specific energy consumption, used for the transportation of a unit of gas, the criteria may be given the following way:
The dimensionless complex may be presented the following way:
The other parameters:,, and , remain the same:
To present the functional relation in criterion form, the following equation is used:
To describe the criteria indicating the specific energy consumption, Equation (16) is used:
The criteria includes the specific energy consumption, used for the transportation of 1 m3 air, and the main characteristics of a given system, such as: the system main geometric parameter—the equivalent diameter of the pipe system and the properties of the transported gas (air).
The criteria includes the parameters that change depending on the selected method of a flow rate regulation: speed for frequency regulation, or the referred length of a pipe system (network) for throttle regulation. By using this dimensionless complex, it is possible to evaluate the impact of properties of a gas (density and dynamic viscosity) on the specific energy consumption, if (for example) the initial temperature is changed.
Therefore, to investigate the impact of a selected method of flow rate regulation and change of gas density on the energy efficiency of a given system, used to transport fluids, the following equation may be used—:
To accomplish an energy analysis of a given fan system, it is necessary to know the work characteristics of the fan, as well as the resistance characteristic of the pipe system.
It is well-known that the energy (work) characteristics of fans are presented graphically by their manufacturers. For the aim for this research work, it is necessary to present analytic expressions for these graphics by using adequate equations. According to [12], in analyzing pump systems, the head vs. flow rate (H-Q) and coefficient of efficiency vs. flow rate (η-Q) characteristics can be described by using a complete second-degree polynomial. Obtaining these equations requires using a specialized software product that enables the scanning of the graphics concerning the pump work characteristics and from the manufacture production catalogues—including the determination of the coordinates of a good number of points belonging to the curves. To process the found data the “least squares method” was used, which enables the determination of the coefficients of the analyzed polynomials. It is possible to apply this method also to a fan system. The work characteristic of the fan—representing the total pressure as a function of the flow rate at given speed with a constant value—may be described the following way:
The equation of the characteristic represents:
The coefficients used in Equations (18) and (19) are found by applying the method described in the above paragraph.
The properties of the air at different physical conditions are determined by taking into account the following relations:
• air density at temperature :
where is the gas constant for humid air; —the partial water vapor pressure in the air; —the atmospheric pressure [20];
• air dynamic viscosity in the range of … [20]:
As it is known, the referred length of the pipe system indicates the geometric length of a given simple pipe with a constant diameter, as well as the equivalent lengths of the existing local resistances. For a given pipe, a change of results from the magnitude change of any variable (adjustable) local resistance. To determine the referred length of a pipe system, the coefficient of its resistance characteristic – k, is used:
where is a pipe coefficient of friction; – referred length coefficient indicating the type and scheme of the current pipe system (network).
Indicating the lack of static heads in fan systems, the relation that is valid for each work regime i, respectively is: . Therefore, the transformation of Equation (22) is as follows:
Then, to estimate the pipe system referred length, the following equation is used
At first assumption, the fluid flow regime of motion is considered to be completely turbulent (belongs to the quadratic area). In this case, for the estimation of the coefficient of friction the following equation is used [5]:
where is the equivalent roughness of the pipe walls.
By taking Equation (25) into account, and using Equation (26), it can be estimated the coefficient of a pipe system resistance characteristic:
For the estimation of the referred pipe system length at given work regime (pressure , flow rate ) the following equation is used:
4. Results
To demonstrate applying the established criteria equations used to evaluate the energy efficiency (energy consumption) of a fan system, we studied such a system containing a centrifugal fan BHCH 9.5, produced by the company Spartak from Burgas (Bulgaria, http://www.spartak.bg/). For the determination of the required coefficients, used in Equations (18) and (19), it is necessary to use the catalog data concerning fan curves at nominal speed, as well as to apply the methodology described in one of the previous paragraphs. Table 2 presents the values of these coefficients.

Table 2.
Values of the coefficients used in Equations (18) and (19).
The nominal work regime of the analyzed fan at speed of has the following parameters: nominal flow rate—, nominal pressure— and nominal coefficient of efficiency—.
The air properties at standard conditions (temperature , absolute pressure pa = 101,325 Pa and relative humidity hu = 0.4) respectively are: density and dynamic viscosity—.
The pipe system has a typical geometric size and for the estimation of the referred length in case that the fan works at its nominal work regime, Equation (27) is used:
For the nominal work regime of the fan the specific energy consumption is:
and the dimensionless complexes and have the following values:
In case of isometric conditions of gas passing through a given pipe system the following relations are valid:
The change of the flow rate is a result of using a given method of flow rate regulation. It is well-known that the most commonly used method of regulating the flow rate of (turbo machine) systems used to transport fluids respectively is the frequency—by changing the machine shaft speed of rotation and throttle—by changing the pipe system resistance characteristic. For this reason, the presented particularities in determining the dimensionless complexes concern these two methods.
4.1. Throttle Regulation of the Flow Rate
In this case, the speed has constant value—n is constant. Using Equations (18) and (19) enables the estimation, respectively, of the pressure for each of the ensured flow rates obtained by applying the throttle regulation, as well as the relevant values of the coefficient of efficiency.
The referred length of the pipe system will be different for each of the achieved flow rates. To determine it, the methodology described in one of the above paragraphs is used—Equation (27).
For the estimation of the dimensionless complexes , the found values and Equations (10)–(13) are used. The referring of the found results to the relevant criteria, determined for the nominal work regime of the analyzed fan, must normalize their values.
4.2. Frequency Regulation of the Flow Rate
In this case, the referred length of the pipe system has a constant value, i.e., LTP is constant. The fan system’s total coefficient of efficiency is also a constant, i.e., η is a constant. These two parameters are determined by using Equations (19) and (28), involving the obtained before regulation system output flow rate.
The required fan speed and pressure for each flow rate can be determined by using the equations of similarity [22]:
where is the flow rate of the initial (output) work regime (before regulation).
The referring of the criteria and to the relevant parameters, concerning the nominal work regime of the fan, has to normalize their values:
and
Figure 1 represents the results found. The analysis is accomplished by taking into account the change of the initial flow rate in the range of: .
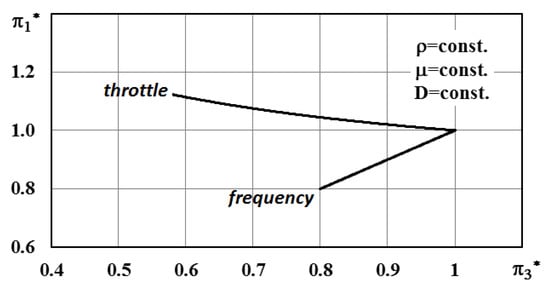
Figure 1.
Change of the specific energy consumption criterion depending on the selected method of flow rate regulation (Source: Author own calculation, based on Excel).
In this case, the initial flow rate is equal to the nominal flow rate, i.e., . If is applied, the nature of the found relation is analogous and for other values of the initial flow rate.
Taking into account Equation (10), it can be seen that for a given pipe system and isothermal conditions of transporting the air, the parameter and therefore the criteria becomes depended by only the specific energy consumption—, i.e., this criteria represents dimensionless specific energy consumption. Due to the decreased flow rate, the criteria also decreases—as in case of applying the frequency or throttle method of flow rate regulation. The reason respectively is the reduced fan’s speed (), and the increased pipe system’s referred length—, accompanied by an increased resistance in the pipe network.
As might be predicted, increasing the degree of regulation (i.e., decreasing the flow rate) leads to decreasing the specific energy consumption (i.e., the criterion ) in case of using the frequency method, while in case of applying the throttle method, it is the opposite. The above statement fully corresponds to the well-known fact that the frequency method is the most effective method of flow rate regulation, in terms of energy efficiency, while the throttle method is associated with the existing of significant additional energy loss.
4.3. Determining the Impact of the Air Temperature on the Energy Consumption of Fan Systems
It is well-known that temperature variation leads to a change of air’s density and viscosity, and therefore a part of the parameters, used for the determination of the established criteria, will also be changed. Indicating that Equations (10) and (11) are used for the estimation of the criteria and , it can be seen that air’s density and dynamic viscosity are taking part.
According to [6], the density variation has no impact on the system’s flow rate, i.e., Q is a constant. In case of a decreased temperature for the density and pressure is valid that and , but at the same time the pipe system resistance characteristic gets steeper, which enables the flow rate to stay constant. The pressure variation leads to a change of the specific energy consumption , as well as the criteria . The density variation has impact on the criterion , and therefore also influences the relation: . The other three criteria keep their constant values independent of density variation. In case of completely turbulent flow (quadratic area), viscosity has no impact on the coefficients of pipe resistance, and therefore it does not affect the determination of the pipe system’s referred length.
Figure 2 represents graphics indicating the change of the specific energy consumption criteria as a function of the criteria for three different work regimes of the analyzed fan system.
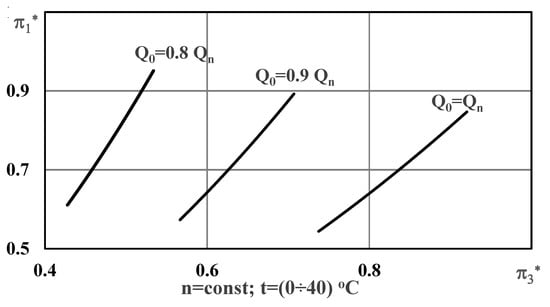
Figure 2.
Change of the specific energy consumption criteria depending on the temperature variation (Source: author’s own calculation, based on Excel).
As it may be expected, decreasing the air’s density (a result of temperature increase) leads to decreasing of specific energy consumption , which is explained with the decreasing of the pressure, used to transport the given flow rate . Due to the simultaneous decreasing of and , the value of the criteria will also decrease.
5. Conclusions
Applying methods of dimensional analysis enables establishing of dimensionless complexes, which can be used for accomplishing a quantitative analysis of the effective energy use of systems transporting fluids. The proposed method can be used in analyzing the work performance, in terms of energy efficiency, of fan systems working with low or medium pressure, when the gas density has a constant value. Another additional restriction for applying this method is the existence of isothermal conditions, in which gas viscosity stays constant.
The proposed criteria includes the specific energy consumption , used for the evaluation of the energy effectiveness of the fluid transportation.
The impact of the applied method of flow rate regulation on the effective energy use of a fan system can be determined by using the criteria . This criteria includes parameters characterizing the selected method of flow rate regulation: speed () for using the frequency method and pipe system’s referred length () for using the throttle method. Change of the properties of a gas also influences these two criteria and this may be used in evaluating the impacts of the variation of density () and dynamic viscosity () on the effective energy use of systems transporting air. With increasing air density resulting from the decreasing temperature, the specific energy consumption increases.
Author Contributions
Conceptualization, G.P.; methodology, G.P., K.K., and B.K.; software, G.P., K.K., and B.K.; validation, G.P.; formal analysis, G.P., K.K., B.K., and R.D.; investigation, G.P., K.K., and B.K.; resources, K.K., B.K., and R.D.; data curation, G.P., K.K., and B.K.; writing—original draft preparation, G.P.; writing—review and editing, K.K. and B.K.; visualization, R.D.; supervision, G.P.; project administration, K.K., B.K., and R.D. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Augustin, T. Energy efficiency and savings in pumping systems—The holistic approach. In Proceedings of the Southern African Energy Efficiency Convention (SAEEC), Johannesburg, South Africa, 14–15 November 2012. [Google Scholar] [CrossRef]
- Dimitrova, R. Methods, Used to Evaluate the Energy Efficiency of Systems for Transporting Fluids. In Proceedings of the 58th Science Conference of Ruse University, Ruse, Bulgaria, 22 October 2019; Volume 58. [Google Scholar]
- Popov, G.; Klimentov, K.; Kostov, B. Investigation of the energy consumption in regulating the flow rate of pump systems. In Proceedings of the 10th Anniversary International Conference an Accomplishment in Electrical and Mechanical Engineering and Information Technology, DEMI’2011, BanjaLuka, Bosnia and Herzegovina, 26–28 May 2011; pp. 481–487. [Google Scholar]
- Kostov, B.; Popov, G.; Klimentov, K. Effective regulation of the flow rate of parallel working pumps. Int. J. Sci. Tech. Innov. Ind. 2013, 6, 57–59. [Google Scholar]
- Kostov, B. Impact of cold water temperature variation on the energy efficiency of a water supply pump system with variable demand. Int. Rev. Mech. Eng. 2018, 7, 604–612. [Google Scholar] [CrossRef]
- Popov, G. Influence of air’s density on the energy consumption of fan systems. Toplotechnika 2014, 1, 72–75. [Google Scholar]
- Popov, G.; Klimentov, K.; Kostov, B. Investigating the influence of the technical state of the pump aggregates on the energy consumption of pump system. Toplotehnika 2012, 3, 64–67. [Google Scholar]
- Popov, G.; Klimentov, K.; Kostov, B. Investigation of the energy consumption in regulating the flow rate of fan systems. In Proceedings of the XXIInd National Conference on Thermodynamics with International Participation NACOT, Galati, Romania, 22–24 May 2019. [Google Scholar] [CrossRef]
- ISO/ASME 14414 Pump System Energy Assessment. 2015. Available online: https://infostore.saiglobal.com/preview/98704299004.pdf?sku=878847_SAIG_NSAI_NSAI_2088410 (accessed on 5 January 2016).
- Popov, G.; Klimentov, K.; Kostov, B. Methods to estimate the energy consumption in regulating the flow rate of pump systems. In Proceedings of the 10th Anniversary International Conferenceon Accomplishments in Electrical and Mechanical Engineering and Information Technology DEMI’2011, Banja Luka, Bosnia and Herzegovina, 26–28 May 2011; pp. 495–500. [Google Scholar]
- EN 13779: 2006 Ventilation for Non-Residential Buildings— Performance Requirements for Ventilation and Room–Conditioning System. Available online: https://www.sis.se/api/document/preview/60957/ (accessed on 5 August 2007).
- Klimentov, K.; Popov, G.; Tujarov, K. Equations of centrifugal pumps’ characteristics. Energetica 2008, 6–7, 60–63. [Google Scholar]
- Munson, R.; Okiisi, T.; Huebsch, W.; Rothmayer, A. Fundamentals of Fluid Mechanics, 7th ed.; John Wiley & Sons, Inc.: New York, NY, USA, 2013. [Google Scholar]
- Smits, J. A Physical Introduction to Fluid Mechanics, 2nd ed.; Prinston University: Prinston, NJ, USA, 2019. [Google Scholar]
- White, M. Mechanical Engineering, 7th ed.; McGraw-Hill: New York, NY, USA, 2011. [Google Scholar]
- Weigand, B.; Simon, V. Laws of similarity in fluid mechanics. In WIT Transactions on State of the Artin Science and Engineering; WIT Press: Southampton, UK, 2006; Volume 3, pp. 20–35. [Google Scholar]
- Bombardelli, W.; DeCamargo, A.; Frizzone, J. Local head loss caused in connections used in micro-irrigation systems. Rev. Bras. Eng. Ambient. 2019, 23, 492–498. [Google Scholar] [CrossRef]
- Perboni, A.; Frizzone, J.; DeCamargo, A.; Pinto, M. Modelling head loss along emitting pipe susing dimensional analysis. J. Braz. Assoc. Agric. Eng. 2015, 35, 442–457. [Google Scholar]
- Khan, A.; Hoque, A. A study on dimensional analysis for air-water flow system. Ganit J. Bangladesh Math. Soc. 2010, 30, 11–18. [Google Scholar] [CrossRef]
- ISO 5801: 2007 Industrial Fans Performance (Testing Using Standardized Airways). Available online: https://infostore.saiglobal.com/preview/257707716276.pdf?sku=859942_SAIG_NSAI_NSAI_2045827 (accessed on 25 October 2017).
- Sardrar, M. Centrifugal Fans: Similarity, Scaling Laws, and Fan Performance. Ph.D. Thesis, Department of Mechanical and Aerospace Engineering and the Faculty of the State University of New York at Buffalo, Buffalo, NY, USA, 2001. [Google Scholar]
- Cory, B. Fans & Ventilation. A Practical Guide; Elsevier and Roles & Associates Ltd.: Oxford, UK, 2005. [Google Scholar]
- Dixon, L. Fluid Mechanics, Thermo dynamics of Turbo-Machinery, 4th ed.; Butterworth-Heinemann Linacre House, Jordan Hill: Oxford, UK, 1998. [Google Scholar]
- El-Naggar, A. A one-dimensional flow analysis for the prediction of centrifugal pump performance characteristics. Int. J. Rotating Mach. 2013. [Google Scholar] [CrossRef]
- Lewis, I. Turbo-machinery performance analysis. In Elsevier Science & Technology Books; Butterworth-Heinemann: Oxford, UK, 1996. [Google Scholar]
- Round, F. Incompressible Flow Turbo Machines: Design, Selection, Application and Theory; Butterworth-Heinemann: Oxford, UK, 2004. [Google Scholar]
- Srinivasan, M. Rotor-Dynamic Pumps (Centrifugal and Axial), 2nd Revised edition; New Academic Science Ltd.: London, UK, 2016. [Google Scholar]
- Patil, A.; Gudigopuram, S.; Ayyildiz, B.; Delgado, A.; Morrison, G. Performance Evaluation and Dimensional Analysis of Multistage Helicoaxial Pump for Two-Phase Flow. Int. J. Turbo Mach. Propuls. Power. 2019. [Google Scholar] [CrossRef]
- Timar, P. Dimensionless characteristics of centrifugal pump. Chem. Pap. Slovak Acad. Sci. 2005, 59, 500–503. [Google Scholar]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).