Optimal Denoising and Feature Extraction Methods Using Modified CEEMD Combined with Duffing System and Their Applications in Fault Line Selection of Non-Solid-Earthed Network
Abstract
1. Introduction
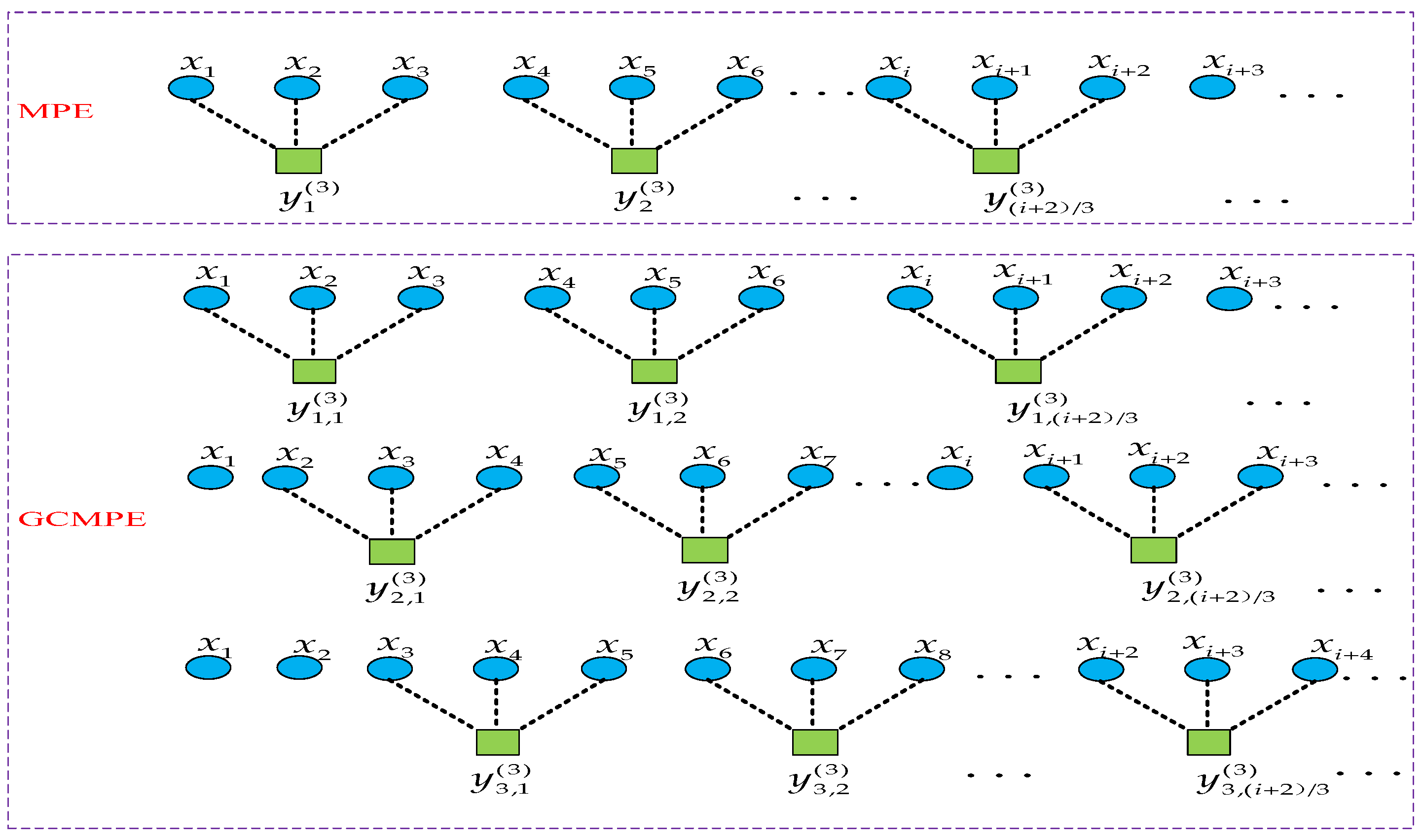
2. Generalized Composite Multiscale Permutation Entropy
2.1. Permutation Entropy
2.2. Multiscale Permutation Entropy
2.3. Generalized Composite Multiscale Permutation Entropy
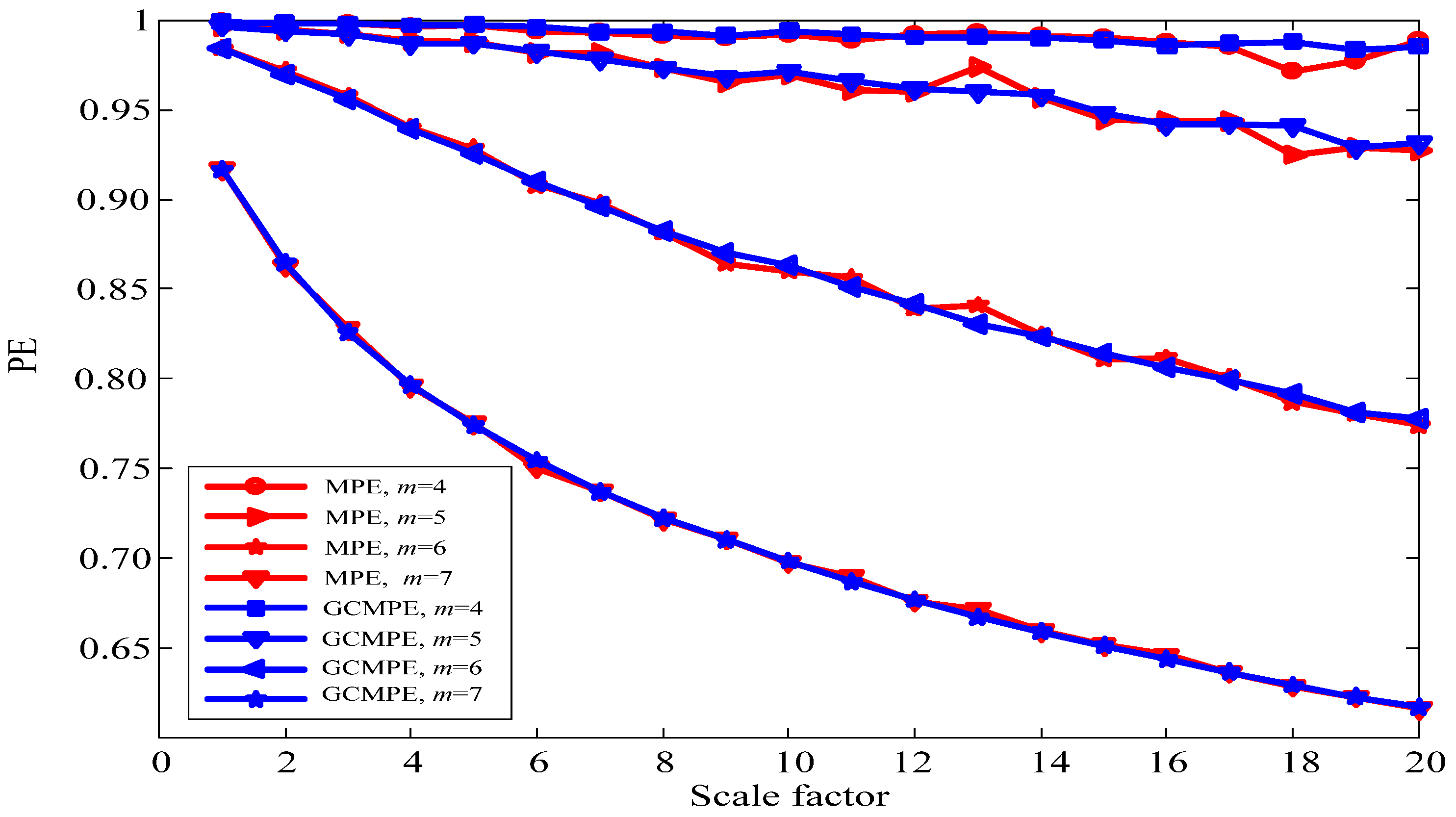
2.4. Parameter Selection and Comparative Analysis
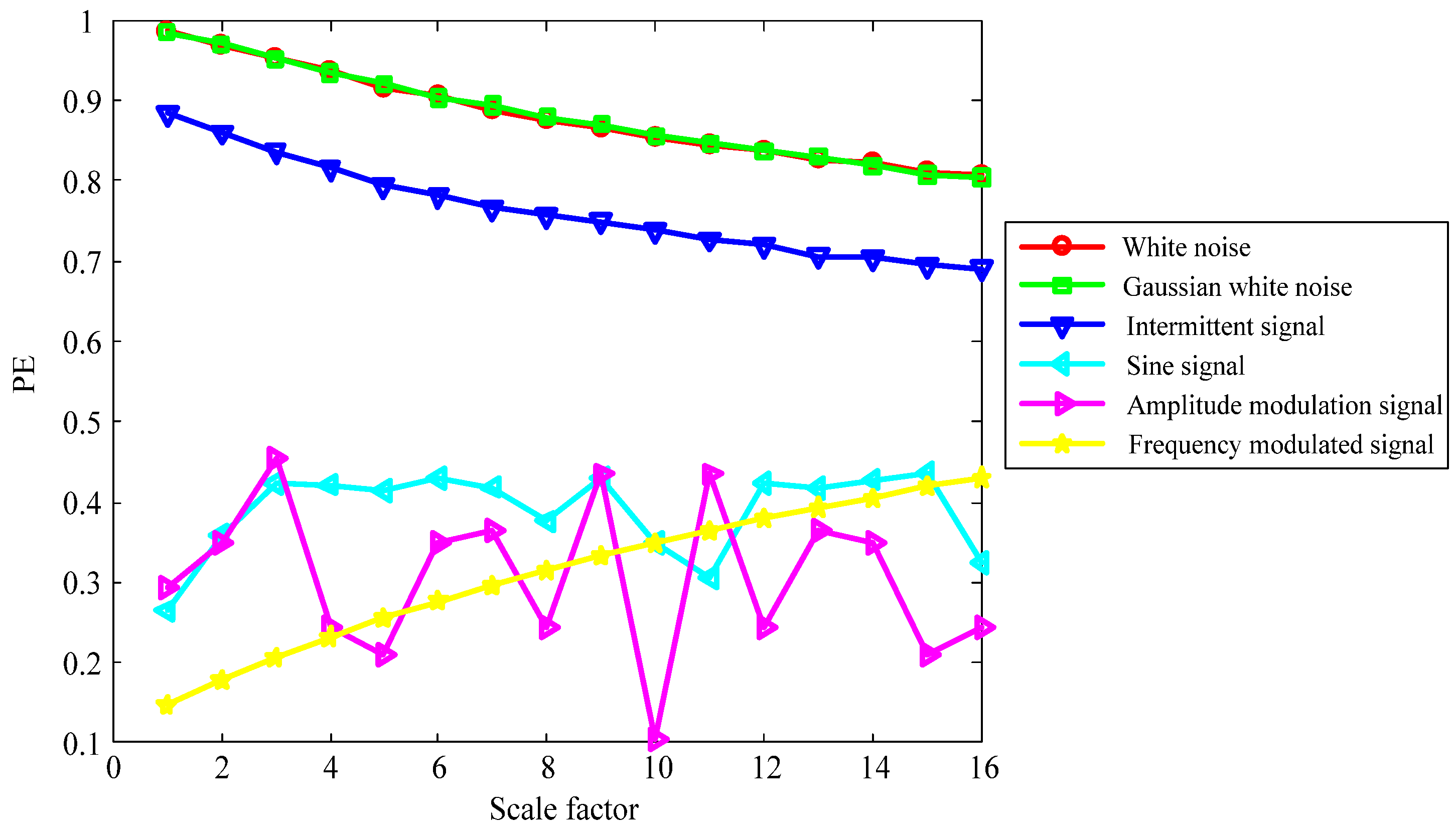
2.5. Signal Randomness Detection
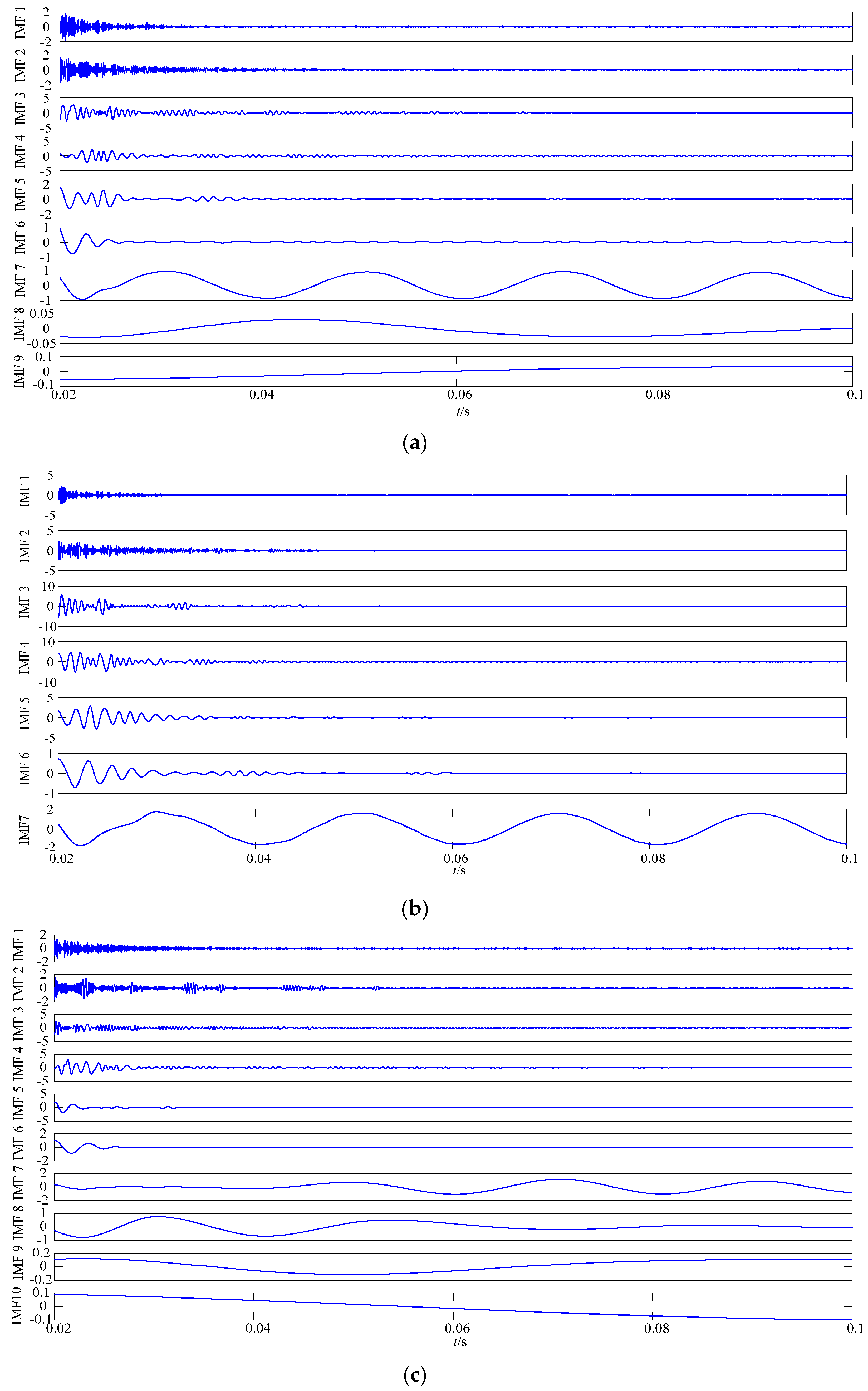
3. MCEEMD Algorithm
3.1. The Steps of MCEEMD
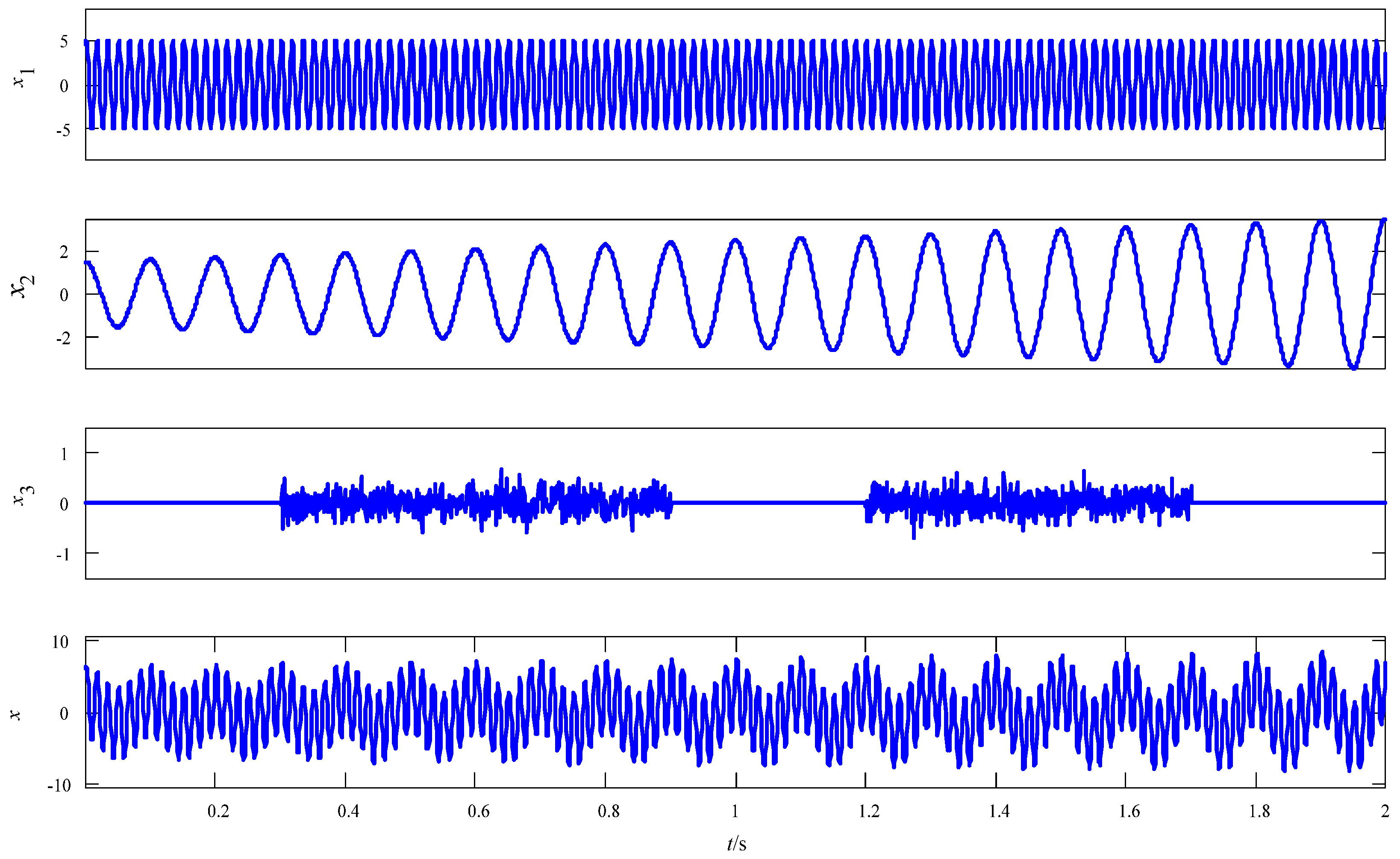
3.2. Analysis of the Simulation Signal Using EMD, CEEMD, and MCEEMD
4. Optimal Smooth Denoising Model
4.1. Optimal Smooth Denoising
4.2. Optimal Smooth Denoising Experiment of Simulation Signal
5. Measuring Principle of Duffing System
5.1. Duffing System Model
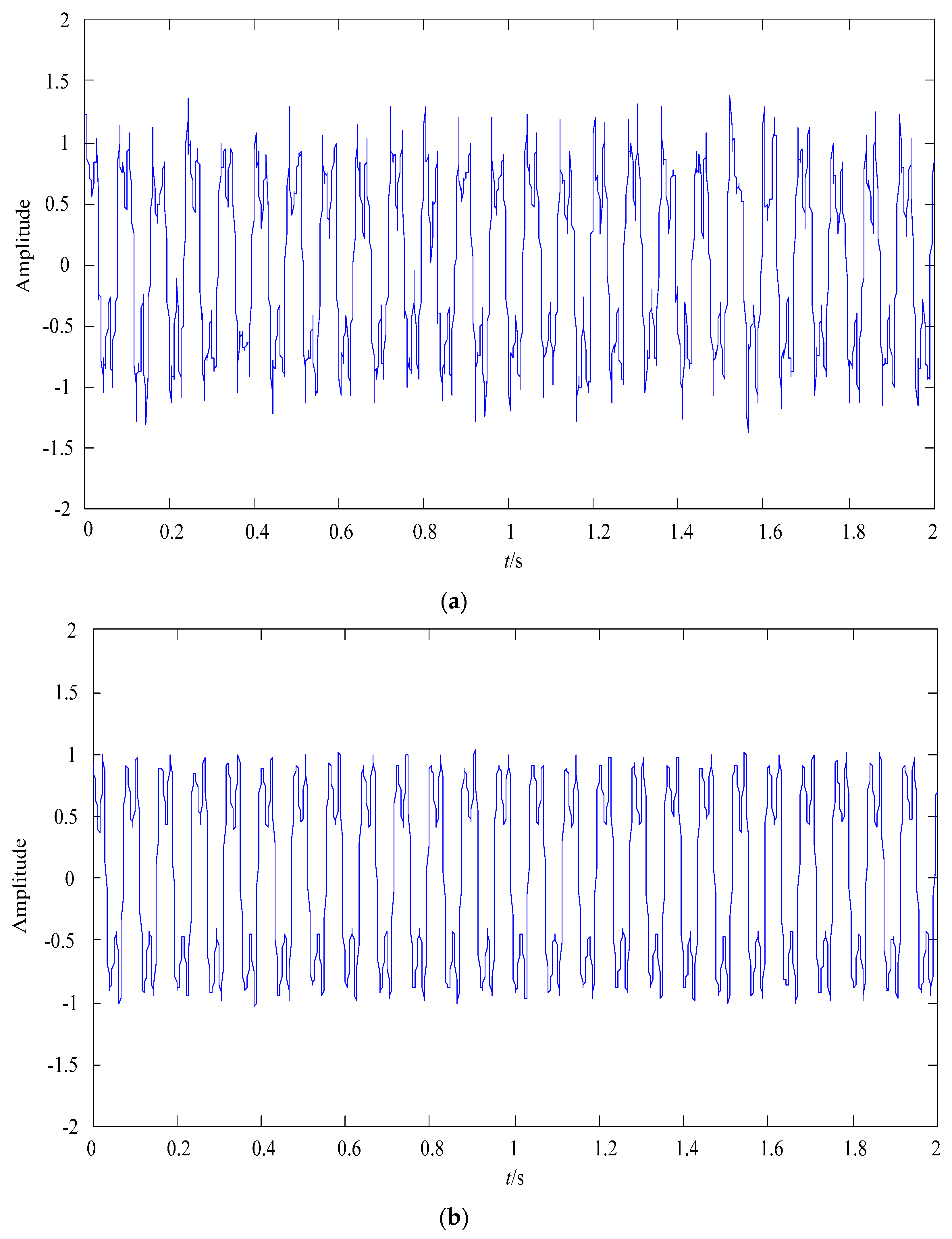
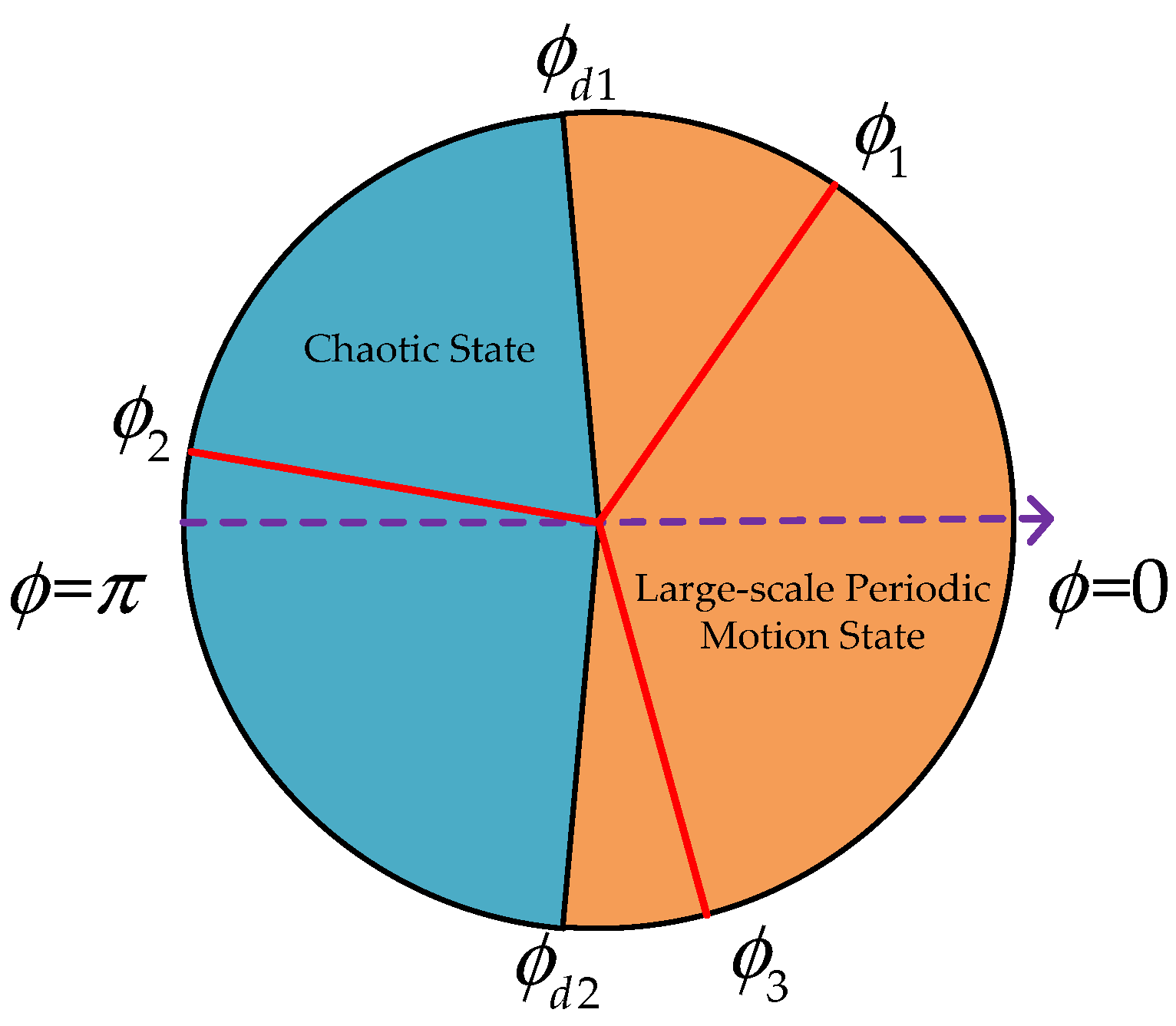
5.2. Trisection Symmetry Phase Estimation
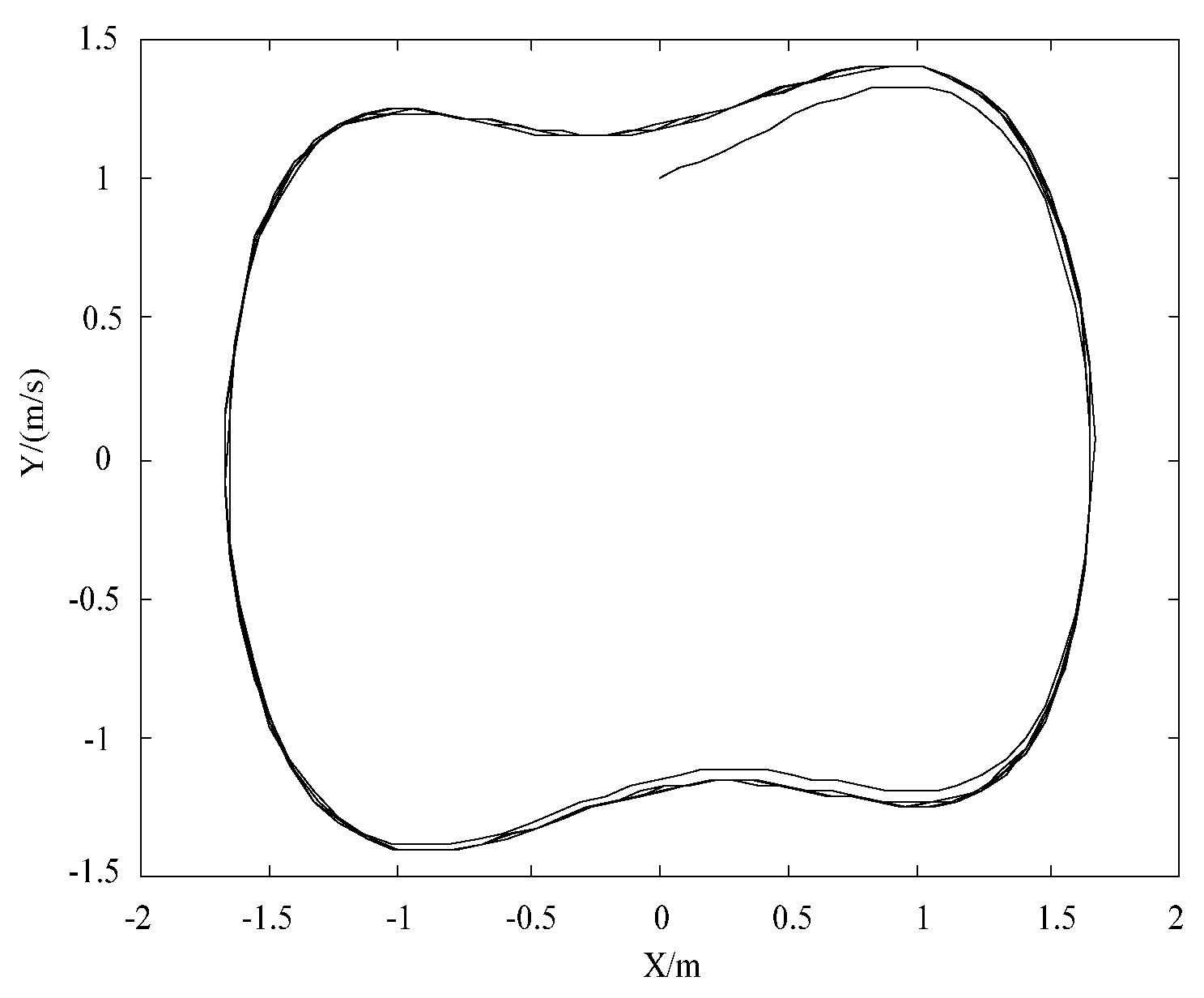
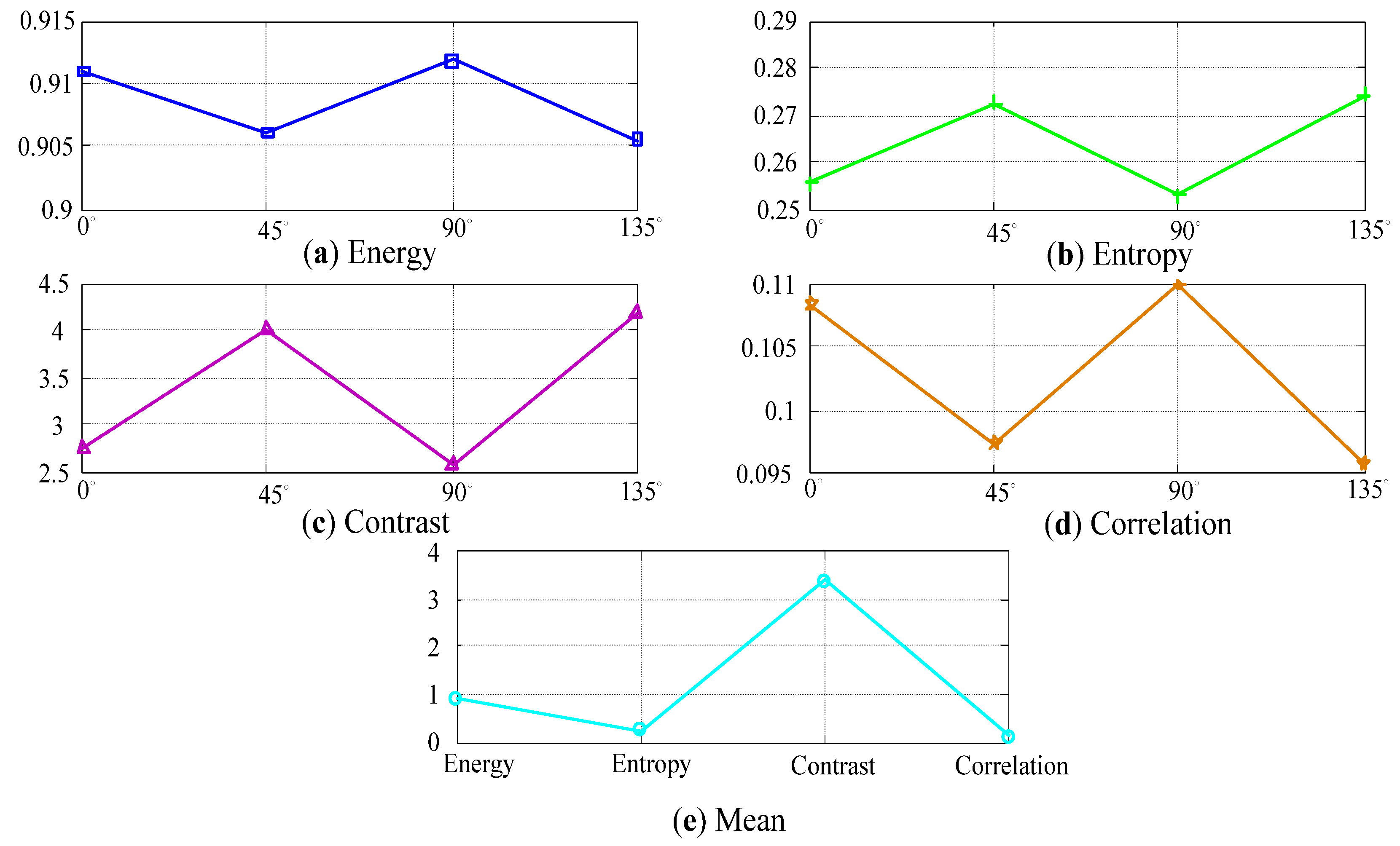
5.3. A Method of Distinguishing Chaotic Characteristics
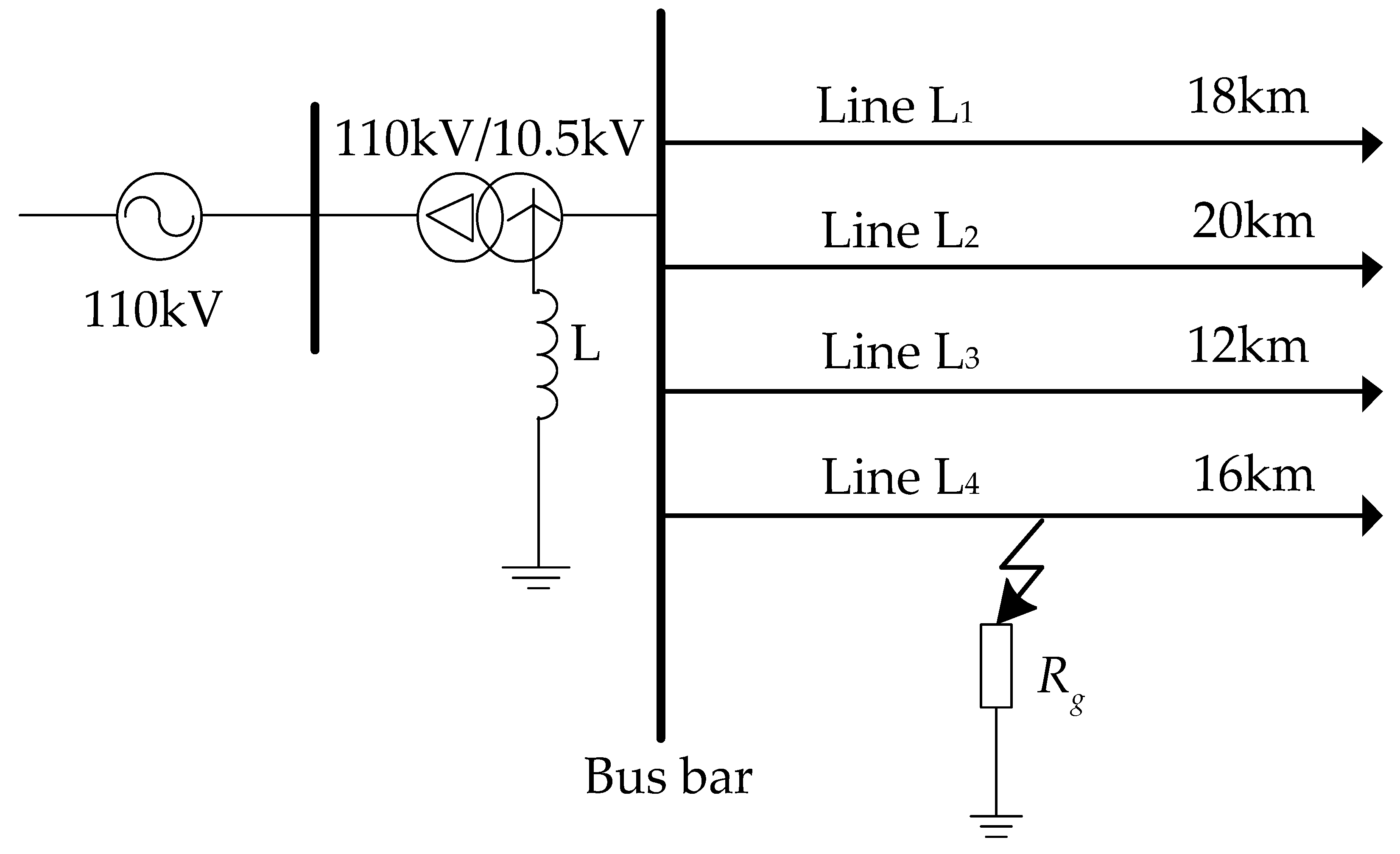
6. Fault Line Selection Steps and Simulation
6.1. Introduction of the Fault Line Selection Steps
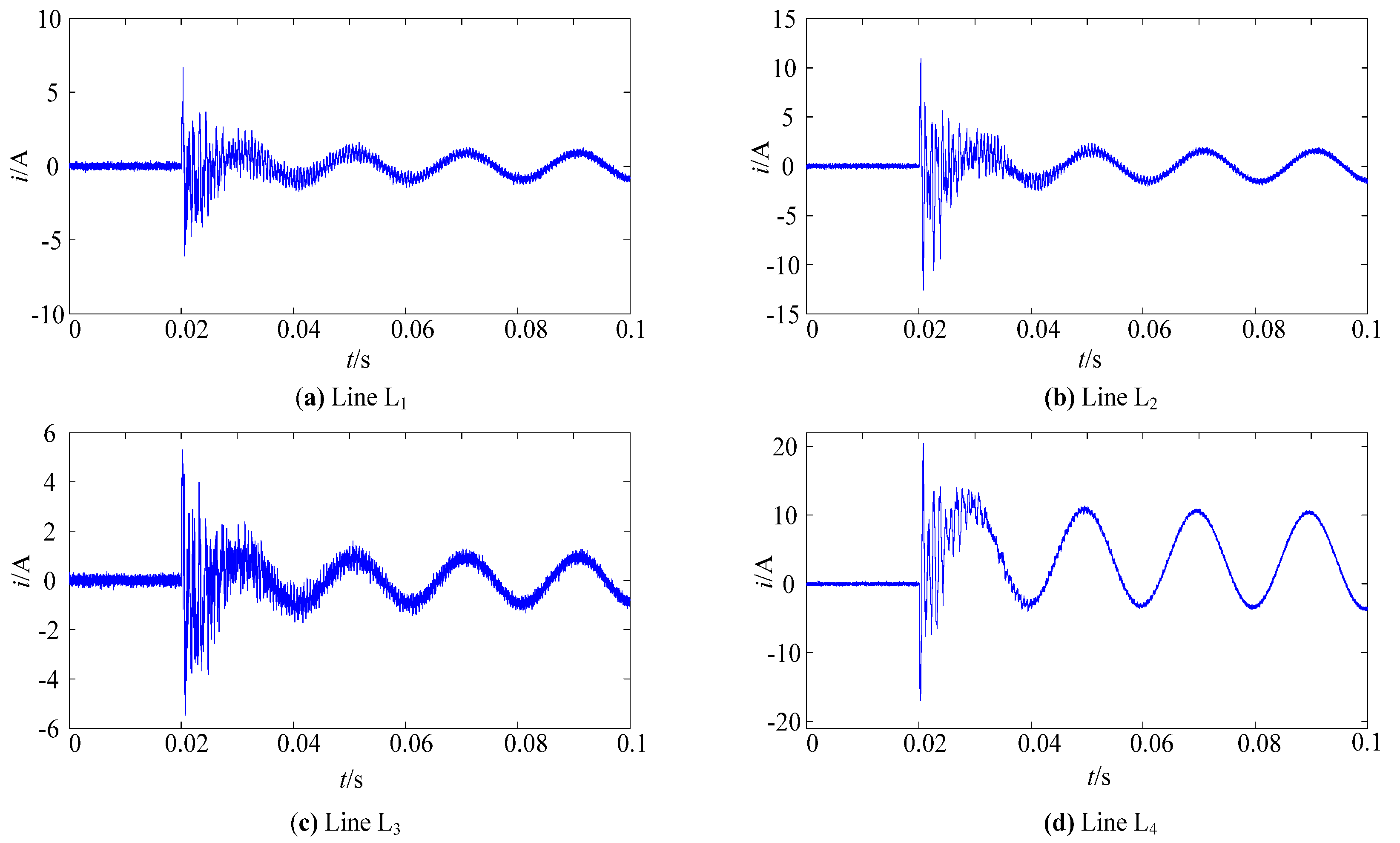
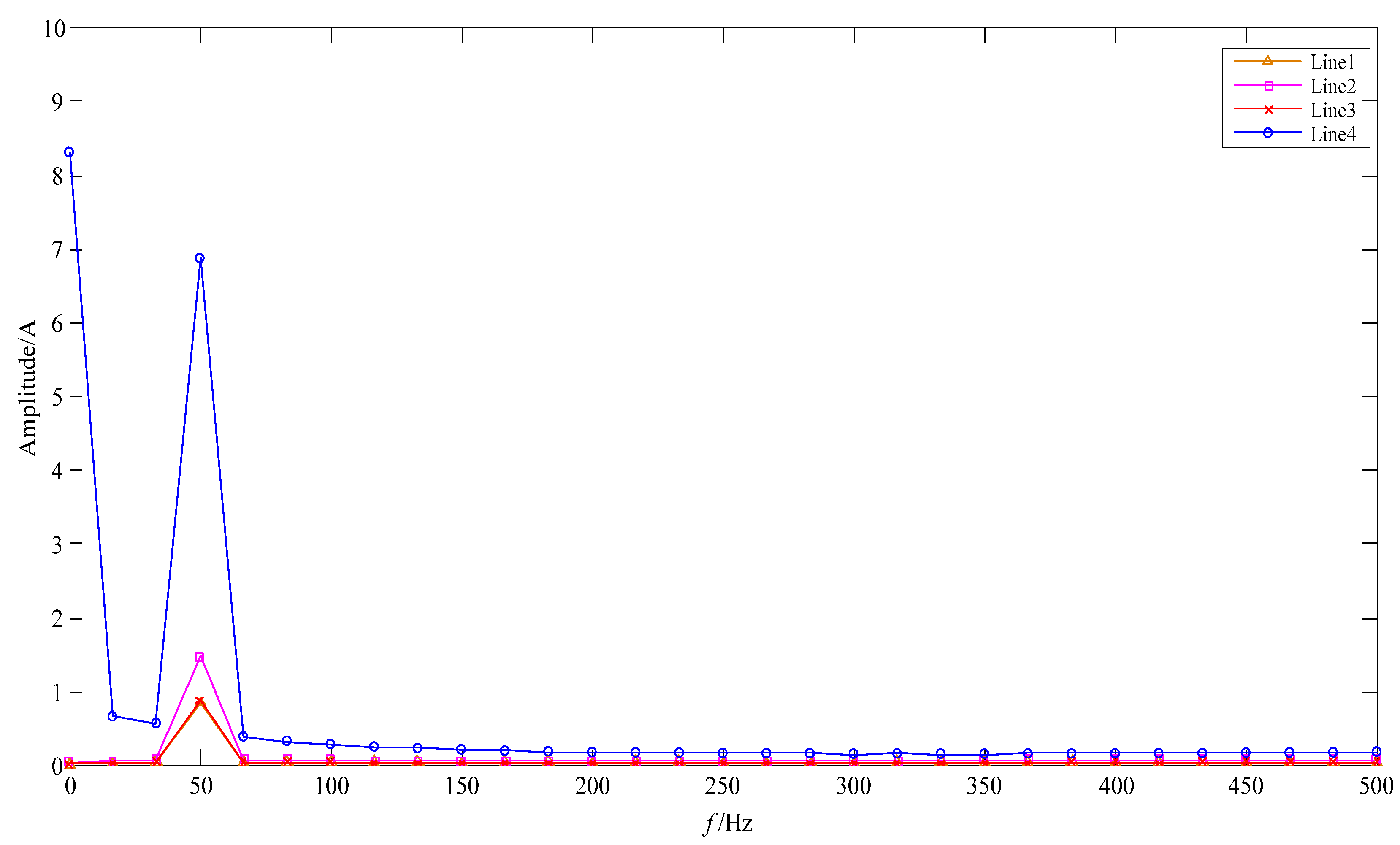
6.2. Simulation Study
7. Conclusions
- (1)
- GCMPE can solve the deficiencies of MPE and has better stability than MPE. Based on GCMPE and SVM for abnormal signal detection, a new denoising algorithm is proposed. The simulation results show that MCEEMD has better decomposition results than the existing algorithms. MCEEMD also has strong adaptability and restrains the mode mixing of EMD.
- (2)
- The optimal smooth denoising model can be determined by balancing the similarity and smoothness of different filtering algorithms. The superior algorithm can retain the useful features of the original signal and reduce the noise and smooth the original signal.
- (3)
- A novel method of identifying chaotic nature based on texture features of the phase diagram is presented. This way can avoid the involvement of human factors and automatically identify chaotic nature by computers.
- (4)
- The fault line in the non-solid-earthed network can be selected with the diagram outputted by the Duffing system. A large number of experimental studies show that the proposed method can accurately select the fault line under different fault situations. The research provides a novel train of thought for the fault line in the non-solid-earthed network.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| MCEEMD | Modified complementary ensemble empirical mode decomposition |
| GCMPE | Generalized composite multiscale permutation entropy |
| SVM | Support vector machine |
| IMF | Intrinsic mode functions |
| EMD | Empirical mode decomposition |
| VMD | Variational mode decomposition |
| EEMD | Ensemble empirical mode decomposition |
| CEEMD | Complementary ensemble empirical mode decomposition |
| CEEMDAN | Complete ensemble empirical mode decomposition with adaptive noise |
| PE | Permutation entropy |
| MPE | Multiscale permutation entropy |
| GLCM | Gray level co-occurrence matrix |
| Ort | Orthogonality |
| FFT | Fast Fourier transform |
References
- Wang, X.; Gao, J.; Song, G.; Cheng, Q.; Wei, X.; Wei, Y. Faulty line selection method for distribution network based on variable scale bistable system. J. Sens. 2016, 2016, 7436841. [Google Scholar] [CrossRef]
- Wang, X.; Wei, Y.; Zeng, Z.; Hou, Y.; Gao, J.; Wei, X. Fault line selection method of small current to ground system based on atomic sparse decomposition and extreme learning machine. J. Sens. 2015, 2015, 678120. [Google Scholar] [CrossRef]
- Shao, W.; Bai, J.; Cheng, Y.; Zhang, Z.; Li, N. Research on a faulty line selection method based on the zero-sequence disturbance power of resonant grounded distribution networks. Energies 2019, 12, 846. [Google Scholar] [CrossRef]
- Lin, X.; Sun, J.; Kursan, I.; Zhao, F.; Li, Z.; Li, X.; Yang, D. Zero-sequence compensated admittance based faulty feeder selection algorithm used for distribution network with neutral grounding through Peterson-coil. Int. J. Electr. Power Energy Syst. 2014, 63, 747–752. [Google Scholar] [CrossRef]
- Zhuang, S.; Miao, X.; Jiang, H.; Guo, M. A line selection method for single-phase high-impedance grounding fault in resonant grounding system of distribution network based on improved euclidean-dynamic time warping distance. Power Syst. Technol. 2020, 44, 273–281. [Google Scholar]
- Dong, X.; Shi, S. Identifying single-phase-to-ground fault feeder in neutral noneffectively grounded distribution system using wavelet transform. IEEE Trans. Power Deliv. 2008, 23, 1829–1837. [Google Scholar] [CrossRef]
- Costa, F.; Souza, B.; Brito, N.; Silva, J.; Santos, W. Real-time detection of transients induced by high-impedance faults based on the boundary wavelet transform. IEEE Trans. Ind. Appl. 2015, 51, 5312–5323. [Google Scholar] [CrossRef]
- Zhang, Z.; Liu, X.; Piao, Z. Fault line detection in neutral point ineffectively grounding power system based on phase-locked loop. IET Gener. Transm. Distrib. 2014, 8, 273–280. [Google Scholar]
- Zhang, S.; Zhai, X.; Dong, X.; Li, L.; Tang, B. Application of EMD and Duffing oscillator to fault line detection in un-effectively grounded system. Proc. Chin. Soc. Electr. Eng. 2013, 33, 161–167. [Google Scholar]
- Kang, X.; Liu, X.; Suonan, J.; Ma, C.; Wang, C.; Yang, L. New method for fault line selection in non-solidly grounded system based on matrix pencil method. Autom. Electr. Power Syst. 2012, 36, 88–93. [Google Scholar]
- Li, Y.; Li, Y.; Chen, X.; Yu, J. Denoising and feature extraction algorithms using NPE combined with VMD and their applications in ship-radiated noise. Symmetry 2017, 9, 256. [Google Scholar] [CrossRef]
- Hou, J.; Wu, Y.; Gong, H.; Ahmad, A.; Liu, L. A novel intelligent method for bearing fault diagnosis based on EEMD permutation entropy and GG clustering. Appl. Sci. 2020, 10, 386. [Google Scholar] [CrossRef]
- Wang, S.; Sun, Y.; Zhou, Y.; Jamil Mahfoud, R.; Hou, D. A new hybrid short-term interval forecasting of PV output power based on EEMD-SE-RVM. Energies 2019, 13, 87. [Google Scholar] [CrossRef]
- Xue, S.; Tan, J.; Shi, L.; Deng, J. Rope tension fault diagnosis in hoisting systems based on vibration signals using EEMD, improved permutation entropy, and PSO-SVM. Entropy 2020, 22, 209. [Google Scholar] [CrossRef]
- Ren, Y.; Suganthan, P.; Srikanth, N. A comparative study of empirical mode decomposition-based short-term wind speed forecasting methods. IEEE Trans. Sustain. Energy 2015, 6, 236–244. [Google Scholar] [CrossRef]
- Zhao, L.; Yu, W.; Yan, R. Rolling bearing fault diagnosis based on CEEMD and time series modeling. Math. Probl. Eng. 2014, 2014, 101867. [Google Scholar] [CrossRef]
- Liu, F.; Gao, J.; Liu, H. The feature extraction and diagnosis of rolling bearing based on CEEMD and LDWPSO-PNN. IEEE Access 2020, 8, 19810–19819. [Google Scholar] [CrossRef]
- Yang, D.; Sun, Y.; Wu, K. Research on CEEMD-AGA denoising method and its application in feed mixer. Math. Probl. Eng. 2020, 2020, 9873268. [Google Scholar] [CrossRef]
- Fuentealba, P.; Illanes, A.; Ortmeier, F. Independent analysis of decelerations and resting periods through CEEMDAN and spectral-based feature extraction improves cardiotocographic assessment. Appl. Sci. 2019, 9, 5421. [Google Scholar] [CrossRef]
- Li, G.; Yang, Z.; Yang, H. A denoising method of ship radiated noise signal based on modified CEEMDAN, dispersion entropy, and interval thresholding. Electronics 2019, 8, 597. [Google Scholar] [CrossRef]
- Tian, S.; Bian, X.; Tang, Z.; Yang, K.; Li, L. Fault diagnosis of gas pressure regulators based on CEEMDAN and feature clustering. IEEE Access 2019, 7, 132492–132502. [Google Scholar] [CrossRef]
- Wang, G.; Chen, D.; Lin, J.; Chen, X. The application of chaotic oscillators to weak signal detection. IEEE Trans. Ind. Electron. 1999, 46, 440–444. [Google Scholar] [CrossRef]
- Xue, W.; Dai, X.; Zhu, J.; Luo, Y.; Yang, Y. A noise suppression method of ground penetrating radar based on EEMD and permutation entropy. IEEE Geosci. Remote Sens. Lett. 2019, 16, 1625–1629. [Google Scholar] [CrossRef]
- Srinu, S.; Mishra, A.K. Cooperative sensing based on permutation entropy with adaptive thresholding technique for cognitive radio networks. IET Sci. Meas. Technol. 2016, 10, 934–942. [Google Scholar] [CrossRef]
- Du, W.; Guo, X.; Wang, Z.; Wang, J.; Yu, M.; Li, C.; Wang, G.; Wang, L.; Guo, H.; Zhou, J.; et al. A new fuzzy logic classifier based on multiscale permutation entropy and its application in bearing fault diagnosis. Entropy 2019, 22, 27. [Google Scholar] [CrossRef]
- Wang, X.; Lu, Z.; Wei, J.; Zhang, Y. Fault diagnosis for rail vehicle axle-box bearings based on energy feature reconstruction and composite multiscale permutation entropy. Entropy 2019, 21, 865. [Google Scholar] [CrossRef]
- Huo, Z.; Zhang, Y.; Shu, L.; Gallimore, M. A new bearing fault diagnosis method based on fine-to-coarse multiscale permutation entropy, laplacian score and SVM. IEEE Access 2019, 7, 17050–17066. [Google Scholar] [CrossRef]
- Humeau-Heurtier, A.; Wu, C.-W.; Wu, S.-D. Refined composite multiscale permutation entropy to overcome multiscale permutation entropy length dependence. IEEE Signal Process. Lett. 2015, 22, 2364–2367. [Google Scholar] [CrossRef]
- Zheng, J.; Liu, T.; Meng, R.; Liu, Q. Generalized composite multiscale permutation entropy and PCA based fault diagnosis of rolling bearings. J. Vib. Shock 2018, 37, 61–66. [Google Scholar]
- Wan, Z.; Yi, S.; Li, K.; Tao, R.; Gou, M.; Li, X.; Guo, S. Diagnosis of elevator faults with LS-SVM based on optimization by K-CV. J. Electr. Comput. Eng. 2015, 2015, 935038. [Google Scholar] [CrossRef]
- Liu, W.; Zhou, X.; Jiang, Z.; Ma, F. Improved empirical mode decomposition method based on optimal feature. J. Jilin Univ. (Eng. Tech. Ed.) 2017, 47, 1957–1963. [Google Scholar]
- Wang, Z.; Qiao, P.; Shi, B. Nonpenetrating damage identification using hybrid lamb wave modes from Hilbert-Huang spectrum in thin-walled structures. Shock Vib. 2017, 2017, 5164594. [Google Scholar] [CrossRef]
- Zheng, Y.; Sun, X.; Chen, J.; Yue, J. Extracting pulse signals in measurement while drilling using optimum denoising methods based on the ensemble empirical mode decomposition. Pet. Explor. Dev. 2012, 39, 750–753. [Google Scholar] [CrossRef]
- Li, G.; Zeng, L.; Zhang, L.; Wu, Q. State identification of Duffing oscillator based on extreme learning machine. IEEE Signal Process. Lett. 2018, 25, 25–29. [Google Scholar] [CrossRef]
- Song, W.; Deng, S.; Yang, J.; Cheng, Q. Tool wear detection based on Duffing-holmes oscillator. Math. Probl. Eng. 2008, 2008, 510406. [Google Scholar] [CrossRef]
- Chang, T. Chaotic motion in forced Duffing system subject to linear and nonlinear damping. Math. Probl. Eng. 2017, 2017, 3769870. [Google Scholar] [CrossRef]
- Li, Y.; Yang, B.; Shi, Y. Chaos-based weak sinusoidal signal detection approach under colored noise background. Acta Phys. Sin. Chin. Ed. 2003, 52, 526–530. [Google Scholar]
- Shang, Q.; Yin, C.; Li, S.; Yang, Y. Study on detection of weak sinusoidal signal by using Duffing oscillator. Proc. Chin. Soc. Electr. Eng. 2005, 25, 66–70. [Google Scholar]
- Suresh, A.; Shunmuganathan, K.L. Image texture classification using gray level co-occurrence matrix based statistical features. Eur. J. Sci. Res. 2012, 75, 591–597. [Google Scholar]
- Luo, J.; Song, D.; Xiu, C.; Geng, S.; Dong, T. Fingerprint classification combining curvelet transform and gray-level cooccurrence matrix. Math. Probl. Eng. 2014, 2014, 592928. [Google Scholar] [CrossRef]
- Liu, X.; Xu, K.; Zhou, P.; Liu, H. Feature extraction with discrete non-separable shearlet transform and its application to surface inspection of continuous casting slabs. Appl. Sci. 2019, 9, 4668. [Google Scholar] [CrossRef]
- Lo, C.; Chen, C.; Yeh, Y.; Chang, C.; Yeh, H. Quantitative analysis of melanosis coli colonic mucosa using textural patterns. Appl. Sci. 2020, 10, 404. [Google Scholar] [CrossRef]
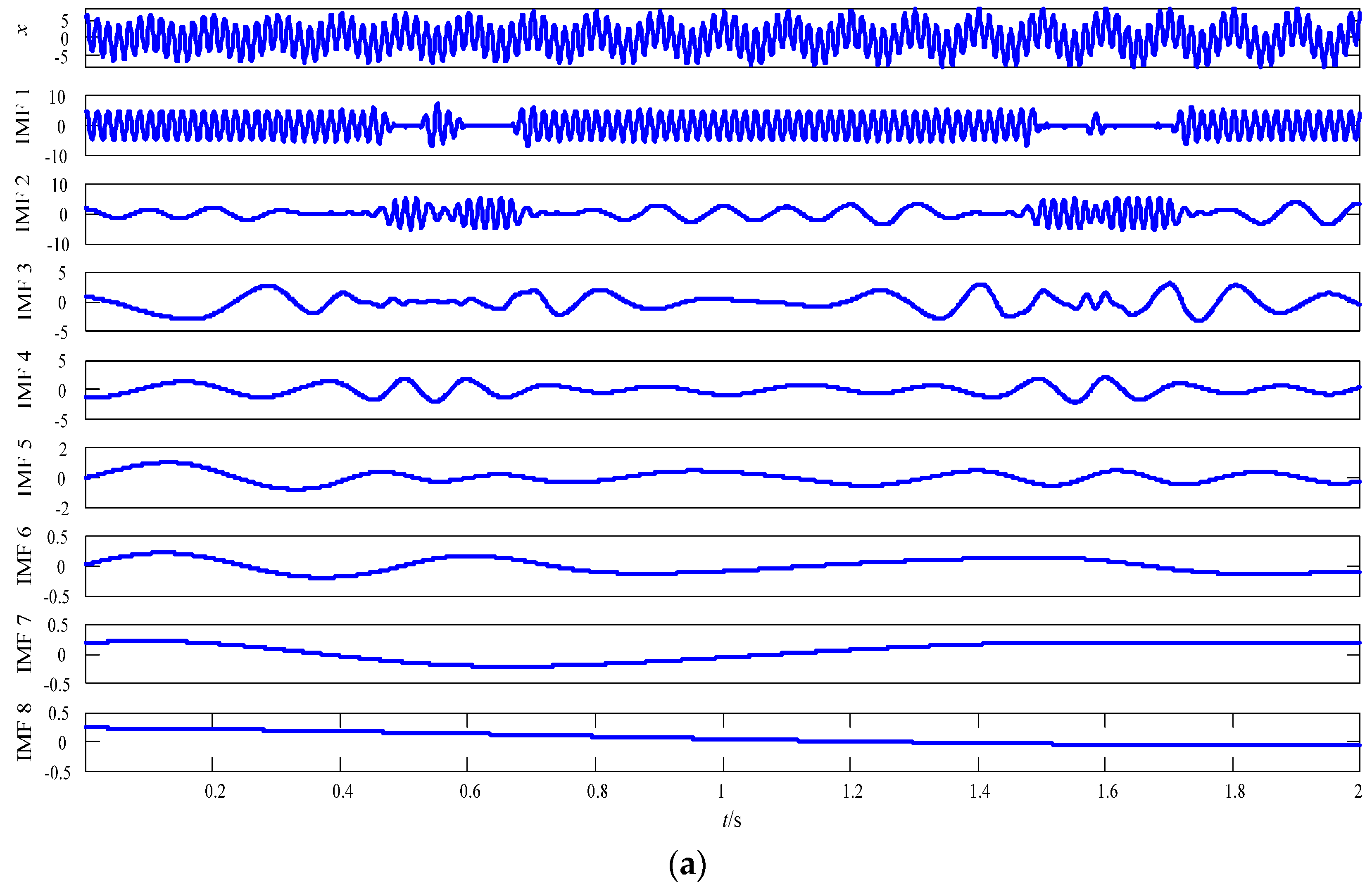
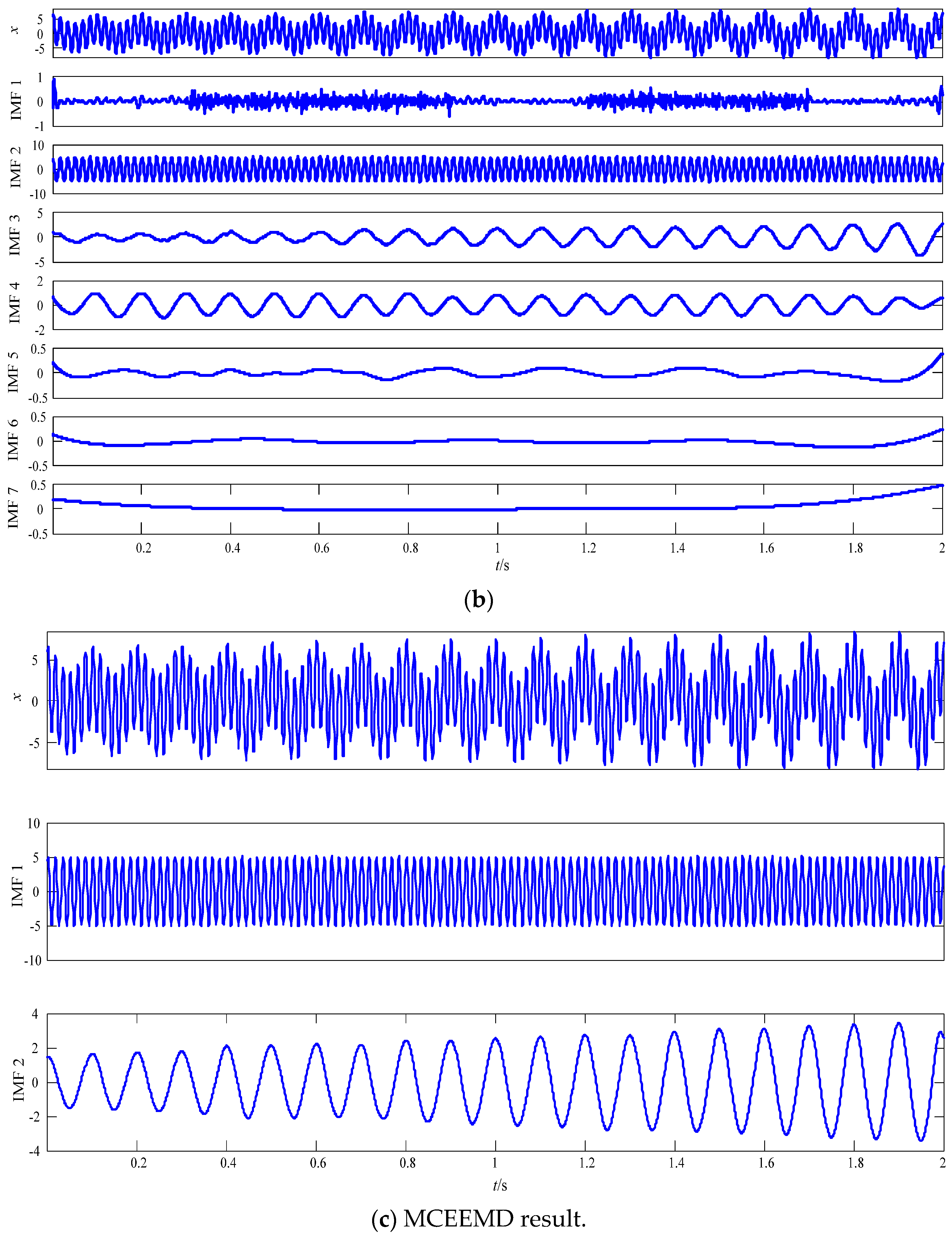
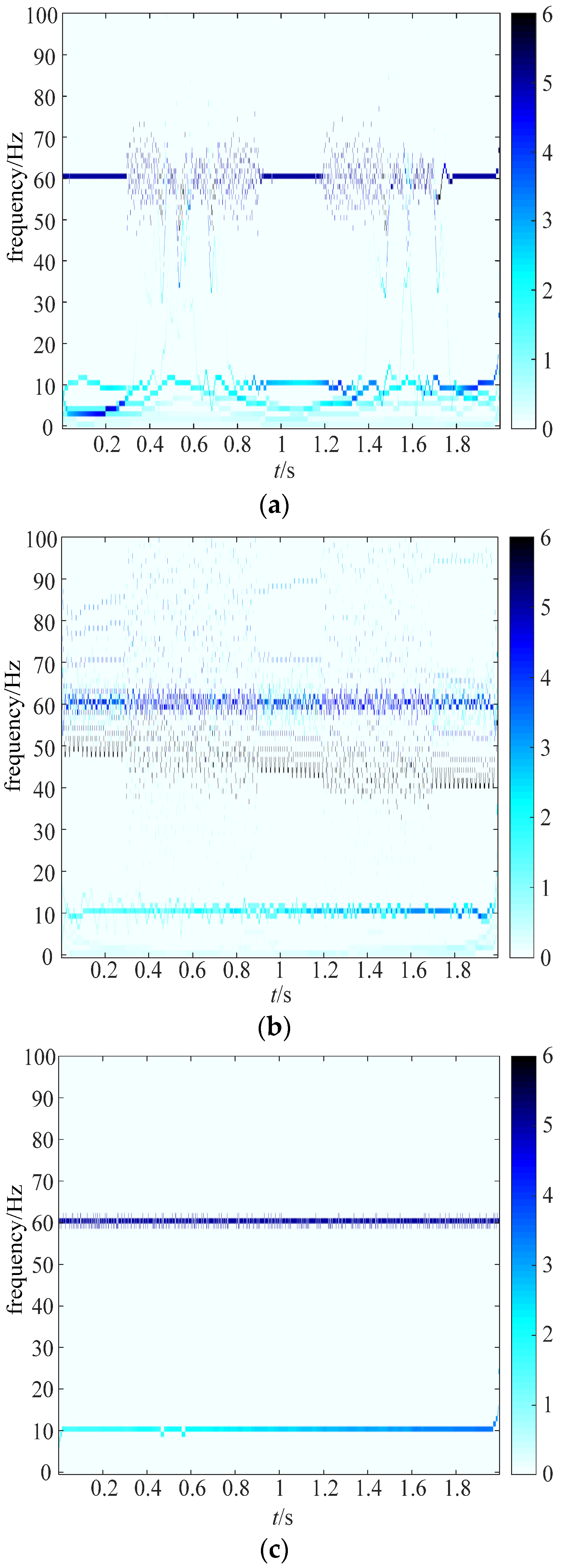

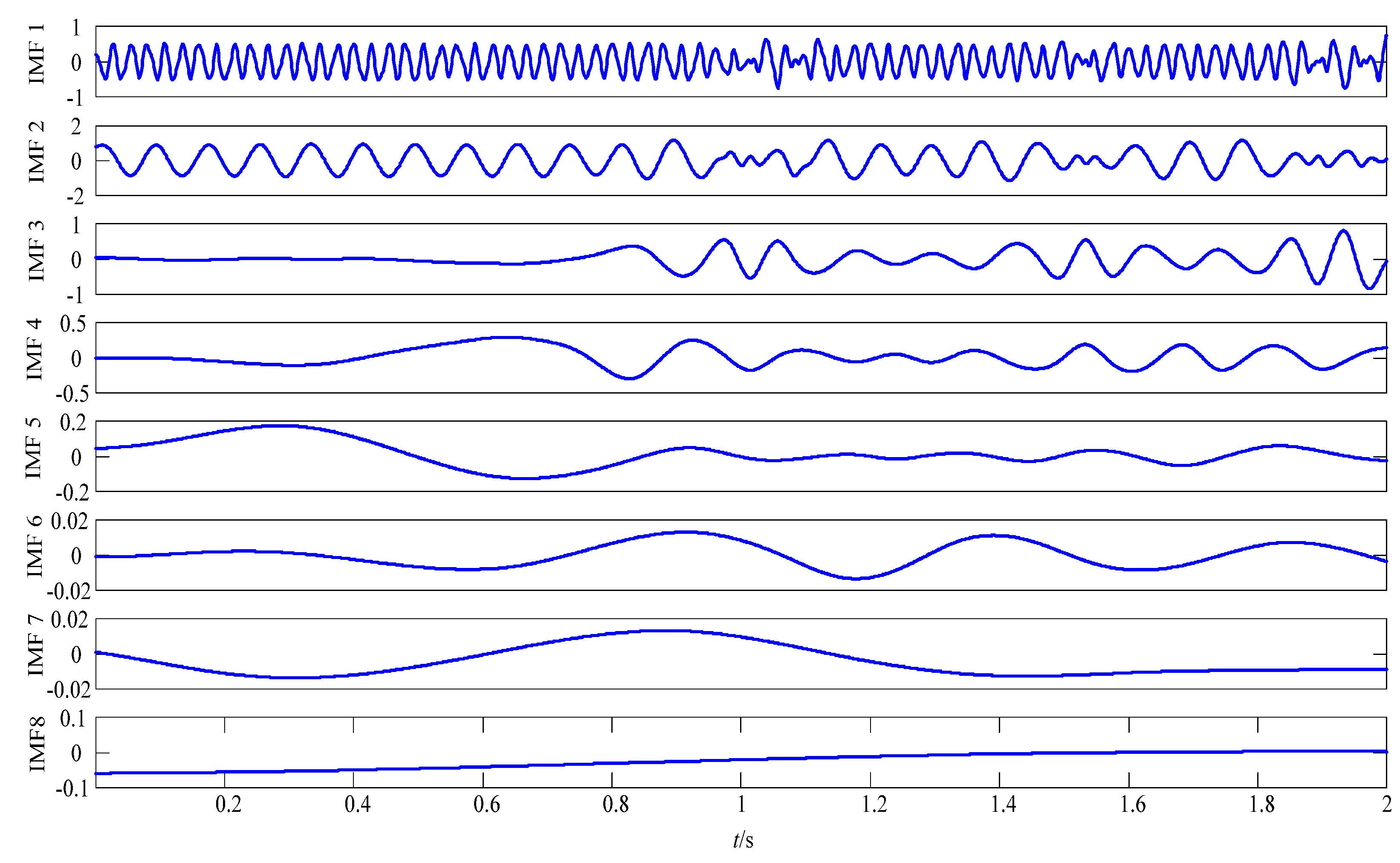

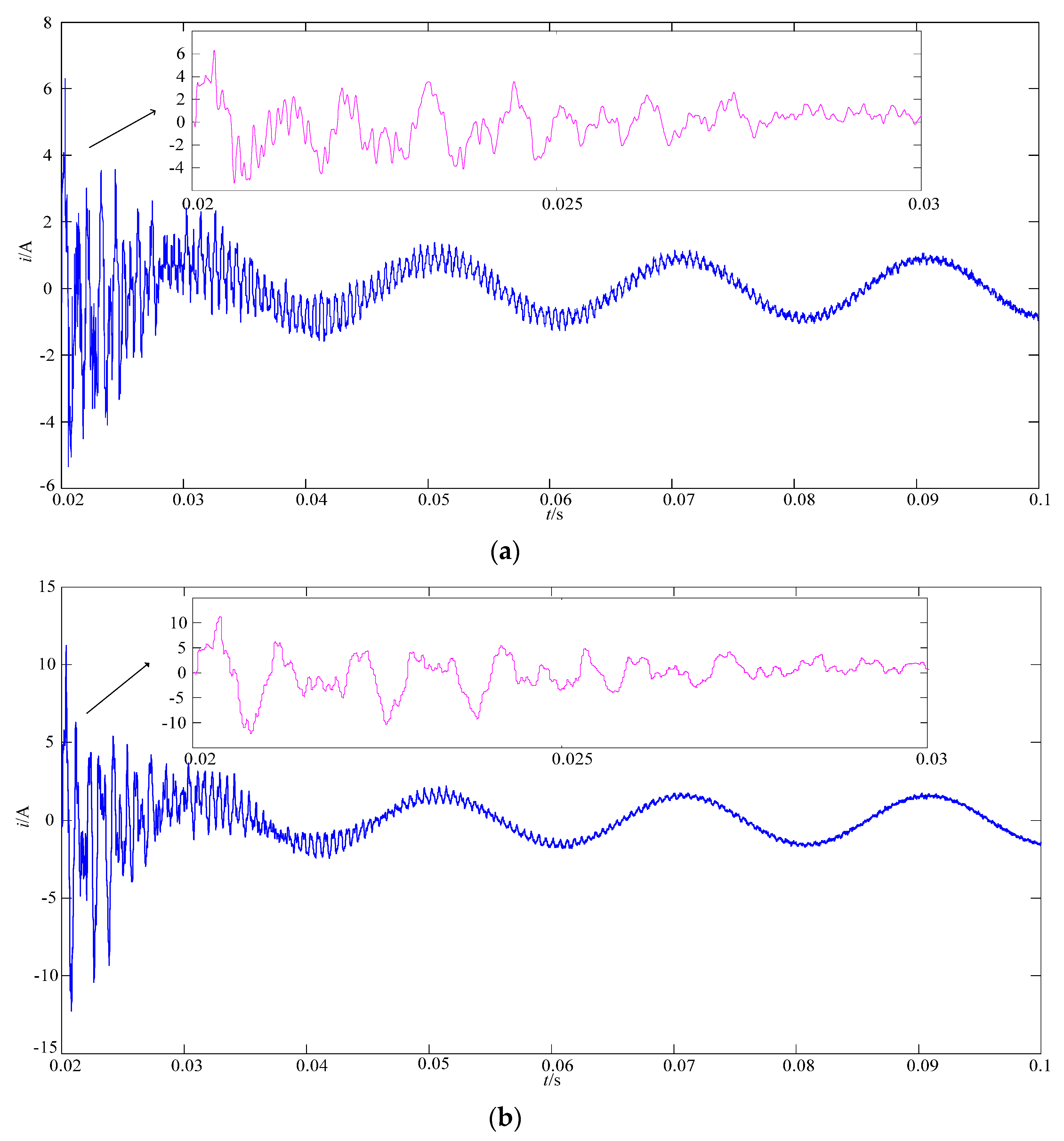
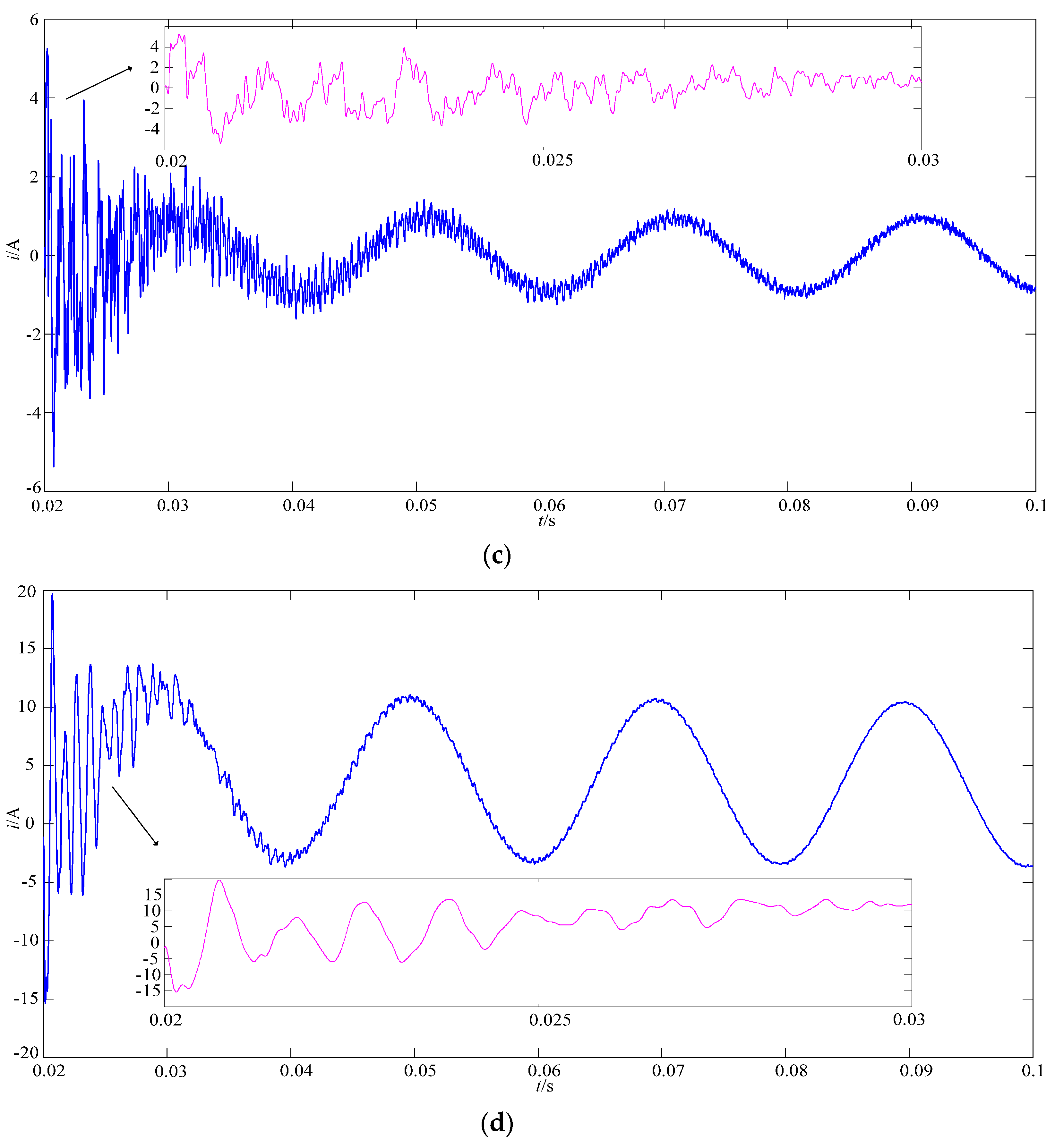
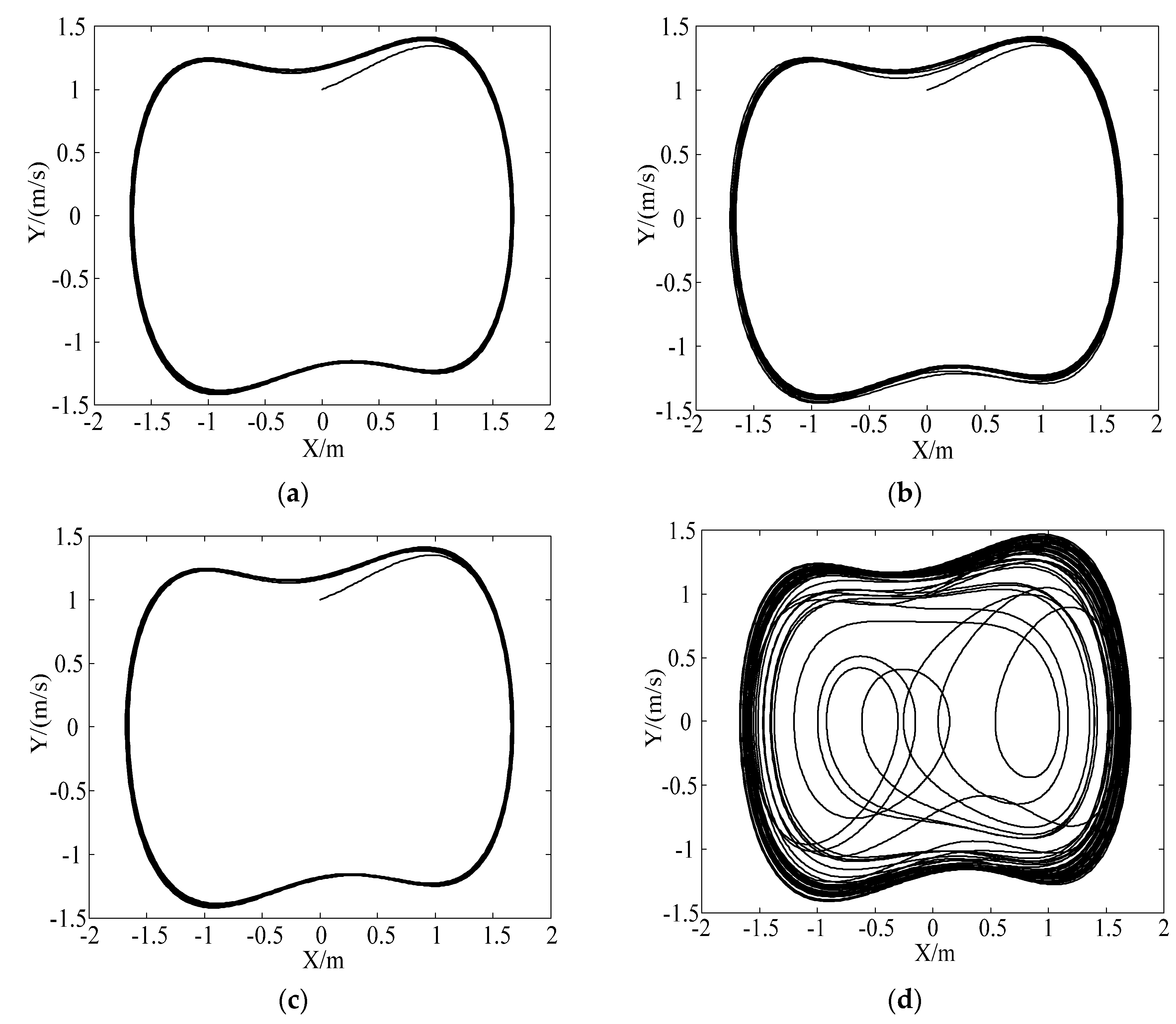
| x1 | x2 | x3 | |
|---|---|---|---|
| IMF1 | 0.9031 | 0.0009 | 0.0489 |
| IMF2 | 0.2889 | 0.4760 | 0.0214 |
| IMF3 | 0.0019 | 0.3790 | 0.0246 |
| IMF4 | −0.0020 | 0.3267 | −0.0277 |
| IMF5 | 0.0007 | 0.0061 | −0.0103 |
| IMF6 | 0.0010 | −0.0030 | 0.0105 |
| IMF7 | 0.0001 | −0.0004 | −0.0012 |
| IMF8 | 0.0032 | −0.0010 | −0.0088 |
| x1 | x2 | x3 | |
|---|---|---|---|
| IMF1 | 0.3952 | −0.0058 | 0.7078 |
| IMF2 | 0.9993 | −0.0035 | −0.0107 |
| IMF3 | 0.0369 | 0.9804 | −0.0156 |
| IMF4 | 0.0005 | 0.9475 | −0.0183 |
| IMF5 | −0.0011 | 0.2294 | −0.0149 |
| IMF6 | −0.0024 | 0.0257 | −0.0005 |
| IMF7 | −0.0028 | 0.0085 | −0.0006 |
| x1 | x2 | x3 | |
|---|---|---|---|
| IMF1 | 0.9995 | 0.0008 | 0.0235 |
| IMF2 | −0.0010 | 0.9992 | −0.0092 |
| Denoising Algorithms | Ort |
|---|---|
| EMD | 0.0891 |
| CEEMD | 0.0671 |
| MCEEMD |
| Filtering Algorithms | Amse | Asmse | Aminf |
|---|---|---|---|
| SR1 | 0.659710 | 0.016383 | 0.402380 |
| SR2 | 0.274279 | 0.016512 | 0.171172 |
| SR3 | 0.158327 | 0.016505 | 0.101598 |
| SR4 | 0.125100 | 0.016505 | 0.081662 |
| SR5 | 0.109698 | 0.016505 | 0.072421 |
| SR6 | 0.109262 | 0.016505 | 0.072159 |
| SR7 | 0.109205 | 0.016505 | 0.072125 |
| SR8 | 0.106914 | 0.016505 | 0.070750 |
| Line | Sequence | Resistance (Ω/km) | Inductance (mH/km) | Capacitance (μF/km) | Length (km) |
|---|---|---|---|---|---|
| L1 | positive-sequence | 0.1820 | 1.1180 | 0.1150 | 18 |
| zero-sequence | 0.3250 | 5.6810 | 0.0096 | ||
| L2 | positive-sequence | 0.1260 | 1.0180 | 0.1200 | 20 |
| zero-sequence | 0.2850 | 4.5600 | 0.0150 | ||
| L3 | positive-sequence | 0.1800 | 2.1580 | 0.1290 | 12 |
| zero-sequence | 0.2730 | 5.5610 | 0.0150 | ||
| L4 | positive-sequence | 0.1320 | 2.2250 | 0.2290 | 16 |
| zero-sequence | 0.2380 | 5.5610 | 0.0235 |
| Line | Energy | Entropy | Contrast | Correlation | Euclidean Distance | Chaotic Nature |
|---|---|---|---|---|---|---|
| L1 | 0.9215 | 0.2262 | 2.0705 | 0.1225 | 1.3151 | Periodical |
| L2 | 0.8932 | 0.2817 | 2.5023 | 0.0885 | 0.8831 | Periodical |
| L3 | 0.9225 | 0.2242 | 2.0689 | 0.1246 | 1.3168 | Periodical |
| L4 | 0.6222 | 0.8270 | 11.9338 | 0.0245 | 8.5726 | Chaotic |
| Fault Situation | Line | Energy | Entropy | Contrast | Correlation | Euclidean Distance | Chaotic Nature | Result |
|---|---|---|---|---|---|---|---|---|
| (L4, 30 Ω, 10 km) | L1 | 0.9172 | 0.2352 | 2.1417 | 0.1153 | 1.2436 | Periodical | L4 |
| L2 | 0.9017 | 0.2665 | 2.1456 | 0.0967 | 1.2393 | Periodical | ||
| L3 | 0.9155 | 0.2395 | 2.1211 | 0.1138 | 1.2641 | Periodical | ||
| L4 | 0.6216 | 0.8195 | 10.8519 | 0.0245 | 7.4935 | Chaotic | ||
| (L4, 500 Ω, 2 km) | L1 | 0.8962 | 0.2766 | 2.0462 | 0.0916 | 1.3388 | Periodical | L4 |
| L2 | 0.8539 | 0.3470 | 2.2218 | 0.0636 | 1.1680 | Periodical | ||
| L3 | 0.8943 | 0.2791 | 2.0082 | 0.0898 | 1.3769 | Periodical | ||
| L4 | 0.5818 | 0.9199 | 15.2676 | 0.0217 | 11.9056 | Chaotic | ||
| (L4, 1000 Ω, 1 km) | L1 | 0.9037 | 0.2616 | 2.1546 | 0.0989 | 1.2303 | Periodical | L4 |
| L2 | 0.8747 | 0.3119 | 2.0104 | 0.0748 | 1.3760 | Periodical | ||
| L3 | 0.9029 | 0.2642 | 2.1641 | 0.0980 | 1.2208 | Periodical | ||
| L4 | 0.5735 | 0.9289 | 15.0723 | 0.0213 | 11.7144 | Chaotic | ||
| (L3, 200 Ω, 6 km) | L1 | 0.9271 | 0.2157 | 2.2960 | 0.1321 | 1.0905 | Periodical | L3 |
| L2 | 0.8999 | 0.2891 | 5.1498 | 0.0876 | 1.7652 | Periodical | ||
| L3 | 0.6155 | 0.8406 | 11.9449 | 0.0240 | 8.5848 | Chaotic | ||
| L4 | 0.9149 | 0.2402 | 2.1099 | 0.1126 | 1.2552 | Periodical | ||
| (L2, 10 Ω, 3 km) | L1 | 0.9212 | 0.2277 | 2.1077 | 0.1221 | 1.2779 | Periodical | L2 |
| L2 | 0.5721 | 0.9310 | 15.0184 | 0.0213 | 11.6578 | Chaotic | ||
| L3 | 0.9225 | 0.2250 | 2.0669 | 0.1248 | 1.3188 | Periodical | ||
| L4 | 0.8874 | 0.2975 | 2.4383 | 0.0842 | 0.9476 | Periodical | ||
| (L2, 100 Ω, 5 km) | L1 | 0.9267 | 0.2162 | 2.2603 | 0.1307 | 1.1261 | Periodical | L2 |
| L2 | 0.6157 | 0.8444 | 12.4470 | 0.0240 | 9.0858 | Chaotic | ||
| L3 | 0.9265 | 0.2167 | 2.2689 | 0.1310 | 1.1166 | Periodical | ||
| L4 | 0.8775 | 0.3338 | 4.7863 | 0.0753 | 1.4038 | Periodical | ||
| (L2, 600 Ω, 1 km) | L1 | 0.9270 | 0.2160 | 2.3471 | 0.1315 | 1.0394 | Periodical | L2 |
| L2 | 0.7612 | 0.5635 | 7.0596 | 0.0389 | 3.6905 | Chaotic | ||
| L3 | 0.9272 | 0.2166 | 2.3373 | 0.1321 | 1.4092 | Periodical | ||
| L4 | 0.9201 | 0.2298 | 2.2778 | 0.1199 | 1.1077 | Periodical | ||
| (L1, 100 Ω, 3 km) | L1 | 0.6806 | 0.7136 | 9.3671 | 0.0291 | 6.0039 | Chaotic | L1 |
| L2 | 0.9165 | 0.2371 | 2.0641 | 0.1152 | 1.3211 | Periodical | ||
| L3 | 0.9251 | 0.2204 | 2.2327 | 0.1293 | 1.1534 | Periodical | ||
| L4 | 0.9135 | 0.2424 | 2.0484 | 0.1107 | 1.3367 | Periodical | ||
| (L1, 300 Ω, 12 km) | L1 | 0.6880 | 0.7058 | 9.4638 | 0.0300 | 6.0994 | Chaotic | L1 |
| L2 | 0.9306 | 0.2093 | 2.4337 | 0.1383 | 0.9536 | Periodical | ||
| L3 | 0.9278 | 0.2137 | 2.3455 | 0.1313 | 1.0412 | Periodical | ||
| L4 | 0.9172 | 0.2363 | 2.1388 | 0.1161 | 1.2465 | Periodical | ||
| (Bus bar, 200 Ω) | L1 | 0.9268 | 0.2157 | 2.2952 | 0.1308 | 1.0912 | Periodical | Bus bar |
| L2 | 0.9316 | 0.2066 | 2.3919 | 0.1397 | 0.9955 | Periodical | ||
| L3 | 0.9268 | 0.2166 | 2.3039 | 0.1309 | 1.0825 | Periodical | ||
| L4 | 0.9160 | 0.2375 | 2.0775 | 0.1141 | 1.3077 | Periodical | ||
| (Bus bar, 1000 Ω) | L1 | 0.9285 | 0.2133 | 2.3596 | 0.1339 | 1.0272 | Periodical | Bus bar |
| L2 | 0.9246 | 0.2208 | 2.3515 | 0.1274 | 1.0347 | Periodical | ||
| L3 | 0.9280 | 0.2143 | 2.3948 | 0.1330 | 0.9920 | Periodical | ||
| L4 | 0.9227 | 0.2247 | 2.2817 | 0.1234 | 1.1041 | Periodical |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hou, S.; Guo, W. Optimal Denoising and Feature Extraction Methods Using Modified CEEMD Combined with Duffing System and Their Applications in Fault Line Selection of Non-Solid-Earthed Network. Symmetry 2020, 12, 536. https://doi.org/10.3390/sym12040536
Hou S, Guo W. Optimal Denoising and Feature Extraction Methods Using Modified CEEMD Combined with Duffing System and Their Applications in Fault Line Selection of Non-Solid-Earthed Network. Symmetry. 2020; 12(4):536. https://doi.org/10.3390/sym12040536
Chicago/Turabian StyleHou, Sizu, and Wei Guo. 2020. "Optimal Denoising and Feature Extraction Methods Using Modified CEEMD Combined with Duffing System and Their Applications in Fault Line Selection of Non-Solid-Earthed Network" Symmetry 12, no. 4: 536. https://doi.org/10.3390/sym12040536
APA StyleHou, S., & Guo, W. (2020). Optimal Denoising and Feature Extraction Methods Using Modified CEEMD Combined with Duffing System and Their Applications in Fault Line Selection of Non-Solid-Earthed Network. Symmetry, 12(4), 536. https://doi.org/10.3390/sym12040536





