A Self-Adaptive Extra-Gradient Methods for a Family of Pseudomonotone Equilibrium Programming with Application in Different Classes of Variational Inequality Problems
Abstract
1. Introduction
2. Preliminaries
- (i)
- strongly monotone if
- (ii)
- monotone if
- (iii)
- strongly pseudomonotone if
- (iv)
- pseudomonotone if
- (v)
- satisfying the Lipschitz-type condition on C if there are two real numbers such thatholds.
- (i)
- For each
- (ii)
- if and only if
- with
- For each exists;
- All sequentially weak cluster point of lies in C;
- for all and f is pseudomonotone on feasible set
- f satisfy the Lipschitz-type condition on with constants and
- for all and satisfy
- need to be convex and subdifferentiable over for all fixed
3. An Algorithm and Its Convergence Analysis
| Algorithm 1 (The Modified Popov’s subgradient extragradient method for pseudomonotone ) |
|
- Initialization: Given and
- Iterative steps: For given and construct a half-space
- where
- Step 1: Compute
- Step 2: Update the stepsize as follows
- and compute
- Then and weakly converge to the solution
4. Solving Variational Inequality Problems with New Self-Adaptive Methods
- monotone on C if ;
- L-Lipschitz continuous on C if ;
- pseudomonotone on C if
- .
- G is monotone on C and is nonempty;
- .
- G is pseudomonotone on C and is nonempty;
- .
- G is L-Lipschitz continuous on C through positive parameter
- .
- for every and satisfying
- Initialization: Choose for a nondecreasing sequence such that and
- Iterative steps: For given and construct a half space
- where
- Step 1: Compute
- Step 2: The stepsize is updated as follows
- and compute
- Then the sequence and weakly converge to of
- Initialization: Choose and
- Iterative steps: For given and construct a half space
- Step 1: Compute
- Step 2: The stepsize is updated as follows
- and compute
- Thus and converge weakly to the solution of
- Initialization: Choose for a nondecreasing sequence such that and
- Iterative steps: For given and construct a half space
- where
- Step 1:
- Step 2: The stepsize is updated as follows
- and compute
- Then the sequences and converges weakly to of
- Initialization: Choose and
- Iterative steps: For given and construct a half space
- Step 1:
- Step 2: The stepsize is updated as follows
- and compute
- Then and converge weakly to of
5. Computational Experiment
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Blum, E. From optimization and variational inequalities to equilibrium problems. Math. Stud. 1994, 63, 123–145. [Google Scholar]
- Facchinei, F.; Pang, J.S. Finite-Dimensional Variational Inequalities and Complementarity Problems; Springer Science & Business Media: New York, NY, USA, 2007. [Google Scholar]
- Konnov, I. Equilibrium Models and Variational Inequalities; Elsevier: Amsterdam, The Netherlands, 2007; Volume 210. [Google Scholar]
- Yang, Q.; Bian, X.; Stark, R.; Fresemann, C.; Song, F. Configuration Equilibrium Model of Product Variant Design Driven by Customer Requirements. Symmetry 2019, 11, 508. [Google Scholar] [CrossRef]
- Muu, L.D.; Oettli, W. Convergence of an adaptive penalty scheme for finding constrained equilibria. Nonlinear Anal. Theory Methods Appl. 1992, 18, 1159–1166. [Google Scholar] [CrossRef]
- Fan, K. A Minimax Inequality and Applications, Inequalities III; Shisha, O., Ed.; Academic Press: New York, NY, USA, 1972. [Google Scholar]
- Yuan, G.X.Z. KKM Theory and Applications in Nonlinear Analysis; CRC Press: Boca Raton, FL, USA, 1999; Volume 218. [Google Scholar]
- Brézis, H.; Nirenberg, L.; Stampacchia, G. A remark on Ky Fan’s minimax principle. Boll. Dell Unione Mat. Ital. 2008, 1, 257–264. [Google Scholar]
- Rehman, H.U.; Kumam, P.; Sompong, D. Existence of tripled fixed points and solution of functional integral equations through a measure of noncompactness. Carpathian J. Math. 2019, 35, 193–208. [Google Scholar]
- Rehman, H.U.; Gopal, G.; Kumam, P. Generalizations of Darbo’s fixed point theorem for new condensing operators with application to a functional integral equation. Demonstr. Math. 2019, 52, 166–182. [Google Scholar] [CrossRef]
- Combettes, P.L.; Hirstoaga, S.A. Equilibrium programming in Hilbert spaces. J. Nonlinear Convex Anal. 2005, 6, 117–136. [Google Scholar]
- Flåm, S.D.; Antipin, A.S. Equilibrium programming using proximal-like algorithms. Math. Program. 1996, 78, 29–41. [Google Scholar] [CrossRef]
- Van Hieu, D.; Muu, L.D.; Anh, P.K. Parallel hybrid extragradient methods for pseudomonotone equilibrium problems and nonexpansive mappings. Numer. Algorithms 2016, 73, 197–217. [Google Scholar] [CrossRef]
- Van Hieu, D.; Anh, P.K.; Muu, L.D. Modified hybrid projection methods for finding common solutions to variational inequality problems. Comput. Optim. Appl. 2017, 66, 75–96. [Google Scholar] [CrossRef]
- Van Hieu, D. Halpern subgradient extragradient method extended to equilibrium problems. Rev. Real Acad. De Cienc. Exactas Fís. Nat. Ser. A Mat. 2017, 111, 823–840. [Google Scholar] [CrossRef]
- Hieua, D.V. Parallel extragradient-proximal methods for split equilibrium problems. Math. Model. Anal. 2016, 21, 478–501. [Google Scholar] [CrossRef]
- Konnov, I. Application of the proximal point method to nonmonotone equilibrium problems. J. Optim. Theory Appl. 2003, 119, 317–333. [Google Scholar] [CrossRef]
- Duc, P.M.; Muu, L.D.; Quy, N.V. Solution-existence and algorithms with their convergence rate for strongly pseudomonotone equilibrium problems. Pacific J. Optim 2016, 12, 833–845. [Google Scholar]
- Quoc, T.D.; Anh, P.N.; Muu, L.D. Dual extragradient algorithms extended to equilibrium problems. J. Glob. Optim. 2012, 52, 139–159. [Google Scholar] [CrossRef]
- Quoc Tran, D.; Le Dung, M.; Nguyen, V.H. Extragradient algorithms extended to equilibrium problems. Optimization 2008, 57, 749–776. [Google Scholar] [CrossRef]
- Santos, P.; Scheimberg, S. An inexact subgradient algorithm for equilibrium problems. Comput. Appl. Math. 2011, 30, 91–107. [Google Scholar]
- Tada, A.; Takahashi, W. Weak and strong convergence theorems for a nonexpansive mapping and an equilibrium problem. J. Optim. Theory Appl. 2007, 133, 359–370. [Google Scholar] [CrossRef]
- Takahashi, S.; Takahashi, W. Viscosity approximation methods for equilibrium problems and fixed point problems in Hilbert spaces. J. Math. Anal. Appl. 2007, 331, 506–515. [Google Scholar] [CrossRef]
- Ur Rehman, H.; Kumam, P.; Cho, Y.J.; Yordsorn, P. Weak convergence of explicit extragradient algorithms for solving equilibirum problems. J. Inequal. Appl. 2019, 2019, 1–25. [Google Scholar] [CrossRef]
- Rehman, H.U.; Kumam, P.; Kumam, W.; Shutaywi, M.; Jirakitpuwapat, W. The Inertial Sub-Gradient Extra-Gradient Method for a Class of Pseudo-Monotone Equilibrium Problems. Symmetry 2020, 12, 463. [Google Scholar] [CrossRef]
- Ur Rehman, H.; Kumam, P.; Abubakar, A.B.; Cho, Y.J. The extragradient algorithm with inertial effects extended to equilibrium problems. Comput. Appl. Math. 2020, 39. [Google Scholar] [CrossRef]
- Argyros, I.K.; d Hilout, S. Computational Methods in Nonlinear Analysis: Efficient Algorithms, Fixed Point Theory and Applications; World Scientific: Singapore, 2013. [Google Scholar]
- Ur Rehman, H.; Kumam, P.; Cho, Y.J.; Suleiman, Y.I.; Kumam, W. Modified Popov’s explicit iterative algorithms for solving pseudomonotone equilibrium problems. Optim. Methods Softw. 2020, 1–32. [Google Scholar] [CrossRef]
- Argyros, I.K.; Cho, Y.J.; Hilout, S. Numerical Methods for Equations and Its Applications; CRC Press: Boca Raton, FL, USA, 2012. [Google Scholar]
- Korpelevich, G. The extragradient method for finding saddle points and other problems. Matecon 1976, 12, 747–756. [Google Scholar]
- Antipin, A. Convex programming method using a symmetric modification of the Lagrangian functional. Ekon. Mat. Metod. 1976, 12, 1164–1173. [Google Scholar]
- Censor, Y.; Gibali, A.; Reich, S. The subgradient extragradient method for solving variational inequalities in Hilbert space. J. Optim. Theory Appl. 2011, 148, 318–335. [Google Scholar] [CrossRef]
- Lyashko, S.I.; Semenov, V.V. A new two-step proximal algorithm of solving the problem of equilibrium programming. In Optimization and Its Applications in Control and Data Sciences; Springer: Cham, Switzerland, 2016; pp. 315–325. [Google Scholar]
- Polyak, B.T. Some methods of speeding up the convergence of iteration methods. USSR Comput. Math. Math. Phys. 1964, 4, 1–17. [Google Scholar] [CrossRef]
- Beck, A.; Teboulle, M. A fast iterative shrinkage-thresholding algorithm for linear inverse problems. SIAM J. Imaging Sci. 2009, 2, 183–202. [Google Scholar] [CrossRef]
- Moudafi, A. Second-order differential proximal methods for equilibrium problems. J. Inequal. Pure Appl. Math. 2003, 4, 1–7. [Google Scholar]
- Dong, Q.L.; Lu, Y.Y.; Yang, J. The extragradient algorithm with inertial effects for solving the variational inequality. Optimization 2016, 65, 2217–2226. [Google Scholar] [CrossRef]
- Thong, D.V.; Van Hieu, D. Modified subgradient extragradient method for variational inequality problems. Numer. Algorithms 2018, 79, 597–610. [Google Scholar] [CrossRef]
- Dong, Q.; Cho, Y.; Zhong, L.; Rassias, T.M. Inertial projection and contraction algorithms for variational inequalities. J. Glob. Optim. 2018, 70, 687–704. [Google Scholar] [CrossRef]
- Yang, J. Self-adaptive inertial subgradient extragradient algorithm for solving pseudomonotone variational inequalities. Appl. Anal. 2019. [Google Scholar] [CrossRef]
- Thong, D.V.; Van Hieu, D.; Rassias, T.M. Self adaptive inertial subgradient extragradient algorithms for solving pseudomonotone variational inequality problems. Optim. Lett. 2020, 14, 115–144. [Google Scholar] [CrossRef]
- Liu, Y.; Kong, H. The new extragradient method extended to equilibrium problems. Rev. Real Acad. De Cienc. Exactas Fís. Nat. Ser. A Mat. 2019, 113, 2113–2126. [Google Scholar] [CrossRef]
- Bianchi, M.; Schaible, S. Generalized monotone bifunctions and equilibrium problems. J. Optim. Theory Appl. 1996, 90, 31–43. [Google Scholar] [CrossRef]
- Goebel, K.; Reich, S. Uniform convexity. In Hyperbolic Geometry, and Nonexpansive; Marcel Dekker, Inc.: New York, NY, USA, 1984. [Google Scholar]
- Kreyszig, E. Introductory Functional Analysis with Applications, 1st ed.; Wiley: New York, NY, USA, 1978. [Google Scholar]
- Tiel, J.V. Convex Analysis; John Wiley: New York, NY, USA, 1984. [Google Scholar]
- Bauschke, H.H.; Combettes, P.L. Convex Analysis and Monotone Operator Theory in Hilbert Spaces; Springer: New York, NY, USA, 2011; Volume 408. [Google Scholar]
- Alvarez, F.; Attouch, H. An inertial proximal method for maximal monotone operators via discretization of a nonlinear oscillator with damping. Set-Valued Anal. 2001, 9, 3–11. [Google Scholar] [CrossRef]
- Opial, Z. Weak convergence of the sequence of successive approximations for nonexpansive mappings. Bull. Am. Math. Soc. 1967, 73, 591–597. [Google Scholar] [CrossRef]
- Dadashi, V.; Iyiola, O.S.; Shehu, Y. The subgradient extragradient method for pseudomonotone equilibrium problems. Optimization 2019. [Google Scholar] [CrossRef]

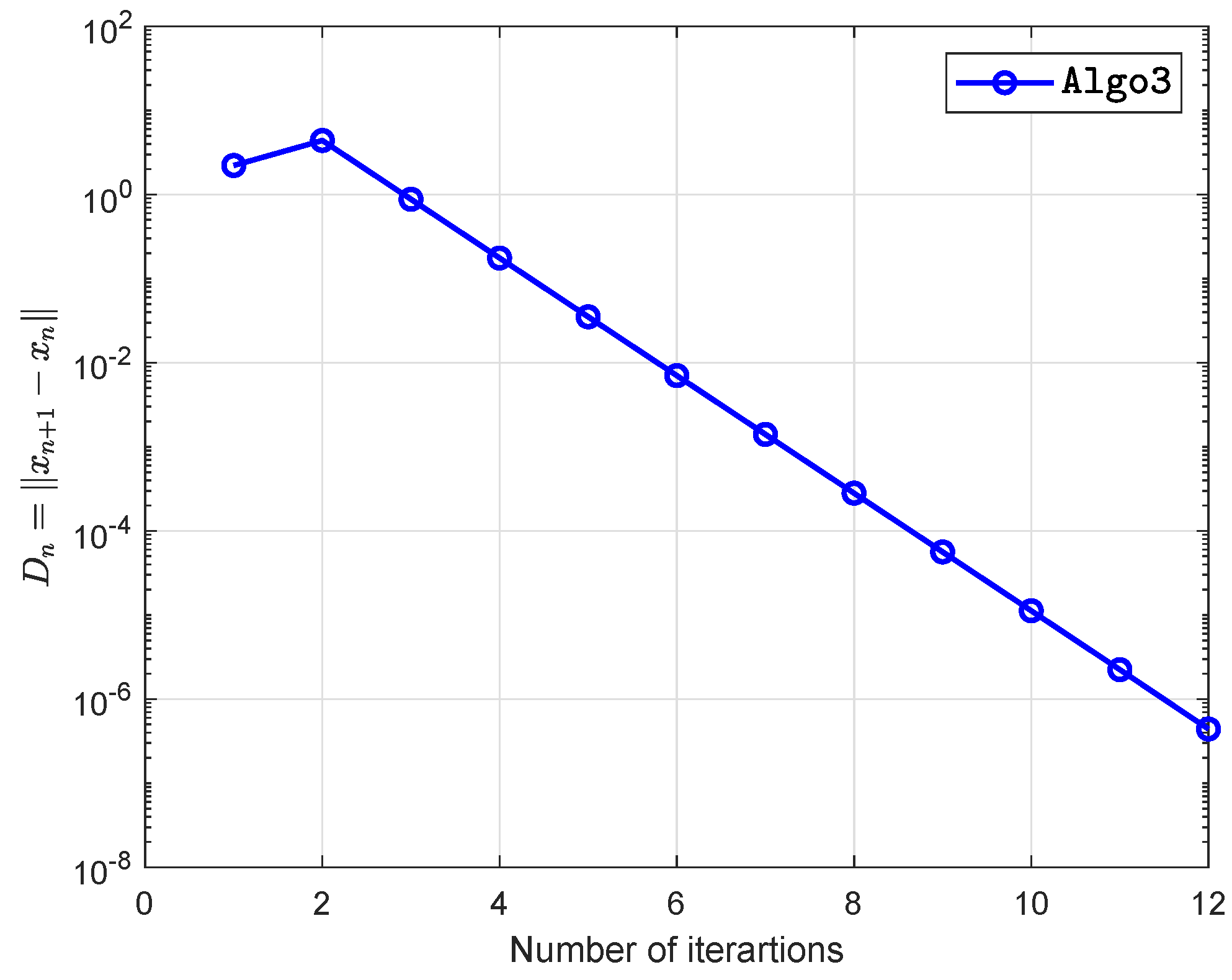
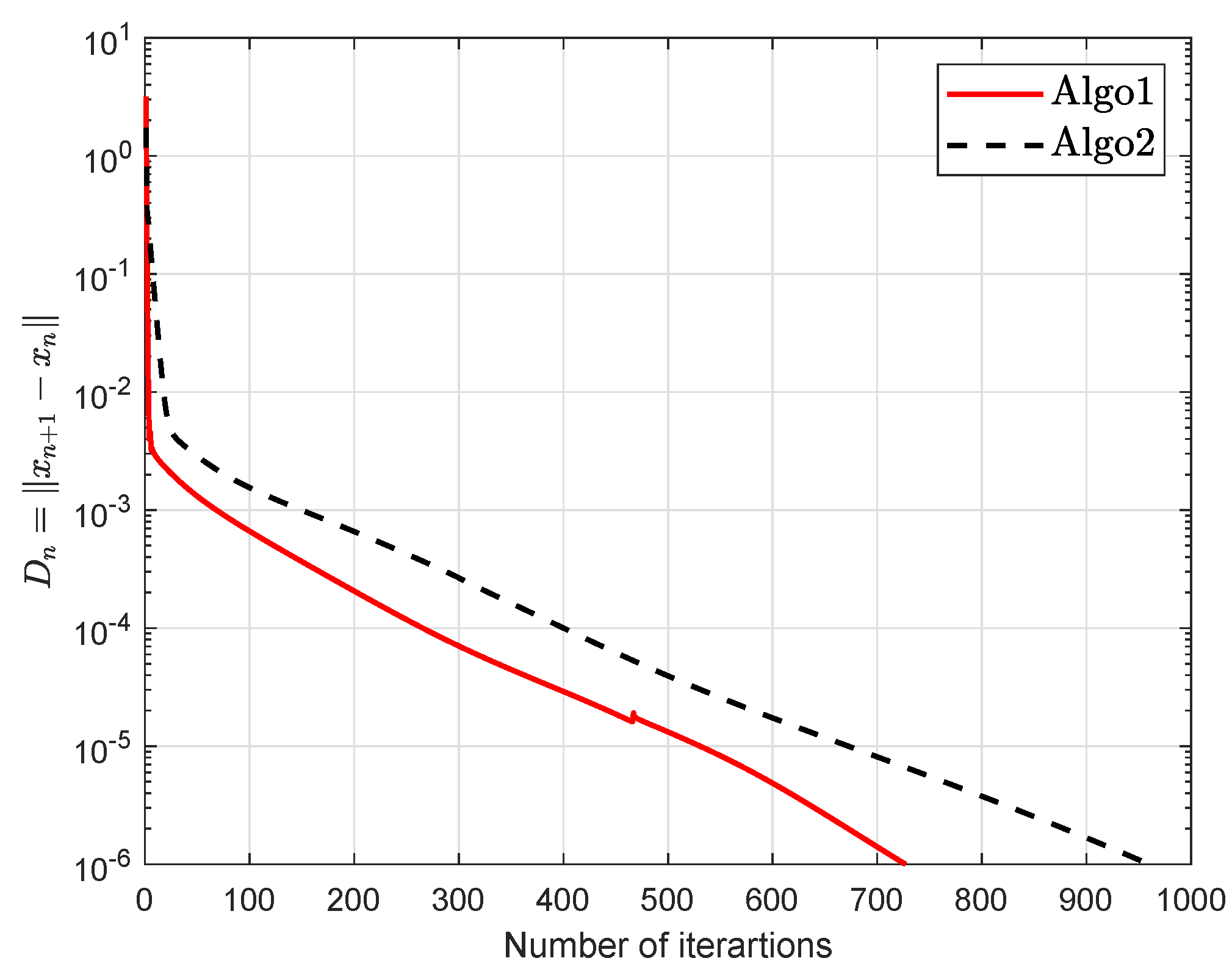
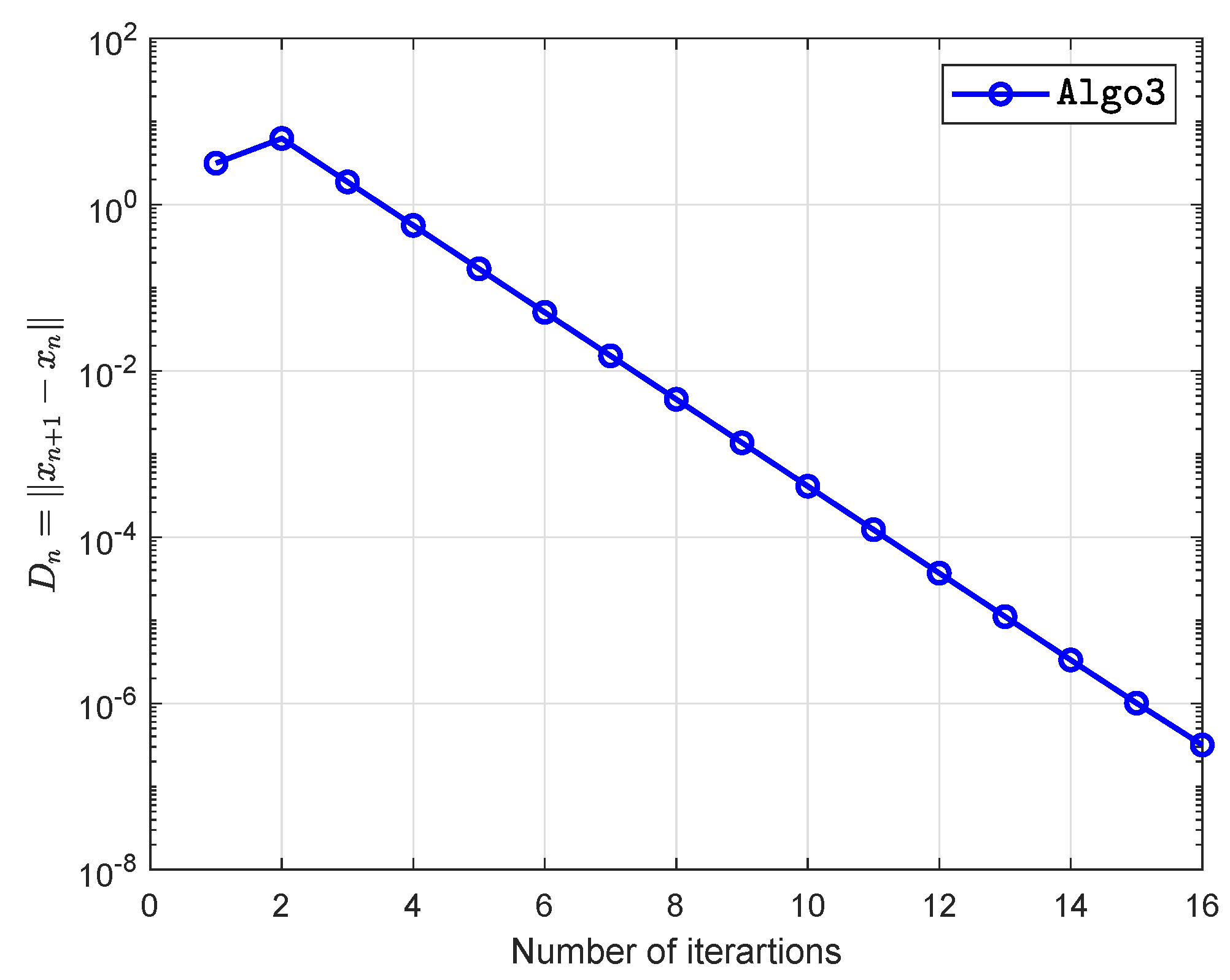
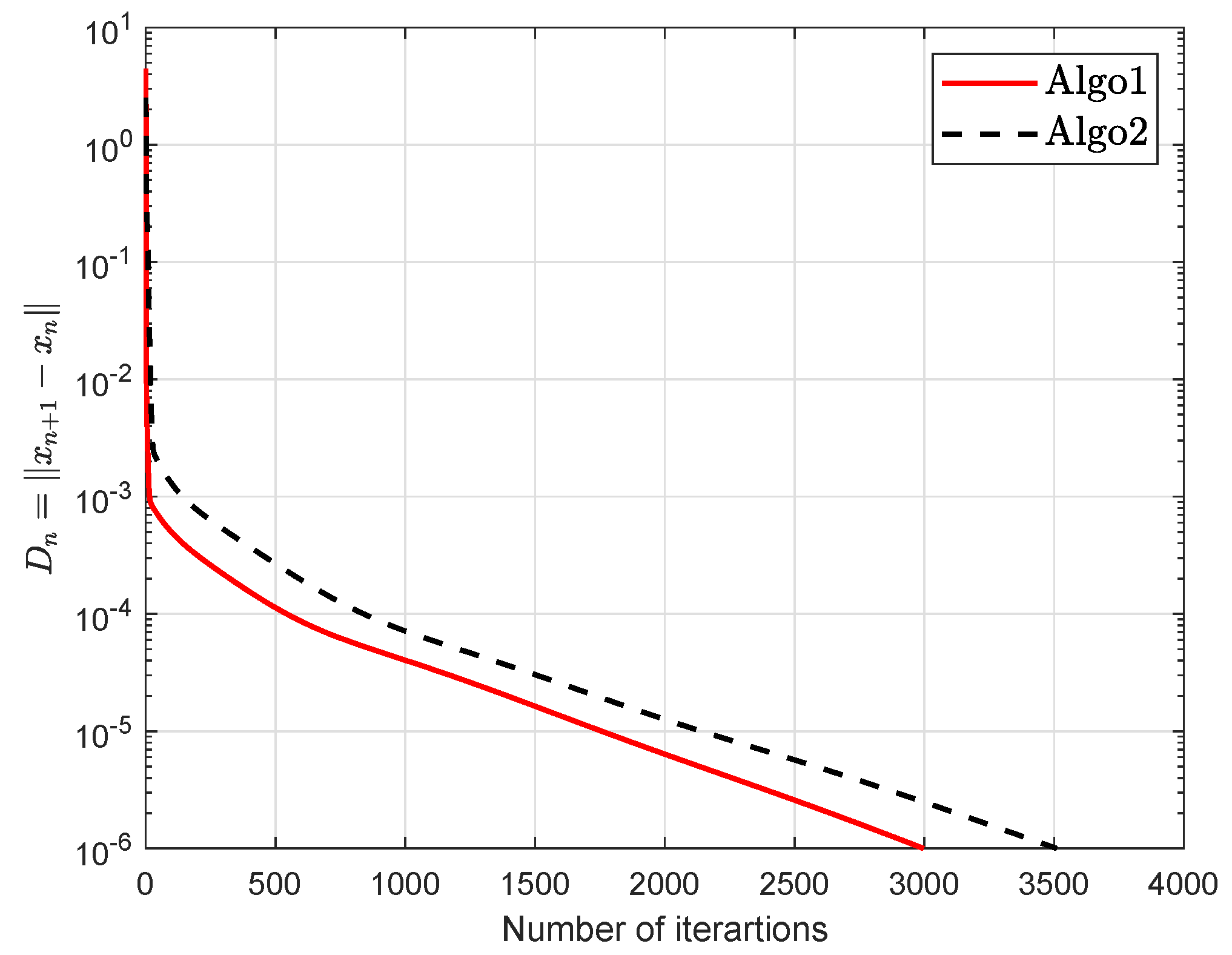
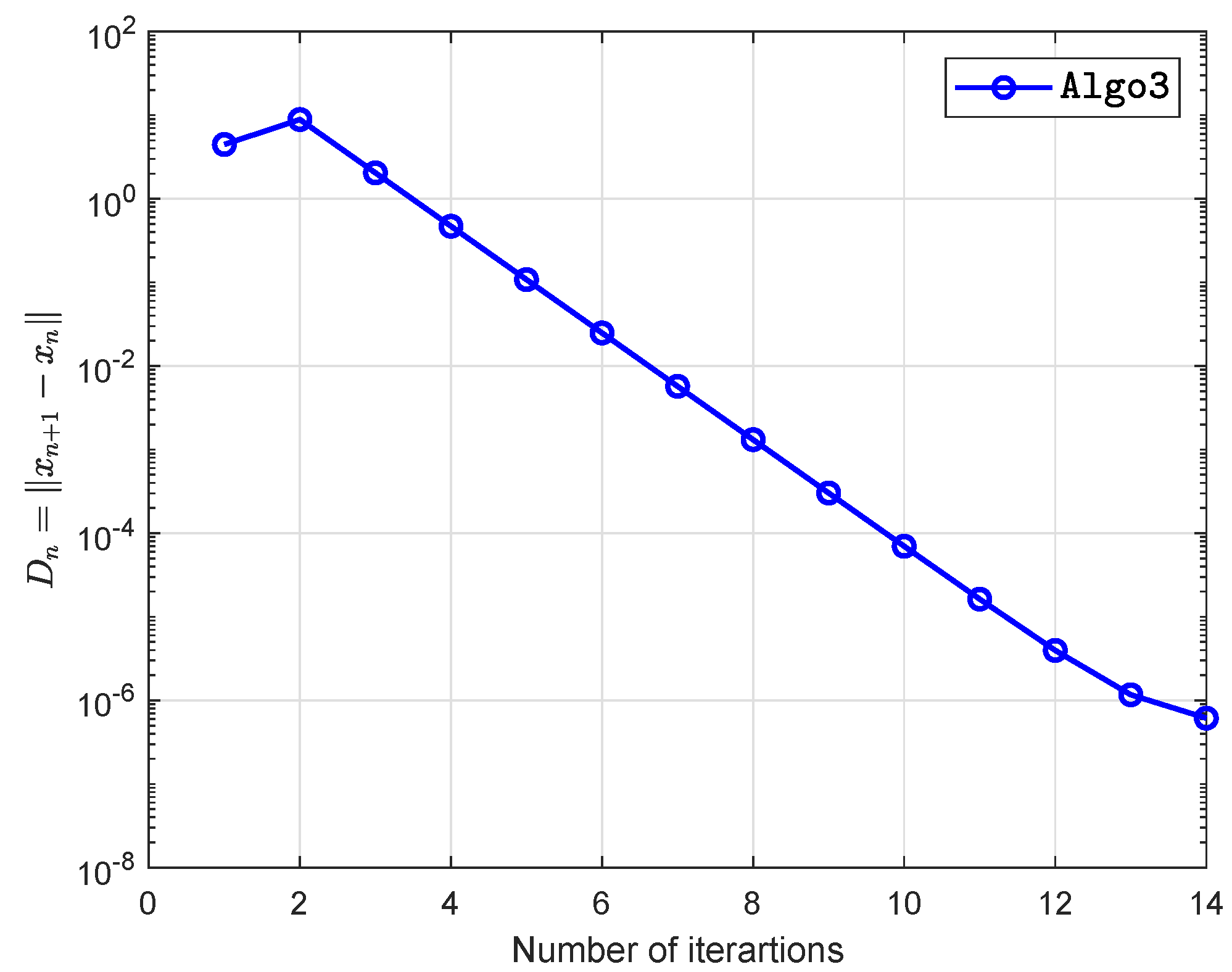

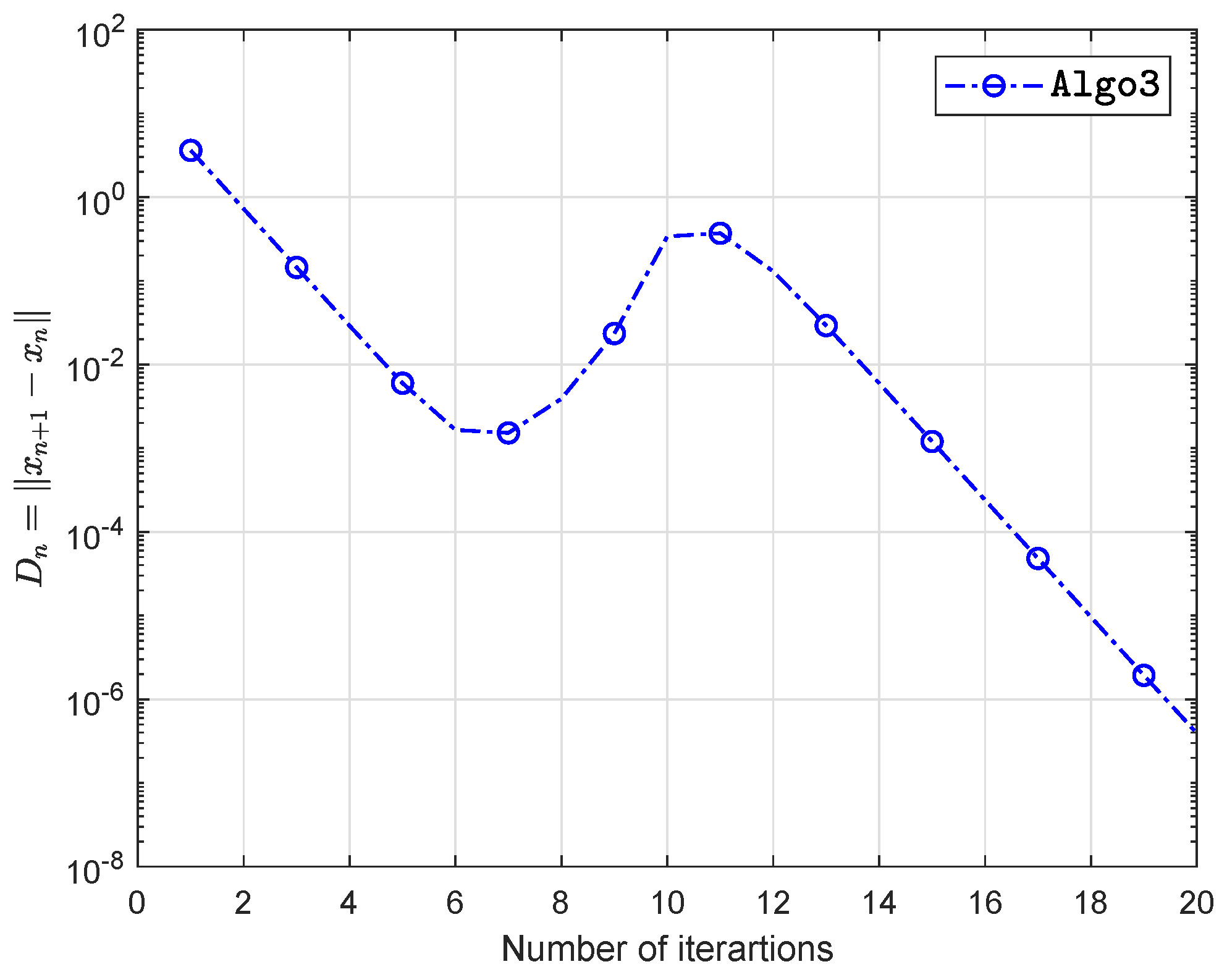
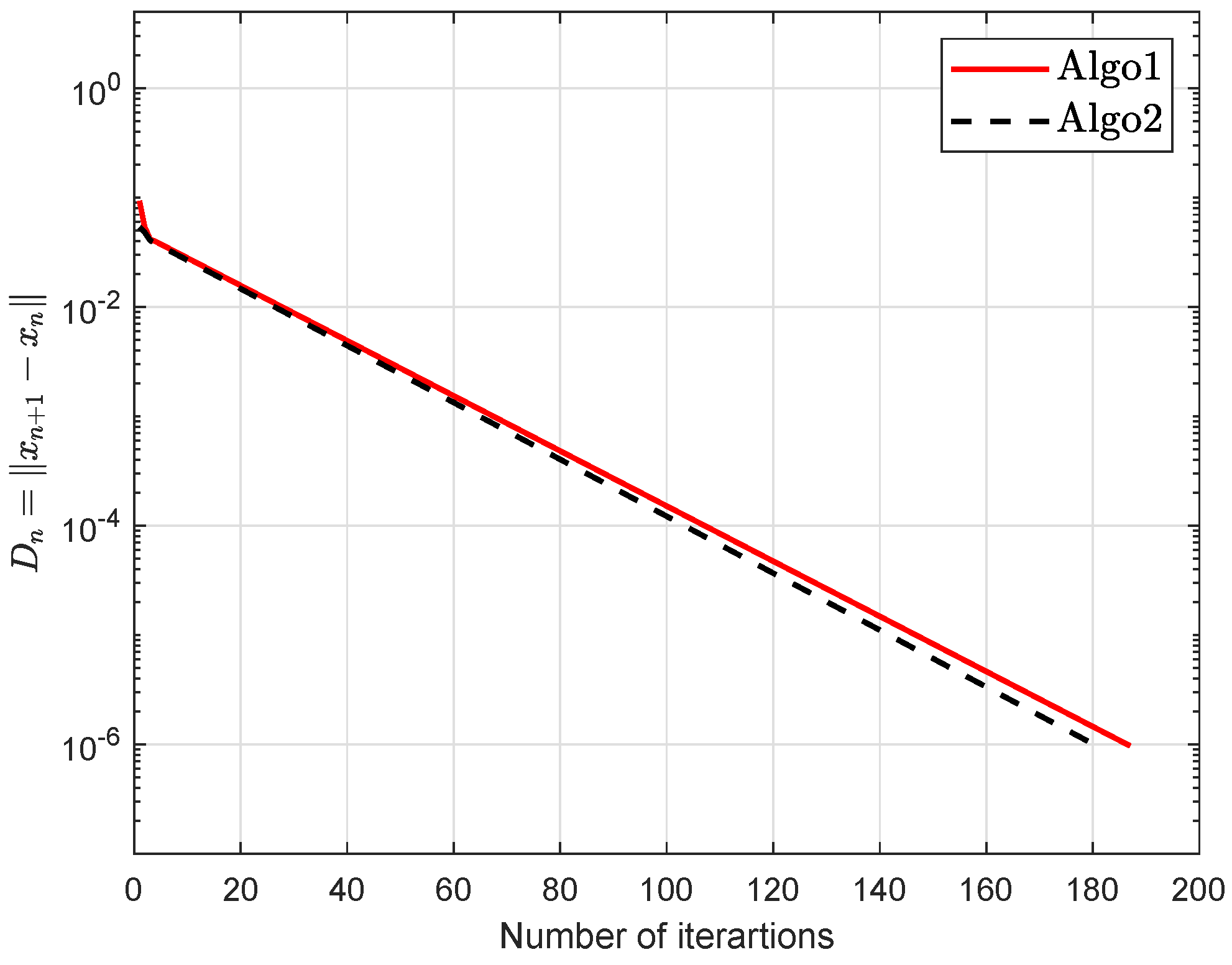

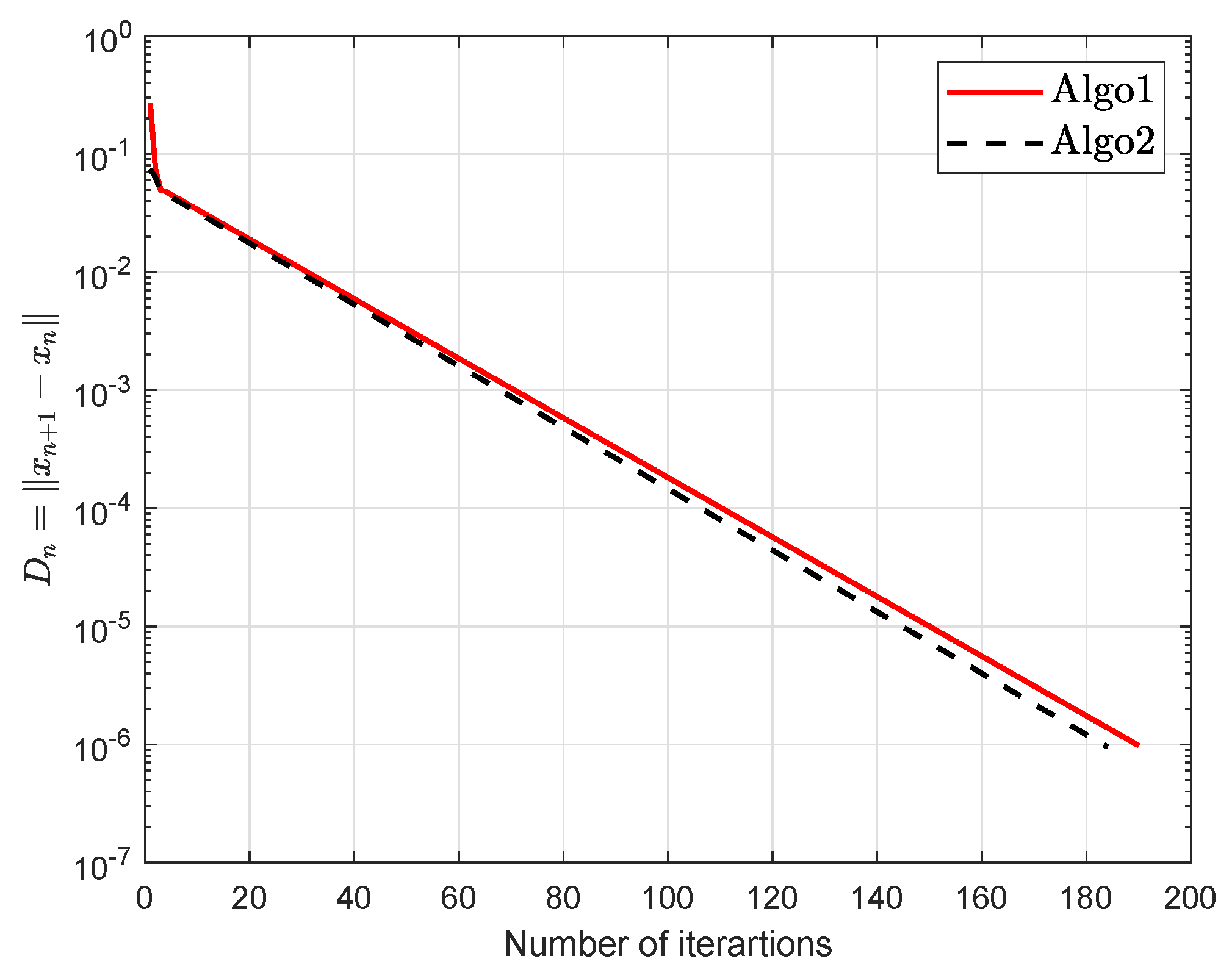
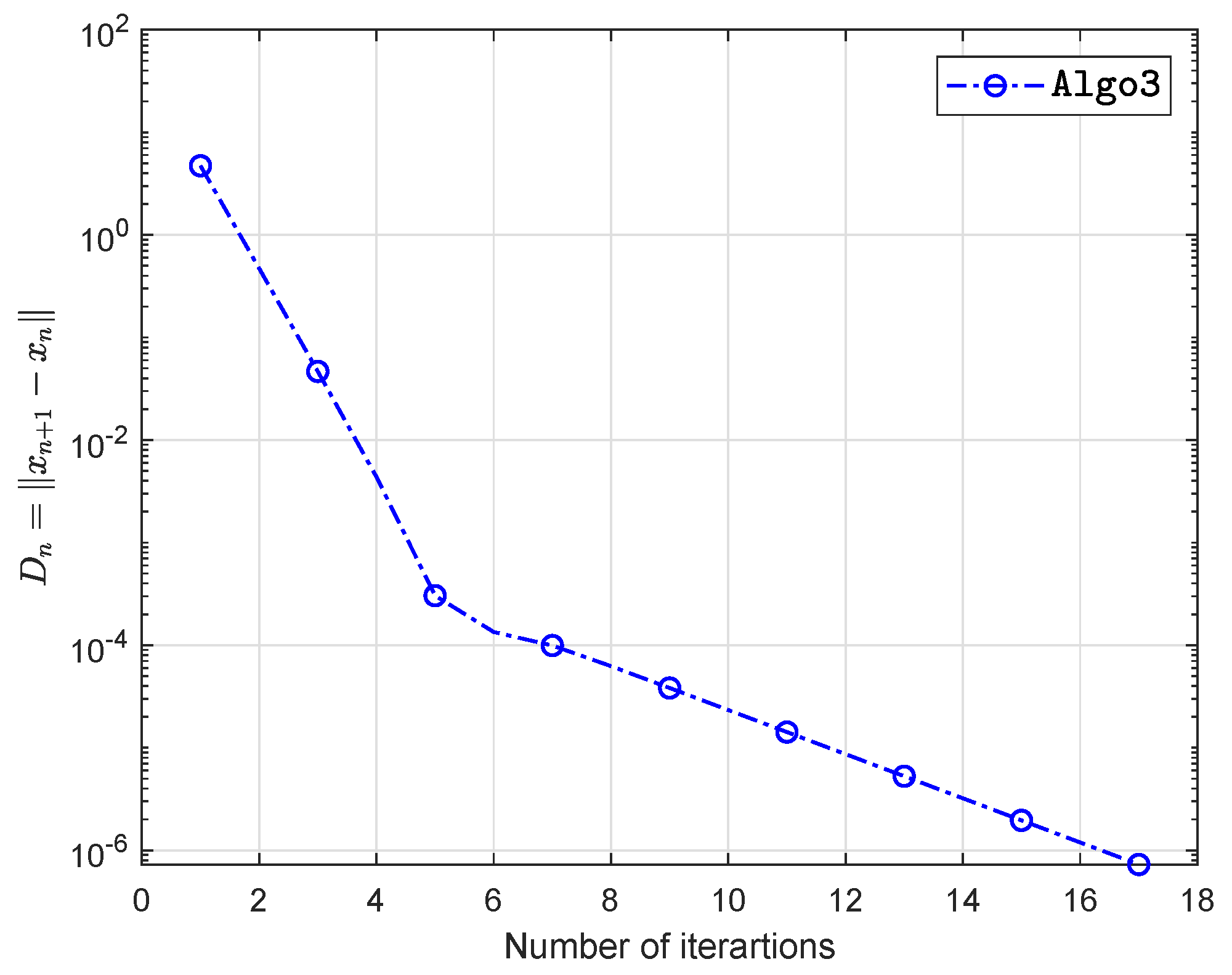
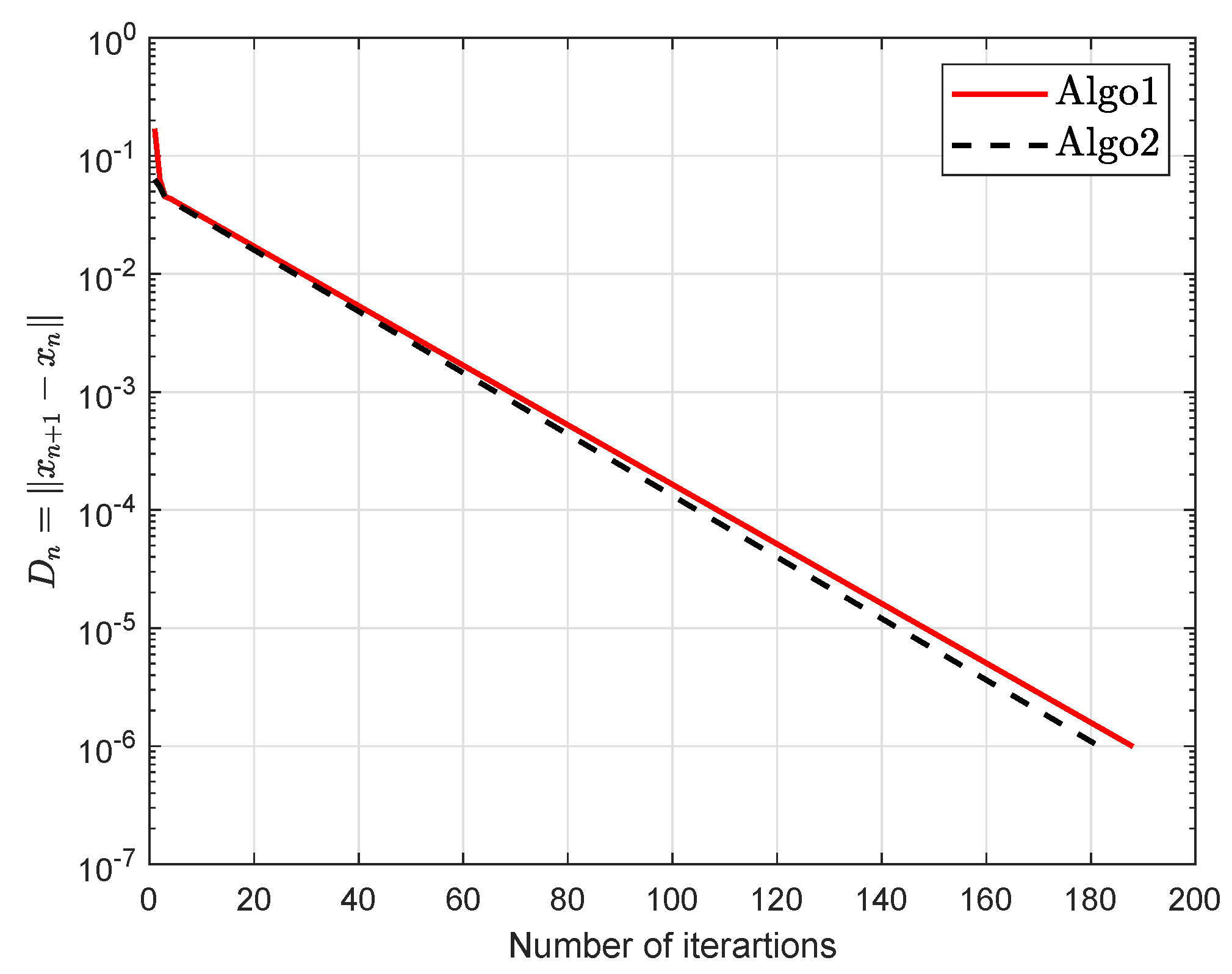
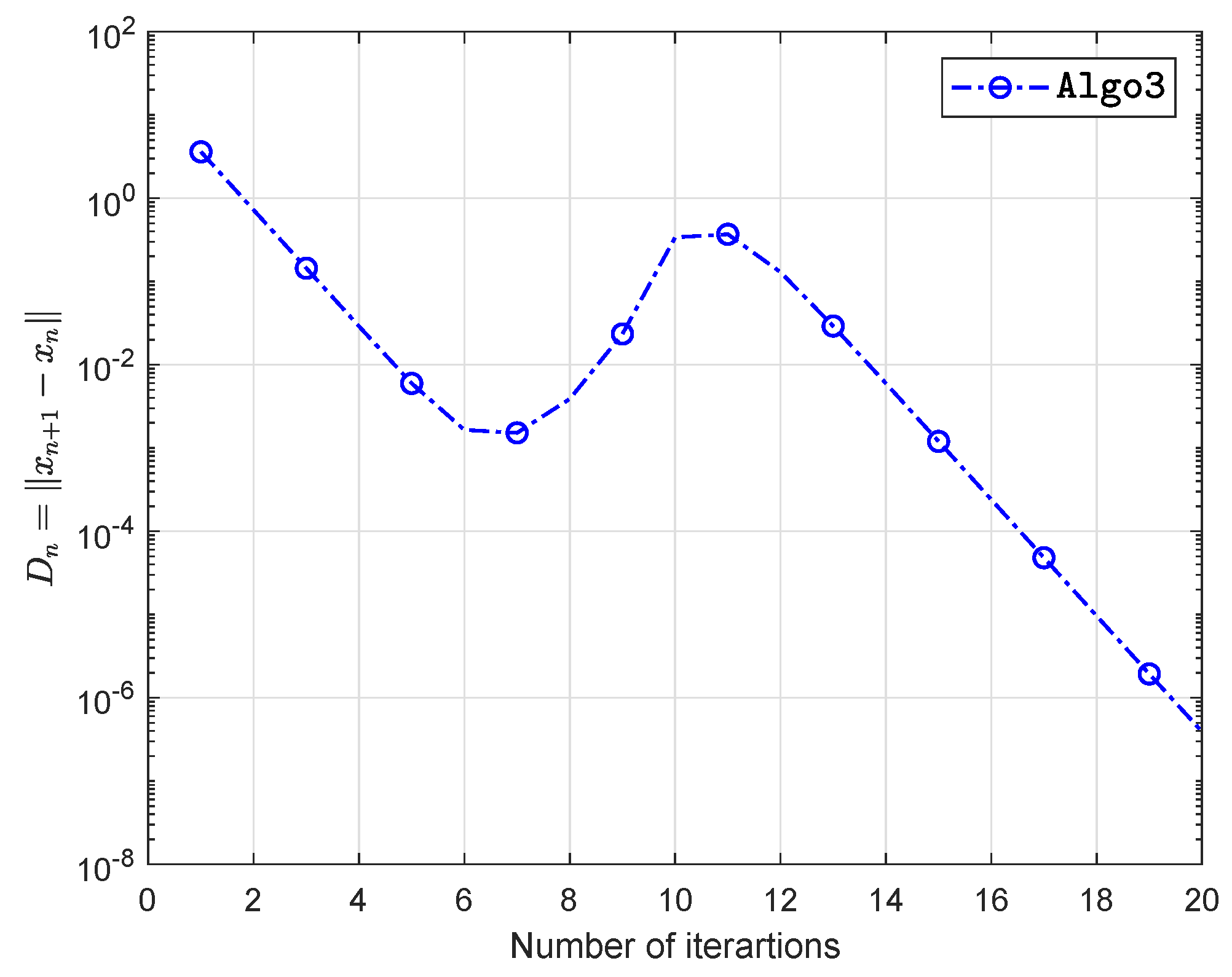
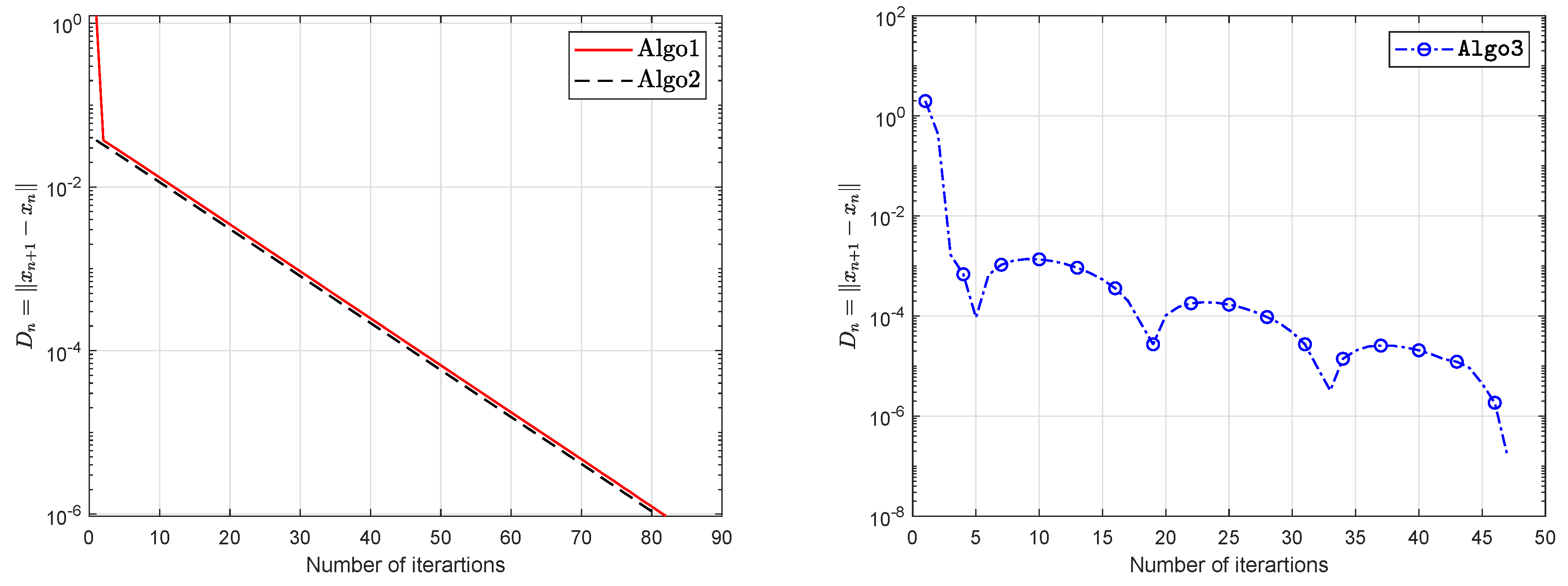

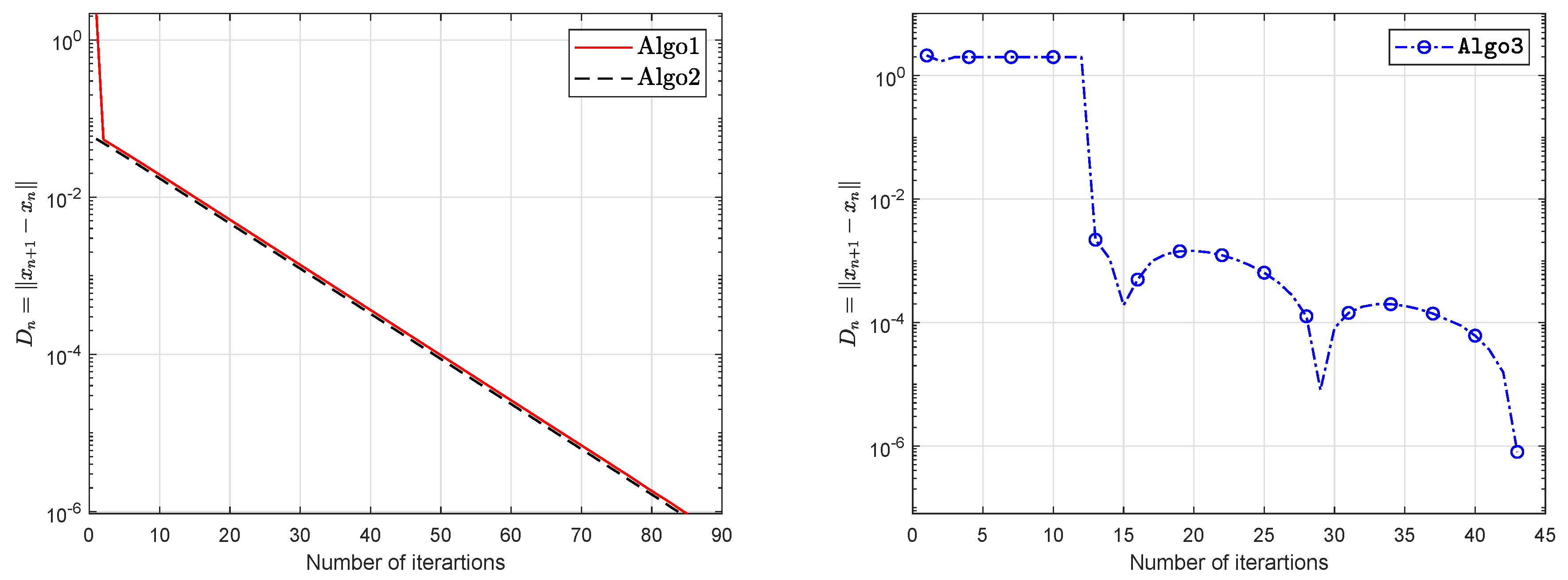
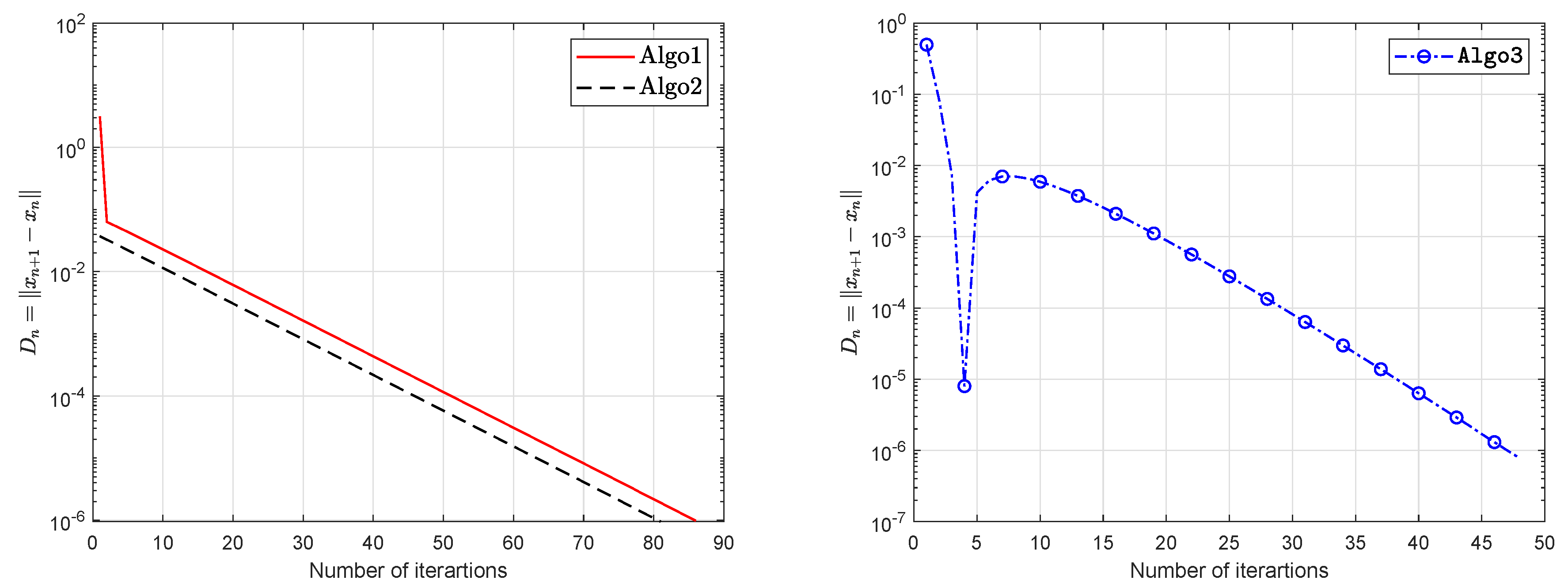
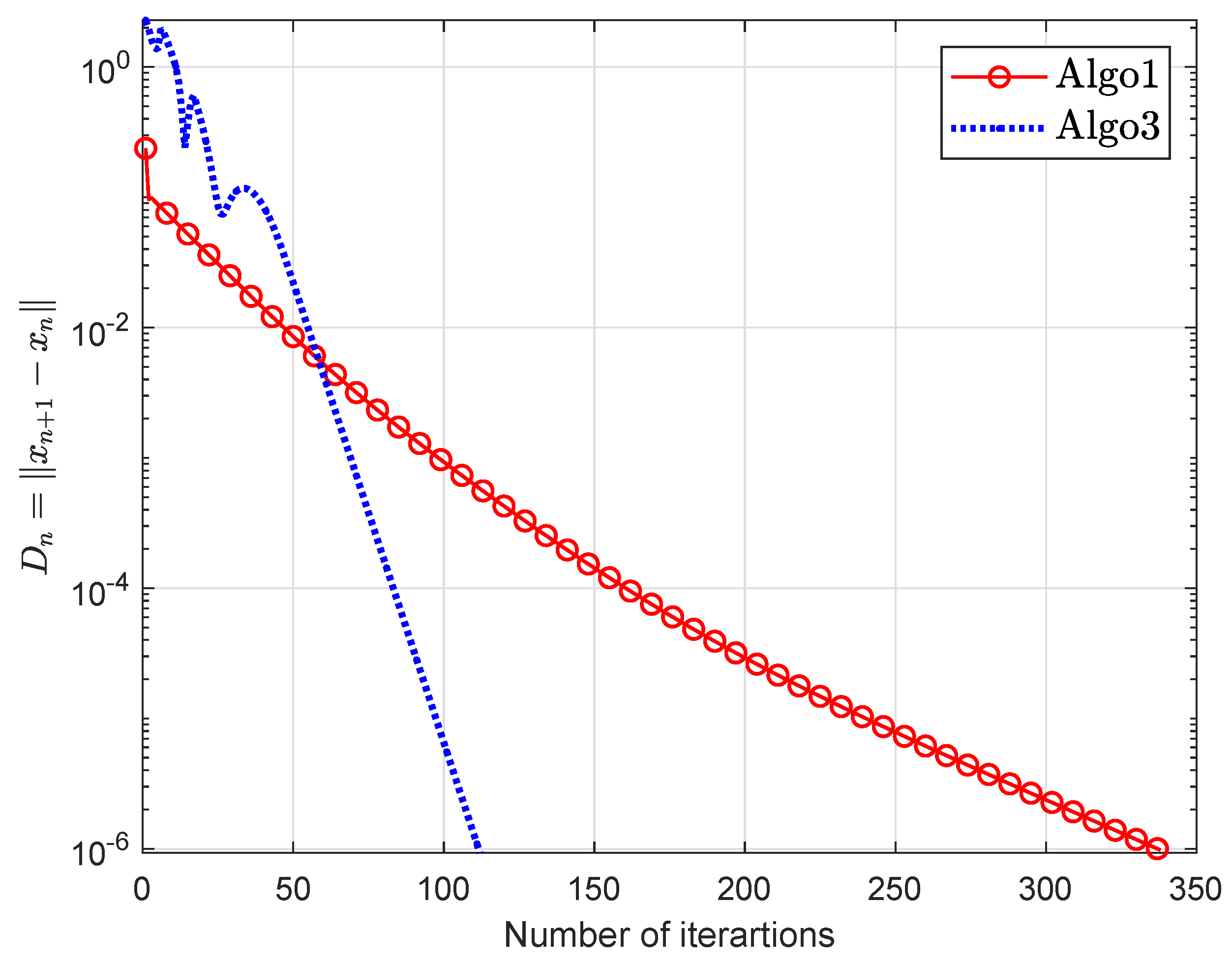
| Algo1 | Algo2 | Algo3 | ||||
| n | Iter. | Exeu.time. | Iter. | Exeu.time. | Iter. | Exeu.time. |
| 5 | 287 | 5.9342 | 281 | 3.5302 | 12 | 0.1204 |
| 10 | 727 | 19.8789 | 960 | 12.8186 | 16 | 0.1584 |
| 20 | 2997 | 72.7622 | 3510 | 3510 | 14 | 0.1624 |
| Algo1 | Algo2 | Algo3 | ||||
| v0 | Iter. | Exeu.time. | Iter. | Exeu.time. | Iter. | Exeu.time. |
| (−1.0, 2.0) | 180 | 1.7844 | 172 | 0.7740 | 20 | 0.1025 |
| (1.5, 1.7) | 187 | 2.1016 | 181 | 0.8069 | 23 | 0.1125 |
| (2.7, 4.6) | 190 | 1.9044 | 184 | 0.7979 | 17 | 0.0881 |
| (2.0, 3.0) | 188 | 1.8635 | 182 | 0.7792 | 20 | 0.1063 |
| Algo1 | Algo2 | Algo3 | ||||
| v0 | Iter. | Exeu.time. | Iter. | Exeu.time. | Iter. | Exeu.time. |
| (1.5, 1.7) | 82 | 2.6525 | 81 | 1.3557 | 47 | 0.9015 |
| (2.0, 3.0) | 82 | 2.7698 | 81 | 1.3698 | 50 | 1.4948 |
| (1.0, 2.0) | 85 | 2.9042 | 84 | 1.4026 | 43 | 1.2657 |
| (2.7, 2.6) | 86 | 2.8937 | 81 | 1.3990 | 48 | 1.4540 |
| Algo1 | Algo3 | |||
| n | Iter. | Exeu.time. | Iter. | Exeu.time. |
| 5 | 338 | 12.6364 | 112 | 8.8393 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rehman, H.u.; Kumam, P.; Argyros, I.K.; Alreshidi, N.A.; Kumam, W.; Jirakitpuwapat, W. A Self-Adaptive Extra-Gradient Methods for a Family of Pseudomonotone Equilibrium Programming with Application in Different Classes of Variational Inequality Problems. Symmetry 2020, 12, 523. https://doi.org/10.3390/sym12040523
Rehman Hu, Kumam P, Argyros IK, Alreshidi NA, Kumam W, Jirakitpuwapat W. A Self-Adaptive Extra-Gradient Methods for a Family of Pseudomonotone Equilibrium Programming with Application in Different Classes of Variational Inequality Problems. Symmetry. 2020; 12(4):523. https://doi.org/10.3390/sym12040523
Chicago/Turabian StyleRehman, Habib ur, Poom Kumam, Ioannis K. Argyros, Nasser Aedh Alreshidi, Wiyada Kumam, and Wachirapong Jirakitpuwapat. 2020. "A Self-Adaptive Extra-Gradient Methods for a Family of Pseudomonotone Equilibrium Programming with Application in Different Classes of Variational Inequality Problems" Symmetry 12, no. 4: 523. https://doi.org/10.3390/sym12040523
APA StyleRehman, H. u., Kumam, P., Argyros, I. K., Alreshidi, N. A., Kumam, W., & Jirakitpuwapat, W. (2020). A Self-Adaptive Extra-Gradient Methods for a Family of Pseudomonotone Equilibrium Programming with Application in Different Classes of Variational Inequality Problems. Symmetry, 12(4), 523. https://doi.org/10.3390/sym12040523









