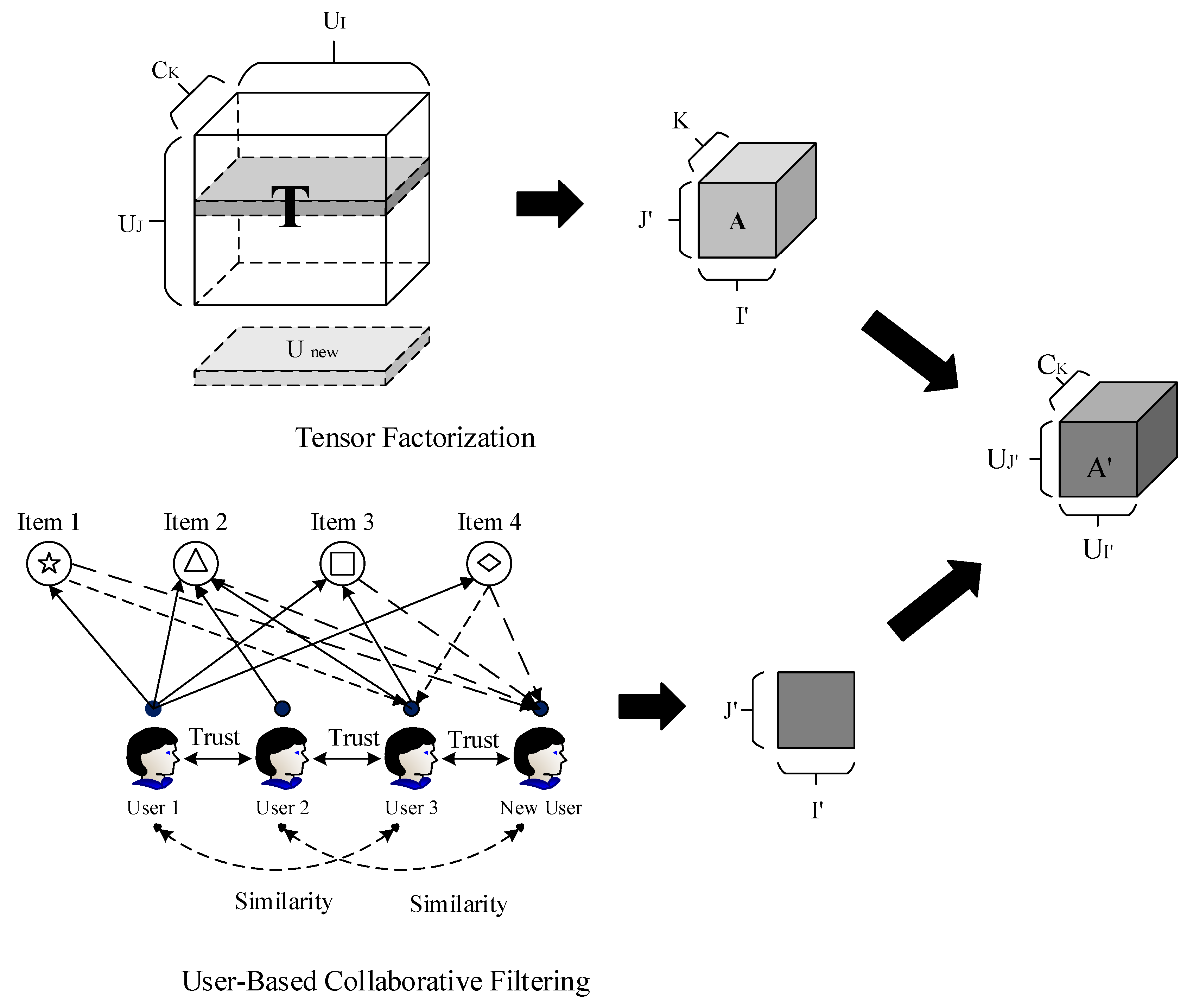
3.2. User-Based Collaborative Filtering
The joint study of sociology and computer science shows that the user’s behavior is influenced by its direct trust of friends. As the saying goes, “Birds of a feather flock together.” Take the movie as an example. If user A likes “Forrest Gump”, “When Happiness Comes Knocking”, “Rain Man”, “Shawshank Redemption”, and other movies, another user B also likes these movies. If he also likes “Wind and Harvard Road”, it is very likely that user A also likes the movie “Wind and Harvard Road”. Therefore, in the recommendation system, when user A needs a personalized recommendation, he can first find a user group M with similar interests. Then, it recommends to A an item that M likes and A has not touched, which is based on the UCF algorithm. As shown in
Figure 1, the focus of this paper is to solve the similarity between trusted users by considering the implicit similarity between the trust relationship between users and user behavior.
Given user U and user V, assume that N(u) represents positive feedback information that user U has ever made on the item set, and N(v) represents positive feedback information that user V has ever made on the item set. Then, we can simply calculate the implicit similarity of interest between user U and user V, as in (1).
In Equation (1), the effect of popular items in the common interest list of user U and user V on their implicit similarity is penalized.
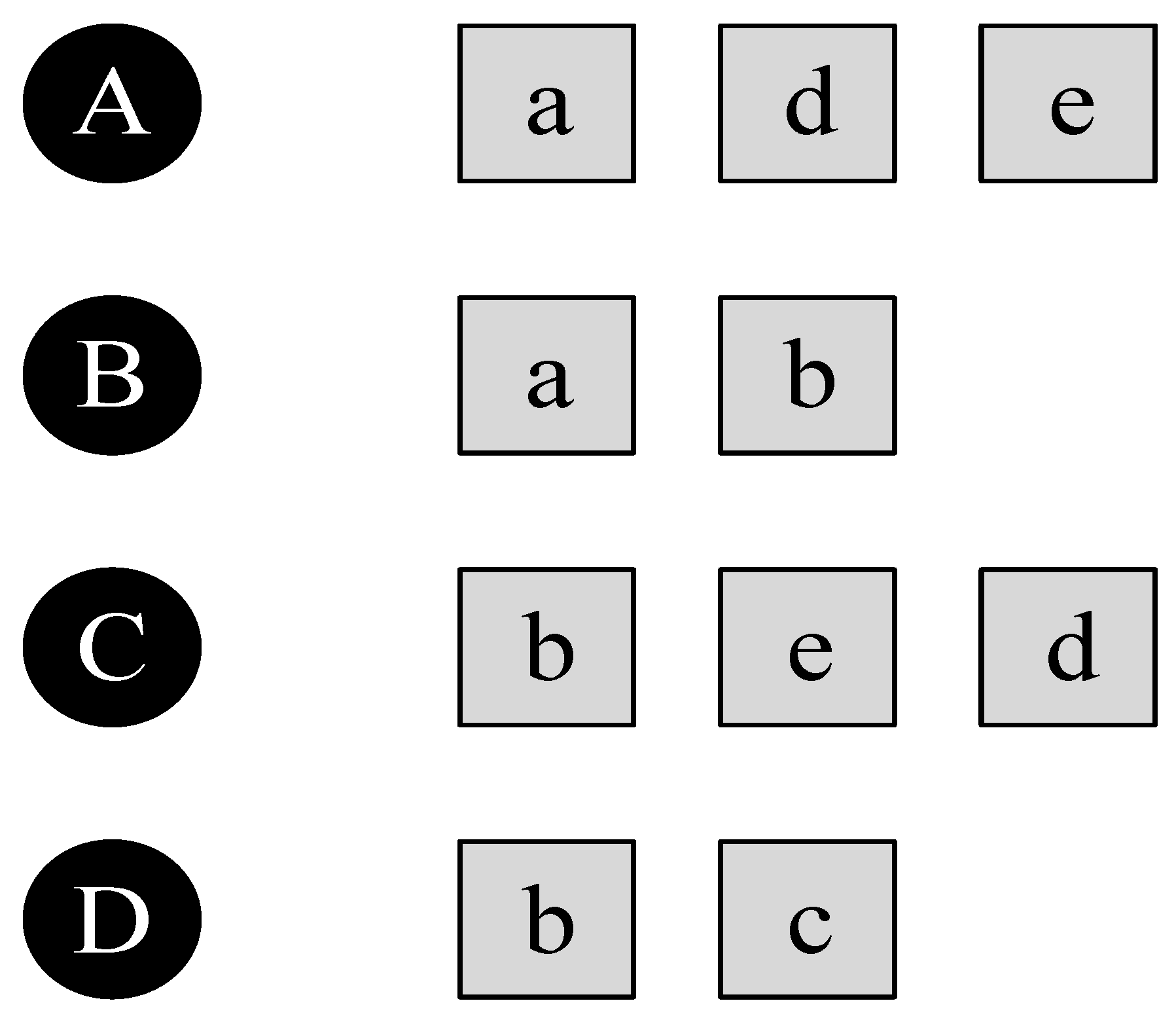
An example analysis is performed, as shown in
Figure 2. It is assumed that user A has evaluated information for item {a, d, e}, and user B has evaluated information for item {a, b}. The implicit similarity between user A and user B is calculated using (1).
By analogy, the implicit similarity between user A and users C and D can be obtained, and as shown in
Table 2, the implicit similarity between user U and user V can be easily calculated by UCF.
3.3. Tensor Tucker Factorization Model
The tensor is the generalized concept of multidimensional arrays. Compared to matrix formats, tensors usually contain more basic structural information. Applying a tensor to a recommendation system can accurately capture the inherent correlations between users through multidimensional data to achieve more effective recommendation results. Although these data can be analyzed by matrix methods after expansion or flattening, such matrixing usually does not take full advantage of the essential tensor structure.
It appears to be natural to directly extend low-rank matrix factorization methods to the low-rank tensor factorization problem. Based on this definition, Ji et al. [
48] further proposed a nonconvex approach. However, these methods involved the singular value decomposition (SVD) of
, which is time-consuming. To address this issue, Xu et al. [
49] adopted low-rank matrix factorization:
where
is the observed data, and
is the projection operator.
In this paper, a third-order tensor is used as an example. As shown in
Figure 3, suppose that T is the tensor of size
, which can be expressed as Tucker factorization:
where, the volume of the core tensor A is
, the user factor matrix is
, the item factor matrix is
, and the context factor matrix is
. Therefore, the score that corresponds to any position on the tensor T is:
The minimum loss function for the score tensor T factorization is:
We solve
,
,
, and
according to the SGD method. The update formula for each iteration is:
where
is the learning rate, and the summation subscripts
,
, and
in the update formula represent the set of position indices of all nonzero elements on the matrix
respectively. This method minimizes the factorization of kernel norms and low-rank tensors to effectively improve the inferiority of potential results.
3.4. A Low-Rank Tensor Factorization Using Implicit Similarity in Trust Relationships (LTF-ISTR)
In a real network, users do not exist independently, and there is a certain social relationship between users. The two users have different preferences for an item based on mutual trust. Therefore, based on the consideration of trusting users, this paper further considers the implicit similarity of users and captures the local information of correlation between users. After obtaining the association relationship of the trusted users, the global information between the users is further explored by low-rank tensor factorization.
This paper proposes a new tensor model, which is a low-rank tensor factorization using implicit similarity in trust relationships. Here, we define a third-order tensor T, where the tensor
represents the score given by the user
in the context of similarity
and the same movie viewed by the trusted user
, as shown in
Figure 1. The matrix
of the user and the trusted user is obtained by user collaborative filtering, and the implicit similarity
between the user
and the trusted user
is obtained. The approximate tensor A is reconstructed to generate a new low-rank tensor
based on the implicit similarity of the trust relationship. Then, Tucker factorization is performed on tensor
. The size of the core tensor
is
, the user
factor matrix is
, and the user
factor matrix is
, hidden. The matrix that contains the similarity factor is
. Therefore, the objective function of the low-rank tensor factorization using implicit similarity in trust relationships is defined as:
here,
and
:
Among them, is a positive regularization parameter, and denotes the L2 norm regularization term of each factor matrix. Our model considers a priori the trust user factor matrix and has a deeper insight into the factor matrix prior. There is further optimization of the low-rank tensor factorization.
Next, we chose the CG method between the SGD method and Newton method in the algorithm optimization problem. The CG method can quickly converge to the optimal solution of the solved problem when solving large linear equations, and it has the advantage of small storage. Its basic idea is to construct a set of conjugate directions in the direction of the negative gradient at the iteration point and then to search the target function extremum along this set of directions. The CG method has a good local search ability, and the solution process is as follows:
Step 1: Select the initial point , given the precision , and let ;
Step 2: Calculate , if , stop; otherwise, ;
Step 3: Calculate ;
Step 4: Calculate ;
Step 5: Calculate , if , stop;
Step 6: Calculate ;
Step 7: Let and go to Step 3.
According to the above steps, for the positive definite quadratic function. First, we initialize the values, and then iteratively update them by Formula (12). The iterative formula of the CG method is:
here,
In these processes, we know that the calculation formula for the coefficient in the search direction contains a symmetric and positive definite matrix A. It can be seen that to extend the CG method of application and quadratic function to general functions, we must first solve that the matrix A cannot be included in the formula.
The solution is:
(1) Use the Fletcher–Reeves CG method [
42] when calculating, that is:
(2)
is obtained by using Wolfe’s linear search criterion, which has quadratic termination [
45].
In our model, the Fletcher-Reeves CG method requires a small amount of storage, is stable and does not require any external parameters, and it greatly improves the computational efficiency. The objective function is optimized by the Fletcher–Reeves CG method. The local minimum parameters , , and are obtained according to the following formula.
Taking as an example, the calculation steps are as follows:
Step 1: Select the initial point , given error accuracy , let ;
Step 2: Calculate , if , stop. Otherwise, take the next step;
Step 3: Construct search direction, let and ;
Step 4: let
and the Wolfe linear search criterion is used to calculate the step size
. A new iteration point is obtained. Return to Step 2.
by the same token,
It should be noted that in the low-rank tensor model of this paper, the user and the user have the same number. Trusting users is part of the overall user. Therefore, a low-rank tensor factorization using implicit similarity in trust relationship is significantly smaller than the traditional tensor model. In addition, there is no need to calculate the overall tensor T when the user updates.
In our model, the low-rank factorization fidelity term is used to capture global information, while the implicit similarity of the trusted user and the regularization term of each factor matrix are used to capture local information. Therefore, our approach utilizes local and global information and is reasonably expected to produce better results.