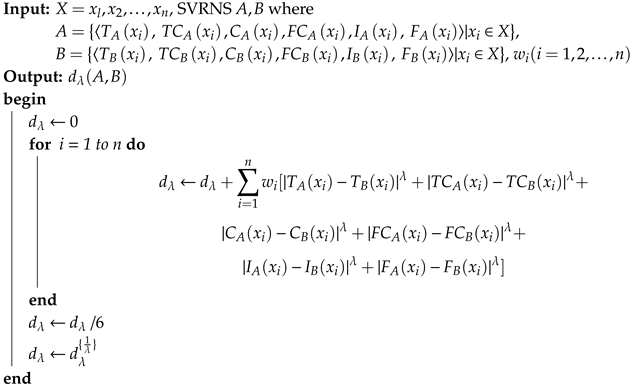1. Introduction
Neutrosophy is an emerging branch in modern mathematics. It is based on philosophy and was introduced by Smarandache and deals with the concept of indeterminacy [
1]. Neutrosophic logic is a generalization of fuzzy logic proposed by Zadeh [
2]. A proposition in Neutrosophic logic is either true (T), false (F) or indeterminate (I). This inclusion of indeterminacy makes the neutrosophic logic capable of analyzing uncertainty in datasets. Hence, it can be used to logically represent the uncertain and often inconsistent information in the real world problems. Single Valued Neutrosophic Sets (SVNS) [
3] are an instance of a neutrosophic set which can be used in real scientific and engineering applications such as Decision-making problems [
4,
5,
6,
7,
8,
9,
10,
11], Image Processing [
12,
13,
14], Social Network Analysis [
15], Social problems [
16,
17] and psychology [
18]. The distance and similarity measures have found practical applications in the fields of psychology for comparing different behavioural and cognitive patterns.
Imaginative or pretend play is one of the fascinating topics in child psychology. It begins around the age of 1 year or so. It is at its most prominent during the preschool years when children begin to interact with other children of their own age and begin to access more toys. It is crucial in child development as it helps in the development of language (sometimes the child language which cannot be deciphered by everyone) and also helps nurture the imagination of tiny-tots. However, the factors determining the level of imaginative play in children are varied and complicated and a study of them would help one to assess their mental development. It is here that fuzzy neutrosophic logic comes into play. In this paper, we propose a new notion of Single Valued Refined Neutrosophic Sets (SVRNS) which is a model structured on indeterminate and imaginary notions, coupled with machine learning techniques such as heat maps, clustering, parallel axes coordinate, etc., to study the factors that determine and influence imaginative play in children and how it differs in children with different abilities and skills.
Every child is born different. The personality and behaviour of children is an interplay of several different factors. Psychology is a complicated and varied science and open to subjective interpretations. The study of child psychology in an objective manner can help one uncover several aspects of child behaviour and also result in early detection of certain mental disorders. One of the key motivations of this research is to uncover the factors that determine the mental abilities of a child and the extent of their imagination which helps in predicting their academic and overall performance in later stages. Machine Learning is slowly but steadily becoming one of the hot topics of computer science. Amalgamation of machine learning algorithms and psychology on the basis of complex and neutrosophic logic is certainly exciting and will help to cover new bounds.
This study primarily focuses on the analysis of imaginative play in children on the basis of neutrosophic logic and draws conclusions on the same with the help of clustering algorithms. The approach is initialized by generating a finite number of complex and neutrosophic sets determined by several cognitive, psychological and biological factors that affect imaginative play in the mentioned age group. The primary advantage here is the ability of such sets to deal with the uncertainty, imagination and indeterminacy present in the study of pretend play in children in the age group from 1 to 10 years. With the help of this study, we aim to distinguish the contribution of several factors of imaginative play in children and conclude from the study whether the child has any mental disorders or not and about the general cognitive skills coupled with imagination. This model will also help in identifying factors which may contribute to potential psychological disorders in young children at an early stage and predict the academic performance of the child.
In this research, a new complex fuzzy neutrosophic set is defined which will be used as a model to study the imaginary and indeterminate behaviour in young children in the age group from 1 to 10 years by giving them suitable stimuli for imaginary play. The data were collected from different sources with the help of a questionnaire, observations, recorded sessions and interviews, and after transforming the data into the proposed new neutrosophic logic, they were fitted into the newly constructed model and conclusions were drawn from them using a child psychologist as an expert. This model attempts to discover the extent to which several factors contribute to imaginative play in children of the specified age group and to detect possibilities of mental disorders such as autism and hyperactivity in young children on the basis of the trained model.
The paper is organized into seven major sections which are further divided into a few subsections. Section one is introductory in nature. A detailed analysis of the works related to neutrosophy and its applications to a few relevant fields are presented in section two. It also provides the gaps that have been identified in those works.
Section 3 introduces Single Valued Refined Neutrosophic Sets (SVRNS) along with their properties, such as distance measures and related algorithms. It also introduces and discusses several machine learning techniques used for assessment. The description of the dataset used for the application of algorithms such as K-means clustering, heat maps, parallel axes coordinate is given in section four. It also includes the approach involved in processing the data obtained appropriately into SVRNSs.
Section 5 provides an illustrative example of the methods described in the preceding section.
Section 6 details the results obtained from the application of the discussed algorithms and their respective visualizations.
Section 7 discusses the conclusions based on our study and its future scope.
2. Related Works
Fink [
19] explored the role of imaginative play in the attainment of conservation and perspectivism with the help of a training study paradigm. Kindergarten children were assigned to certain conditions such as free play in the presence of an experimenter and a control group. The method of their data collection was observation. The results indicate that imaginative play can result in new cognitive structures. The relationship between different types of play experiences and the construction of certain physical or social concepts were also discussed, along with educational implications.
Udwin [
20] studied a group of children who had been removed from harmful family backgrounds and placed in institutional care. These children were exposed to imaginative play training sessions. These subjects showed an increase in imaginative behaviour. Age, non-verbal intelligence and fantasy predisposition were determinants of the subjects’ response to the training programme, with younger, high-fantasy and high-IQ children being most susceptible to the influence of the training exercises.
Huston-Stein [
21] attempted to establish a relationship between social structure and child psychology by employing methods of direct observations of field experiments. The behaviour was then categorised on the basis of a set of defined behavioural categories and evaluated on the basis of suitable metrics. The results focus on establishing correlations between these behavioural categories and classroom structure and draw conclusions on how such social structures impact imaginative play.
Bodrova [
22] related another important parameter, namely academic performance, to imaginative play. They have established imaginative play as a necessary prerequisite and one of the major sources of child development. They deduced how imaginative play scenarios require a certain knowledge of environmental setting and how it affects the academic excellence of a child.
Seja [
23] explored another important factor in child psychology—emotions. They attempted to determine how imaginative play helps to understand the emotional integration of children. The source of data collected in this study is elementary school children who were tested on verbal intelligence and by standard psychological tests. Conclusions were drawn on the basis of an extensive statistical analysis which also attempted to investigate gender differences.
Neutrosophy has given importance to the imprecision and complexity of data. This is an important reason behind using neutrosophic logic in real life applications. Dhingra et al. [
24] attempted to classify a given leaf as diseased or healthy based on the membership functions of the neutrosophic sets. Image segmentation into true, false and indeterminate regions after preprocessing was used to extract features and several classifiers were used to arrive at a classification. A comparative analysis of these classifiers was also provided.
Several researchers [
25,
26,
27,
28,
29,
30] dealt with algebraic structures of neutrosophic duplets, which are a special case of neutrality. Single Valued Neutrosophic Sets (SVNS), which is particular cases of triplet following the fuzzy neutrosphic membership concepts in their mathematical properties and operations are dealt by Haibin [
31].
Haibin [
31] gave the notion of Single Valued Neutrosophic Sets (SVNS) along with their mathematical properties and set operations. Properties such as inclusion, complement and union were defined on SVNS. They also gave examples of how such sets can be used in practical engineering applications. SVNS has found a major application in medical diagnosis. Shehzadi [
32] presented the use of Hamming distance and similarity measures of given SVNSs to diagnose a patient as having Diabetes, Dengue or Tuberculosis. The three membership functions (truth, falsity and indeterminacy) were assigned suitable values and distance and similarity measures were applied on them. These measures were then used to provide a medical diagnosis. Smarandache and Ali [
33] provided the notion of complex neutrosophic sets (CNS). Membership values given to them were of the form a+bi. Several properties of these sets were defined. These sets find applications in electrical engineering and decision-making fields. Neutrosophic Refined Sets where defined in [
34].
A more refined and precise view of indeterminacy is provided by Kandasamy [
35]. The indeterminacy membership function was further categorized as indeterminacy tending towards truth and indeterminacy tending towards false. Hence, resulting in Double-Valued Neutrosophic Set (DVNS). Their properties, such as complement, union and equality were also discussed and distance measures were also defined on them. On the basis of these properties, minimum spanning trees and clustering algorithms were described [
36]. Dice measures on DVNS were proposed in [
37]. The importance given to the indeterminacy of incomplete and imprecise data, as often found in the real world, is a major advantage of the DVNS and hence, is more apt for several engineering and medical applications.
The model of Triple Refined Indeterminate Neutrosophic Set (TRINS) was also introduced by Kandasamy and Smarandache [
38]. It categorizes indeterminacy membership function as leaning towards truth and leaning towards false in addition to the traditional three membership functions of neutrosophic sets. After defining the several properties and distance measures, the TRINS was used for personality classification. The personality classification using TRINS has been found to be more accurate and realistic as compared to SVNS and DVNS. Indeterminate Likert scaling using five point scale was introduced in [
39] and a sentiment analysis using Neutrosophic refined sets was conducted in [
40,
41].
To date, the study of imaginative play in children has not been analysed using neutrosophy coupled with an imaginary concept; thus, to cover this unexplored area, the new notion of Single Valued Refined Neutrosophic Sets (SVRNS) that represent imaginary and indeterminate memberships individually were defined. A study of imaginative play in children using Neutrosophic Cognitive Maps (NCM) model was carried out in [
42].
3. Single Valued Refined Neutrosophic Set (SVRNS) and Its Properties
This section presents the definition of Single Valued Refined Neutrosophic Set (SVRNS). These sets are based on the essential concepts of real, complex and neutrosophic values which takes membership from the fuzzy interval [0,1]. In a way this can be realized as a mixture of refined neutrosophic sets coupled with real membership values for imaginary aspect. However SVRNS are different from traditional neutrosophic sets. The neutrosophic logic is powerful and can model concepts of arbitrary complexity covering incomplete and imprecise data. Children’s behaviour is one such complicated and the imprecise branch that can be modelled as objectively as possible by coupling imaginary or complex nature of data with its indeterminacy.
The concept of SVRNS are defined, developed and described in the following.
3.1. Single Valued Refined Neutrosophic Set (SVRNS)
Definition 1. Let X be a space of points (objects), with a generic element in X denoted by x. A neutrosophic set A in X is characterised by a truth membership function , a true tending towards complex membership function , a complex membership function , a false tending towards complex membership function , an indeterminacy membership function , and a falsity membership function . For each point x in X, there are , , , , , and Therefore, a Single Valued Refined Neutrosophic Set (SVRNS) A can be represented by 3.2. Distance Measures of SVRNS
The distance measures of SVRNSs are defined in this section and the related algorithm for determining the distance is given.
Definition 2. Consider two SVRNSs A and B in a universe of discourse, which are denoted byandwhere , , , , , , , , , , for every . Let be the weight of an element , with and . Then, the generalised SVRNS weighted distance is defined as follows:where . The above equation reduces to the SVRNS weighted Hamming distance and the SVRNS weighted Euclidean distance, when λ = 1, 2, respectively. The SVRNS weighted Hamming distance is given aswhere λ = 1. The SVRNS weighted Euclidean distance is given aswhere λ = 2. The algorithm to obtain the generalized SVRNS weighted distance
between two SVRNS
A and
B is given in Algorithm 1.
| Algorithm 1: Generalized SVRNS weighted distance |
![Symmetry 12 00402 i001 Symmetry 12 00402 i001]() |
The related flowchart is given in
Figure 1.
The generalised SVRNS weighted distance for λ > 0 satisfies the following properties:
if and only if A = B
If , C is a SVRNS in X, then and
3.3. K-Means Algorithm
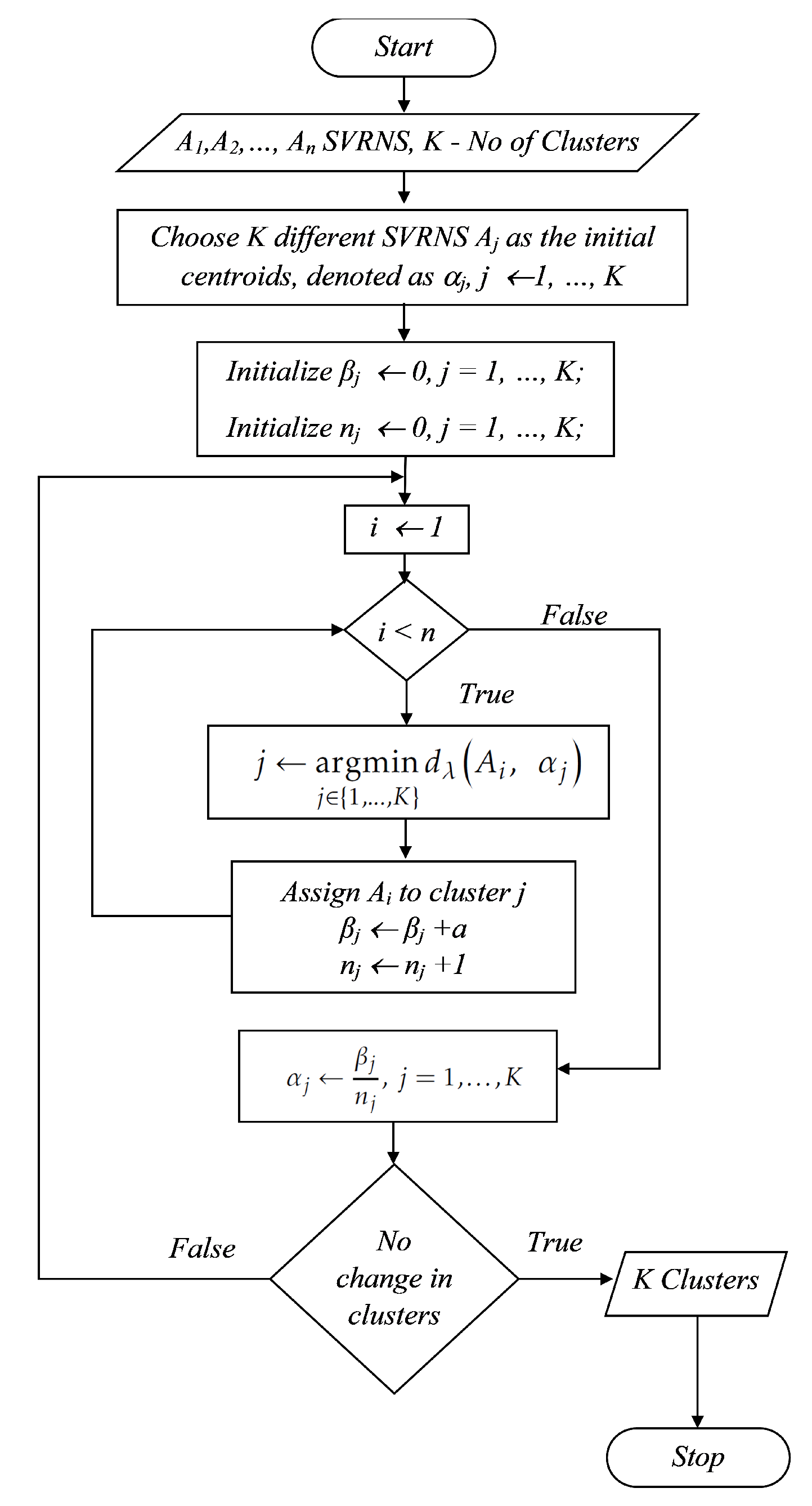
The K-means algorithm for SVRNS is given in Algorithm 2.
| Algorithm 2: K-means algorithm for clustering SVRNS values |
![Symmetry 12 00402 i002 Symmetry 12 00402 i002]() |
The related flowchart is given in
Figure 2.
We used the following machine learning techniques in this paper after obtaining and processing the data.
3.4. Other Machine Learning Techniques
The Elbow method is a technique used to find the value of appropriate value of K(Number of clusters) in K-means clustering. It makes the cluster analysis design consistent. A heat map is a data visualization technique used to show correlation between two attributes in the form of a matrix where each value is represented as colours. The Principal Component Analysis (PCA) makes use of orthogonal transformation to convert a set of observations of variables which might be possibly correlated, into a set of values of linearly uncorrelated variables called principal components. It is a widely used statistical technique. Parallel coordinates (also known as Parallel Axes Chart (PAC)) are highly used for the visualization of multi-dimensional geometry and analysis of multivariate data. Easy visualization of multiple dimensions is an innate feature of PAC plot, making it simple to analyse attributes which are associated with other attributes in a similar manner.
4. Dataset Description
Imaginative play is defined as “a form of symbolic play where children use objects, actions or ideas to represent other objects, actions, or ideas using their imaginations to assign roles to inanimate objects or people”. During the early stage, “toddlers begin to develop their imaginations, with sticks becoming boats and brooms becoming horses. Their play is mostly solitary, assigning roles to inanimate objects like their dolls and teddy bears”. It has proven to be highly beneficial as it results in early use of language and proper use of tenses and adjectives. It gives the children a sense of freedom and allows them to be creative in their own space. It helps children make sense of the physical world and also their inner selves. It can develop with the help of the most basic tools such as a toy mobile or a cardboard tube.
The data regarding imaginative play in children were collected from the local school and an orphanage in Vellore, India.
A child psychologist was present throughout the sessions, analyzed and suggested the various parameters and recorded the observations about each session. The session at each of these places began with the expert talking to the child about general things and everyday life as an ice-breaker exercise. This included talking about his/her favourite subjects, parents and treating him/her with biscuits or chocolates. The surroundings were made as comfortable as possible. The child was then asked to conduct an imaginary phone call in whichever way he/she liked. The imaginary conversation was then recorded as video on a phone. The expert made observations that were recorded on paper in a running hand description. This signified the end of the session.
Overall, 10 such sessions were conducted at the school and 2 were conducted at the orphanage. The children belonged to the age group of 6 to 8 years. Additionally, in order to make the dataset diverse as suggested by the expert, 7 videos were taken from the internet in which children conducted imaginary conversations over the phone. The running hand description thus collected was used by this expert to assign values to the six membership functions based on which the SVRNS is constructed.
Table 1 provides the parameters which have been used to study imaginative play along with their description. The parameters 1 to 11 are available in [
19] and the other 4 parameters from 12 to 15 are introduced by us.
Method of Evaluation
The running hand description of the above-mentioned parameters was transformed into a complex fuzzy neutrosophic sets by the expert/child psychologist, for applying machine learning algorithms discussed in the earlier section. The methods of evaluation for each parameter as suggested by the expert are discussed below.
Imaginative Theme: An imaginative theme that is based on the real situation will result in the increase in the truth membership function and otherwise if the theme is entirely imaginative. However, since there is always a degree of complex and indeterminacy in this parameter, the complex and indeterminate membership functions was also assigned certain values from [0,1].
Physical Movements: If physical movements are made, the value of truth membership function will increase else the falsity membership function will increase. Complex and indeterminacy values from [0,1] shall be assigned values if movements are difficult to interpret properly or happened to be imaginary.
Gestures: Similar to physical movements, any gestures made in accordance with the imaginative activity will result in an increase in the truth membership value and in falsity value otherwise. Any indeterminate or complex feature will result in values being assigned to indeterminate and complex respectively from [0,1].
Facial Expressions: Any facial expressions made in accordance with the imaginative activity conducted will lead to an increase in the truth membership and in falsity membership function otherwise. Complex and indeterminacy membership functions shall be assigned values if facial expressions are difficult to interpret properly.
Nature and Length of Social Interaction: Any interaction that is made in accordance with the play activity will result in an increase in truth membership functions and in falsity membership functions otherwise. Indeterminate and complex membership functions shall be assigned values if the interactions are difficult to interpret properly.
Play Materials Used: These are nouns and need not be translated to SVRNS.
Way Play Materials were Used: Any usage of play materials in a realistic manner will lead to an increase in the truth membership and in falsity membership function otherwise. Complex and indeterminacy membership functions shall be assigned values if usage is difficult to interpret properly.
Verbalisation: Any verbalisation that is made in accordance with the play activity will result in an increase in truth membership functions and in falsity membership functions otherwise. Complex and indeterminacy membership functions shall be assigned values if the verbalization is difficult to interpret properly.
Tone of Voice: If the tone of voice is in accordance with the situation of play activity and high, it will result in an increase in truth membership functions and in falsity membership functions otherwise. Complex and indeterminacy membership functions shall be assigned values if the interactions are difficult to interpret properly.
Role Identification: Any role identification that is realistic will lead to an increase in the truth membership and in falsity membership function otherwise. Complex and indeterminacy membership functions shall be assigned values if role identification is difficult to interpret properly.
Engagement Level: If the engagement level is high but the theme and role identification are realistic, truth membership function value increases. If the engagement level is high but the theme and role identification are imaginative, falsity membership function value increases. Other combinations of engagement level, theme and role identification will result in assigning values to the other membership functions.
Eye Reaction: Any eye reaction that is made in accordance with the play activity will result in an increase in truth membership functions and in falsity membership functions otherwise. Complex and indeterminacy membership functions shall be assigned values if the eye reaction is difficult to interpret properly.
Cognitive Response: Any cognitive response that is made in accordance with the play activity will result in an increase in truth membership functions and in falsity membership functions otherwise. Complex and indeterminacy membership functions shall be assigned values if the cognitive is difficult to interpret properly.
Grammar and Linguistics: If the grammar, sentence structure and syntax are correct, the value of truth membership function will increase. Any error in grammar, syntax or sentence structure will lead to an increase in the value of falsity membership function. If, however, the linguistics are difficult to comprehend, indeterminate and complex membership functions’ value will increase.
Coherence: If the sentences made are related to one another, the value of truth membership function will increase. Any incoherence, i.e., making sentences are not related to one another will lead to an increase in the value of falsity membership function. If, however, the coherence of sentences is difficult to comprehend, indeterminate and complex membership functions’ value will increase.
5. Illustrative Example
This section provides an example on processing of the data obtained as a running hand description. On the basis of this description, the expert estimated and evaluated the child. The following example is based on a video of 3-year-old child and the following observations given by the expert are made in form of running hand descriptions of the 15 parameters given in
Table 2.
Table 2 depicts a running hand description of the discussed parameters. These parameters are then assigned real values by the expert. These values are discussed in
Table 3.
Likewise the SVRNS tuples for the other data sets was done with the help of the expert. Then these SVRNS sets are used for analysis using machine learning algorithms.
6. Results and Discussions
Several libraries such as pandas, numpy, matplotlib, sklearn, seaborn and pylab associated with Python were used for data visualization. Programming was carried out using python for the visualization of the previous discussed algorithms, based on the result of elbow curve, K-means clustering was done. Logical conclusions have been drawn from these visualizations and the role several determinants play in determining the imaginative capabilities of the child has also been highlighted.
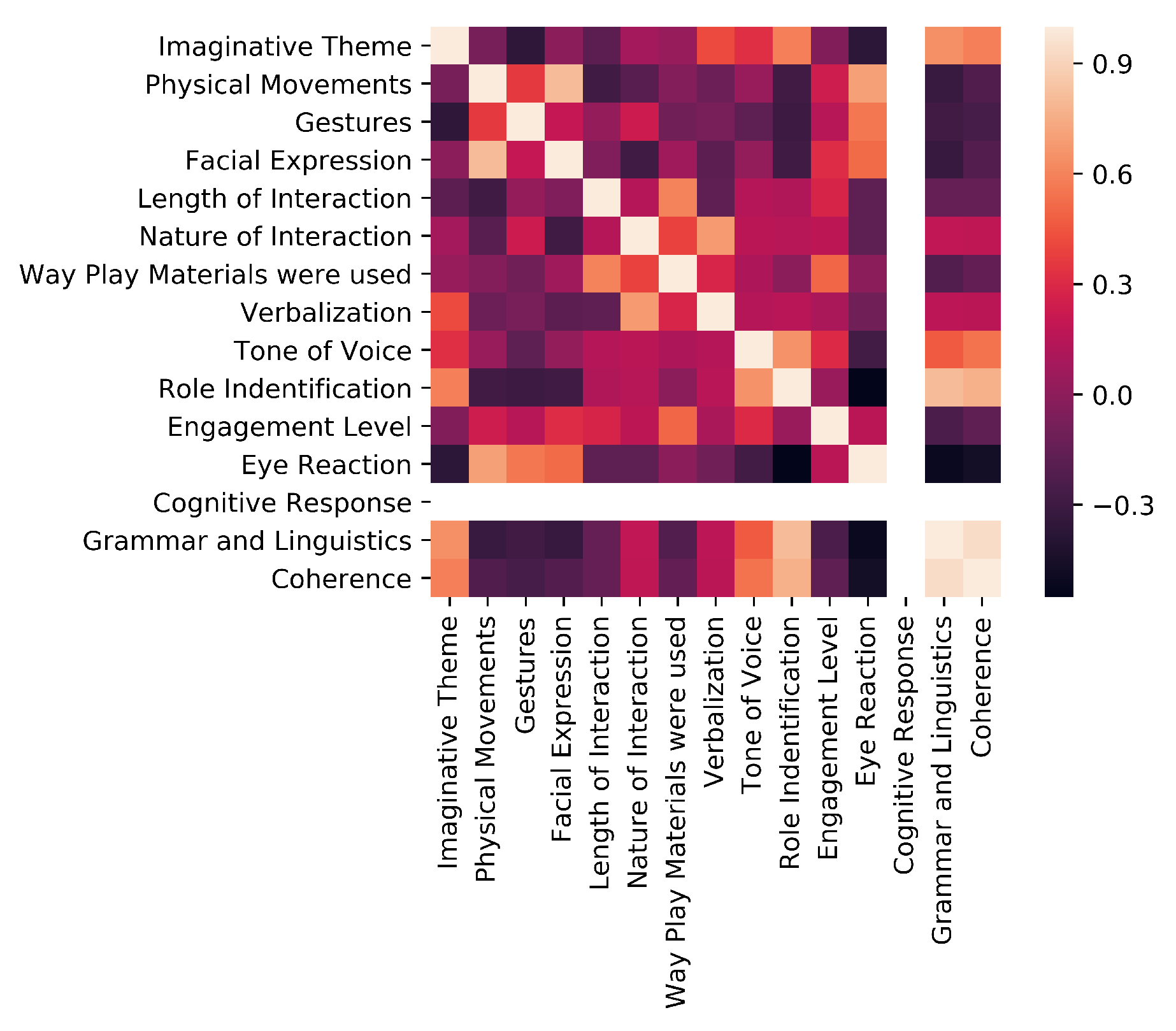
Heat map, which strongly demonstrates the factors of correlation and associativity, has a colour scale in which lighter shades signify positive correlation and darker shades signify a negative correlation. Correlation between any two parameters signifies their associated relation. Positive correlation happens when an increase in one attribute shows an increase in another attribute as well. Negative correlation happens when an increase in one attribute shows a decrease in another attribute. The heat map, which strongly demonstrates the factors of correlation and associativity, has a colour scale in which lighter shades signify positive correlation and darker shades signify a negative correlation. For example, in
Figure 3, which is a heat map for feature T, Grammar and Coherence show extremely positive correlation whereas Eye Reaction and Role Identification show a negative correlation.
The results from the
Figure 3 shows the heatmap for feature T (Truth membership).
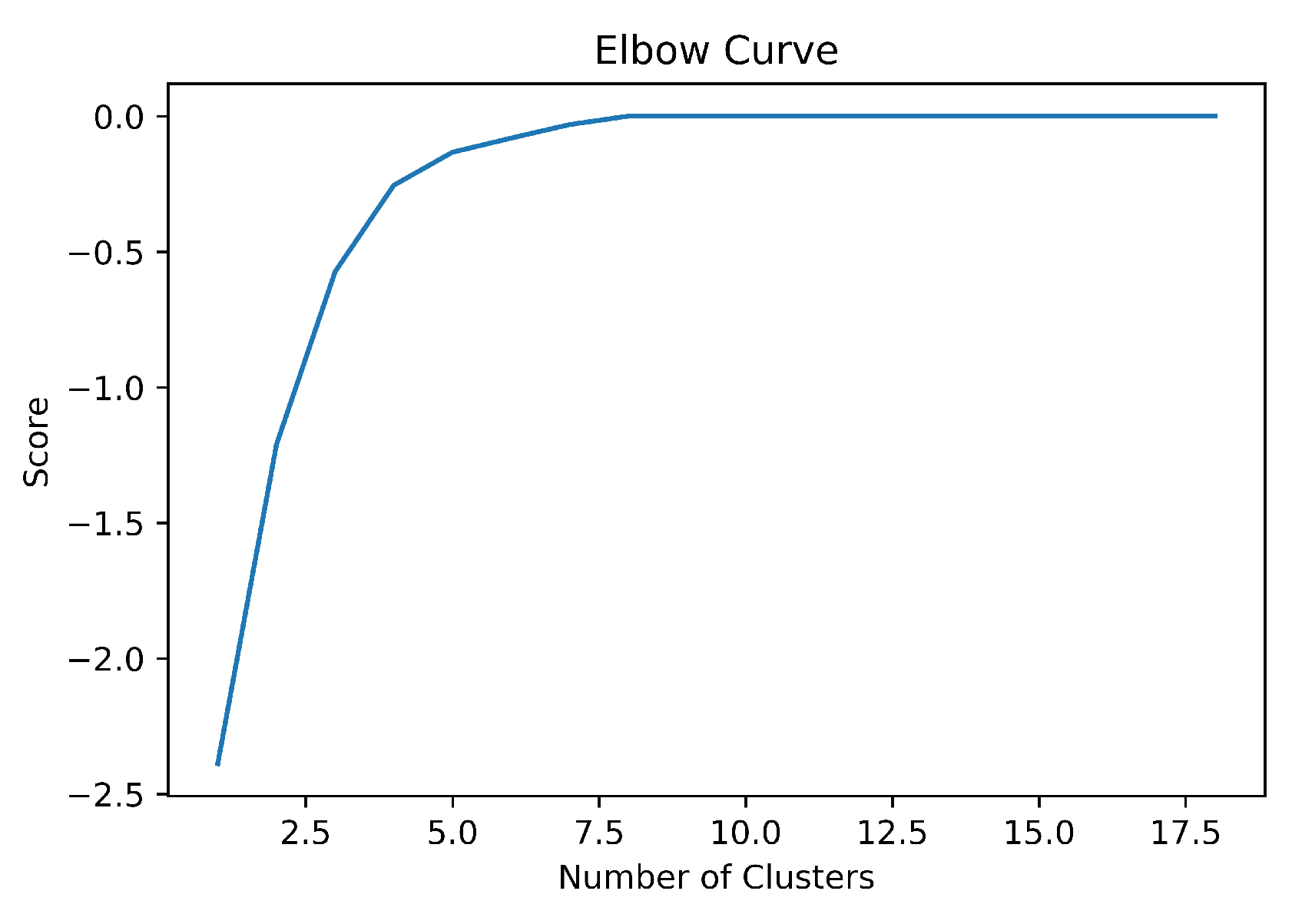
An elbow curve was plotted to determine the optimal number of clusters for K-means and PCA K-means clustering.
Figure 4 shows our elbow curve for feature T where we can see that the sharp bend comes at k = 4, thus, 4 clusters are optimal.
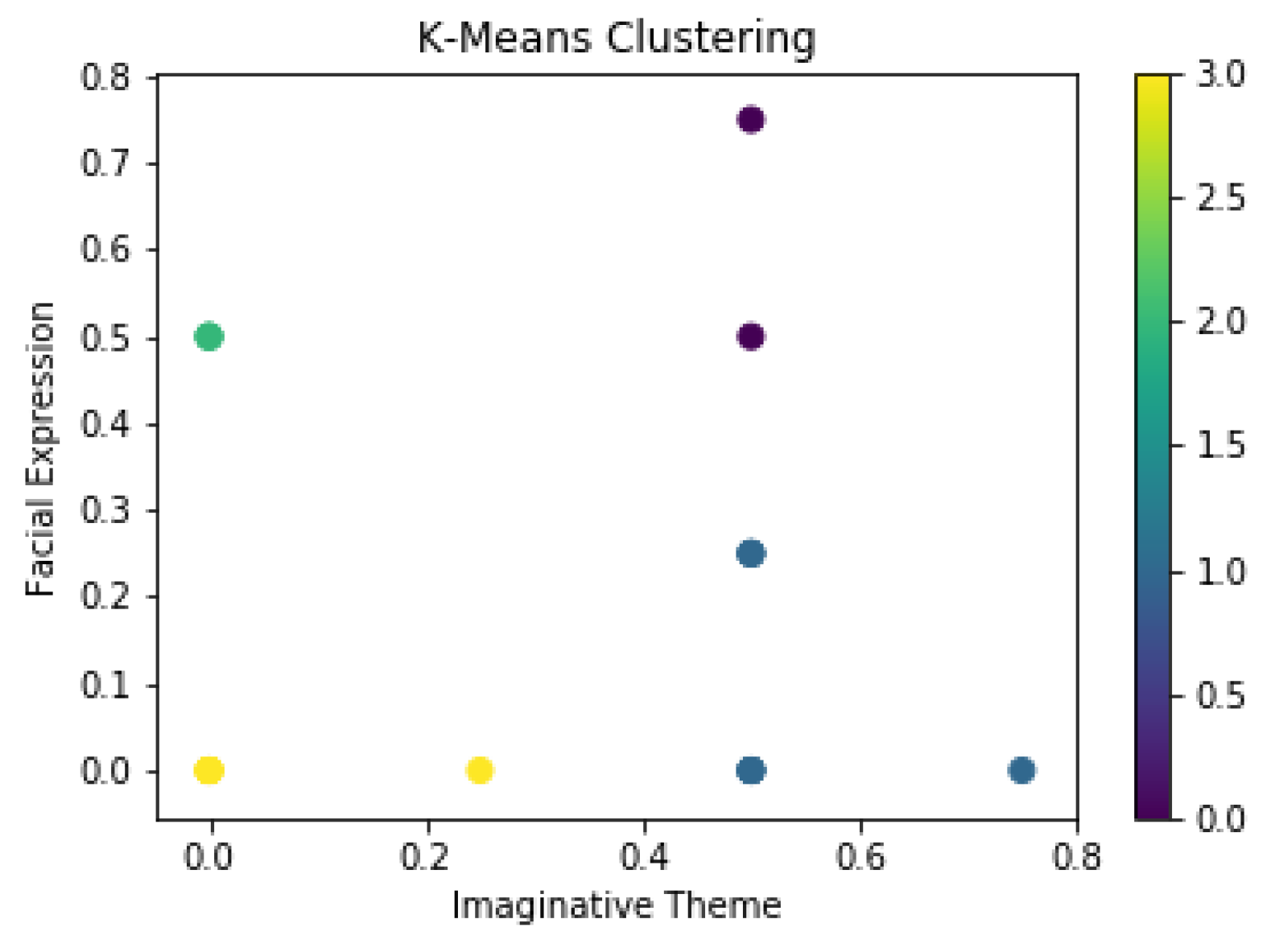
In
Figure 5, while testing K-means on feature T for the parameters ‘Facial Expression’ on the y-axis against ‘Imaginative Theme’ on the x-axis, it was found that higher concentration of points lies near x = 0.5 and y = 0.2.
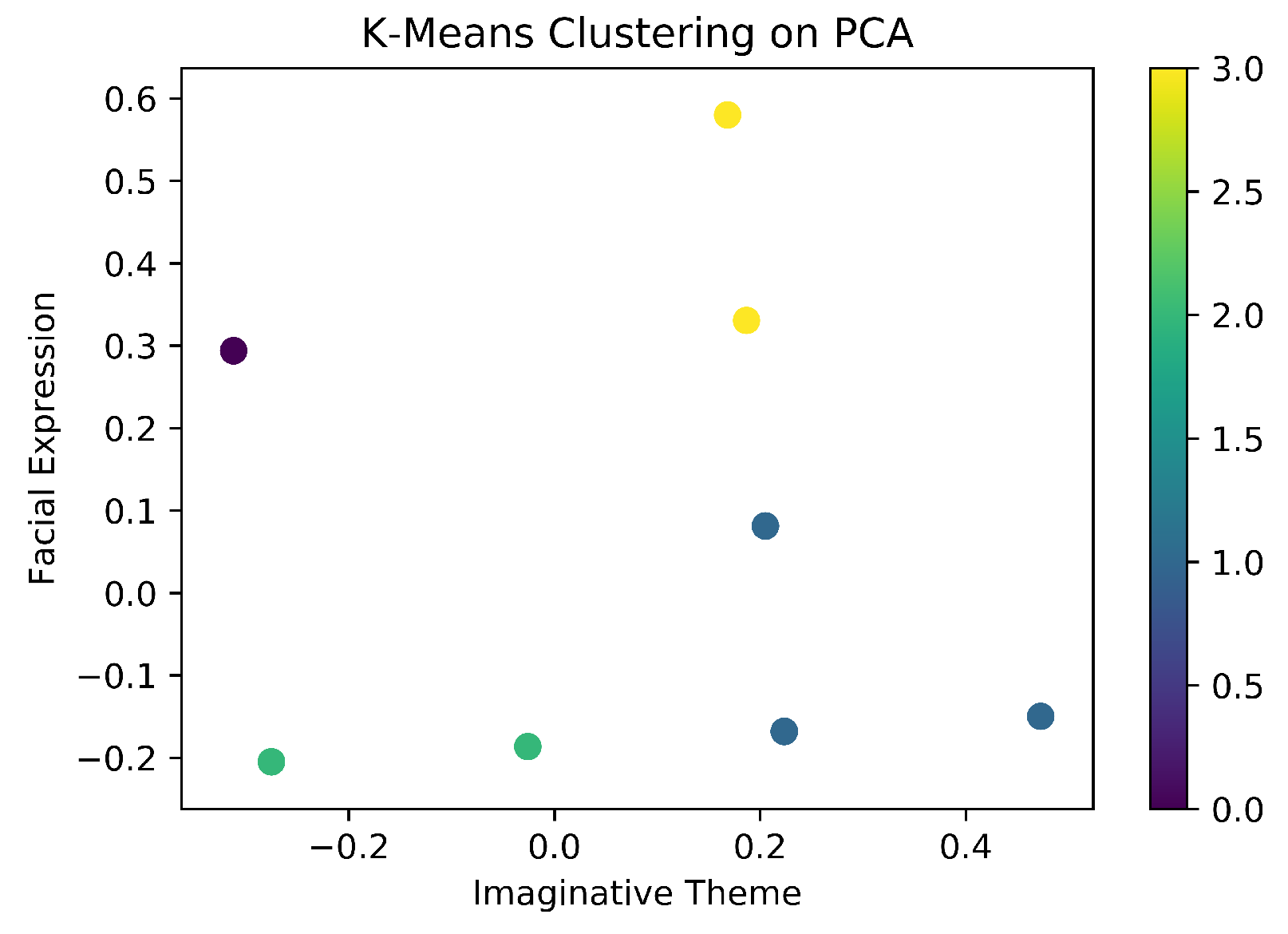
Then, the data was resolved along its principal components, thus giving a new spatial arrangement of the feature, which was then clustered again using K-Means.
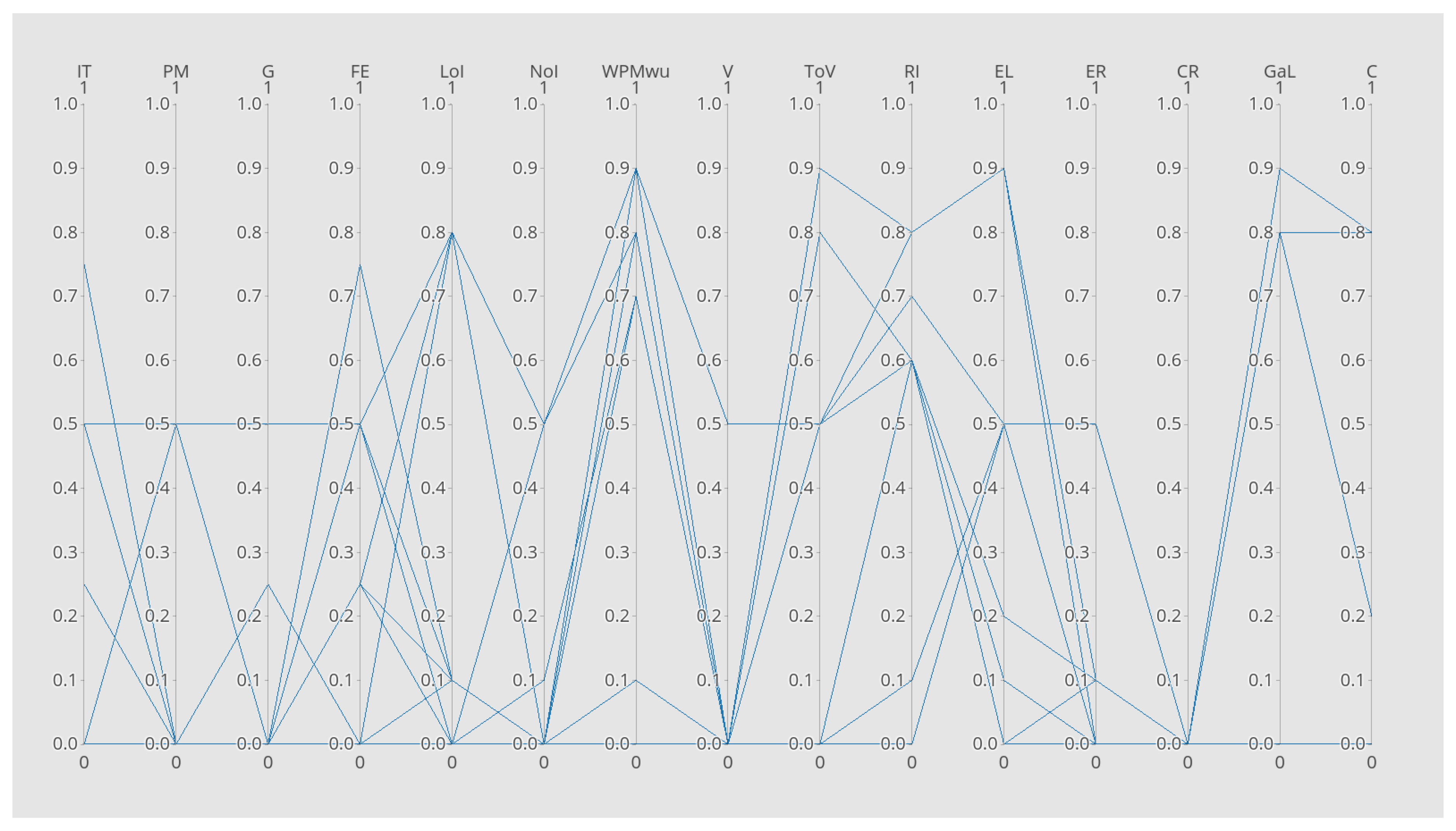
Figure 6 shows the output for PCA K-Means Clustering for T. A significant deviation of the spatial arrangement of data points is seen in the figure. Now, the higher concentration of points shift to x = 0.2, y = 0.08. ‘Tone of Voice’ and ‘Engagement Level’ are similarly associated with ‘Role Identification’ as the co-ordinate axis is symmetrical about it, as shown in
Figure 7.
The comparative analysis in
Table 4 focuses on five common factors between the four algorithms. The correlation between any two parameters signifies their associated relation. A positive correlation happens when an increase in one attribute shows an increase in another attribute as well. A negative correlation happens when an increase in one attribute shows a decrease in another attribute. The heat map, which strongly demonstrates the factors of correlation and associativity, has a colour scale in which lighter shades signify positive correlation and darker shades signify a negative correlation. For example, in
Figure 3, which is a heat map for feature T, Grammar and Coherence show extremely positive correlation whereas Eye Reaction and Role Identification show a negative correlation. The visibility of data points is best observed in the PAC graph while the least was observed in the Heat Map, which focused more on their associativity. Associativity, the reverse of this happened in PAC Graphs and Heat Maps where associativity in the former decreased due to conflict of interest in the arrangement of axes. The dynamicity of PAC, unlike for all other graphs, is the highest because the axes can be rearranged to see which arrangement gives us the best results. However, in K-Means, PCA K-Means and Heat map, the axes are static and rearranging them does not show any significant change. Scalability is a measure of how many data points can be represented in the same graph without the loss of visibility. This was found to be strongest in K-Means and PCA K-means as each point could be seen uniquely on a 2D Cartesian space.
7. Conclusions and Future Work
The authors have defined the new concept of Single Valued Refined Neutrosophic Sets (SVRNS) which is a generalized version of neutrosophic sets which functions using six memberships values. Furthermore, these SVRNS make use of imaginary values for the memberships. This newly defined concept of SVRNS was used to study the imaginative play in children. The model proposed also consists of distance measures such as Hamming distance and Euclidean distance for two given SVRNSs.
On the basis of expert opinion, the data was successfully transformed into SVRNS. These sets were helpful in drawing clusters, heat maps, parallel axes coordinate and so on. The pictorial representation of the results of these algorithms has helped to gain useful insight into the data collected. We were able to objectively interpret, for instance, the role of factors such as grammar in imaginative play in children.
On the basis of the data collected and processed to form SVRNSs, we will be able to successfully develop an artificial neural network (ANN), decision trees and other supervised learning algorithms in this domain for future research and they will be useful for drawing insights into the role of these parameters by varying the values of the parameters. Other quality measures such as p-value, confusion matrix and accuracy can also be drawn from it. Since the data under consideration were small, we were not able to construct ANN.
For future work, we will study the mentally retarded children in this age group and perform a comparative analysis with the normal children in this age group.
The model will help us in identifying children with autism and attention deficit hyperactivity disorder (ADHD) and other psychological disorders. The detection of such disorders if any at an early stage with the help of our model will help parents and doctors to use the necessary measures to treat and control them quickly.
The model can be further used for other psychological studies like for modeling destructive behaviours of alcoholics and bulimic children and/or adults.
With this given dataset, cross culture validation was not done. For future research, we shall consider the study of cross culture among children and try to generate a variation from cross culture and its effect or influence on the cognitive and language abilities of children.