Approximate Solutions of the LRS Bianchi Type-I Cosmological Model
Abstract
1. Introduction
2. Cosmological Model
3. Basic Formulation of HPM
4. Application of HPM
4.1. Solution for
4.2. Solution for
4.3. Solution for
4.4. Solution for
4.5. Solution for
4.6. Special Case
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Morris, M.S.; Thorne, K.S. Wormholes in spacetime and their use for interstellar travel: A tool for teaching general relativity. Am. J. Phys. 1988, 56, 395–412. [Google Scholar] [CrossRef]
- Sharif, M.; Jawad, A. Phantom-like generalized cosmic chaplygin gas and traversable wormhole solutions. Eur. Phys. J. Plus 2014, 129, 15. [Google Scholar] [CrossRef]
- Lobo, F.S.N.; Parsaei, F.; Riazi, N. New asymptotically flat phantom wormhole solutions. Phys. Rev. D 2013, 87, 084030. [Google Scholar] [CrossRef]
- Kim, S.-W.; Lee, H. Exact solutions of a charged wormhole. Phys. Rev. D 2001, 63, 064014. [Google Scholar] [CrossRef]
- Copeland, E.J.; Sami, M.; Tsujikawa, S. Dynamics of Dark Energy. Int. J. Mod. Phys. D 2006, 15, 1753–1936. [Google Scholar] [CrossRef]
- De Leon, J.P. Mass and charge in brane-world and noncompact Kaluza-KLEin theories in 5 dim. Gen. Relativ. Gravit. 2003, 35, 1365–1384. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshitz, E.M. The Classical Theory of Fields, 3rd ed.; Pergamon Press: Oxford, UK, 1971; Volume 2. [Google Scholar]
- Sushkov, S.V.; Kim, S.W. Wormholes supported by the kink-like configuration of a scalar field. Class Quant Graw 2002, 19, 4909–4922. [Google Scholar] [CrossRef]
- He, J.H. Homotopy perturbation technique. Comput. Meth. Appl. Mech. Eng. 1999, 178, 257262. [Google Scholar] [CrossRef]
- Cveticanin, L. Homotopy-perturbation method for pure nonlinear differential equation. Chaos Solitons Fractals 2006, 30, 12211230. [Google Scholar] [CrossRef]
- He, J.H. Application of homotopy perturbation method to nonlinear wave equations. Chaos Solitons Fractals 2005, 26, 695700. [Google Scholar] [CrossRef]
- He, J.H. Limit cycle and bifurcation of nonlinear problems. Chaos Solitons Fractals 2005, 26, 827833. [Google Scholar] [CrossRef]
- He, J.H. Homotopy perturbation method for solving boundary value problems. Phys. Lett. A 2006, 350, 8788. [Google Scholar] [CrossRef]
- He, J.H. A coupling method of homotopy technique and perturbation technique for nonlinear problems. Int. J. Nonlinear Mech. 2000, 35, 3743. [Google Scholar] [CrossRef]
- He, J.H. Comparison of homotopy perturbation method and homotopy analysis method. Appl. Math. Comput. 2004, 156, 527539. [Google Scholar] [CrossRef]
- He, J.H. Homotopy perturbation method: A new nonlinear analytical technique. Appl. Math. Comput. 2003, 135, 7379. [Google Scholar] [CrossRef]
- He, J.H. Homotopy perturbation method with two expanding parameters. Indian J. Phys. 2014, 88, 193–196. [Google Scholar] [CrossRef]
- Farasat Shamir, M. Locally Rotationally Symmetric Bianchi Type I Cosmology in f(R,T) Gravity. Eur. Phys. J. C 2015, 75, 354. [Google Scholar] [CrossRef]
- Mustafa, G.; Abbas, G.; Shahzad, M.R.; Xia, T. Stable wormholes existence under non-commutative distributed background in Rastall theory. Can. J. Phys. 2019, 17, 0026. [Google Scholar] [CrossRef]
- Mustafa, G.; Shahzad, M.R.; Abbas, G.; Xia, T. Stable wormholes solutions in the background of Rastall theory. Mod. Phys. Lett. 2020, 33, 2050035. [Google Scholar] [CrossRef]
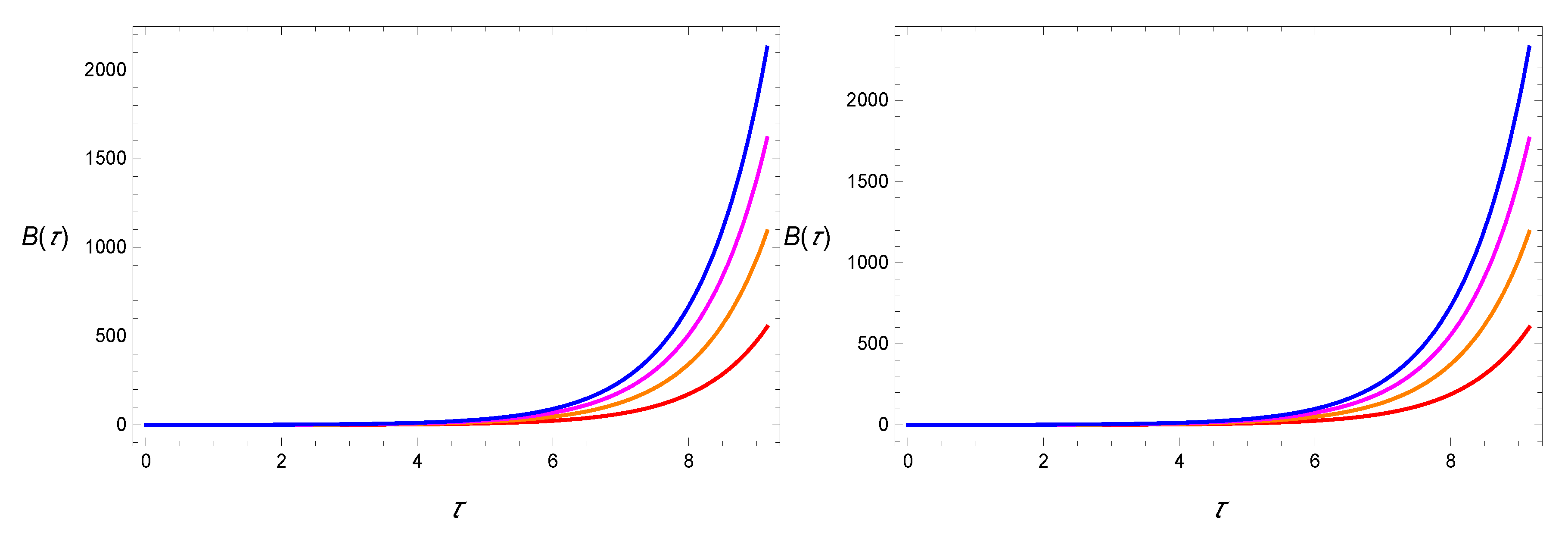
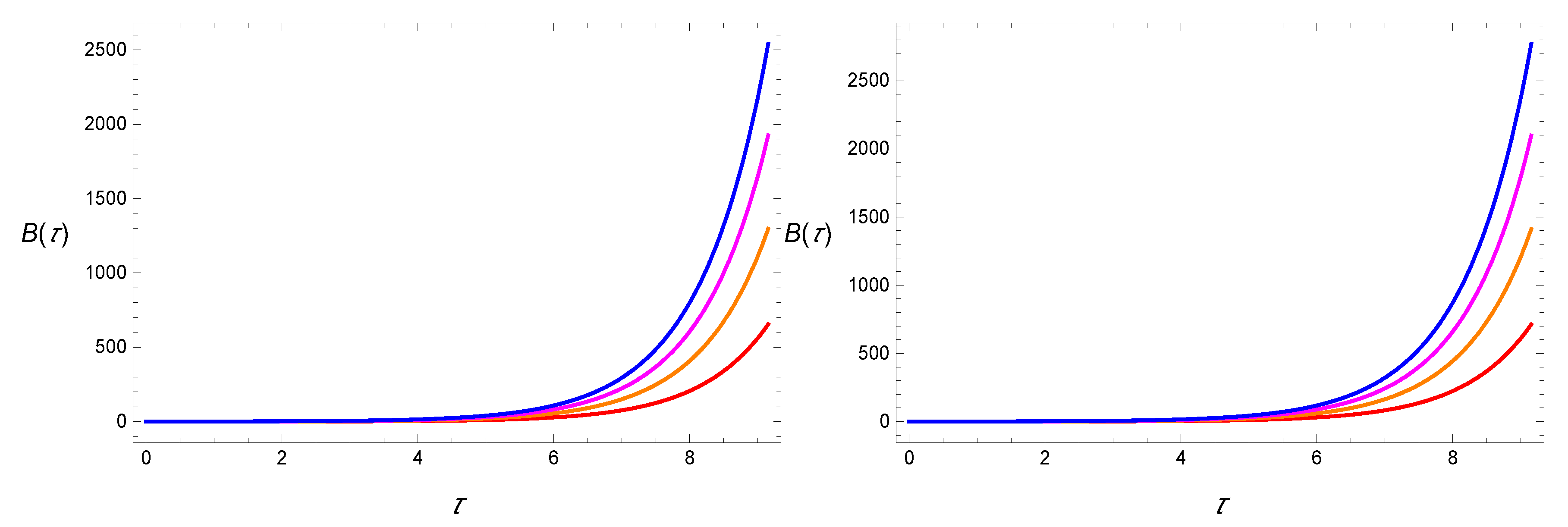
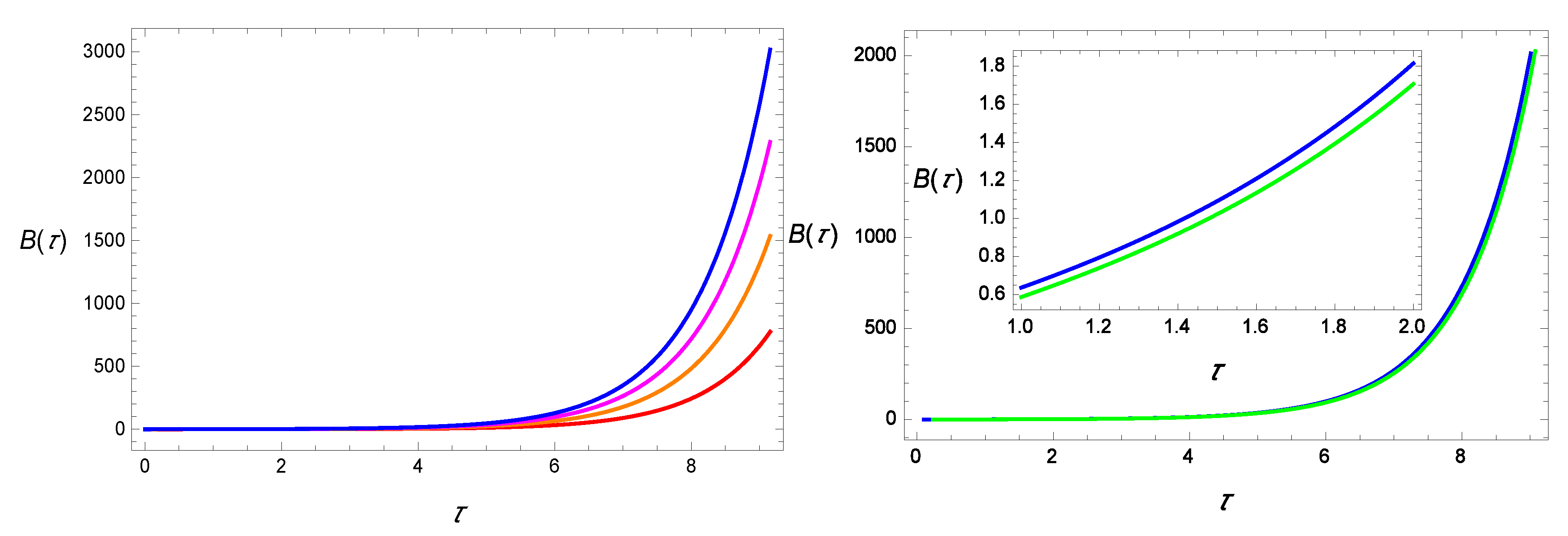
| and | ||
|---|---|---|
| HPM | Exact | |
| 0.3 | 0.198989 | 0.100976 |
| 0.8 | 0.499301 | 0.451041 |
| 1.3 | 0.885666 | 0.827151 |
| 1.8 | 1.483150 | 1.393510 |
| 2.3 | 2.453730 | 2.308390 |
| 2.8 | 4.048630 | 3.809900 |
| 3.3 | 6.676200 | 6.282930 |
| 3.8 | 11.00760 | 10.35930 |
| 4.3 | 18.14860 | 17.07990 |
| 4.8 | 29.92210 | 28.16000 |
| 5.3 | 49.33320 | 46.42800 |
| 5.8 | 81.33670 | 76.54680 |
| 6.3 | 134.1020 | 126.2040 |
| 6.8 | 221.0960 | 208.0760 |
| 7.3 | 364.5260 | 343.0590 |
| 7.8 | 601.0010 | 565.6090 |
| 8.3 | 990.8840 | 932.5310 |
| 8.8 | 1633.690 | 1537.480 |
| 9.3 | 2693.500 | 2534.880 |
| 9.8 | 4440.830 | 4179.320 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feng, Y.; Hou, L. Approximate Solutions of the LRS Bianchi Type-I Cosmological Model. Symmetry 2020, 12, 403. https://doi.org/10.3390/sym12030403
Feng Y, Hou L. Approximate Solutions of the LRS Bianchi Type-I Cosmological Model. Symmetry. 2020; 12(3):403. https://doi.org/10.3390/sym12030403
Chicago/Turabian StyleFeng, Yihu, and Lei Hou. 2020. "Approximate Solutions of the LRS Bianchi Type-I Cosmological Model" Symmetry 12, no. 3: 403. https://doi.org/10.3390/sym12030403
APA StyleFeng, Y., & Hou, L. (2020). Approximate Solutions of the LRS Bianchi Type-I Cosmological Model. Symmetry, 12(3), 403. https://doi.org/10.3390/sym12030403





