Abstract
For the numerical integration of differential equations with oscillatory solutions an exponentially fitted explicit sixth-order hybrid method with four stages is presented. This method is implemented using variable step-size while its derivation is accomplished by imposing each stage of the formula to integrate exactly where the frequency μ is imaginary. The local error that is employed in the step-size selection procedure is approximated using an exponentially fitted explicit fourth-order hybrid method. Numerical comparisons of the new and existing hybrid methods for the spring-mass and other oscillatory problems are tabulated and discussed. The results show that the variable step exponentially fitted explicit sixth-order hybrid method outperforms the existing hybrid methods with variable coefficients for solving several problems with oscillatory solutions.
1. Introduction
Computation of the solutions of the special second order initial value problems
in which the first derivative does not appear explicitly has spawned many numerical algorithms and approaches. These problems often emerge in engineering and applied sciences and may be directly solved using numerical methods such as Runge–Kutta–Nystrom methods, multistep methods and hybrid methods.
In general, numerical methods are divided into two categories: (1) methods with constant coefficients and (2) methods with variable coefficients. In the development of methods with constant coefficients, one has to consider the algebraic order, the phase-lag order, the dissipation order, the strategy of minimizing the error constant and the size of interval of periodicity or the interval of absolute stability of the resulting methods (e.g., [1,2,3,4,5]). Meanwhile, development of methods with variable coefficients involves the usage of various techniques such as phase-fitting, amplification-fitting, trigonometric-fitting and exponential-fitting (e.g., [6,7,8]). These techniques are used to get methods specially adapted to the certain behavior or the structure of the solution of the problem, hence the methods with variable coefficients usually depend on the frequency of the problem. For variable step-size implementation where the step-size varies throughout the integration, accuracy and the computational cost are very much depending on the formulation of the numerical methods and the step-size control algorithm. In the step-size control algorithm, a certain procedure is usually employed to keep the local error smaller than the desired tolerance. The local error may be approximated by a pair of embedded formulas with different algebraic orders (e.g., [9,10]) or phase lag orders (e.g., [11]). In previous work, it is observed that more attention is paid to the algebraic orders and phase-lag properties than the interval of absolute stability in the development of embedded formulas for variable step-size implementation.
In this paper, we attempt to derive an exponentially fitted explicit sixth-order hybrid method by taking into consideration the strategy of maximizing the interval of absolute stability. The method is implemented using a variable step-size in which a lower order embedded formula of hybrid method is employed for the local error estimation.
Our interest is confined to the class of explicit hybrid methods proposed by Franco [12].
where h is the step-size while and represent and respectively. These methods require s – 1 function evaluations or stages at each step of integration. In Butcher tableau notation, these methods can be represented by
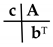 where A = [aij], bT = [b1 b2 … bs] and cT = [c1 c2 … cs]. Order conditions for this class of methods are as listed in [13] while the leading term of the local truncation error for a pth-order hybrid method is defined to be
where ti ∈ T2 and ρ(ti) = p + 2. The error constant is the quantity
where is the number of trees of order p + 2 [12].
where A = [aij], bT = [b1 b2 … bs] and cT = [c1 c2 … cs]. Order conditions for this class of methods are as listed in [13] while the leading term of the local truncation error for a pth-order hybrid method is defined to be
where ti ∈ T2 and ρ(ti) = p + 2. The error constant is the quantity
where is the number of trees of order p + 2 [12].
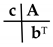
2. Stability Analysis
The stability analysis is presented for hybrid methods with constant coefficients and for hybrid methods with coefficients depending on the multiplication of frequency and the step-size.
Consider the standard equation
with exact solution . Let H = λh, and e = (1 1 … 1)T. Applying the hybrid methods defined in Equation (1) with constant coefficients to the differential Equation (2) yields the following equation
where
The characteristic polynomial, which determines the solution of Equation (3), is
Theory of linear stability analysis requires that the characteristic polynomial (Equation (4)) must be Schur stable to guarantee the stability of the corresponding method. Thus, all roots of Equation (4) must lie inside a unit circle in a complex plane. Hence, the following definitions give conditions for the interval of periodicity and the interval of absolute stability of the methods.
Definition 1.
For hybrid methods corresponding to Equation (4), the interval (0, Hp) is called the interval of periodicity ifandfor all H ∈ (0, Hp).
Definition 2.
For hybrid methods corresponding to Equation (4), the interval (0, Ha) is called the interval of absolute stability ifandfor all H ∈ (0, Ha).
If the coefficients of hybrid methods defined in Equation (1) are functions of v = μh where μ is the frequency of the problem and h is the step-size, then the interval of absolute stability is generalized to the region of stability. Setting μ = iw, w is real to match the oscillatory behavior of the exact solution of Equation (2), and θ = wh, we arrive at the following definition.
Definition 3.
A region of stability is a region of the θ-H plane throughout whichand.
3. Derivation of the New Method
3.1. Exponentially Fitted Sixth-Order Method
Consider coefficients of a class of four-stage explicit hybrid methods given by Table 1:

Table 1.
Coefficients of a class of four-stage explicit hybrid methods.
Setting and solving equations of conditions for a sixth-order hybrid method, we get
The free parameter is chosen to maximize the interval of absolute stability. Applying the transformation to the characteristic polynomial (Equation (4)) yields the equation:
This transformation maps the interior of a unit circle to the left half plane Re (ζ) < 0 while the boundary of the unit circle to the imaginary axis. For stability, the points should satisfy the inequalities arising from the Routh–Hurwitz criterion. A graph with a region of feasible solutions to the Routh-Hurwitz criterion is depicted. In order to extend the interval of absolute stability, the point with the biggest possible interval (0, H) apparent in the graph is chosen. Here, we choose . Consequently, all other coefficients are
The interval of absolute stability is (0, 4.42) while the error constant E = 2.08 × 10−3 [14]. Using these coefficients, the characteristic polynomial (Equation (4)) is a Schur polynomial if H < 4.42. The Schur polynomial is symmetric and a basis of all symmetric polynomials.
Next, we assume that the coefficients are functions of θ while other coefficients remain constants. Then, we associate each stage formula of four-stage explicit hybrid methods with the linear operator Li[y(t)] as follows:
Setting , and with and results in coefficients ,, ,, and :
with their respective Taylor series expansions
Setting with and , coefficients are obtained:
with the Taylor series expansions:
Based on the Taylor series expansions, it is obvious that the coefficients of the exponentially fitted sixth-order hybrid method (denoted as EXH6) will be equal to their original constant values if θ = 0. The region of stability of the method is shown in Figure 1.
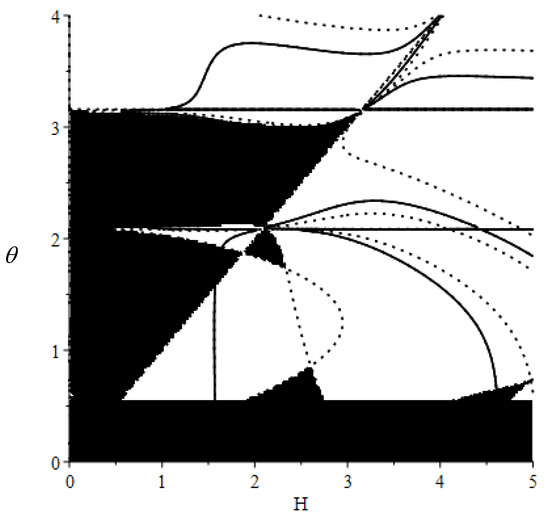
Figure 1.
Region of stability of the exponentially fitted explicit sixth-order hybrid method.
3.2. Exponentially Fitted Fourth-Order Method
This section discusses the derivation of the exponentially fitted fourth-order method to be used as a tool for local error estimation. Consider a class of three-stage explicit hybrid method represented by Table 2:

Table 2.
Coefficients of a class of three-stage explicit hybrid methods.
The fourth-order method has the same c and A values as the sixth-order method with constant coefficients described in Section 3.1. Using the order conditions for a fourth-order explicit hybrid method as listed in [13], we obtain
, , and [14].
Assume that are functions of θ. Setting the following linear operator
to zero for and , we have
with the Taylor series expansions:
In the variable step-size setting, the local error estimation is calculated using the formula
where and are solutions obtained from the exponentially fitted sixth-order hybrid method and the exponentially fitted fourth-order hybrid method respectively. If “tol” is the user-specified tolerance, then the step-size is selected by this procedure:
If LTE < tol, then the step is accepted and the new step-size is unchanged
If LTE ≥ tol, then the step is rejected and the new step-size is computed using the formula
4. Results
In our numerical experiments, the new and existing methods were coded using Microsoft Visual C++ software and abbreviated as follows.
EXH6: The exponentially fitted explicit sixth-order hybrid method with four stages derived in this paper. This method was implemented in variable step.
TSI6: The exponentially fitted explicit sixth-order hybrid method with four stages proposed by Tsitouras and Simos [15]. This method was implemented using the same step-size selection procedure as that for EXH6. The rational approximations of the coefficients in [15] were implemented to control the local error.
EEHM6(4): The exponentially fitted explicit sixth-order hybrid method proposed in [16] and implemented using the step-size selection procedure as discussed in [16].
The performance of the new and existing methods was measured by the number of function evaluations and maximum global errors for specified tolerances. We have set all maximum global errors to 16 digits of precision. Table 3, Table 4, Table 5, Table 6 and Table 7 show the numerical results obtained for the new and existing methods. In the tables, SSTEP and FSTEP each denotes the number of successful steps of integration that was being accepted and rejected respectively. Other abbreviations are:

Table 3.
Numerical results of EXH6, TSI6 and EEHM6(4) for Problem 1.

Table 4.
Numerical results of EXH6, TSI6 and EEHM6(4) for Problem 2.

Table 5.
Numerical results of EXH6, TSI6 and EEHM6(4) for Problem 3.

Table 6.
Numerical results of EXH6, TSI6 and EEHM6(4) for Problem 4.

Table 7.
Numerical results of EXH6, TSI6 and EEHM6(4) for Problem 5.
MAXGE: Maximum global error
NFE: Number of function evaluations
TOL: Tolerance
Problem 1 (Perturbed system)
Source: [8]
with and
Exact solution:
For the first component of this problem, w was chosen to be 10 while for the second component, w was chosen to be 5
Problem 2 (Linear oscillatory problem)
Source: [12]
Exact solution:
For this problem, w was chosen to be 5.
Problem 3 (The undamped Duffing’s equation)
Source: [17]
where and v = 1.01. The approximate solution computed by the Galerkin method with a precision of is given by
where A1 = 0.200179477536, A3 = 2.46946143 ⋅ 10−4, A5 = 3.04014 ⋅ 10−7, A7 = 3.74 ⋅ 10−10, A9 = 0.000000000000.
For this problem, we chose w = 1.
Problem 4 (The nonlinear oscillatory problem)
Source: [12]
Exact solution:
For this problem, w = 1.
Problem 5 (Application to the spring-mass model for running)
Source: [18]
where r(t) is the radial motion over time t, k is the stiffness of the leg spring, is the rest length and g is the gravitational acceleration. It is also noted that denotes the angular velocity with the touch-down condition and the spring amplitude ρ. Assume that the initial values are given by
The exact solution of this problem is
We solved the problem by choosing as an example k = 11, g = 9.81, , m = 80 and ρ = 0.001 for 0 ≤ t ≤ 100. For all methods, the selected w was .
5. Discussion and Conclusions
In this paper, the development of the sixth-order explicit hybrid method with an extended interval of absolute stability is described along with the exponential-fitting technique used to obtain the exponentially-fitted sixth-order hybrid method which is denoted by EXH6. In the technique, each stage formula is imposed to exactly integrate where μ is imaginary. This method is compared with the existing methods in [15] and [16] for several oscillatory problems. The derivation of TSI6 involved nullifying the phase-lag along with the phase-lag first and second derivatives [15] while the derivation of EEHM6(4) involved the usage of the exponential-fitting technique to the sixth-order hybrid method derived in [12] having an interval of periodicity (0, 2.75).
Of all methods, EXH6 gives high accuracy with a reasonable number of function evaluations for all tolerances considered in Problem 1 (the perturbed system) and has the smallest number of function evaluations for solving Problem 2 (the linear oscillatory problem). For Problem 3, EEHM6(4) has the smallest number of function evaluations followed by EXH6, while EEHM6(4) and EXH6 both perform well for Problem 4 (the nonlinear oscillatory problem). Application of the methods to the spring-mass model for running in Problem 5 shows that EXH6 can reach up to fifteenth order of accuracy while EEHM6(4) and TSI6 can only reach up to the third order and eleventh order of accuracy even for stringent tolerances. For tolerances and , the accuracy of EXH6 is slightly bigger than that for tolerance due to round off errors. Furthermore, TSI6 has the biggest number of function evaluations compared to the EXH6 and EEHM6(4) methods for most of the tolerances in all problems considered. This fact indicates that TSI6 needs more computational cost than that needed by EXH6 and EEHM6(4). In conclusion, the new method outperforms the existing hybrid methods for solving several special second order problems. Hence, these results offer evidence that variable step methods with variable coefficients are more efficient if the derivation of the methods takes into account the strategy of maximizing the interval of stability.
Author Contributions
Conceptualization, F.S.; methodology, F.S.; investigation, F.S.; software, E.S.I.; funding acquisition, F.S.; writing—original draft preparation, F.S.; writing—review and editing, E.S.I. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Universiti Kebangsaan Malaysia, grant number GGPM-2017-074.
Acknowledgments
The authors would like to thank Kamaruzaman Jusoff for his suggestions that led to this research.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Franco, J.M.; Randez, L. Eight-order explicit two-step hybrid methods with symmetric nodes and weights for solving orbital and oscillatory IVPs. Int. J. Mod. Phys. C 2018, 29, 18. [Google Scholar] [CrossRef]
- Senu, N.; Suleiman, M.; Ismail, F.; Othman, M. A zero dissipative Runge-Kutta-Nystrom method with minimal phase-lag. Math. Probl. Eng. 2010, 591341. [Google Scholar] [CrossRef]
- Chawla, M.M. A new class of explicit two-step fourth order methods for y″ = f(t, y) with extended intervals of periodicity. J. Comput. Appl. Math. 1986, 14, 467–470. [Google Scholar] [CrossRef]
- Stavroyiannis, S.; Simos, T.E. Optimization as a function of the phase-lag order of nonlinear explicit two-step P-stable method for linear periodic IVPs. Appl. Numer. Math. 2009, 59, 2467–2474. [Google Scholar] [CrossRef]
- Franco, J.M.; Palacios, M. High-order P-stable multistep methods. J. Comput. Appl. Math. 1990, 30, 1–10. [Google Scholar] [CrossRef]
- Ahmad, N.A.; Senu, N.; Ismail, F. Phase-fitted and amplification-fitted higher order two-derivative Runge-Kutta method for the numerical solution of orbital and related periodical IVPs. Math. Probl. Eng. 2017, 1871278. [Google Scholar] [CrossRef]
- Yang, H.; Wu, X. Trigonometrically-fitted ARKN methods for perturbed oscillators. Appl. Numer. Math. 2008, 58, 1375–1395. [Google Scholar] [CrossRef]
- Franco, J.M. Exponentially fitted explicit Runge-Kutta-Nystrom methods. J. Comput. Appl. Math. 2004, 167, 1–19. [Google Scholar] [CrossRef]
- Van de Vyver, H. A Runge-Kutta-Nystrom pair for the numerical integration of perturbed oscillators. Comput. Phys. Commun. 2005, 167, 129–142. [Google Scholar] [CrossRef]
- Raptis, A.D.; Cash, J.R. A variable step method for the numerical integration of the one-dimensional Schrodinger equation. Comput. Phys. Commun. 1985, 36, 113–119. [Google Scholar] [CrossRef]
- Simos, T.E.; Williams, P.S. New insights in the development of Numerov-type methods with minimal phase-lag for the numerical solution of the Schrodinger equation. Comput. Chem. 2001, 25, 77–82. [Google Scholar] [CrossRef]
- Franco, J.M. A class of explicit two-step hybrid methods for second-order IVPs. J. Comput. Appl. Math. 2006, 187, 41–57. [Google Scholar] [CrossRef]
- Coleman, J.P. Order conditions for a class of two-step methods for y” = f(x,y). IMA J. Numer. Anal. 2003, 23, 197–220. [Google Scholar] [CrossRef]
- Samat, F.; Razak, N. Derivation of explicit 6(4) pair of hybrid methods for special second order ordinary differential equations. In Proceedings of the 25th National Symposium on Mathematical Sciences, AIP Conference Proceedings, Pahang, Malaysia, 27–29 August 2017; American Institute of Physics: College Park, MD, USA, 2018; Volume 1974, p. 020077. [Google Scholar]
- Tsitouras, C.; Simos, T.E. Trigonometric-fitted explicit Numerov-type method with vanishing phase-lag and its first and second derivatives. Mediterr. J. Math. 2018, 15, 168. [Google Scholar] [CrossRef]
- Samat, F.; Ismail, F.; Suleiman, M.B. A variable step-size exponentially fitted explicit hybrid method for solving oscillatory problems. Int. J. Math. Math. Sci. 2011, 2011, 328197. [Google Scholar] [CrossRef]
- Simos, T.E.; Dimas, E.; Sideridis, A.B. A Runge-Kutta-Nystrom method for the numerical integration of special second-order periodic initial-value problem. J. Comput. Appl. Math. 1994, 51, 317–326. [Google Scholar] [CrossRef][Green Version]
- Geyer, H.; Seyfarth, A.; Blickhan, R. Spring-mass running: Simple approximate solution and application to gait stability. J. Theor. Biol 2005, 232, 315–328. [Google Scholar] [CrossRef] [PubMed]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).