2. The Birth of the Universe. Modernization of the Process of Baryon Asymmetry
For the production of the observed number of particles (10
88), the model of a slowly swelling Universe as the result of the multiple reproductions of cosmological cycles arises naturally. Eventually, it had passed off to a modern de Sitter regime by tunneling [
6]. Besides, the cyclic solution is an attractor [
9]. As pointed out in article [
10] many years ago, entropy produced during one cycle would add to the entropy produced in the next, causing each cycle to be longer than the one before it. Details of the cyclic model and propagation through singularity can be found in articles [
11,
12]. On
Figure 1 illustration of a slowly swelling Universe is presented.
The term “nothing” denotes an extremely compactified empty space (without particles): analog of a classical singularity. Our initial conditions were: topology is closed; N
0 ~ 10
4–10
6 cm
−3, RPT is the second order on scale E ~ 10
16 GeV, and the generation of a new phase continuously occurs. The Universe born out of “nothing” in an anisotropic state (for example, Bianchi type IX) relaxed quickly to some equilibrium state including metric. We considered a quantitative model of the RPT [SU(5)]
SUSY→[U(1)xU(2)xSU(3)]
SUSY. A chain of phase transitions in the early Universe might be:
Here G is the local super symmetry group joining all physical fields and interactions; D
4 is the group of diffeomorphisms corresponding to gravitational interaction; [SU(5)]
SUSY is the group Grand Unification with global super symmetry; U(1)xSU(2)xSU(3) is the group symmetry of Standard Model. The only trace of the first RPT is the initial Λ-term. The remaining RPT are described by modern theories of elementary particles. During RPT, with the cooling of the cosmological plasma, vacuum condensates of quantum fields with a negative energy density were produced p = −ε. Thus, the RPT series was accompanied by the generation of negative contributions to the cosmological Λ-term. At first, a gravitation vacuum condensate (topological defects of different dimensions) was produced which gave a start to beginning time in our Universe. After a large number of oscillations (~10
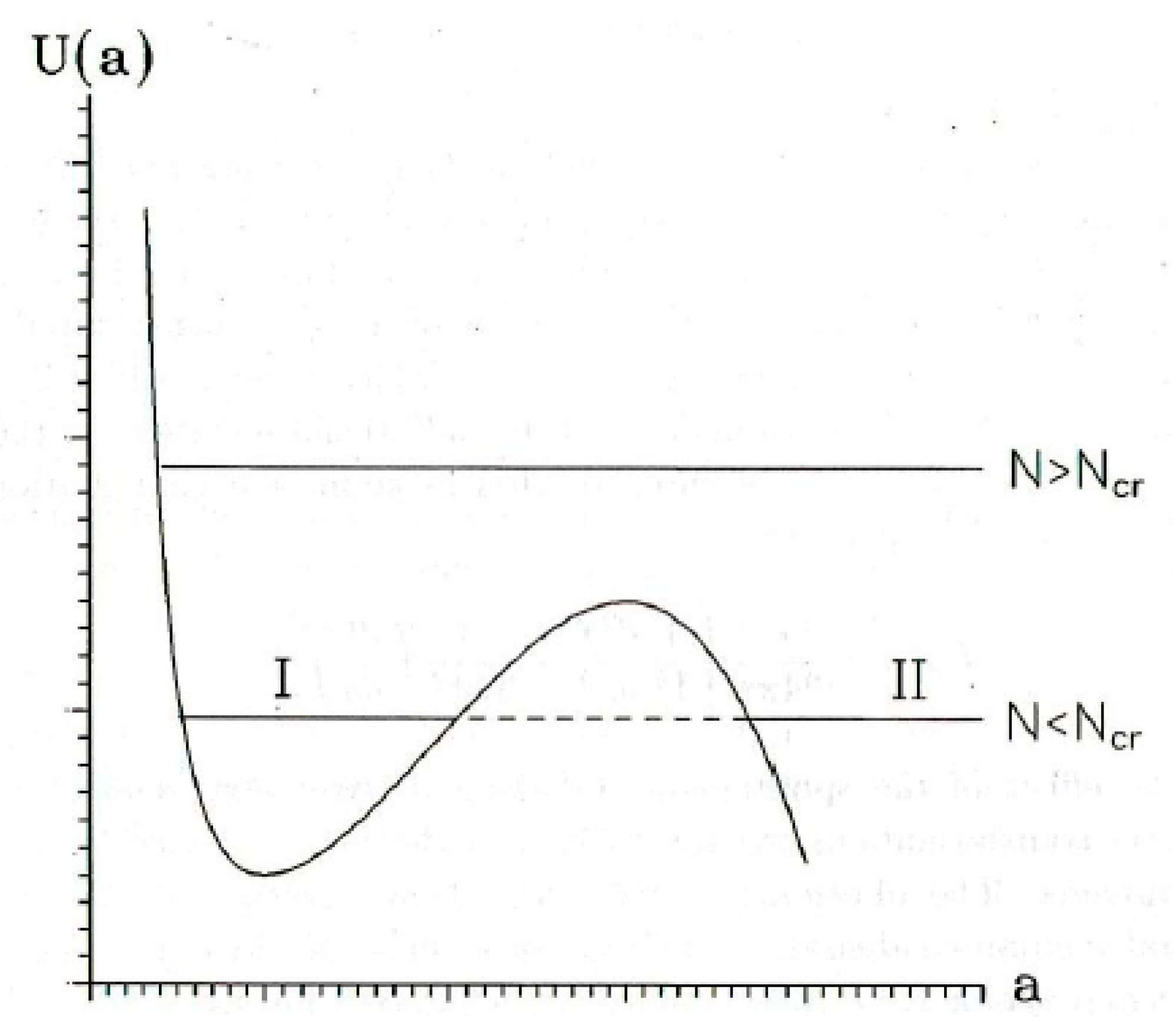
5), the Universe underwent a tunneling transition in the high-symmetry thermodynamically unstable phase (
Figure 2) when expansion in the de Sitter regime became inevitable.
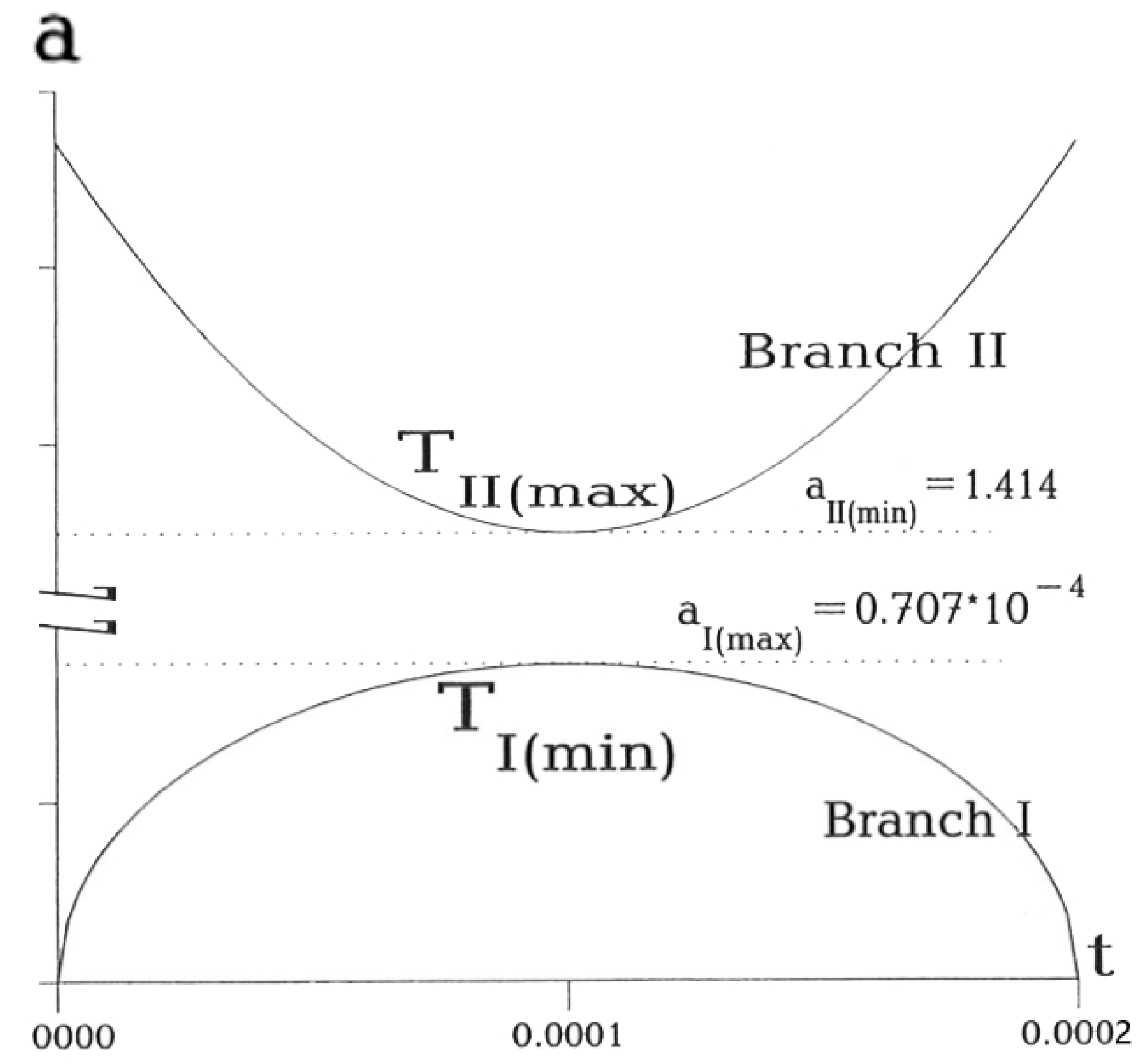
The hypothesis about quantum bounce of the Universe from singularity and quasi-classical oscillations after its creation from “nothing” lead to the conclusion that the probability of tunneling from branch I to branch II increases monotonously with an increasing number of oscillation cycles in region I (
Figure 3). With the increase of the number of oscillation cycles, eventually the tunneling will take place in spite of the small probability of tunneling on each separate oscillation cycle. The relation of radii is the characteristic parameter describing the effect of spontaneous increasing of the universe size:
If the initial number of particles is 5 ×10
5<N
cr, N
cr ≈5 × 10
11 cm
−3 [
7], then the radius increases by a factor of 2 × 10
4 as the result of quantum tunneling. This phenomenon can be considered as an analogue of classical inflation. On calculated energy (10
16 GeV), we got the number of particles 10
60 only. As previously mentioned, the observed particle number ~10
88 has been created after multiple cosmological cycles containing all series of relativistic phase transitions [
6,
7]. It was a slow swell.
The key moment of the very early universe evolution is production of baryon asymmetry, which is characterized by the relation:
It is most likely that the Universe was born in the baryon symmetric state, which was more energetic profit but now
. The right (standard) mechanism of baryon asymmetry production has been proposed more than 40 years ago in [
13]. Recently, we modernized this mechanism by introduction of magnetic monopoles in the composition of super heavy gauge bosons—dyon-lepto-quarks with mass ~10
16 GeV [
14]. It is known that magnetic particles have a huge force attraction. An important dependence was derived by Dirac in the article [
15]:
Here: e—electric charge; g—magnetic charge; k—the monopole quantum number. Relation of thin structure constants for magnetic and electric particles characterized attractive force for k = 1 and g = 68.5 is:
For k = 2 g = 137 and α
m/α
е = 18769. J. Schwinger [
16] proposed to take only even means for k in the early universe (a more symmetrical case). For the realization of baryon asymmetry of the Universe, it is necessary to carry out Sakharov’s conditions [
17]:
- (1)
nonconservation of baryon number B;
- (2)
violation of C and CP symmetries;
- (3)
violation of thermodynamical equilibrium.
These conditions are practically impossible to carry out in standard model of particle physics. It is most likely that super-heavy dyon-lepto-quarks and their antiparticles were decayed to create the baryon asymmetry of our Universe Ƞ
b. Note, that standard scenario [
13] gives only η
В ~ 10
-6. We hope that the introduction of magnetic monopoles in composition of gauge bosons with mass 10
16 GeV will give Ƞ
b~ 10
−10 for the decay of the dyon and the antidyon-lepto-quarks [
14]. The ideology of baryon asymmetry creation can be found in the early reviews [
18,
19] and in the recent book [
20]. In any case, the baryon asymmetry in the Universe furnishes clear evidence that a new physics is called for beyond the standard model of physics of particles and the standard cosmological model.
3. Dark Energy
Most likely, dark energy is not clean vacuum energy and it is a dynamical value. Three dynamical periods might take place during dark energy evolution: quintessence period, vacuum energy period, and phantom period, which is now, likely. An equation state might weakly change near
w ≡ p/ρ = −1 during the evolution of the Universe. It lost more than 32 orders of magnitude in temperature. A quintessence period is connected with evolution of dark energy on 78 orders. The cosmological constant (Λ-term) problem existed for many years, because there was not an understanding of its vast reduction by 123 orders of magnitude [
21]. The problem was even called a crisis of physics. Indeed, this crisis existed before the introduction of the holographic principle [
22] and entropic force [
23] in physics. A cosmological constant was introduced by Einstein [
24] in his field equation as a property of space to preserve a static universe:
A. Einstein rewrote the rules of our physical world by this equation 100 years ago. However, not all was that smooth. A. Friedmann [
25] showed that the static solution of Einstein’s equation (5) is unstable and a minuscule matter density fluctuation leads to collapse or perpetual expansion. Einstein then abandoned the Λ-term, because it became known that the Universe is expanding. Much later, in 1947, in Lemaitre’s letter to Einstein [
26] the idea of the cosmological constant seemed brilliant to G. Lemaitre. He interpreted it as the vacuum energy density, i.e., the Λ-term is the vacuum energy of the Universe. If we move the Λ-term to the right-hand side of Einstein’s Equation (5), then this will be a form of energy that was called dark energy. A vacuum with the equation of state
p = −ρ is a stable state of quantum fields without any excitation of wave modes (nonwave modes are condensates). Consequently, the vacuum of the Universe consists of quantum field condensates that are diluted and, of course, fluctuate during its expansion. The energy density of the present vacuum at red shift
z = 0 differs significantly from the energy density at the birth of the Universe, i.e., at
z = ∞:
Here we have a difference in vacuum energy density by 123 orders of magnitude that were reduced through rather peculiar physical processes during the evolution of the Universe. Our Universe was probably born by the tunneling from an oscillating regime to that of Friedmann and began to expand owing to thermodynamical instability after tunneling on branch II (
Figure 2). New microstates arose during its expansion (evolution).
V. Fock’s ideas [
27] should be used to construct the space of new quantum states. However, we can take a different path. An entropic force emerges as the Universe expands, with the energy losses being inevitable due to its presence. Only the vacuum energy can be an energy source. The entropic force F was proposed by E. Verlinde [
23] as a microscopic force:
Here: ΔS is the change in entropy at a displacement Δx, and Nis the information about the holographic system in bits. In cosmology, the idea of an entropic force was already applied in [
28] for the same “crisis” purposes, but unsuccessfully, although the very existence of an entropic force allows one to talk about the energy (FΔx) that, in this case, is taken away from the vacuum energy as the Universe expands. Thus, the ideas of holography should be applied more accurately, i.e., formally, only in the classical regime. J. Maldacena [
29] pointed out that all of the information about a gravitational system is coded at its boundary. In the holographic limit, the vacuum energy density of the universe is then [
30]:
M
pl is the Planck mass. In addition, J. Bekenstein [
31] showed that the entropy (the number of microstates) of a black hole is 1/4 of the area of the event horizon expressed in Planck units. The idea of a similarity in the thermodynamics of a black hole in special coordinates to the thermodynamics of a de Sitter universe belonging to S. Hawking [
32] turned out to be very useful, as did Jacobson’s idea [
33] that gravity on the macroscopic scale is a manifestation of vacuum thermodynamics. We used these ideas to solve the Λ-term problem.
Our Universe after its birth [
6] passed the quantum stage of its evolution, when the holographic ideas cannot be used, because holography is a classical phenomenon. In the initial regime, our Universe probably lost its high symmetry, extra dimensions, and parity, but, at the same time, some bunches of particles were produced, including the dark ones. Of course, there was also a transitional regime between the quantum and classical regimes. Upon sharp cooling after the birth of the universe, when its high symmetry was lost, a number of phase transitions occurred. Their condensates compensated 78 orders of vacuum energy [
34,
35], because the forming condensates made negative contributions to the positive vacuum energy density.
Thus, phase transitions in the very early Universe have quenched more than 78 orders of the dark energy. At the beginning of the last phase transition the Universe had a density of ~10
−2 GeV
4, or 10
16 g cm
−3. By now (
z = 0) the vacuum energy must diminish further by a factor of
ρQCD/
ρDE≈ (0.265/1.8 × 10
−12)
4 ≈ 5 × 10
44 to quench all 123 orders. How can the vacuum energy losses by 44 orders of magnitudes be obtained and what process is “guilty” of this? We have a physical basis, the entropic force that emerges as the Universe expands, and Hawking’s assertion about a similarity of the thermodynamics of a de Sitter Universe to the thermodynamics of a black hole. In addition, the authors of [
30] argue that the entropy of the Universe is bound by its surface measured in Planck units: S≤ π
R2M
Pl2. This surface serves as a holographic screen. In the holographic limit the vacuum energy density of the Universe is then related to the entropy by a very simple formula,
ρ= 3M
Pl4/8S, that for calculations in the classical regime is:
At
z = 0, we have
ρ(0) = 0.375 × 10
−47 GeV
4 if
R(0) = 10
28 cm. In the classical regime of evolution, the vacuum energy could be reduced by a factor of (3/8)(10
28/3 × 10
4)
2 ≈ 4 × 10
46 in 4 × 10
17 s. If the beginning of classical (Friedmann) evolution is taken at a size of 3 × 10
5 cm, then we will have a coincidence of the reduction in vacuum energy with the “required” value:
Note that there is some arbitrariness in the estimates here because we do not know how long the transitional regime was. On the other hand, this almost exact coincidence cannot be fortuitous. Here, it is important to make some remarks on holography. General relativity provides a dramatic example of the holographic theory, while the existence of a horizon in the universe gives a strong argument for the holographic approximation in cosmology. The growth of the information entropy in the universe during its expansion is obvious. The existence of a holographic limit [
36] constrains the number of degrees of freedom (the number of microstates) that can exist in a bounded volume. Both sizes, R
QCD= 3 × 10
5 cm and R= 10
28 cm, can be causal horizons in the holographic thermodynamics of the Universe. Einstein’s equations are obtained from the proportionality of the entropy to the event horizon, given the Clausius fundamental relation dS=dQ/T, where dS is the change in entropy, dQ is the change in energy flow through the horizon, and T is the Unruh temperature seen by an accelerated observer inside the horizon [
30]. In a de Sitter Universe, the event horizon coincides with the apparent horizon. Some cosmological models dispense with the event horizon, but the apparent horizon always exists. Finally, the dark energy of our universe has evolved from the Planck time until now. The Universe lost ~123 (4 × 10
78 × 4 × 10
44) orders in this form of energy during 4 × 10
17 s in the process of creating new microstates as it expanded (in the quantum regime the phase transitions were more effective in this reduction). Thus, the crisis of physics related to the cosmological constant that lasted for many decades can be overcome. There are also other dark energy models. Besides, the dark energy may not be a pure vacuum energy, but probably, has a small admixture of a scalar field [
37]. Some experiments on dark energy have been prepared and an international consortium exists—
www.darkenergysurvey.org. The Dark Energy Camera will remain mounted on the Blanco telescope at Cerro Tololo (Chile) for another five to 10 years and will continue to be a useful instrument for scientific collaborations around the world.
Probably dark energy evolution has three phases: quintessence, vacuum and phantom phase. Now w = −1.028 ± 0.031 [
38]. Of course, the boundaries of these phases have been washed off.
4. Dark Matter
Some portion of particles has arisen in our universe during oscillations and tunneling for its creation [
6]. Compelling evidence has indicated that about one quarter of composition of the Universe shows itself as a dark matter. Fresh cosmological parameters are presented by Planck and SABRE collaborations [
39,
40]. DM particles from familons, the existence of three generations of particles, the existence of distinguished scales in the Universe, a fractal distribution of baryons and DM structures are the natural phenomenon in a composite (preon) model of elementary particles [
41]. The Standard Model has three generations of particles: the first generation of particles consists of stable particles; second and third generations consist of unstable particles. The whole set of elementary particles can be described in the preon version. For example, we have:
| Particle | Preon Composition | Electric Charge |
| Positron | + + + | +1 |
| Down quark | − □□ | −1/3 |
| Upper antiquark | − − □ | −2/3 |
| Electronic antineutrino | □□□ | 0 |
| W+ | + + + 0 0 0 | +1 |
| γ | + − | 0 |
It is suggested that there are preons of two types: preon “+” with the electric charge +1/3 and preon “0”, without an electric charge. The antipreon “−“ has the electric charge −1/3, and the neutral antipreon is marked as “□”. In the article [
41], we considered the simplest boson-fermion-preon model of left chiral quarks and leptons. The basic elements of this model are the chiral fermion preons U
αL D
αL and the scalar preons of quark φ
iαa type and lepton χ
αl type. Then, in this model, the internal structure of elementary particles is:
Inside quarks and leptons, the metagluonic fields G
ωμνand the scalar preon fields are in the state of confinement. This effect is similar by its physical nature to the confinement of quarks and gluons inside hadrons, providing the existence of nonperturbative metagluonic and preon condensates. These condensates are described by the following:
Here, Λ
mcis the energy scale of preon confinement, V
ab, V
lmare the condensate matrices. The condensates (15) and (16), together with the gluonic condensates <0I(α
c/π) G
aμνG
μνaI0>and the quark condensates
provide a quark mass creation mechanism for all three particle generations. In the framework of this theory, DM is a system of familon collective excitations of the heterogeneous nonperturbative vacuum. This system consists of three subsystems: (1) familons of the upper-quark type; (2) familons of the lower-quark type; (3) familons of the lepton type. Small masses of familons are the result of super weak interactions of Goldstone fields with nonperturbative vacuum condensates. The value of these masses is limited:
The effect of familons mass production corresponds formally with the appearance of mass terms in the Lagrangian of Goldstone fields. From general consideration, one can propose that massive terms may arise as with “right” and with “wrong” signs. The sign of the massive terms predetermines the destiny of residual symmetry of Goldstone fields. In the case of “wrong” sign for low temperatures, T < T
c ~ m
familons ~ 0.1–10
5 K, a Goldstone condensate is produced and the symmetry of familon gas spontaneously breaks. The negative square mass of the complex scalar field means that for T < T
c(up) ~
│m
f│ pseudo-Goldstone vacuum is unstable that is when T = T
c(up) in gas of pseudo-Goldstone bosons there should be a relativistic phase transition to a state with spontaneous breaking U(1) symmetry. The phase transition in the cosmological familon gas is a first-order phase transition with a wide temperature range of phase coexistence. A numerical simulation of such relativistic phase transition has shown [
41] that a spatial interchange of high-symmetry and low-symmetry phases took place in the Universe with the density contrast
δρ/ρ ~ 0.1. Of course, the thermodynamic temperature of the familon gas does not necessarily coincide with the thermodynamic temperature of all other subsystems of the Universe. In the modern epoch, this fact can manifest itself in that the temperature of the familon gas as a part of dark matter can differ from the CMB (Cosmic Microwave Background) temperature). To explain the scale hierarchy of baryon structures, our model implements at least three relativistic phase transitions since there are three familon subsystems in the Universe [
41]. Baryons repeated this block-phase structure which produced particles of DM (familons). Eventually, they produced: galaxies, clusters of galaxies and superclusters of galaxies. The formation of primary galactic nuclei during phase transitions in the early Universe was discussed in the article [
42]. Probably, dark matter medium must be a multi component system as and the Standard Model.
5. Conclusions
In this review, we summarized the birth of the Universe and modernization of baryon asymmetry from a theoretical point of view, the role of dark components of the Universe, i.e., dark energy and dark matter, and reviewed the preon model. Here, it is necessary to note that authors of a recent article [
43] discussed our idea [
7] in a more refined form that the Universe was born in an anisotropic state (Bianchi type IX, as example) and quickly relaxed to an equilibrium state, including metric, vacuum condensate, and distribution function of plasma particles. Besides, it is necessary to note two reviews on baryon asymmetry in which spontaneous and gravitation baryogenesis considered [
44,
45]. We note that the identification of dark matter particles is of the highest scientific priority. Dark matter particles search in dozens of experiments. The masses of particles constituting the dark matter can lie within the range from 10
−15 to 10
15 GeV, while the cross section for their interaction with nucleons and the cross-section for their annihilation into SM particles can occupy the range 10
−76–10
−41 cm
2 [
46]. Light, weak interacting massive particles (WIMP) search conducts in collaboration CDEX - China Dark Matter Experiment [
47]. They have provided the limit on the mass of WIMP m
χ< 6 GeV/c
2. In our review we did not discuss a darkogenesis, in which the asymmetric dark matter was produced the same mechanism as and the baryon component [
48,
49]. In the recent article [
50] authors proposed the next generation of colliders may open dark matter particles for evaporation of microscopic black holes through Hawking radiation.
We predicted the dynamics of dark energy and the occurrence of voids in a large-scale distribution of dark matter from familons. The detection of the next fundamental level of matter on colliders is also very probable. In the nearest future, the experiments on DE and DM will be able to solve (or to disprove) some of the cosmological problems discussed in this review.