Multi-Scale Insights on the Threshold Pressure Gradient in Low-Permeability Porous Media
Abstract
1. Introduction
2. A Novel Semi-Empirical Formula for the Threshold Pressure Gradient (TPG)
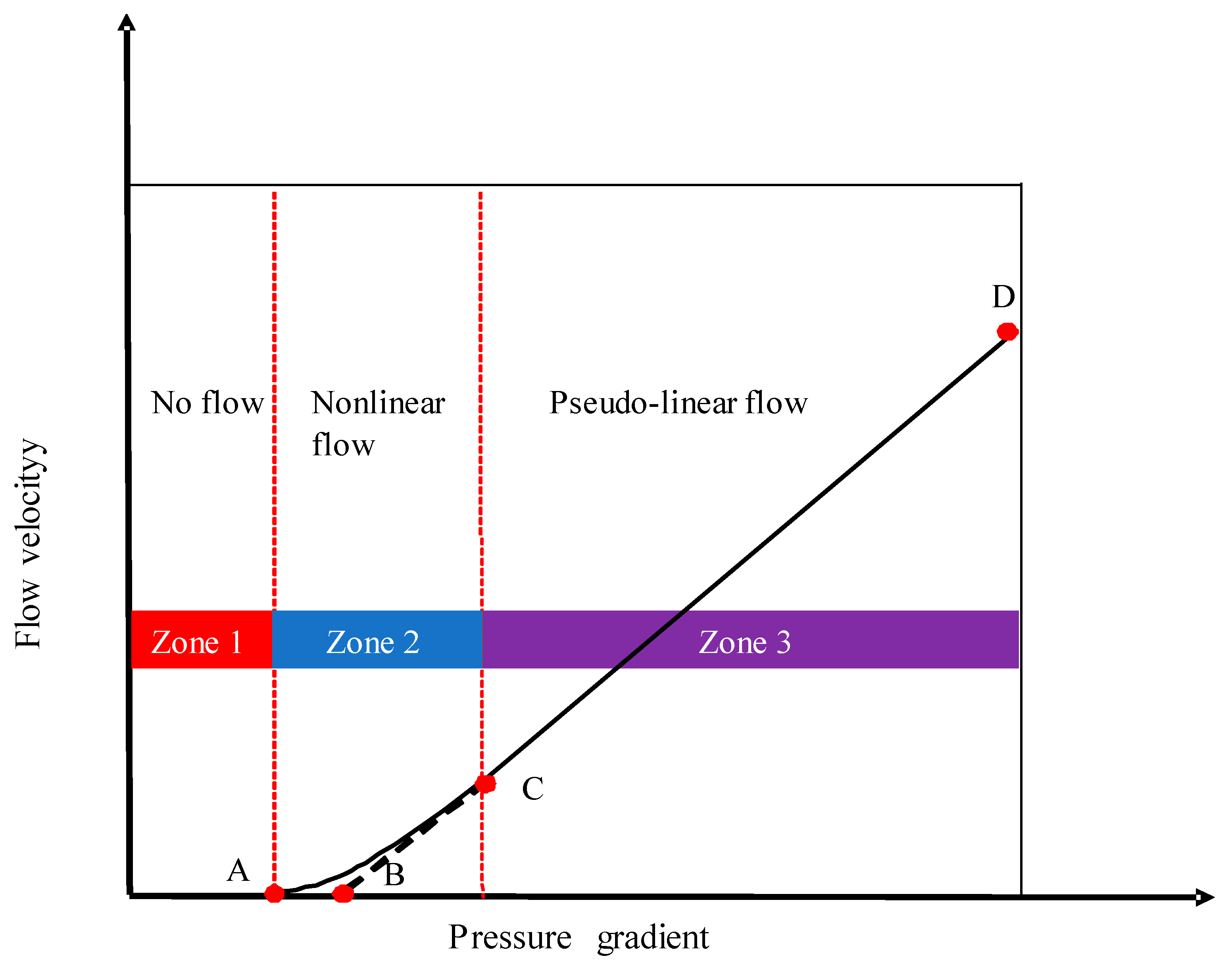
2.1. Effects of Macroscopic Parameters on TPG
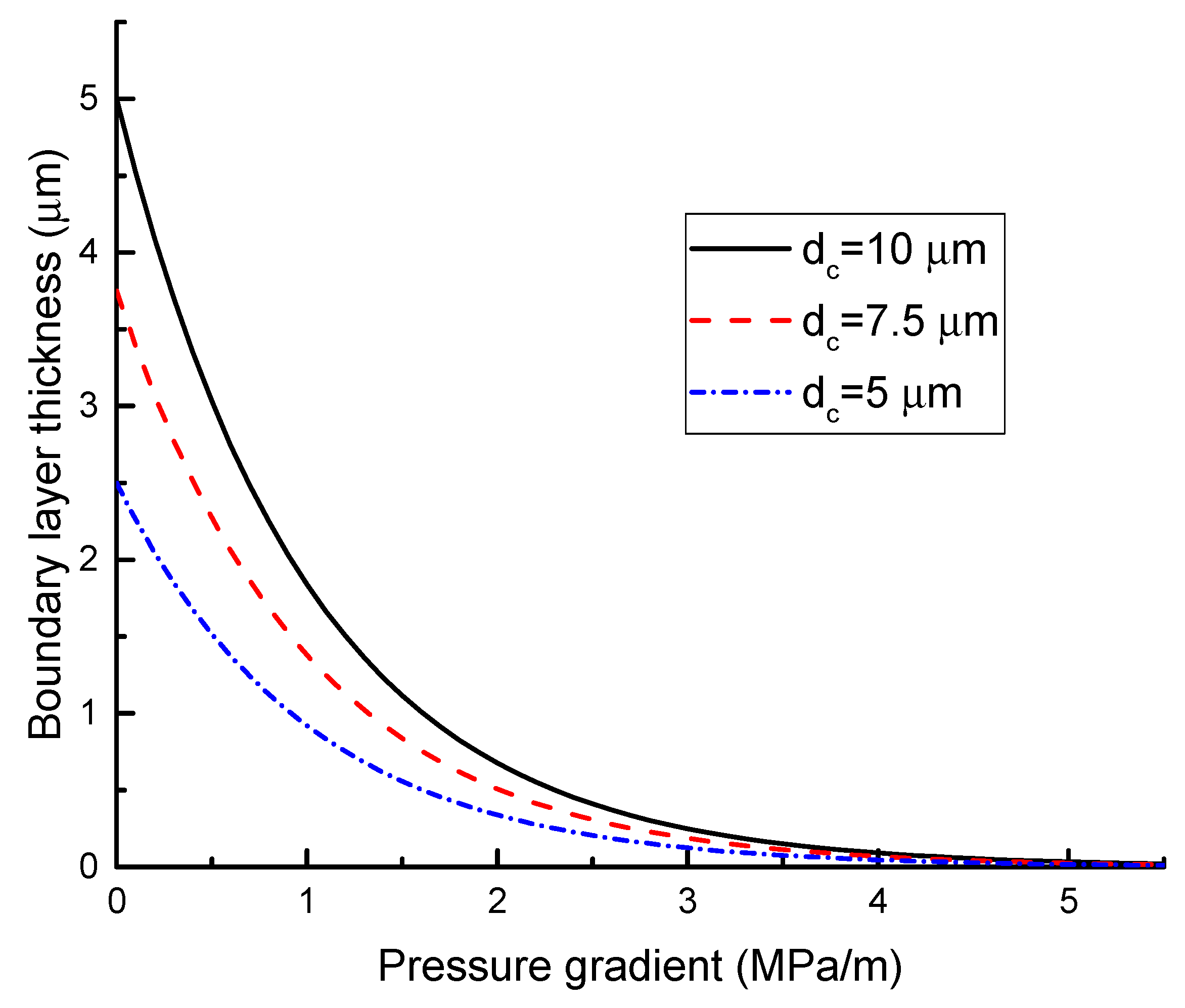
2.1.1. Effect of Boundary Layer
2.1.2. Effect of Capillary Pressure
2.1.3. Effect of Stress Sensitivity
2.2. Verification of the Proposed TPG Model Using Experimental Data
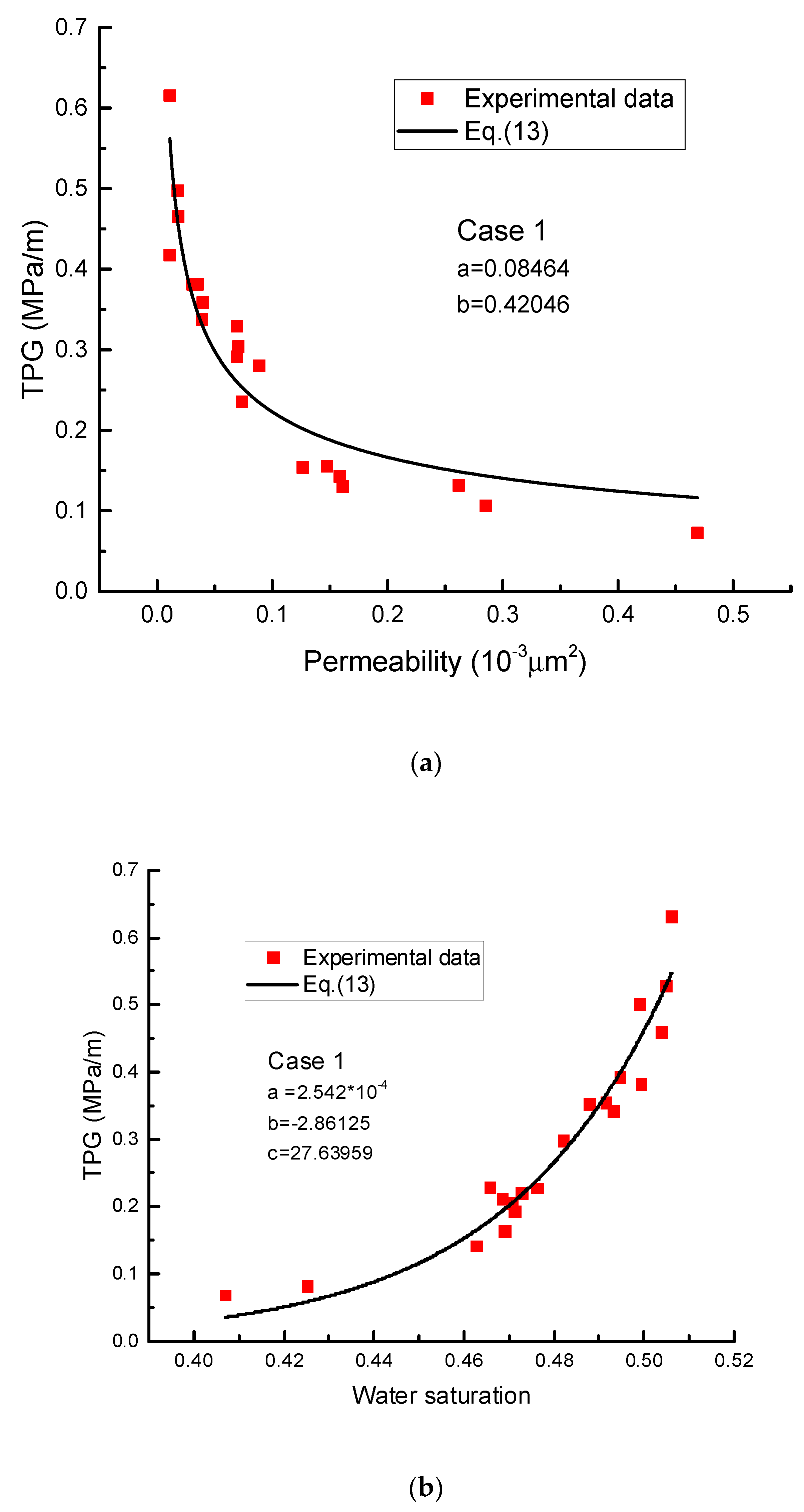
2.2.1. Case 1: Correlation of the TPG with Permeability and Water Saturation
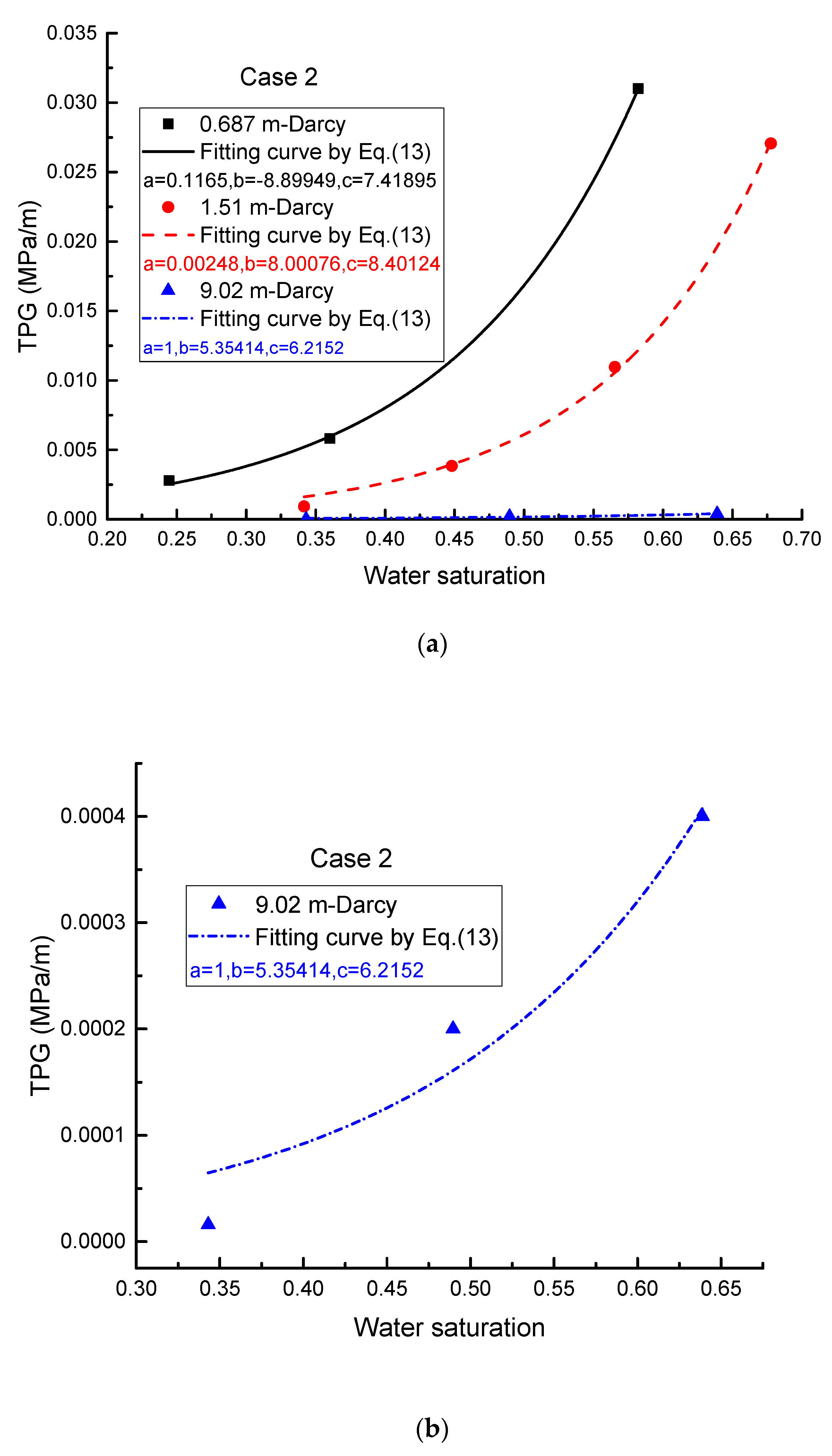
2.2.2. Case 2: Correlation of the TPG with Water Saturation at Different Permeabilities
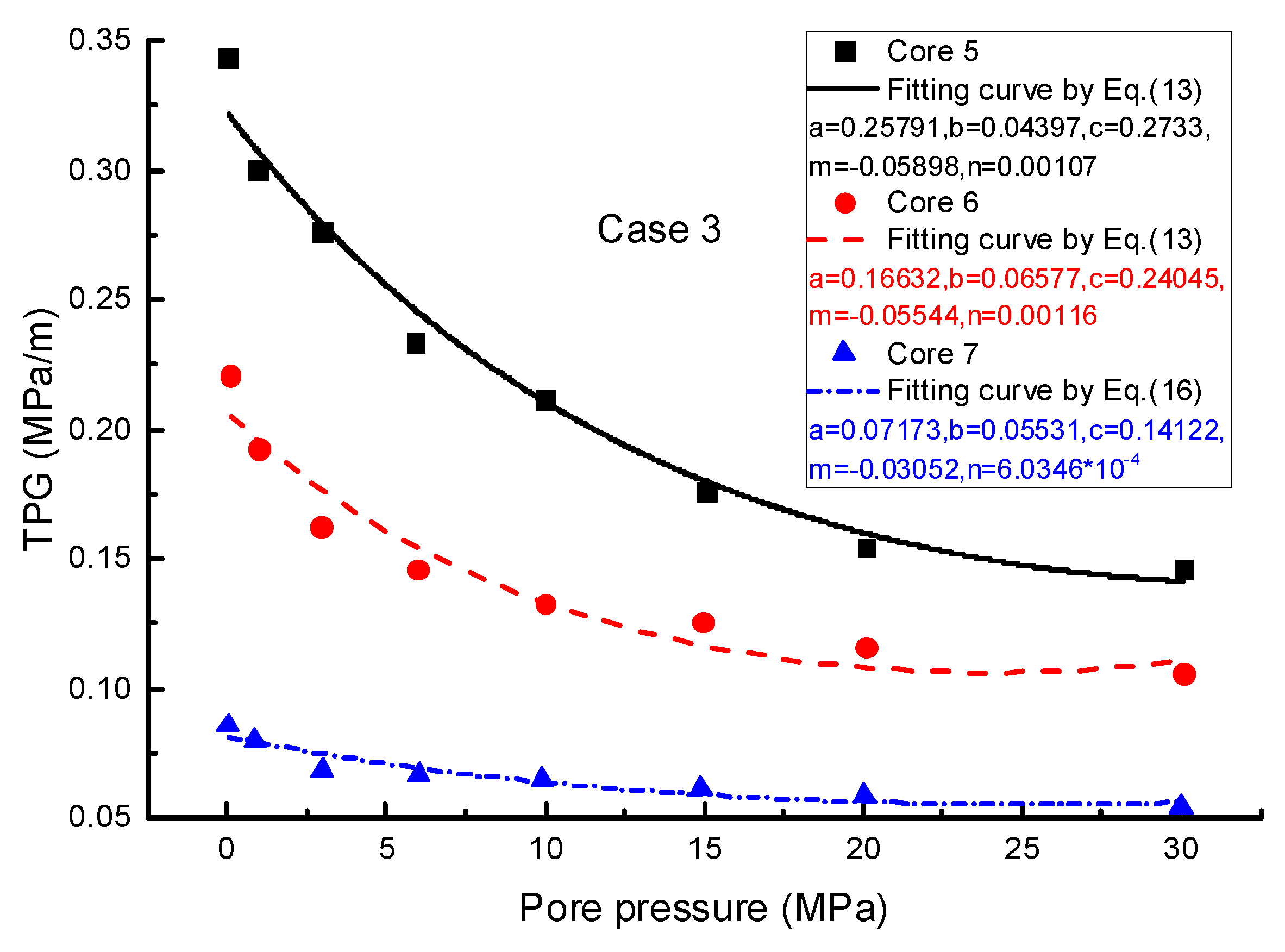
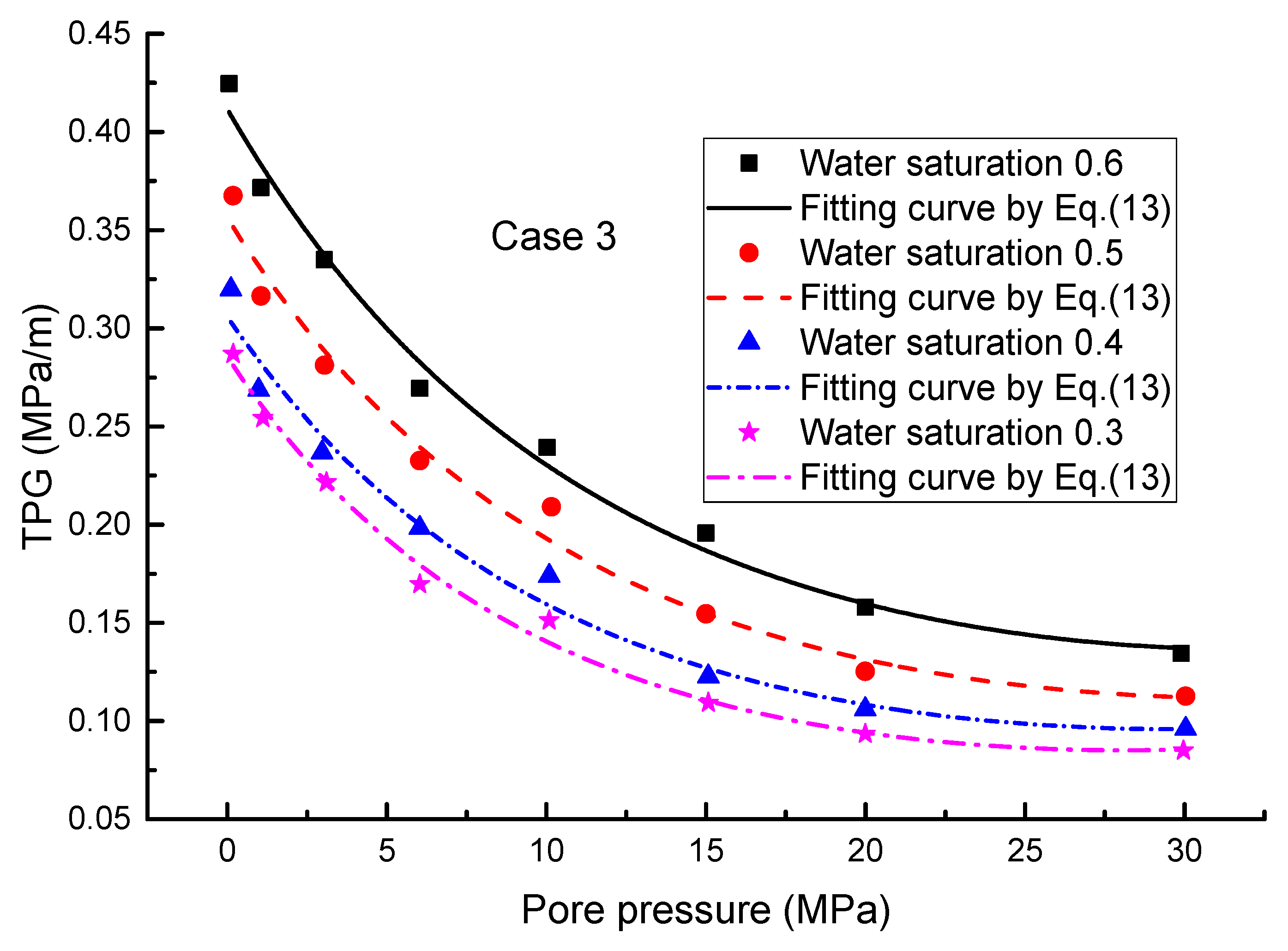
2.2.3. Case 3: Correlation of the TPG with Pore Pressure
3. A Fractal Model for the Threshold Pressure Gradient
3.1. Derivation of Threshold Pressure Gradient Based on Fractal Theory
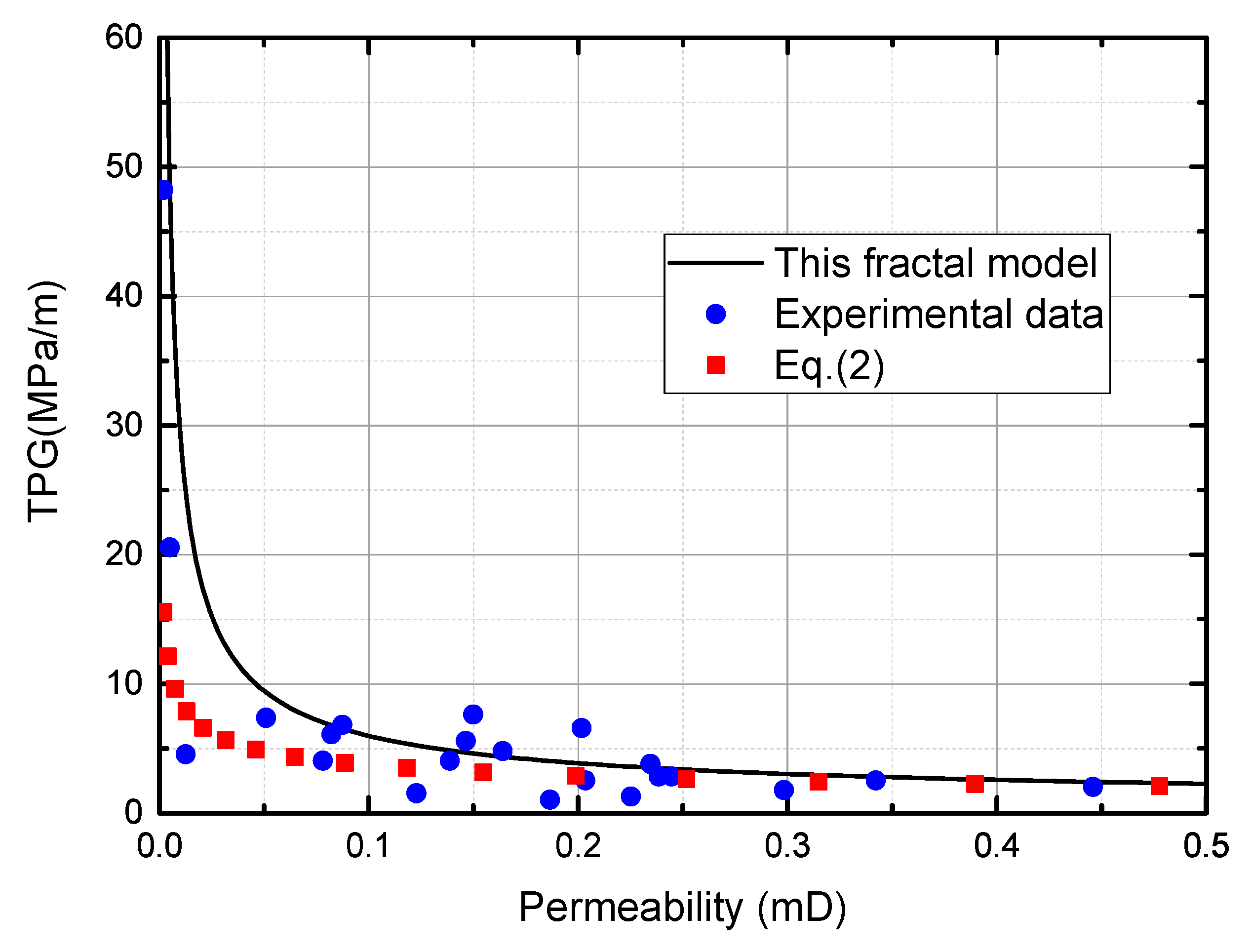
3.2. Model Validation and Analysis
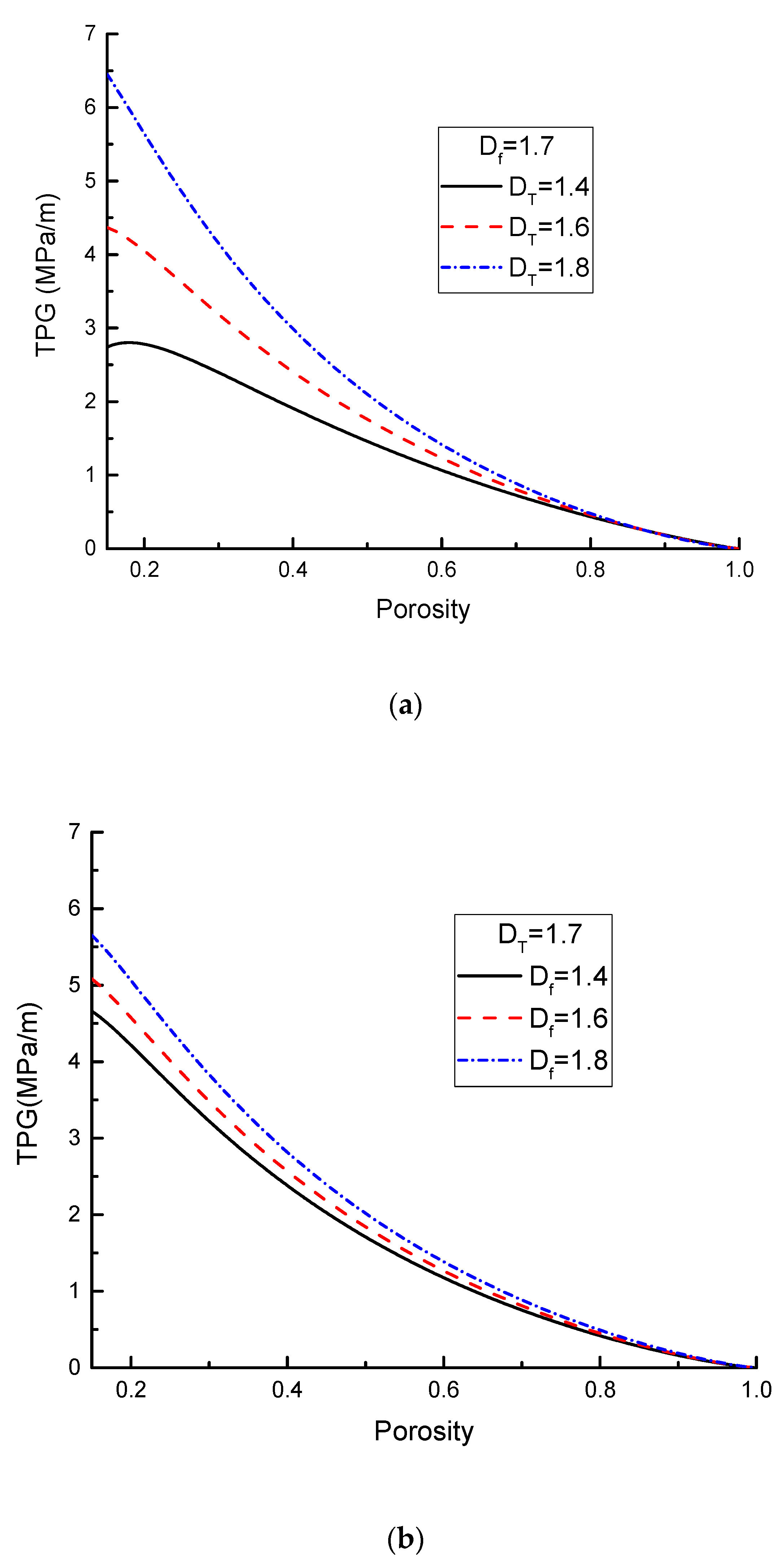
3.3. Effect of Fractal Dimensions
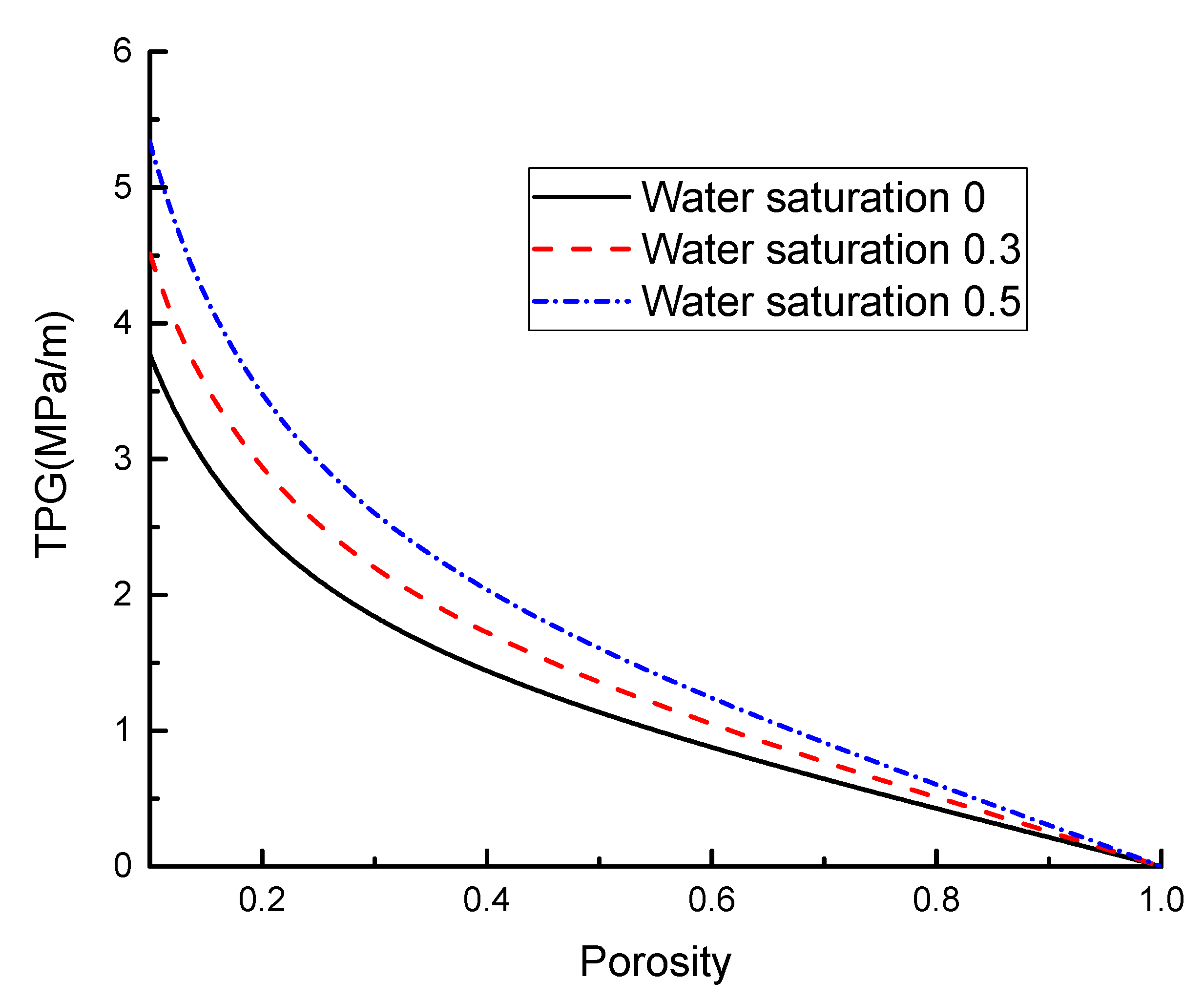
3.4. Effect of Residual Water Saturation
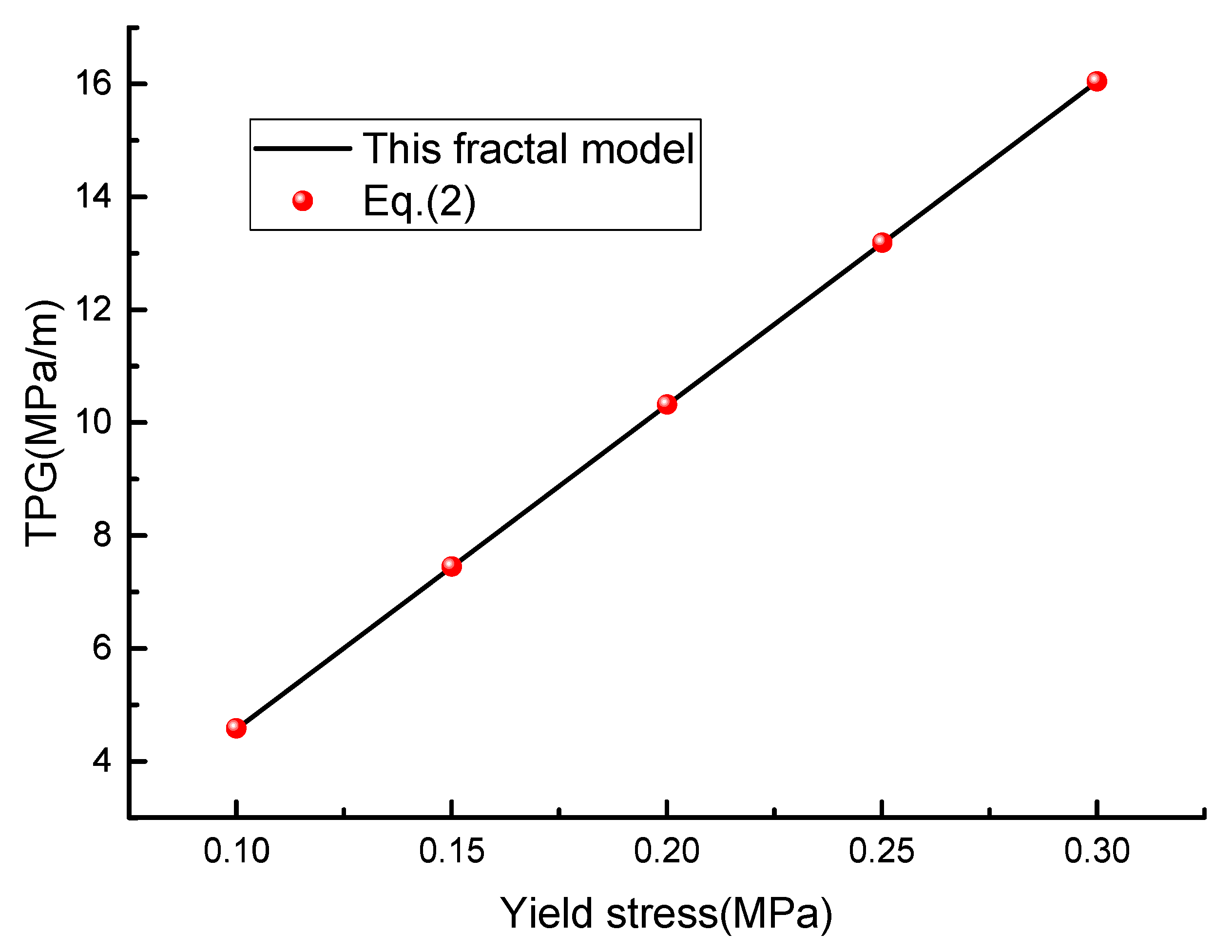
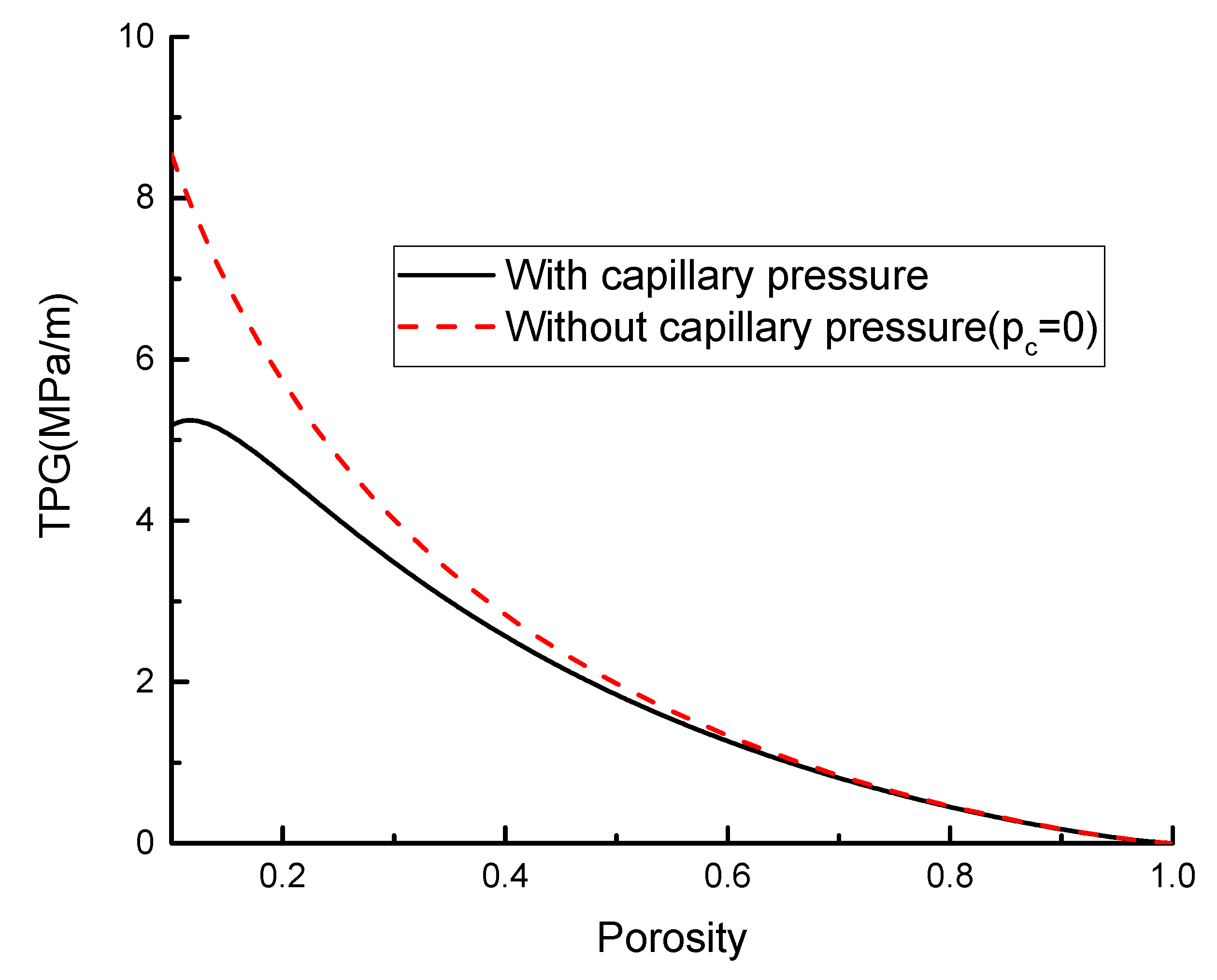
3.5. Effect of Capillary Pressure
4. Conclusions
- The gas flow in low-permeability reservoirs exhibits a strong non-Darcy behavior. The boundary layer effect and fluid plasticity play the main role in this nonlinear behavior.
- The threshold pressure gradient is directly related to permeability, water saturation, and pore pressure. An approximate power function can describe the relationship between permeability and the TPG. An exponential relationship is more consistent with the effects of water saturation and pore pressure.
- Both pore-size distribution in the fractal dimension and tortuosity fractal dimension can increase the TPG by characterizing the complexity of the pore structure. However, the tortuosity fractal dimension has a more significant enhancement effect.
- Complex pore structure has a significant effect on the TPG only in the range of low porosity, but water saturation and yield stress have a wider influence range. A linear relationship between yield stress and TPG can be observed.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A: Derivation of Fractal Parameters
References
- Ahmad, F.; Adhami, A.Y.; Smarandache, F. Neutrosophic optimization model and computational algorithm for optimal shale gas water management under uncertainty. Symmetry 2019, 11, 544. [Google Scholar] [CrossRef]
- Jia, C.; Zheng, M.; Zhang, Y. Unconventional hydrocarbon resources in China and the prospect of exploration and development. Pet. Explor. Dev. 2012, 39, 139–146. [Google Scholar] [CrossRef]
- Cai, J. A fractal approach to low velocity non-Darcy flow in a low permeability porous medium. Chin. Phys. B 2014, 23, 44701. [Google Scholar] [CrossRef]
- Song, H.; Cao, Y.; Yu, M.; Wang, Y.; Killough, J.E.; Leung, J. Impact of permeability heterogeneity on production characteristics in water-bearing tight gas reservoirs with threshold pressure gradient. J. Nat. Gas Sci. Eng. 2015, 22, 172–181. [Google Scholar] [CrossRef]
- Li, D.; Zha, W.; Liu, S.; Wang, L.; Lu, D. Pressure transient analysis of low permeability reservoir with pseudo threshold pressure gradient. J. Pet. Sci. Eng. 2016, 147, 308–316. [Google Scholar] [CrossRef]
- Tian, W.; Li, A.; Ren, X.; Josephine, Y. The threshold pressure gradient effect in the tight sandstone gas reservoirs with high water saturation. Fuel 2018, 226, 221–229. [Google Scholar] [CrossRef]
- Zhu, W.; Song, H.; Huang, X.; Liu, X.; He, D.; Ran, Q. Pressure characteristics and effective deployment in a water-bearing tight gas reservoir with low-velocity non-Darcy flow. Energy Fuels 2011, 25, 1111–1117. [Google Scholar] [CrossRef]
- Wang, X.; Sheng, J.J. Effect of low-velocity non-Darcy flow on well production performance in shale and tight oil reservoirs. Fuel 2017, 190, 41–46. [Google Scholar] [CrossRef]
- Ding, J.; Yang, S.; Nie, X.; Wang, Z. Dynamic threshold pressure gradient in tight gas reservoir. J. Nat. Gas Sci. Eng. 2014, 20, 155–160. [Google Scholar] [CrossRef]
- Huang, L.; Shi, J.; Yang, L.; Zang, J.; Zhang, L.; Yu, P. Experimental research and analysis on threshold pressure gradient in low-permeability gas reservoir. Fault-Block Oil Gas Field. 2016, 23, 610–614. [Google Scholar]
- Zhang, R.H.; Zhang, L.H.; Wang, R.H.; Zhao, Y.L.; Huang, R. Simulation of a multistage fractured horizontal well in a water-bearing tight fractured gas reservoir under non-Darcy flow. J. Geophys. Eng. 2018, 15, 877–894. [Google Scholar] [CrossRef]
- Song, F.; Wang, J.; Liu, H. Static threshold pressure gradient characteristics of liquid influenced by boundary wettability. Chin. Phys. Lett. 2010, 27, 24704. [Google Scholar]
- Huang, Y.; Yang, Z.; He, Y.; Wang, X.; Luo, Y. Nonlinear porous flow in low permeability porous media. Mech. Pract. 2013, 35, 1–8. [Google Scholar] [CrossRef]
- Wang, F.; Liu, Z.; Cai, J.; Gao, J. A fractal model for low-velocity non-Darcy flow in tight oil reservoirs considering boundary-layer effect. Fractals 2018, 26, 1850077. [Google Scholar] [CrossRef]
- Miller, R.J.; Low, P.F. Threshold gradient for water flow in clay systems 1. Soil Sci. Soc. Am. J. 1963, 27, 605–609. [Google Scholar] [CrossRef]
- Prada, A.; Civan, F. Modification of Darcy’s law for the threshold pressure gradient. J. Pet. Sci. Eng. 1999, 22, 237–240. [Google Scholar] [CrossRef]
- Wang, S.; Huang, Y.; Civan, F. Experimental and theoretical investigation of the Zaoyuan field heavy oil flow through porous media. J. Pet. Sci. Eng. 2006, 50, 83–101. [Google Scholar] [CrossRef]
- Liu, W.; Yao, J.; Wang, Y. Exact analytical solutions of moving boundary problems of one-dimensional flow in semi-infinite long porous media with threshold pressure gradient. Int. J. Heat Mass Transf. 2012, 55, 6017–6022. [Google Scholar] [CrossRef]
- Li, S.; Cheng, L.; Li, X.; Hao, F. Nonlinear seepage flow of ultralow permeability reservoirs. Pet. Explor. Dev. 2008, 35, 606–612. [Google Scholar] [CrossRef]
- Zeng, B.; Cheng, L.; Hao, F. Experiment and mechanism analysis on threshold pressure gradient with different fluids. Presented at the Nigeria Annual International Conference and Exhibition, Calabar, Nigeria, 31 July–7 August 2010. SPE-140678MS. [Google Scholar]
- Yang, R.; Jiang, R.; Liu, S.; Zhang, X.; Liu, H. Numerical simulation of nonlinear seepage in ultra-low permeability reservoirs. Acta Pet. Sin. 2011, 32, 299–306. [Google Scholar]
- Chen, X.; He, P.; Qin, Z. Damage to the microstructure and strength of altered granite under wet–dry cycles. Symmetry 2018, 10, 716. [Google Scholar] [CrossRef]
- Bornstein, M.M.; Fernández-Martínez, M.; Guirao, J.L.; Gómez-García, F.J.; Guerrero-Sánchez, Y.; López-Jornet, P. On the symmetry of the bone structure density over the nasopalatine foramen via accurate fractal dimension analysis. Symmetry 2019, 11, 202. [Google Scholar] [CrossRef]
- Yu, B.; Cheng, P. A fractal model for permeability of bi-dispersed porous media. Int. J. Heat Mass Transf. 2002, 45, 2983–2993. [Google Scholar] [CrossRef]
- Wang, S.; Yu, B. A fractal model for the starting pressure gradient for Bingham fluids in porous media embedded with fractal-like tree networks. Int. J. Heat Mass Transf. 2011, 54, 4491–4494. [Google Scholar] [CrossRef]
- Ye, W.; Wang, X.; Cao, C.; Yu, W. A fractal model for threshold pressure gradient of tight oil reservoirs. J. Pet. Sci. Eng. 2019, 179, 427–431. [Google Scholar] [CrossRef]
- Li, J.; Chen, Z.; Wu, K.; Li, R.; Xu, J.; Liu, Q.; Qu, S.; Li, X. Effect of water saturation on gas slippage in tight rocks. Fuel 2018, 225, 519–532. [Google Scholar] [CrossRef]
- Cai, J.; Lin, D.; Singh, H.; Zhou, S.; Meng, Q.; Zhang, Q. A simple permeability model for shale gas and key insights on relative importance of various transport mechanisms. Fuel. 2019, 252, 210–219. [Google Scholar] [CrossRef]
- Huo, D.; Benson, S.M. Experimental investigation of stress-dependency of relative permeability in rock fractures. Transp. Porous Media 2016, 113, 567–590. [Google Scholar] [CrossRef]
- Su, H.B. A flow model reflecting dynamic kick-off pressure gradient for low permeability reservoirs. J. Southwest Pet. Univ. 2015, 37, 105–111. [Google Scholar]
- Wang, Q.; Tang, H.; Lv, L.; Peng, D.; Guo, F. An experimental study on threshold pressure gradient in low pernteability reservoir. Pet. Geol. Recovery Effic. 2011, 18, 97–100. [Google Scholar]
- Hao, F.; Cheng, L.S.; Hassan, O.; Hou, J.; Liu, C.Z.; Feng, J.D. Threshold pressure gradient in ultra-low permeability reservoirs. Pet. Sci. Technol. 2008, 26, 1024–1035. [Google Scholar] [CrossRef]
- Bachu, S.; Bennion, B. Effects of in-situ conditions on relative permeability characteristics of CO2-brine systems. Environ. Geol. 2008, 54, 1707–1722. [Google Scholar] [CrossRef]
- Thomas, L.K.; Katz, D.L.; Tek, M.R. Threshold pressure phenomena in porous media. Soc. Pet. Eng. J. 1968, 8, 174–184. [Google Scholar] [CrossRef]
- Wu, D.; Ju, B.; Wu, S.; Brantson, E.T.; Fu, Y.; Lei, Z. Investigation of productivity decline in inter-salt argillaceous dolomite reservoir due to formation damage and threshold pressure gradient: Laboratory, mathematical modeling and application. Energy Explor. Exploit. 2017, 35, 33–53. [Google Scholar] [CrossRef]
- Hu, B.; Wang, J.G.; Wu, D.; Wang, H. Impacts of zone fractal properties on shale gas productivity of a multiple fractured horizontal well. Fractals 2019, 27, 1950006. [Google Scholar] [CrossRef]
- Bird, R.B.; Stewart, W.E.; Lightfoot, E.N.; Meredith, R.E. Transport phenomena. J. Electrochem. Soc. 1961, 108, 78C–79C. [Google Scholar] [CrossRef]
- Ahn, K.J.; Seferis, J.C.; Berg, J.C. Simultaneous measurements of permeability and capillary pressure of thermosetting matrices in woven fabric reinforcements. Polym. Compos. 1991, 12, 146–152. [Google Scholar] [CrossRef]
- Yu, B. Fractal character for tortuous streamtubes in porous media. Chin. Phys. Lett. 2005, 22, 158. [Google Scholar]
- Yu, B.; Li, J. Some fractal characters of porous media. Fractals 2001, 9, 365–372. [Google Scholar] [CrossRef]
- Xu, P.; Qiu, S.; Yu, B.; Jiang, Z. Prediction of relative permeability in unsaturated porous media with a fractal approach. Int. J. Heat Mass Transf. 2013, 64, 829–837. [Google Scholar] [CrossRef]

| TPG Correlations | Core Data | Reference |
|---|---|---|
| Core flooding using brine | Prada and Civan [16] | |
| Core flooding using oil | Li et al. [19] | |
| Core flooding using oil | Li et al. [19] | |
| Core flooding using formation water | Zeng et al. [20] | |
| Core flooding using oil | Yang et al. [21] |
| Fitting Coefficients | a | b | c | m | n | ||
|---|---|---|---|---|---|---|---|
| Case 1 (permeability effect [10]) | Figure 3a | 0.08464 | 0.42046 | ||||
| Figure 3b | −2.86125 | 27.63959 | |||||
| Case 2 (water saturation effect [7]) | Figure 4a | Core 1 | 0.1165 | −8.89949 | 7.41895 | ||
| Core 2 | 0.00248 | 8.00076 | 8.40124 | ||||
| Figure 4b | Core 3 | 1 | 5.35414 | 6.2152 | |||
| Case 3 (pore pressure effect [9]) | Figure 5 | Core 5 | 0.25791 | 0.04397 | 0.2733 | −0.05898 | 0.00107 |
| Core 6 | 0.16632 | 0.06577 | 0.24045 | −0.05544 | 0.00116 | ||
| Core 7 | 0.07173 | 0.05531 | 0.14122 | −0.03052 | |||
| Figure 6 (Core 5) | Sw 0.6 | 0.30482 | 0.05371 | 0.25039 | −0.0687 | 0.00107 | |
| Sw 0.5 | 0.25943 | 0.05661 | 0.31669 | −0.07261 | 0.00114 | ||
| Sw 0.4 | 0.18415 | 0.09078 | 0.635 | −0.07849 | 0.00133 | ||
| Sw 0.3 | 0.16559 | 0.0973 | 0.90743 | −0.08621 | 0.00154 | ||
| Case 1 (permeability effect [10]) | Range of permeability (mD) | Average permeability (mD) | Range of porosity (%) | Average porosity (%) | |
| 0.011–0.47 | 0.11 | 2.62–14.21 | 6.16 | ||
| Case 2 (water saturation effect [7]) | Core Number | Permeability (mD) | Length (cm) | Diameter (cm) | Driving pressure (MPa) |
| Core 1 | 0.687 | 5 | 2.5 | 0.504 | |
| Core 2 | 1.51 | 5 | 2.5 | 0.401 | |
| Core 3 | 9.02 | 5 | 2.5 | 0.053 | |
| Case 3 (pore pressure effect [9]) | Core Number | Permeability (mD) | Length (cm) | Diameter (cm) | Porosity (%) |
| Core 5 | 0.061 | 5.962 | 2.534 | 6.15 | |
| Core 6 | 0.193 | 6.28 | 2.538 | 8.32 | |
| Core 7 | 0.317 | 6.286 | 2.54 | 12.08 | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.; Wang, J.; Wang, X.; Chan, A. Multi-Scale Insights on the Threshold Pressure Gradient in Low-Permeability Porous Media. Symmetry 2020, 12, 364. https://doi.org/10.3390/sym12030364
Wang H, Wang J, Wang X, Chan A. Multi-Scale Insights on the Threshold Pressure Gradient in Low-Permeability Porous Media. Symmetry. 2020; 12(3):364. https://doi.org/10.3390/sym12030364
Chicago/Turabian StyleWang, Huimin, Jianguo Wang, Xiaolin Wang, and Andrew Chan. 2020. "Multi-Scale Insights on the Threshold Pressure Gradient in Low-Permeability Porous Media" Symmetry 12, no. 3: 364. https://doi.org/10.3390/sym12030364
APA StyleWang, H., Wang, J., Wang, X., & Chan, A. (2020). Multi-Scale Insights on the Threshold Pressure Gradient in Low-Permeability Porous Media. Symmetry, 12(3), 364. https://doi.org/10.3390/sym12030364







