Fractional Dynamics in Soccer Leagues
Abstract
1. Introduction
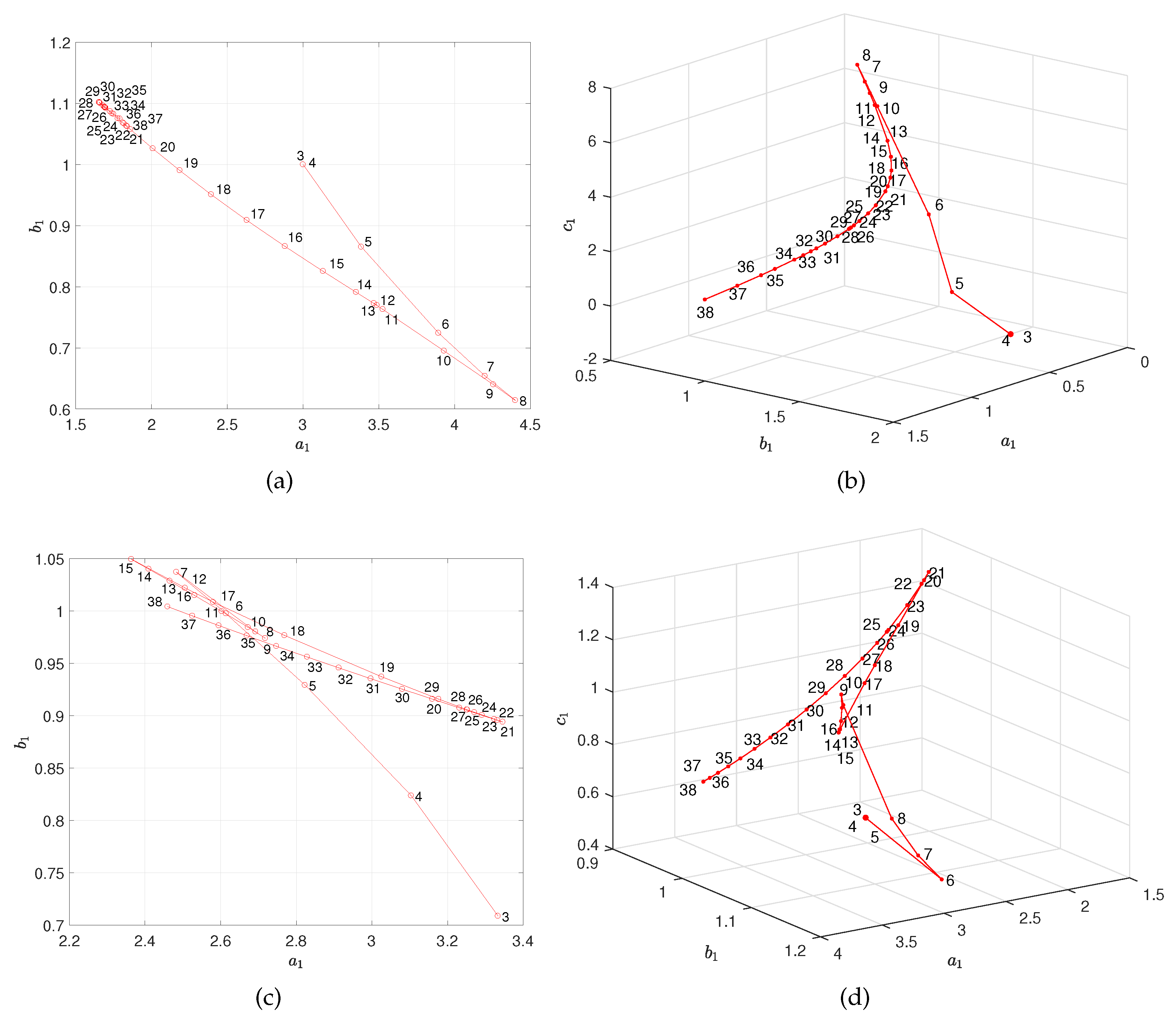
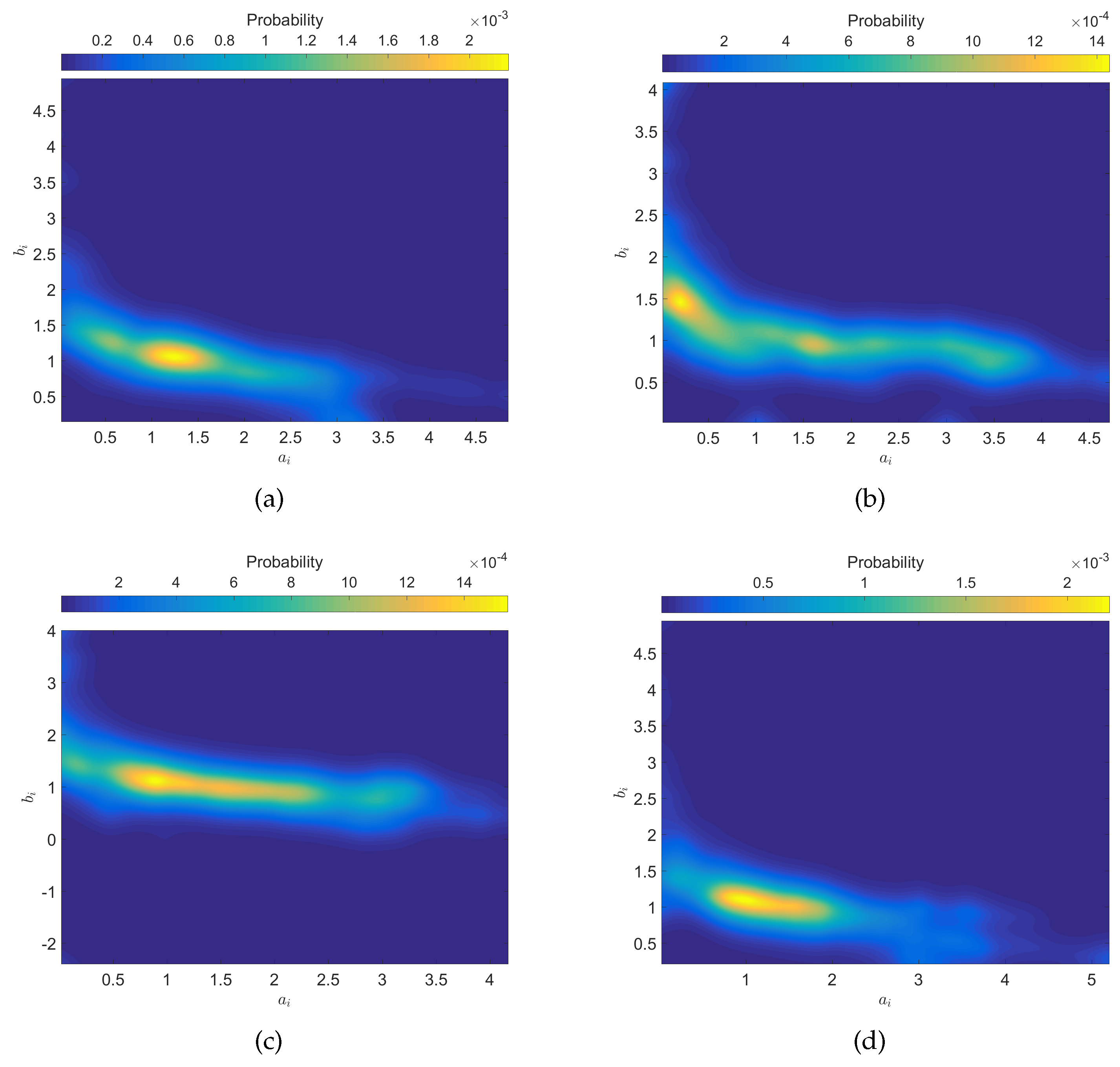
2. Modeling the Teams’ Dynamics
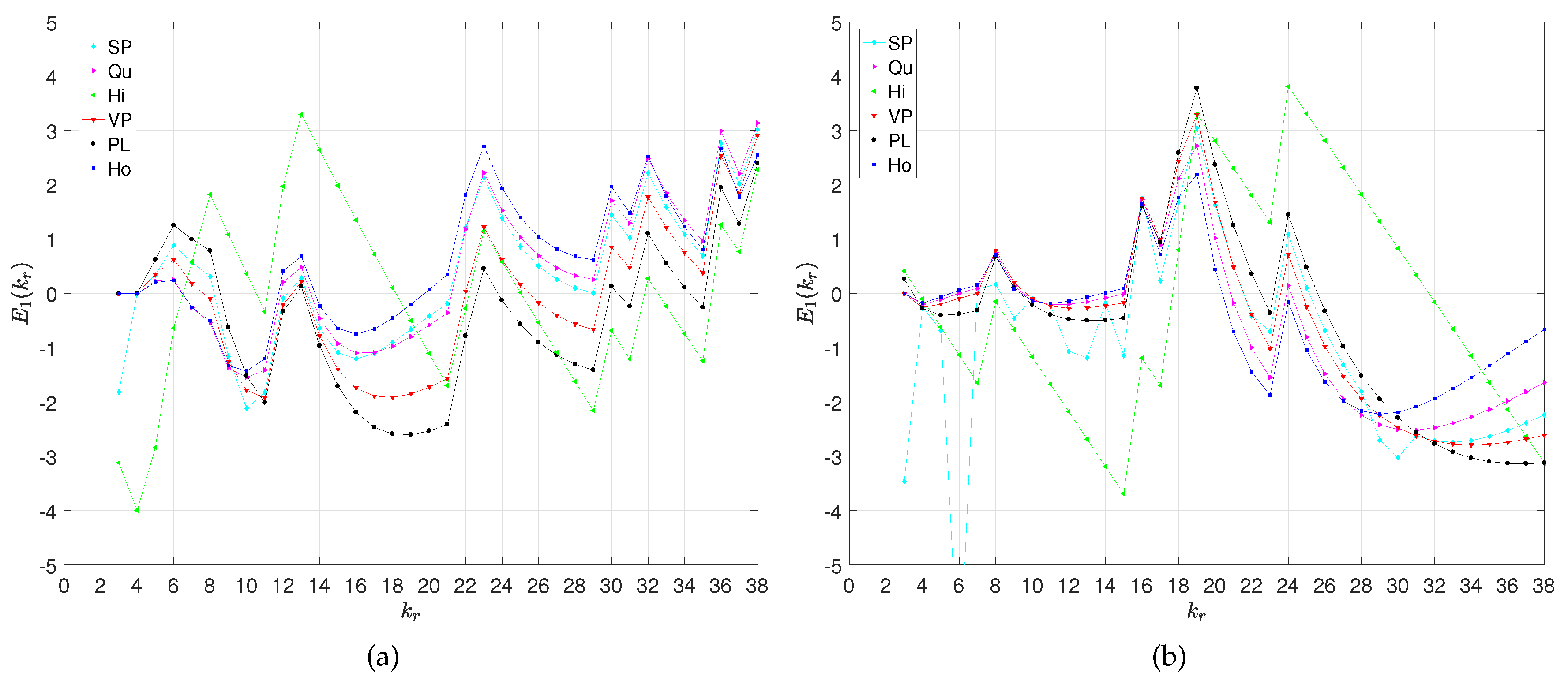
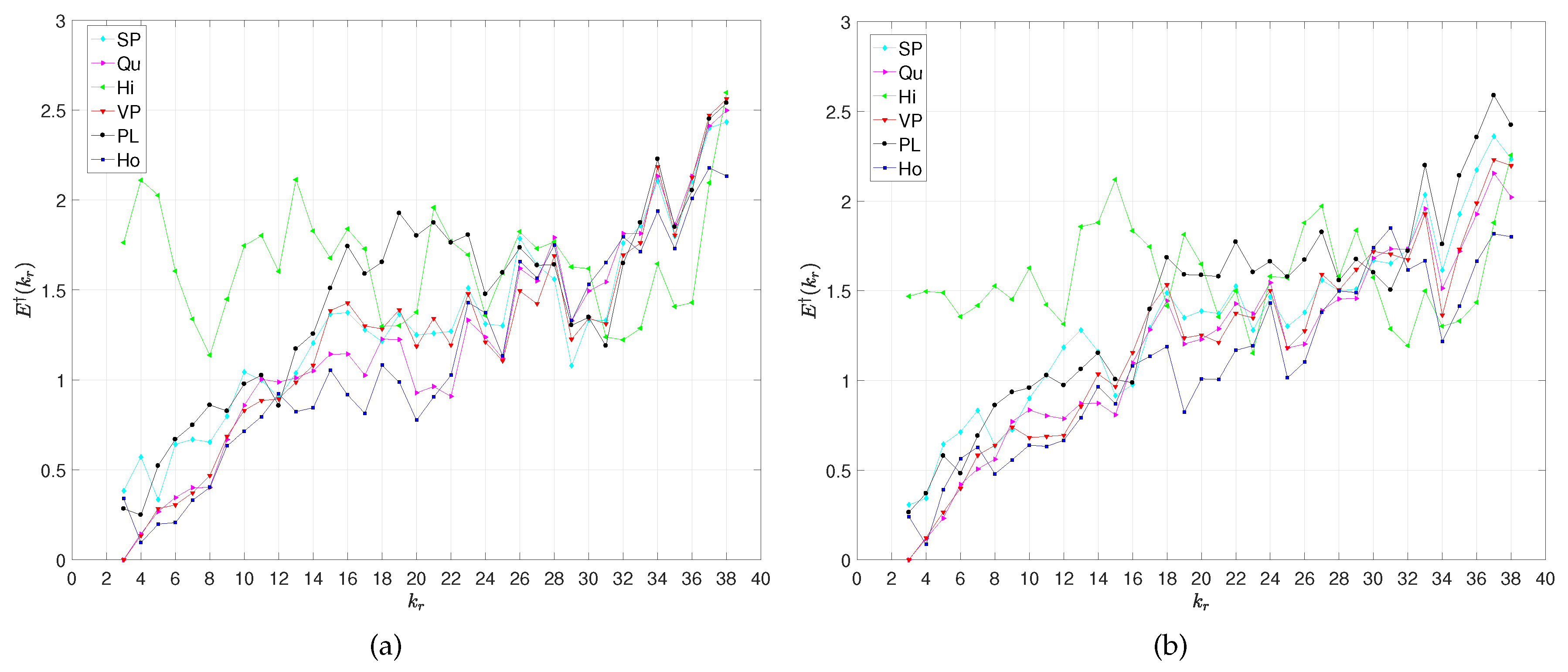
3. Entropy of the Spatio-Temporal Patterns of the Models’ Parameters
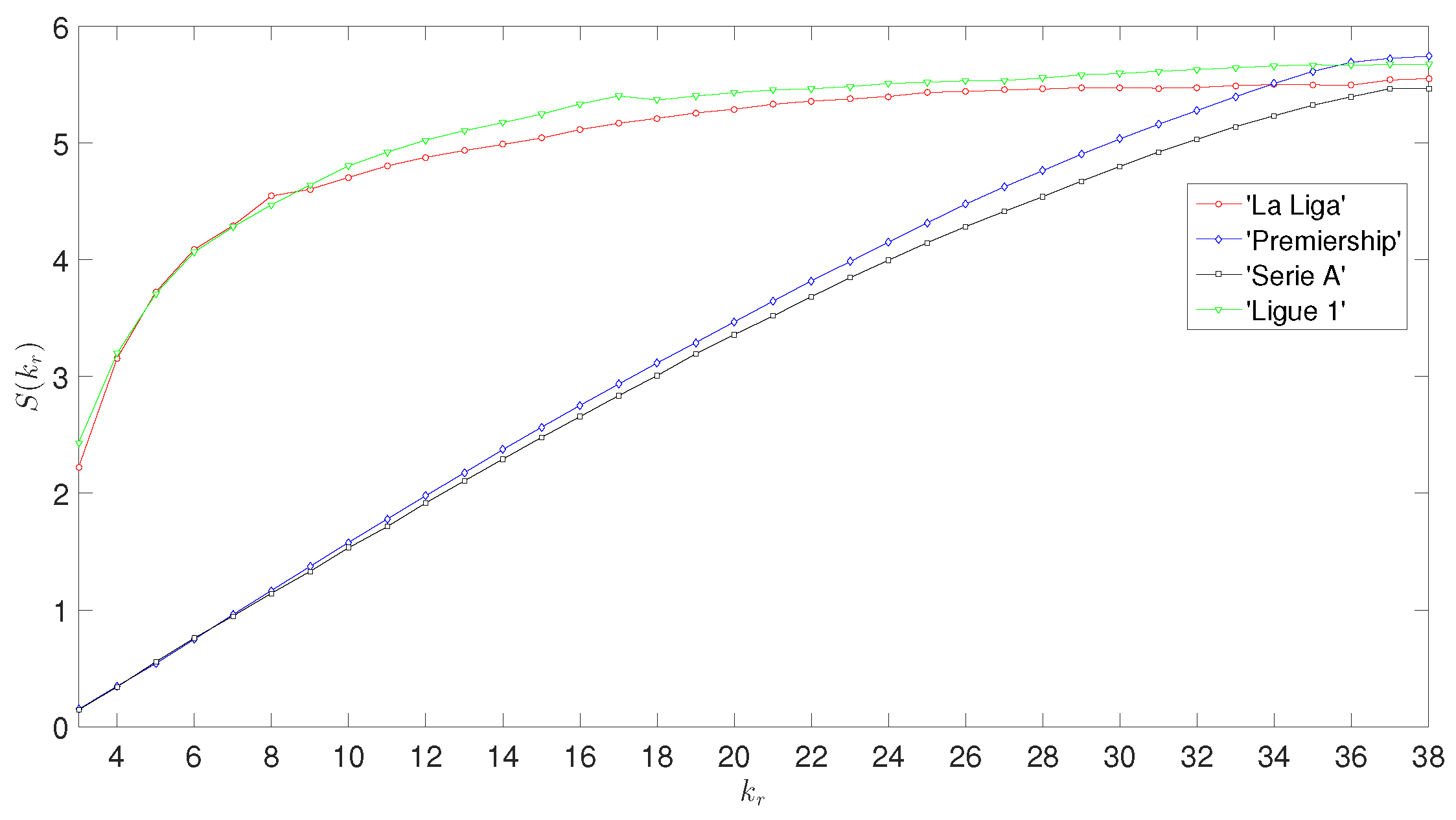
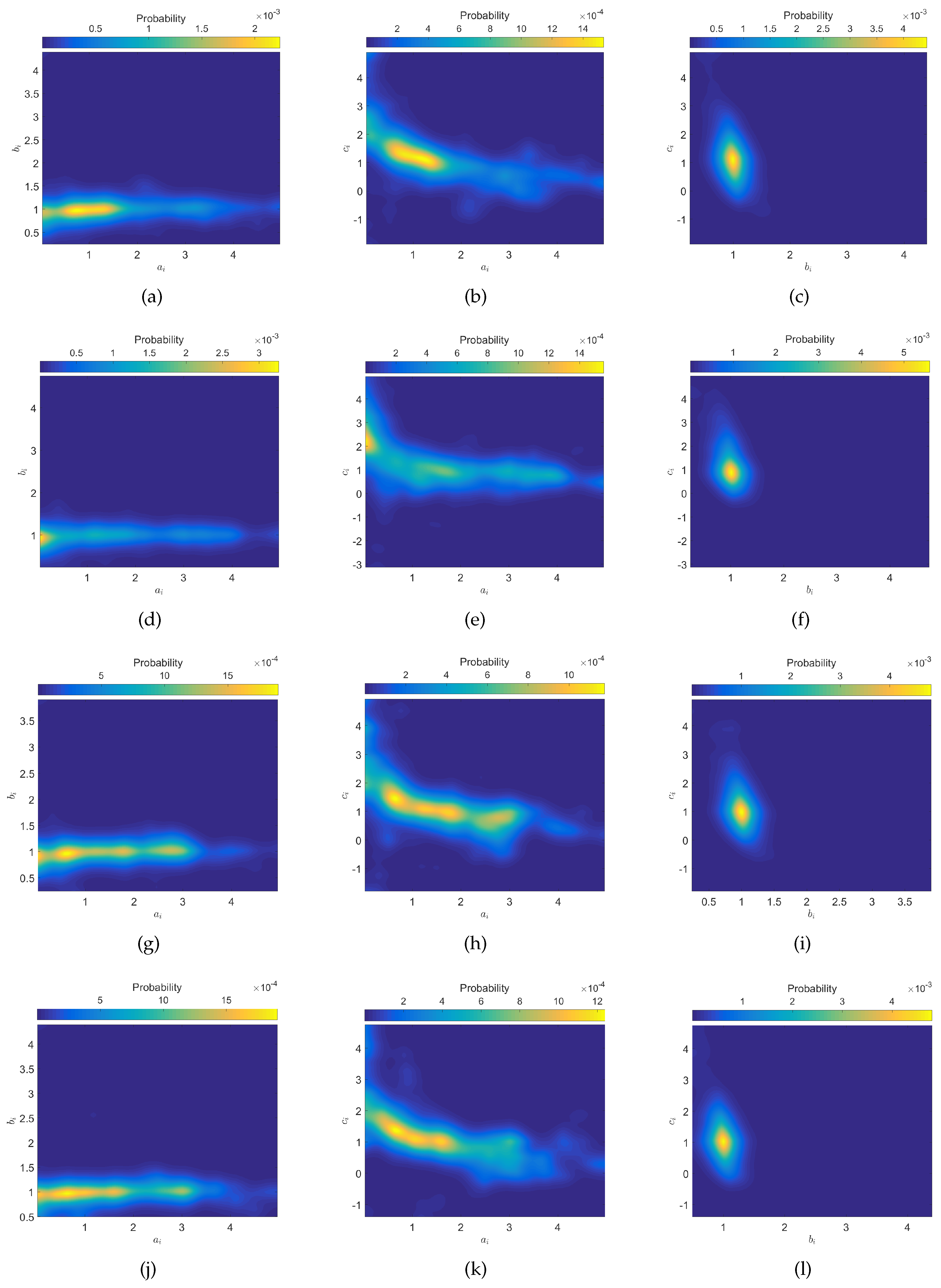
3.1. The Entropy of the PL Model
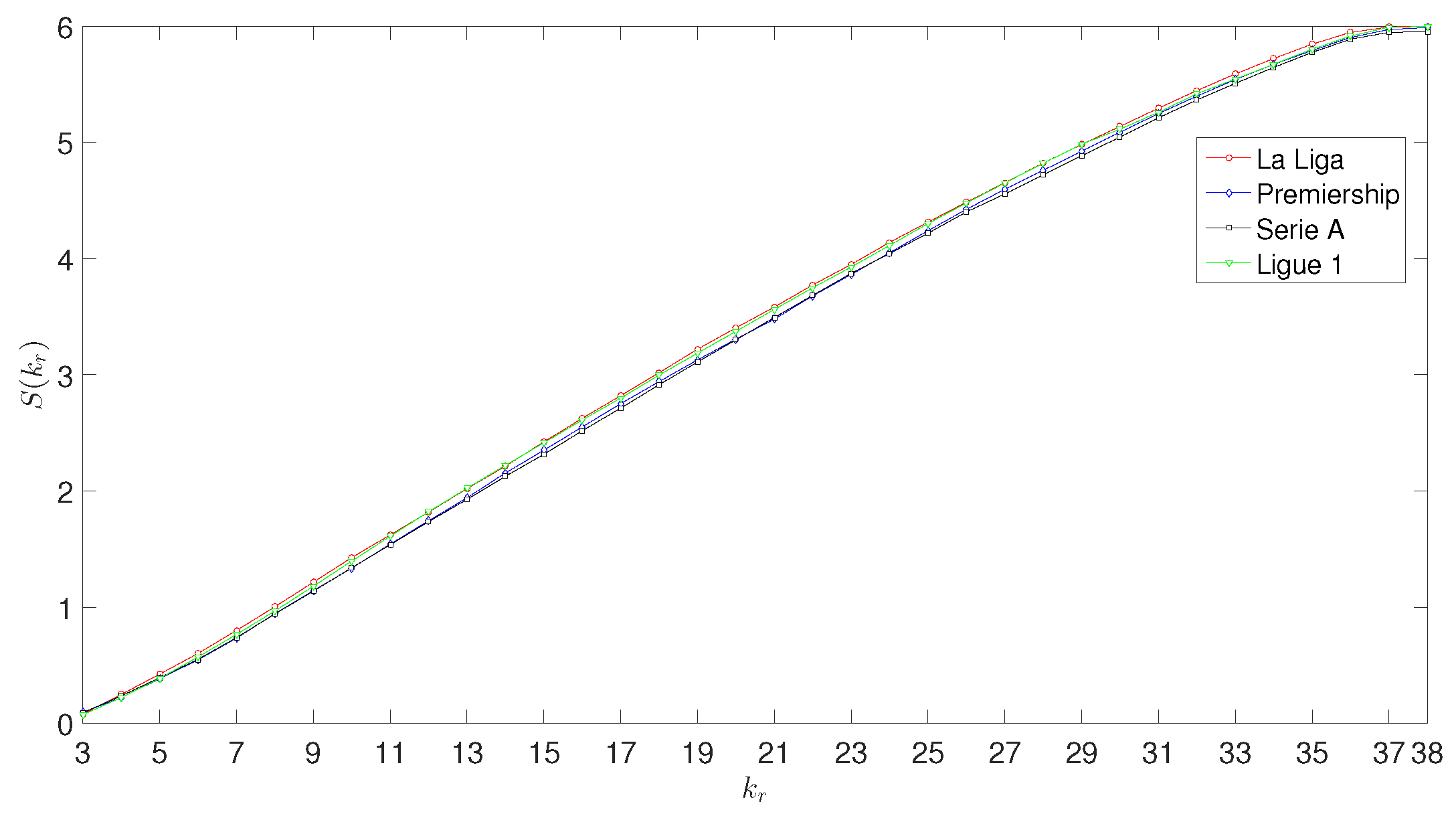
3.2. The Entropy of the Ho Model
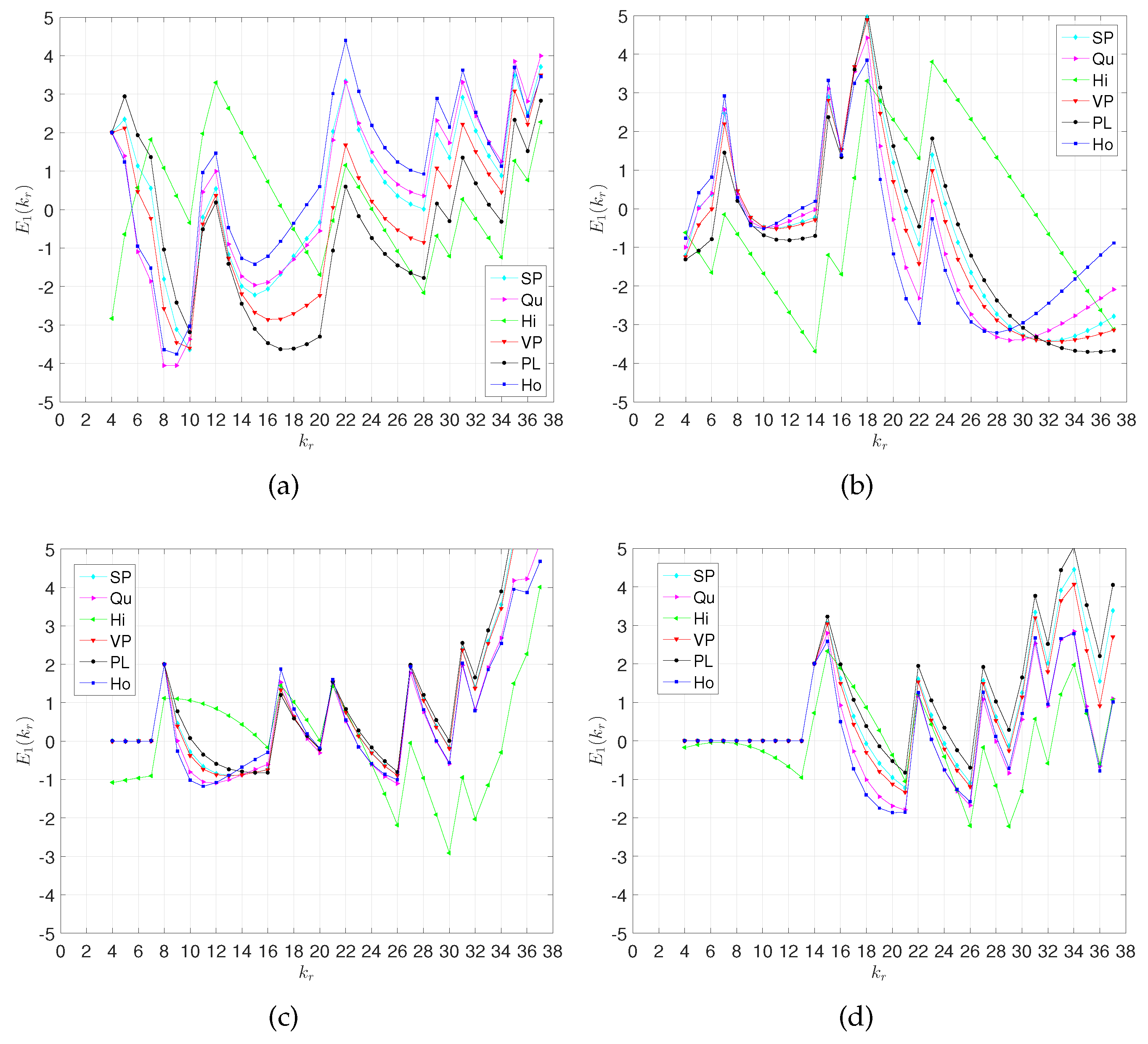
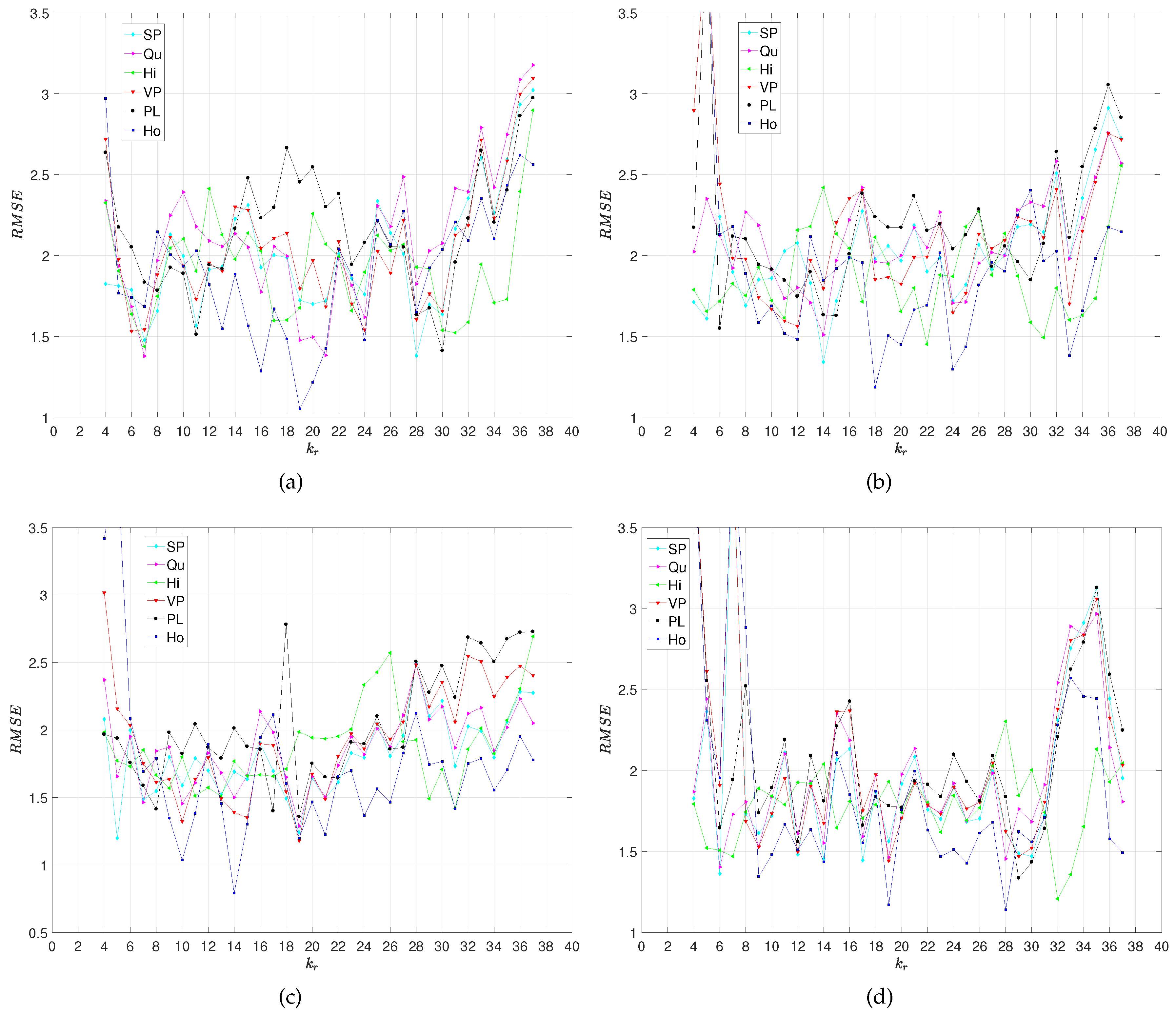
4. Predicting the Teams’ Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Carling, C.; Williams, A.M.; Reilly, T. Handbook of Soccer Match Analysis: A Systematic Approach to Improving Performance; Routledge: Abingdon, UK, 2007. [Google Scholar]
- Giulianotti, R. Football. In The Wiley-Blackwell Encyclopedia of Globalization; Wiley: Hoboken, NJ, USA, 2012. [Google Scholar]
- Brocas, I.; Carrillo, J.D. Do the “three-point victory” and “golden goal” rules make soccer more exciting? J. Sport. Econ. 2004, 5, 169–185. [Google Scholar] [CrossRef]
- Miller, K.S.; Ross, B. An Introduction to the Fractional Calculus and Fractional Differential Equations; Wiley: Hoboken, NJ, USA, 1993. [Google Scholar]
- Tenreiro Machado, J.A.; Kiryakova, V. Recent history of the fractional calculus: Data and statistics. In Handbook of Fractional Calculus with Applications: Basic Theory; Kochubei, A., Luchko, Y., Eds.; De Gruyter: Berlin, Germany, 2019; Volume 1, pp. 1–21. [Google Scholar]
- Machado, J.T.; Pinto, C.M.; Lopes, A.M. A review on the characterization of signals and systems by power law distributions. Signal Process. 2015, 107, 246–253. [Google Scholar] [CrossRef]
- Parsa, B.; Dabiri, A.; Machado, J.A.T. Application of Variable order Fractional Calculus in Solid Mechanics. In Handbook of Fractional Calculus with Applications: Applications in Engineering, Life and Social Sciences, Part A; Baleanu, D., Lopes, A.M., Eds.; De Gruyter: Berlin, Germany, 2019; Volume 7, pp. 207–224. [Google Scholar]
- Machado, J.T.; Lopes, A.M. Fractional Electromagnetics. In Handbook of Fractional Calculus with Applications: Applications in Physics, Part B; Tarasov, V.E., Ed.; De Gruyter: Berlin, Germany, 2019; Volume 5, pp. 1–23. [Google Scholar]
- Lopes, A.M.; Machado, J. Fractional order models of leaves. J. Vib. Control. 2014, 20, 998–1008. [Google Scholar] [CrossRef]
- Machado, J.T.; Lopes, A.M. On the mathematical modeling of soccer dynamics. Commun. Nonlinear Sci. Numer. Simul. 2017, 53, 142–153. [Google Scholar] [CrossRef]
- Machado, J.; Mata, M.E.; Lopes, A.M. Fractional state space analysis of economic systems. Entropy 2015, 17, 5402–5421. [Google Scholar] [CrossRef]
- Valério, D.; Ortigueira, M.; Machado, J.T.; Lopes, A.M. Continuous-time fractional linear systems: Steady-state behaviour. In Handbook of Fractional Calculus with Applications: Applications in Engineering, Life and Social Sciences, Part A; Petráš, I., Ed.; De Gruyter: Berlin, Germany, 2019; Volume 6, pp. 149–174. [Google Scholar]
- Couceiro, M.S.; Clemente, F.M.; Martins, F.M.; Machado, J.A.T. Dynamical stability and predictability of football players: The study of one match. Entropy 2014, 16, 645–674. [Google Scholar] [CrossRef]
- Silva, P.; Duarte, R.; Esteves, P.; Travassos, B.; Vilar, L. Application of entropy measures to analysis of performance in team sports. Int. J. Perform. Anal. Sport 2016, 16, 753–768. [Google Scholar] [CrossRef]
- Machado, J.T.; Lopes, A.M. Multidimensional scaling analysis of soccer dynamics. Appl. Math. Model. 2017, 45, 642–652. [Google Scholar] [CrossRef]
- Neuman, Y.; Israeli, N.; Vilenchik, D.; Cohen, Y. The adaptive behavior of a soccer team: An entropy-based analysis. Entropy 2018, 20, 758. [Google Scholar] [CrossRef]
- Lopes, A.M.; Tenreiro Machado, J. Entropy Analysis of Soccer Dynamics. Entropy 2019, 21, 187. [Google Scholar] [CrossRef]
- Berrar, D.; Lopes, P.; Davis, J.; Dubitzky, W. Guest editorial: Special issue on machine learning for soccer. Mach. Learn. 2019, 108, 1–7. [Google Scholar] [CrossRef]
- Karlis, D.; Ntzoufras, I. Analysis of sports data by using bivariate Poisson models. J. R. Stat. Soc. Ser. D (The Stat.) 2003, 52, 381–393. [Google Scholar] [CrossRef]
- Baio, G.; Blangiardo, M. Bayesian hierarchical model for the prediction of football results. J. Appl. Stat. 2010, 37, 253–264. [Google Scholar] [CrossRef]
- Hvattum, L.M.; Arntzen, H. Using ELO ratings for match result prediction in association football. Int. J. Forecast. 2010, 26, 460–470. [Google Scholar] [CrossRef]
- Berrar, D.; Lopes, P.; Dubitzky, W. Incorporating domain knowledge in machine learning for soccer outcome prediction. Mach. Learn. 2019, 108, 97–126. [Google Scholar] [CrossRef]
- Murphy, K.P. Machine Learning: A Probabilistic Perspective; MIT Press: Cambridge, MA, USA, 2012. [Google Scholar]
- Van Haaren, J.; Van den Broeck, G. Relational learning for football-related predictions. In Latest Advances in Inductive Logic Programming; World Scientific: Singapore, 2015; pp. 237–244. [Google Scholar]
- Hubáček, O.; Šourek, G.; Železnỳ, F. Learning to predict soccer results from relational data with gradient boosted trees. Mach. Learn. 2019, 108, 29–47. [Google Scholar] [CrossRef]
- Tsokos, A.; Narayanan, S.; Kosmidis, I.; Baio, G.; Cucuringu, M.; Whitaker, G.; Király, F. Modeling outcomes of soccer matches. Mach. Learn. 2019, 108, 77–95. [Google Scholar] [CrossRef]
- Edla, D.R.; Lingras, P.; Venkatanareshbabu, K. Advances in Machine Learning and Data Science: Recent Achievements and Research Directives; Springer: Berlin, Germany, 2018. [Google Scholar]
- Abu-Mostafa, Y.S.; Magdon-Ismail, M.; Lin, H.T. Learning from Data; AMLBook: New York, NY, USA, 2012. [Google Scholar]
- Lawson, C.L.; Hanson, R.J. Solving Least Squares Problems; SIAM: Philadelphia, PA, USA, 1974; Volume 161. [Google Scholar]
- Draper, N.R.; Smith, H.; Pownell, E. Applied Regression Analysis; Wiley: New York, NY, USA, 1966; Volume 3. [Google Scholar]
- Lopes, A.; Tenreiro Machado, J.; Galhano, A. Empirical laws and foreseeing the future of technological progress. Entropy 2016, 18, 217. [Google Scholar] [CrossRef]
- Lopes, A.; Tenreiro Machado, J. Complexity Analysis of Global Temperature Time Series. Entropy 2018, 20, 437. [Google Scholar] [CrossRef]
- Machado, J.T.; Lopes, A.M. The persistence of memory. Nonlinear Dyn. 2015, 79, 63–82. [Google Scholar] [CrossRef]
- Machado, J.; Lopes, A.M. Analysis of natural and artificial phenomena using signal processing and fractional calculus. Fract. Calc. Appl. Anal. 2015, 18, 459–478. [Google Scholar] [CrossRef]
- Shannon, C. A Mathematical Theory of Communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Jaynes, E. Information Theory and Statistical Mechanics. Phys. Rev. 1957, 106, 620–630. [Google Scholar] [CrossRef]
- Pinto, C.M.; Lopes, A.M.; Machado, J.T. A review of power laws in real life phenomena. Commun. Nonlinear Sci. Numer. Simul. 2012, 17, 3558–3578. [Google Scholar] [CrossRef]
| SP | Qu | Hi | VP | PL | Ho | ||
|---|---|---|---|---|---|---|---|
| ‘La Liga’ | 1.3182 | 1.1832 | 1.5852 | 1.2051 | 1.4118 | 1.0782 | |
| 0.4986 | 0.5441 | 0.2592 | 0.5607 | 0.5746 | 0.4736 | ||
| ‘Premiership’ | 1.2354 | 1.1082 | 1.5061 | 1.1699 | 1.3368 | 1.0394 | |
| 0.5233 | 0.5529 | 0.2240 | 0.5984 | 0.5496 | 0.5112 | ||
| ‘Serie A’ | 1.1749 | 1.0574 | 1.5783 | 1.1596 | 1.3800 | 1.0045 | |
| 0.4426 | 0.4865 | 0.2966 | 0.5977 | 0.5963 | 0.4251 | ||
| ‘Ligue 1’ | 1.3035 | 1.2053 | 1.6562 | 1.2313 | 1.4357 | 1.1333 | |
| 0.5155 | 0.6144 | 0.3093 | 0.6080 | 0.5627 | 0.5813 |
| SP | Qu | Hi | VP | PL | Ho | ||
|---|---|---|---|---|---|---|---|
| ‘La Liga’ | 2.0137 | 2.1177 | 1.9397 | 2.0604 | 2.1631 | 1.9172 | |
| 0.3807 | 0.4339 | 0.3076 | 0.3945 | 0.3684 | 0.4173 | ||
| ‘Premiership’ | 1.9765 | 1.9543 | 1.9936 | 2.0860 | 2.0926 | 1.9036 | |
| 0.5519 | 0.4019 | 0.2198 | 0.6336 | 0.5226 | 0.6672 | ||
| ‘Serie A’ | 1.8093 | 1.8717 | 1.8765 | 1.9462 | 2.0468 | 1.7322 | |
| 0.2930 | 0.2764 | 0.3042 | 0.4216 | 0.4139 | 0.5888 | ||
| ‘Ligue 1’ | 2.0407 | 2.1022 | 1.9912 | 2.1400 | 2.1935 | 1.9337 | |
| 0.3226 | 0.2835 | 0.2657 | 0.4683 | 0.4653 | 0.5536 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lopes, A.M.; Tenreiro Machado, J.A. Fractional Dynamics in Soccer Leagues. Symmetry 2020, 12, 356. https://doi.org/10.3390/sym12030356
Lopes AM, Tenreiro Machado JA. Fractional Dynamics in Soccer Leagues. Symmetry. 2020; 12(3):356. https://doi.org/10.3390/sym12030356
Chicago/Turabian StyleLopes, António M., and Jose A. Tenreiro Machado. 2020. "Fractional Dynamics in Soccer Leagues" Symmetry 12, no. 3: 356. https://doi.org/10.3390/sym12030356
APA StyleLopes, A. M., & Tenreiro Machado, J. A. (2020). Fractional Dynamics in Soccer Leagues. Symmetry, 12(3), 356. https://doi.org/10.3390/sym12030356






