A Novel Secure Occupancy Monitoring Scheme Based on Multi-Chaos Mapping

Abstract

Smart building control, managing queues for instant points of service, security systems, and customer support can benefit from the number of occupants information known as occupancy. Due to interrupted real-time continuous monitoring capabilities of state-of-the-art cameras, a vision-based system can be easily deployed for occupancy monitoring. However, processing of images or videos over insecure channels can raise several privacy concerns due to constant recording of an image or video footage. In this context, occupancy monitoring along with privacy protection is a challenging task. This paper presents a novel chaos-based lightweight privacy preserved occupancy monitoring scheme. Persons’ movements were detected using a Gaussian mixture model and Kalman filtering. A specific region of interest, i.e., persons’ faces and bodies, was encrypted using multi-chaos mapping. For pixel encryption, Intertwining and Chebyshev maps were employed in confusion and diffusion processes, respectively. The number of people was counted and the occupancy information was sent to the ThingSpeak cloud platform. The proposed chaos-based lightweight occupancy monitoring system is tested against numerous security metrics such as correlation, entropy, Number of Pixel Changing Rate (NPCR), Normalized Cross Correlation (NCC), Structural Content (SC), Mean Absolute Error (MAE), Mean Square Error (MSE), Peak to Signal Noise Ratio (PSNR), and Time Complexity (TC). All security metrics confirm the strength of the proposed scheme.

1. Introduction

The widespread use of visual surveillance indicates that it is not only indispensable as a security measure, but also valuable in providing an accessible solution for other applications such as smart buildings management, occupancy systems, and retail traffic analysis. Visual occupancy counting techniques have several advantages over other methods such as Radio Frequency (RF) and Passive Infrared (PIR)-based methods [1,2,3,4,5,6,7]. In comparison to other traditional technologies, including RF and PIR-based, the camera-based occupancy system is affordable due to decreasing prices of the camera and vision-based technologies [1,2,3,4,5,6,7]. Moreover, a video-based solution is considered as one of the most feasible solutions that can be easily deployment in indoor settings [4]. The aforementioned advantages have made camera-based people counting systems to become the most widely used technique. However, numerous privacy concerns can arise with the use of camera-based occupancy systems if measures are not taken to protect the person’s identity [8,9].

Progression in computer networks, computer storage devices, and imaging tools that are used these days, provides strong possibilities for leaking/disclosing individual privacy [10]. The digital images used for occupancy count are highly susceptible to a number of attacks including statistical, key space, and brute force attacks. Data privacy and authentication of multimedia data are two main concerns these days [11]. Security of multimedia data through encryption is one of the most significant techniques which received special attention from the research community over the last decades. In encryption, digital bit-streams of data are transformed in such away that an adversary could not reveal the original information. Decryption is the reverse process of encryption and only an authorized person can access the original content. A cryptosystem consists of a set of algorithms that convert plaintext data into encrypted and ciphetext data into decrypted format. Cryptosystems are categorized based upon the distribution of the keys: (i) symmetric key encryption and (ii) asymmetric key encryption [12].

Currently, protecting the privacy of the data is one of the most critical issues. It is imperative to provide safety to sensitive information against eavesdropping. Secure encryption scheme must prove that an unauthorized person could not get access to sensitive data. Sensitive information should be read-only by an authorized person and should resist cryptographic attacks [11]. Building occupancy count has numerous advantages including queue monitoring, capacity alerts, real-time count, and efficient building energy management. Furthermore, a monitoring system can be utilized in customer services, intelligent smart building. One of the accurate building occupancy monitoring systems is the vision/camera-based system. Occupancy via real-time video is more accurate as well as precise when compared to other traditional methods [8,9]. However, vision-based occupancy system must also be protected from attackers and illegal access and the privacy of the individual should not be compromised. Along with higher accuracy, privacy protection in real-time vision-based systems is a challenging task. To mitigate the privacy issues in vision-based occupancy system, we proposed a chaotic cryptosystem to provide security for digital images/videos which capture the images through an overhead camera. In the proposed system, the encryption process transforms the actual image contents for security purposes and data is converted to a secured form known as the ciphered image. The ciphered image is an unreadable form of the image, and the original contents and privacy of individuals are protected.

In the proposed work, each frame/image is protected via confusion followed by a diffusion step. Once the ROI (face) is properly detected, it is encrypted with the chaos-based system. The ROI (face) image pixels are scrambled through chaos-based pseudorandom numbers. One of the challenges in vision-based occupancy monitoring system is lightweight and secure privacy protection. Our proposed system is lightweight and secure against many attacks, which is proven in the security analysis section.

2. Background and Related Knowledge

The symmetric key-based distribution uses the same key for data encryption and decryption. The key that is used to encrypt the confidential digital information must be sent to the recipient through a proper secure digital channel. The asymmetric public-key encryption uses separate keys for encryption and decryption of digital content. It is evident from previous research [11,12,13,14,15,16,17] that the secure communication can be achieved through encryption. Encryption uses cryptographic primitives and is responsible for changing the confidential data into an unintelligible form. In the case of images, pixels are converted into such a form that does not convey any meaningful information [12,13,14,15,16]. The flow charts for image encryption and decryption schemes are shown in Figure 1 and Figure 2. From Figure 1 and Figure 2, one can see that a cryptographic algorithm and primitives are applied for image encryption. In image encryption, random numbers are generated through random phenomena and image pixels are substituted with some random number during the confusion stage of an algorithm. The substitution process scrambles the pixels of the original image and increases the entropy which makes it suitable to transmit it through a public/insecure network. However, substitution-only methods are not secured and some more steps should be added to secure an image [11,18,19,20,21,22].

Figure 1. The schematic chart of encryption phase.

Figure 2. The schematic chart of decryption phase.

Encryption of image pixels is an important step for protecting the integrity and privacy of individual in an image through two steps known as confusion and diffusion, which was initially introduced by Claude Shannon in 1949 [23,24]. This was one of the groundbreaking works providing a foundation for protecting critical information. Both confusion and diffusion have been widely used for protecting digital images. During the confusion stage, image pixels are permuted through some random number generators (RNG). However, due to low security, researchers are proposing new schemes that are based on both confusion and diffusion. In diffusion, pixels values are also changed through some mechanism, for example, XOR operations and substitution boxes (S-Boxes) [25,26,27,28,29,30,31]. Since last decade, research on the Substitution Boxes (S-Boxes) design has gained special attention from the cryptographers. A number of S-Boxes are available in literature that is used as a confusion step [32,33,34,35,36]. Some of the S-boxes are based on chaos theory, which is highly sensitive to initial conditions and by changing the starting conditions will change the entire attractor [36]. Chaotic systems are deterministic if the original keys are known to an authorized person. Such a system produce highly random numbers, which could be employed in the design of S-Boxes and then can be deployed in encryption algorithms.

Researchers have proposed several encryption algorithms that provide a solution for confidentiality. Commonly used schemes are Advanced Encryption Standard (AES), Rivest–Shamir– Adleman (RSA), Data Encryption Standard (DES), and International Data Encryption Algorithm (IDEA), but these algorithm are not well-suited for images/videos, as they are mainly used for text encryption [37,38,39,40,41,42,43,44,45]. The major reasons why these algorithms are not suited for video/images are as follows. (i) Traditional methods such as AES, etc., require high computation. Moreover, images are typically larger in volume and highly correlated, thus AES, DES, etc. are not suited for images. (ii) DES and AES algorithms cause real-time latency and therefore do not work in real-time scenarios.

Video encryption is scrambling of video content in such as a way that an intruder is incapable of obtaining the video content with a meaningful quality. Such requirement strongly demand innovative techniques for achieving the desired level of video/image security. Conventional cryptographic techniques are not efficient for real-time data processing [37,38,39,40,41,42,43,44,45]. Therefore, to fulfill such requirements, selective/partial encryption is becoming a popular choice for cryptographers. When partial encryption-based techniques are employed, one is able to encrypt only a part of the data and therefore computational complexity of the scheme is significantly reduced. This enables us to achieve the required level of video security while drastically reducing the amount of data that needs to be processed. Such characteristics make partial/selective encryption particularly useful in real-time applications [46,47,48,49]. This work has the following main contributions.

1. A detailed background of chaos theory is provided. 1. Chaos and Region-of-Interest-based new image encryption scheme with the person(s) counter algorithm is proposed.

2. Extensive security analysis including statistical and key space tests in a real-world environment are presented in this article.

The rest of paper is organized as follows. An introduction to chaotic maps and its application in image encryption is provided in Section 2.The proposed scheme is explained in Section 3. Experimental analysis and security test are discussed in Section 4. Finally, conclusions and future work are given in Section 5.

From previous literature, it is well-known that a close relationship exists between chaotic maps and cryptography [46,47,48,49]. Encryption based on these techniques (for example, logistic and tent maps) share similar characteristics such as strong reliance on initial conditions and difficult prediction of the outputs. Mathematically, the logistic map is written as

$$x_{n+1}=\mu x_n\left(1-x_n\right)$$

(1)

where $x_n$$\in (0,1)$, $\mu \in (0,4]$; however, for obtaining random numbers, the range of $\mu$ must be $\in (3.5699456,4]$.

Xiang et al. [50] used the logistic chaotic map and develop a lightweight encryption method. The proposed method was applied to the text of blocks and were shuffled randomly through the random sequences generated from the logistic map. The scheme was fast and computationally efficient. However, the proposed scheme was proven to be insecure due to its low keyspace. Many authors have critically examined this scheme [50] and reported that due to the lower key space Xiang et al. scheme is susceptible to cryptographic attacks. Pareek et al. [51] proposed a simple and secure chaos-based cryptographic algorithm utilizing two logistic maps. An external key was produced with the logistic map and image was encrypted through several rounds of permutation and random sequences were applied for achieving a reliable, and secret data. The proposed scheme was secure but it was also proved insecure due to lower keyspace [52]. Khan et al. [52] proposed a secure system based on quantum dynamical spinning and rotation using quantum cryptography for higher security. The proposed scheme has good computational speed when compared to other traditional cryptosystems [52]. The computational speed of a quantum-based system is approximately 100 times faster than classical computers. Mainly, Khan et al. work is based on a spinning operator. In this work, keys were encrypted, and subsequently, the digital image is encoded. The proposed cryptosystem was validated with numerous statistical tests [52].

Wang et al. [53] proposed an algorithm based on zigzag transform and deoxyribonucleic acid (DNA) coding. The cryptosystem was dependent on the initial values for the chaotic dynamical system, the (DNA) coding, and zigzag transform, and from the generated random numbers, images were encrypted. The test image was scrambled using zigzag transformation before pixel sorting. The image is further diffused through DNA-based random numbers and was bit-wise XORed with chaos-based random numbers. The security of the proposed scheme was further strengthened by adding an extra layer of security using a hybrid technique and therefore system was strongly resistant against any differential attack. Behnia et al. [37] presented a new encryption based on multiple chaotic maps. Digital images were scrambled through the proposed method using coupled lattice maps and one-dimensional chaotic map. The proposed system has higher keyspace and sufficient security. However, the system showed low sensitivity to the initial conditions.

Gao et al. [54] proposed a secure scheme based on a hyperchaotic map and scrambled the contents of the plain image. Due to the use of hyperchaos maps, the randomness in the proposed scheme was increased compared to other chaotic maps. The proposed scheme used a matrix shuffling process which permuted the pixels of images followed by a diffusion process using a hyperchaotic map. Ahmad et al. [55] presented a survey on chaos and non-chaos schemes. In a chaos-based scheme, pixels positions were shuffled using Bernoulli’s shift map; subsequently, the map is employed to modify the original pixels of the digital images. Jawad et al. outlined that chaos-based schemes have higher keyspace and images were highly secured than non-chaos based schemes. The other study, Jawad et al. [56] proposed a novel scheme for digital multimedia security using lightweight cryptography and random numbers obtained from Chebyshev and Intertwining maps. The chaotically coupled combination of the maps added confusion and diffusion property to the presented scheme. The proposed cryptosystem had good statistical security results. Zhang et al. [57] proposed a symmetric key-based secure scheme for image encryption. The system was combined using linear and nonlinear coupled lattices. The combination of linear and nonlinear lattices overwhelmed the issues of the periodic windows. The proposed scheme uses a combination of permutation and diffusion of the pixels. Mirzaei et al. [58] proposed a new scheme based on parallel steps for confusion and diffusion. Image pixels were divided into four equal blocks. Chaotic maps were employed to shuffled the image blocks. In the final phase, all blocks were encrypted and each pixel is distorted using random numbers obtained from chaotic maps. All security tests validated the proposed system. Belazi et al. [59] proposed a scheme based on improved scrambling techniques. The cryptosystem consists of novel method for scrambling. The suggested technique employed several chaotic maps such logistic map, S-box and a number of permutation functions.

Recently, Masood et al. [60] proposed a novel scheme for secure communication. Confusion and diffusion were carried out using chaotic maps and all required security steps were followed, which were initially proposed by Claude Shannon in 1949 [23,24]. This cryptosystem utilised the complex values created through a complex Mandelbrot set of fractals which was originally developed by Benoit Mandelbrot. The Mandelbrot fractals generated complex random numbers. In the proposed scheme, imaginary numbers were neglected while the real numbers were utilized in the encryption algorithm. The random numbers were multiplied with a sequence produced from Fibonacci series. An extra security layer was added through chaotic Kaplan Yorke map and fractals. The Mandelbrot fractals used in Masood et al. scheme is written as

$$Z_{n+1}={Z_n}^2+c$$

(2)

According to recent research [60], over a thousand papers based on chaos were published until to date. It is, however, unfortunate that many of these techniques are susceptible to a number of attacks [60]. Additionally, many techniques are either computationally extensive or impractical due to low keyspace.

3. The Proposed Chaos-Based Secure Occupancy Scheme

Intertwining and Chebyshev chaotic maps exhibit desirable characteristics such as a positive Lyapunov exponent, zero correlation in the total field, and an equiprobable distribution, and therefore it can be used for video/image encryption. The proposed scheme utilizes both Intertwining and Chebyshev chaotic maps because they offer the aforementioned desirable properties and a larger keyspace which resist brute force attacks. Intertwining map can be written as [61]

$$\begin{array}{c}{A}_{n+1}=(\lambda \times \alpha \times B_n\times (1-A_n)+C_n)mod(1),\hfill \\ B_{n+1}=({\displaystyle \frac{\lambda \times \beta \times B_n+C_n}{1+{(A_{n+1})}^2}})mod(1),\\ \hfill C_{n+1}=(\lambda \times (A_{n+1}+B_{n+1}+\gamma )\times sin(C_n)mod(1),\end{array}$$

(3)

where $A_n,B_n$ and $C_n\in (0,1)$, $0\le \lambda \le 3.999$, $\left|\alpha \right|>33.5,\left|\beta \right|>37.9,\left|\gamma \right|>35.7$. The Key space of Intertwining map is (${10}^{60}\approx 2^{200}$) which is greater than traditional Logistic map and tent maps. Compared to other maps, random number generated through Intertwining Logistic map is distributed more evenly [61]. Chebyshev map can be defined as [62,63]

$$T_{\mu }(z)=cos(\mu \times arccos(z)),$$

(4)

where $\mu$ = 0, 1, 2, ..., and $z\in [-1,1]$. Huang suggested $\mu =4$ for less computation and efficient use of Chebyshev map. In the proposed scheme, we utilize $\mu =4$ and such type of Chebyshev function can be written as

$$f(z_i)=8z_{i-1}^4-8z_{i-1}^2+1,i=1,2,\dots$$

(5)

The main goal of the proposed scheme is the detection of an object in a video sequence, followed by encryption and then counting of the objects. Flow chart of the encryption process used in the scheme is shown in Figure 3. The pseudo-random key streams are generated using the scheme proposed in our previous research [10].

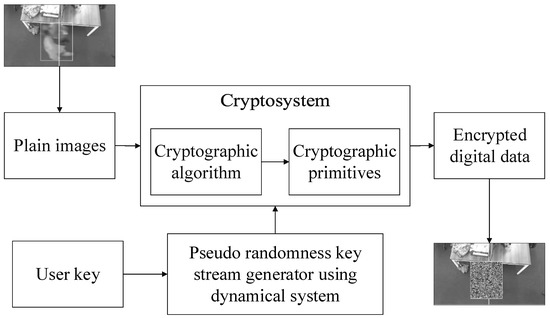
Figure 3. The systematic process of image encryption.

To obtain an image it is necessary to use background modeling. For moving object detection, there are a plethora of methods available in the literature each having its own advantages and disadvantages. In our case, we used Gaussian Mixture Model (GMM) technique due to its accuracy and real-time applicability. Mathematically, GMM is written as

$${\displaystyle P(x_t)={\displaystyle \sum }_{j=1}^K{w}_{j,t}\eta (x_t;{\varphi }_j,t,\sum _{j,t}),}$$

(6)

In Equation (6), $x_t$ is incoming pixel value at a time t, $w_{j,t}$ is weight of $j^{th}$ distribution at time t, and $\eta (x_t,{\varphi }_{j,t},{\displaystyle \sum _{j,t}})$ is probability Gaussian distribution function. Based on value of $w/\sigma$, K distribution is sorted and the background model can be written as follows,

$$B=argmi{n}_b\left({\displaystyle \sum }_{j=1}^b{w}_k>T\right),$$

(7)

Each Gaussian which is greater than the threshold T is classified as background. More details about GMM can be found in [2]. For every Gaussian variable with a value larger than T, a background is classified.

The Kalman filter is widely popular and used extensively in signal estimation, navigation systems, and control systems. Essentially, the Kalman filter is used to provide optimal estimation in the form of mathematical equations. The results are optimal despite the presence of Additive White Gaussian Noise (AWGN). In the proposed method, the Kalman filter is used to forecast the position of moving object. This is followed by tracking of the person as the frames continue. In discrete-time, the Kalman filter with a state transition given by $\widehat{X}$ at k is written as

$${\widehat{X}}_k=A{\widehat{X}}_{(k-1)}+B{u}_k+W_k,$$

(8)

where A is $n\times 1$ system state transition vector; B represents the control parameter, which relates $u_k$ with state ${\widehat{X}}_k$; and $W_k$ is a vector representing additive noise. Mathematically, measurement Z in terms of state ${\widehat{X}}_k$ can be defined as

$$Z_k=H_k{\widehat{X}}_k+V_k,$$

(9)

where H relates the measured vector Z to the state vector ${\widehat{X}}_k$, whereas $V_k$ is measured noise. Therefore, in essence, the Kalman filter is responsible for estimating the next state given the current state and the noise values, which allows for prediction. Figure 2 highlights the process flow of the filter. One can see from Figure 2 that the Kalman filter is an iterative technique used for prediction and correction of state variables.

Detail Steps of the Proposed Occupancy Scheme:

Step 1: A series of frames are acquired with the use of the single overhead camera. For the sake of simplicity, the algorithm uses grayscale frames by converting RGB frames to grayscale.

Step 2: The background is denoted as B. It is challenging to obtain a fixed background due to changes in the environment’s illumination levels. To remedy this, GMM is used in the proposed system. In this case, GMM work as a foreground detector. There are two main parameters of GMM, i.e., the threshold $\alpha$ and the Gaussian number (K). Values for these parameters are set as 0.7 and 3, respectively.

Step 3: Generally, algorithms confuse shadows as objects, determining them to be the foreground. Therefore, for every frame, shadows must be removed. This is achieved by converting the frame’s color space to YCbCr. Then, apply morphological closing and opening operations. Mathematically, closing (PC) and opening (PO) are written as

$$PC=Erode(Dilate(P),K_r),$$

$$PO=Dilate(Erode(P),K_r),$$

here $K_r$ denotes the kernel.

Step 4: The threshold defines where the background ends and the foreground begins. Subtract the current frame $PO$ from B, which identifies the objects in motion that exists in the foreground that is the ROI.

Step 5: The seed values for Intertwining and Chebyshev maps are selected as a secret key.

Step 6: Iterate the Intertwining and Chebyshev maps $H\times W$ times, which is the same size as the size of ROI bound obtained in step 4. Pixels in ROI is shuffled using random indices obtained through Intertwining maps.

Step 7: The shuffled data matrix is diffused using the random matrix obtained through Chebyshev map. XORed operation is applied on shuffled ROI and random chaos valued obtained from Chebyshev. Lastly, the Advanced Encryption Standard (AES) substitution is applied to get the encrypted ROI.

Step 8: The Kalman filter estimate, the position of moving objects, and the Hungarian cost matrix $\psi$ are obtained, which assigns the costs between the track and detection D.

Step 9: Finally, the number of people in the encrypted domain is counted.

4. Experimental Test and Security Analysis

The Logitech camera (2.0 megapixels) was installed in T10 office at Glasgow Caledonian University, United Kingdom. The frame size of the Logitec camera was set to a low value for efficient computation, i.e., $180\times 320$ pixels. The camera was installed 1.7 meters above the ground. The video was processed for occupancy counting using the aforementioned steps in the proposed method. Each frame is encrypted for obtaining higher security. A plaintext image frame selected ROI encrypted complete image and encrypted ROI are shown in Figure 4, respectively. From Figure 4, one can see that the privacy of an individual is secure, and the desired region is encrypted; however, it is compulsory to prove the encryption strength through mathematical security parameters. Security measures are carried out and discussed in very detail.

Figure 4. Plain image, Encrypted region of interest (ROI) image, and Retrieved Encrypted image.

4.1. Histogram Analysis

Histogram analysis is one of the most significant security measures that represents the occurrence of the pixels in a defined range. The uniformity of pixels validates that the confidential information is encrypted; thus, the eavesdropper will have no clue of the original information. The histogram is applied to the plain text image. The peaks of the plain image pixels are compared to the uniform and equally distributed pixels of the encrypted image shown in Figure 5. The regular distribution of pixels that are shown in Figure 5 depicts that the proposed scheme is secure.

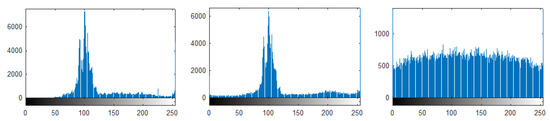
Figure 5. Plain ROI image histogram, encrypted ROI image histogram, and retrieved Encrypted image histogram.

4.2. Correlation Coefficient Analysis

The correlation coefficient defines the distribution of the pixels in a plain and encrypted digital image. Pixels that are similar to each other show that they are highly correlated with each other. Such pixels that are not similar to each other show that the pixels have a lower correlation. Such tests highlight lower correlation in encrypted image. Mathematically, the correlation coefficient is written as

$${\gamma }_{XY}=\frac{{\delta }_{XY}}{\sqrt{{\delta }_X^2{\delta }_Y^2}},$$

(10)

where as ${\delta }_{XY}$ in the aforementioned Equation (10) is covariance of the random variables X and Y, ${\delta }_X^2$ and ${\delta }_Y^2$ are the variance that in the random variable X and Y. Each term is defined as follows,

$${\delta }_{XY}={\displaystyle \sum }_{j=1}^N\frac{\left(X_j-{\mu }_j\right)\left(Y_j-{\mu }_Y\right)}{N},$$

(11)

$${\delta }_X^2={\displaystyle \sum }_{j=1}^N\frac{\left(X_j-E{(X)}^2\right)}{N},$$

(12)

$${\delta }_Y^2={\displaystyle \sum }_{j=1}^N\frac{\left(Y_j-E{(Y)}^2\right)}{N},$$

(13)

where ${\mu }_X$ and ${\mu }_Y$ are the expected values of the random variables X and Y. The correlation coefficient values are between −1 and 1. The value 1 indicates the maximum value of correlation and shows that a digital plain and the encrypted image is similar. In contrast, a value “−1” shows that the encrypted image is negative of the original image. Ideally, the correlation value should be near 0. A value near to zero depicts that the suggested scheme is highly secure.

Plain digital image values for the horizontal, diagonal, and vertical directions are 0.9086, 0.8313, and 0.9053, respectively, with a mean value for all three directions is 0.8817. For encrypted image values for, horizontal, diagonal, and vertical directions are 0.0005, −0.0047, and 0.1313, respectively, with the calculated mean value is 0.042, which is close to 0 as shown in the Table 1. The evaluated values are also compared to several existing algorithms and it can be seen the proposed system perform better. Furthermore, image pixels are examined for a plain and encrypted images that are shown in Figure 6 and Figure 7 in horizontal, diagonal, and vertical directions, respectively. It is clear from correlation plots that encrypted image is highly scattered and therefore reveals that encrypted pixels are not similar.

Table 1. Correlation coefficient values for each direction: H-D = Horizontal direction, D-D = Diagonal direction, V-D = Vertical direction, A-V = Cumulative average value.

		Plain Image Directions				Encrypted Image Directions
	Images	H-D	D-D	V-D	A-V	H-D	D-D	V-D	A-V
1	Proposed	0.9086	0.8313	0.9053	0.8817	0.0005	−0.0047	0.1313	0.042
2	Ref. [4]	0.9727	0.9204	0.9573	-	−0.0394	−0.0194	−0.0223	-
3	Ref. [64]	-	-	-	-	0.0681	0.0128	0.0049	-
4	Ref. [65]	-	-	-	-	0.0965	0.0362	−0.0581	-
5	Ref. [66]	-	-	-	-	0.1257	0.0226	0.0581	-

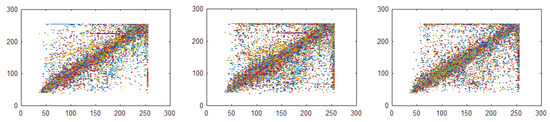
Figure 6. Plain image horizontal direction pixels, plain image diagonal direction pixels, and plain image vertical direction pixels.

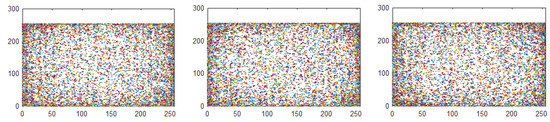
Figure 7. Encrypted image horizontal direction pixels, encrypted image diagonal direction pixels, and encrypted image vertical direction pixels.

4.3. Peak to Signal Noise Ratio

The quality of an encrypted image can be evaluated through the peak to signal noise ratio (PSNR) test. PSNR can be written as

$$\mathbf{PSNR}=10{log}_2\frac{I^{2}max}{MSE},$$

(14)

where $I_{max}$ in the above Equation (14) is the highest value of the pixel in the test image. For a good cryptosystem, a low value of PSNR is required, which depicts a significant difference between plain and encrypted images. The effectiveness of the proposed technique is evaluated using PSNR in decibel. The average value should be equal to 9.50 (dB), while for the proposed scheme is 9.26 (dB), which is less than 9.50 (dB), indicating a higher quality of encryption.

4.4. Mean Square Error

To assess the proposed scheme further, Mean Square Error (MSE) test is performed. MSE can be written as

$$\mathbf{MSE}=\frac{1}{M\times N}{\sum }_{i-1}^M{\sum }_{j-1}^N\left(P_{(i,j)}-C_{(i,j)}\right),$$

(15)

In the preceding Equation (15), $M\times N$ is the cumulative size of the image consisting of total pixels equal to $180\times 320$. $P_{i,j}$ and $C_{i,j}$ are plain and cipher digital image at $i^{th}$ row and $j^{th}$ column. In the condition of mean square error (MSE), it is necessary to attain higher value. We studied the mean square error (MSE) test on the proposed scheme and computed its value which is equal to $7775.0$. Moreover, the proposed system is also compared to the standards of AES, AES-CBC, AES-Counter, AES-Feedback and AES-Stream. The MSE test values are equal to 4600, 4637, 4938, 4577, and 4911 for AES, AES-CBC, AES-Counter, AES-Feedback, and AES-Stream, respectively, as shown in Table 2. These values are smaller than the proposed scheme values and therefore through MSE test a higher security of the proposed scheme is validated.

Table 2. MSE value and comparison with existing cryptosystems.

S. No.	Algorithms	MSE Values
1	Proposed	7775.0
2	AES	4600
3	AES-CBC	4637
4	AES-Counter	4938
5	AES-Feedback	4577
6	AES-Stream	4911

4.5. Entropy Analysis

The output encrypted image should be highly random which can be evaluated through entropy test. Mathematically, entropy is written as

$$\mathbf{H}=-{\displaystyle \sum }_{J=0}^{N-1}p\left(x_j\right){log}_{b}p\left(x_j\right),$$

(16)

where $p(x_j)$ is the probability mass function for the event $x_j$. The b in the above Equation (16) indicates the logarithmic base. X is the random variable which takes n outcomes. For an ideal encryption scheme, value of entropy should be close to 8. The proposed scheme, entropy value is $7.99\approx 8$. The value of $7.99$ highlights that the proposed system is highly robust against differential attack. Moreover, the proposed system has higher entropy values than other traditional schemes (Table 3).

Table 3. Comparison of entropy values.

S. No.	Algorithms	Entropy Values
1	Ideal	8.0000
2	Proposed	7.9911
3	Baptisa’s algorithm [67]	7.9260
4	Wong’s algorithm [67]	7.9690
5	Rhouma et al. [64]	7.9732
6	Huang et al. [66]	7.7703
7	Hongjun at al. [65]	7.9845

4.6. Mean Absolute Error

Mean absolute error (MAE) is the other security parameter that is used to investigate the probability of the differential attack. In other words, it determines the maximum difference between a plain image and the encrypted image. MAE is written as

$$\mathbf{MAE}=\frac{1}{M\times N}{\displaystyle \sum }_{i=0}^{M-1}{\displaystyle \sum }_{j=0}^{N-1}\left|\left(C_{(i,j)}-P_{(i,j)}\right)\right|,$$

(17)

whereas $M\times N$ is the total size of an image. The $C_{i,j}$ in the Equation (17) depicts the secure cipher image at $ith$ row and $jth$ column, whereas $P_{i,j}$ is the plain image at $ith$ row and $jth$ column. The greater the value of mean absolute error (MAE), the less chance of occurrence of a successful attack. A value of 114 is accomplished after the test parameter, which shows that the proposed scheme has sufficient strength of opposing attack. The computed values is compared to several existing algorithms which is shown in Table 4. One can see from Table 4 that proposed system has lower MAE that highlight the security of the proposed scheme.

Table 4. Mean absolute error (MAE) comparison.

S. No.	Algorithms	MAE Values
1	Proposed	114
2	[14]-Lena image	77.35
3	[14]-Baboon image	73.91
4	[60]	92
5	Norouzi et al. [68]-Lena	77.82
6	Norouzi et al. [68]-Tiffany image	94.36
7	Norouzi et al. [68]-Splash	76.78

4.7. Number of Pixel Changing Rate

The test is used to find the sensitivity of pixel change rate when plain image or key is slightly changed. For analyzing Number of Pixel Change Rate (NPCR), consider $C_1(i,j)$ and $C_2(i,j)$, which are encrypted and the plaintext was only a pixel different. NPCR can be computed as

$$\mathbf{NPCR}=\frac{\left({\sum }_{i,j}{V}_{i,j}\right)}{M\times N}\times 100,$$

(18)

where as: $V_{i,j}=\left\{\begin{array}{cc}0\hfill & C_{1(i,j)}=C_{2(i,j)}\hfill \\ 1\hfill & C_{1(i,j)}\ne C_{2(i,j)}\hfill \end{array}\right.$

The NPCR in the proposed scheme was more than 99% that indicates higher security of the proposed system.

4.8. Normalized Cross Correlation

The Normalized Cross-Correlation (NCC) is one of the essential security measures which is used for testing the security of an encryption algorithm. This test is mainly dependent on two parameters: (i) mean and (ii) variance. NCC is calculated as

$$\mathbf{NCC}=\frac{1}{N}\times \frac{sum[x_n-mea{n}_x]\times [y_n-mea{n}_y]}{\sqrt{va{r}_x\times va{r}_y}}$$

(19)

whereas in the above Equation (19), the var is a variance between x and y, $mea{n}_x$ and $mea{n}_y$ are the average values between x and y, respectively. The output range of NCC is between [1, −1]. The value of 1 indicates that the pixels are highly correlated to each other. In contrast, a value less than 1 shows that the pixels are dissimilar, and the proposed system is secure. The achieved value for the proposed system is ($0.6883<1$) depicts sufficient security and resistance against differential attacks.

4.9. Time Complexity of the Proposed System

It is crucial to have a good cryptosystem and must use the least resources and should be computationally efficient. Such a cryptographic algorithm which are computationally inefficient and requires much time for encryption/decryption, cannot be used as a real-time security solution. We have carried out the time complexity test of the proposed cryptosystem and the processing time was only 8.6 msec. The examination is carried out on MATLAB 2019(a) with a system having 8GB RAM. The calculated computational time for the proposed system is compared to several existing systems as shown in the in Table 5 that highlight the real-time applicability of the proposed system.

Table 5. Time complexity values and its comparison.

S. No.	Algorithms	Time Complexity (s)
1	Proposed	8.6 ms
2	Ahmad et al. [10]-Lena image	2.25 s
3	Ahmad et al. [10]-Pepper image	2.76 s
4	Ahmad et al. [10]-Sailboat image	2.66 s
5	Ahmad et al. [10]-Baboon image	2.55 s
6	Ahmad et al. [69]-Lena image	3.23 s
7	Ahmad et al. [69]-Pepper image	3.68 s
8	Ahmad et al. [69]-Sailboat image	3.55 s
9	Ahmad et al. [69]-Baboon image	3.53 s

4.10. Structural Content

Similarity between plain image and cipher image is calculated via Structural Content (SC) test. It determine the similarity between the plain and encrypted image. Mathematically, SC is written as

$$\mathbf{SC}=\frac{{\sum }_{i=1}^M{\sum }_{j=1}^N{\left(O_{i,j}\right)}^2}{{\sum }_{i=1}^M{\sum }_{j=1}^N{\left(E_{(i,j)}\right)}^2},$$

(20)

whereas $O_{i,j}$ and $E_{i,j}$ in Equation (20) are original and encrypted images at ith row and jth column, respectively. The value of SC is between (1, −1). A value less than 1 indicates that the proposed system is secure while a value close to 1 highlights that the scheme is insecure for digital images. In the proposed scheme, SC is 0.6257 which is less than 1 and therefore it indicates higher security of the proposed scheme.

5. Conclusions

This paper presents a novel privacy preserved occupancy monitoring system. The number of people can be counted along with the Region of Interest (ROI) based encryption. Such ROI-based encryption offers improved computation speed. Intertwining and Chebyshev maps are used to encrypt moving objects in the foreground which drastically improve the performance. The results show that the chaotic maps used in this paper are highly sensitive to the initial seed parameters. Such properties of chaos maps protect an attacker from numerous attacks. The proposed scheme is tested in a real-time office environment and the security is proved via a number of security parameters is reported in this research. These parameters include entropy, correlation, mean square error, mean absolute error, peak to signal noise ratio, number of pixel change rate, normalized cross correlation, and structural content. Results from these tests confirm the usefulness of the proposed technique in real-time environment and verify a higher level of security. Our future goal is to test the proposed method with other chaotic maps, and furthermore compare it with a number of other conventional encryption schemes.