Confidence Intervals for the Mixture Transition Distribution (MTD) Model and Other Markovian Models

Abstract

The Mixture Transition Distribution (MTD) model used for the approximation of high-order Markov chains does not allow a simple calculation of confidence intervals, and computationnally intensive methods based on bootstrap are generally used. We show here how standard methods can be extended to the MTD model as well as other models such as the Hidden Markov Model. Starting from existing methods used for multinomial distributions, we describe how the quantities required for their application can be obtained directly from the data or from one run of the E-step of an EM algorithm. Simulation results indicate that when the MTD model is estimated reliably, the resulting confidence intervals are comparable to those obtained from more demanding methods.

1. Introduction

Markovian models such as homogeneous Markov chains, Mixture Transition Distribution (MTD) models and Hidden Markov Models (HMMs) are widely used for the analysis of time series. They are, for instance, a standard tool in speech recognition and DNA analysis, and they are becoming more and more popular in psychology, finance, and social sciences. However, some aspects of these models have not been fully studied yet, including the construction of confidence intervals (CIs). At least two reasons can explain this: (i) Markov chains were often used in a theoretical framework which does not require real data; (ii) even if models such as HMMs are of standard use today, they are often applied in fields where the number of available data is very large, limiting the need to worry about sample size and confidence intervals. When confidence intervals are nevertheless required, the most common solution is to rely on resampling methods such as bootstrap. This approach can be used with all Markovian models, but on the other hand, it can be very computationally intensive [1,2]. Therefore, the aim of this article is to provide an easy-to-calculate method for the evaluation of confidence intervals in the case of the MTD model, and then to extend the same approach to other Markovian models.

The approach described in this paper can be viewed as a development of a method already applied to homogeneous Markov chains: Since the transition matrix of a Markov chain can be seen as a set of multinomial distributions, it is possible to rely on methods developed for computing simultaneous confidence intervals on multinomial distributions. For instance, the R package markovchain [3] includes an implementation of this principle based on the work of Sison and Glaz [4]. This approach works well, because in empirical situations, the number of data points used to estimate each element of the transition matrix is generally known. However, this is not the case for the MTD and the HMM models. In the case of HMMs, there exists a theoretical solution using the Hessian matrix, but it cannot be applied on large samples [5] or when some of the parameters are on the boundary of the parameter space [2], and as far as we know there is still no published method for the construction of analytical confidence intervals in the case of the MTD model.

The purpose of this paper is to show that existing methods can also be applied to the MTD model and other advanced Markovian models, the only requirement being a way for correctly estimating the number of observations entering in the computation of each transition probability. The paper is organized as follows: In Section 2 we recall some principles used to build confidence intervals in the case of multinomial distributions. In Section 3, we show how to apply these principles in the case of the MTD model, and we extend the same approach to hidden models in Section 4. Numerical simulations are provided in Section 5, and a Discussion ends the paper.

2. Simultaneous Confidence Intervals for Multinomial Distributions

Let $({\theta }_1,{\theta }_2,\dots ,{\theta }_c)$ be the theoretical probability distribution of a categorical random variable Y taking values in $\{1,\dots ,c\}$. Let $(n_1,n_2,\dots ,n_c)$ be the observed frequency distribution computed from a sample of size $n={\sum }_{i=1}^c{n}_i$, and let $(p_1,p_2,\dots ,p_c)$ be the corresponding empirical probability distribution. The objective is to provide simultaneous confidence intervals for $p_1,\dots ,p_c$. One approach is to consider the related problem of the minimal sample size required to achieve a given precision of the estimation. Mathematically, we have to find the minimal n such that

$$P\left(\bigcap _{i=1}^c\left(\right|p_i-{\theta }_i|\le d)\right)\ge 1-\alpha$$

where $\alpha$ is the type I error, and where d is the precision of the estimation, that is the maximal difference allowed between any element of the theoretical probability distribution and its empirical estimation, or equivalently the half-length confidence interval around the empirical estimations.

This problem has been adressed several times. An easy to used, but imprecise solution, is to provide intervals of the form ${\widehat{p}}_i\pm d$, and to simply compute d as $1/\sqrt{n}$, what is similar to the confidence interval computed for a single binomial proportion. Following Adcock [6], d can also be obtain from the following equation:

$$n=0.25\frac{{\chi }_{[1,\alpha /c]}^2}{d^2}$$

where ${\chi }_{[1,\alpha /c]}^2$ is the threshold of a chi-square distribution with one degree of freedom and probability equal to $\alpha /c$. This method is very easy to use, but it suffers some shortcomings, among them the fact that the resulting confidence interval is a function of c, the number of categories. Thompson [7] proposed to consider instead

$$n=\underset{c\ge 1}{max}\left\{\frac{\frac{1}{c}(1-\frac{1}{c}){\chi }_{[1,\alpha /c]}^2}{d^2}\right\}$$

(1)

Even if this rule is not perfect, its degree of conservatism being unknown, it presents the advantage to provide a precision d independent from the number of categories.

Thompson provided the quantity $d^{2}n$ for different values of $\alpha$, for instance $d^{2}n$ = 1.00635 for $\alpha =10\%$, 1.27359 for $\alpha =5\%$, and 1.96986 for $\alpha =1\%$. Dividing this value by the desired $d^2$ gives the required sample size, whatever the number of categories of the distribution. For instance, $d=0.1$ and $\alpha =5\%$ lead to $n=1.27359/{0.1}^2=127.359$, so a sample of at least 128 data points should be used.

Now, considering the reverse problem, it is possible to compute the actual half-length confidence interval d given the number of data used for the estimation. If we have for instance $n=300$ data points and we use $\alpha =5\%$, the precision is then equal to $d=\sqrt{1.27359/300}=0.0652$, what means that all probabilities of the multinomial distribution have been estimated with a precision of $\pm 0.0652$.

Confidence intervals derived from the above formulas have in common the fact that d is equal for each probability of the distribution. This is a limitation, because we can expect the number of data available for estimating each probability to influence the width of the confidence interval. Different solutions for the computation of non-equal simultaneous confidence intervals have been proposed by, e.g., Sison and Glaz [4], Bailey [8], Fitzpatrick and Scott [9], Goodman [10], Hou, Chiang and Tai [11], Quesenberry and Hurst [12]. To our best knowledge, no published results do systematically compare from a theoretical point of view the performance of all of these approaches. Nevertheless, the simulation studies of Cherry [13] suggest that the method proposed by Bailey performs generally well at a very light computational cost. The lower bound of the confidence interval for the i-th element of a multinomial distribution, including continuity correction, is written

$$p_i^{-}=\frac{{\left(\sqrt{A}-\sqrt{C(C+1-A)}\right)}^2}{{(C+1)}^2}$$

(2)

and the upper bound is given by

$$p_i^{+}=\frac{{\left(\sqrt{B}+\sqrt{C(C+1-B)}\right)}^2}{{(C+1)}^2}$$

(3)

where $A=(n_i-1/8)/(n+1/8)$, $B=(n_i+7/8)/(n+1/8)$, and C is the upper ($\alpha /c$)100th percentile of the one degree of freedom chi-square distribution divided by $4n$.

Without entering into the discussion about the comparison of the different approaches cited above, what is not the purpose of this paper, we note that all these methods require the knowledge not only of the empirical probability distribution $(p_1,p_2,\dots ,p_c)$, but also of the corresponding frequency distribution $(n_1,n_2,\dots ,n_c)$. When these quantities are generally known in the case of a single multinomial distribution or of an homogeneous Markov chain of any order, this is not the case for more complex models such as the MTD model. This is the reason why confidence intervals for these models are usually obtained only by the mean of bootstrap, what can be very time consuming. In contrast, the method developed hereafter does not require repetitive computations on many different samples, so the computation cost is reduced.

3. Mixture Transition Distribution Models

In many cases, the use of high-order Markov chains is not possible, because the number of parameters increases exponentially with the dependence order. Different modelings have been proposed to reduce this problem. Among them, the Mixture Transition Distribution (MTD) model introduced by Raftery [14] proved to be very interesting, combining parsimony with quality of modeling [15]. Let $Y_t$ be a categorical random variable taking values in $\{1,\dots ,c\}$. The principle of the MTD model is to consider independently the influence of each lag upon the present. The basic equation is

$$\begin{array}{ccc}\hfill P(Y_t=i_0|Y_{t-f}=i_f,\dots ,Y_{t-1}=i_1)& =& \sum _{g=1}^f{\lambda }_{g}P(Y_t=i_0|Y_{t-g}=i_g)\hfill \\ & =& \sum _{g=1}^f{\lambda }_g{q}_{i_g{i}_0}\hfill \end{array}$$

where f is the order of the Markov chain, $\Lambda =({\lambda }_1,\dots ,{\lambda }_f)$, ${\sum }_i{\lambda }_i=1$, is a vector of lag weights, and where

$$Q=\left(\begin{array}{ccc}{q}_{11}& \dots & q_{1c}\\ ⋮& ⋮\\ q_{c1}& \dots & q_{cc}\end{array}\right)$$

is a transition matrix of the same size as the transition matrix associated with the first-order homogeneous Markov chain. This model is very parsimonious since each new lag adds only one parameter to the model.

The parameters of the MTD model can be decomposed into $c+1$ different distributions: The c rows of the transition matrix Q and the vector of weights $\Lambda$. When the elements of $\Lambda$ are constrained to be non-negative, the usual case, the $c+1$ sets of parameters are all probability distributions. The requirement for applying the methods of Section 2 is then to be able to estimate the numbers of data used to compute each of these $c+1$ distributions. That can be done using a principle similar to the E-step of an EM algorithm [16]. Suppose that we have $n+f$ successive observations of a random variable numbered from $Y_{-f+1}$ to $Y_n$. Suppose that at each time t, the probability distribution was generated by one of the f lags and let $Z_t$ be a length f indicator vector defined as:

$$Z_t\left(g\right)=\left\{\begin{array}{c}1,\mathrm{if}\mathrm{lag}g\mathrm{explains}{Y}_t\hfill \\ 0,\mathrm{otherwise}\hfill \end{array}\right.$$

The lag really used to explain $Y_t$ being unobserved, we say that the model includes a hidden component. Following Böhning [17], the expectation of $Z_t\left(g\right)$ is computed as

$$\begin{array}{c}\hfill {\tilde{z}}_t\left(g\right)=\frac{{\lambda }_g{q}_{i_g{i}_0}}{{\sum }_{k=1}^f{\lambda }_k{q}_{i_k{i}_0}}\end{array}$$

The weight coefficient for the g-th lag is then estimated as

$${\widehat{\lambda }}_g=\frac{{\sum }_{t=1}^n{\tilde{z}}_t\left(g\right)}{n}$$

and the vector

$$\left(\sum _{t=1}^n{\tilde{z}}_t\left(1\right),\dots ,\sum _{t=1}^n{\tilde{z}}_t\left(f\right)\right)=\left(n{\widehat{\lambda }}_1,\dots ,n{\widehat{\lambda }}_f\right)$$

(4)

gives an estimation of the number of data points used to compute coefficients ${\lambda }_1,\dots ,{\lambda }_f$. Confidence intervals are then obtained by using one of the methods of Section 2.

The computation of confidence intervals for the parameters of the transition matrix Q is very similar: In a MTD model of order f, the transition matrix Q is used to represent the relationship between each of the f lags of the model and the present situation. Therefore, each transition probability of the form $q_{k{i}_0}$ represents the f following situations where the lag takes value k and the current observation is state $i_0$: ($y_{t-f}=k$ and $y_t=i_0$), ($y_{t-f+1}=k$ and $y_t=i_0$), …, ($y_{t-1}=k$ and $y_t=i_0$). Let $\widehat{N}$ be a $(c\times c)$ matrix whose element $(k,i_0)$ is defined as

$${\widehat{n}}_{k{i}_0}=\sum _{\begin{array}{c}t=1\\ y_t=i_0\end{array}}^n\sum _{\begin{array}{c}g=1\\ y_{t-g}=k\end{array}}^f{\tilde{z}}_t\left(g\right)$$

This matrix contains estimates of the number of data used to calculate each element of Q. From there, the use of the methods described in Section 2 becomes possible.

After estimation, the MTD model can be used to construct an approximation of the high order transition matrix of the Markov chain. The number of data used to compute the probability corresponding to $Y_{t-f}=i_f,\dots ,Y_t=i_0$ is estimated by

$${\widehat{m}}_{i_f,\dots ,i_0}=\sum _{g=1}^f{\widehat{\lambda }}_g{\widehat{n}}_{i_g{i}_0}$$

and the total number of data used for the row defined by $Y_{t-f}=i_f,\dots ,Y_{t-1}=i_1$ is

$${\widehat{m}}_{i_f,\dots ,·}=\sum _{j=1}^c{\widehat{m}}_{i_f,\dots ,i_0}$$

These quantities are then used to compute confidence intervals for the probabilities in the order f transition matrix.

The basic MTD model allows many extensions, among them the MTDg model in which a different matrix is used to represent the transition process between each lag and the present. There are then f transition matrices ${\widehat{Q}}_1,\dots ,{\widehat{Q}}_f$ and f corresponding matrices ${\widehat{N}}^{\left(1\right)},\dots ,{\widehat{N}}^{\left(f\right)}$, the element $(k,i_0)$ of ${\widehat{N}}^{\left(g\right)}$ being defined as

$${\widehat{n}}_{k{i}_0}^{\left(g\right)}=\sum _{\begin{array}{c}t=1\\ y_t=i_0\\ y_{t-g}=k\end{array}}^n{\tilde{z}}_t\left(g\right)$$

The number of data used to compute the probability defined by $Y_{t-f}=i_f,\dots ,Y_t=i_0$ in the order f transition matrix is then estimated by

$${\widehat{m}}_{i_f,\dots ,i_0}=\sum _{g=1}^f{\widehat{\lambda }}_g{\widehat{n}}_{i_g{i}_0}^{\left(g\right)}$$

4. Extension to Hidden Markov Models

The principles developed in the context of the MTD model can also be applied to hidden models. In a Hidden Markov Model (HMM), the state taken by the Markov chain at time t is unknown. We observe instead a second random variable whose distribution depends on the state taken by the hidden chain. Let $X_t$ be a categorical random variable taking values in $\{1,\dots ,k\}$ and governed by a hidden Markov chain of order ℓ. Let $Y_t$ be a categorical random variable taking values in $\{1,\dots ,c\}$. To each of the k states of $X_t$ correspond a different probability distribution for $Y_t$, the distribution actually used at time t being unknown. See, e.g., Zucchini and MacDonald [2] for a good introduction to HMMs.

We consider a first-order hidden transition matrix and n successive observations of $Y_t$ numbered from $Y_1$ to $Y_n$. Three different sets of probabilities are used to fully identify the model: The unconditional distribution of the first hidden state, denoted by $\pi$, the transition matrix between hidden states, A, and the distribution of the random variable $Y_t$ given each of the k hidden states, $C_1,\dots ,C_k$.

Theoretically, assuming the asymptotic normality of the parameter maximum likelihood estimators around their true value, it is possible to compute an exact confidence interval for each parameter of a HMM [18]. In practice, however, it is not possible to use this method when the series of interest is more than about n = 100 data points long [5]. At least three alternative methods have been introduced: Finite-differences approximation [19], bootstrap [20], and likelihood profiles [21]. These methods present the advantage of being usable on long time series. On the other hand, as noted by Visser, Raijmakers and Molenaar [5], results can be very sensible to truncations and rounding errors. Moreover, the required computations are very intensive. Finite-differences approximation of the Hessian matrix is obtained by considering the second-order partial derivative of the log-likelihood. This approximation is necessary, because the true Hessian matrix cannot be computed on large samples. Bootstrap consists in generating a large number of new samples by sampling with replaceemnt from the original data. Then, the model of interest is estimated on each sample, which provides an approximation of the distribution of each parameter. Likelihood profiling consists in comparing the likelihood of the optimal model with the likelihood of a model in which the value of one of the parameters was slightly increased by an amount a. Different trials are performed in order to find the maximal value a for which the likelihood of the original and modified models are still statistically identical. The resulting a value is then considered as the upper bound of the confidence interval for the parameter. Repeating the same procedure with a negative value of a provides the lower bound of the interval. The same method is successively applied to each parameter of the model.

We show now that the approach proposed for MTD models can also be applied to HMMs at a very low cost. The percentage of the time the model is using each of the k possible distributions for the observed random variable $Y_t$ is unknown. However, this percentage can be estimated as follows: HMM parameters are estimated using the Baum-Welch algorithm [22], a customized version of the Expectation-Maximization (EM) algorithm. Similarly to what we did for the MTD model, we suppose that at each time t, one of the k possible distributions was used. Let $Z_t$ be a size k vector indicating which distribution was used at time t:

$$Z_t\left(g\right)=\left\{\begin{array}{c}1,\mathrm{if}\mathrm{distribution}{C}_g\mathrm{was}\mathrm{active}\mathrm{at}\mathrm{time}t\hfill \\ 0,\mathrm{otherwise}\hfill \end{array}\right.$$

During the E-step of the estimation algorithm, the expectation of $Z_t\left(g\right)$ is computed as follows: First, we define two auxiliary quantities:

$$\begin{array}{ccc}{\alpha }_t\left(g\right)\hfill & =& P(Y_1,\dots ,Y_t,X_t=g|\pi ,A,C_1,\dots ,C_k),t=1,\dots ,n\hfill \\ {\beta }_t\left(g\right)\hfill & =& P(Y_{t+1},\dots ,Y_n|X_t=g,\pi ,A,C_1,\dots ,C_k),t=1,\dots ,n\hfill \end{array}$$

Using ${\alpha }_1\left(g\right)=\pi \left(g\right)C_g\left(y_1\right)$ and ${\beta }_n\left(g\right)=1$, $g=1,\dots ,k$, to initialize the computation, we obtain iteratively

$$\begin{array}{ccc}\hfill {\alpha }_{t+1}\left(g\right)& =& \left(\sum _{i=1}^k{\alpha }_t\left(i\right)a(i,g)\right)C_g\left(y_{t+1}\right),t=2,\dots ,n\hfill \\ \hfill {\beta }_t\left(g\right)& =& \sum _{i=1}^k{C}_g\left(y_{t+1}\right){\beta }_{t+1}\left(g\right)a(i,g),t=n-1,\dots ,1\hfill \end{array}$$

The expectation of $Z_t\left(g\right)$ is then

$$\begin{array}{c}\hfill {\tilde{z}}_t\left(g\right)=\frac{{\alpha }_t\left(g\right){\beta }_t\left(g\right)}{L(Y_1,\dots ,Y_n)}\end{array}$$

where $L(Y_1,\dots ,Y_n)={\sum }_{i=1}^k{\alpha }_n\left(i\right)$ is the likelihood of the observed data. The total number of data points used to compute $C_g$ is estimated as

$$\sum _{t=1}^n{\tilde{z}}_t\left(g\right)$$

and this quantity is used to compute confidence intervals for the probabilities in $C_g$. Notice that multiplying the above quantity by the r-th element of $C_g$ provides an estimation of the number of data used to compute this r-th element.

By definition of the model, each observation of $Y_t$ is directly linked to a hidden state, so the length of the unobserved sequence of hidden states is n. The probability distribution of the first hidden state is given by $({\tilde{z}}_1\left(1\right),\dots ,{\tilde{z}}_1\left(k\right))$, and the sum of this vector, one, is the number of data used to compute $\pi$. Obviously, one data is not enough to obtain a reliable estimation, but in practice, when only one time-series is used to identify the model, the precise knowledge of the active state at the beginning of the series is generally useless. On the other hand, when a HMM is estimated from several independent samples, the total number of data used to compute each vector $Z_t$, and in particular $Z_1$, is equal to the number of independent samples, what can lead to a reliable estimation of $\pi$.

The number of data entering in the computation of the g-th row of the hidden transition matrix A is estimated as

$$\sum _{t=1}^{n-1}{\tilde{z}}_t\left(g\right)$$

and this quantity is used to obtain confidence intervals for the elements of this g-th row. The summation is taken up to $n-1$ rather than n, because the transition matrix expresses the relation between two successive hidden states, and a sample of size n contains only $n-1$ transitions.

We turn now to the case of a high-order HMM, that is a HMM with a transition matrix A of order $f>1$. In addition to the computation of the first hidden state distribution, $\pi$, the complete identification of the model requires the computation of the distribution of the second hidden state given the first one, ${\pi }_{2|1}$, the distribution of the third hidden state given the first two, ${\pi }_{3|1,2}$, and so on until ${\pi }_{f|1,\dots ,f-1}$. In the Baum-Welch algorithm, the vectors ${\tilde{Z}}_t$ are replaced by the computation of matrices giving the expectation of observing f successive hidden states and we define

$${\tilde{z}}_t(i_{f-1},\dots ,i_0)=P(X_{t-f+1}=i_{f-1},\dots ,X_t=i_0|Y_1,\dots ,Y_t),t=f,\dots ,n$$

(5)

For $t<f$, we define matrices giving the expectation of observing t successive hidden states:

$${\tilde{z}}_t(i_{t-1},\dots ,i_0)=P(X_1=i_{t-1},\dots ,X_t=i_0|Y_1,\dots ,Y_t),t=1,\dots ,f-1$$

(6)

The number of data used to compute a probability distribution in the model is then estimated by summing up the corresponding elements in ${\tilde{z}}_t(i_{f-1},\dots ,i_0)$ and in ${\tilde{z}}_t(i_{t-1},\dots ,i_0)$.

Finally, it is also possible to use the same principle to compute confidence intervals in the case of the Double Chain Markov Model (DCMM). This model, first introduced by Paliwal [23] in the context of speech recognition and then developed and generalized by Berchtold [24,25], is an extension of the basic HMM in which the hypothesis of conditional independence between successive observations of the random variable $Y_t$ is removed, the relation being instead modeled by the mean of a Markov chain. The probability distributions $C_1,\dots ,C_k$ are then replaced by k transition matrices, $Q_1,\dots ,Q_k$, possibly of high-order.

5. Simulation Studies

We present two simulation studies designed to compare different methods of calculating confidence intervals. The first simulation study considers a MTD model and compares confidence intervals obtained through Bailey’s approach with reference intervals obtained from a bootstrap procedure. The second simulation study extends results previously published by Visser, Raijmakers and Molenaar [5] in the case of a first-order HMM by adding confidence intervals based on both Thompson’s and Bailey’s approaches. The R statistical environment was used for all computations [26]. Markovian models were optimized using the march R package [27]. Additional R codes, as well as the dataset used in the second simulation study, are available here: https://drive.switch.ch/index.php/s/Qo8mjJvJw9Rd8CH. Alternatively, the Windows standalone version of march [28] can also be used for most computations.

5.1. MTD Simulation Study

The objective of this study was to compare the confidence intervals that can be obtained for a MTD model through Bailey’s approach (Equations (2) and (3)) with reference confidence intervals obtained by a bootstrap procedure. We considered a second-order model ($f=2$) with three different states ($c=3$). First, a second-order transition matrix (see below for details) was used to generate, after a burn-in period of 50 sequences, a dataset of 200 independent sequences of length 52. Since a second-order model requires two initial data to be initialized, the length of 52 was chosen to have exactly 50 data points in the log-likelihood of each sequence.

The order of the dataset was checked by estimating the homogeneous first- and second-order Markov chains, and by comparing them using the Bayesian Information Criterion [29], but in practice the second-order hypothesis was never rejected. Then, a second-order MTD model was fitted to the data and the 95% Bailey’s confidence intervals were computed for all parameters.

In a second step, a bootstrap procedure with 2000 replications was performed on the dataset: For each replication, a new dataset of 200 sequences was obtained by sampling sequences with replacement from the original dataset, and the second-order MTD model was fitted. Finally, 95% confidence intervals were computed by taking the corresponding quantiles of the distribution of the parameters obtained from the 2000 replications. The full procedure was replicated 100 times.

Three different types of second-order matrices were used to generate the original datasets, leading to three different simulation studies:

• Fully random: A matrix of size ($c^f\times c$) is populated with random values distributed uniformly between 0 and 1. Each row is then normalized by the sum of its elements, leading to a second-order transition matrix in reduced form.
• MTD: A transition matrix Q of size ($c\times c$) and a vector $\Lambda$ of size two are populated with random values distributed uniformly between 0 and 1. The rows of Q and the vector are then normalized by the sum of their elements, leading to the transition matrix and the lag vector defining a second-order MTD model. The second-order transition matrix corresponding to the MTD model is then built.
• Constrained MTD: The generating mechanism is similar to the MTD mechanism, but with the two following differences: (a) The random values generated on the diagonal of the Q matrix are multiplied by 5 in order to obtain more persistent states. (b) The weight of the second lag, ${\lambda }_2$, is constrained to be not lower than 0.2, the goal being to limit the risk of obtaining a degenerated first-order solution to the model.

We used these three different generating mechanisms, because the MTD model cannnot reproduce the full range of autocorrelations that are possible in time-series [15,30]. Consequently, the MTD model can become very complicated to optimize on datasets with specific autocorrelations. This is further complicated by the fact that the MTD model is not completely identified, and that several combinations of parameters can correspond to the same optima of the solution space [31]. The above fully random generating matrix can lead to situations in which the MTD model behaves poorly, which implies that simulation results could be difficult to understand, the quality of confidence intervals depending not only on the principles they are based on, but also on the quality of the MTD model itself. On the other hand, the constrained MTD matrix should avoid such problems, and the MTD matrix represents an intermediate case.

Figure 1 summarizes our results. It combines the different elements necessary to accurately compare the Bailey’s CIs with the bootstrap CIs which are considered the reference in this experiment. In addition to the relative width of the intervals provided by each method, it is possible to check whether these intervals are constructed around the same point estimate or not. In this way, the differences between the two methods are clearly visible. Reporting results as correlations between CIs obtained from both methods would not have been informative enough, because, for instance, a tendency of one method to slightly over- or under-estimate the variability of a coefficient could not have been put in evidence. For each of the three generating mechanisms, the results of the 100 simulations are plotted on a same graph. For each parameter, the 95% confidence interval is represented as a rectangle whose base gives the width of the bootstrap CI, and whose height gives the width of the corresponding Bailey’s CI. The more square the rectangle, the closer the width of the two intervals. Blue rectangles indicate that the bootstrap interval is larger than Bailey’s interval, and red rectangles indicate the reverse. A rectangle not centered on the diagonal indicates that the two CIs are centered around different point estimates.

The left column of Figure 1 presents CIs for the parameters of the MTD model (both $\Lambda$ and Q). Results are poor for the simulation using the fully random second-order generating mechanism. As explained before, this was expected, since some of the correlations that can be generated by a second-order model cannot be fully reproduced by a MTD modeling. In some of the 100 replications, the MTD model fitted on each bootstrap sample took entirely different parameter values, leading to very large confidence intervals. On the other hand, the corresponding Bailey’s CI stayed much narrower, since they were computed from only one run of the MTD model. However, we should not conclude that Bailey’s intervals are in this case preferable, because the problem lies in the use of the MTD itself. Note that this problem with the possible range of use of the MTD model is distinct from the well-known label switching problem that ocurs with mixture models [32]. Label switching occurs when the different components of a mixture are not ordered a priori, which is not the case with the MTD model, where each component is associated with a different lag of the dependent variable. The poor results presented in the upper left graph of Figure 1 are therefore not an indication of a problem with the computation of confidence intervals, but an indication of the limits of the MTD principle.

The middle and bottom graphs in the left column of Figure 1 correspond to the two MTD generating mechanisms, and the results are much better than those produced by the fully-random mechanism. In particular, in the case of the constrained MTD, all confidence intervals lie close to the diagonal without significant difference between the two computation methods. Finally, a few intervals are problematic when using the unconstrained MTD generating mechanism, but they remain the exception, not the rule.

The second column of Figure 1 summarizes confidence intervals for the probabilities in the second-order transition matrix computed from the MTD model. Since these probabilites are estimated from a combination of several parameters of the MTD model, errors in the MTD parameters not only propagate to high order transition probabilities, but they can accumulate. This explains why these CIs are in average larger than those of the MTD parameters, and why some of them are further from the diagonal. However, we come to the same general conclusion that the results are much better when the generation mechanism itself is compatible with the MTD principle.

On average, calculating bootstrap CIs took 6500 times more processor time than calculating Bailey’s CIs. This ratio is a function of the characteristics of the bootstrap procedure. For example, if we had relied on 1000 replications instead of 2000, then the ratio would have decreased to 3250.

5.2. HMM Comparison Study

Visser, Raijmakers and Molenaar [5] used the following two-hidden states, three output values HMM model to generate a dataset of length 2000:

$$A=\left(\begin{array}{cc}{a}_{11}& a_{12}\\ a_{21}& a_{22}\end{array}\right)=\left(\begin{array}{cc}0.9& 0.1\\ 0.3& 0.7\end{array}\right)$$

$$C_1=\left(\begin{array}{ccc}{c}_{11}& c_{12}& c_{13}\end{array}\right)=\left(\begin{array}{ccc}0.6& 0.0& 0.4\end{array}\right)$$

$$C_2=\left(\begin{array}{ccc}{c}_{21}& c_{22}& c_{23}\end{array}\right)=\left(\begin{array}{ccc}0.0& 0.3& 0.7\end{array}\right)$$

They estimated then the same HMM from the generated dataset and they computed confidence intervals using likelihood profiling, 500 and 1000 sample bootstrap, and finite-differences approximation of the Hessian. As discussed by Visser, Raijmakers and Molenaar, confidence intervals obtained from likelihood profiles and bootstrap are very similar, when confidence intervals obtained from finite-differences approximation of the Hessian are generally narrower. For the purpose of comparison, we report in

Table 1. Comparison of confidence intervals obtained using different methods. The first column gives the parameters of the Hidden Markov Model (HMM) defined in Visser, Raijmakers and Molenaar [5]. The second column gives the estimated parameters obtained by maximization of the log-likelihood on a sample of size 2000. The third and fourth columns report the 5% confidence intervals obtained by Visser et al. using, respectively, 1000 samples bootstrap and finite-differences approximation of the Hessian. The last two columns provide the 5% confidence intervals derived, respectively, from the Thompson’s and Bailey’s equations.

Parameter	Estimated Value	Bootstrap CI	Approximated Hessian CI	Thompson’s CI	Bailey’s CI
$a_{11}$	0.8843	(0.8563, 0.9123)	(0.8574, 0.9112)	(0.8544, 0.9142)	(0.8686, 0.9024)
$a_{12}$	0.1157	(0.0877, 0.1437)	(0.0888, 0.1426)	(0.0858, 0.1456)	(0.0972, 0.1359)
$a_{21}$	0.2864	(0.2363, 0.3365)	(0.2174, 0.3554)	(0.2392, 0.3336)	(0.2442, 0.3304)
$a_{22}$	0.7136	(0.6635, 0.7637)	(0.6446, 0.7826)	(0.6664, 0.7608)	(0.6684, 0.7548)
$c_{11}$	0.6163	(0.5784, 0.6542)	(0.5835, 0.6491)	(0.5864, 0.6462)	(0.5845, 0.6468)
$c_{12}$	0.0	-	-	-	-
$c_{13}$	0.3837	(0.3458, 0.4216)	(0.3509, 0.4165)	(0.3538, 0.4136)	(0.3526, 0.4149)
$c_{21}$	0.0	-	-	-	-
$c_{22}$	0.3102	(0.2582, 0.3622)	(0.2715, 0.3489)	(0.2631, 0.3573)	(0.2640, 0.3580)
$c_{23}$	0.6898	(0.6378, 0.7418)	(0.6511, 0.7285)	(0.6427, 0.7369)	(0.6406, 0.7346)

the confidence intervals obtained from 1000 bootstrap samples and from finite-differences approximation of the Hessian, along with the corresponding Thomson’s and Bailey’s intervals obtained using the approach presented in this paper. Note that, since the Thomson’s and Bailey’s CIs were calculated after one run of the EM optimization algorithm, when bootstrap CIs were obtained after 1000 independent runs of the same EM algorithm, the ratio of processor time between the two approaches is exactly 1000 against the bootstrap approach.

As can be seen in Table 1, results are slightly different from one method to another, but this is consistent with previous comparison studies [4,11,13]. Confidence intervals obtained from Thompson’s and Bailey’s equations are close to those obtained through bootstrap and approximation of the Hessian matrix. No systematic difference, in the sense of an over- or under-estimation of the width of the intervals, do appear. These results confirm the usefulness of our approach, since it is possible to obtain reliable confidence intervals at only a fraction of the computational cost of other methods.

6. Discussion

The computation of confidence intervals for the parameters of Markovian models is made difficult because of the possible large number of parameters involved, and because parts of these models are sometimes not directly observed (hidden models). However, these issues are tractable using appropriate principles and algorithms. First of all, the parameters of Markovian models can be decomposed into a set of probability distributions. Secondly, when parameters of a model are hidden, it is possible to estimate the number of data points entering in their computation though the use of one iteration of the E-step of an EM algorithm. Putting these two elements together leads to the possibility of using established formulas to estimate confidence intervals.

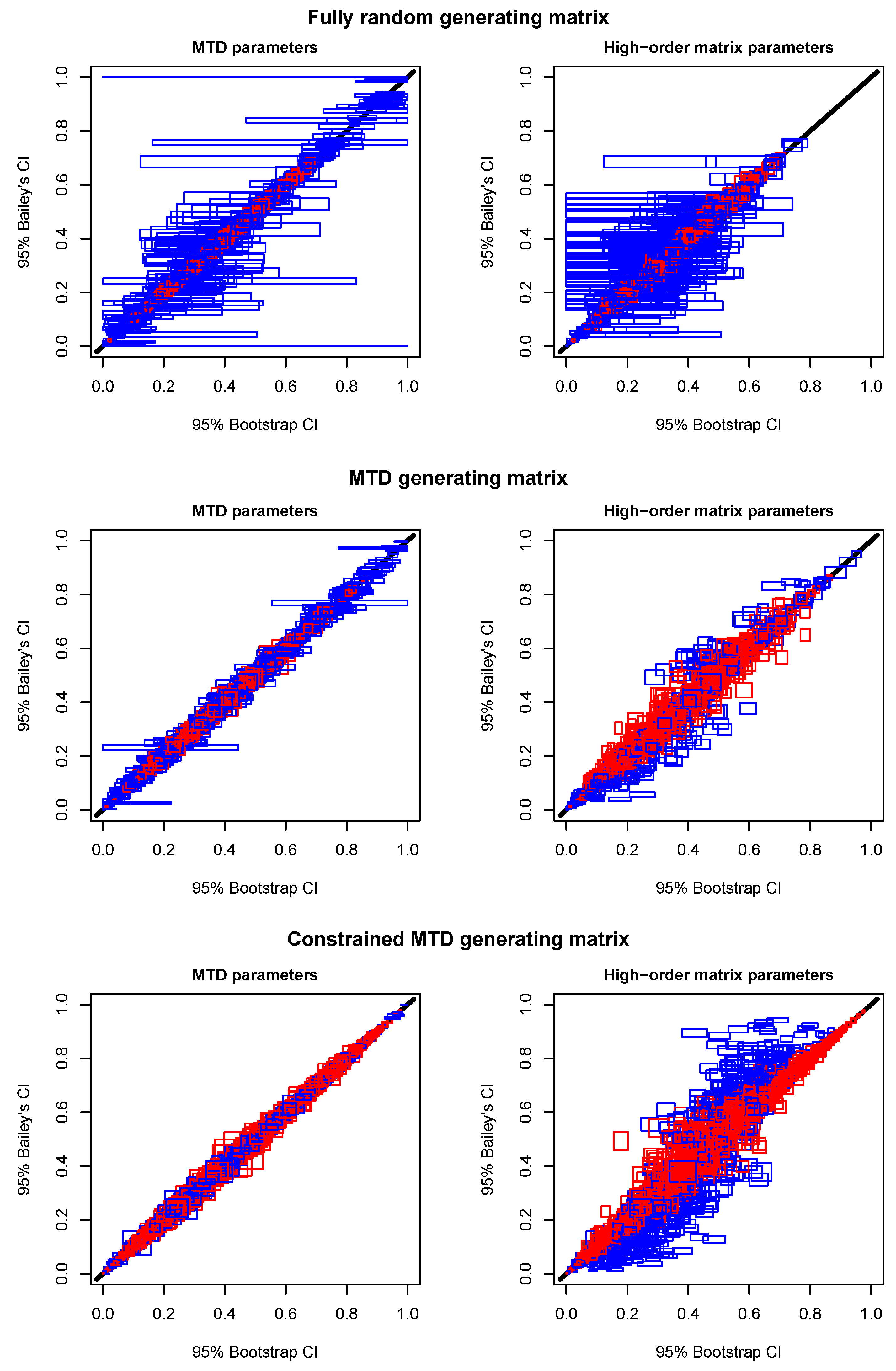
Other methods have been proposed for the construction of confidence intervals in Markovian models, but as mentioned previously, exact computation is only feasible on very short data sequences. Alternative methods such as likelihood profiling and bootstrap answer to this issue, but they are very computationally intensive, as shown through our simulations. For instance, bootstrap implies to optimize repetitively the same model on thousands of different samples, and likelihood profiling must be performed separately for finding the lower and upper bounds of each confidence interval of a model. Even if the bootstrap can be considered as the current gold standard for calculating CIs in Markovian models, its use is made difficult when the available processor time is limited, or when the model of interest is difficult to optimize. On the other hand, the approach developed in this article is much more effective, because, whatever the number of parameters of the model, the calculations required are mainly based on a single execution of the optimization algorithm. It could therefore prove to be very interesting for the development of real time or near real time applications.

Simulation results indicate that confidence intervals obtained from our approach are consistent with those obtained from previous methods. Moreover, our approach presents the advantage of unifying the computation of confidence intervals for homogeneous Markov chains, MTD models, and hidden models in a same theoretical framework. However, it must be recalled that the optimization of some models can prove very difficult, and that a given model is not always able to correctly represent the data. In such situations, the computation of confidence intervals may be misleading, giving a false idea of accuracy. Therefore, it is always necessary to question the merits of using one model rather than another, and to select the correct model for the function of the data to be analyzed. As demonstrated by the first simulation study, the standard MTD model, for example, is not suitable for all types of autocorrelation, and in some cases it does not necessarily represent the best choice.