Optimal Location and Sizing of PV Sources in DC Networks for Minimizing Greenhouse Emissions in Diesel Generators
Abstract
1. Introduction
2. Mathematical Model
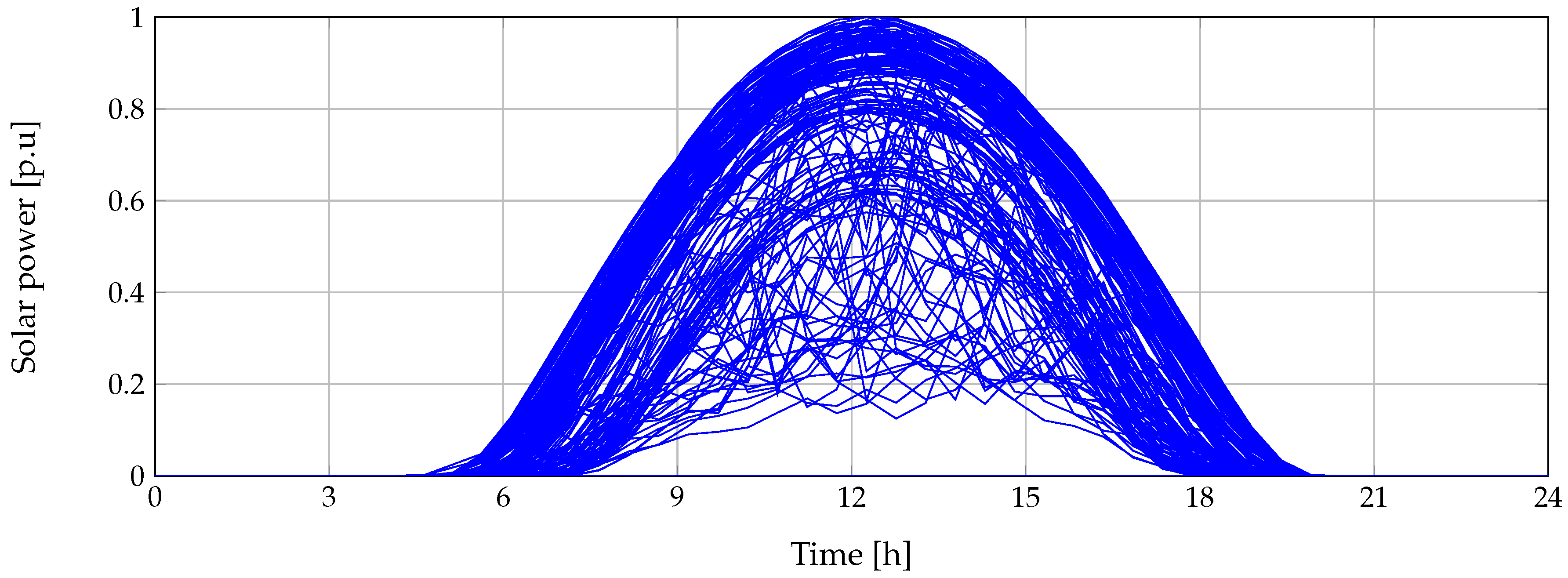
3. Solar Generation Forecasting
Artificial Neural Network
4. Optimization Strategy
| Algorithm 1: Main steps for solving the proposed MINLP model in GAMS [57] |
|
5. Test System and Numerical Validations
5.1. Test System
5.2. Objective Function and Daily Curves
5.3. Simulation Scenarios
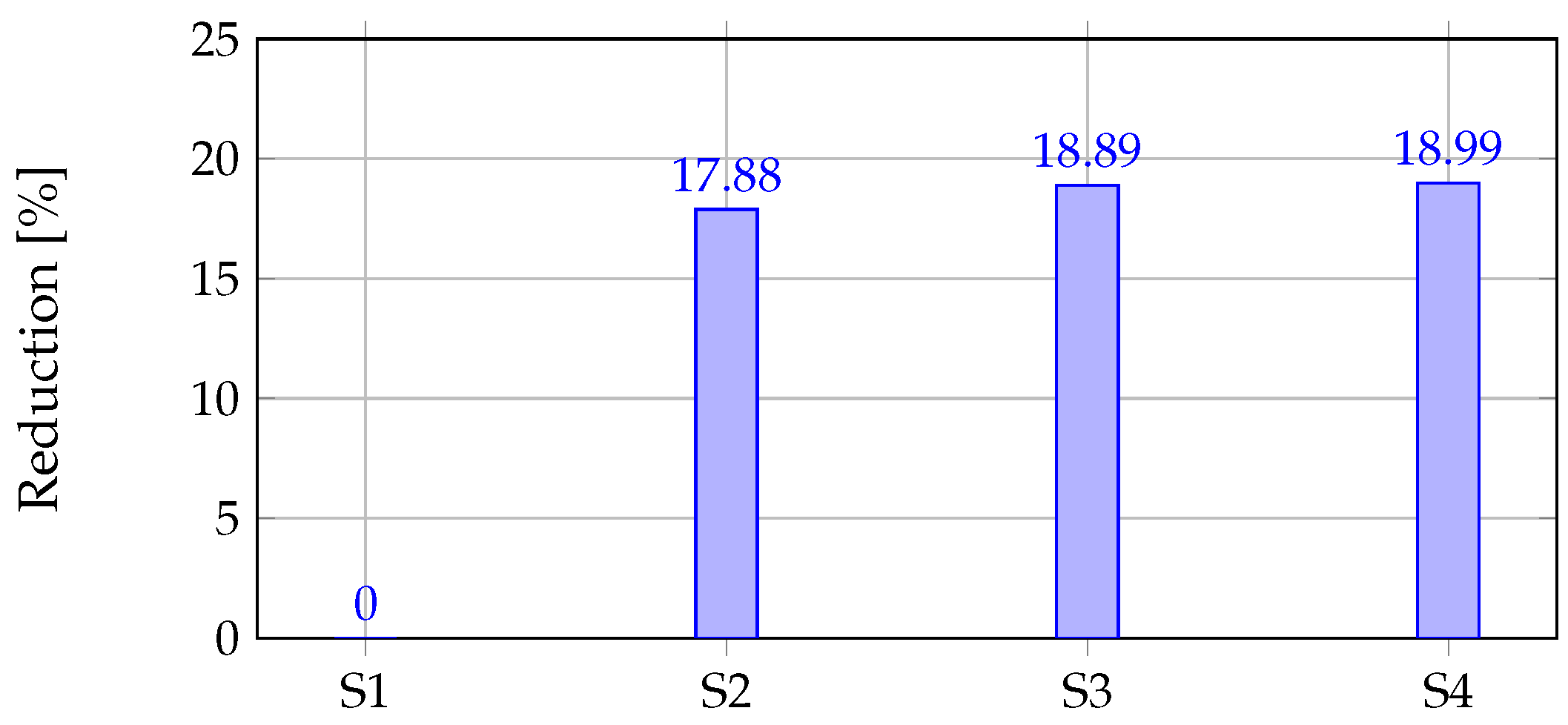
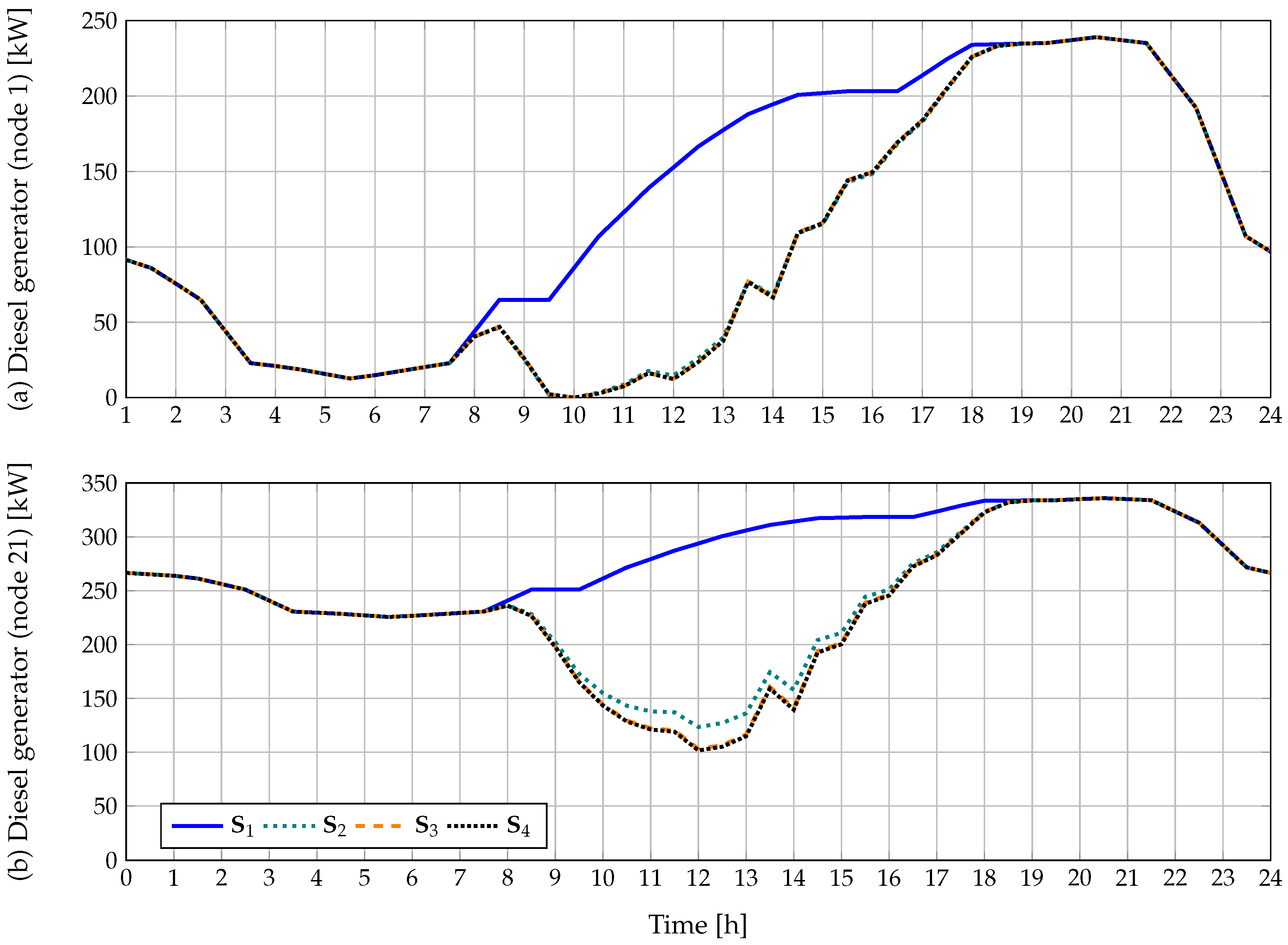
5.4. Numerical Results
6. Conclusions and Future Works
Author Contributions
Funding
Conflicts of Interest
References
- Blaabjerg, F.; Chen, Z.; Kjaer, S.B. Power electronics as efficient interface in dispersed power generation systems. IEEE Trans. Power Electron. 2004, 19, 1184–1194. [Google Scholar] [CrossRef]
- Wandhare, R.G.; Agarwal, V. Novel Integration of a PV-Wind Energy System With Enhanced Efficiency. IEEE Trans. Power Electron. 2015, 30, 3638–3649. [Google Scholar] [CrossRef]
- Montoya, O.D.; Gil-González, W.; Garces, A. Distributed energy resources integration in single-phase microgrids: An application of IDA-PBC and PI-PBC approaches. Int. J. Electr. Power Energy Syst. 2019, 112, 221–231. [Google Scholar] [CrossRef]
- Gil-González, W.; Montoya, O.D.; Holguín, E.; Garces, A.; Grisales-Noreña, L.F. Economic dispatch of energy storage systems in dc microgrids employing a semidefinite programming model. J. Energy Storage 2019, 21, 1–8. [Google Scholar] [CrossRef]
- Grisales, L.F.; Montoya, O.D.; Grajales, A.; Hincapie, R.A.; Granada, M. Optimal Planning and Operation of Distribution Systems Considering Distributed Energy Resources and Automatic Reclosers. IEEE Lat. Am. Trans. 2018, 16, 126–134. [Google Scholar] [CrossRef]
- Montoya, O.D.; Grajales, A.; Garces, A.; Castro, C.A. Distribution Systems Operation Considering Energy Storage Devices and Distributed Generation. IEEE Lat. Am. Trans. 2017, 15, 890–900. [Google Scholar] [CrossRef]
- Di Noia, L.P.; Genduso, F.; Miceli, R.; Rizzo, R. Optimal Integration of Hybrid Supercapacitor and IPT System for a Free-Catenary Tramway. IEEE Trans. Ind. Appl. 2019, 55, 794–801. [Google Scholar] [CrossRef]
- Jayasinghe, S.D.G.; Vilathgamuwa, D.M.; Madawala, U.K. A Dual Inverter-Based Supercapacitor Direct Integration Scheme for Wind Energy Conversion Systems. IEEE Trans. Ind. Appl. 2013, 49, 1023–1030. [Google Scholar] [CrossRef]
- Montoya, O.D.; Garcés, A.; Serra, F.M. DERs integration in microgrids using VSCs via proportional feedback linearization control: Supercapacitors and distributed generators. J. Energy Storage 2018, 16, 250–258. [Google Scholar] [CrossRef]
- Gil-González, W.; Montoya, O.D.; Garces, A. Control of a SMES for mitigating subsynchronous oscillations in power systems: A PBC-PI approach. J. Energy Storage 2018, 20, 163–172. [Google Scholar] [CrossRef]
- Shen, L.; Cheng, Q.; Cheng, Y.; Wei, L.; Wang, Y. Hierarchical control of DC micro-grid for photovoltaic EV charging station based on flywheel and battery energy storage system. Electr. Power Syst. Res. 2020, 179, 106079. [Google Scholar] [CrossRef]
- Huang, C.N.; Chen, Y.S. Design of magnetic flywheel control for performance improvement of fuel cells used in vehicles. Energy 2017, 118, 840–852. [Google Scholar] [CrossRef]
- Murad, M.A.A.; Milano, F. Modeling and Simulation of PI-Controllers Limiters for the Dynamic Analysis of VSC-Based Devices. IEEE Trans. Power Syst. 2019, 34, 3921–3930. [Google Scholar] [CrossRef]
- Schiffer, J.; Seel, T.; Raisch, J.; Sezi, T. Voltage Stability and Reactive Power Sharing in Inverter-Based Microgrids With Consensus-Based Distributed Voltage Control. IEEE Trans. Control Syst. Technol. 2016, 24, 96–109. [Google Scholar] [CrossRef]
- Joung, K.W.; Kim, T.; Park, J. Decoupled Frequency and Voltage Control for Stand-Alone Microgrid with High Renewable Penetration. IEEE Trans. Ind. Appl. 2019, 55, 122–133. [Google Scholar] [CrossRef]
- Simpson-Porco, J.W.; Shafiee, Q.; Dörfler, F.; Vasquez, J.C.; Guerrero, J.M.; Bullo, F. Secondary Frequency and Voltage Control of Islanded Microgrids via Distributed Averaging. IEEE Trans. Ind. Electron. 2015, 62, 7025–7038. [Google Scholar] [CrossRef]
- Garces, A. Uniqueness of the power flow solutions in low voltage direct current grids. Electr. Power Syst. Res. 2017, 151, 149–153. [Google Scholar] [CrossRef]
- Montoya, O.D.; Gil-González, W.; Garces, A. Power flow approximation for DC networks with constant power loads via logarithmic transform of voltage magnitudes. Electr. Power Syst. Res. 2019, 175, 105887. [Google Scholar] [CrossRef]
- Montoya, O.D.; Gil-González, W.; Garces, A. Optimal Power Flow on DC Microgrids: A Quadratic Convex Approximation. IEEE Trans. Circuits Syst. II 2019, 66, 1018–1022. [Google Scholar] [CrossRef]
- Li, J.; Liu, F.; Wang, Z.; Low, S.H.; Mei, S. Optimal Power Flow in Stand-Alone DC Microgrids. IEEE Trans. Power Syst. 2018, 33, 5496–5506. [Google Scholar] [CrossRef]
- Parhizi, S.; Lotfi, H.; Khodaei, A.; Bahramirad, S. State of the Art in Research on Microgrids: A Review. IEEE Access 2015, 3, 890–925. [Google Scholar] [CrossRef]
- Montoya, O.D.; Gil-González, W.; Garces, A. Sequential quadratic programming models for solving the OPF problem in DC grids. Electr. Power Syst. Res. 2019, 169, 18–23. [Google Scholar] [CrossRef]
- Montoya, O.D.; Gil-González, W.; Grisales-Noreña, L.F. Vortex Search Algorithm for Optimal Power Flow Analysis in DC Resistive Networks with CPLs. IEEE Trans. Circuits Syst. II 2019. [Google Scholar] [CrossRef]
- Garcés, A. On the Convergence of Newton’s Method in Power Flow Studies for DC Microgrids. IEEE Trans. Power Syst. 2018, 33, 5770–5777. [Google Scholar] [CrossRef]
- Montoya, O.D.; Garrido, V.M.; Gil-González, W.; Grisales-Noreña, L.F. Power Flow Analysis in DC Grids: Two Alternative Numerical Methods. IEEE Trans. Circuits Syst. II 2019, 66, 1865–1869. [Google Scholar] [CrossRef]
- Yu, S.Y.; Kim, H.J.; Kim, J.H.; Han, B.M. SoC-Based Output Voltage Control for BESS with a Lithium-Ion Battery in a Stand-Alone DC Microgrid. Energies 2016, 9, 924. [Google Scholar] [CrossRef]
- Robinson, S.; Papadopoulos, S.; Jadraque Gago, E.; Muneer, T. Feasibility Study of Integrating Renewable Energy Generation System in Sark Island to Reduce Energy Generation Cost and CO2 Emissions. Energies 2019, 12, 4722. [Google Scholar] [CrossRef]
- Gil-González, W.; Montoya, O.D.; Garces, A. Modeling and control of a small hydro-power plant for a DC microgrid. Electr. Power Syst. Res. 2020, 180, 106104. [Google Scholar] [CrossRef]
- Hassan, M.A.; Li, E.; Li, X.; Li, T.; Duan, C.; Chi, S. Adaptive Passivity-Based Control of dc–dc Buck Power Converter With Constant Power Load in DC Microgrid Systems. IEEE J. Emerg. Sel. Top. Power Electron. 2019, 7, 2029–2040. [Google Scholar] [CrossRef]
- Shadmand, M.B.; Balog, R.S.; Abu-Rub, H. Model Predictive Control of PV Sources in a Smart DC Distribution System: Maximum Power Point Tracking and Droop Control. IEEE Trans. Energy Convers. 2014, 29, 913–921. [Google Scholar] [CrossRef]
- Vafamand, N.; Khooban, M.H.; Dragičević, T.; Blaabjerg, F. Networked Fuzzy Predictive Control of Power Buffers for Dynamic Stabilization of DC Microgrids. IEEE Trans. Ind. Electron. 2019, 66, 1356–1362. [Google Scholar] [CrossRef]
- Ghiasi, M.I.; Golkar, M.A.; Hajizadeh, A. Lyapunov Based-Distributed Fuzzy-Sliding Mode Control for Building Integrated-DC Microgrid With Plug-In Electric Vehicle. IEEE Access 2017, 5, 7746–7752. [Google Scholar] [CrossRef]
- Mokhtar, M.; Marei, M.I.; El-Sattar, A.A. An Adaptive Droop Control Scheme for DC Microgrids Integrating Sliding Mode Voltage and Current Controlled Boost Converters. IEEE Trans. Smart Grid 2019, 10, 1685–1693. [Google Scholar] [CrossRef]
- Liu, X.; Liu, Y.; Liu, J.; Xiang, Y.; Yuan, X. Optimal planning of AC-DC hybrid transmission and distributed energy resource system: Review and prospects. CSEE J. Power Energy Syst. 2019, 5, 409–422. [Google Scholar] [CrossRef]
- Wogrin, S.; Gayme, D.F. Optimizing Storage Siting, Sizing, and Technology Portfolios in Transmission-Constrained Networks. IEEE Trans. Power Syst. 2015, 30, 3304–3313. [Google Scholar] [CrossRef]
- Sachs, J.; Sawodny, O. A Two-Stage Model Predictive Control Strategy for Economic Diesel-PV-Battery Island Microgrid Operation in Rural Areas. IEEE Trans. Sustain. Energy 2016, 7, 903–913. [Google Scholar] [CrossRef]
- Adefarati, T.; Bansal, R.C.; John Justo, J. Techno-economic analysis of a PV–wind–battery–diesel standalone power system in a remote area. J. Eng. 2017, 2017, 740–744. [Google Scholar] [CrossRef]
- Moradi, M.; Abedini, M. A combination of genetic algorithm and particle swarm optimization for optimal DG location and sizing in distribution systems. Int. J. Electr. Power Energy Syst. 2012, 34, 66–74. [Google Scholar] [CrossRef]
- Gandomkar, M.; Vakilian, M.; Ehsan, M. A Genetic–Based Tabu Search Algorithm for Optimal DG Allocation in Distribution Networks. Electr. Power Components Syst. 2005, 33, 1351–1362. [Google Scholar] [CrossRef]
- Nekooei, K.; Farsangi, M.M.; Nezamabadi-Pour, H.; Lee, K.Y. An Improved Multi-Objective Harmony Search for Optimal Placement of DGs in Distribution Systems. IEEE Trans. Smart Grid 2013, 4, 557–567. [Google Scholar] [CrossRef]
- Sultana, S.; Roy, P.K. Krill herd algorithm for optimal location of distributed generator in radial distribution system. Appl. Soft Comput. 2016, 40, 391–404. [Google Scholar] [CrossRef]
- Grisales-Noreña, L.F.; Gonzalez Montoya, D.; Ramos-Paja, C.A. Optimal Sizing and Location of Distributed Generators Based on PBIL and PSO Techniques. Energies 2018, 11, 1018. [Google Scholar] [CrossRef]
- Kaur, S.; Kumbhar, G.; Sharma, J. A MINLP technique for optimal placement of multiple DG units in distribution systems. Int. J. Electr. Power Energy Syst. 2014, 63, 609–617. [Google Scholar] [CrossRef]
- Montoya, O.D.; Gil-González, W.; Grisales-Noreña, L. An exact MINLP model for optimal location and sizing of DGs in distribution networks: A general algebraic modeling system approach. Ain Shams Eng. J. 2019. [Google Scholar] [CrossRef]
- Montoya, O.D.; Gil-González, W.; Grisales-Noreña, L. Relaxed convex model for optimal location and sizing of DGs in DC grids using sequential quadratic programming and random hyperplane approaches. Int. J. Electr. Power Energy Syst. 2020, 115, 105442. [Google Scholar] [CrossRef]
- Montoya, O.D. A convex OPF approximation for selecting the best candidate nodes for optimal location of power sources on DC resistive networks. Eng. Sci. Technol. Int. J. 2019. [Google Scholar] [CrossRef]
- Grisales-Noreña, L.F.; Garzon-Rivera, O.D.; Montoya, O.D.; Ramos-Paja, C.A. Hybrid Metaheuristic Optimization Methods for Optimal Location and Sizing DGs in DC Networks. In Workshop on Engineering Applications; Chapter Applied Computer Sciences in Engineering; Figueroa-García, J., Duarte-González, M., Jaramillo-Isaza, S., Orjuela-Cañon, A., Díaz-Gutierrez, Y., Eds.; Springer: Cham, Switzerland, 2019; Volume 1052, pp. 214–225. [Google Scholar] [CrossRef]
- Montoya, O.D.; Garrido, V.M.; Grisales-Noreña, L.F.; Gil-González, W.; Garces, A.; Ramos-Paja, C.A. Optimal Location of DGs in DC Power Grids Using a MINLP Model Implemented in GAMS. In Proceedings of the 2018 IEEE 9th Power, Instrumentation and Measurement Meeting (EPIM), Salto, Uruguay, 14–16 November 2018; pp. 1–5. [Google Scholar] [CrossRef]
- Maleki, A.; Pourfayaz, F.; Hafeznia, H.; Rosen, M.A. A novel framework for optimal photovoltaic size and location in remote areas using a hybrid method: A case study of eastern Iran. Energy Convers. Manag. 2017, 153, 129–143. [Google Scholar] [CrossRef]
- Montoya, O.D.; Gil-González, W.; Grisales-Noreña, L.; Orozco-Henao, C.; Serra, F. Economic Dispatch of BESS and Renewable Generators in DC Microgrids Using Voltage-Dependent Load Models. Energies 2019, 12, 4494. [Google Scholar] [CrossRef]
- Simpson-Porco, J.W.; Dörfler, F.; Bullo, F. On Resistive Networks of Constant-Power Devices. IEEE Trans. Circuits Syst. II 2015, 62, 811–815. [Google Scholar] [CrossRef]
- Zhang, L. Artificial Neural Network Architecture Design for EEG Time Series Simulation Using Chaotic System. In Proceedings of the 2018 Joint 7th International Conference on Informatics, Electronics Vision (ICIEV) and 2018 2nd International Conference on Imaging, Vision Pattern Recognition (icIVPR), Kitakyushu, Japan, 25–29 June 2018; pp. 388–393. [Google Scholar] [CrossRef]
- Du, Y.C.; Stephanus, A. Levenberg-Marquardt Neural Network Algorithm for Degree of Arteriovenous Fistula Stenosis Classification Using a Dual Optical Photoplethysmography Sensor. Sensors 2018, 18, 2322. [Google Scholar] [CrossRef]
- Wilson, P.; Mantooth, H.A. Chapter 10—Model-Based Optimization Techniques. In Model-Based Engineering for Complex Electronic Systems; Wilson, P., Mantooth, H.A., Eds.; Newnes: Oxford, UK, 2013; pp. 347–367. [Google Scholar] [CrossRef]
- Naghiloo, A.; Abbaspour, M.; Mohammadi-Ivatloo, B.; Bakhtari, K. GAMS based approach for optimal design and sizing of a pressure retarded osmosis power plant in Bahmanshir river of Iran. Renew. Sustain. Energy Rev. 2015, 52, 1559–1565. [Google Scholar] [CrossRef]
- Montoya, O.D. Solving a Classical Optimization Problem Using GAMS Optimizer Package: Economic Dispatch Problem Implementation. Ingenieria y Ciencia 2017, 13, 39–63. [Google Scholar] [CrossRef]
- GAMS Development Corp. GAMS Free Demo Version. Available online: https://www.gams.com/download/ (accessed on 14 February 2020).

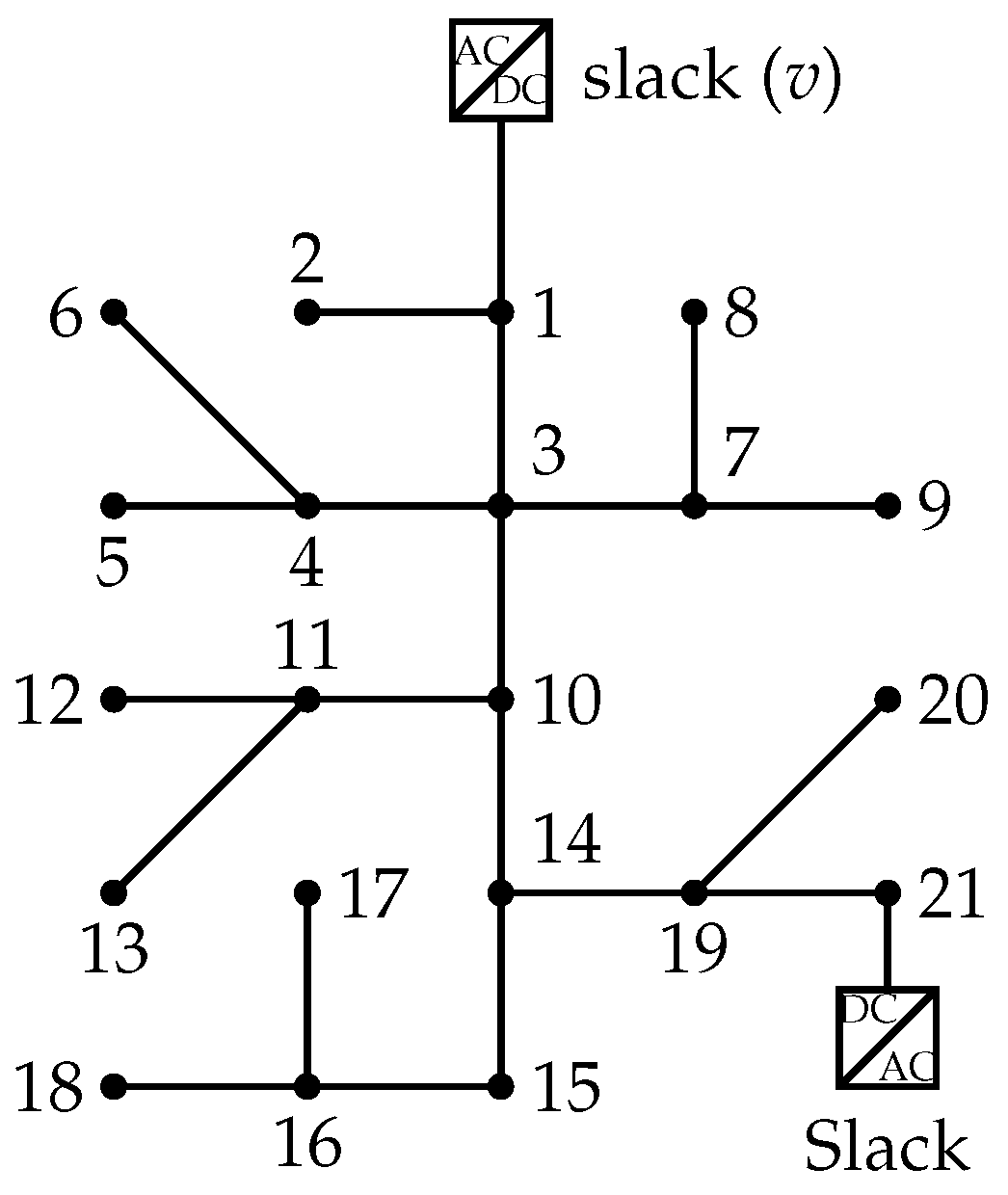
| Node i | Node j | [pu] | [pu] | Node i | Node j | [pu] | [pu] |
|---|---|---|---|---|---|---|---|
| 1(slack) | 2 | 0.0053 | 0.70 | 11 | 12 | 0.0079 | 0.68 |
| 1 | 3 | 0.0054 | 0.00 | 11 | 13 | 0.0078 | 0.10 |
| 3 | 4 | 0.0054 | 0.36 | 10 | 14 | 0.0083 | 0.00 |
| 4 | 5 | 0.0063 | 0.04 | 14 | 15 | 0.0065 | 0.22 |
| 4 | 6 | 0.0051 | 0.36 | 15 | 16 | 0.0064 | 0.23 |
| 3 | 7 | 0.0037 | 0.00 | 16 | 17 | 0.0074 | 0.43 |
| 7 | 8 | 0.0079 | 0.32 | 16 | 18 | 0.0081 | 0.34 |
| 7 | 9 | 0.0072 | 0.80 | 14 | 19 | 0.0078 | 0.09 |
| 3 | 10 | 0.0053 | 0.00 | 19 | 20 | 0.0084 | 0.21 |
| 10 | 11 | 0.0038 | 0.45 | 19 | 21(slack) | 0.0082 | -0.21 |
| Type of Emission | Chemical Symbol | Rank [lb/MWh] |
|---|---|---|
| Carbon dioxide | 1000–1700 | |
| Sulfur dioxide | 0.40–3.00 | |
| Nitrogen oxides | 10–41 | |
| Carbon monoxide | 0.40–9.00 | |
| Heavy particles | 0.40–3.00 |
| Period | Real [pu] | Forec. [pu] | Load [pu] | Period | Real [pu] | Forec. [pu] | Load [pu] |
|---|---|---|---|---|---|---|---|
| 1 | 0.000 | 0.000 | 0.633 | 25 | 1.000 | 0.976 | 0.814 |
| 2 | 0.000 | 0.000 | 0.619 | 26 | 0.975 | 1.000 | 0.842 |
| 3 | 0.000 | 0.000 | 0.605 | 27 | 0.771 | 0.978 | 0.869 |
| 4 | 0.000 | 0.000 | 0.578 | 28 | 0.889 | 0.790 | 0.886 |
| 5 | 0.000 | 0.000 | 0.550 | 29 | 0.630 | 0.883 | 0.902 |
| 6 | 0.000 | 0.000 | 0.495 | 30 | 0.593 | 0.604 | 0.905 |
| 7 | 0.000 | 0.000 | 0.440 | 31 | 0.404 | 0.606 | 0.908 |
| 8 | 0.000 | 0.000 | 0.435 | 32 | 0.366 | 0.357 | 0.908 |
| 9 | 0.000 | 0.000 | 0.429 | 33 | 0.231 | 0.328 | 0.908 |
| 10 | 0.000 | 0.000 | 0.421 | 34 | 0.203 | 0.142 | 0.935 |
| 11 | 0.000 | 0.000 | 0.413 | 35 | 0.130 | 0.142 | 0.963 |
| 12 | 0.000 | 0.000 | 0.419 | 36 | 0.053 | 0.073 | 0.987 |
| 13 | 0.000 | 0.000 | 0.426 | 37 | 0.008 | 0.019 | 0.988 |
| 14 | 0.000 | 0.000 | 0.433 | 38 | 0.000 | 0.008 | 0.989 |
| 15 | 0.000 | 0.026 | 0.440 | 39 | 0.000 | 0.000 | 0.990 |
| 16 | 0.024 | 0.052 | 0.495 | 40 | 0.000 | 0.000 | 0.995 |
| 17 | 0.124 | 0.110 | 0.550 | 41 | 0.000 | 0.000 | 1.000 |
| 18 | 0.272 | 0.263 | 0.550 | 42 | 0.000 | 0.000 | 0.995 |
| 19 | 0.439 | 0.431 | 0.550 | 43 | 0.000 | 0.000 | 0.990 |
| 20 | 0.604 | 0.594 | 0.605 | 44 | 0.000 | 0.000 | 0.935 |
| 21 | 0.733 | 0.730 | 0.660 | 45 | 0.000 | 0.000 | 0.880 |
| 22 | 0.810 | 0.830 | 0.701 | 46 | 0.000 | 0.000 | 0.770 |
| 23 | 0.860 | 0.875 | 0.743 | 47 | 0.000 | 0.000 | 0.660 |
| 24 | 0.984 | 0.899 | 0.778 | 48 | 0.000 | 0.000 | 0.633 |
| Simulation Scenario | Objective Function [lb] () | Processing Time [s] |
|---|---|---|
| 13,428.91 | 6.224 | |
| 11,027.19 | 11.001 | |
| 10,892.80 | 18.478 | |
| 10,878.18 | 19.063 |
| Simulation Scenario | Location [node] | Size [kW] | Total Penetration [kW] | ||||
|---|---|---|---|---|---|---|---|
| — | — | — | — | — | — | 0 | |
| 17 | — | — | 320.37 | — | — | 320.372 | |
| 17 | 19 | — | 141.30 | 191.098 | — | 332.400 | |
| 12 | 17 | 19 | 91.33 | 101.582 | 139.485 | 332.400 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Montoya, O.D.; Grisales-Noreña, L.F.; Gil-González, W.; Alcalá, G.; Hernandez-Escobedo, Q. Optimal Location and Sizing of PV Sources in DC Networks for Minimizing Greenhouse Emissions in Diesel Generators. Symmetry 2020, 12, 322. https://doi.org/10.3390/sym12020322
Montoya OD, Grisales-Noreña LF, Gil-González W, Alcalá G, Hernandez-Escobedo Q. Optimal Location and Sizing of PV Sources in DC Networks for Minimizing Greenhouse Emissions in Diesel Generators. Symmetry. 2020; 12(2):322. https://doi.org/10.3390/sym12020322
Chicago/Turabian StyleMontoya, Oscar Danilo, Luis Fernando Grisales-Noreña, Walter Gil-González, Gerardo Alcalá, and Quetzalcoatl Hernandez-Escobedo. 2020. "Optimal Location and Sizing of PV Sources in DC Networks for Minimizing Greenhouse Emissions in Diesel Generators" Symmetry 12, no. 2: 322. https://doi.org/10.3390/sym12020322
APA StyleMontoya, O. D., Grisales-Noreña, L. F., Gil-González, W., Alcalá, G., & Hernandez-Escobedo, Q. (2020). Optimal Location and Sizing of PV Sources in DC Networks for Minimizing Greenhouse Emissions in Diesel Generators. Symmetry, 12(2), 322. https://doi.org/10.3390/sym12020322