Abstract
When analyzing the dynamic behavior of multi-body elastic systems, a commonly used method is the finite element method conjunctively with Lagrange’s equations. The central problem when approaching such a system is determining the equations of motion for a single finite element. The paper presents an alternative method of calculation theses using the Gibbs–Appell (GA) formulation, which requires a smaller number of calculations and, as a result, is easier to apply in practice. For this purpose, the energy of the accelerations for one single finite element is calculated, which will be used then in the GA equations. This method can have advantages in applying to the study of multi-body systems with elastic elements and in the case of robots and manipulators that have in their composition some elastic elements. The number of differentiation required when using the Gibbs–Appell method is smaller than if the Lagrange method is used which leads to a smaller number of operations to obtain the equations of motion.
1. Introduction
The common method to obtain the equations of motion for a finite element belonging to an elastic element of a multibody system is represented by Lagrange equations. In this way, the most important step in the analysis of the multi-body systems with elastic elements is solved, the rest of the procedures being the classical ones currently used in the finite element method FEA and verified by practice. So, it is possible to determine the dynamic response of a single finite element. Using the known assembly methods and introducing loads and proper boundary conditions, the set of differential equations describing the behavior of the entire elastic system is obtained.
In this process, the type of finite element chosen will determine the shape functions that will be used and which will give the final form of the coefficients of the matrix appearing in the equations of motion. In such an analysis, it is considered that the deformations are small enough to not have influence on the general, rigid motion of the multibody system. Thus, a large class of systems has been studied, having in their structure elastic elements modeled with one-dimensional, two-dimensional or three-dimensional finite elements. One-dimensional finite elements were among the first studied. We can mention here [1,2,3,4,5,6,7]. The method was then extended naturally to bi- and three-dimensional elements [8,9,10].
The basic hypothesis used was that the rigid motion of the multibody system is known and, as a consequence, the velocity and acceleration field of each solid of every element of the system. It is also considered that this rigid motion does not influence the elastic behavior of each element.
Customary Lagrange’s equations were used to determine the dynamic response of a single element. For this, it is necessary to determine, as the first step, the Lagrangian composed by kinetic energy, internal energy and the mechanical work of the external loads. The studied elements were considered linear elastic. Thus, the evolution equations of a finite element are obtained. The use of Lagrange’s equations proved to be a useful and practical method and was, generally, the only method used to solve this type of problem. Recent works in the field use Lagrange’s equations for the study of multi-body systems with elastic elements [11,12,13,14,15,16,17]. Theoretically, however, other methods of solving these dynamic systems can be applied, which will ultimately lead to the same equations of motion. In this paper, we will deal with the use of Gibbs–Appell (GA) equations, which have advantages in terms of the number of operations required to obtain the final results and thus prove more economical.
One problem which led to the GA equations was to deduce the differential equations of motion, which are easier to apply in the case of non-holonomic systems but which can also be applied to the holonomic systems. This method was discovered by Gibbs in 1879 [18] and, independently, by Appell in 1899 [19]. The function of Lagrange or Hamilton is replaced, in this formalism, by the energy of accelerations and represents an application of the well-known Gauss principle of least constraint being equivalent to the other formulations currently used in classical mechanics.
The modern mechanical systems are characterized by ultra-fast movements and velocities and include serial structures of robots as well. The fast movements are generally characterized by a time variation law for accelerations and lead to the occurrence of accelerations of higher orders. The last decades are characterized by a sustained development of the use of robots in the industry. This involves studies that allow good control of such systems, especially when working with high speeds and forces. In the case of such systems, which give very high working speeds and especially important speed variations, accelerations become significant. In these cases, the GA method becomes interesting. This type of formalism is useful for a wide class of engineering problems. For example, it can be used to analyze rigid dynamical systems, considering quasi-velocities [20]. The equations of motion can be easily obtained, both for holonomic systems and for non-holonomic systems. It is thus possible to eliminate at this step Lagrange’s multipliers and thus reduce the number of unknowns with which they work. The method can be applied both to linear and nonlinear problems. An example is presented in [21] where are obtained the motion equations for an N-link robot, with flexible elements. Experimental procedures validate the result obtained using the GA formalism. In the last period, this formalism tends to become a usual procedure. There are many papers presenting this kind of approach, like [22], where an application consists of an N-flexible-link manipulator used in the cooperative flexible mobile manipulator. The main advantage of recursive GA formulation is used to determine the motion equations without classical use of Lagrange multipliers. Some new methods to study the dynamic behavior of the multibody system have, as the central piece in approach, this formalism. As an example, in [23], such a system is defined using a classic set of coupled differential equations and a set of algebraic equations for expressing the liaisons (constraints). The use of Lagrange formalism asks a large number of derivatives in the governing equations. In these cases, the use of the recursive GA formalism becomes easier to apply. In this mode, it is possible to obtain the equations of motion automatically. In [24], the main advantage of this formulation used in applications is that it is not necessary to eliminate Lagrange’s multipliers and, as a consequence, the computational complexity decrease. Identically the formalism is also used in [25]. Dynamical response and motion equations can be obtained via recursive GA formulation and represent the way used to reduce the computational effort, significant for this application. The main advantage is fewer mathematical calculations compared to other formulations. There are a lot of papers using this formalism in the study of the dynamical system [26]. Interesting results are presented in [27,28,29]. The present paper only aims at obtaining the equations of motion for a three-dimensional finite element with a general motion.
The problems regarding the accuracy of the results and the accuracy of the models used in the case of the mechanisms, which have significant displacements and deformations, were not developed in the paper. These very interesting and current study domains themselves represent a distinct field of research. In this paper, we only dealt with the presentation of an alternative method, which presents advantages of calculation, of determining the equations of motion for a single element. The other operations used then in the method of finite elements were considered the ones currently used in practice.
2. Gibbs–Appell Formalism
In the case of scleronomic liaisons, the acceleration of a point i of a system of material points having n degree of freedom has, generally, the expression:
where is the position vector of the point and represent the independent coordinates. In the following, the dot placed above a scalar, vector or matrix size means the derivative of the respective size with respect to time. The notion energy of accelerations for a system of material points is defined as [27]:
The form of this expression is similar to the expression of kinetic energy but the mechanical significance is different. In the case of a solid body, the definition can be extended to the whole domain of the body as:
where the acceleration of a certain point of the solid is similar to Equation (1):
Introducing Equation (3a) in Equation (3) we get:
where:
contains terms that have no accelerations,
represents the terms in which the accelerations intervene linearly and:
represents the quadratic terms in accelerations.
GA equations are given by relations:
where it represents the generalized force corresponding to the generalized coordinate qj.
3. Basic Hypothesis
Now consider a finite element modeling a domain of an elastic element from the structure of a multibody system. The aim of the paper is to determine the motion equations of this element. The generalized coordinates will be the displacements of the nodes. The displacements of an arbitrary point of the continuous domain modeled by the finite element shall be expressed using a finite number of nodal coordinates. The finite element shall be related to the mobile reference frame, which participates in the general rigid motion (Figure 1). With , we shall note the velocity, and with , the acceleration of the origin of the local reference frame relative to the global reference frame OXYZ. We shall note with the angular velocity and with the angular acceleration. Generally, a multibody system consists of several solids. Every solid is characterized by these two vectors, and the number of pairs of such vectors is equal to the number of distinct bodies. The relations between the components of a vector in the local coordinate system and the components of the same vector in a global coordinate system are obtained using a matrix of rotation :
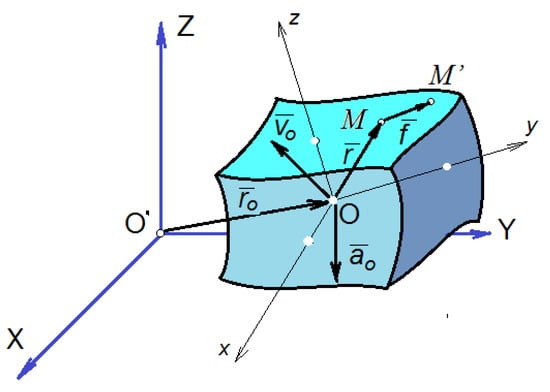
Figure 1.
Three-dimensional finite element.
If an arbitrary point M of the finite element has a displacement changing into M’, we may write:
where is the position vector of point M’ with components expressed in the global coordinate system. The continuous displacement field noted is approximated, using the finite element method, by relation:
where the matrix elements , the shape functions, will depend on the type of the finite element chosen and are the independent nodal coordinates. The velocity of point M’ will be:
and the acceleration will be:
These expressions will be used to determine the energy of accelerations. In the future, the index G mark the vector with the components expresses in the global reference system, the index L mark the vector with the components expresses in the local reference frame and the non-indexed vectors are considered to be written in the local coordinate system. The derivatives of the positional matrix occur in the previous relations. These derivatives will define angular velocities and angular accelerations. From the orthogonality conditions written for the positional matrix we have:
where is the unit matrix, the following relation can be obtained:
which is a skew symmetric matrix angular velocity, with components in global coordinate system, corresponding to the angular velocity:
Obviously, we have, too:
The angular acceleration operator is defined by:
and:
It will result after some elementary calculus:
whereas:
We have, too:
These relations will be useful in the following considerations.
4. Motion Equations
In the following, the equations of motion for a finite element will be established using the GA formalism. For this, it is necessary to first determine the energy of the accelerations of a finite element. If we use Expression (13) determined previously for the acceleration of a point, the energy of the accelerations for the considered finite element is given by the expression [30]:
The quadratic terms can be easily identified in the accelerations of the independent coordinates , noted with :
the terms in which these accelerations appear linear :
and the terms that do not contain at all accelerations and which do not have importance in GA equations, :
The potential energy (internal work) has a classical form:
where is the stress tensor and the strains tensor:
Writing the Hooke law as follows:
and of the differential relations between strains and finite deformations:
where represents the differentiation operator [31] and, using Equations (13), (15) and (16), the internal work becomes [31]:
where is the classical stiffness matrix:
If noted with , the vector of body forces per unit volume, then the external work of these is:
The concentrated forces in the nodes of the element will give an external work:
The equations of motion are obtained by applying the GA equations previously presented:
By , we understand:
In our case:
and:
After a series of elementary calculations and rearranging of terms, we get the equations of motion for the finite element considered:
We shall note with , the row i of matrix and with:
where:
therefore:
where it is denoted:
The term does not contain and, consequently:
Finally, the motion equations can be written in the condensed form:
These equations are related to the local system of coordinates. Similar formulas can be obtained, and we consider the global reference frame. The matrix coefficients can be calculated after choosing the shape functions and the independent nodal coordinates for expressing the displacement of a point.
5. Conclusions and Discussions
In the classical Lagrangian formalism, to determine the equations of motion for a three-dimensional finite element, the main step of the calculation is the Lagrangian, based essentially on the kinetic energy of the deformable finite element. The Lagrangian is:
where are given, respectively, by the Relations (31), (33) and (34) and the kinetic energy has the expression:
Lagrange’s equations are:
Leaving aside the other derivatives, which have a low weight in the computing economy, the term most significant in this formulation is the term kinetic energy. In this expression, there are four terms containing the vector and four terms containing the vector . If we look at the expression of Lagrange’s equations, it follows that we will have four differentiation operations for , another four for and then the derivatives with respect to the time of the terms .
Using the Gibbs–Appell equations that have the form of Equation (31), we have to differentiate the energy of the accelerations given by the Relations (24)–(26) and (37). The role of kinetic energy is play in these equations by the energy of accelerations . Note that of the three terms of kinetic energy, only two contain the vector of accelerations. The size has a single term that contains this vector and has four terms that contain the vector and which are differentiated. The total number of differentiation to be made in this case is five.
The conclusion from these two approaches is that the number of operations to be performed when using the Gibbs–Appell equations is lower than when Lagrange’s method is applied. The use of this method has the advantage that we are familiar with the calculation of kinetic energy of a solid and to determine the energy of the accelerations it is sufficient to replace the speeds, in the kinetic energy formula, with the accelerations. The use of these equations will result in an economy in the computational effort we make to determine the equations of motion for a single finite element.
An application was made for a rod within a wind pumping mechanism (Figure 2). The mechanism proposed for the study is a mechanism with two degrees of freedom of type “kinematic chain closed by inertia” [32].
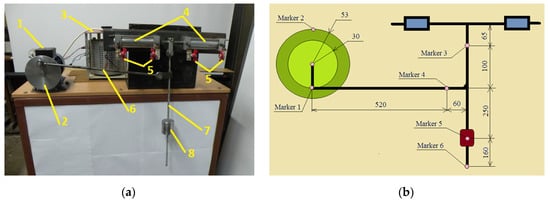
Figure 2.
(a) Experimental test stand and (b) sketch of the mechanism with the positioning of the markers (dimensions are in mm). 1—engine; 2—rotating disk; 3—invertor; 4—pumps; 5—valves; 6—rod; 7—pendulum rod; 8—weight.
Table 1 presents a comparison between the number of differentiation required when using Lagrange’s method and the number of differentiation required if the Gibbs–Appell method is applied. It is noted that the number of these operations is reduced to less than half. For a large number of finite elements used, in the case of complex structures, the reduction can be significant and can reduce the computational effort. We mention that after obtaining the matrix coefficients of the system of differential equations, the next procedures in the two methods become identical, so also the necessary computer times.

Table 1.
Comparison between the Lagrange and Gibbs–Appell methods. Number of differentiations.
Another problem that arises is the accuracy of the results. In the case of finite element analysis of a mechanism that can have large displacements, specific problems arise, very delicate, related to the accuracy of the results obtained and the correctness of the models used. During the present paper, we did not deal with these aspects, especially interesting and exciting. By themselves, these aspects define a field of research. The purpose of the paper was to provide an alternative way of writing the equations of motion, which would have the advantage of a smaller number of operations to perform.
The test mechanism on which the considerations were made, presented in Figure 2, can be considered, at this level as regards the accuracy of the results, accessible through the classical methods. In Figure 3 and Figure 4, we presented the space of the possible positions that can be occupied by the elements of this mechanism, to justify our hypothesis.
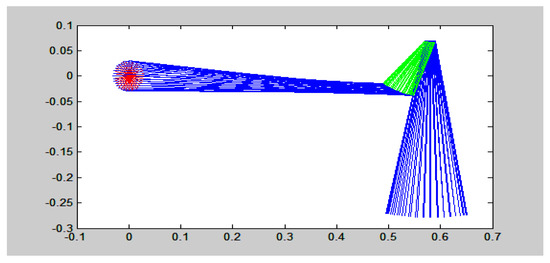
Figure 3.
Sketch of the motion of the two degree of freedom system for the angular speed 16 rad/s.

Figure 4.
Sketch of the motion of the two degree of freedom system for the angular speed 19 rad/s.
Author Contributions
Conceptualization, S.V. and I.N.; methodology, S.V. and M.L.S.; software, M.M.; validation, S.V., I.N. and M.M.; formal analysis, S.V. and M.L.S.; investigation, M.L.S.; resources, S.V.; writing—original draft preparation, S.V. and I.N.; writing—review and editing, M.L.S.; visualization, M.M.; supervision, I.N. and M.M.; project administration, S.V.; funding acquisition, S.V., I.N., M.M. and M.L.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Erdman, A.G.; Sandor, G.N.; Oakberg, A. A General Method for Kineto-Elastodynamic Analysis and Synthesis of Mechanism. Journal of Engineering for Industry. ASME Trans. 1972, 94, 1193. [Google Scholar]
- Bagci, C. Elastodynamic Response of Mechanical Systems using Matrix Exponential Mode Uncoupling and Incremental Forcing Techniques with Finite Element Method. In Proceedings of the Sixth Word Congress on Theory of Machines and Mechanisms, New Delhi, India, 15–20 December 1983; Volume 472. [Google Scholar]
- Bahgat, B.M.; Willmert, K.D. Finite Element Vibrational Analysis of Planar Mechanisms. Mech. Mach. Theory 1976, 11, 47–71. [Google Scholar] [CrossRef]
- Cleghorn, W.L.; Fenton, E.G.; Tabarrok, K.B. Finite Element Analysis of High-Speed Flexible Mechanisms. Mech. Mach. Theory 1981, 16, 407–424. [Google Scholar] [CrossRef]
- Christensen, E.R.; Lee, S.W. Nonlinear finite element modelling of the dynamics of unrestrained flexible structures. Comput. Struct 1986, 23, 819–829. [Google Scholar] [CrossRef]
- Midha, A.; Erdman, A.G.; Frohrib, D.A. Finite element approach to mathematical modeling of high-speed elastic linkages. Mech. Mach. Theory 1978, 13, 603–618. [Google Scholar] [CrossRef]
- Nath, P.K.; Ghosh, A. Steady-state response of mechanism with elastic links by finite element methods. Mech. Mach. Theory 1980, 15, 199–211. [Google Scholar] [CrossRef]
- Vlase, S.; Marin, M.; Öchsner, A.; Scutaru, M.L. Motion equation for a flexible one-dimensional element used in the dynamical analysis of a multibody system. Contin. Mech. Thermodyn. 2019. [Google Scholar] [CrossRef]
- Vlase, S. Dynamical Response of a Multibody System with Flexible Elements with a General Three-Dimensional Motion. Rom. J. Phys. 2012, 57, 676–693. [Google Scholar]
- Vlase, S.; Dănăşel, C.; Scutaru, M.L.; Mihălcică, M. Finite Element Analysis of a Two-Dimensional Linear Elastic Systems with a Plane "rigid Motion. Rom. J. Phys. 2014, 59, 476–487. [Google Scholar]
- Deü, J.-F.; Galucio, A.C.; Ohayon, R. Dynamic responses of flexible-link mechanisms with passive/active damping treatment. Comput. Struct. 2008, 86, 258–265. [Google Scholar] [CrossRef]
- Hou, W.; Zhang, X. Dynamic analysis of flexible linkage mechanisms under uniform temperature change. J. Sound Vib. 2009, 319, 570–592. [Google Scholar] [CrossRef]
- Neto, M.A.; Ambrósio, J.A.C.; Leal, R.P. Composite materials in flexible multibody systems. Comput. Methods Appl. Mech. Eng. 2006, 195, 6860–6873. [Google Scholar] [CrossRef]
- Piras, G.; Cleghorn, W.L.; Mills, J.K. Dynamic finite-element analysis of a planar high-speed, high-precision parallel manipulator with flexible links. Mech. Mach. Theory 2005, 40, 849–862. [Google Scholar] [CrossRef]
- Shi, Y.M.; Li, Z.F.; Hua, H.X.; Fu, Z.F.; Liu, T.X. The Modeling and Vibration Control of Beams with Active Constrained Layer Damping. J. Sound Vib. 2001, 245, 785–800. [Google Scholar] [CrossRef]
- Zhang, X.; Erdman, A.G. Dynamic responses of flexible linkage mechanisms with viscoelastic constrained layer damping treatment. Comput. Struct. 2001, 79, 1265–1274. [Google Scholar] [CrossRef]
- Zhang, X.; Lu, J.; Shen, Y. Simultaneous optimal structure and control design of flexible linkage mechanism for noise attenuation. J. Sound Vib. 2007, 299, 1124–1133. [Google Scholar]
- Gibbs, J.W. On the fundamental formulae of dynamics. Am. J. Math. 1879, 2, 49–64. [Google Scholar] [CrossRef]
- Appell, P. Sur une forme générale des equations de la dynamique. C.R. Acad. Sci. Paris 1899, 129, 459–460. [Google Scholar]
- Mirtaheri, S.M.; Zohoor, H. The Explicit Gibbs-Appell Equations of Motion for Rigid-Body Constrained Mechanical System. In Book Series: RSI International Conference on Robotics and Mechatronics ICRoM; IEEE: Piscataway, NJ, USA, 2018; pp. 304–309. [Google Scholar]
- Mehrjooee, O.; Dehkordi, S.F.; Korayem, M.H. Dynamic modeling and extended bifurcation analysis of flexible-link manipulator. Mech. Based Des. Struct. Mach. 2019, 1–24. [Google Scholar] [CrossRef]
- Korayem, M.H.; Dehkordi, S.F. Motion equations of cooperative multi flexible mobile manipulator via recursive Gibbs-Appell formulation. Appl. Math. Model. 2019, 65, 443–463. [Google Scholar] [CrossRef]
- Shafei, A.M.; Shafei, H.R. A systematic method for the hybrid dynamic modeling of open kinematic chains confined in a closed environment. Multibody Syst. Dyn. 2017, 38, 21–42. [Google Scholar] [CrossRef]
- Amini, S.; Dehkordi, S.F.; Fahraji, S.H. Motion equation derivation and tip-over evaluations for K mobile manipulators with the consideration of motors mass by the use of Gibbs-Appell formulation. In Proceedings of the 5th RSI International Conference on Robotics and Mechatronics (IcRoM), Tehran, Iran, 25–27 October 2017. [Google Scholar]
- Korayem, M.H.; Dehkordi, S.F. Derivation of dynamic equation of viscoelastic manipulator with revolute-prismatic joint using recursive Gibbs-Appell formulation. Nonlinear Dyn. 2017, 89, 2041–2064. [Google Scholar] [CrossRef]
- Shafei, A.M.; Korayem, M.H. Theoretical and experimental study of dynamic load-carrying capacity for flexible robotic arms in point-to-point motion. Optim. Control Appl. Methods 2017, 38, 963–972. [Google Scholar] [CrossRef]
- Negrean, I.; Kacso, K.; Schonstein, C.; Duca, A. Mechanics, Theory and Applications; UTPRESS: Cluj-Napoca, Romania, 2012. [Google Scholar]
- Negrean, I.; Crișan, A.-D. Synthesis on the Acceleration Energies in the Advanced Mechanics of the Multibody Systems. Symmetry 2019, 11, 1077. [Google Scholar] [CrossRef]
- Negrean, I.; Crișan, A.-D.; Vlase, S. A New Approach in Analytical Dynamics of Mechanical Systems. Symmetry 2020, 12, 95. [Google Scholar] [CrossRef]
- Vlase, S. Elimination of Lagrangian Multipliers. Mech. Res. Commun. 1987, 14, 17. [Google Scholar] [CrossRef]
- Massonet, C.; Deprez, G.; Maquoi, R.; Muller, R.; Fonder, G. Calcul des Structures sur Ordinateur; EYROLLES: Paris, France, 1972. [Google Scholar]
- Scutaru, M.L.; Mitrica, B. Dynamical Analysis of the Mechanical System with Two Degrees of Freedom Applied to the Transmission of the Wind Turbine. Math. Probl. Eng. 2016, 2016, 3821083. [Google Scholar] [CrossRef][Green Version]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).