Mixed Type Nondifferentiable Higher-Order Symmetric Duality over Cones

Abstract

A new mixed type nondifferentiable higher-order symmetric dual programs over cones is formulated. As of now, in the literature, either Wolfe-type or Mond–Weir-type nondifferentiable symmetric duals have been studied. However, we present a unified dual model and discuss weak, strong, and converse duality theorems for such programs under higher-order $\mathcal{F}$- convexity/higher-order $\mathcal{F}$- pseudoconvexity. Self-duality is also discussed. Our dual programs and results generalize some dual formulations and results appeared in the literature. Two non-trivial examples are given to show the uniqueness of higher-order $\mathcal{F}$- convex/higher-order $\mathcal{F}$- pseudoconvex functions and existence of higher-order symmetric dual programs.

1. Introduction

The study of higher-order duality has computational advantages over the first-order duality when approximations are used, as it provides tighter bound for the value of the objective function. Mangasarian [1] formulated a class of higher-order duality in nonlinear problems. Later on, Mond and Zhang [2] obtained various higher-order duality results under higher-order invexity assumptions. Chen [3] discussed Mond–Weir-type higher-order symmetric duality involving F-convex functions, whereas Mishra [4] obtained Mond–Weir-type higher-order symmetric duality theorems under generalized invexity. Khurana [5] presented symmetric duality results for a Mond–Weir-type dual programs over arbitrary cones under cone-pseudoinvexity and strongly cone-pseudoinvexity. Later on, a higher-order Mond–Weir-type nondifferentiable multiobjective dual problem is formulated and established duality relations involving higher-order $(F,\alpha ,\rho ,d)$ type-I fuctions by Ahmad et al. [6]. In [7], Gupta and Jayswal obtained multiobjective higher-order symmetric duality results under higher-order K-preinvexity/K-pseudoinvexity.

The theoretical and algorithmic concepts of mixed duality in nonlinear programming problems are interesting and useful. Under K-preinvexity and K-pseudoinvexity assumptions, Ahmad and Husain [8] formulated multiobjective mixed type symmetric dual programs over cones and proved duality results. Chandra et al. [9] studied mixed type symmetric duality results. Xu [10] proved duality theorems for two mixed type duals of a multiobjective programming problem. Yang et al. [11] presented mixed type symmetric duality for nondifferentiable nonlinear programming problems. By ignoring nonnegativity constraints of symmetric dual given in [12], Ahmad [13] presented multiobjective mixed type symmetric duality results. Recently, Verma et al. [14] formulated a higher-order nondifferentiable mixed symmetric dual model and duality results are studied under higher-order invexity/generalized invexity.

In the present paper, a new mixed type nondifferentiable higher-order symmetric dual programs over cones are formulated. As of now, in the literature, either Wolfe-type or Mond–Weir-type nondifferentiable symmetric dual programs have been discussed. However, our model unifies both dual programs. Under higher-order $\mathcal{F}$- convexity/higher-order $\mathcal{F}$- pseudoconvexity, appropriate duality theorems are proved. Self-duality is also discussed. Our study extends and generalizes the existing results appeared in [15,16,17,18,19,20,21]. Two non-trivial examples are given to show the uniqueness of higher-order $\mathcal{F}$- convex/higher-order $\mathcal{F}$- pseudoconvex functions and existence of higher-order symmetric dual programs.

2. Preliminaries

We consider the following nonlinear programming problem.

$(P)\mathrm{Minimize} F(x)$

$x\in X,$

where $X\subseteq {\mathbb{R}}^n$ and $F:X\to \mathbb{R}$.

2.1. Definitions

(a)

The support function $s(x|E)$ of E is given by

$$s(x|E)=\max \left\{x^{T}y:y\in E\right\}.$$

The subdifferential of $s(x|E)$ is defined by

$$\partial s(x|E)=\left\{z\in E:z^{T}x=s(x|E)\right\}.$$

The normal cone for any convex set $S\subset {\mathbb{R}}^n$ at a point $x\in S$ is defined by

$$N_S(x)=\{y\in {\mathbb{R}}^n:y^T(z-x)\le 0\mathrm{for} \mathrm{all}z\in S\}.$$

It is readily verified that for a compact convex set D, y is in $N_D(x)$ if and only if

$$s(y|D)=x^{T}y.$$

(b)

Let C be a closed convex cone in ${\mathbb{R}}^n$ with nonempty interior. The positive polar cone $C^{*}$ of C is given by

$$C^{*}=\left\{q\in {\mathbb{R}}^n:x^{T}q\ge 0\mathrm{for} \mathrm{all}x\in C\right\}.$$

(c)

A function $\mathcal{F}:X\times X\times {\mathbb{R}}^n\mapsto \mathbb{R}$ (where $X\subseteq {\mathbb{R}}^n$) is sublinear in its third component, if for all $x,y\in X:$

(i)

$\mathcal{F}(x,y;b_1+b_2)\le \mathcal{F}(x,y:b_1)+\mathcal{F}(x,y:b_2),$ for all $b_1,b_2\in {\mathbb{R}}^n;$ and

(ii)

$\mathcal{F}(x,y;\alpha b)=\alpha \mathcal{F}(x,y;b),$ for all $\alpha \in \mathbb{R},$ for all $b\in {\mathbb{R}}^n.$

(d)

Reference [3] A function $\varphi :{\mathbb{R}}^n\mapsto \mathbb{R}$ is called higher-order $\mathcal{F}-$ convex at $u\in {\mathbb{R}}^n$ with respect to $g:{\mathbb{R}}^n\times {\mathbb{R}}^n\mapsto \mathbb{R},$ if for all $(x,p)\in {\mathbb{R}}^n\times {\mathbb{R}}^n$,

$$\varphi (x)-\varphi (u)-g(u,p)+p^T{\nabla }_{p}g(u,p)\ge \mathcal{F}(x,u;{\nabla }_x\varphi (u)+{\nabla }_{p}g(u,p)).$$

(e)

Reference [3] A function $\varphi :{\mathbb{R}}^n\mapsto \mathbb{R}$ is called higher-order $\mathcal{F}-$ pseudoconvex at $u\in {\mathbb{R}}^n$ with respect to $g:{\mathbb{R}}^n\times {\mathbb{R}}^n\mapsto \mathbb{R},$ if for all $(x,p)\in {\mathbb{R}}^n\times {\mathbb{R}}^n$,

$$\mathcal{F}(x,u;{\nabla }_x\varphi (u)+{\nabla }_{p}g(u,p))\ge 0\Rightarrow \varphi (x)-\varphi (u)-g(u,p)+p^T{\nabla }_{p}g(u,p)\ge 0.$$

The above definitions (d) and (e) are validated by the following example.

2.2. Example

Consider $\varphi (x)=e^{-x}+x^2,F_{x,u}(a)=|a|(x^2-u^2)$, $g(u,p)=\frac{p}{u+1}$ and $X=\{x:x\ge 1\}$.

Now, we show that the function $\varphi (x)$ is a higher-order $\mathcal{F}$- pseudoconvex at $u=1$ and for all $x\ge 1$.

$$\begin{array}{cc}\hfill F(x,u;{\nabla }_x\varphi (u)+{\nabla }_{p}g(u,p))& =|{\nabla }_x\varphi (u)+{\nabla }_{p}g(u,p)|(x^2-u^2)\hfill \\ & =|-e^{-u}+2u+\frac{1}{u+1}|(x^2-u^2),\hfill \end{array}$$

For $u=1$, the above expression reduces to

$$F(x,1;{\nabla }_x\varphi (1)+{\nabla }_{p}g(1,p))=|-e^{-1}+2+\frac{1}{2}|(x^2-1)\ge 0,forx\ge 1,$$

(1)

Now,

$$\varphi (x)-\varphi (u)-g(u,p)+p^T{\nabla }_{p}g(u,p)=e^{-x}+x^2-e^{-u}-u^2-\frac{p}{u+1}+\frac{p}{u+1}.$$

At $u=1,$ the above equality becomes

$$\varphi (x)-\varphi (u)-g(u,p)+p^T{\nabla }_{p}g(u,p)=e^{-x}+x^2-\frac{1}{e}-1\ge 0,forx\ge 1,$$

(2)

The Equations (1) and (2) show that function $\varphi (x)$ is a higher-order $\mathcal{F}-$ pseudoconvex at $u=1$ and for all $x\ge 1$ (see Figure 1, Figure 2 and Figure 3).

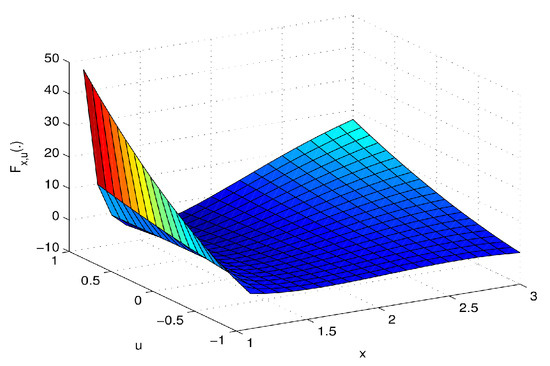
Figure 1. Graph of $F_{x,u}(.)$ against x and u.

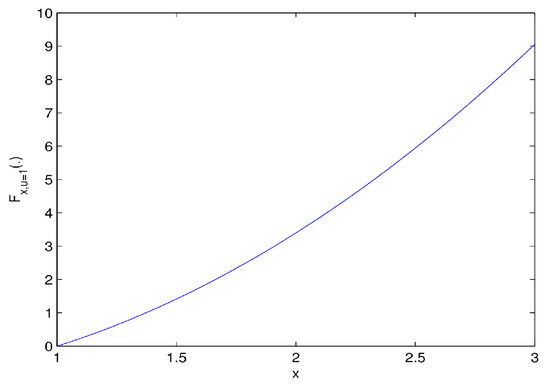
Figure 2. Graph of $F_{x,u}(.)$ against x.

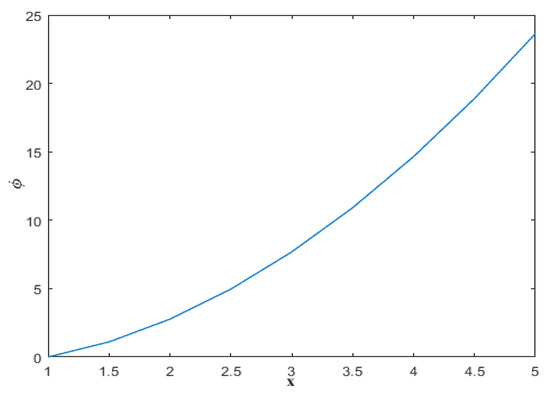
Figure 3. Graph of $\varphi$ against x.

Now, we determine whether $\varphi (x)$ is a higher-order $\mathcal{F}-$ convex function.

$$\begin{array}{c}\varphi (x)-\varphi (u)-g(u,p)+p^T{\nabla }_{p}g(u,p)-F(x,u;{\nabla }_x\varphi (u)+{\nabla }_{p}g(u,p))\\ =e^{-x}+x^2-e^{-u}-u^2-\frac{p}{u+1}+\frac{p}{u+1}-|-e^{-u}+2u+\frac{1}{u+1}|(x^2-u^2).\end{array}$$

At $u=1$

$$\begin{array}{cc}\hfill =& e^{-x}+x^2-\frac{1}{e}-1-|-e^{-1}+2+\frac{1}{2}|(x^2-1)\equiv \chi ,\hfill \\ & \ngeqq 0,(forx\ge 2),\hfill \end{array}$$

which shows that the function $\varphi (x)$ is not a higher-order $\mathcal{F}-$ convex (see Figure 4) at $u=1$ and $x=2$. This concludes that every higher-order $\mathcal{F}-$ convex function is a higher-order $\mathcal{F}-$ pseudoconvex function, but the converse is not necessarily true. (See Appendix A for codes of Figure 1, Figure 2, Figure 3 and Figure 4).

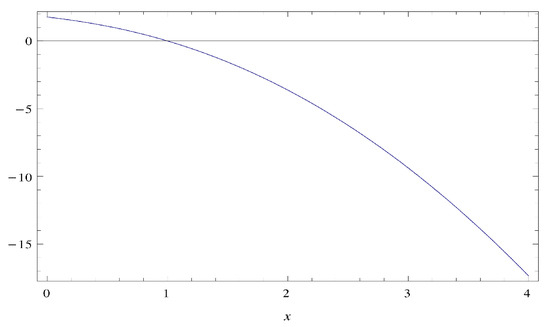
Figure 4. Graph of $\chi$ against x.

3. Higher-Order Mixed Type Symmetric Duality over Cones

For N = {1, 2, 3, …, n} and H = {1, 2, 3, …, h}, let us assume $A_1\subset N,B_1\subset H$ and $A_2=N\backslash A_1$ and $B_2=H\backslash B_1$, where $|A_1|$ denotes the number of elements in the set $A_1$, also $|A_2|$, $|B_1|$ and $|B_2|$ are defined similarly.

Again if $|A_1|=0$, then $|A_2|=n$ and therefore ${\mathbb{R}}^{|A_1|}$ is a zero-dimensional Euclidean space and ${\mathbb{R}}^{|A_2|}$ is n-dimensional Euclidean space.

Now $x\in {\mathbb{R}}^n$ if and only if $x=\{x^1,x^2\}$, i.e., $x^1\in {\mathbb{R}}^{|A_1|},x^2\in {\mathbb{R}}^{|A_2|}$. Similarly, any $y\in {\mathbb{R}}^h$ if and only if $y=\{y^1,y^2\}$, i.e., $y^1\in {\mathbb{R}}^{|B_1|},y^2\in {\mathbb{R}}^{|B_2|}$. Let

(i)

$f^1:{\mathbb{R}}^{|A_1|}\times {\mathbb{R}}^{|B_1|}\to \mathbb{R}$,

(ii)

$f^2:{\mathbb{R}}^{|A_2|}\times {\mathbb{R}}^{|B_2|}\to \mathbb{R}$,

(iii)

$h^1:{\mathbb{R}}^{|A_1|}\times {\mathbb{R}}^{|B_1|}\times {\mathbb{R}}^{|A_1|}\to \mathbb{R}$,

(iv)

$h^2:{\mathbb{R}}^{|A_2|}\times {\mathbb{R}}^{|B_2|}\times {\mathbb{R}}^{|A_2|}\to \mathbb{R}$,

(v)

$g^1:{\mathbb{R}}^{|A_1|}\times {\mathbb{R}}^{|B_1|}\times {\mathbb{R}}^{|B_1|}\to \mathbb{R}$ and

(vi)

$g^2:{\mathbb{R}}^{|A_2|}\times {\mathbb{R}}^{|B_2|}\times {\mathbb{R}}^{|B_2|}\to \mathbb{R}$

be twice differentiable functions.

Now we formulate the following mixed type nondifferentiable higher-order symmetric dual programs over cones.

Primal Problem(MHP):

$$\begin{array}{cc}\hfill \mathrm{Minimize} G(x,y,z,p)& =f^1(x^1,y^1)+s(x^1|E_1)+f^2(x^2,y^2)+s(x^2|E_2)-{(y^1)}^T{z}^1\hfill \\ & +g^1(x^1,y^1,p^1)+g^2(x^2,y^2,p^2)-{(p^1)}^T{\nabla }_{p^1}{g}^1(x^1,y^1,p^1)\hfill \\ & -{(p^2)}^T{\nabla }_{p^2}{g}^2(x^2,y^2,p^2)-{(y^2)}^T[{\nabla }_{y^2}{f}^2(x^2,y^2)+{\nabla }_{p^2}{g}^2(x^2,y^2,p^2)]\hfill \end{array}$$

subject to

$$-({\nabla }_{y^1}{f}^1(x^1,y^1)-z^1+{\nabla }_{p^1}{g}^1(x^1,y^1,p^1))\in C_3^{*},$$

(3)

$$-({\nabla }_{y^2}{f}^2(x^2,y^2)-z^2+{\nabla }_{p^2}{g}^2(x^2,y^2,p^2))\in C_4^{*},$$

(4)

$${(y^1)}^T[{\nabla }_{y^1}{f}^1(x^1,y^1)-z^1+{\nabla }_{p^1}{g}^1(x^1,y^1,p^1)]\ge 0,$$

(5)

$${(p^1)}^T[{\nabla }_{y^1}{f}^1(x^1,y^1)-z^1+{\nabla }_{p^1}{g}^1(x^1,y^1,p^1)]\ge 0,$$

(6)

$${(p^2)}^T[{\nabla }_{y^2}{f}^2(x^2,y^2)-z^2+{\nabla }_{p^2}{g}^2(x^2,y^2,p^2)]\ge 0,$$

(7)

$$x^1\in C_1,x^2\in C_2,y^2\ge 0,$$

(8)

$$z^1\in D_1,z^2\in D_2.$$

(9)

Dual Problem(MHD):

$$\begin{array}{cc}\hfill \mathrm{Maximize} H(u,v,w,r)& =f^1(u^1,v^1)-S(v^1|D_1)+f^2(u^2,v^2)-S(v^2|D_2)+{(u^1)}^T{w}^1\hfill \\ & +h^1(u^1,v^1,r^1)+h^2(u^2,v^2,r^2)-{(r^1)}^T{\nabla }_{r^1}{h}^1(u^1,v^1,r^1)\hfill \\ & -{(r^2)}^T{\nabla }_{r^2}{h}^2(u^2,v^2,r^2)-{(u^2)}^T[{\nabla }_{u^2}{f}^2(u^2,v^2)+{\nabla }_{r^2}{h}^2(u^2,v^2,r^2)]\hfill \end{array}$$

subject to

$$({\nabla }_{u^1}{f}^1(u^1,v^1)+w^1+{\nabla }_{r^1}{h}^1(u^1,v^1,r^1))\in C_1^{*},$$

(10)

$$({\nabla }_{u^2}{f}^2(u^2,v^2)+w^2+{\nabla }_{r^2}{h}^2(u^2,v^2,r^2))\in C_2^{*},$$

(11)

$${(u^1)}^T[{\nabla }_{u^1}{f}^1(u^1,v^1)+w^1+{\nabla }_{r^1}{h}^1(u^1,v^1,r^1)]\le 0,$$

(12)

$${(r^1)}^T[{\nabla }_{u^1}{f}^1(u^1,v^1)+w^1+{\nabla }_{r^1}{h}^1(u^1,v^1,r^1)]\le 0,$$

(13)

$${(r^2)}^T[{\nabla }_{u^2}{f}^2(u^2,v^2)+w^2+{\nabla }_{r^2}{h}^2(u^2,v^2,r^2)]\le 0,$$

(14)

$$v^1\in C_3,v^2\in C_4,u^2\ge 0,$$

(15)

$$w^1\in E_1,w^2\in E_2,$$

(16)

where, $p^1\in {\mathbb{R}}^{|B_1|}$, $p^2\in {\mathbb{R}}^{|B_2|}$, $r^1\in {\mathbb{R}}^{|A_1|}$, $r^2\in {\mathbb{R}}^{|A_2|}$ and $E_1,E_2,D_1$, and $D_2$ are compact convex sets in ${\mathbb{R}}^{|B_1|},{\mathbb{R}}^{|B_2|},{\mathbb{R}}^{|A_1|}$, and ${\mathbb{R}}^{|A_2|}$, respectively.

4. Remark

The above dual programs generalize several models that appeared in the literature can be seen below.

(A)

If $|B_1|=0,|A_1|=0,C_1={{\mathbb{R}}^n}_{+}$ and $C_2={{\mathbb{R}}^h}_{+}$, then the above programs reduce to non-differentiable Wolfe-type dual programs (see [18]).

(B)

Let $|B_2|=0,|A_2|=0,C_1={{\mathbb{R}}^n}_{+}$ and $C_2={{\mathbb{R}}^h}_{+}$. Then the above programs become non-differentiable Mond–Weir-type dual programs (see [18]).

(C)

Let $C_1={{\mathbb{R}}^n}_{+}$ and $C_2={{\mathbb{R}}^h}_{+}$ in (MHP) and (MHD), respectively. Then we get the programs proposed by Verma et al. [14].

(D)

Let $C_1={{\mathbb{R}}^n}_{+}$, $C_2={{\mathbb{R}}^h}_{+}$, $E=0$ and $D=0$ in (MHP) and (MHD), respectively. Then we get the programs discussed by Verma et al. [22].

5. Duality Theorems

In this section, we establish the relations between primal problem (MHP) and dual problem (MHD).

Theorem 1.

(Weak Duality) Let$(x^1,x^2,y^1,y^2,z^1,z^2,p^1,p^2)$be feasible for (MHP) and$(u^1,u^2,v^1,v^2,w^1,w^2,r^1,r^2)$be feasible for (MHD). Suppose that

(i) 

$f^1(.,v^1)+{(.)}^T{w}^1$is higher-order$\mathcal{F}-$pseudo-convex function at$u^1$with respect to$h^1(u^1,v^1,r^1)$,

(ii) 

$-f^1(x^1,.)+{(.)}^T{z}^1$is higher-order$\mathcal{F}-$pseudo-convex function at$y^1$with respect to$-g^1(x^1,y^1,p^1)$,

(iii) 

$f^2(.,v^2)+{(.)}^T{w}^2$is higher-order$\mathcal{F}-$convex function at$u^2$with respect to$h^2(u^2,v^2,r^2)$,

(iv) 

$-f^2(x^2,.)+{(.)}^T{z}^2$is higher-order$\mathcal{F}-$convex function at$y^2$with respect to$-g^2(x^2,y^2,p^2)$,

(v) 

$\mathcal{F}(x^1,u^1;{\psi }^1)+{(u^1)}^T{\psi }^1+{(r^1)}^T{\psi }^1\ge 0,\forall x^1,u^1\in C_1,{\psi }^1\in C_1^{*},$

(vi) 

$\mathcal{F}(v^1,y^1;{\psi }^2)+{(y^1)}^T{\psi }^2+{(p^1)}^T{\psi }^2\ge 0,\forall v^1,y^1\in C_3,{\psi }^2\in C_3^{*},$

(vii) 

$\mathcal{F}(x^2,u^2;{\psi }^3)+{(u^2)}^T{\psi }^3+{(r^2)}^T{\psi }^3\ge 0,\forall x^2,u^2\in C_2,{\psi }^3\in C_2^{*}$and

(viii) 

$\mathcal{F}(v^2,y^2;{\psi }^4)+{(y^2)}^T{\psi }^4+{(p^2)}^T{\psi }^4\ge 0,\forall v^2,y^1\in C_4,{\psi }^4\in C_4^{*}.$

Then

$$G(x^1,x^2,y^1,y^2,z^1,z^2,p^1,p^2)\ge H(u^1,u^2,v^1,v^2,w^1,w^2,r^1,r^2).$$

(17)

Proof. 

From hypotheses (iii) and (iv), we get

$$\begin{gathered} f^2(x^2,v^2)+{(x^2)}^T{w}^2-f^2(u^2,v^2)-{(u^2)}^T{w}^2-h^2(u^2,v^2,p^2)+{(p^2)}^T{\nabla }_{p^2}{h}^2(u^2,v^2,p^2) \\ \ge \mathcal{F}(x^2,u^2;{\nabla }_{x^2}{f}^2(u^2,v^2)+w^2+{\nabla }_{r^2}{g}^2(u^2,v^2,r^2)) \end{gathered}$$

(18)

and

$$\begin{gathered} f^2(x^2,y^2)-{(y^2)}^T{z}^2-f^2(x^2,v^2)+{(v^2)}^T{z}^2+g^2(x^2,y^2,p^2)-{(p^2)}^T{\nabla }_{p^2}{g}^2(x^2,y^2,p^2) \\ \ge \mathcal{F}(v^2,y^2;-({\nabla }_{y^2}{f}^2(x^2,y^2)-z^2+{\nabla }_{p^2}{h}^2(x^2,y^2,p^2)). \end{gathered}$$

(19)

Let

$${\psi }^3=({\nabla }_{u^2}{f}^2(u^2,v^2)+w^2+{\nabla }_{r^2}{h}^2(u^2,v^2,r^2))\in C_2^{*}$$

and

$${\psi }^4=-({\nabla }_{y^2}{f}^2(x^2,y^2)-z^2+{\nabla }_{p^2}{g}^2(x^2,y^2,p^2))\in C_4^{*}.$$

Now from hypotheses (vii) and (viii), we get

$$\begin{array}{cc}\mathcal{F}(x^2,u^2;{\nabla }_{x^2}{f}^2(u^2,v^2)+w^2+{\nabla }_{r^2}{g}^2(u^2,v^2,r^2))+& u^2[{\nabla }_{x^2}{f}^2(u^2,v^2)+w^2+{\nabla }_{r^2}{g}^2(u^2,v^2,r^2)]\\ & \ge -r^2[{\nabla }_{x^2}{f}^2(u^2,v^2)+w^2+{\nabla }_{r^2}{g}^2(u^2,v^2,r^2)]\end{array}$$

and

$$\begin{array}{cc}\hfill \mathcal{F}(v^2,y^2;-({\nabla }_{y^2}{f}^2(x^2,y^2)-z^2+{\nabla }_{p^2}{h}^2(x^2,y^2,p^2)))& -y^2[{\nabla }_{y^2}{f}^2(x^2,y^2)-z^2+{\nabla }_{p^2}{h}^2(x^2,y^2,p^2)]\hfill \\ & \ge p^2[{\nabla }_{y^2}{f}^2(x^2,y^2)-z^2+{\nabla }_{p^2}{h}^2(x^2,y^2,p^2)].\hfill \end{array}$$

The above inequalities along with inequalities (7) and (14) imply that

$$\mathcal{F}(x^2,u^2;{\nabla }_{x^2}{f}^2(u^2,v^2)+w^2+{\nabla }_{r^2}{g}^2(u^2,v^2,r^2))\ge -u^2[{\nabla }_{x^2}{f}^2(u^2,v^2)+w^2+{\nabla }_{r^2}{g}^2(u^2,v^2,r^2)]$$

and

$$\mathcal{F}(v^2,y^2;-({\nabla }_{y^2}{f}^2(x^2,y^2)-z^2+{\nabla }_{p^2}{h}^2(x^2,y^2,p^2)))\ge y^2[{\nabla }_{y^2}{f}^2(x^2,y^2)-z^2+{\nabla }_{p^2}{h}^2(x^2,y^2,p^2)].$$

The above inequalities along with Equations (18) and (19) give

$$\begin{gathered} f^2(x^2,v^2)+{(x^2)}^T{w}^2-f^2(u^2,v^2)-{(u^2)}^T{w}^2-h^2(u^2,v^2,p^2)+{(p^2)}^T{\nabla }_{p^2}{h}^2(u^2,v^2,p^2) \\ \ge -u^2[{\nabla }_{x^2}{f}^2(u^2,v^2)+w^2+{\nabla }_{r^2}{g}^2(u^2,v^2,r^2)] \end{gathered}$$

and

$$\begin{gathered} f^2(x^2,y^2)-{(y^2)}^T{z}^2-f^2(x^2,v^2)+{(v^2)}^T{z}^2+g^2(x^2,y^2,p^2)-{(p^2)}^T{\nabla }_{p^2}{g}^2(x^2,y^2,p^2) \\ \ge y^2[{\nabla }_{y^2}{f}^2(x^2,y^2)-z^2+{\nabla }_{p^2}{h}^2(x^2,y^2,p^2)]. \end{gathered}$$

Now adding the above two inequalities, we obtain

$$\begin{gathered} \begin{array}{c}{f}^2(x^2,y^2)+{(x^2)}^T{w}^2-{(y^2)}^T{z}^2+g^2(x^2,y^2,p^2)-{(p^2)}^T{\nabla }_{p^2}{g}^2(x^2,y^2,p^2)-y^2[{\nabla }_{y^2}{f}^2(x^2,y^2) \\ -z^2+{\nabla }_{p^2}{h}^2(x^2,y^2,p^2)]\\ \ge f^2(u^2,v^2)+{(u^2)}^T{w}^2-{(v^2)}^T{z}^2+h^2(u^2,v^2,p^2)-{(p^2)}^T{\nabla }_{p^2}{h}^2(u^2,v^2,p^2)-u^2[{\nabla }_{x^2}{f}^2(u^2,v^2) \\ +w^2+{\nabla }_{r^2}{g}^2(u^2,v^2,r^2)].\end{array} \end{gathered}$$

Noting that ${(x^2)}^T{w}^2\le s(x^2|E_2)$ and ${(v^2)}^T{z}^2\le s(v^2|D_2),$ we have

$$\begin{gathered} f^2(x^2,y^2)+s(x^2|E_2)+g^2(x^2,y^2,p^2)-y^2[{\nabla }_{y^2}{f}^2(x^2,y^2)+{\nabla }_{p^2}{h}^2(x^2,y^2,p^2)] \\ \ge f^2(u^2,v^2)-s(v^2|D_2)+h^2(u^2,v^2,p^2) \\ -{(p^2)}^T{\nabla }_{p^2}{h}^2(u^2,v^2,p^2)-u^2[{\nabla }_{x^2}{f}^2(u^2,v^2)+{\nabla }_{r^2}{h}^2(u^2,v^2,r^2)]. \end{gathered}$$

(20)

By taking

$${\psi }^1=({\nabla }_{u^1}{f}^1(u^1,v^1)+w^1+{\nabla }_{r^1}{h}^1(u^1,v^1,r^1))\in C_1^{*}$$

and

$${\psi }^2=-({\nabla }_{y^1}{f}^1(x^1,y^1)-z^1+{\nabla }_{p^1}{g}^1(x^1,y^1,p^1))\in C_3^{*},$$

we have

$$\begin{array}{c}\hfill \mathcal{F}(x^1,u^1;{\nabla }_{u^1}{f}^1(u^1,v^1)+w^1+{\nabla }_{r^1}{g}^1(u^1,v^1,r^1))\ge -(u^1+r^1)[{\nabla }_{u^1}{f}^1(u^1,v^1)+w^1+{\nabla }_{r^1}{g}^1(u^1,v^1,r^1)]\\ \hfill (\mathrm{by}\mathrm{the}\mathrm{hypothesis}(v))\end{array}$$

and

$$\begin{array}{c}\hfill \mathcal{F}(v^1,y^1;-({\nabla }_{y^1}{f}^1(x^1,y^1)-z^1+{\nabla }_{p^1}{h}^1(x^1,y^1,p^1)))\ge (y^1+p^1)[{\nabla }_{y^1}{f}^1(x^1,y^1)-z^1+{\nabla }_{p^1}{h}^1(x^1,y^1,p^1)]\\ \hfill (\mathrm{by}\mathrm{the}\mathrm{hypothesis}(vi)).\end{array}$$

The above two inequalities along with inequalities (5), (6), (12), and (13) give

$$\mathcal{F}(x^1,u^1;{\nabla }_{u^1}{f}^1(u^1,v^1)+w^1+{\nabla }_{r^1}{g}^1(u^1,v^1,r^1))\ge 0$$

and

$$\mathcal{F}(v^1,y^1;-({\nabla }_{y^1}{f}^1(x^1,y^1)-z^1+{\nabla }_{p^1}{h}^1(x^1,y^1,p^1)))\ge 0,$$

which by hypotheses (i) and (ii) imply

$$f^1(x^1,v^1)+{(x^1)}^T{w}^1-f^1(u^1,v^1)-{(v^1)}^T{w}^1-h^1(u^1,v^1,p^1)+{(p^1)}^T{\nabla }_{p^1}{h}^1(u^1,v^1,p^1)\ge 0$$

and

$$f^1(x^1,y^1)+{(v^1)}^T{z}^1-f^1(x^1,v^1)-{(y^1)}^T{z}^1+g^1(x^1,y^1,p^1)-{(p^1)}^T{\nabla }_{p^1}{g}^1(x^1,y^1,p^1)\ge 0.$$

Adding the above two inequalities, we obtain

$$\begin{gathered} f^1(x^1,y^1)-{(y^1)}^T{z}^1+{(x^1)}^T{w}^1+g^1(x^1,y^1,p^1)-{(p^1)}^T{\nabla }_{p^1}{g}^1(x^1,y^1,p^1) \\ \hspace{1em}\hspace{1em}\hspace{1em}\ge f^1(u^1,v^1)+{(v^1)}^T{w}^1-{(v^1)}^T{z}^1+h^1(u^1,v^1,p^1)-{(p^1)}^T{\nabla }_{p^1}{h}^1(u^1,v^1,p^1). \end{gathered}$$

Using ${(x^1)}^T{w}^1\le s(x^1|E_1)$ and ${(v^1)}^T{z}^1\le s(v^1|D_1),$ we have

$$\begin{gathered} f^1(x^1,y^1)-{(y^1)}^T{z}^1+s(x^1|E_1)+g^1(x^1,y^1,p^1)-{(p^1)}^T{\nabla }_{p^1}{g}^1(x^1,y^1,p^1) \\ \ge f^1(u^1,v^1)+{(v^1)}^{T}w-s(v^1|D_1)+h^1(u^1,v^1,p^1)-{(p^1)}^T{\nabla }_{p^1}{h}^1(u^1,v^1,p^1). \end{gathered}$$

(21)

Combining inequalities (20) and (21), we get

$$G(x^1,x^2,y^1,y^2,z^1,z^2,p^1,p^2)\ge H(u^1,u^2,v^1,v^2,w^1,w^2,r^1,r^2).$$

 □

Theorem 2.

(StrongDuality)

Let$({\overline{x}}^1,{\overline{x}}^2,{\overline{y}}^1,{\overline{y}}^2,{\overline{z}}^1,{\overline{z}}^2,{\overline{p}}^1,{\overline{p}}^2)$be an optimal solution of (MHP). Suppose that

(i) 

${\nabla }_{p^1{p}^1}{g}^1({\overline{x}}^1,{\overline{y}}^1,{\overline{p}}^1)$is positive or negative definite matrix and${\nabla }_{p^2{p}^2}{g}^2({\overline{x}}^2,{\overline{y}}^2,{\overline{p}}^2)$is negative definite matrix,

(ii) 

${\nabla }_{y^1}{f}^1({\overline{x}}^1,{\overline{y}}^1)-{\overline{z}}^1+{\nabla }_{p^1}{g}^1({\overline{x}}^1,{\overline{y}}^1,{\overline{p}}^1)\ne 0$and${\nabla }_{y^2}{f}^2({\overline{x}}^2,{\overline{y}}^2)-{\overline{z}}^2+{\nabla }_{p^2}{g}^2({\overline{x}}^2,{\overline{y}}^2,{\overline{p}}^2)\ne 0,$

(iii) 

${({\overline{p}}^1)}^T[{\nabla }_{y^1}{f}^1({\overline{x}}^1,{\overline{y}}^1)-{\overline{z}}^1+{\nabla }_{p^1}{g}^1({\overline{x}}^1,{\overline{y}}^1,{\overline{p}}^1)]=0\Rightarrow {\overline{p}}^1=0$

and 

${\overline{y}}^2[{\nabla }_{y^2}{g}^2({\overline{x}}^2,{\overline{y}}^2,{\overline{p}}^2)-{\nabla }_{p^2}{g}^2({\overline{x}}^2,{\overline{y}}^2,{\overline{p}}^2)+{\nabla }_{y^2{y}^2}{f}^2({\overline{x}}^2,{\overline{y}}^2){\overline{p}}^2]=0\Rightarrow {\overline{p}}^2=0,$

(iv) 

$g^1({\overline{x}}^1,{\overline{y}}^1,0)=h^1({\overline{x}}^1,{\overline{y}}^1,0),{\nabla }_{x^1}{g}^1({\overline{x}}^1,{\overline{y}}^1,0)={\nabla }_{r^1}{h}^1({\overline{x}}^1,{\overline{y}}^1,0)$,

${\nabla }_{y^1}{g}^1({\overline{x}}^1,{\overline{y}}^1,0)={\nabla }_{p^1}{g}^1({\overline{x}}^1,{\overline{y}}^1,0)$,$g^2({\overline{x}}^2,{\overline{y}}^2,0)=h^2({\overline{x}}^2,{\overline{y}}^2,0)$and

${\nabla }_{x^2}{g}^2({\overline{x}}^2,{\overline{y}}^2,0)={\nabla }_{r^2}{h}^2({\overline{x}}^2,{\overline{y}}^2,0).$

Then,

(I) 

$({\overline{x}}^1,{\overline{x}}^2,{\overline{y}}^1,{\overline{y}}^2,{\overline{w}}^1,{\overline{w}}^2,{\overline{r}}^1=0,{\overline{r}}^2=0)$is feasible for (MHD), and

(II) 

$G({\overline{x}}^1,{\overline{x}}^2,{\overline{y}}^1,{\overline{y}}^2,{\overline{z}}^1,{\overline{z}}^2,{\overline{p}}^1,{\overline{p}}^2)=H({\overline{x}}^1,{\overline{x}}^2,{\overline{y}}^1,{\overline{y}}^2,{\overline{w}}^1,{\overline{w}}^2,{\overline{r}}^1,{\overline{r}}^2).$

Furthermore, if the hypotheses of Theorem 1 are satisfied for all feasible solutions of (MHP) and (MHD), then$({\overline{x}}^1,{\overline{x}}^2,{\overline{y}}^1,{\overline{y}}^2,{\overline{w}}^1,{\overline{w}}^2,{\overline{r}}^1=0,{\overline{r}}^2=0)$is an optimal solution for (MHD).

Proof. 

As $({\overline{x}}^1,{\overline{x}}^2,{\overline{y}}^1,{\overline{y}}^2,{\overline{z}}^1,{\overline{z}}^2,{\overline{p}}^1,{\overline{p}}^2)$ is an optimal solution of (MHP), by the Fritz John necessary optimality conditions [23,24], there exist $\alpha ,\gamma ,{\delta }^1,{\delta }^2\in \mathbb{R}$, ${\beta }^1\in {\mathbb{R}}^{|B_1|}$, ${\beta }^2,\eta \in {\mathbb{R}}^{|B_2|}$, ${\xi }^1\in {\mathbb{R}}^{|A_1|}$, ${\xi }^2\in {\mathbb{R}}^{|A_2|}$ such that the following conditions are satisfied at $({\overline{x}}^1,{\overline{x}}^2,{\overline{y}}^1,{\overline{y}}^2,{\overline{z}}^1,{\overline{z}}^2,{\overline{p}}^1,{\overline{p}}^2):$

$$\begin{gathered} \{\alpha [{\nabla }_{x^1}{f}^1({\overline{x}}^1,{\overline{y}}^1)+{\xi }^1+{\nabla }_{x^1}{g}^1({\overline{x}}^1,{\overline{y}}^1,{\overline{p}}^1)-{\nabla }_{p^1{x}^1}{g}^1({\overline{x}}^1,{\overline{y}}^1,{\overline{p}}^1){\overline{p}}^1]+[{\nabla }_{y^1{x}^1}{f}^1({\overline{x}}^1,{\overline{y}}^1) \\ +{\nabla }_{p^1{x}^1}{g}^1({\overline{x}}^1,{\overline{y}}^1,{\overline{p}}^1)]({\beta }^1-\gamma {\overline{y}}^1-{\delta }^1{\overline{p}}^1)\}(x^1-{\overline{x}}^1)\ge 0,\mathrm{for}\mathrm{all}{x}^1\in C_1, \end{gathered}$$

(22)

$$\begin{gathered} \{\alpha [{\nabla }_{x^2}{f}^2({\overline{x}}^2,{\overline{y}}^2)+{\xi }^2+{\nabla }_{x^2}{g}^2({\overline{x}}^2,{\overline{y}}^2,{\overline{p}}^2)]+\left\{{\nabla }_{p^2{x}^2}{g}^2({\overline{x}}^2,{\overline{y}}^2,{\overline{p}}^2)\right\}({\beta }^2-\alpha {\overline{y}}^2-\alpha {\overline{p}}^2 \\ -{\delta }^2{\overline{p}}^2)+\left\{{\nabla }_{y^2{x}^2}{f}^2({\overline{x}}^2,{\overline{y}}^2)\right\}({\beta }^2-\alpha {\overline{y}}^2-{\delta }^2{\overline{p}}^2)\}(x^2-{\overline{x}}^2)\ge 0,\mathrm{for}\mathrm{all}{x}^2\in C_2, \end{gathered}$$

(23)

$$\begin{gathered} \alpha [{\nabla }_{y^1}{f}^1({\overline{x}}^1,{\overline{y}}^1)-{\overline{z}}^1+{\nabla }_{y^1}{g}^1({\overline{x}}^1,{\overline{y}}^1,{\overline{p}}^1)-{\nabla }_{p^1{y}^1}{g}^1({\overline{x}}^1,{\overline{y}}^1,{\overline{p}}^1){\overline{p}}^1]+({\nabla }_{y^1{y}^1}{f}^1({\overline{x}}^1,{\overline{y}}^1) \\ +{\nabla }_{p^1{y}^1}{g}^1({\overline{x}}^1,{\overline{y}}^1,{\overline{p}}^1))({\beta }^1-\gamma {\overline{y}}^1-{\delta }^1{\overline{p}}^1)-\gamma [{\nabla }_{y^1}{f}^1({\overline{x}}^1,{\overline{y}}^1)-{\overline{z}}^1+{\nabla }_{p^1}{g}^1({\overline{x}}^1,{\overline{y}}^1,{\overline{p}}^1)]=0, \\ \mathrm{for}\mathrm{all},y^1\in {\mathbb{R}}^{|B_1|}, \end{gathered}$$

(24)

$$\begin{gathered} \left\{{\nabla }_{p^2{y}^2}{g}^2({\overline{x}}^2,{\overline{y}}^2,{\overline{p}}^2)\right\}({\beta }^2-\alpha {\overline{y}}^2-\alpha {\overline{p}}^2-{\delta }^2{\overline{p}}^2)+\alpha [{\nabla }_{y^2}{g}^2({\overline{x}}^2,{\overline{y}}^2,{\overline{p}}^2)-{\nabla }_{p^2}{g}^2({\overline{x}}^2,{\overline{y}}^2,{\overline{p}}^2)] \\ +\left\{{\nabla }_{y^2{y}^2}{f}^2({\overline{x}}^2,{\overline{y}}^2)\right\}({\beta }^2-\alpha {\overline{y}}^2-{\delta }^2{\overline{p}}^2)-\eta =0\mathrm{for}\mathrm{all},y^2\in {\mathbb{R}}^{|B_2|}, \end{gathered}$$

(25)

$$\begin{gathered} \left\{{\nabla }_{p^1{p}^1}{g}^1({\overline{x}}^1,{\overline{y}}^1,{\overline{p}}^1)\right\}({\beta }^1-\alpha {\overline{p}}^1-\gamma {\overline{y}}^1-{\delta }^1{\overline{p}}^1) \\ -{\delta }^1[{\nabla }_{y^1}{f}^1({\overline{x}}^1,{\overline{y}}^1)-{\overline{z}}^1+{\nabla }_{p^1}{g}^1({\overline{x}}^1,{\overline{y}}^1,{\overline{p}}^1)]=0, \end{gathered}$$

(26)

$$\begin{gathered} \left\{{\nabla }_{p^2{p}^2}{g}^2({\overline{x}}^2,{\overline{y}}^2,{\overline{p}}^2)\right\}({\beta }^2-\alpha {\overline{y}}^2-\alpha {\overline{p}}^2-{\delta }^2{\overline{p}}^2) \\ -{\delta }^2[{\nabla }_{y^2}{f}^2({\overline{x}}^2,{\overline{y}}^2)-{\overline{z}}^2+{\nabla }_{p^2}{g}^2({\overline{x}}^2,{\overline{y}}^2,{\overline{p}}^2)]=0, \end{gathered}$$

(27)

$${\beta }^1[{\nabla }_{y^1}{f}^1({\overline{x}}^1,{\overline{y}}^1)-{\overline{z}}^1+{\nabla }_{p^1}{g}^1({\overline{x}}^1,{\overline{y}}^1,{\overline{p}}^1)]=0,$$

(28)

$${\beta }^2[{\nabla }_{y^2}{f}^2({\overline{x}}^2,{\overline{y}}^2)-{\overline{z}}^2+{\nabla }_{p^2}{g}^2({\overline{x}}^2,{\overline{y}}^2,{\overline{p}}^2)]=0,$$

(29)

$$\gamma {\overline{y}}^1[{\nabla }_{y^1}{f}^1({\overline{x}}^1,{\overline{y}}^1)-{\overline{z}}^1+{\nabla }_{p^1}{g}^1({\overline{x}}^1,{\overline{y}}^1,{\overline{p}}^1)]=0,$$

(30)

$${\delta }^1{\overline{p}}^1[{\nabla }_{y^1}{f}^1({\overline{x}}^1,{\overline{y}}^1)-{\overline{z}}^1+{\nabla }_{p^1}{g}^1({\overline{x}}^1,{\overline{y}}^1,{\overline{p}}^1)]=0,$$

(31)

$${\delta }^2{\overline{p}}^2[{\nabla }_{y^2}{f}^2({\overline{x}}^2,{\overline{y}}^2)-{\overline{z}}^2+{\nabla }_{p^2}{g}^2({\overline{x}}^2,{\overline{y}}^2,{\overline{p}}^2)]=0,$$

(32)

$$(\alpha -\gamma )y^1+{\beta }^1-{\delta }^1{p}^1\in N_{D_1}({\overline{z}}^1),$$

(33)

$${\beta }^2-{\delta }^2{p}^2\in N_{D_2}({\overline{z}}^2),$$

(34)

$${({\xi }^1)}^T{\overline{x}}^1=S(x^1|E_1),{\xi }^1\in C_1,$$

(35)

$${({\xi }^2)}^T{\overline{x}}^2=S(x^2|E_2),{\xi }^2\in C_2,$$

(36)

$$\eta {\overline{y}}^2=0,$$

(37)

$$(\alpha ,{\beta }^1,{\beta }^2,\gamma ,{\delta }^1,{\delta }^2,\eta )\ne 0,$$

(38)

$$(\alpha ,{\beta }^1,{\beta }^2,\gamma ,{\delta }^1,{\delta }^2,\eta )\ge 0.$$

(39)

Premultiplying Equations (26) and (27) by $({\beta }^1-\alpha {\overline{p}}^1-\gamma {\overline{y}}^1-{\delta }^1{\overline{p}}^1)$ and $({\beta }^2-\alpha {\overline{p}}^2-\alpha {\overline{y}}^2-{\delta }^2{\overline{p}}^2)$, respectively, and then using Equations (28)–(32), we get

$${({\beta }^1-\alpha {\overline{p}}^1-\gamma {\overline{y}}^1-{\delta }^1{\overline{p}}^1)}^T{\nabla }_{p^1{p}^1}{g}^1({\overline{x}}^1,{\overline{y}}^1,{\overline{p}}^1)({\beta }^1-\alpha {\overline{p}}^1-\gamma {\overline{y}}^1-{\delta }^1{\overline{p}}^1)=0,$$

(40)

and

$$\begin{gathered} ({\beta }^2-\alpha {\overline{p}}^2-\alpha {\overline{y}}^2-{\delta }^2{\overline{p}}^2){\nabla }_{p^2{p}^2}{g}^2({\overline{x}}^2,{\overline{y}}^2,{\overline{p}}^2)({\beta }^2-\alpha {\overline{p}}^2-\alpha {\overline{y}}^2-{\delta }^2{\overline{p}}^2) \\ =-\alpha {\delta }^2{\overline{y}}^2[{\nabla }_{y^2}{f}^2({\overline{x}}^2,{\overline{y}}^2)-{\overline{z}}^2+{\nabla }_{p^2}{g}^2({\overline{x}}^2,{\overline{y}}^2,{\overline{p}}^2)]. \end{gathered}$$

(41)

Using hypothesis (i) in (40), we get

$${\beta }^1=\alpha {\overline{p}}^1+\gamma {\overline{y}}^1+{\delta }^1{\overline{p}}^1.$$

(42)

Further, using inequalities (4), (8), and (39) in (41), we obtain

$$({\beta }^2-\alpha {\overline{p}}^2-\alpha {\overline{y}}^2-{\delta }^2{\overline{p}}^2){\nabla }_{p^2{p}^2}{g}^2({\overline{x}}^2,{\overline{y}}^2,{\overline{p}}^2)({\beta }^2-\alpha {\overline{p}}^2-\alpha {\overline{y}}^2-{\delta }^2{\overline{p}}^2)\ge 0,$$

which on using hypothesis (i), we obtain

$${\beta }^2=\alpha {\overline{p}}^2+\alpha {\overline{y}}^2+{\delta }^2{\overline{p}}^2.$$

(43)

From Equations (26), (27), along with hypothesis (ii), we obtain

$${\delta }^1=0$$

(44)

and

$${\delta }^2=0.$$

(45)

Now suppose, $\alpha =0.$ Then, Equations (43) and (45) give ${\beta }^2=0$. The Equation (24) with hypothesis (ii) implies $\gamma =0$, and Equation (42) yields ${\beta }^1=0$. Therefore, Equation (25) implies $\eta =0.$ Thus $(\alpha ,{\beta }^1,{\beta }^2,\gamma ,{\delta }^1,{\delta }^2,\eta )=0$, which contradicts the Equation (38). Therefore,

$$\alpha >0.$$

(46)

From Equations (28), (30) and (31), we have

$${({\beta }^1-\gamma {\overline{y}}^1-{\delta }^1{\overline{p}}^1)}^T[{\nabla }_{y^1}{f}^1({\overline{x}}^1,{\overline{y}}^1)-{\overline{z}}^1+{\nabla }_{p^1}{g}^1({\overline{x}}^1,{\overline{y}}^1,{\overline{p}}^1)]=0,$$

which along with (42), gives

$$\alpha {({\overline{p}}^1)}^T[{\nabla }_{y^1}{f}^1({\overline{x}}^1,{\overline{y}}^1)-{\overline{z}}^1+{\nabla }_{p^1}{g}^1({\overline{x}}^1,{\overline{y}}^1,{\overline{p}}^1)]=0.$$

(47)

Using hypothesis (iii), we get

$${\overline{p}}^1=0.$$

(48)

Further, from Equations (25), (37), and (43), we obtain

$$\alpha {\overline{y}}^2[{\nabla }_{y^2}{g}^2({\overline{x}}^2,{\overline{y}}^2,{\overline{p}}^2)-{\nabla }_{p^2}{g}^2({\overline{x}}^2,{\overline{y}}^2,{\overline{p}}^2)+{\nabla }_{y^2{y}^2}{f}^2({\overline{x}}^2,{\overline{y}}^2){\overline{p}}^2]=0,$$

(49)

which by hypothesis (iii) and Equation (46) implies

$${\overline{p}}^2=0.$$

(50)

Therefore, (42) and (43) reduce to

$${\beta }^1=\gamma {\overline{y}}^1$$

(51)

and

$${\beta }^2=\alpha {\overline{y}}^2.$$

(52)

Now from Equations (24), (42), and (48) with hypotheses (ii) and (iv), we get

$$\alpha =\gamma >0.$$

(53)

Therefore, Equation (52) implies

$${\overline{y}}^2=\frac{{\beta }^2}{\alpha }\ge 0.$$

(54)

Now, Equations (22) and (23) along with (42), (43), (50) and hypothesis (iv), we obtain

$$\alpha [{\nabla }_{x^1}{f}^1({\overline{x}}^1,{\overline{y}}^1)+{\overline{\xi }}^1+{\nabla }_{r^1}{g}^1({\overline{x}}^1,{\overline{y}}^1,{\overline{p}}^1)](x^1-{\overline{x}}^1)\ge 0,\mathrm{for}\mathrm{all}{x}^1\in C_1$$

(55)

and

$$\alpha [{\nabla }_{x^2}{f}^2({\overline{x}}^2,{\overline{y}}^2)+{\overline{\xi }}^2+{\nabla }_{r^2}{g}^2({\overline{x}}^2,{\overline{y}}^2,{\overline{p}}^2)](x^2-{\overline{x}}^2)\ge 0,\mathrm{for}\mathrm{all}{x}^2\in C_2.$$

(56)

Let $x^1\in C_1,$ then ${\overline{x}}^1+x^1\in C_1$. Then above inequality (55) implies

$${({\overline{x}}^1)}^T[{\nabla }_{x^1}{f}^1({\overline{x}}^1,{\overline{y}}^1)-{\overline{\xi }}^1+{\nabla }_{r^1}{g}^1({\overline{x}}^1,{\overline{y}}^1,{\overline{p}}^1)]\ge 0,\mathrm{for}\mathrm{all}{x}^1\in C_1.$$

(57)

Similarly,

$${({\overline{x}}^2)}^T[{\nabla }_{x^2}{f}^2({\overline{x}}^2,{\overline{y}}^2)+{\overline{\xi }}^2+{\nabla }_{r^2}{g}^2({\overline{x}}^2,{\overline{y}}^2,{\overline{p}}^2)]\ge 0,\mathrm{for}\mathrm{all}{x}^2\in C_2.$$

(58)

Therefore,

$${\nabla }_{x^1}{f}^1({\overline{x}}^1,{\overline{y}}^1)+{\overline{\xi }}^1+{\nabla }_{r^1}{g}^1({\overline{x}}^1,{\overline{y}}^1,{\overline{p}}^1)\in {C_1}^{*}$$

(59)

$${\nabla }_{x^2}{f}^2({\overline{x}}^2,{\overline{y}}^2)+{\overline{\xi }}^2+{\nabla }_{r^2}{g}^2({\overline{x}}^2,{\overline{y}}^2,{\overline{p}}^2)\in {C_2}^{*}.$$

(60)

If we take ${\overline{\xi }}^1={\overline{w}}^1$ and ${\overline{\xi }}^2={\overline{w}}^2$, then $({\overline{x}}^1,{\overline{x}}^2,{\overline{y}}^1,{\overline{y}}^2,{\overline{w}}^1,{\overline{w}}^2,{\overline{r}}^1=0,{\overline{r}}^2=0)$ satisfies the dual constraints (10)–(15). Therefore, it is feasible solution for (MHD).

Now from Equations (34), (46), (50), and (52), we get ${\overline{y}}^2\in N_{D_2}({\overline{z}}^2).$ As $D_2$ is a compact convex set in ${\mathbb{R}}^{|A_2|}$,

$${({\overline{y}}^2)}^T{\overline{z}}^2=S({\overline{y}}^2|D_2).$$

(61)

Moreover, since ${\beta }^1=\gamma {\overline{y}}^1$ and $\gamma >0$ then from Equations (33), (48), and (53), we obtain ${\overline{y}}^1\in N_{D_1}({\overline{z}}^1).$ As $D_1$ is a compact convex set in ${\mathbb{R}}^{|A_1|}$,

$${({\overline{y}}^1)}^T{\overline{z}}^1=S({\overline{y}}^1|D_1).$$

(62)

Therefore by Equations (35), (36), (48), (50), (61), (62), and hypothesis (iv), we get the equal objective functions value of (MHP) and (MHD) at $({\overline{x}}^1,{\overline{x}}^2,{\overline{y}}^1,{\overline{y}}^2,{\overline{z}}^1,{\overline{z}}^2,{\overline{p}}^1=0,{\overline{p}}^2=0)$ and $({\overline{x}}^1,{\overline{x}}^2,{\overline{y}}^1,{\overline{y}}^2,{\overline{w}}^1,{\overline{w}}^2,{\overline{r}}^1=0,{\overline{r}}^2=0)$. From Theorem 1, we get that $({\overline{x}}^1,{\overline{x}}^2,{\overline{y}}^1,{\overline{y}}^2,{\overline{w}}^1,{\overline{w}}^2,{\overline{r}}^1=0,{\overline{r}}^2=0)$ is an optimal solution for (MHD). □

Theorem 3.

(Converse Duality) Let$({\overline{u}}^1,{\overline{u}}^2,{\overline{v}}^1,{\overline{v}}^2,{\overline{w}}^1,{\overline{w}}^2,{\overline{r}}^1,{\overline{r}}^2)$be an optimal solution of (MHD). Suppose that

(i) 

${\nabla }_{r^1{r}^1}{h}^1({\overline{u}}^1,{\overline{v}}^1,{\overline{r}}^1)$is positive or negative definite matrix and${\nabla }_{r^2{r}^2}{h}^2({\overline{u}}^2,{\overline{v}}^2,{\overline{r}}^2)$is negative definite matrix,

(ii) 

${\nabla }_{v^1}{f}^1({\overline{u}}^1,{\overline{v}}^1)+{\overline{w}}^1+{\nabla }_{r^1}{h}^1({\overline{u}}^1,{\overline{v}}^1,{\overline{r}}^1)\ne 0$and${\nabla }_{v^2}{f}^2({\overline{u}}^2,{\overline{v}}^2)+{\overline{w}}^2+{\nabla }_{r^2}{g}^2({\overline{u}}^2,{\overline{v}}^2,{\overline{r}}^2)\ne 0,$

(iii) 

${({\overline{r}}^1)}^T[{\nabla }_{u^1}{f}^1({\overline{u}}^1,{\overline{v}}^1)+{\overline{w}}^1+{\nabla }_{r^1}{h}^1({\overline{u}}^1,{\overline{v}}^1,{\overline{r}}^1)]=0\Rightarrow {\overline{r}}^1=0$

and 

${\overline{u}}^2[{\nabla }_{u^2}{h}^2({\overline{u}}^2,{\overline{v}}^2,{\overline{r}}^2)-{\nabla }_{r^2}{h}^2({\overline{u}}^2,{\overline{v}}^2,{\overline{r}}^2)+{\nabla }_{u^2{u}^2}{f}^2({\overline{u}}^2,{\overline{v}}^2){\overline{r}}^2]=0\Rightarrow {\overline{r}}^2=0,$

(iv) 

$h^1({\overline{u}}^1,{\overline{v}}^1,0)=g^1({\overline{u}}^1,{\overline{v}}^1,0),{\nabla }_{u^1}{h}^1({\overline{u}}^1,{\overline{v}}^1,0)={\nabla }_{p^1}{g}^1({\overline{u}}^1,{\overline{v}}^1,0)$,

${\nabla }_{v^1}{h}^1({\overline{u}}^1,{\overline{v}}^1,0)={\nabla }_{r^1}{h}^1({\overline{u}}^1,{\overline{v}}^1,0),h^2({\overline{u}}^2,{\overline{v}}^2,0)=g^2({\overline{u}}^2,{\overline{v}}^2,0)$and

${\nabla }_{u^2}{h}^2({\overline{u}}^2,{\overline{v}}^2,0)={\nabla }_{p^2}{g}^2({\overline{u}}^2,{\overline{v}}^2,0).$

Then,

(I) 

$({\overline{u}}^1,{\overline{u}}^2,{\overline{v}}^1,{\overline{v}}^2,{\overline{z}}^1,{\overline{z}}^2,{\overline{p}}^1=0,{\overline{p}}^2=0)$is feasible for (MHP), and

(II) 

$G({\overline{u}}^1,{\overline{u}}^2,{\overline{v}}^1,{\overline{v}}^2,{\overline{z}}^1,{\overline{z}}^2,{\overline{p}}^1,{\overline{p}}^2)=H({\overline{u}}^1,{\overline{u}}^2,{\overline{v}}^1,{\overline{v}}^2,{\overline{w}}^1,{\overline{w}}^2,{\overline{r}}^1,{\overline{r}}^2).$

Furthermore, if the hypotheses of Theorem 1 are satisfied for all feasible solutions of (MHP) and (MHD), then$({\overline{u}}^1,{\overline{u}}^2,{\overline{v}}^1,{\overline{v}}^2,{\overline{z}}^1,{\overline{z}}^2,{\overline{p}}^1=0,{\overline{p}}^2=0)$is an optimal solution for (MHP).

Proof. 

The proof follows on the line of Theorem 2. □

5.1. Self Duality

In general, primal problem (MHP) and dual problem (MHD) are not self-duals without including restrictions on $f,h$ and g. If we assume $D_1=D_2,E_1=E_2$, $f^1:{\mathbb{R}}^{|A_1|}\times {\mathbb{R}}^{|B_1|}\to \mathbb{R}$, $f^2:{\mathbb{R}}^{|A_2|}\times {\mathbb{R}}^{|B_2|}\to \mathbb{R}$, $h^1:{\mathbb{R}}^{|A_1|}\times {\mathbb{R}}^{|B_1|}\times {\mathbb{R}}^{|A_1|}\to \mathbb{R}$, $h^2:{\mathbb{R}}^{|A_2|}\times {\mathbb{R}}^{|B_2|}\times {\mathbb{R}}^{|A_2|}\to \mathbb{R}$, $g^1:{\mathbb{R}}^{|A_1|}\times {\mathbb{R}}^{|B_1|}\times {\mathbb{R}}^{|B_1|}\to \mathbb{R},$$g^2:{\mathbb{R}}^{|A_2|}\times {\mathbb{R}}^{|B_2|}\times {\mathbb{R}}^{|B_2|}\to \mathbb{R}$ are skew symmetric, that is,

$$f^i(u^1,v^1)=-f^i(v^1,u^1),i=1,2,$$

$$h^i(u^1,v^1,r^1)=-h^i(v^1,u^1,r^1),i=1,2,$$

$$C_1=C_3$$

and

$$C_2=C_4.$$

By rewriting the dual problem (MHD) as a minimization problem, we get

$$\begin{array}{c}\mathrm{Minimize} H(u,v,w,r)=-\{f^1(u^1,v^1)-S(v^1|D_1)+f_2(u^2,v^2)-S(v^2|D_2)+{(u^1)}^T{w}^1\\ +h^1(u^1,v^1,r^1)+h_2(u^2,v^2,r^2)-{(r^1)}^T{\nabla }_{r^1}{h}^1(u^1,v^1,r^1)-{(r^2)}^T{\nabla }_{r^2}{h}^2(u^2,v^2,r^2)\\ -{(u^2)}^T[{\nabla }_{u^2}{f}^2(u^2,v^2)+{\nabla }_{r^2}{h}^2(u^2,v^2,r^2)]\}\end{array}$$

subject to

$${\nabla }_{u^1}{f}^1(u^1,v^1)+w^1+{\nabla }_{r^1}{h}^1(u^1,v^1,r^1)\in C_1^{*},$$

$${\nabla }_{u^2}{f}^2(u^2,v^2)+w^2+{\nabla }_{r^2}{h}^2(u^2,v^2,r^2)\in C_2^{*},$$

$${(u^1)}^T[{\nabla }_{u^1}{f}^1(u^1,v^1)+w^1+{\nabla }_{r^1}{h}^1(u^1,v^1,r^1)]\le 0,$$

$${(r^1)}^T[{\nabla }_{u^1}{f}^1(u^1,v^1)+w^1+{\nabla }_{r^1}{h}^1(u^1,v^1,r^1)]\le 0,$$

$${(r^2)}^T[{\nabla }_{u^2}{f}^2(u^2,v^2)+w^2+{\nabla }_{r^2}{h}^2(u^2,v^2,r^2)]\le 0,$$

$$v^1\in C_3,v^2\in C_4,u^2\ge 0,$$

As $f,h$ and g are skew symmetric, therefore

$${\nabla }_{u^1}{f}^1(u^1,v^1)=-{\nabla }_{u^1}{f}^1(v^1,u^1),{\nabla }_{u^1}{f}^2(u^2,v^2)=-{\nabla }_{u^1}{f}^2(v^2,u^2),$$

$${\nabla }_{u^1}{h}^1(u^1,v^1,r^1)=-{\nabla }_{u^1}{h}^1(v^1,u^1,r^1), \mathrm{and}{\nabla }_{u^1}{h}^2(u^2,v^2,r^2)=-{\nabla }_{u^1}{h}^2(v^2,u^2,r^2).$$

Now the above problem becomes:

$$\begin{array}{c}\mathrm{Minimize} H(u,v,w,r)=f^1(v^1,u^1)+S(v^1|D_1)+f^2(v^2,u^2)+S(v^2|D_2)-{(u^1)}^T{w}^1\\ +h^1(v^1,u^1,r^1)+h^2(v^2,u^2,r^2-{(r^1)}^T{\nabla }_{r^1}{h}^1(v^1,u^1,r^1)\\ -{(r^2)}^T{\nabla }_{r^2}{h}^2(v^2,u^2,r^2)-{(u^2)}^T[{\nabla }_{u^2}{f}^2(v^2,u^2)+{\nabla }_{r^2}{g}^2(v^2,u^2,r^2)]\end{array}$$

subject to

$$-({\nabla }_{u^1}{f}^1(v^1,u^1)+w^1+{\nabla }_{r^1}{h}^1(v^1,u^1,r^1))\in C_3^{*},$$

$$-({\nabla }_{u^2}{f}^2(v^2,u^2)+w^2+{\nabla }_{r^2}{h}^2(v^2,u^2,r^2))\in C_4^{*},$$

$${(u^1)}^T[{\nabla }_{u^1}{f}^1(v^1,u^1)+w^1+{\nabla }_{r^1}{h}^1(v^1,u^1,r^1)]\ge 0,$$

$${(r^1)}^T[{\nabla }_{u^1}{f}^1(v^1,u^1)+w^1+{\nabla }_{r^1}{h}^1(v^1,u^1,r^1)]\ge 0,$$

$${(r^2)}^T[{\nabla }_{u^2}{f}^2(v^2,u^2)+w^2+{\nabla }_{r^2}{h}^2(v^2,u^2,r^2)]\ge 0,$$

$$v^1\in C_1,v^2\in C_2,u^2\ge 0,$$

which is identical to (MHP), that is, the objective function and the constraint functions of (MHP) and (MHD) are identical. Thus, (MHP) is a self-dual.

Thus, if $(x^1,x^2,y^1,y^2,w^1,w^2,p^1,p^2)$ is feasible for (MHP), then $(y^1,y^2,x^1,x^2,w^1,w^2,p^1,p^2)$ is feasible for (MHD) and vice versa.

The weak and strong duality theorems are verified by the following example.

5.2. Example

Let $f(x,y)=(x_1^2+y_1^2+x_1+y_1+x_2^2+y_2^2+x_2+y_2)$, $s(x|E)=\frac{x+|x|}{2}$, $g(x,y,p)=\frac{1}{2}{p}^T({\nabla }_{yy}f(x,y)p)$, $h(x,y,r)=\frac{1}{2}{r}^T({\nabla }_{yy}f(x,y)r)$ and $C_1=C_2=C_3=C_4={\mathbb{R}}_{+}^2.$ Then, the problems (MHP) and (MHD) are as follows.

Primal Problem(MHP):

$$\begin{array}{c}\mathrm{Minimize} \mathrm{G}(\mathrm{x},\mathrm{y},\mathrm{z},\mathrm{p})=\hfill \\ x_1^2+x_2^2+x_1+x_2+y_1^2+y_2^2+y_1+y_2+\frac{x_1+|x_1|}{2}+\frac{x_2+|x_2|}{2}-y_1{z}_1-p_1^2-p_2^2-y_2(2y_2+1+2p_2)\hfill \end{array}$$

subject to

• $$(2y_1+1-z_1+2p_1)\le 0,$$
• $$(2y_2+1-z_2+2p_2)\le 0,$$
• $$(2y_1^2+y_1-y_1{z}_1+2p_1{y}_1)\ge 0,$$
• $$(2p_1{y}_1+p_1-p_1{z}_1+2p_1^2)\ge 0,$$
• $$(2p_2{y}_2+p_2-p_2{z}_2+2p_2^2)\ge 0,$$
• $$x,z,y_2\ge 0.$$

Dual Problem(MHD):

$$\begin{array}{c}\mathrm{Maximize} \mathrm{H}(\mathrm{u},\mathrm{v},\mathrm{w},\mathrm{r})=\hfill \\ u_1^2+u_2^2+u_1+u_2+v_1^2+v_2^2+v_1+v_2-\frac{v_1+|v_1|}{2}-\frac{v_2+|v_2|}{2}+u_1{w}_1-r_1^2-r_2^2-u_2(2u_2+1+2r_2)\hfill \end{array}$$

subject to

• $$(2u_1+1+w_1+2r_1)\ge 0,$$
• $$(2u_2+1+w_2+2r_2)\ge 0,$$
• $$(2u_1^2+u_1+u_1{w}_1+2r_1{u}_1)\le 0,$$
• $$(2r_1{u}_1+r_1+r_1{w}_1+2r_1^2)\le 0,$$
• $$(2r_2{u}_2+r_2+r_2{w}_2+2r_2^2)\le 0,$$
• $$v,w,u_2\ge 0,$$

where

(i) 

$f(x,y):{\mathbb{R}}^2\times {\mathbb{R}}^2⟶\mathbb{R}$,

(ii) 

$g(x,y,p):{\mathbb{R}}^2\times {\mathbb{R}}^2\times {\mathbb{R}}^2⟶\mathbb{R}$ and

(iii) 

$h(x,y,r):{\mathbb{R}}^2\times {\mathbb{R}}^2\times {\mathbb{R}}^2⟶\mathbb{R}$.

Let $\overline{x}=\overline{y}=\overline{u}=\overline{v}=\overline{w}=\overline{z}=\overline{p}=\overline{r}=$ $\left(\begin{array}{c}0\\ 0\end{array}\right).$

Then, $(x,y,z,p)$ is feasible for (MHP) and $(u,v,w,r)$ is feasible for (MHD).

Now, $f^1(.,v)+{(.)}^T{w}^1=(u_1^2+u_1+u_1{w}_1)$ is a higher-order $\mathcal{F}$- pseudo-convex function at ${\overline{u}}^1=0$ with respect to $h^1$ and $-f^1(x,.)+{(.)}^T{z}^1=(-y_1^2-y_1+y_1{z}_1)$ is a higher-order $\mathcal{F}$-pseudo-convex function at ${\overline{y}}^1=0$ with respect to $-g^1$. Now, $f^2(.,v)+{(.)}^T{w}^2=(u_2^2+u_2+u_2{w}_2)$ is a higher-order $\mathcal{F}$-convex function at ${\overline{u}}^2=0$ with respect to $h^2$. Similarly, $-f^2(x,.)+{(.)}^T{z}^2=(-y_2^2-y_2+y_2{z}_2)$ is a higher-order $\mathcal{F}$-convex function at ${\overline{y}}^2=0$ with respect to $-g^2$.

Also conditions (v) to (viii) of weak duality theorem (Theorem 1) are satisfied for $\overline{x}=\overline{y}=\overline{u}=\overline{v}=\overline{w}=\overline{z}=\overline{p}=\overline{r}=$ $\left(\begin{array}{c}0\\ 0\end{array}\right).$ Therefore, weak duality theorem is satisfied.

Furthermore,

(i)

${\nabla }_{p^1{p}^1}{g}^1(\overline{x},\overline{y},\overline{p})=$$\left(\begin{array}{cc}2& 0\\ 0& 2\end{array}\right)$ is positive definite matrix

and

${\nabla }_{p^2{p}^2}{g}^2(\overline{x},\overline{y},\overline{p})=$$\left(\begin{array}{cc}-2& 0\\ 0& -2\end{array}\right)$ is negative definite matrix,

(ii)

$\{{\nabla }_{y^1}{f}^1(\overline{x},\overline{y})-{\overline{z}}^1+{\nabla }_{p^1}{g}^1(\overline{x},\overline{y},\overline{p}),{\nabla }_{y^2}{f}^2(\overline{x},\overline{y})-{\overline{z}}^2+{\nabla }_{p^2}{g}^2(\overline{x},\overline{y},\overline{p})\}=\left(\begin{array}{c}1\\ 1\end{array}\right),$

(iii)

${({\overline{p}}^1)}^T\{{\nabla }_{y^1}{f}^1(\overline{x},\overline{y})-{\overline{z}}^1+{\nabla }_{p^1}{g}^1(\overline{x},\overline{y},\overline{p})\}=0⟹{\overline{p}}^1=0$ and

${\overline{y}}^2[{\nabla }_{y^2}{g}^2({\overline{x}}^2,{\overline{y}}^2,{\overline{p}}^2)-{\nabla }_{p^2}{g}^2({\overline{x}}^2,{\overline{y}}^2,{\overline{p}}^2)+{\nabla }_{y^2{y}^2}{f}^2({\overline{x}}^2,{\overline{y}}^2){\overline{p}}^2]=0⟹{\overline{p}}^2=0.$

(As $\overline{p}$ initially taken as zero).

(iv)

$h^i(\overline{x},\overline{y},0)=g^i(\overline{x},\overline{y},0)$, ${\nabla }_x{h}^i(\overline{x},\overline{y},0)={\nabla }_r{g}^i(\overline{x},\overline{y},0)$, ${\nabla }_{y^1}{g}^1({\overline{x}}^1,{\overline{y}}^1,0)={\nabla }_{p^1}{g}^1({\overline{x}}^1,{\overline{y}}^1,0),$ for $i=1,2$.

Therefore, all the assumptions of strong duality theorem (Theorem 2) are also satisfied. Now objective function value is equal to $\mathbf{0}$.

6. Special Cases

(i)

Let $C_1={{\mathbb{R}}^n}_{+}$, $C_2={{\mathbb{R}}^h}_{+}$, $|B_1|=0$, $|A_1|=0$, $E_1=0$ and $D_1=0$ in (MHP) and (MHD). Then, we get the programs proposed by Verma and Gulati [21].

(ii)

If $C_1={{\mathbb{R}}^n}_{+}$, $C_3={{\mathbb{R}}^h}_{+}$, removed the higher-order and non-differentiable terms and omission of inequalities (6), (7), (13), and (14), then we get the model presented by Chandra et al. [9].

(iii)

Let $C_1={{\mathbb{R}}^n}_{+}$ and $C_3={{\mathbb{R}}^h}_{+}$, $|A_2|=0,|B_2|=0$, $p=0$ and $r=0$. Then, our programs are reduced to the programs presented in [25].

(iv)

If $C_1=-C_1$, $C_3=-C_3$, $|B_2|=0$, $|A_2|=0$, $E_1=0$, $D_1=0$ and omission of inequalities (7) and (14), then we get the dual programs discussed in [26].

(v)

If $C_2=-C_2$, $C_4=-C_4$, $|B_1|=0$, $|A_1|=0$, $E_2=0$, $D_2=0$ and omission of inequalities (6) and (13), then we get the dual programs studied in [26].

(vi)

If $C_2=-C_2$, $C_4=-C_4$, $|B_1|=0$, $|A_1|=0$, $E_2=0$, $D_2=0$, $g(x,y,p)=(1/2)p^T{\nabla }_{yy}f(x,y)p$ and $h(u,v,r)=(1/2)r^T{\nabla }_{xx}f(u,v)r$, and omission of inequalities (6) and (13), then we get the dual programs is equal to obtained in [27].

For $C_2={{\mathbb{R}}^n}_{+}$, $C_4={{\mathbb{R}}^h}_{+}$, and omission of inequalities (6) and (13), we get the following special cases (vii) to (viii):

(vii)

If $|B_1|=0$ and $|A_1|=0$, then we get the programs considered in [17].

(viii)

Let $|B_1|=0$, $|A_1|=0$, $g(x,y,p)=(1/2)p^T{\nabla }_{yy}f(x,y)p$ and $h(u,v,r)=(1/2)r^T{\nabla }_{xx}f(u,v)r$. Then, our programs become the programs presented in [16].

For $C_1={{\mathbb{R}}^n}_{+}$, $C_3={{\mathbb{R}}^h}_{+}$, and omission of inequalities (7) and (14), we get the following special cases (ix) to (xiii):

(ix)

If $g(x,y,p)=(1/2)p^T{\nabla }_{yy}f(x,y)p$ and $h(u,v,r)=(1/2)r^T{\nabla }_{xx}f(u,v)r$, then we get the programs obtained in [15].

(x)

If $|B_2|=0$, $|A_2|=0$, $g(x,y,p)=(1/2)p^T{\nabla }_{yy}f(x,y)p$ and $h(u,v,r)=(1/2)r^T{\nabla }_{xx}f(u,v)r$, then we get the dual programs derived in [19].

(xi)

If $|B_2|=0$, $|A_2|=0$, $E_1=0$, $D_1=0$, $g(x,y,p)=(1/2)p^T{\nabla }_{yy}f(x,y)p$ and $h(u,v,r)=(1/2)r^T{\nabla }_{xx}f(u,v)r$, then we get the dual programs studied in [4].

(xii)

If $|B_2|=0$, $|A_2|=0$, $g(x,y,p)=(1/2)p^T{\nabla }_{yy}f(x,y)p$, $h(u,v,r)=(1/2)r^T{\nabla }_{xx}f(u,v)r$, $E_1=0$ and $D_1=0$, then we get the dual programs presented in [28].

(xiii)

Let $C_1=-C_1$, $C_3=-C_3$, $|A_2|=0,|B_2|=0$, $p=0,r=0$, $E_1=0$ and $D_1=0$. Then, we obtain symmetric dual programs [29,30].

7. Conclusions

A new mixed type nondifferentiable higher-order symmetric dual programs over cones has been formulated. It is also shown the uniqueness of higher-order $\mathcal{F}$-convexity/higher-order $\mathcal{F}$-pseudoconvexity by a non-trivial example. Under these assumptions, the weak, strong, and converse duality theorems have been derived, and verified by an example. Self-duality has been also discussed. The presented programs and results generalize some existing duals and their corresponding theorems appeared in the literature. The symmetric duality between (MHP) and (MHD) can be extended for fractional and multiobjective programming problems over cones.