Modulated Viscosity-Dependent Parameters for MHD Blood Flow in Microvessels Containing Oxytactic Microorganisms and Nanoparticles
Abstract
:1. Introduction
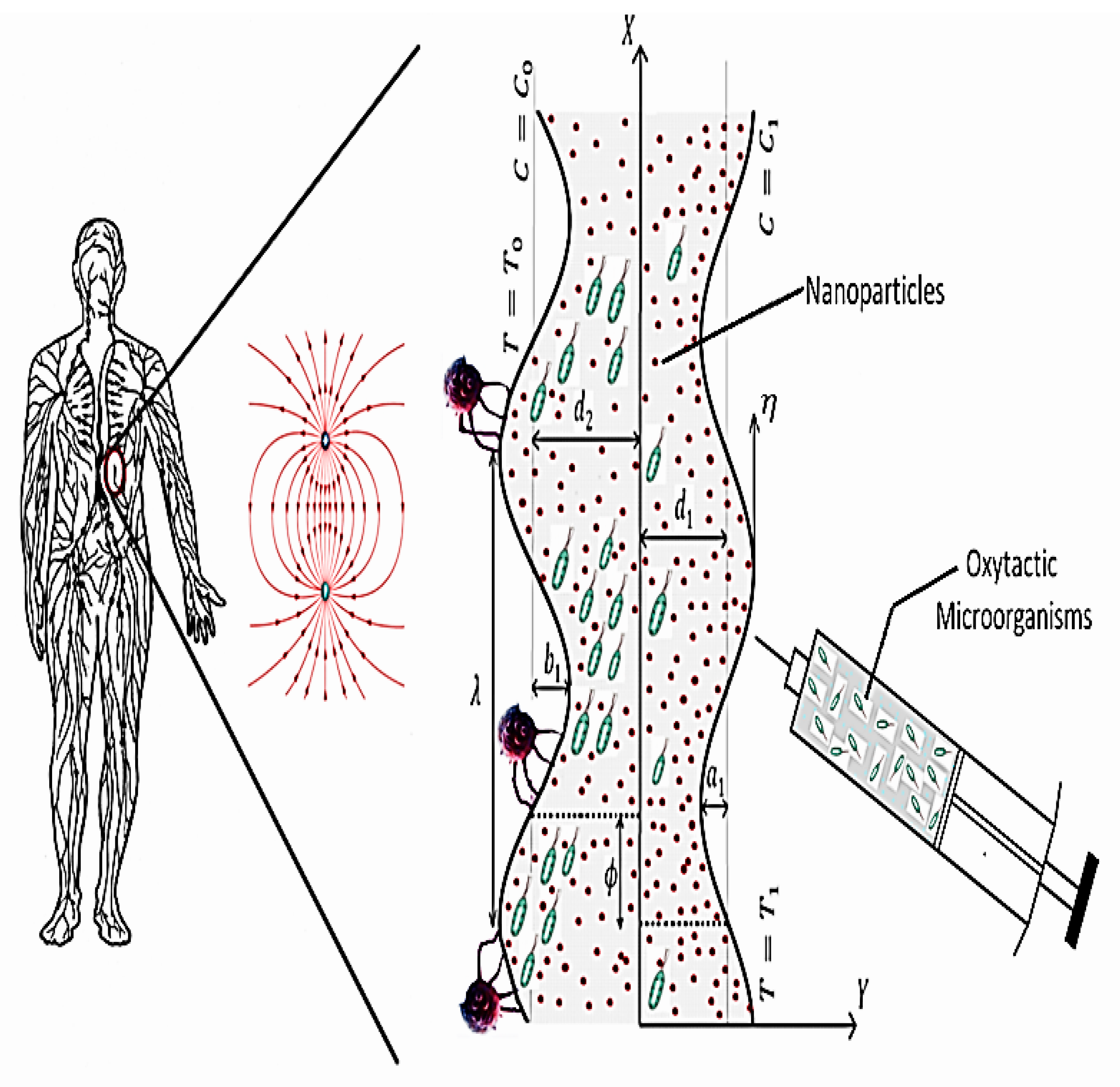
2. Physical Description
2.1. The Carreau–Yasuda Model
2.2. Model Formulation
2.3. Governing Equations
2.4. Transformations and Simplifications
2.5. Variable Non-Dimensional Parameters
2.6. Boundary Conditions
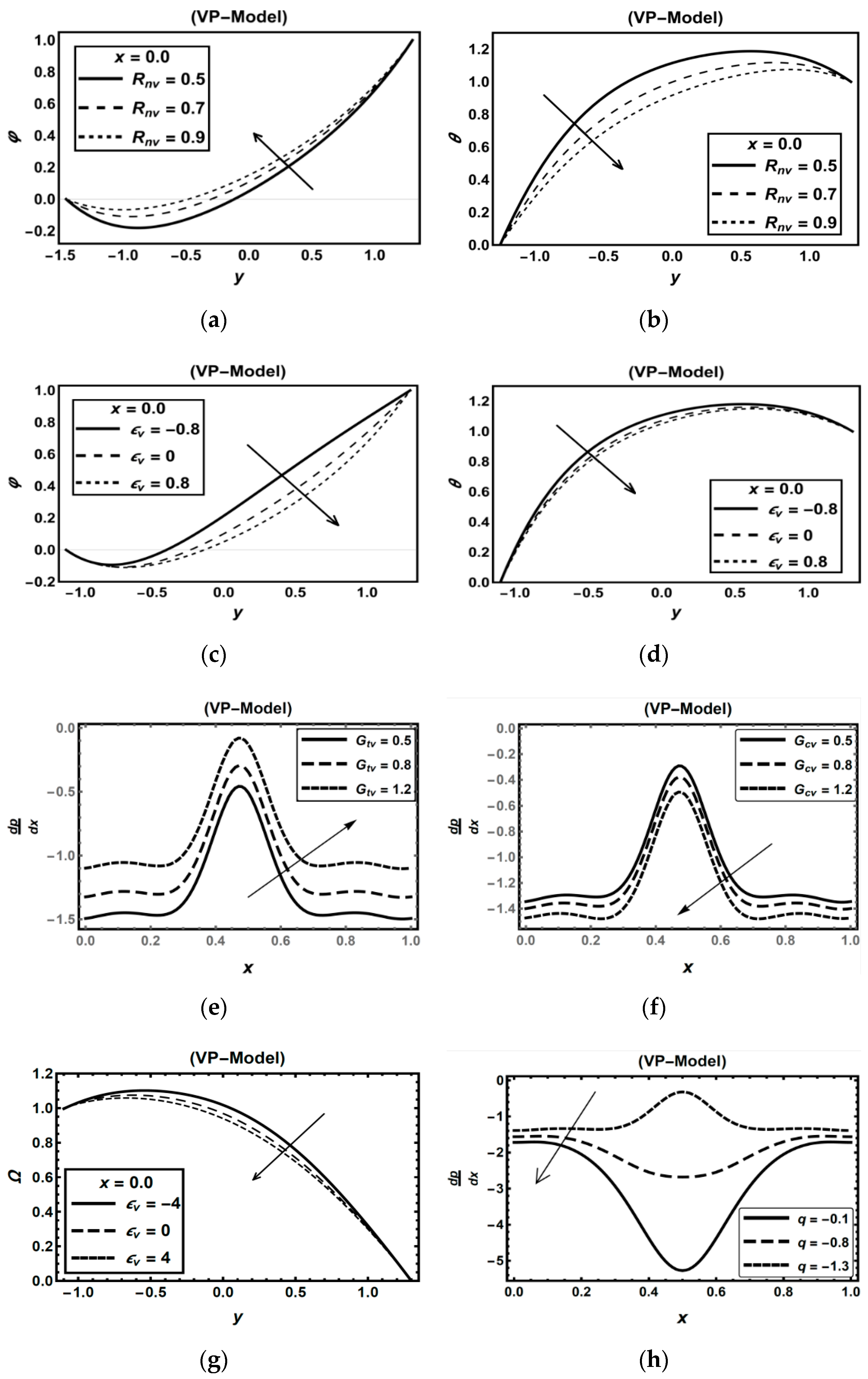
3. Results and Discussion
- (1)
- Show that the VP-Model is more reliable than the CP-Model.
- (2)
- Investigate the features of adding oxytactic microorganisms (as oxygen repellents) to the upstream of the blood flow.
- (3)
- Examine the magnetic field parameters’ role in the presence/absence of the Joule heating effect for the VP-Model case.
- (4)
- Discuss the theoretical significance of the current study’s ambient parameters supported with experimental agreements and theoretical studies whenever possible.
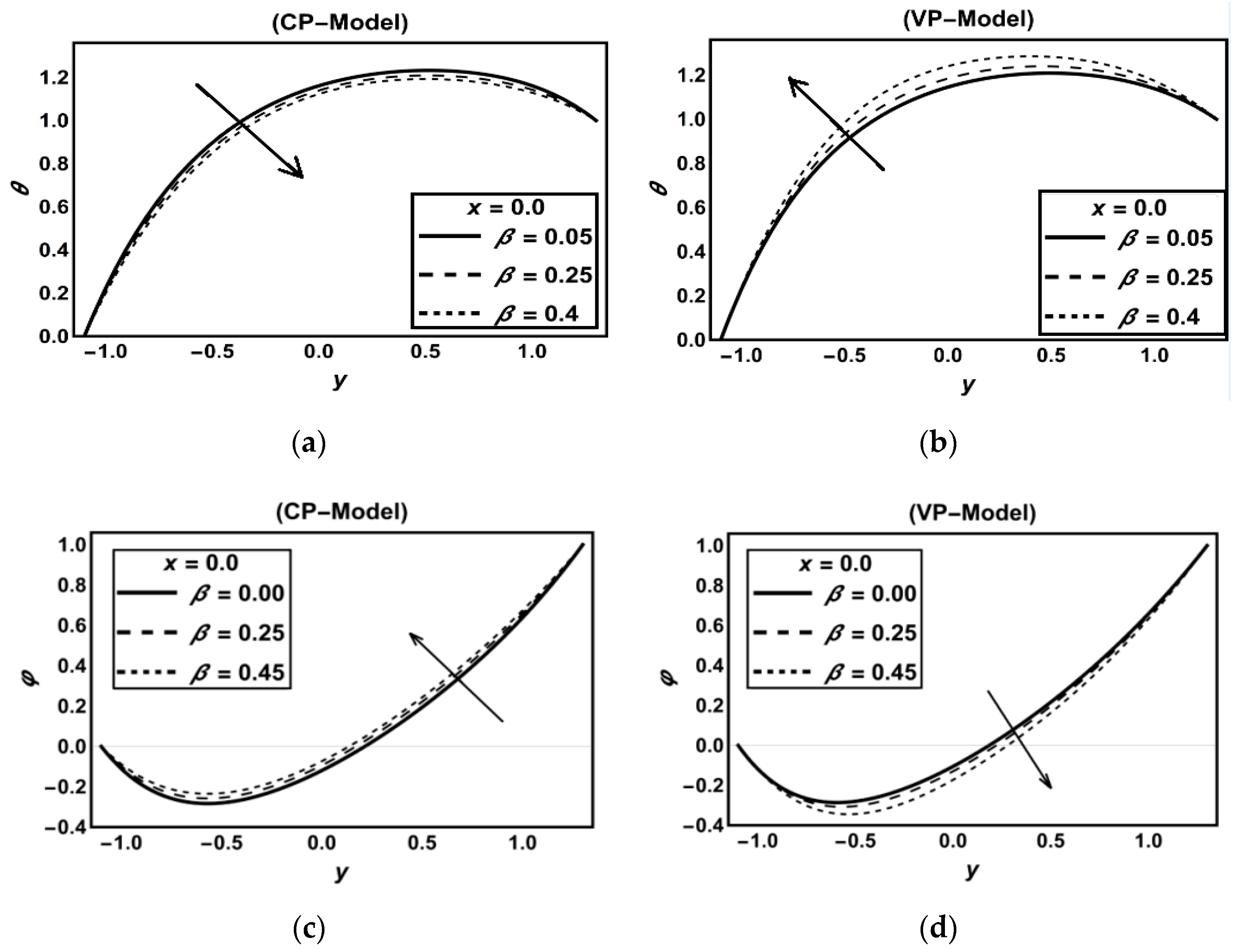
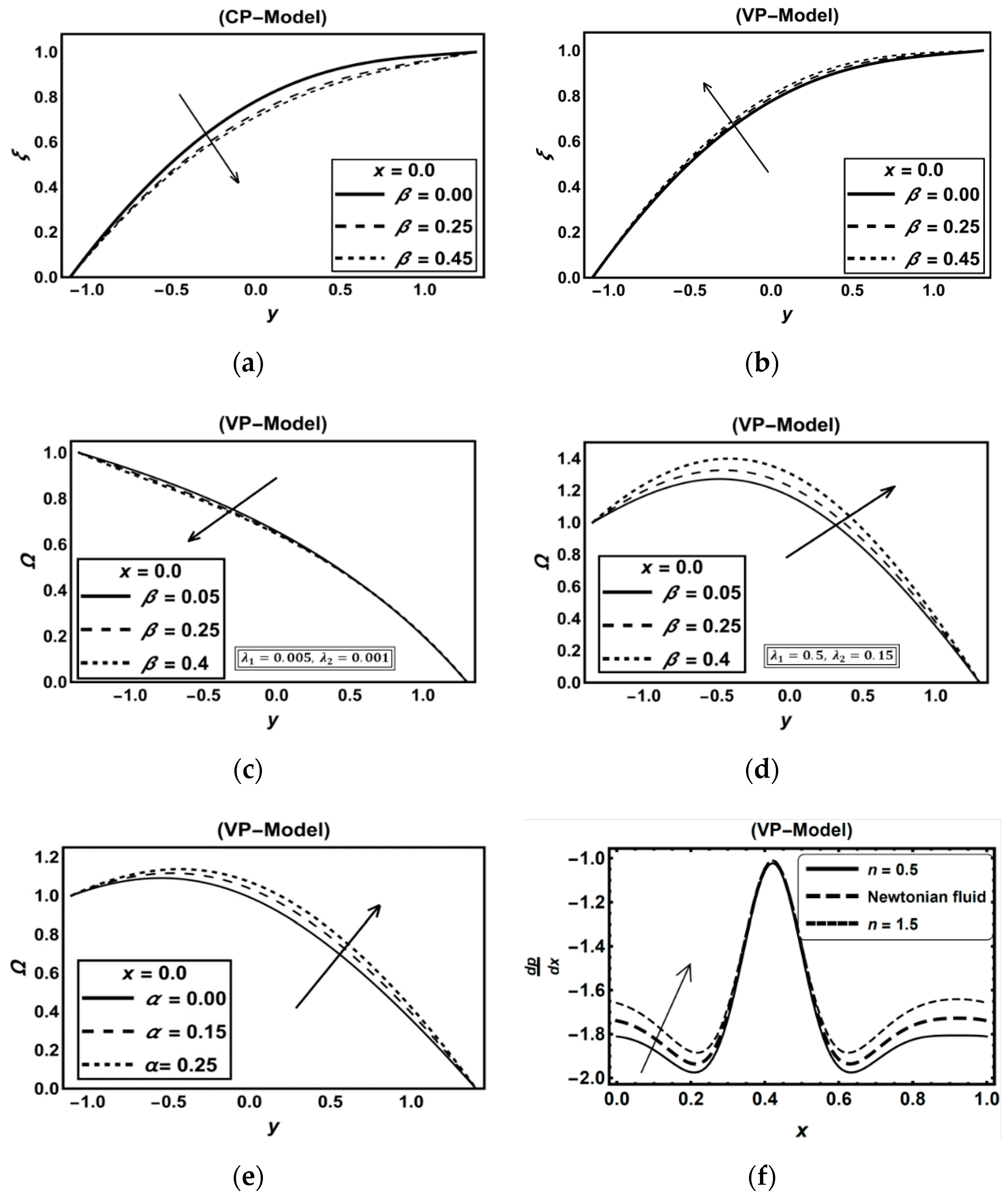
3.1. CP-Model Versus VP-Model
Discussion on Some Previous Works
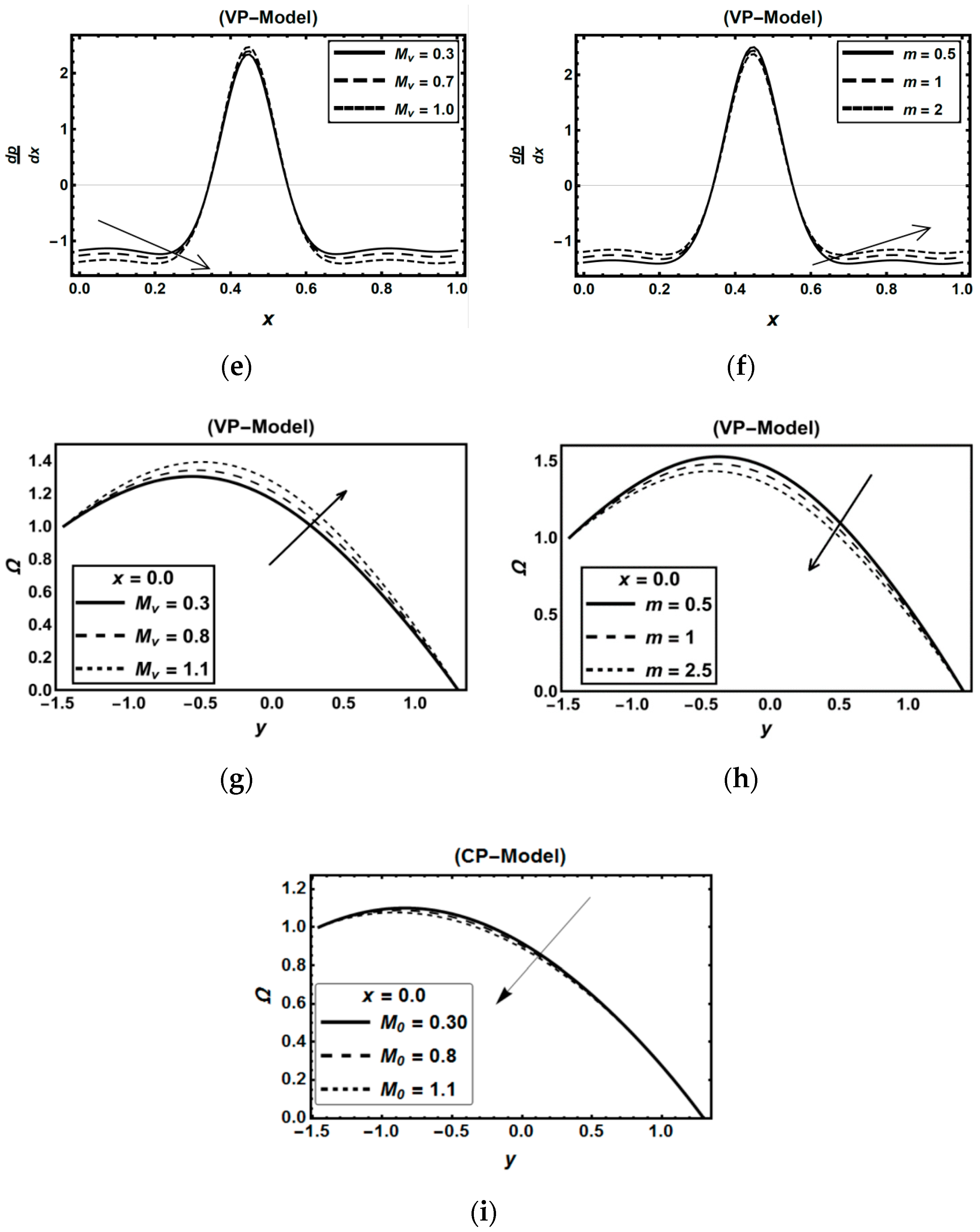
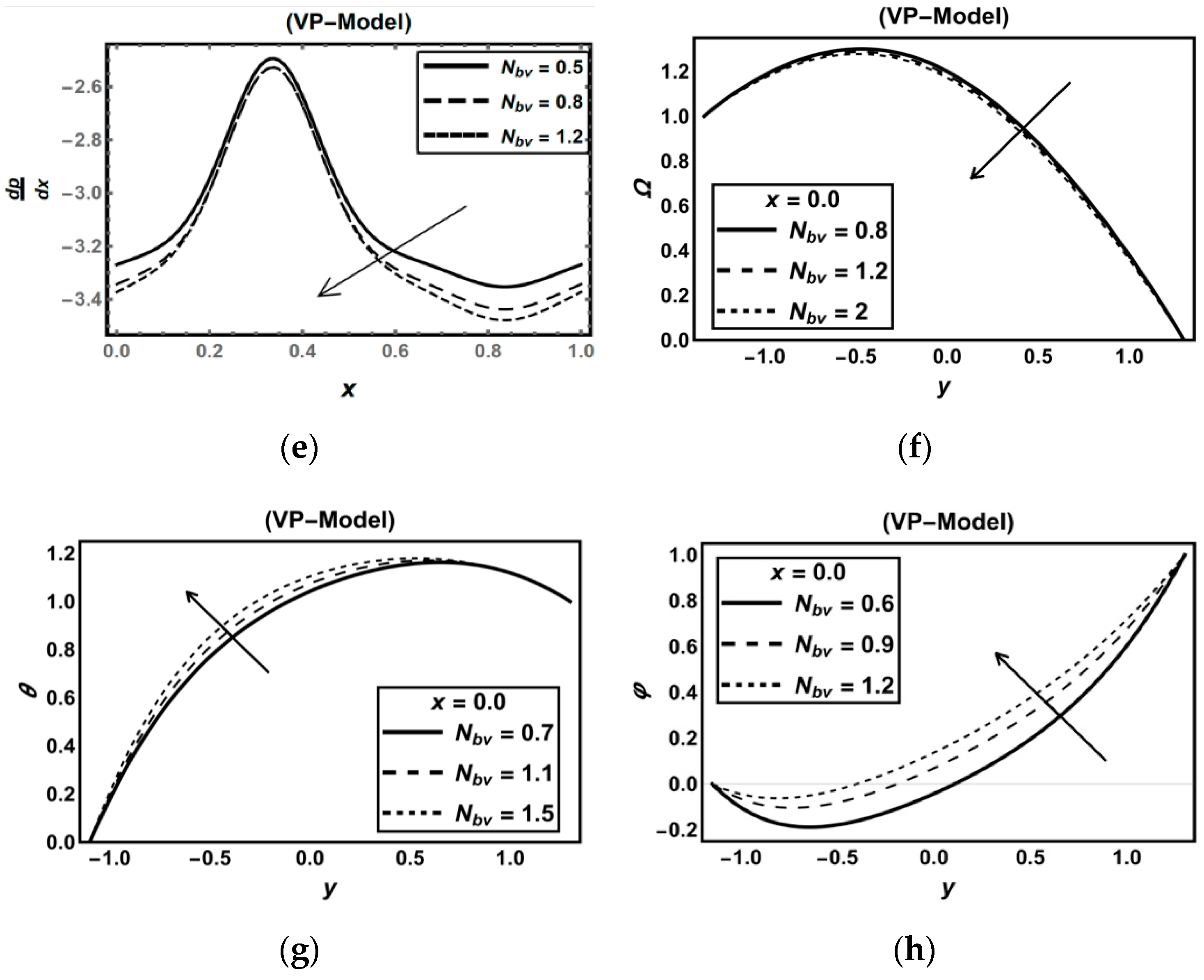
3.2. Oxytactic Microorganism Parameters
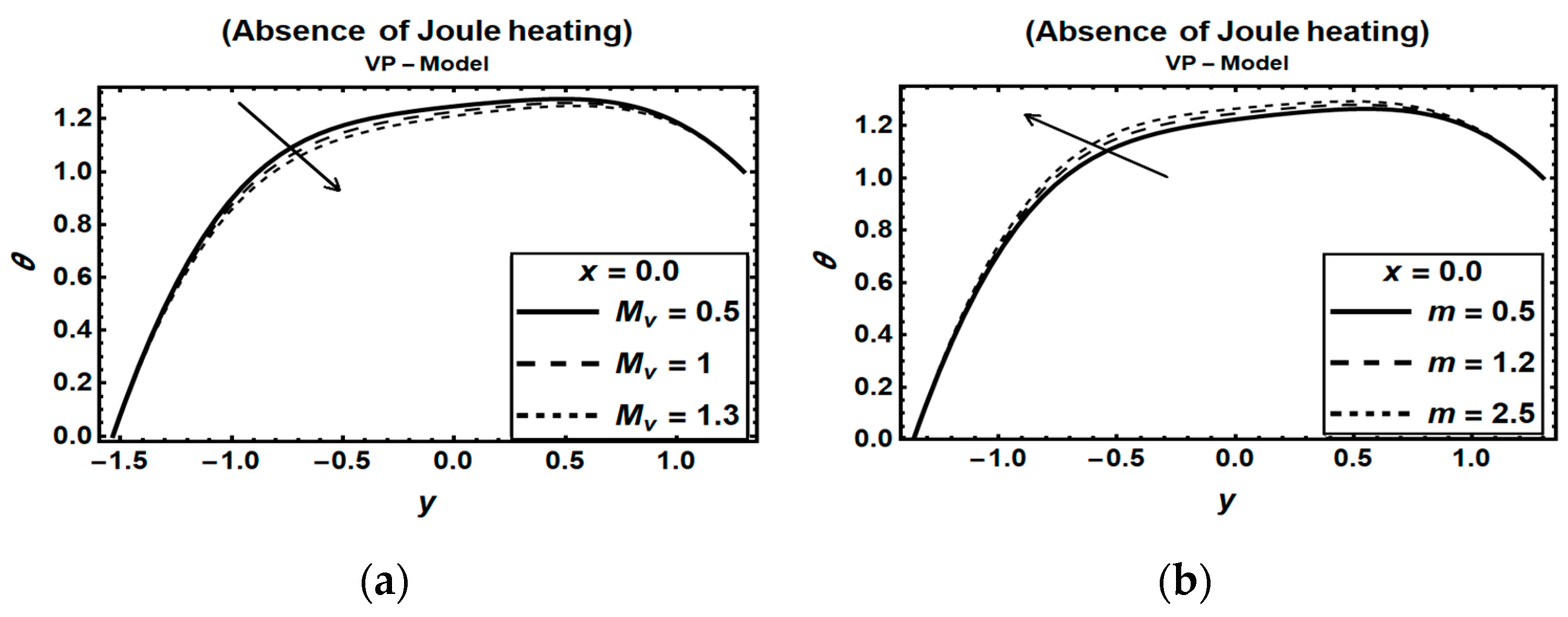
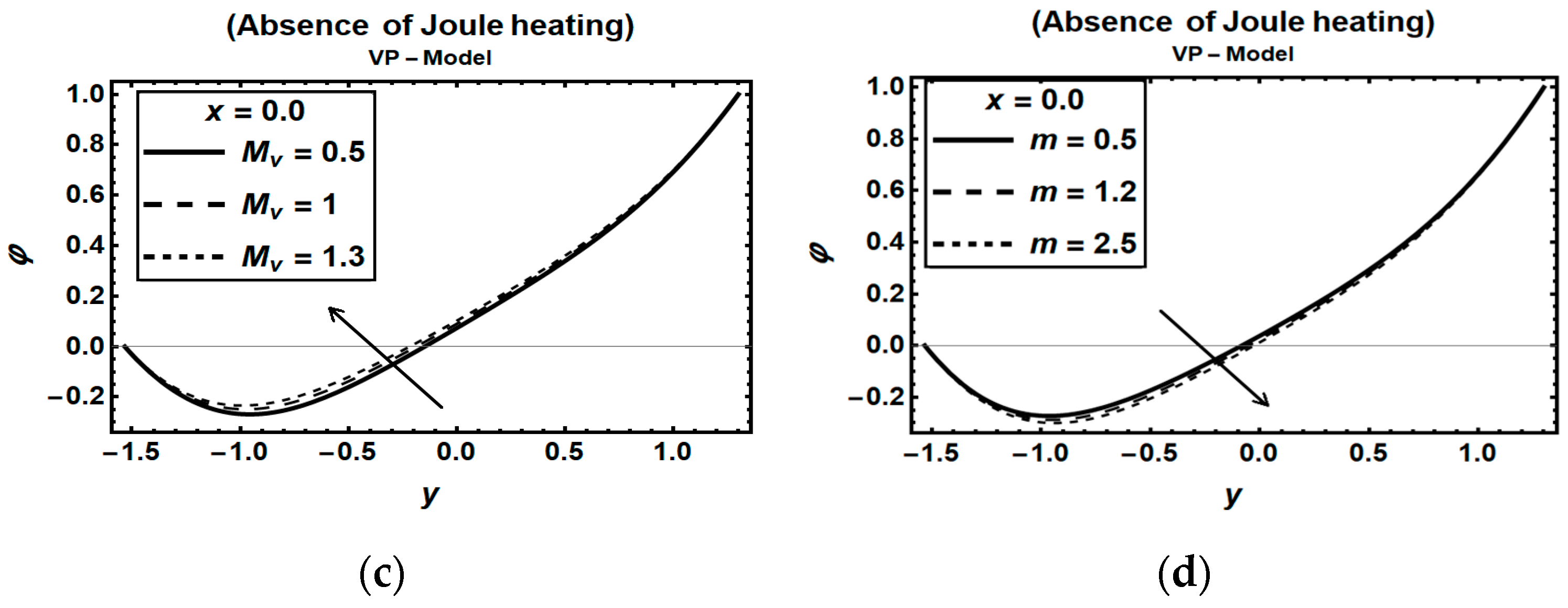
3.3. Magnetic Field Parameters and Joule Heating Effects
3.4. Role of Nanoparticles Parameters
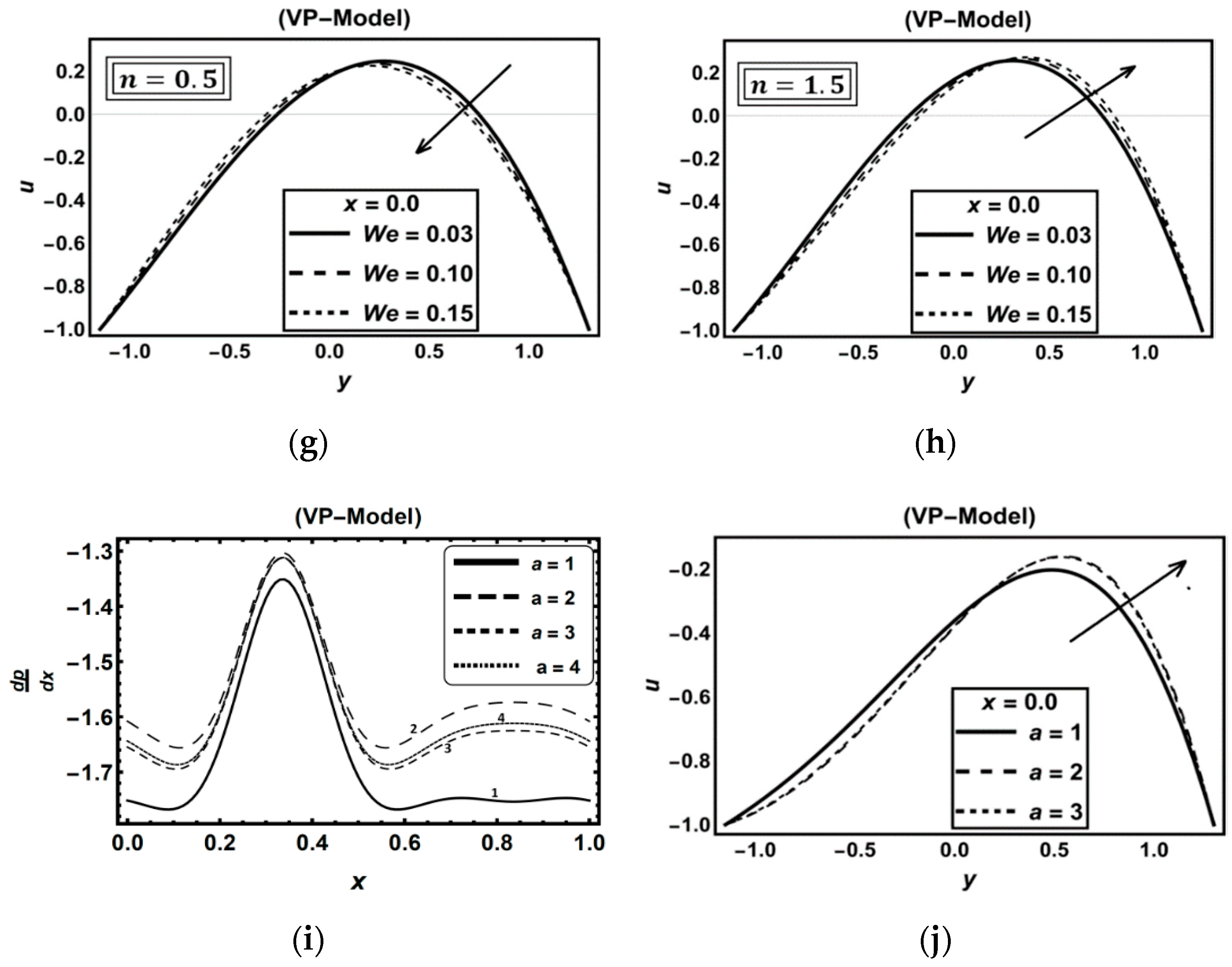
3.5. Role of Carreau–Yasuda Fluid Parameters
3.6. Role of Thermal Radiation, Buoyancy, Chemical Reaction and Flow Rate Effects
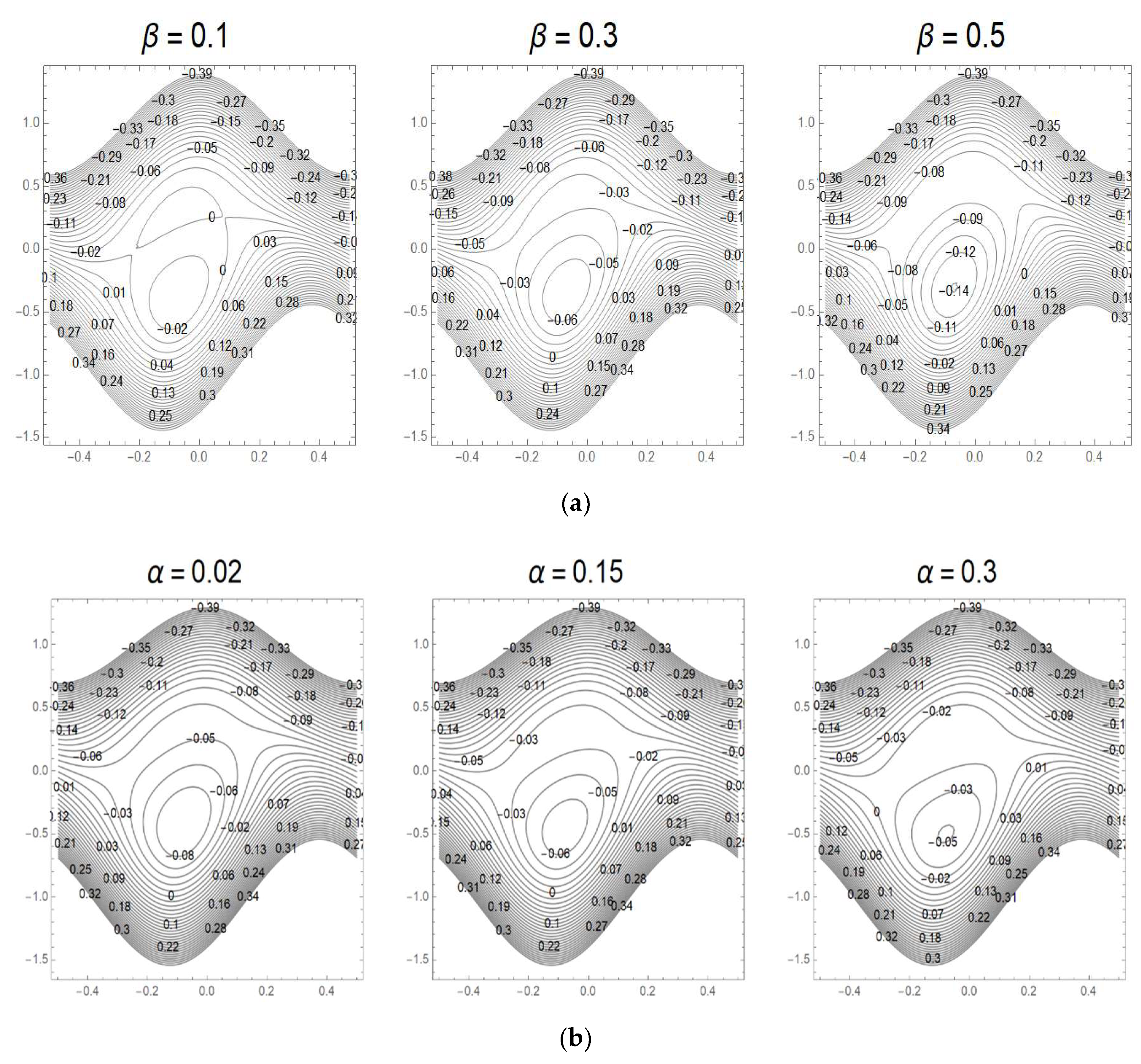
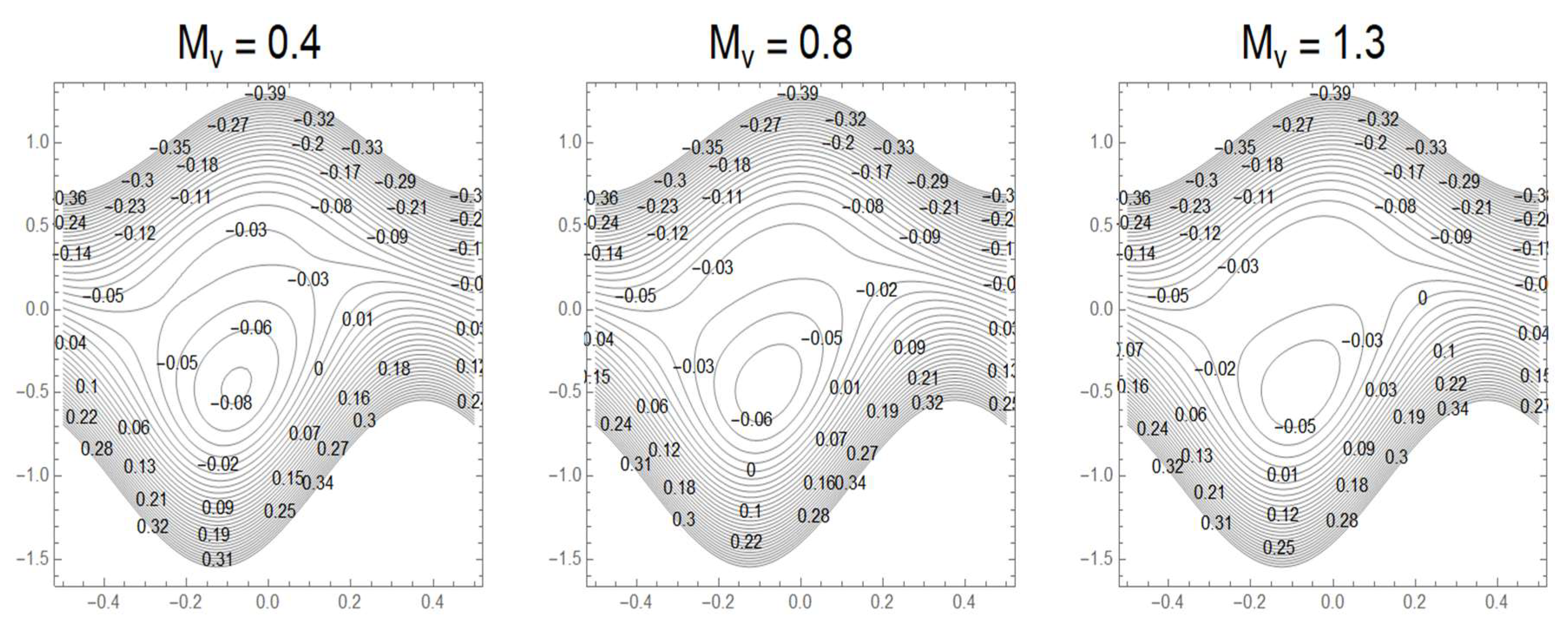
3.7. Streamlines and Trapping
4. Conclusions
- (1)
- We have confirmed the VP-Model’s reliability over the CP-Model by referring to physical phenomena and past experimental results.
- (2)
- Disregarding the Joule heating effects in modeling MHD flow problems in the presence of heat and mass transfer will result in unrealistic outcomes.
- (3)
- Microorganism density is an increasing function ofand whereas it decreases with increasing and.
- (4)
- Rising in oxygen concentrations causes the microorganism density to increase in the direction towards the hypoxic tumor regions; even a reduction in blood viscosity is regarded.
- (5)
- The impacts ofon the temperature and nanoparticle volume fraction profiles are quite the opposite. On the other hand, the influences of on the nanoparticle volume fraction and temperature profiles are similar.
- (6)
- In the presence of a generative chemical reaction, the temperature, nanoparticle concentration, and microorganism density profiles are boosted, but the opposite trend occurred for a destructive chemical reaction.
- (7)
- It is remarkable to observe that the impact of on velocity in blood shear-thinning is quite the opposite of the case of blood shear-thickening.
- (8)
- Surprisingly, it is noticed that the pressure gradient starts showing an alternating increase/decrease behavior upon substituting positive constitutive integer values for the Carreau–Yasuda index parameter The maximum pressure gradient occurs for the case of the Carreau fluid).
- (9)
- The number and size of the trapped bolus decreases with an increase in and , while increasing with an increase of
Author Contributions
Funding
Conflicts of Interest
References
- Nakhchi, M.E.; Hatami, M.; Rahmati, M. A numerical study on the effects of nanoparticles and their fins on performance improvement of phase change thermal energy storage. Energy 2021, 215, 119112. [Google Scholar]
- Nakhchi, M.E.; Esfahani, J.A. CFD approach for two-phase CuO nanofluid flow through heat exchangers enhanced by double perforated louvered strip insert. Powder Technol. 2020, 367, 877–888. [Google Scholar] [CrossRef]
- Nakhchi, M.E.; Rahmati, M.T. Entropy generation of turbulent Cu-water nanofluid flows inside thermal systems equipped with transverse-cut twisted turbulators. J. Therm. Anal. Calorim. 2019, 138, 1423–1436. [Google Scholar] [CrossRef]
- Ostwald, W. Ueber die rechnerische Darstellung des Strukturgebietes der Viskositat. Kolloid Z. 1929, 47, 176–187. [Google Scholar] [CrossRef]
- Carreau, P.J. Rheological equations from molecular network theories. Trans. Soc. Rheol. 1972, 16, 99–127. [Google Scholar] [CrossRef]
- Yasuda, K. Investigation of the Analogies between Viscometric and Linear Viscoelastic Properties of Polystyrene Fluids. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 1979. [Google Scholar]
- Nitesh, K.; Abdul-Khader, S.M.; Pai, B.R.; Kyriacou, P.A.; Khan, S.H.; Prakashinic, K. Computational fluid dynamic study on effect of Carreau-Yasuda and Newtonian blood viscosity models on hemodynamic parameters. J. Comput. Methods Sci. Eng. 2019, 19, 465–477. [Google Scholar]
- Gijsen, F.H.; van de Vosse, F.N.; Janssen, J.D. Wall shear stress in backward-facing step flow of a red blood cell suspension. Biorheology 1998, 35, 263–279. [Google Scholar]
- Alshare, A.; Tashtoush, B.; El-Khalil, H.H. Computational modeling of non-Newtonian blood flow through stenosed arteries in the presence of magnetic field. J. Biomech. Eng. 2011, 135, 114503. [Google Scholar] [CrossRef]
- Hong, H.; Song, J.M.; Yeom, E. Variations in pulsatile flow around stenosed microchannel depending on viscosity. PLoS ONE 2019, 14, e0210993. [Google Scholar] [CrossRef] [Green Version]
- Bernsdorf, J.; Wang, D. Non-Newtonian blood flow simulation in cerebral aneurysms. Comput. Math. Appl. 2009, 58, 1024–1029. [Google Scholar] [CrossRef] [Green Version]
- Hayat, T.; Abbasi, M.F.; Alsaedi, A.; Alsaedi, F. Hall and ohmic heating effects on the peristaltic transport of a carreau-yasuda fluid in an asymmetric channel. Z. Naturforsch. 2014, 69, 43–51. [Google Scholar] [CrossRef]
- Hayat, T.; Shafiquea, M.; Tanveera, A.; Alsaedi, A. Hall and ion slip effects on peristaltic flow of Jeffrey nanofluid with Joule heating. J. Magn. Magn. Mater. 2016, 407, 51–59. [Google Scholar] [CrossRef]
- Ramesh, K. Influence of heat and mass transfer on peristaltic flow of couple stress fluid through porous medium in the presence of inclined magnetic field in an asymmetric channel. J. Mol. Liq. 2016, 219, 256–271. [Google Scholar]
- Abbasi, F.M.; Hayat, T.; Alsaedi, A. Numerical analysis for MHD peristaltic transport of Carreau-Yasuda fluid in a curved channel with hall effects. J. Mol. Liq. 2015, 382, 104–110. [Google Scholar] [CrossRef]
- Eldabe, N.T.; Elogail, M.A.; Elshaboury, S.M.; Hasan, A.A. Hall effects on the peristaltic transport of Williamson fluid through a porous medium with heat and mass transfer. Appl. Math. Mod. 2016, 40, 315–328. [Google Scholar] [CrossRef]
- Hayat, T.; Farooq, S.; Alsaedi, A.; Ahmed, B. Hall and radial magnetic effects on radiative peristaltic flow of Carreau-Yasuda fluid in a channel with convective heat and mass transfer. J. Magn. Magn. Mater. 2016, 412, 207–216. [Google Scholar] [CrossRef]
- Bhatti, M.M.; Rashidi, M.M. Study of heat and mass transfer with Joule heating on magnetohydrodynamic (MHD) peristaltic blood flow under the influence of Hall effect. Propuls. Power Res. 2017, 6, 177–185. [Google Scholar] [CrossRef]
- Hayat, T.; Naseema, A.; Rafiq, M.; Alsaadi, F.E. Hall and Joule heating effects on peristaltic flow of Powell–Eyring liquid in an inclined symmetric channel. Results Phys. 2017, 7, 518–528. [Google Scholar]
- Ramesh, K.; Tripathi, D.; Beg, O.A.; Kadir, A. Slip and hall current effects on Jeffrey fluid suspension flow in a peristaltic hydromagnetic blood micropump. Iran. J. Sci. Technol. Trans. Mech. Eng. 2019, 43, 675–692. [Google Scholar] [CrossRef]
- Rafiq, M.; Yasmin, H.; Hayat, T.; Alsaadi, F. Effect of hall and ion-slip on the peristaltic transport of a nanofluid: A biomedical application. Chin. J. Phys. 2019, 60, 208–227. [Google Scholar] [CrossRef]
- Abdelsalam, S.I.; Bhatti, M.M. New insight into AuNP applications in Tumour treatment and cosmetics through wavy annuli at the nanoscale. Sci. Rep. 2019, 9, 260. [Google Scholar] [CrossRef] [PubMed]
- Hayat, T.; Abbasi, F.M.; Ahmed, B.; Alsaedi, A. Mhd mixed convection peristaltic flow with variable viscosity and thermal conductivity. Sains Malays. 2014, 43, 1583–1590. [Google Scholar]
- Hussain, Q.; Hayat, T.; Ashgar, S.; Ahmed, B.; Alsaadi, F. Heat and mass transfer analysis in variable viscosity peristaltic flow with hall current and ion-slip. J. Mech. Med. Biol. 2016, 16, 1650047. [Google Scholar]
- Alvi, N.; Latif, T.; Hussain, Q.; Asghar, S. Peristalsis of nonconstant viscosity Jeffrey fluid with nanoparticles. Results Phys. 2016, 6, 1109–1125. [Google Scholar] [CrossRef] [Green Version]
- Abbasi, F.M.; Hayat, T.; Ahmad, B. Hydromagnetic peristaltic transport of variable viscosity fluid with heat transfer and porous medium. Appl. Math. Inf. Sci. 2016, 10, 2173–2181. [Google Scholar] [CrossRef]
- Hayat, T.; Riaz, A.; Tanveer, A.; Alsaedi, A. Peristaltic transport of tangent hyperbolic fluid with variable viscosity. Therm. Sci. Eng. Prog. 2018, 6, 217–225. [Google Scholar] [CrossRef]
- Elogail, M.A.; Elshekhipy, A.A. Approximate analytical solutions to non-linear peristaltic flow with temperature-dependent viscosity parameters: Application of multi-step differential transform method (MsDTM). Can. J. Phys. 2018, 96, 287–299. [Google Scholar] [CrossRef]
- Ordal, G.W.; Goldman, D.J. Chemotactic repellents of Bacillus subtilis. J. Mol. Biol. 1976, 100, 103–108. [Google Scholar]
- Zhulin, I.B.; Bespalov, V.A.; Johnson, M.S.; Taylor, B.L. Oxygen taxis and proton motive force in Azospirillum brasilense. J. Bacteriol. 1996, 178, 5199–5204. [Google Scholar] [CrossRef] [Green Version]
- Shioi, J.; Dang, C.V.; Taylor, B.L. Oxygen attractant and repellent in Bacterial chemotaxis. J. Bacteriol. 1987, 169, 3118–3123. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhang, Z.; Li, Z.; Yu, W.; Li, K.; Xie, Z.; Shi, Z. Propulsion of liposomes using bacterial motors. Nanotechnology 2013, 24, 185103. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Martel, S. Swimming microorganisms acting as nanorobots versus artificial nanorobotic agents: A perspective view from an historical retrospective on the future of medical nanorobotics in the largest known three-dimensional biomicrofluidic networks. Biomicrofluidics 2016, 10, 021301. [Google Scholar] [CrossRef] [PubMed]
- Dogra, N.; Izadi, H.; Vanderlick, T. Micro-motors: A motile bacteria based system for liposome cargo transport. Sci. Rep. 2016, 6, 29369. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Felfoul, O.; Mohammadi, M.; Taherkhani, S.; Lanauze, D.; Zhong, X.Y.; Loghin, D.; Essa, S.; Jancik, S.; Houle, D.; Lafleur, M.; et al. Magneto-aerotactic bacteria deliver drug-containing nanoliposomes to tumour hypoxic regions. Nat. Nanotechnol. 2016, 11, 941–947. [Google Scholar] [CrossRef]
- Taktikos, J. Modeling the Random Walk and Chemotaxis of Bacteria: Aspects of Biofilm Formation. Doctoral Thesis, Technische Universität Berlin, Berlin, Germany, 2013. [Google Scholar]
- Charteris, N.; Khain, E. Modeling chemotaxis of adhesive cells: Stochastic lattice approach and continuum description. New. J. Phys. 2014, 16, 025002. [Google Scholar] [CrossRef] [Green Version]
- Hillen, T.; Painter, K.J. A user’s guide to PDE models for chemotaxis. J. Math. Biol. 2008, 58, 183–217. [Google Scholar] [CrossRef]
- Kuznetsov, A.V. Non-oscillatory and oscillatory nanofluid bio-thermal convection in a horizontal layer finite depth. Eur. J. Mech. B/Fluids 2011, 30, 156–165. [Google Scholar] [CrossRef]
- Amirsom, N.A.; Uddin, M.J.; Basir, M.F.; Kadir, A.; Bég, O.A.; Ismail, A.I. Computation of melting dissipative magnetohydrodynamic nanofluid bioconvection with second-order slip and variable thermophysical properties. Appl. Sci. 2019, 9, 2493. [Google Scholar] [CrossRef] [Green Version]
- Kim, Y.-C. Diffusivity of bacteria. Korean J. Chem. Eng. 1996, 13, 282–287. [Google Scholar]
- Hayat, T.; Aslam, N.; Khan, M.I.; Alsaedi, A. Mixed convective peristaltic flow of Carreau-Yasuda fluid in an inclined symmetric channel. Microsyst. Technol. 2019, 25, 609–620. [Google Scholar] [CrossRef]
- Eldabe, N.T.; Abo-Seida, O.M.; Abo-Seliem, A.A.; Elshekhipy, A.A.; Hegazy, N. Magnetohydrodynamic peristaltic flow of Williamson nanofluid with heat and mass transfer through a non-Darcy porous medium. Microsyst. Technol. 2018, 24, 3751–3776. [Google Scholar] [CrossRef]
- Eldabe, N.T.; Gabr, M.E.; Zaher, S.A. Two dimensional boundary layer flow with heat and mass transfer of magneto hydrodynamic non-Newtonian nanofluid through porous medium over a semi-infinite moving plate. Microsyst. Technol. 2018, 24, 2919–2928. [Google Scholar] [CrossRef]
- Mekheimer, Kh.S.; Zaher, A.Z.; Hasona, W.M. Entropy of AC electro-kinetics for blood mediated gold or copper nanoparticles as a drug agent for thermotherapy of oncology. Chin. J. Phys. 2020, 65, 123–138. [Google Scholar] [CrossRef]
- Kim, N.; Reddy, J.N. 3-D least-squares finite element analysis of flows of generalized Newtonian fluids. J. Nonnewton Fluid Mech. 2019, 266, 143–159. [Google Scholar] [CrossRef]
- Morrison, F.A. Understanding Rheology; Oxford University Press: New York, NY, USA, 2001; pp. 225–256. [Google Scholar]
- Miao, L.; Massoudi, M. Effects of shear dependent viscosity and variable thermal conductivity on the flow and heat transfer in a slurry. Energies 2015, 8, 11546–11574. [Google Scholar] [CrossRef] [Green Version]
- Elogail, M.A. Comments on “ ’combined effects of magnetohydrodynamic and temperature-dependent viscosity on peristaltic flow of Jeffrey nanofluid through a porous medium: Application to oil refinement’ by W.M. Hasona, A.A. El-Shekhipy and M.G. Ibrahim, International Journal of Heat and Mass Transfer, 2018, 126: 700–714”. Int. J. Heat Mass Transf. 2019, 128, 976–979. [Google Scholar]
- Mekheimer, Kh.S.; El-Kot, M.A. Influence of magnetic field and Hall currents on blood flow through a stenotic artery. Appl. Math. Mech. 2008, 29, 1093–1104. [Google Scholar] [CrossRef]
- Hayat, T.; Iqbal, R.; Tanveer, A.; Alsaedi, A. Mixed convective peristaltic transport of Carreau-Yasuda fluid in a tapered asymmetric channel. J. Mol. Liq. 2016, 223, 1100–1113. [Google Scholar] [CrossRef]
- Hayat, T.; Bilal, A.; Alsaedi, A.; Abbasi, F.M. Numerical study for peristalsis of Carreau-Yasuda nanomaterial with convective and zero mass flux condition. Results Phys. 2018, 8, 1168–1177. [Google Scholar]
- Khan, W.A.; Makinde, O.D. MHD nanofluid bioconvection due to gyrotactic microorganisms over a convectively heat stretching sheet. Int. J. Therm. Sci. 2014, 81, 118–124. [Google Scholar] [CrossRef]
- Kuznetsov, A.V. Nanofluid bioconvection in water-based suspensions containing nanoparticles and oxytactic microorganisms: Oscillatory instability. Nanoscale Res. Lett. 2011, 6, 100. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Buongiorno, J. Convective transport in nanofluids. J. Heat Trans. 2006, 128, 240–250. [Google Scholar] [CrossRef]
- Abd-elmaboud, Y.; Mekheimer, Kh.S.; Abdellateef, A.I. Thermal properties of couple-stress fluid flow in an asymmetric channel with peristalsis. J. Heat Trans. 2013, 135, 044502. [Google Scholar] [CrossRef]
- Demirel, Y. Nonequilibrium Thermodynamics, 3rd ed.; Elsevier: Amsterdam, The Netherlands, 2014; p. 82. [Google Scholar]
- Cengel, Y.A.; Cimbala, J.M.; Turner, R.H. Fundamentals of Thermal-Fluid Sciences, 5th ed.; Mc Graw Hill: New York, NY, USA, 2008; p. 428. [Google Scholar]
- Marini, C.P.; Russo, G.C.; Nathan, I.M.; Jurkiewicz, A.; McNiels, J. Effect of hematocrit on regional oxygen delivery and extraction in an adult respiratory distress syndrome animal model. Am. J. Surg. 2000, 180, 108–114. [Google Scholar] [CrossRef]
- Most, A.S.; Ruocco, N.A.; Gewirtz, H. Effect of a reduction in blood viscosity on maximal myocardial oxygen delivery distal to a moderate coronary stenosis. Circulation 1986, 74, 1085–1092. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Asha, S.K.; Sunitha, G. Effect of joule heating and MHD on peristaltic blood flow of Eyring–Powell nanofluid in a non-uniform channel. J. Taibah Univ. Sci. 2018, 13, 155–168. [Google Scholar] [CrossRef] [Green Version]



| Figure | Dimensionless Constant Parameters | |||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Figure 2a | 0.3 | 0.5 | 1.1 | 0.9 | - | 0.8 | 1.1 | 0.9 | 0.5 | 0.7 | 0.8 | 0.5 | 3 | 0.25 | 0.6 | 0.15 | 1 | 4 | 0.1 | 0.5 | 0.15 | 0.5 | 0.5 | |||
| Figure 2c | 0.3 | 0.5 | 1.1 | 0.9 | - | 0.8 | 1.1 | 0.9 | 0.5 | 0.6 | 0.6 | 0.5 | 1 | 0.25 | 0.6 | 0.25 | 1 | 4 | 0.15 | 0.3 | 0.1 | 0.5 | 0.2 | |||
| Figure 4i | 0.3 | 0.5 | 1.1 | - | 0.35 | 0.8 | 1.2 | 0.5 | 0.5 | 0.5 | 0.7 | 0.5 | 2 | 0.25 | 0.5 | 0.25 | 1 | 3 | 0.15 | 0.5 | 0.15 | 0.5 | 0.8 | |||
| Figure 7a | 0.3 | 0.5 | 1.1 | 0.7 | - | 0.85 | 0.8 | 0.8 | 0.6 | 0.6 | 0.8 | 0.5 | 1 | 0.25 | 0.7 | 0.25 | 1 | 3 | 0.15 | 0.5 | 0.1 | 0.5 | 0.4 | |||
| Figure | Dimensionless Variable Parameters | |||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Figure 2b | 0.3 | 0.5 | 1.1 | 0.9 | - | 0.8 | 1.1 | 0.9 | 0.5 | 0.7 | 0.8 | 0.5 | 3 | 0.25 | 0.6 | 0.15 | 1 | 4 | 0.1 | 0.5 | 0.15 | 0.5 | 0.5 | |||
| Figure 2d | 0.3 | 0.5 | 1.1 | 0.9 | - | 0.8 | 1.1 | 0.9 | 0.5 | 0.6 | 0.6 | 0.5 | 1 | 0.25 | 0.6 | 0.25 | 1 | 0 | 1 | 0.1 | 0.3 | 0.1 | 0.5 | 0.2 | ||
| Figure 3a | 0.3 | 0.5 | 1.0 | 0.8 | 0.15 | - | 1.2 | 0.8 | 0.9 | 0.7 | 0.7 | 0.5 | 2 | 0.25 | 0.6 | 0.2 | 1 | 3 | 0.1 | 0.5 | 0.15 | 0.5 | 0.4 | |||
| Figure 3b | 0.4 | 0.5 | 1.0 | 0.8 | 0.2 | 0.7 | 1.2 | 0.7 | 0.5 | 0.6 | - | 0.5 | 1 | 0.25 | 0.6 | 0.15 | 1 | 3 | 0.1 | 0.5 | 0.15 | 0.5 | 0.8 | |||
| Figure 3c | 0.3 | 0.5 | 1.1 | 0.9 | 0.2 | 0.7 | 1.3 | 0.8 | 0.6 | 0.6 | 0.8 | 0.5 | 1 | 0.25 | 0.7 | 0.15 | 1 | 3 | 0.15 | - | 0.15 | 0.5 | 0.4 | |||
| Figure 3d | 0.3 | 0.5 | 1.1 | 0.9 | 0.2 | 0.7 | 1.3 | 0.8 | 0.6 | 0.6 | 0.8 | 0.5 | 1 | 0.25 | 0.7 | 0.15 | 1 | 3 | 0.15 | - | 0.15 | 0.5 | 0.4 | |||
| Figure 3e | 0.3 | 0.5 | 1.1 | 0.9 | 0.2 | 0.7 | 1.3 | 0.8 | 0.6 | 0.6 | 0.8 | 0.5 | 1 | 0.25 | 0.7 | 0.15 | 1 | . | 3 | 0.15 | 0.5 | - | 0.5 | 0.4 | ||
| Figure 3f | 0.3 | 0.5 | 1.1 | 0.9 | 0.2 | 07 | 1.3 | 0.8 | 0.6 | 0.6 | 0.8 | 0.5 | 1 | 0.25 | 0.7 | 0.15 | 1 | 3 | 0.15 | 0.5 | - | 0.5 | 0.4 | |||
| Figure 3g | 0.3 | 0.5 | 1.1 | 0.8 | 0.4 | 0.7 | 1.2 | 0.9 | 0.7 | 0.7 | 0.5 | 0.5 | - | 0.25 | 0.6 | 0.15 | 1 | 4 | 0.15 | 0.5 | 0.15 | 0.5 | 0.8 | |||
| Figure 3h | 0.3 | 0.5 | 1.1 | 0.8 | 0.3 | 0.9 | 1.2 | 0.6 | 0.7 | 0.8 | 0.6 | 0.5 | - | 0.25 | 0.7 | 0.15 | 1 | 3 | 0.15 | 0.5 | 0.15 | 0.5 | 0.4 | |||
| Figure 4a | 0.3 | 0.5 | 1.1 | - | 0.25 | 0.9 | 1.1 | 0.7 | 0.6 | 0.6 | 0.8 | 0.5 | 1 | 0.25 | 0.7 | 0.2 | 1 | 3 | 0.15 | 0.5 | 0.15 | 0.5 | 0.5 | |||
| Figure 4b | 0.4 | 0.5 | 1.1 | - | 0.25 | 0.9 | 1.1 | 0.7 | 0.6 | 0.6 | 0.8 | 0.5 | 1 | 0.25 | 0.7 | 0.2 | 1 | 3 | 0.15 | 0.5 | 0.15 | 0.5 | 0.2 | |||
| Figure 4c | 0.3 | 0.5 | 1.1 | 0.9 | 0.25 | 0.9 | 1.1 | 0.7 | 0.6 | 0.6 | 0.8 | 0.5 | 1 | 0.25 | - | 0.2 | 1 | 3 | 0.15 | 0.5 | 0.15 | 0.5 | 0.2 | |||
| Figure 4d | 0.4 | 0.5 | 1.1 | 0.9 | 0.25 | 0.9 | 1.1 | 0.7 | 0.6 | 0.6 | 0.8 | 0.5 | 1 | 0.25 | - | 0.2 | 1 | . | 3 | 0.15 | 0.5 | 0.15 | 0.5 | 0.2 | ||
| Figure 4e | 0.4 | 0.7 | 1.1 | - | 0.3 | 0.7 | 1.2 | 0.7 | 0.7 | 0.8 | 0.7 | 0.5 | 1 | 0.25 | 0.9 | 0.25 | 1 | 3 | 0.15 | 0.5 | 0.12 | 0.5 | 0.5 | |||
| Figure 4f | 0.4 | 0.7 | 1.1 | 0.6 | 0.3 | 0.7 | 1.2 | 0.8 | 0.7 | 0.8 | 0.7 | 0.5 | 3 | 0.25 | - | 0.25 | 1 | 3 | 0.15 | 0.5 | 0.15 | 0.5 | 0.5 | |||
| Figure 4g | 0.3 | 0.5 | 1.1 | - | 0.35 | 0.8 | 1.2 | 0.5 | 0.5 | 0.5 | 0.7 | 0.5 | 2 | 0.25 | 0.5 | 0.25 | 1 | 4 | 0.15 | 0.5 | 0.15 | 0.5 | 0.8 | |||
| Figure 4h | 0.4 | 0.5 | 1.1 | 0.9 | 0.35 | 0.8 | 1.2 | 0.5 | 0.6 | 0.5 | 0.7 | 0.5 | 2 | 0.25 | - | 0.25 | 1 | 4 | 0.15 | 0.5 | 0.15 | 0.5 | 0.8 | |||
| Figure 5a | 0.3 | 0.5 | 1.1 | - | 0.4 | 0.6 | 1.4 | 1.1 | 0.9 | 0.5 | 0.7 | 0.5 | 4 | 0.25 | 1 | 0.2 | 1 | 5 | 0.15 | 0.5 | 0.15 | 0.5 | 0.2 | |||
| Figure 5b | 0.3 | 0.5 | 1.1 | 1.1 | 0.45 | 0.6 | 1.4 | 0.9 | 0.8 | 1.4 | 0.7 | 0.5 | 4 | 0.25 | - | 0.2 | 1 | 5 | 0.15 | 0.5 | 0.15 | 0.5 | 0.2 | |||
| Figure 5c | 0.3 | 0.5 | 1.1 | - | 0.4 | 0.5 | 1.4 | 0.9 | 0.8 | 1.1 | 0.6 | 0.5 | 4 | 0.3 | 0.6 | 0.2 | 1 | 5 | 0.15 | 0.5 | 0.15 | 0.5 | 0.2 | |||
| Figure 5d | 0.3 | 0.4 | 1.1 | 1.3 | 0.3 | 0.6 | 0.9 | 0.8 | 0.8 | 1.4 | 0.6 | 0.5 | 1 | 0.3 | - | 0.2 | 1 | 5 | 0.1 | 0.5 | 0.15 | 0.5 | 0.2 | |||
| Figure 6a | 0.3 | 0.5 | 1 | 0.8 | 0.3 | 0.7 | 1.2 | - | 0.7 | 0.5 | 0.7 | 0.5 | 4 | 0.25 | 0.7 | 0.25 | 1 | 4 | 0.15 | 0.5 | 0.1 | 0.5 | 0.2 | |||
| Figure 6b | 0.3 | 0.4 | 1.1 | 0.9 | 0.4 | 0.7 | 1.4 | - | 0.5 | 0.5 | 0.7 | 0.5 | 1 | 0.25 | 0.7 | 0.25 | 1 | 3 | 0.15 | 0.4 | 0.1 | 0.5 | 0.5 | |||
| Figure 6c | 0.4 | 0.5 | 1.1 | 0.9 | 0.35 | 0.8 | 1.1 | - | 0.6 | 0.6 | 0.7 | 0.5 | 1 | 0.25 | 0.7 | 0.25 | 1 | 3 | 0.15 | 0.5 | 0.15 | 0.5 | 0.4 | |||
| Figure 6d | 0.4 | 0.5 | 1.1 | 0.9 | 0.4 | 0.7 | 1.3 | - | 0.5 | 0.5 | 0.7 | 0.5 | 1 | 0.25 | 0.7 | 0.25 | 1 | 3 | 0.15 | 0.4 | 0.12 | 0.5 | 0.5 | |||
| Figure 6e | 0.3 | 0.5 | 1 | 0.8 | 0.3 | 0.7 | - | 0.7 | 0.8 | 0.5 | 0.8 | 0.5 | 4 | 0.25 | 0.7 | 0.25 | 1 | 4 | 0.15 | 0.5 | 0.15 | 0.5 | 0.5 | |||
| Figure 6f | 0.3 | 0.5 | 0.9 | 0.6 | 0.4 | 0.8 | - | 1 | 0.8 | 0.7 | 0.7 | 0.5 | 1 | 0.25 | 0.6 | 0.25 | 1 | 3 | 0.15 | 0.5 | 0.15 | 0.5 | 0.4 | |||
| Figure 6g | 0.3 | 0.5 | 1.1 | 0.9 | 0.35 | 0.8 | - | 1 | 0.8 | 0.6 | 0.6 | 0.5 | 1 | 0.25 | 0.5 | 0.25 | 1 | 3 | 0.15 | 0.5 | 0.15 | 0.5 | 0.4 | |||
| Figure 6h | 0.3 | 0.5 | 0.9 | 0.7 | 0.3 | 0.7 | - | 0.6 | 0.5 | 0.5 | 0.7 | 0.5 | 1 | 0.25 | 0.8 | 0.25 | 1 | 3 | 0.15 | 0.4 | 0.12 | 0.5 | 0.5 | |||
| Figure 7b | 0.3 | 0.4 | 1.1 | 0.7 | - | 0.85 | 1.3 | 0.8 | 0.6 | 0.6 | 0.8 | 0.5 | 1 | 0.25 | 0.7 | 0.25 | 1 | 0 | 3 | 0.15 | 0.5 | 0.1 | 0.5 | 0.4 | ||
| Figure 7c | 0.3 | 0.5 | 1.1 | 0.9 | - | 0.8 | 1.3 | 0.7 | 0.7 | 0.9 | 0.8 | 0.5 | 2 | 0.25 | 0.6 | 0.2 | 1 | 4 | 0.15 | - | - | 0.5 | 0.5 | |||
| Figure 7d | 0.3 | 0.5 | 1.1 | 0.9 | - | 0.8 | 1.3 | 0.7 | 0.7 | 0.9 | 0.8 | 0.5 | 2 | 0.25 | 0.6 | 0.2 | 1 | 4 | 0.15 | - | - | 0.5 | 0.5 | |||
| Figure 7e | 0.4 | 0.6 | 1.1 | 0.8 | 0.25 | 1 | 1.2 | 0.7 | 0.6 | 0.7 | 0.5 | 0.5 | 2 | 0.25 | 0.6 | - | 1 | 4 | 0.1 | 0.5 | 0.1 | 0.5 | 0.25 | |||
| Figure 7f | 0.3 | 0.5 | 0.9 | 0.8 | 0.4 | 0.7 | 1.3 | 0.6 | 0.7 | 0.8 | 0.5 | 0.5 | 1 | 0.25 | 0.6 | 0.2 | 1 | 4 | 0.15 | 0.5 | 0.15 | - | 0.4 | |||
| Figure 7g | 0.3 | 0.5 | 0.9 | 0.7 | 0.3 | 0.7 | 1.1 | 0.7 | 0.6 | 0.8 | 0.7 | 0.5 | 3 | 0.25 | 0.8 | 0.2 | 1 | 3 | - | 0.5 | 0.15 | - | 0.4 | |||
| Figure 7h | 0.3 | 0.5 | 0.9 | 0.7 | 0.3 | 0.7 | 1.1 | 0.7 | 0.6 | 0.8 | 0.7 | 0.5 | 3 | 0.25 | 0.6 | 0.2 | 1 | 3 | - | 0.5 | 0.15 | - | 0.4 | |||
| Figure 7i | 0.3 | 0.5 | 1 | 0.9 | 0.3 | 0.7 | 1.3 | 0.8 | 0.7 | 1.2 | 0.7 | 0.5 | 2 | 0.25 | 0.7 | 0.2 | - | 4 | 0.3 | 0.5 | 0.12 | 0.5 | 0.5 | |||
| Figure 7j | 0.3 | 0.5 | 0.9 | 0.8 | 0.4 | 1 | 1.1 | 0.7 | 0.6 | 0.8 | 0.7 | 0.5 | 4 | 0.25 | 1 | 0.25 | - | 3 | 0.1 | 0.5 | 0.15 | 0.5 | 0.6 | |||
| Figure 8a | 0.3 | 0.5 | 1.1 | 0.8 | 0.3 | 0.8 | 1.1 | 0.8 | 0.6 | 0.7 | 0.7 | - | 3 | 0.25 | 0.7 | 0.2 | 1 | 3 | 0.15 | 0.5 | 0.15 | 0.5 | 0.4 | |||
| Figure 8b | 0.3 | 0.5 | 0.9 | 0.8 | 0.4 | 0.8 | 1.1 | 0.7 | 0.6 | 0.7 | 0.7 | - | 3 | 0.25 | 0.7 | 0.25 | 1 | 3 | 0.1 | 0.5 | 0.15 | 0.5 | 0.4 | |||
| Figure 8c | 0.3 | 0.5 | 1.1 | 0.8 | 0.25 | 0.7 | 1.2 | 0.7 | 0.8 | 0.8 | 0.7 | 0.5 | 1 | 0.25 | 0.6 | 0.15 | 1 | 3 | 0.15 | 0.5 | 0.12 | 0.5 | - | |||
| Figure 8d | 0.3 | 0.5 | 1.1 | 0.8 | 0.25 | 0.7 | 1.2 | 0.7 | 0.8 | 0.8 | 0.8 | 0.5 | 1 | 0.25 | 0.6 | 0.15 | 1 | 3 | 0.15 | 0.5 | 0.12 | 0.5 | - | |||
| Figure 8e | 0.3 | 0.5 | 1.1 | 0.8 | 0.4 | 0.8 | 1.2 | 0.6 | 0.7 | - | 0.7 | 0.5 | 1 | 0.2 | 0.6 | 0.25 | 1 | 3 | 0.15 | 0.5 | 0.15 | 0.5 | 0.5 | |||
| Figure 8f | 0.3 | 0.5 | 1.1 | 0.8 | 0.4 | 0.8 | 1.1 | 0.6 | - | 0.7 | 0.7 | 0.5 | 1 | 0.25 | 0.6 | 0.25 | 1 | 3 | 0.1 | 0.5 | 0.15 | 0.5 | 0.5 | |||
| Figure 8g | 0.3 | 0.5 | 1.1 | 0.5 | 0.6 | 0.6 | 1 | 0.9 | 0.6 | 0.7 | 0.9 | 0.5 | 5 | 0.25 | 0.6 | 0.15 | 1 | 4 | 0.15 | 0.5 | 0.15 | 0.5 | - | |||
| Figure 8h | 0.3 | 0.5 | 1.1 | 0 | 0.8 | 0.4 | 0.8 | 1 | 0.6 | 0.5 | 0.7 | 0.7 | 0.5 | 1 | 0.25 | 0.6 | 0.25 | 1 | - | 4 | 0.1 | 0.5 | 0.15 | 0.5 | 0.5 | |
| Figure 9a | 0.4 | 0.5 | 1.1 | 0.8 | - | 0.8 | 1 | 0.5 | 0.8 | 0.8 | 0.7 | 0.5 | 1 | 0.25 | 0.7 | 0.15 | 1 | 4 | 0.15 | 0.5 | 0.15 | 0.5 | - | |||
| Figure 9b | 0.3 | 0.5 | 1.1 | 0.8 | 0.3 | 0.8 | 1.2 | 0.5 | 0.8 | 0.8 | 0.7 | 0.5 | 1 | 0.25 | 0.7 | - | 1 | 4 | 0.15 | 0.5 | 0.15 | 0.5 | 0.5 | |||
| Figure 9c | 0.3 | 0.5 | 1.1 | - | 0.3 | 0.8 | 1.2 | 0.5 | 0.8 | 0.8 | 0.7 | 0.5 | 1 | 0.25 | 0.7 | 0.15 | 1 | 4 | 0.15 | 0.5 | 0.15 | 0.5 | 0.5 | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Elogail, M.A.; Mekheimer, K.S. Modulated Viscosity-Dependent Parameters for MHD Blood Flow in Microvessels Containing Oxytactic Microorganisms and Nanoparticles. Symmetry 2020, 12, 2114. https://doi.org/10.3390/sym12122114
Elogail MA, Mekheimer KS. Modulated Viscosity-Dependent Parameters for MHD Blood Flow in Microvessels Containing Oxytactic Microorganisms and Nanoparticles. Symmetry. 2020; 12(12):2114. https://doi.org/10.3390/sym12122114
Chicago/Turabian StyleElogail, M. A., and Kh. S. Mekheimer. 2020. "Modulated Viscosity-Dependent Parameters for MHD Blood Flow in Microvessels Containing Oxytactic Microorganisms and Nanoparticles" Symmetry 12, no. 12: 2114. https://doi.org/10.3390/sym12122114
APA StyleElogail, M. A., & Mekheimer, K. S. (2020). Modulated Viscosity-Dependent Parameters for MHD Blood Flow in Microvessels Containing Oxytactic Microorganisms and Nanoparticles. Symmetry, 12(12), 2114. https://doi.org/10.3390/sym12122114






