1. Introduction
The Moutard transformation [
1] is a very interesting form of discrete symmetry of second-order linear equations with variable coefficients. Consider the differential equation
where
is the two-dimensional Euclidean Laplacian. Let
and
be two partial solutions of this equation, i.e., its solutions for two different Cauchy problems (with different initial conditions). The function
we will call the prop solution because it will play the role of a foundation on which we will build the Moutard’s mathematical apparatus. This apparatus, known as the Moutard symmetry is to be defined as the following transformation:
where
and we used the following (standard) tensor notations:
;
;
is a fully antisymmetric tensor with
; and, as usual, we have a summation over the repeated indices. Note that the one-form being integrated in (
3) will be closed (i.e its derivative will be equal to zero) when both
and
are solutions of (
2). Hence, the shape of the contour of integration
in (
3) is irrelevant.
If we switch from
to the cone variables
x and
y, then the Equation (
1) will take a new form:
To define the Moutard symmetry in the new cone variables one has to override the closed one-form
. Namely, let
and
be two solutions of the (
4):
Define a differential form
such that
and
Note that since by definition both
and
are solutions of (
5), the one-form is closed too, i.e.,
and thus the shape of the contour of integration
is irrelevant.
The Moutard symmetry has the form
It is worth pointing out at this step that
rather then zero.
The Moutard symmetry in usual variables can be formally reduced in a one-dimensional limit to the Darboux transformation (originally introduced in 1882 in article [
2] and further developed by Crum in [
3]). In other words, the Moutard symmetry group includes the Darboux transformation group as a subgroup. This is potentially a very significant observation since the group structure of the Darboux transformation is associated with a subalgebra of the Kats–Moody algebra of the group SU(2) by means of the following commutation relation:
where
are the structure constants of the group SU(2) (i.e., the group of unitary
matrices with determinant 1, whose generators are the famous Pauli matrices.) [
4]. It is important to note, however, that while the Darboux transformation is indeed a limit case of the Moutard transformation in the one-dimensional limit, there still exist a crucial difference between the two. While both require two eigenfunctions to jump start the process of transformation, in the case of Darboux transformation these eigenfunctions might belong to different eigenvalues, as long as the prop function is positively defined everywhere (to ensure the regularity of a new dressed potential). In contrast to that, the Moutard transformation only accepts two eigenfunctions belonging to the same eigenvalue, which in this paper for simplicity is set equal to zero.
Another interesting property of the Moutard symmetries is that they ((
8), (
11), (
9) or (
2), (
3)) can be iterated several times, and the result of their application can be expressed via the corresponding Pfaffian forms [
5]. The Moutard symmetries have a number of interesting physical applications, ranging from the Maxwell equations in a 2D inhomogeneous medium [
6] to the problems of quantum cosmology and the Wheeler–DeWitt equation [
7], as well as the quantum (phantom) modified gravity models [
8]. However, the Moutard transformations are most effective in the theory of integrable evolutionary equations in (1 + 2) dimensions. And this is a good time to introduce one of these equations, which will be the key subject of our article. But in order to do tat, we’ll have to take a little detour to very end of XX century.
It was the year 1984, and two Soviet mathematicians, Sergey Novikov and Aleksander Veselov, have made a very important discovery [
9]. At that time they were studying the class of two-dimensional Schrödinger operators
L with a property of a “finite-zoneness w.r.t. a single energy level”, originally introduced in 1976 by Dubrovin, Krichever and Novikov in [
10], and is a property of a Schrödinger operator
L whose Bloch functions (i.e., the eigenfunctions that
L shares with the periodic operators of spatial translations) on a single energy level is meromorphic (i.e., holomorphic everywhere except for a few isolated poles) on a Riemann surface of a finite genus ([
10], see also [
11]). More specifically, Veselov and Novikov were interested in those “finite-zone” 2D Schrödinger operators
L that are simultaneously real and purely potential. For that end, a theorem has been proven that for eigenfunction
of such an operator to be meromorphic everywhere except at two points and possess the required asymptotes (see [
9] for details), those eigenfunctions necessarily have to satisfy the following system of equations:
where the overhead bar denotes complex conjugate, the operators
and the coefficients
and
V are uniquely defined by the aforementioned asymptotes.
The pair of operators
L and
A coupled by the system (
12) deeply resembles the famous Lax pair
[
12]: two time-dependent operators that satisfy the condition
which in turn produces a new
-dimensional differential equation—with such notable examples as, Korteweg–de Vries (KdV), sine–Gordon and the nonlinear Schrödinger equations (for more details cf. [
5,
12], see also [
13]). However, in the case of (
12) the proper “entanglement” between the
L and
A was a tad more complex, and required an additional operator
(similar in form to
albeit with its own coefficients):
In other words, the system (
12) was essentially a letter of acquaintance from an infinitely diverse family of novel
dimensional equations. The very first (and the simplest) member of that very family was the
equation (with
) that has been henceforth known as the Novikov–Veselov equation (NV) [
9]:
Subsequent studies of NV equation has produced a lot of very interesting observation: for example, in a one-dimensional case (i.e., when both
u and
are independent of
y variable) the (
14) reduces to the KdV equation; whereas if we add to (
14) one additional term,
, and then take a limit
, we will instead wound up with either one of two Kadomtsev–Petviashvili equations [
14]—another famous
generalization of KdV! In fact, a huge and ever-growing body of works related to the study of NV equations has been established (see, for example, Refs. [
15,
16,
17,
18] for a rather extensive review of a recent literature on the subject). In particular, a lot of spotlight has been focused on the solutions of (
14) and (
15). For example, the article [
19] shows how the method of superposition originally proposed in [
20] can be used to obtain a 2-solitary wave solution of the Novikov–Veselov equation. The more general N-solitons solutions were subsequently constructed in [
21]. A conspicuous absence of exponentially localized solitons for NV equation with a positive energy was explored and explained in [
22], whereas the impossibility of such solutions for the negative energy NV was proven in [
23]. Many articles were dedicated to unusual and fascinating properties of the multi-dimensional solutions, including those for seemingly ordinary flat waves. In particular, in [
24] it has been shown that plane wave soliton solutions of NV equation are not stable for transverse perturbations; the paper [
18] demonstrates that NV equation permits such interesting solutions as multi-solitons, ring solitons, and the breathers; while the authors of [
25] construct a Mach-type soliton of the NV equation. One of the most effective mathematical tools for studying the NV equation is the inverse scattering method. It was developed and applied in many articles, such as, for example, Refs. [
16,
26]. We must also mention an important paper [
17], which looked at a zero-energy Novikov–Veselov equation for the initial data of conductivity type. Taking into account that the
nonlinear equations to this day remain mostly “terra incognita”, it generates a lot of attention when someone manages to establish a relationship between the various members of a small group of currently known integrable models. As one such example we can refer to the article [
27] which has uncovered a curious relationship between the hyperbolic NV equation and the stationary Davey–Stewartson II equation—here the adjective “hyperbolic” simply means that the
L Equation (
4) is hyperbolic, i.e., that both
x and
y variables are real (accordingly, since the “original” NV equation is associated with the system (
12), it can be called “elliptic”). Finally, a lot of literature has been written on the subject of various generalizations of NV equations, of their properties and of their solutions [
28,
29,
30], and see also [
31], where the analogue of NV equations is shown to arise in the nonlinear optics in a dispersion-free limit.
The observant reader will of course notice that one of the most prominent aspects of the majority of the articles we have mentioned is an almost universal adoption of an inverse scattering method as a primary tool for conducting the research and finding the exact solutions of NV. However, in this article we wish to discuss an alternative method of solving the Cauchy problem for NV (the hyperbolic version). This method, albeit simple in principle, appears to be deep enough to be applicable to a very broad class of equations, NV being just the first one – just as it is the but a first member of the Novikov–Veselov hierarchy.
The article is organized as follows. In
Section 2 we introduce all the necessary ingredients of our proposed method, namely: the Lax pair for the hyperbolic (real-valued) NV equation, the Moutard transformation and the Airy functions—and describe how to use them to produce the exact solutions to the NV equation. In the next section,
Section 3, we up the ante by adding the initial conditions into the mix—and show how to make sure the new solution satisfies those conditions. Finally, in
Section 4 we discuss the generalization of the proposed method to the higher-order equations from the Novikov–Veselov hierarchy.
2. The Moutard Transformation
Let us start by introducing the hyperbolic NV equation:
where from now on the indices will denote the partial derivatives w.r.t. the corresponding variables. This system allows for a Lax pair of the following type:
If one knows two linearly independent solutions
and
for (
16), then one can utilize the famous Moutard transformation to construct a new function
that will serve as a solution to the same Equation (
16) albeit with a new potential
. The new potential will then satisfy the relation
Let us assume that
. Then the entire system (
16) simplifies to
The Equation (
18) can be resolved by separating the variables. The resulting solution will be of a form:
where
are two arbitrary functions that are continuously differentiable by
x and
y, correspondingly. Substituting (
20) into (
17) yields a following post-Moutard form of function
:
As follows from (
21), our next goal should lie in ascertaining the exact forms of the functions
and
. This task can be accomplished by looking at the Equation (
19) which we have ignored so far. We will rewrite it as a standard Cauchy problem by introducing the initial conditions for
and rewriting the (
19) as a system
where
is an arbitrary time-dependent function. The apparently symmetric nature of (
23) allows us to restrict our attention on just one of the equations therein, namely—the first one.
We begin by introducing the Fourier transform
of the function
:
This transformation is handy because of the identity
which, after being substituted into (
23), yields the equation
The Equation (
25) must be satisfied for all
x and
p, and therefore leads to:
(
26) is a nonhomogeneous linear O.D.E. of first order. Its general solution is
where
is a function, determinable from the initial conditions (
22). Using the inverse Fourier transform (
24) we come to the following conclusion:
According to (
22),
so the unknown
is an inverse Fourier transform of the initial condition
, i.e.,:
and we subsequently end up with the following general formula for the function
:
The (
29) can be further simplified by pointing out the similarity between the integrals with respect to variable
p and the Airy function
. The Airy function is a particular solution of the eponymous Airy equation:
that has a following integral representation:
Using this fact together with the apparent identity:
together with the Equation (
29) and the similar one written for
finally yields:
So, we end up with both the solution
of the Lax pair (
18), (
19), and, as a courtesy of Moutard transform (
17), with a solution
of the NV Equation (
15) as well. In other words, to find a non-zero solution of the NV equation, it will suffice to start with
, impose the boundary conditions (
22) on the Lax pair (
18), (
19), use (
32) to find its solution and conclude the calculations by finding a function
via the Moutard transformation (
17). As straightforward as it is, there is one question we should ask: what would happen should we try to invert the process and instead start out with he boundary conditions for the NV equation itself?
3. The Cauchy Problem for the Novikov–Veselov Equation
In the previous chapter we have shown that there shall exist a solution
to the NV equation, whose exact form can be derived via the Moutard transformation (
21) from the solutions of the system (
18) and (
19), provided we are given the initial conditions (
22). What would happen if the exact forms of the functions
and
are unknown and we are instead given the initial conditions for the NV equation itself, and would it still be possible to find the required
? In other words, is it possible to find an analytic solution to the Cauchy problem for the NV equation provided we only know that the solution has a general structure (
21)? In short, the answer is “yes”.
Let us start by introducing the set of initial and boundary conditions for the NV equation:
where
is some constant that is given to us together with the boundary conditions
and
. Since we know that
satisfies the Moutard transformation, we also know that:
where
and
are defined as in
Section 2, and
and · denote the partial derivatives with respect to
x and
y variables correspondingly. From (
34) and (
33) it immediately follows that
The first two differential equations in (
35) can be easily integrated; for example, the first one after the integration with respect to the variable
x yields
which leads us to the following conclusion:
where we have introduced the notation:
,
,
and
. In a similar fashion, the boundary condition
and its derivative will satisfy:
The system (
36) and (
37) depends on four constants:
,
,
and
. Three of them can be chosen arbitrarily, whereas the fourth one would have to satisfy the Equation (
35), namely:
Curiously, this choice does not affect the Cauchy problem of the NV equation in the least, for it can be shown by direct substitution into (
34) that:
i.e., the initial condition
depends only on the known initial boundary conditions
,
and
C.
We are now ready to answer the question posed in the beginning of this section: provided we know the initial conditions (
38), how do we solve the corresponding Cauchy problem of the hyperbolic real-valued Novikov–Veselov equation? The answer lies in repeating the Moutard transformation process we described in
Section 2! Indeed, since the unknown functions
and
satisfy the relations (
36) and (
37), all we really have to do is substitute them into the system (
32), derive
and
, and substitute them in Equation (
21) to find out the sought after
, which will conclude the problem.
Lets summarize everything we have said so far. In order to find an exact solution
to the hyperbolic real-valued Novikov–Veselov equation
with the given initial boundary conditions
that correspond to the initial condition
one shall:
Choose a differentiable function
and four numbers
,
,
and
that satisfy the condition,
Find two support function
and
via the formulas
Substitute
and
into the equations
Substitute the new functions
and
into the equation
The resulting function
will be a proper solution of the Cauchy problem since by construction it will satisfy both the NV Equation (
39), and the initial conditions
. We would like to emphasize here that this procedure does not involve anything more complicated than partial differentiation and integration and can therefore be used for both the analytic study of the properties of the solutions of NV equation and the corresponding numerical calculations.
Before we conclude this section, we would like to offer two interesting examples of Cauchy problems that might be used for the algorithm we have described above and that serve as the proof that even the seemingly simple case of (
18) with
can lead to some rather interesting problems.
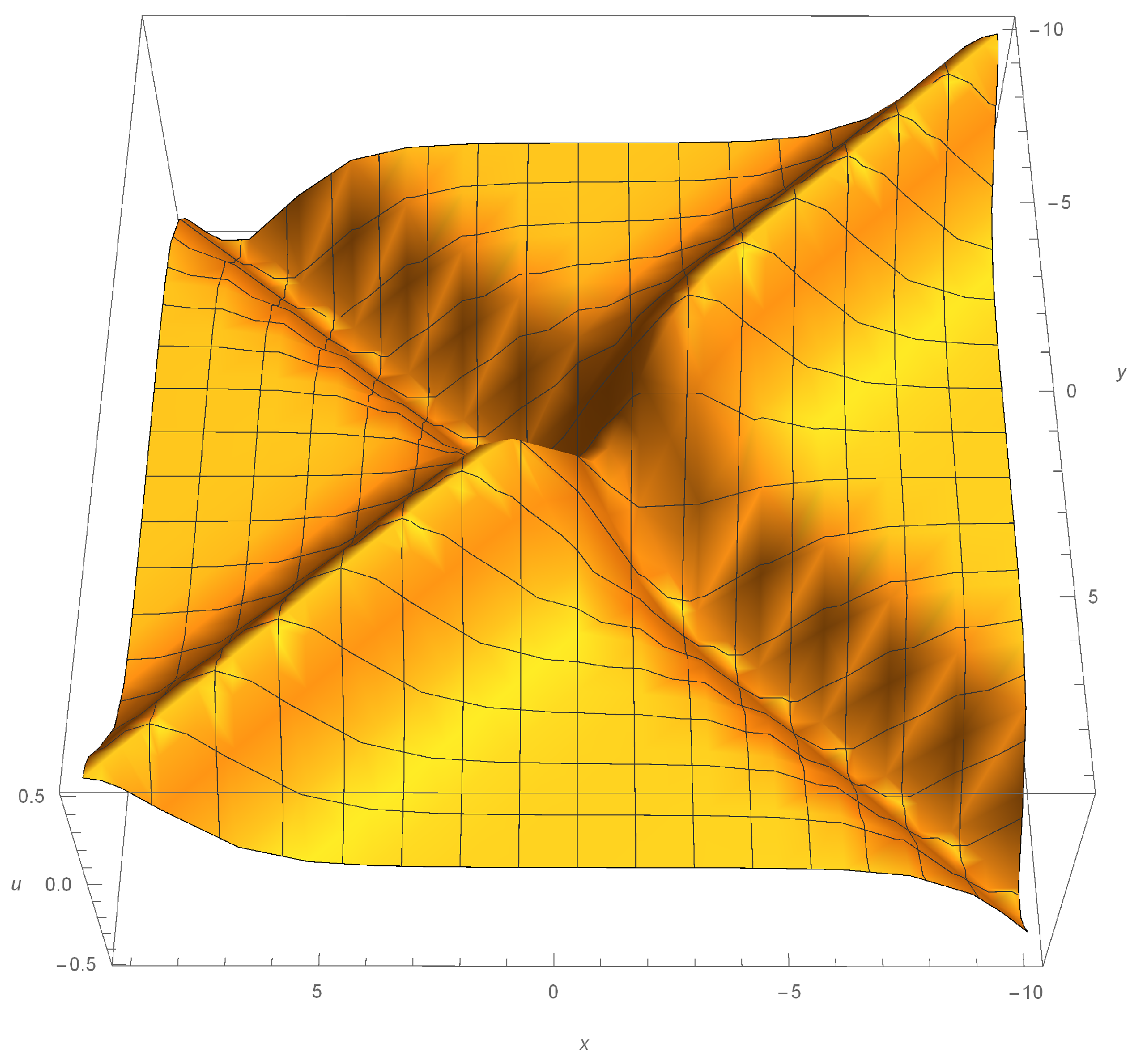
The first is based on the solution of (
20) of the form:
, where
. According to (
21) it corresponds to the following dromion solution:
depicted on
Figure 1. It is important to note that
and
must be non-zero constants, otherwise the functions
and
in (
40) will be identically zero. Any other choice for
, however, would be fine and will result in nontrivial solutions of the NV equation. Additionally, a little note is in order. The solution we have just produced is the exponentially exponentially localized soliton localized on the 2D plane. The solutions of this have been previously constructed for the Davey–Stewartson-I (DS) equation in [
32,
33,
34], while the term “dromion” itself stems from the 1989 paper by Fokas and Santini [
35]. The DS equations describe two interacting fields, and in the case of the dromion on of them describes a certain exponentially localized (on a plane) structure, while the other has orthogonal equipotential lines. It is thanks to this very property that we are at liberty to call the solution (
42) a “dromion”.
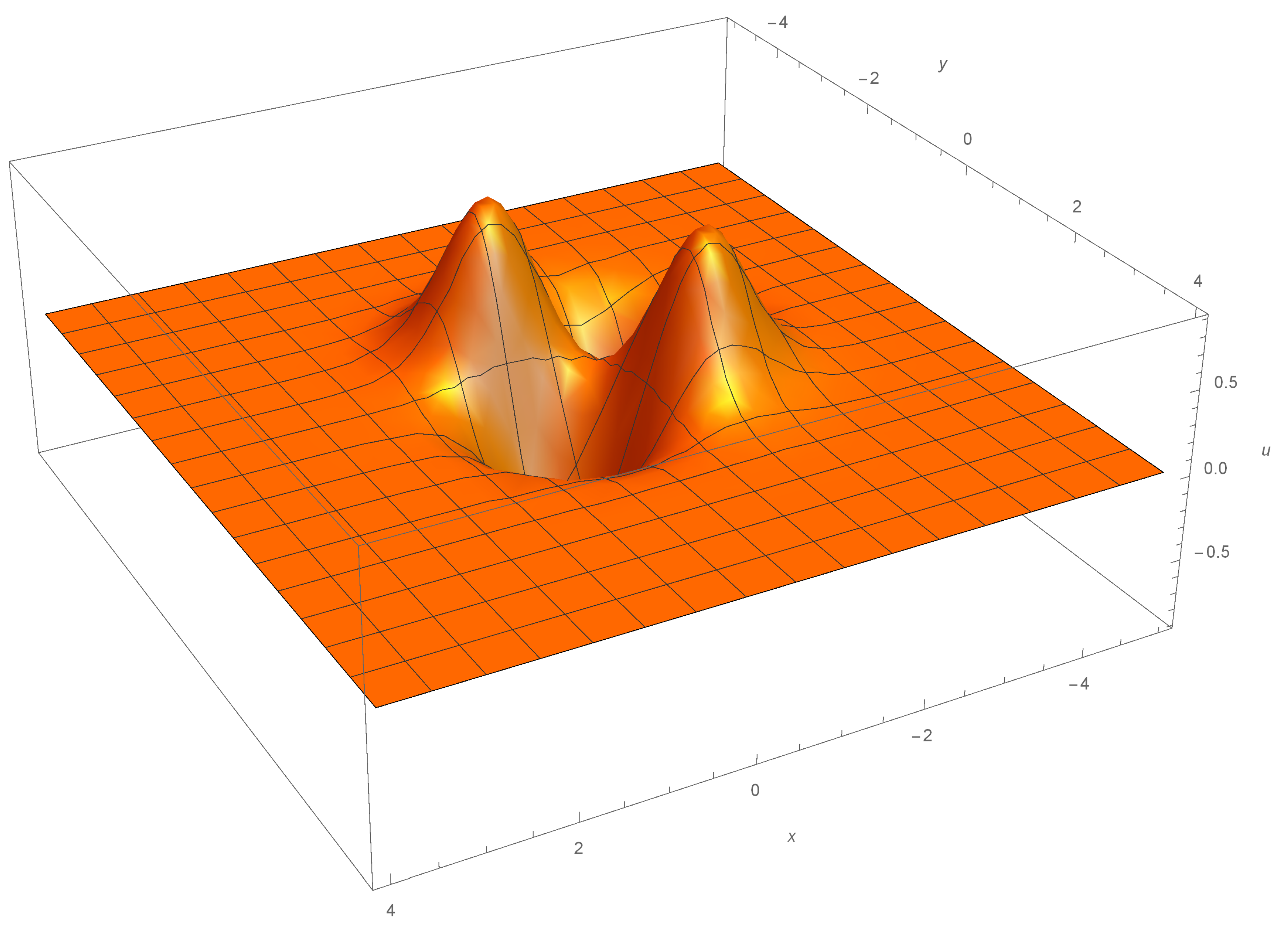
The second solution is based on the function:
, where
. The solution
then has the form:
depicted on
Figure 2, and it is easy to see that on the plane
it describes an exponentially localized structure, centered around the point
.
4. Generalization of the Method: The Higher-Order Equations
Let us now say a few words about the more general problem. First of all, let us look at the following operator-type Lax pair:
where
in some non-zero natural number. This system will correspond to a family of Lax equations, with the special case
corresponding to the hyperbolic NV equation. It will still allow for the Moutard transformation, and therefore the crux of our discussion would still be applicable for arbitrary
n. However, one thing that must change is the exact form of the equations for
and
. This is due to a very simple reason: the Fourier transform
for the function
had to satisfy the Equation (
26), where one of the terms had a specific factor
. It is this very factor that had allowed us to introduce the Airy function and derive the exact formula for
. Unfortunately, this very factor is endemic to the Veselov–Novikov equation, and in the more general case of (
44) it must be replaced with the factor
—destroying any relationship with the Airy function proper. As a result, the entire formula (
40) becomes no longer applicable for the general case and thus should be properly replaced. In order to find out the suitable replacement, we shall separately consider two alternative cases: when
n is odd and when
n is even.
Case 1: Odd n. Let
, where
. Following our previous discussion, let us consider the special case
. Then the system (
44) turns into
Since the first equation requires that
, the system subsequently splits into the following equations:
where for simplicity we have omitted the arbitrary function
. Using the Fourier transformation
we end up with the differential equation
Solving it and returning back to
as described in
Section 2 yields
As we know, in the special case
(i.e.,
) the inner integral in (48) can be rewritten in terms of the Airy function
which serves as a solution to the Airy equation
and is easily derived using either Fourier or Laplace transformation; in case of the Laplace transformation the contour of integration must be chosen lying inside of a sector where the polar angle
satisfies the condition
.
Similarly, it is easy to show that one of a solutions to a more general equation
will be a higher-order generalization of the Airy function:
which means that the required functions
and
can be derived from the initial conditions
and
by the following formulas:
Side note: We would like to remind the reader that in literature the term generalized Airy function is commonly assigned to the solutions of the second order O.D.E. ; hence the addition of the term-order in our case is necessary to avoid a possible confusion.
Case 2: Even n. Let
, where
. This time let us utilize not a Fourier but a Laplace transform:
where we have introduced the equation for
is
so the required function
will satisfy the equation
It is not difficult to show that the Laplace transformation method applied to the ordinary differential equation
will yield a following solution
and so the even case produces the formulas that are quite similar to the old ones, namely:
Note the appearance of a negative sign under the root in (
50), which serves as a indication of an ill-posedness of our problem for
.
Side note: The choice of the lower limit in the Laplace transform being equal to
is neither random nor capricious—it is necessary so that during the integration by parts (which is required to get the solution (
49)) all the boundary terms will vanish.
In order to conclude this section, we have to produce a sample of a differential equation that allows for a Moutard transformation and whose Lax pair reduces to (
44) when
. It is possible to demonstrate that no such equation exists for
, which gives a very strong indication that the method is intricately tied up to the Novikov–Veselov hierarchy. Indeed, if we consider the following Lax pair:
with the functions
a,
b and
satisfying the conditions:
then we end up with the second equation from the Novikov–Veselov hierarchy, which has the following form:
which exactly satisfies both of our underlying assumptions whenever we set
, or, more generally, choose
, where
. Subsequent application of the proposed method to this equation (plus the initial conditions) for the case
we leave to the reader.