1. Introduction
The block cipher is an important branch of cryptography, which can be used not only to encrypt information directly, but also as an effective means to construct hash functions and digital signatures [
1,
2,
3]. The block cipher has been widely applied to the field of information security because of high speed, easy standardization, and convenience for hardware and software implementation. S-box is the only nonlinear component in the symmetric block cipher. Its performance directly determines the security strength of the block cipher. Therefore, the construction of a secure and efficient S-box has become one of the key factors in the design of the block cipher [
4,
5,
6].
In traditional cryptography, Advanced Encryption Standard (AES) uses algebraic methods to construct the S-box. Although high nonlinearity can be obtained because there are only nine algebraic formulas, its structure is too simple and the affine transformation period and iterative output period are too short, so the differential performance is relatively weak and it is difficult to resist algebraic attacks [
7,
8]. Meanwhile, the AES uses static S-box, and its form content is both public and unchanged, which is easy to be analyzed and utilized by the deciphers. Chaos is a deterministic, random-like process in nonlinear dynamic systems.With the deepening of S-box research and the development of chaos theory, dynamic S-box is constructed based on nonlinearity, randomness, initial sensitivity and unpredictability of chaos to realize information confusion, which has been gradually recognized by cryptographers and has made considerable development [
9,
10,
11,
12,
13,
14]. The inherent characteristic of the chaotic system provides a good foundation for constructing the S-box. However, the performance of S-box may be unstable due to the degradation of dynamic characteristics and local periodic phenomenon of digital chaos, so there are some security risks. With the dynamic characteristics degradation and the local periodic phenomenon of digital chaos, and the security problems caused by them becoming more and more prominent, the efficient generation of the chaotic S-box with security guarantees remains to be further studied.
In recent years, intelligent algorithms have been widely developed. Their feasibility and superiority in solving optimization problems have gradually attracted the attention of cryptographers, and have also provided a new idea for constructing the chaotic S-box. A design method of S-box based on chaos and genetic algorithm is proposed in the literature [
15]. The crossover mutation of genetic algorithm is used to generate the chaotic S-box with better nonlinearity. The performance of generated S-box would be easily affected by the dynamic characteristics degradation of digital chaos. A construction method of S-box based on chaos and firefly algorithm is proposed in the literature [
16]. The firefly algorithm is adopted to optimize the generated chaotic S-box set, but the construction efficiency is not high. The convergence time of the algorithm is long, and the performance is also restricted by the chaotic S-box set. A design scheme for constructing high nonlinear chaotic S-box based on genetic algorithm is proposed in the literature [
17], which takes nonlinearity as the only optimization objective leads to little improvement in other cryptographic performances of the chaotic S-box.
Compared with the exhaustive search algorithm, the heuristic algorithm can use some of the searched information to change its own search strategy. If the parameters are set properly, the search efficiency of the heuristic algorithm is more efficient than the exhaustive algorithm [
18,
19]. MSAA is an improvement of the traditional simulated annealing algorithm (SAA). It can overcome the “forgetfulness” in the process of optimization by memorizing the optimal solution currently encountered. Thus, MSAA improves the efficiency and accuracy of global optimal search, which is especially suitable for solving combinatorial optimization problems. Compared to other heuristic algorithms, MSAA is a probabilistic local search method. It can efficiently find the approximate optimal solution of the problem due to its asymptotic convergence [
20]. In this paper, the chaotic S-box set is generated iteratively by digital cascaded chaotic mapping, and the composite objective function is constructed based on the analysis of the S-box performance index. The MSAA is used to efficiently optimize the chaotic S-box set, which can not only obtain the S-box with relatively better cryptographic performance, but also ensure the stability of the S-box security performance. Meanwhile, the chaotic S-box obtained by optimization is transformed by matrix segmentation and scrambling operations to get rid of the performance restriction of the chaotic S-box set, and further enhance the cryptographic performance of the chaotic S-box.
The rest of this paper is as follows: the second section introduces the digital cascaded chaotic mapping. The third section describes the MSAA. The fourth section introduces a design scheme of chaotic S-box based on MSAA. The fifth section analyzes the evaluation indexes and experimental results of S-box performance. The sixth section gives the conclusions of this paper.
2. Chaotic System
Chaos is a deterministic, random-like phenomenon in nonlinear dynamic systems. This process is aperiodic, non-convergent but bounded and extremely sensitive to initial values [
21]. In order to design a secure and efficient chaotic S-box, the application of chaotic systems should follow the following principles. One is that the selected chaotic system should be easy to implement and have efficient iteration, the other is that it can overcome the local periodic problem of the digitization process of the chaotic system. With the dynamic characteristics degradation and the local periodic phenomenon of digital chaos, the security problems caused by them become more and more prominent. The cryptographers are committed to the study of mathematical chaotic models with excellent performance, simple structure, and easy implementation, so that they can better play the chaotic characteristics in the construction of S-box.
To improve the pseudo-random performance and dynamic characteristics of digital chaotic sequences, a digital cascaded chaotic mapping has been proposed in the literature [
22] based on one-dimensional discrete chaotic mappings Logistic and Tent. The iterative output of Logistic chaotic mapping is used as the iterative input of Tent chaotic mapping, and the iterative output of Tent chaotic mapping is used as the input of the next iteration of Logistic chaotic mapping. Then, the one-dimensional discrete chaotic mapping equation after cascading is
In Equation (
1), system parameter
, initial value
, substituting the real-valued chaotic sequence generated by cyclic iteration into Equation (
2) for digital quantization. Then, the digital cascaded chaotic sequence can be obtained:
In Equation (
2), take
,
, which exactly corresponds to the unsigned integer range represented by 8 bits.
The studies have shown that digital cascaded chaotic mapping has efficient iteration and is easy to implement. The mapping has higher complexity, larger parameter space, and stronger initial value sensitivity. A large number of pseudo-random sequences with excellent performance and the great difference can be obtained by tiny changes in initial values and system parameters. The S-box is constructed by using the nonlinearity and randomness of the dynamic iteration of the digital cascaded chaotic mapping. The construction method is simple to operate but can effectively enhance the confusion effect, thus providing a reliable guarantee for the security and efficiency of the S-box construction.
3. Optimization Process of MSAA
The traditional SAA jumps out of the local optimal solution through “probability judgment” and tends to the global optimal [
23,
24]. However, this method may also cause the algorithm to ignore the optimal solution currently encountered. It is difficult to ensure that the final solution must be the global optimal solution. The MSAA proposed by literature [
25] can memorize the optimal solution encountered in the search process. When the search process is over, the searched optimal solution is compared with the memorized optimal solution, and the better one is taken as the final result. The accuracy of the optimization result would be further improved. Since the time required to realize the memory function is extremely short, the MSAA still has high search efficiency.
As shown in
Figure 1, the optimization process of the MSAA is illustrated as follows:
Step 1. In the solution space, set the initial solution , the initial temperature , the minimum temperature , the number of iterations L for each T value, and calculate the objective function of the initial solution . The attenuation function of temperature T is , where , .
Step 2. A new solution is randomly generated near the initial solution , and the objective function of the new solution is calculated.
Step 3.
is compared with
. If
is better than
, that is,
, then accept the new solution
and assign
and
to
and
, respectively. Otherwise, memorize the current optimal solution
, and accept the new solution
according to the probability of Mctropolis criterion. The Mctropolis criterion takes
and temperature
T as input, and the output is the acceptance probability between 0 and 1. Its expression is
Step 4. If the number of iterations L is reached, it is judged whether the termination criterion is met. When the temperature is lower than the minimum temperature or the memorized optimal solution has no changes for multiple consecutive times, then the optimization search is terminated. Otherwise, return to step 2.
Step 5. If the number of iterations L is reached and the termination criterion is met, the searched optimal solution is compared with the memorized optimal solution, and the better one is output as the result. Otherwise, decrease the temperature, reset the number of iterations, and return to step 2.
4. Construction Method of Chaotic S-Box
As shown in
Figure 2, the iterated digital cascaded chaotic sequence is traversed and screened to generate the set of chaotic S-boxes. The set is optimized by MSAA to obtain the chaotic S-box with excellent performance. Then, the chaotic S-box obtained is segmented and scrambled to generate the final chaotic S-box.
The specific construction process is described as follows:
Step 1. Set the initial conditions of the digital cascaded chaotic mapping, that is, , , and the iterative operation is performed.
Step 2. The iterative interval of digital cascaded chaotic mapping is evenly divided into 256 intervals . If the iterative output exists in the interval , the corresponding value is saved and the iteration continues; if does not exist in the interval or has already been saved, the value is not saved and the iteration continues until 256 intervals have been traversed.
Step 3. The outputs are arranged line-by-line in the order of generation and converted into a table of 16 × 16, which is the constructed 8 × 8 S-box. By slightly changing the initial value, the set of chaotic S-boxes can be obtained through the dynamic iteration of the digital cascaded chaotic mapping.
Step 4. Set the initial conditions of the MSAA, the initial temperature is
, the lowest temperature is
, the number of iterations for each
T value is
. In the generated chaotic S-box set, one S-box is randomly selected as the initial solution
, other chaotic S-boxes encountered during the optimization process of MSAA will be used as new solution
. The objective function of new solution
would be compared with the objective function of initial solution
. Since the nonlinearity and difference uniformity are the two most important performance indexes to measure the security performance of S-box, a composite objective function is constructed as
In Equation (
4),
is the nonlinearity of the S-box,
is the difference uniformity of the S-box. The greater the nonlinearity of the S-box and the smaller the difference uniformity, the better its security performance. Therefore, the larger the composite objective function
, the better the cryptographic performance of the S-box. Based on the constructed composite objective function, the MSAA is used to efficiently optimize the set of chaotic S-boxes, and a chaotic
S-box with excellent cryptographic performance would be obtained.
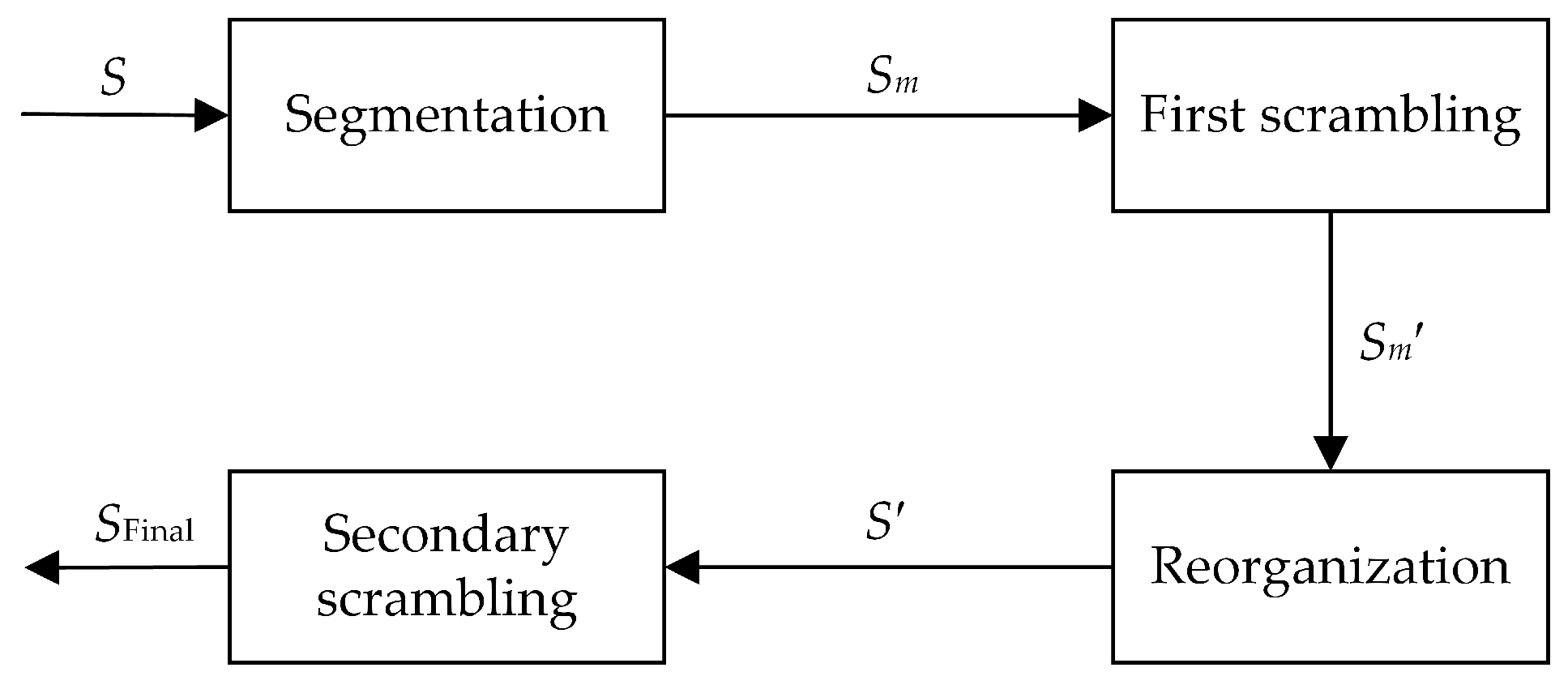
Step 5. As is shown in
Figure 3, the matrix segmentation and scrambling operations are performed on the optimized chaotic
S-box, and the 16 × 16 chaotic
S-box is segmented by matrix according to the following rule:
Then, the four segmented matrices are performed on scrambling operation respectively according to the following rule:
In Equation (
7),
,
,
T represents the transpose of the matrix,
means that
rows and
n rows of the matrix are interchanged, then
A secondary scrambling operation is performed to
according to the following rule
In Equation (
10),
. The output
is the final chaotic
-box shown in
Table 1, and repeat the above method to generate chaotic
-box and chaotic
-box.
5. Testing and Analysis of Performance
5.1. Nonlinearity
Comprehensive analysis of existing research shows that the design of an S-box usually has five criteria: nonlinearity, difference uniformity, strict avalanche criterion (SAC), bit independence criterion (BIC), and bijectivity. The larger the nonlinearity value of the S-box, the stronger its ability to resist linear cryptographic attacks.
Although the S-boxes used in block ciphers are all presented in the form of tables, their essence is a nonlinear combination function of multiple inputs and multiple outputs mapping from
to
. A
S-box can generally be represented as
, which is composed of
mn-bit Boolean functions
, that is,
Let Boolean function
,
,
,
,
, and the dot product of
x and
w be defined as
Then, the first-order Walsh cyclic spectrum of an
n-ary Boolean function
is defined as
For the convenience of calculation, the nonlinearity of
represented by the Walsh cyclic spectrum is defined as
For the 8 × 8 chaotic S-box constructed in this paper, the Walsh cyclic spectrums output by eight Boolean functions are substituted into Equation (
14), respectively. In turn, the nonlinearity values can be obtained. As shown in
Table 2, the three chaotic S-boxes generated by the method of this paper are marked as
-box,
-box, and
-box, the nonlinearities of which are all above 104 and the average values are 108, 108, and 107.5, respectively. The three chaotic S-boxes randomly generated based on the the digital cascaded chaotic sequence in this paper are marked as
-box,
-box, and
-box, the average values of their nonlinearities are 103, 108, and 106.5, respectively. Through comparison, it can be seen that the method of this paper can overcome the instability of the S-box performance caused by the dynamic characteristics degradation and the local periodic phenomenon of digital chaos. At the same time, compared with other chaotic S-boxes generated based on intelligent algorithms, the chaotic S-box proposed has better and more stable nonlinear characteristics and can effectively resist the best linear approximation attack.
5.2. Difference Uniformity
Differential analysis is one of the most effective attacks of block ciphers. In order to measure the ability of a cipher to resist the differential analysis, the concept of difference uniformity has been introduced. The differential analysis mainly realizes the attack through the imbalance of the input/output XOR distribution. If the S-box has an equal probability of input/output XOR distribution, it can effectively resist the differential analysis.
In practice, the input/output XOR distribution of
is generally described by difference approximation probability
In Equation (
15),
means the maximum probability that the output difference is
when the input difference is
.
X represents the set of all possible inputs of
x, and
is the number of all elements in the set
X. The smaller the value of the difference approximation probability
of S-box, the stronger its ability to resist differential attacks.
For the given input difference
, calculate
x to take all possible values and maximum number for
in turn. Then, the table of final difference uniformity distribution can be obtained. As shown in
Table 3, the maximum of the input and output difference of the chaotic
-box in this paper is 10. As shown in
Table 4, the difference approximation probabilities of the three chaotic S-boxes generated by the method of this paper are all 3.9062%. The difference approximation probabilities of the three chaotic S-boxes randomly generated based on the cascaded chaotic sequence in this paper are 4.6875%, 3.9062%, and 3.9062%, respectively. Through comparison, it can be seen that the method of this paper can overcome the instability of the S-box performance caused by the dynamic characteristics degradation and the local periodic phenomenon of digital chaos. At the same time, compared with other chaotic S-boxes generated based on intelligent algorithms, the chaotic S-box proposed has better and more stable difference approximation probabilities, indicating that it has excellent and stable ability to resist differential attacks [
28].
5.3. Strict Avalanche Criterion
In order to resist the attack method based on relatively large change in the output caused by the input change, the SAC is proposed in the literature [
29]. Half of the output result would be changed if one input bit is changed, and the construction of a correlation matrix to judge whether
meets the SAC. Each element value
of the correlation matrix represents the correlation strength between the
i bit of the ciphertext and the
j bit of the plaintext. If the values of each element of the correlation matrix are all close to 0.5, it can indicate that
meets the SAC. The correlation matrix of the chaotic
-box generated by the method of this paper is shown in
Table 5, as shown in
Table 6, the average values of the correlation matrix of the three chaotic S-boxes in this paper are 0.5007, 0.5007, and 0.5008, respectively, which are all closer to 0.5. The SAC performances of the three chaotic S-boxes randomly generated based on the cascaded chaotic sequence in this paper are 0.4836, 0.5012, and 0.5048, respectively. Through comparison, it can be seen that the method of this paper can overcome the instability of the S-box performance caused by the dynamic characteristics degradation and the local periodic phenomenon of digital chaos. At the same time, compared with other chaotic S-boxes generated based on intelligent algorithms, the chaotic S-box proposed has better and more stable SAC performance.
5.4. Bit Independence Criterion
The BIC is one of the essential analysis elements in the design of the S-box. For the Boolean functions and between any two output bits of the S-box, if the S-box meets the BIC-nonlinearity, should meet the characteristics of nonlinearity. If the S-box meets BIC-SAC, should meet the SAC.
As shown in
Table 7, the nonlinearity value of
of the chaotic
-box is larger, indicating that it meets the characteristics of nonlinearity. As shown in
Table 8, the values of each element of the correlation matrix of
of the chaotic
-box are all close to 0.5, indicating that it meets the SAC. As shown in
Table 9, the BIC-nonlinearity average values of the three chaotic S-boxes generated by the method of this paper are 104.21, 104.21, and 104.20, respectively, the BIC-SAC average values of the three chaotic S-boxes are 0.5012, 0.5012, and 0.5011, respectively. The BIC-nonlinearity averages of the three chaotic S-boxes randomly generated based on the cascaded chaotic sequence in this paper are 101.90, 104.21, and 103.53, respectively, and the BIC-SAC averages are 0.4954, 0.5016, and 0.5038, respectively. Through comparison, it can be seen that the method of this paper can overcome the instability of the S-box performance caused by the dynamic characteristics degradation and the local periodic phenomenon of digital chaos. At the same time, compared with other chaotic S-boxes generated based on intelligent algorithms, the chaotic S-box proposed has better and more stable BIC.
5.5. Bijectivity
Generally, the S-box must also satisfy bijectivity in the application. Ref. [
30] has given the condition to satisfy the bijectivity of S-box
In Equation (
16),
,
,
is the Boolean function of each component of the S-box, and
is the Hamming weight.
The standard value of bijectivity of an S-box is 128. It can be seen from the calculation that the sums of linear operations of the Boolean function of each component of the chaotic S-box in this paper are all 128 and have different output values between [0,255], so bijectivity is satisfied.
5.6. Implementation Efficiency
The S-box construction should also consider implementation performance. The experiment is performed on a computer whose central processing unit (CPU) is Intel Core i5-6200 2.4 GHz (Manufacturer location: Santa Clara, California, USA). The function simulation of S-box is carried out on ModelSim-Altera SE 6.6d (Manufacturer location: Santa Clara, California, USA) software using Verilog HDL, and the execution time is about 0.050 s. Under the same conditions, the execution time for SubBytes of AES is 55.067 s. The calculation of SubBytes transformation is obtained by taking the inverse of the multiplication in GF() and performing affine transformation. Generally speaking, the SubBytes transformation is often implemented in look-up-tables (LUT). The execution time of LUT implementation is 0.059 s. Therefore, the required storage space by the method in this paper is less than by LUT and SubBytes of AES.
The hardware is realized by using the storage blocks integrated within field programmable gate array (FPGA) to generate LUT. The target device is Altera Cyclone III EP3C16F484C6 (Manufacturer location: San Jose, CA, USA). The Altera Quartus II 11.0 software is used for a logic synthesis test of the designed S-box. As shown in
Table 10, the chaotic S-box proposed consumes 73 logic elements (LEs), and the highest clock frequency is 192.93 MHz. Compared with the typical LUT-based S-boxes and logic circuits of the SubBytes in AES, the chaotic S-box proposed has less area consumptions and higher clock frequency.
6. Conclusions
A construction method of chaotic S-box based on MSAA is proposed in this paper. The dynamic iteration of the digital cascaded chaotic mapping is used to generate the chaotic S-box set, which effectively alleviates the adverse effect of the dynamic characteristics degradation of digital chaos on the security performance of the S-box. The construction of the composite objective function and the application of the MSAA improve the accuracy and efficiency of the optimization of the chaotic S-box set. The matrix segmentation and scrambling operations are adopted to further enhance the confusion of chaotic S-box, which makes it get rid of the restriction of the performance of the chaotic S-box set. The chaotic S-boxes constructed by this method are tested and analyzed for five cryptographic performances, and compared with other chaotic S-boxes generated based on intelligent algorithms. The results show that the method proposed in this paper can stably and efficiently generate chaotic S-boxes with better cryptographic performance, thus providing a reliable security guarantee for its application.
Author Contributions
Conceptualization, J.W.; Data curation, J.W.; Formal analysis, C.Z.; Funding acquisition, J.W.; Investigation, J.W., Y.Z., C.Z. and Z.Q.; Methodology, J.W.; Project administration, J.W.; Resources, J.W.; Software, C.Z.; Supervision, J.W.; Validation, J.W. and Z.Q.; Visualization, Y.Z.; Writing–original draft, J.W.; Writing–review & editing, J.W. and Y.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Heilongjiang Fundamental Research Foundation for the Local Universities; Science and Technology Innovation Foundation of Harbin, Grant No. 2017RAQXJ031; Heilongjiang University of Science and Technology Graduate Innovation Research Foundation, Grant No. YJSCX2020-223HKD.
Acknowledgments
The authors are thankful to the reviewers for their comments and suggestions to improve the quality of the manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Hussain, I.; Shah, T. Literature survey on nonlinear components and chaotic nonlinear components of block ciphers. Nonlinear Dyn. 2013, 74, 869–904. [Google Scholar] [CrossRef]
- Lu, J.Q.; Seo, H. An investigation of an S-box mechanism in modern block cipher design. In Proceedings of the TENCON 2017—2017 IEEE Region 10 Conference, Penang, Malaysia, 5–8 November 2017; pp. 145–152. [Google Scholar]
- Matheis, K.; Steinwandt, R.; Corona, A.S. Algebraic Properties of the Block Cipher DESL. Symmetry Basel 2019, 11, 1411. [Google Scholar] [CrossRef] [Green Version]
- Mohamed, K.; Pauzi, M.N.M.; Ali, F.H.H.M.; Ariffin, S. Study of S-box properties in block cipher. In Proceedings of the 2014 International Conference on Computer, Communications, and Control Technology (I4CT), Langkawi, Malaysia, 2–4 September 2014; pp. 362–366. [Google Scholar]
- Lu, J.Q.; Seo, H. A Key Selected S-Box Mechanism and Its Investigation in Modern Block Cipher Design. Secur. Commun. Netw. 2020, 2020, 1–26. [Google Scholar] [CrossRef]
- Tian, Y.; Lu, Z. Chaotic S-Box: Intertwining Logistic Map and Bacterial Foraging Optimization. Math. Probl. Eng. 2017, 2017, 1–11. [Google Scholar] [CrossRef]
- Liu, J.; Wei, B.; Wang, X. One AES S-box to increase complexity and its cryptanalysis. J. Syst. Eng. Electron. 2007, 18, 427–433. [Google Scholar]
- Cui, J.; Huang, L.; Zhong, H.; Chang, C.; Yang, W. An improved AES S-Box and its performance analysis. Int. J. Innov. Comput. Inf. Control. 2011, 7, 2291–2302. [Google Scholar]
- Hussain, I.; Anees, A.; Al-Maadeed, T.A.; Mustafa, M.T. Construction of S-Box Based on Chaotic Map and Algebraic Structures. Symmetry Basel 2019, 11, 351. [Google Scholar] [CrossRef] [Green Version]
- Ozkaynak, F.; Celik, V.; Ozer, A.B. A new S-box construction method based on the fractional-order chaotic Chen system. Signal Image Video Process. 2017, 11, 659–664. [Google Scholar] [CrossRef]
- Lu, Q.; Zhu, C.X.; Wang, G.J. A Novel S-Box Design Algorithm Based on a New Compound Chaotic System. Entropy 2019, 21, 1004. [Google Scholar] [CrossRef] [Green Version]
- Liu, G.J.; Yang, W.W.; Liu, W.W.; Dai, Y.W. Designing S-boxes based on 3D four-wing autonomous chaotic system. Nonlinear Dyn. 2015, 82, 1867–1877. [Google Scholar] [CrossRef]
- Lambic, D. A novel method of S-box design based on discrete chaotic map. Nonlinear Dyn. 2017, 87, 2407–2413. [Google Scholar] [CrossRef]
- Belazi, A.; Abd El-Latif, A.A. A simple yet efficient S-box method based on chaotic sine map. Optik 2017, 130, 1438–1444. [Google Scholar] [CrossRef]
- Guesmi, R.; Ben Farah, M.A.; Kachouri, A.; Samet, M. A Novel Design of Chaos Based S-Boxes Using Genetic Algorithm Techniques. In Proceedings of the 2014 IEEE/ACS 11th International Conference on Computer Systems and Applications (AICCSA), Doha, Qatar, 10–13 November 2014; pp. 678–684. [Google Scholar]
- Ahmed, H.A.; Zolkipli, M.F.; Ahmad, M. A novel efficient substitution-box design based on firefly algorithm and discrete chaotic map. Neural Comput. Appl. 2019, 31, 7201–7210. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, Z.Q.; Zhang, L.Y.; Feng, J.; Gao, J.; Lei, P. A genetic algorithm for constructing bijective substitution boxes with high nonlinearity. Inf. Sci. 2020, 523, 152–166. [Google Scholar] [CrossRef]
- Fabian, V. Simulated annealing simulated. Comput. Math. Appl. 1997, 33, 81–94. [Google Scholar] [CrossRef] [Green Version]
- Pendharkar, P.C. Exhaustive and heuristic search approaches for learning a software defect prediction model. Eng. Appl. Artif. Intell. 2010, 23, 34–40. [Google Scholar] [CrossRef]
- Amine, K. Multiobjective Simulated Annealing: Principles and Algorithm Variants. Adv. Oper. Res. 2019, 2019, 1–13. [Google Scholar] [CrossRef]
- Ozkaynak, F. On the effect of chaotic system in performance characteristics of chaos based s-box designs. Phys. a-Stat. Mech. Its Appl. 2020, 550, 124072. [Google Scholar] [CrossRef]
- Wang, J.; Lu, Y.; Ding, Q. The Design of S-box Based on Cascaded Integer Chaos Applied to Wireless Sensor Network. Int. J. Future Gener. Commun. Netw. 2016, 9, 97–106. [Google Scholar] [CrossRef]
- Siddique, N.; Adeli, H. Simulated Annealing, Its Variants and Engineering Applications. Int. J. Artif. Intell. Tools 2016, 25, 1630001. [Google Scholar] [CrossRef]
- Shao, W.; Guo, G.B. Multiple-Try Simulated Annealing Algorithm for Global Optimization. Math. Probl. Eng. 2018, 2018, 1–11. [Google Scholar] [CrossRef]
- Sari, Y.A.; Kumral, M. An improved meta-heuristic approach to extraction sequencing and block routing. J. South. Afr. Inst. Min. Metall. 2016, 116, 673–680. [Google Scholar] [CrossRef] [Green Version]
- Ahmad, M.; Bhatia, D.; Hassan, Y. A Novel Ant Colony Optimization Based Scheme for Substitution Box Design. Procedia Comput. Sci. 2015, 57, 572–580. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.; Pan, B.; Tang, C.; Ding, Q. Construction Method and Performance Analysis of Chaotic S-Box Based on Fireworks Algorithm. Int. J. Bifurc. Chaos 2019, 29, 1950158. [Google Scholar]
- Zhang, W.G.; Pasalic, E. Highly Nonlinear Balanced S-Boxes With Good Differential Properties. IEEE Trans. Inf. Theory 2014, 60, 7970–7979. [Google Scholar] [CrossRef]
- Webster, A.F.; Tavares, S.E. On the Design of S-Boxes. In Proceedings of Advances in Cryptology—CRYPTO ’85 Proceedings; Springer: Berlin/Heidelberg, Germany, 1986; pp. 523–534. [Google Scholar]
- Jakimoski, G.; Kocarev, L. Chaos and cryptography: Block encryption ciphers based on chaotic maps. IEEE Trans. Circuits Syst. Fundam. Theory Appl. 2001, 48, 163–169. [Google Scholar] [CrossRef]
| Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).