Matrix Method by Genocchi Polynomials for Solving Nonlinear Volterra Integral Equations with Weakly Singular Kernels

Abstract

In this study, we present a spectral method for solving nonlinear Volterra integral equations with weakly singular kernels based on the Genocchi polynomials. Many other interesting results concerning nonlinear equations with discontinuous symmetric kernels with application of group symmetry have remained beyond this paper. In the proposed approach, relying on the useful properties of Genocchi polynomials, we produce an operational matrix and a related coefficient matrix to convert nonlinear Volterra integral equations with weakly singular kernels into a system of algebraic equations. This method is very fast and gives high-precision answers with good accuracy in a low number of repetitions compared to other methods that are available. The error boundaries for this method are also presented. Some illustrative examples are provided to demonstrate the capability of the proposed method. Also, the results derived from the new method are compared to Euler’s method to show the superiority of the proposed method.

1. Introduction

Spectral schemes are invaluable tools for the numerical solution of fractional partial differential equations (FPDEs), ordinary differential equations (ODEs), integral equations (IEs), and integrodifferential equations (IDEs).

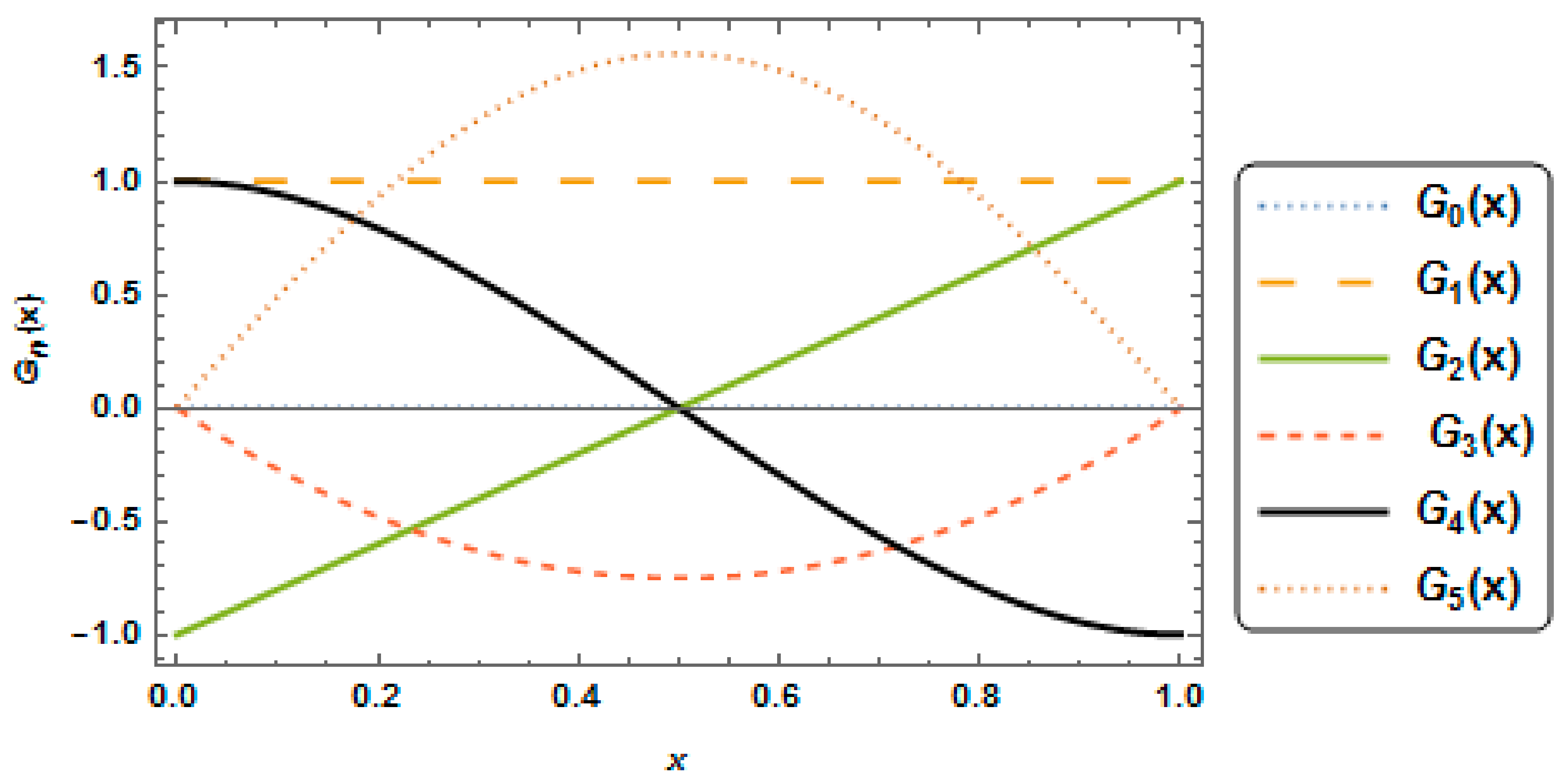
Spectral approaches are a class of schemes used in applied mathematics and scientific computing to numerically solve certain differential equations and nonlinear integral equations. In recent years, these approaches have been used in modeling of many problems of physical phenomena, engineering and chemical processes in chemical kinetics [1], super fluidity biology and economics [2], axially symmetric problems in the case of an elastic body containing an inclusion [3], and fluid dynamics [4], and the Hammerstein integral equation is employed for modeling nonlinear physical phenomena such as electromagnetic fluid dynamics reformulation of boundary value problems with a nonlinear boundary condition [5].

Various numerical approaches have been presented for solving a class of nonlinear singular integral equations including Abel’s integral equation, Hammerstein integral equation, Volterra integral equation, etc. For example, Noeiaghdam et al. in [6] applied the Laplace homotopy analysis method to solve Abel’s integral equation, and validation of this method was discussed in [7]. Also, the numerical studies on the Volterra integral equation with discontinuous kernels can be found in [8,9]. Allaei et al. in [10] presented an analytical and computational method for a class of nonlinear singular integral equations. Maleknejad et al. in [11] proposed a new numerical approach for solving the nonlinear integral equations of Hammerstein and Volterra–Hammerstein. In [12], the authors applied the operational Tau method (OTM) to find a numerical solution for weakly singular Volterra integral equations (WSVIEs) and Abel’s equation.

Other researchers have attempted to solve nonlinear integral equations in recent years. Among them, in recent years, Mehdi Dehghan et al. in [13] solved nonlinear fractional integrodifferential equations (NFIDEs) by using the collocation numerical method. Li Zhu and Qibin Fan in [14] presented a spectral method based on the second Chebyshev wavelet (SCW) operational matrix for solving the fractional nonlinear Fredholm integrodifferential equation, and the Ferdholm and Volterra integral equations.

Nemati in [15] applied a numerical approach for solving nonlinear fractional integrodifferential equations with weakly singular kernels by using a modification of hat functions. Somveer et al. [16] presented an efficient spectral method based on shifted Legendre polynomials for solving nonlinear Volterra singular partial integrodifferential equations (PIDEs) which involve both integrals and derivatives of a function.

Recently, with the effort of other scientists, many of the nonlinear differential and integral equations which appear in different fields of physical phenomena and engineering were solved by using numerical methods, and nonlinear differential and integral equations have also been explored in delayed scaled consensus problems [17,18,19,20,21,22,23,24].

In the study of many nonlinear problems in heat conduction, boundary-layer heat transfer, chemical kinetics, and superfluidity, we are often led to singular Volterra integral equations for which real answers are hard to find [10]. In this article, we use efficient functions such as Genocchi polynomials and their operational matrices to solve nonlinear Volterra integral equations with weakly singular kernels of the following form:

$$y(t)=f(t)-{\displaystyle {\int }_0^t\frac{s^{\beta }}{{(t-s)}^{\alpha }}g(y(s))ds},\hspace{1em}\hspace{1em}t>0,$$

(1)

where $f\left(t\right)$ is in $L^2\left(\Re \right)$ on the interval $0\le t,s\le T$; $g$ is locally Lipchitz continuous, smooth, and a Hammerstein nonlinear function; and $\alpha , \beta$ are real positive numbers.

For future works, we can use other polynomials like Chebyshev, Lagger, etc. for implementation, and by comparing the archived results, we can expand the present method and implement it on the system of nonlinear Volterra integral equations or nonlinear Volterra integral equations of mixed type. Because of important applications of the first kind of Volterra integral equations with discontinuous kernels in load leveling problems and power engineering systems, the proposed method can also be used for future works.

The rest of the article is organized as follows: In Section 2, we state some necessary basic definitions and properties of Genocchi polynomials. Numerical implementation of the suggested technique based on Genocchi polynomials is shown in Section 3. Section 4 estimates the error analysis of our proposed technique. In Section 5, two examples with tables and graphs are presented to show the efficiency and accuracy of the proposed scheme. Section 6 provides some discussion and concluding remarks.

2. Genocchi Polynomials and Their Properties

2.1. Definition of the Genocchi Polynomials

Genocchi polynomials and Genocchi numbers have been widely applied in many branches of mathematics and physics such as complex analytic number theory, homotopy theory, differential topology, and quantum physics (quantum groups) [25,26]. The Genocchi polynomials $G_n(x)$ and numbers $G_n$ are usually expressed by using the exponential generating functions $Q(t,x)$ and $Q(t)$ respectively as follows:

$$Q(t)=\frac{2t}{e^t+1}={\displaystyle \sum _{n=0}^{\infty }{G}_n\frac{t^n}{n!}},\hspace{1em}(\left|t\right|<\pi ),$$

(2)

$$Q(t,x)=\frac{2t{e}^{xt}}{e^t+1}={\displaystyle \sum _n^{\infty }{G}_n(x)\frac{t^n}{n!}},\hspace{1em}(\left|t\right|<\pi ),$$

(3)

where $G_n(x)$ is the well-known Genocchi polynomials of order $n$. Also, we note that the Genocchi polynomials can be determined as follows:

$$G_n(x)={\displaystyle \sum _{k=0}^n\left(\begin{array}{c}n\\ k\end{array}\right)}{G}_{n-k}{x}^k=2B_n(x)-2^{n+1}{B}_n(x),$$

(4)

where the Genocchi number $G_{n-k}$ is obtained by the following relation:

$$G_n=2(1-2^n)B_n,$$

(5)

$B_n$ is the famous Bernoulli number.

The first few Genocchi numbers are given in the table below:

$n$	0	1	2	4	6
$G_n$	0	1	−1	1	−3

We also have to pay attention that $G_{2n+1}=0,\hspace{1em}n=1,2,3,\dots$. We list the first few Genocchi polynomials that are given as follows:

$$\begin{array}{l}{G}_0(x)=0,\\ G_1(x)=1,\\ G_2(x)=2x-1,\\ G_3(x)=3x^2-3x,\\ G_4(x)=4x^3-6x^2+1,\\ G_5(x)=5x^4-10x^3+5x.\end{array}$$

(6)

The Genocchi polynomials are depicted in Figure 1 for different $n$:

Therefore, some of the important basic properties of the Genocchi polynomials are as follows:

$${\displaystyle {\int }_0^1{G}_n(x)G_m(x)}dx=\frac{2{(-1)}^{n}n!m!}{(n+m)!}{G}_{m+n},\hspace{1em}n,m\ge 1,$$

(7)

$$\frac{d{G}_n(x)}{dx}=n{G}_{n-1}(x),\hspace{1em}n\ge 1,$$

(8)

$$G_n(1)+G_n(0)=0,\hspace{1em}n>1,$$

(9)

Also, by using them in Relations (5) and (9), we can write the following:

$$G_n(x)={\displaystyle {\int }_0^{x}n{G}_{n-1}(x)dx}+G_n,\hspace{1em}n\ge 1.$$

(10)

For more information, you can refer to References [27] and [28], which discuss the Genocchi polynomials extensively.

2.2. Approximation of Arbitrary Function by Applying Genocchi Polynomials

The approximation theory plays an important role in solving a variety of differential equations. The main goal of this section is to approximate the arbitrary function $f(x)\in L^2[0,1]$ by Genocchi polynomials. Let $\{G_1(x),G_2(x),\dots ,G_N(x)]\subseteq L^2[0,1]$ be the set of Genocchi polynomials and $P=span\{G_1(x),G_2(x),\dots ,G_N(x)\}$. Since $P$ is a finite dimensional subspace of the $L^2[0,1]$ space, therefore $f(x)$ as an arbitrary element of the $L^2[0,1]$ space has a unique best approximation in $P$, say $f^{*}(x)$, such that

$${‖f(x)-f^{*}(x)‖}_2\le {‖f(x)-y(x)‖}_2:\hspace{0.33em}\forall \hspace{0.33em}y(t)\in P.$$

(11)

Therefore, inequality (11) requires that the following equation to be true.

$$\langle f(x)-f^{*}(x),y(t)\rangle =0:\hspace{0.33em}\forall \hspace{0.33em}y(t)\in P.$$

(12)

where $\langle .,.\rangle$ denotes the inner product.

Any arbitrary function $f(x)\in L^2[0,1]$ can be expanded in the finite series to the number of the Genocchi polynomials as follows:

$$f(x)\approx f^{*}(x)={\displaystyle \sum _{n=1}^N{c}_n{G}_n(x)=C^{T}G(x)},$$

(13)

where $T$ means transpose and the Genocchi coefficient vector $C$ and Genocchi vector $G(x)$ are given by the following:

$$C={[c_1,c_2,\dots ,c_N]}^T,\hspace{1em}\hspace{1em}G(x)={[G_1(x),G_2(x),\dots ,G_N(x)]}^T.$$

(14)

Hence, the coefficient $c_n$ can be obtained using the Genocchi polynomials as follows:

$$c_n=\frac{1}{2n!}\left(f^{(n-1)}(0)+f^{(n-1)}(1)\right),\hspace{1em}\hspace{1em}n=1,\dots ,N.$$

(15)

Of course, we have to note the important fact that calculating the approximation coefficient by the Genocchi polynomials in Equation (15) for a function that is not $(n-1)$ differentiable at the points $x=0,\hspace{1em}x=1$ leads to failure. The following example illustrates the problem.

Let $N=3,\hspace{1em}f(x)=x^{3/2},\hspace{1em}f(x)={\displaystyle \sum _{n=1}^3{c}_n{G}_n(x)}=c_1{G}_1(x)+c_2{G}_2(x)+c_3{G}_3(x);$

$$\begin{array}{l}{c}_3=\frac{1}{2\times 3!}\left[{\left.\frac{d^2}{d{x}^2}{x}^{3/2}\right|}_{x=0}+{\left.\frac{d^2}{d{x}^2}{x}^{3/2}\right|}_{x=1}\right]\\ =\frac{1}{2\times 3!}\left[{\left.\frac{1}{4\sqrt{x}}\right|}_{x=0}+{\left.\frac{1}{4\sqrt{x}}\right|}_{x=1}\right].\end{array}$$

(16)

To avoid this problem for functions that are not $(n-1)$ differentiable at points $x=0,\hspace{1em}x=1$, we use the matrix approach taken in the next section to compute the unknown approximation coefficients.

2.3. Using the Matrix Approach to Compute the Genocchi Approximation Coefficients

In this section, we compute the Genocchi coefficient vector $C$ using the matrix method. Before we apply this approach, we need to demonstrate and verify the following theorems. We first introduce Theorem 1, which gives the expression and proof of integration of the two Genocchi polynomials on arbitrary interval $[a,b],\hspace{1em}0\le a\le b$ which will be used to prove Theorem 2. Therefore, the proof of Theorem 1 is of particular important.

Theorem 1.

Let us assume that$G_n(x)$and$G_m(x)$are twoGenocchi polynomials for$x\ge 0$:

$$\begin{array}{lll}{\gamma }_{n,m}(x)& =& {\displaystyle {\int }_0^x{G}_n(x)G_m(x)dx}\\ & =& {\displaystyle \sum _{r=0}^{n-1}{(-1)}^r\frac{n_{(r)}}{{(m+1)}^{(r+1)}}\left(G_{n-r}(x)G_{m+1+r}(x)-G_{n-r}(0)G_{m+1+r}(0)\right)},\end{array}$$

(17)

where  $n_{(r)},\hspace{1em}{(m+1)}^{(r+1)}$ are respectively the falling and rising factorials. In particular, we have the following relations for $[a,b],\hspace{1em}0\le a\le b$:

$$\begin{array}{lll}{\gamma }_{n,m}^{(a,b)}& =& {\displaystyle {\int }_a^b{G}_n(x)G_m(x)dx}={\gamma }_{n,m}(b)-{\gamma }_{n,m}(a)\\ & =& {\displaystyle \sum _{r=0}^{n-1}{(-1)}^r\frac{n_{(r)}}{{(m+1)}^{(r+1)}}\left(G_{n-r}(b)G_{m+1+r}(b)-G_{n-r}(a)G_{m+1+r}(a)\right)},\\ {\gamma }_{n,m}^{(0,1)}& =& {\displaystyle \sum _{r=0}^{n-1}{(-1)}^r\frac{n_{(r)}}{{(m+1)}^{(r+1)}}\left(G_{n-r}(1)G_{m+1+r}(1)-G_{n-r}(0)G_{m+1+r}(0)\right)},\end{array}$$

(18)

Proof. 

See [26]. □

On the other hand, by applying Theorem 1, we can calculate the arbitrary function approximation coefficients with the matrix approach by using the following theorem.

Theorem 2.

Suppose that$f(x)\in L^2[0,1]$is an arbitrary function and $\{G_i(x):\hspace{1em}i=1,\dots ,N\}$is the set of the Genocchi polynomials up to order$N$. Let$Y=span\{G_1,\dots ,G_N\}$. Since$Y$is a finitedimensional closed subspace of$L^2[0,1]$, then$\exists f^{*}(x)\in Y$is the unique best approximation in the Genocchi polynomials such that any arbitrary function$f(x)$can be expressed in terms of the Genocchi polynomials by unique coefficient$c_n,\hspace{1em}n=0,1,\dots ,N$:

$$f(x)\approx f^{*}(x)={\displaystyle \sum _{n=1}^N{c}_n{G}_n(x)=C^{T}G(x)},$$

(19)

where$C$consisting of the unique coefficient is called the Genocchi coefficient matrix$C$ given by the following:

$$C^T=F^T{T}^{{(0,1)}^{-1}},$$

(20)

where $F={\displaystyle {\int }_0^{1}f(x)G_m(x)dx ,\hspace{1em}m=0,1,\dots ,N }$ and $T^{(0,1)}={\left[{\displaystyle {\int }_0^1{G}_n(x)G_m(x)dx}\right]}_{N\times N}$ is the matrix derived in Theorem 1.

Proof. 

Assume that $f(x)\in L^2[0,1]$. Therefore, this arbitrary function can be approximated using Equation (13) as follows:

$$f(x)\approx {\displaystyle \sum _{n=1}^N{c}_n{G}_n(x)=C^{T}G(x)},$$

(21)

Therefore,

$$\begin{array}{lll}{\displaystyle {\int }_0^{1}f(x)G_m(x)dx}& =& {\displaystyle {\int }_0^1\left({\displaystyle \sum _{n=1}^N{c}_n{G}_n(x)}\right)}{G}_m(x)dx\\ & =& {\displaystyle \sum _{n=1}^N{c}_n{\displaystyle {\int }_0^1{G}_n(x)G_m(x)dx}}.\end{array}$$

(22)

Let the first side of Equation (22) have $f_m={\displaystyle {\int }_0^{1}f(x)G_m(x)dx }$ alternatives; thus, we have the following:

$$\begin{array}{lll}{f}_m& =& {\displaystyle {\int }_0^1\left({\displaystyle \sum _{n=1}^N{c}_n{G}_n(x)}\right)}{G}_m(x)dx\\ & =& {\displaystyle \sum _{n=1}^N{c}_n{\displaystyle {\int }_0^1{G}_n(x)G_m(x)dx}},\\ m& =& 1,\dots ,N.\end{array}$$

(23)

In fact, we can construct Equation (23) as a system of $N$ equations for which the matrix representation of the device is as follows:

$$\begin{array}{l}\left[\begin{array}{c}{f}_1\\ \begin{array}{l}.\\ .\\ .\end{array}\\ f_N\end{array}\right]=\left[c_1,\dots ,c_N\right]\hspace{0.33em}\left[\begin{array}{ccc}{\gamma }_{1,1}^{(0,1)}& \dots & {\gamma }_{1,N}^{(0,1)}\\ {\gamma }_{2,1}^{(0,1)}& \dots & {\gamma }_{2,N}^{(0,1)}\\ .& ....& .\\ .& \dots & .\\ .& \dots & .\\ {\gamma }_{N,1}^{(0,1)}& \dots & {\gamma }_{N,N}^{(0,1)}\end{array}\right],\\ \\ { \mathrm{F}}^T=C^T{T}^{(0,1)}\end{array}$$

(24)

Therefore, we have the Genocchi coefficient matrix $C$ as follows:

$$C^T=F^T{T}^{{(0,1)}^{-1}},$$

(25)

where ${\gamma }_{i,j}$ can be calculated by using Theorem 1. □

3. Implementation of the Genocchi Polynomial Method for Solving Nonlinear Volterra Integral Equations with Weakly Singular Kernels

In this section, we implement a new spectral approach based on the Genocchi polynomials to solve the following equation:

$$y(t)=f(t)-{\displaystyle {\int }_0^t\frac{s^{\beta }}{{(t-s)}^{\alpha }}g(y(s))ds}\hspace{0.33em},\hspace{1em}\hspace{1em}t>0,$$

where $f\left(t\right)$ is in $L^2\left(\Re \right)$ on the interval $0\le t,s\le T$; $g$ is locally Lipchitz continuous, smooth, and a Hammerstein nonlinear function; and $\alpha , \hspace{0.33em}\beta$ are real positive numbers.

Let us assume that function $f(x)\in L^2[0,1]$ is arbitrary; then, we can approximate it, as follows:

$$f(x)\approx {\displaystyle \sum _{n=1}^N{c}_n{G}_n(x)=C^{T}G(x)}=C^{T}G{X}_x,$$

(26)

where $C={[c_1,c_1,\dots ,c_N]}^T$ is a vector of unknown coefficient; $X_x={[1,x,x^2,\dots ,x^n]}^T$; and $G(x)={[G_1(x),G_2(x),\dots ,G_N(x)]}^T=G{X}_x$, where $G$ is a $n\times n$ matrix of coefficients that can be approximated by $X_x$.

Thus, we need to compute the following integral before applying the new approach to solve Equation (1).

$${\displaystyle {\int }_0^x\frac{t^m}{{(x-t)}^{\alpha }}dt}=\frac{\mathsf{\Gamma }(1-\alpha )\mathsf{\Gamma }(m+1)}{\mathsf{\Gamma }(m-\alpha +2)}{x}^{(m-\alpha +1)}\hspace{0.33em},\hspace{1em}m=0,1,\dots .$$

(27)

Therefore, by considering Relation (27), we let

$$z(s)=g(y(s)),\hspace{1em}0\le s\le 1.$$

(28)

since we have

$$y(t)=f(t)-{\displaystyle {\int }_0^t\frac{s^{\beta }}{{(t-s)}^{\alpha }}g(y(s))ds}\hspace{0.33em},\hspace{1em}\hspace{1em}t>0.$$

(29)

By substituting Equation (29) into Equation (28), we have

$$z(t)=g(f(t)-{\displaystyle {\int }_0^t\frac{s^{\beta }}{{(t-s)}^{\alpha }}g(y(s))ds}),\hspace{1em}0\le t\le 1.$$

(30)

We approximate Equation (30) as follows:

$$C^{T}G(t)=g(f(t)-{\displaystyle {\int }_0^t\frac{s^{\beta }}{{(t-s)}^{\alpha }}{C}^{T}G{X}_{s}ds}),\hspace{1em}0\le t\le 1,$$

(31)

and

$$C^{T}G(t)=g(f(t)-C^T\hspace{0.33em}G{\displaystyle {\int }_0^t\frac{s^{\beta }}{{(t-s)}^{\alpha }}{X}_{s}ds}),\hspace{1em}0\le t\le 1.$$

(32)

Thus, we need to convert the integral part of Equation (32) to the matrix form. Therefore, by assuming $X_s={\left[1,s,s^2,\dots ,s^n\right]}^T$, we can write the following:

$$\begin{array}{lll}{\displaystyle {\int }_0^t\frac{s^{\beta }}{{(t-s)}^{\alpha }}.X_{s}ds}& =& {\left[{\displaystyle {\int }_0^t\frac{s^{\beta }}{{(t-s)}^{\alpha }}ds,\hspace{0.33em}{\displaystyle {\int }_0^t\frac{s^{\beta }}{{(t-s)}^{\alpha }}.sds,\hspace{0.33em}\dots ,{\displaystyle {\int }_0^t\frac{s^{\beta }}{{(t-s)}^{\alpha }}.s^{n}ds,\hspace{0.33em}\dots }}}\right]}^T\\ & =& {\left[{\displaystyle {\int }_0^t\frac{s^{\beta }}{{(t-s)}^{\alpha }}ds,\hspace{0.33em}{\displaystyle {\int }_0^t\frac{s^{\beta +1}}{{(t-s)}^{\alpha }}ds,\hspace{0.33em}\dots ,{\displaystyle {\int }_0^t\frac{s^{\beta +n}}{{(t-s)}^{\alpha }}ds,\hspace{0.33em}\dots }}}\right]}^T,\end{array}$$

(33)

and using Equation (27), we have

$${\displaystyle {\int }_0^t\frac{s^{\beta +m}}{{(t-s)}^{\alpha }}ds}=\frac{\mathsf{\Gamma }(1-\alpha )\mathsf{\Gamma }(\beta +m+1)}{\mathsf{\Gamma }(\beta +m-\alpha +2)}{t}^{(\beta +m-\alpha +1)}\hspace{0.33em},\hspace{1em}m=0,1,2,\dots .$$

(34)

Therefore, by using Relation (34), we can rewrite Equation (33) as follows:

$$\begin{array}{c}{\displaystyle {\int }_0^t\frac{s^{\beta }}{{(t-s)}^{\alpha }}.X_{s}ds}=\left[\frac{\mathsf{\Gamma }(1-\alpha )\mathsf{\Gamma }(\beta +1)}{\mathsf{\Gamma }(\beta -\alpha +2)}{t}^{(\beta -\alpha +1)}\hspace{0.33em},\hspace{1em}\frac{\mathsf{\Gamma }(1-\alpha )\mathsf{\Gamma }(\beta +2)}{\mathsf{\Gamma }(\beta -\alpha +3)}{t}^{(\beta -\alpha +2)}\hspace{0.33em},\dots \right.\\ {\left. ,\frac{\mathsf{\Gamma }(1-\alpha )\mathsf{\Gamma }(\beta +m+1)}{\mathsf{\Gamma }(\beta +m-\alpha +2)}{t}^{(\beta +m-\alpha +1)}\hspace{0.33em},\dots \right]}^T.\end{array}$$

(35)

If we consider ${\gamma }_{m,m}=\frac{\mathsf{\Gamma }(1-\alpha )\mathsf{\Gamma }(\beta +m+1)}{\mathsf{\Gamma }(\beta +m-\alpha +2)}\hspace{0.33em},\hspace{1em}m=0,1,2,\dots$, then, we can reconstruct Equation (35) in the matrix form as follows:

$${\displaystyle {\int }_0^t\frac{s^{\beta }}{{(t-s)}^{\alpha }}.X_{s}ds}=\left[\begin{array}{ccccc}{\gamma }_{0,0}& 0& 0& \cdots & 0\\ 0& {\gamma }_{1,1}& 0& 0& 0\\ 0& 0& {\gamma }_{2,2}& 0& 0\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ 0& 0& 0& \cdots & {\gamma }_{m,m}\end{array}\right]\left[\begin{array}{c}{t}^{\beta -\alpha +1}\\ t^{\beta -\alpha +2}\\ ⋮\\ t^{\beta +m-\alpha +1}\\ ⋮\end{array}\right]=\mathsf{\Omega }\hspace{0.33em}\mathsf{\Pi },$$

(36)

where $\mathsf{\Omega }$ is an infinite diagonal matrix and

$$\mathsf{\Pi }={\left[t^{\beta -\alpha +1},t^{\beta -\alpha +2},\cdots ,t^{\beta +m-\alpha +1},\cdots \right]}^T.$$

(37)

Now, each element of infinite vector $\mathsf{\Pi }$ can be approximated by using the Genocchi polynomials as follows:

$$t^{\beta +m-\alpha +1}={\displaystyle \sum _{i=1}^{\infty }{a}_{m,i}{G}_i(t)={\partial }_m}G{X}_t\hspace{0.33em},\hspace{1em}{\partial }_m=\left[a_{m,1},a_{m,2},\dots \right],\hspace{1em}m=0,1,\dots ,$$

(38)

and we obtain

$$\mathsf{\Pi }={\left[{\partial }_{1}G{X}_t,{\partial }_{2}G{X}_t,\dots ,{\partial }_{m}G{X}_t,\dots \right]}^T=AG{X}_t,\hspace{1em}A={\left[{\partial }_1,{\partial }_2,\dots ,{\partial }_m,\dots \right]}^T.$$

(39)

Substituting (39) in (32), we have

$${\displaystyle {\int }_0^t\frac{s^{\beta }}{{(t-s)}^{\alpha }}.X_{s}ds}==\mathsf{\Omega }AG{X}_t.$$

(40)

By using Equations (40) and (39), we get

$$C^{T}G(t)=g(f(t)-C^T\hspace{0.33em}G\mathsf{\Omega }AG{X}_t),\hspace{1em}0\le t\le 1.$$

(41)

We select $N$ nodal points of the Newton–Cotes rule for finding vector $C$ as follows:

$$x_p=\frac{2p-1}{2N},\hspace{1em}p=1,2,\dots ,N,$$

(42)

By collocating Equation (41) at the points $x_p$, we have

$$\begin{array}{l}{C}^{T}G(x_p)=g(f(x_p)-C^T\hspace{0.33em}G\mathsf{\Omega }AG{X}_{x_p}),\hspace{1em}0\le t\le 1,\\ p=1,2,\dots ,N.\end{array}$$

(43)

We can solve the nonlinear system (43) by using the Newton iteration scheme to calculate unknown vector $C.$ After calculating unknown vector $C$ by solving the nonlinear Equation (43), we use Equations (29), (31), and (32) to obtain the approximate solution of Equation (1), as follows:

$$y_n(t)=f(t)-C^T\hspace{0.33em}G\mathsf{\Omega }AG(t),\hspace{1em}0\le t\le 1.$$

(44)

4. Error Analysis

In this section, we perform error estimation of the approximation solution to find the error boundaries of the new numerical approach by applying the Genocchi polynomials. Consider the nonlinear Volterra integral equations with weakly singular kernels of the form Equation (1),

We suppose that $\mathsf{\Omega }=L^2[0,1]$, $\{G_1(t),\hspace{0.33em}{G}_2(t),\dots ,G_n(t)\}\subset \mathsf{\Omega }$, and $T=Span\{G_1(t),\hspace{0.33em}{G}_2(t),\dots ,G_n(t)\}$. Here, we let $y(t)$ be an arbitrary function of $\mathsf{\Omega }$, so, it has the best approximation of $T$. Let $y_n\in T$, that is,

$$\exists y_n\in T\hspace{0.33em}:\hspace{0.33em}\forall h\in T\hspace{1em}{‖y-y_n‖}_2\le {‖y-h‖}_2\hspace{0.33em},$$

(45)

where ${‖y(t)‖}_2^2={{\displaystyle {\int }_0^1\left|y(t)\right|}}^{2}dt$. $y(t)$ is approximated by using the truncated Genocchi polynomials:

$$y(t)\simeq y_n={\displaystyle \sum _{n=1}^N{c}_n{G}_n(t)=C^{T}G(t),}$$

(46)

where $C^T=[c_1,c_2,\dots ,c_N]$ and $G(x)={[G_1(x),G_2(x),\dots ,G_N(x)]}^T$.

In the following study, we present an upper bound for the error of Equation (45). Let $e_n(t)=y(t)-y_n(t)$ be the error function of Equation (1), where $y(t),y_n\left(t\right)$ are the exact and approximate solutions

Therefore, the mean error bound is presented as follows:

$$\begin{array}{lll}{‖e_n(t)‖}_2^2& =& {‖y(t)-y_n(t)‖}_2={\displaystyle {\int }_0^1{\left|y(t)-y_n(t)\right|}^{2}dt}\\ & =& {\displaystyle {\int }_0^1{\left|\left(f(t)-{\displaystyle {\int }_0^t\frac{s^{\beta }}{{(t-s)}^{\alpha }}g(y(s))ds}\right)-\left(f(t)-{\displaystyle {\int }_0^t\frac{s^{\beta }}{{(t-s)}^{\alpha }}g(y_n(s))ds}\right)\right|}^{2}dt}\\ & =& {\displaystyle {\int }_0^1{\left|{\displaystyle {\int }_0^t\frac{s^{\beta }}{{(t-s)}^{\alpha }}\left(g(y(s))-g(y_n(s))\right)ds}\right|}^{2}dt}.\end{array}$$

(47)

On the other hand, $g(s)$ is continuous on the interval $[0,1]$ and locally Lipchitz continuous in $s\in R$; therefore, there is a constant $C_1>0$ such that

$$\left|g(y(s))-g(y_n(s))\right|\le C_1\left|y(s)-y_n(s)\right|.$$

(48)

Then, by using Equations (47) and (48), we have

$$\begin{array}{lll}{‖e_n(t)‖}_2^2& \le & {\displaystyle {\int }_0^1{\left({\displaystyle {\int }_0^t\frac{s^{\beta }}{{(t-s)}^{\alpha }}·C_1\left|y(s)-y_n(s)\right|ds}\right)}^{2}dt}\\ & =& {\displaystyle {\int }_0^1{\left({\displaystyle {\int }_0^t\frac{s^{\beta }}{{(t-s)}^{\alpha }}·C_1\left|y(s)-{\displaystyle \sum _{n=1}^N{c}_n{G}_n(s)}\right|ds}\right)}^{2}dt}\\ & =& {\displaystyle {\int }_0^1{\left({\displaystyle {\int }_0^t\frac{s^{\beta }}{{(t-s)}^{\alpha }}·C_1\left|{\displaystyle \sum _{n=N+1}^{\infty }{c}_n{G}_n(s)}\right|ds}\right)}^{2}dt}\\ & \le & {\displaystyle {\int }_0^1{\left({\displaystyle {\int }_0^t\frac{s^{\beta }}{{(t-s)}^{\alpha }}·C_1{\displaystyle \sum _{n=N+1}^{\infty }\left|c_n\right|\left|G_n(s)\right|}ds}\right)}^{2}dt}.\end{array}$$

(49)

By substituting (4) into (49), we get

$$\begin{array}{lll}{‖e_n(t)‖}_2^2& \le & {\displaystyle {\int }_0^1{\left({\displaystyle {\int }_0^t\frac{s^{\beta }}{{(t-s)}^{\alpha }}·C_1{\displaystyle \sum _{n=N+1}^{\infty }\left|c_n\right|\left|{\displaystyle \sum _{k=0}^n\left(\begin{array}{c}n\\ k\end{array}\right)}{G}_{n-k}{s}^k\right|}ds}\right)}^{2}dt}\\ & \le & {\displaystyle {\int }_0^1{\left({\displaystyle {\int }_0^t\frac{s^{\beta }}{{(t-s)}^{\alpha }}·C_1{\displaystyle \sum _{n=N+1}^{\infty }\left|c_n\right|{\displaystyle \sum _{k=0}^n\left(\begin{array}{c}n\\ k\end{array}\right)\left|G_{n-k}\right|s^k}}ds}\right)}^{2}dt}\\ & =& {{\displaystyle {\int }_0^1\left({\displaystyle \sum _{k=0}^n{\displaystyle \sum _{n=N+1}^{\infty }·C_1\left|c_n\right|\left(\begin{array}{c}n\\ k\end{array}\right)\left|G_{n-k}\right|{\displaystyle {\int }_0^t\frac{s^{\beta +k}}{{(t-s)}^{\alpha }}ds}}}\right)}}^{2}dt,\end{array}$$

(50)

where $\gamma (t,\beta ,\alpha )$ is defined by

$$\gamma (t,\beta ,\alpha )={\displaystyle {\int }_0^t\frac{s^{\beta }}{{(t-s)}^{\alpha }}ds=B(1-\alpha ,1+\beta )t^{1-\alpha +\beta }.}$$

(51)

On the other hand, $B(\alpha ,\beta )$ is the beta function that is usually defined by

$$B(\alpha ,\beta )={\displaystyle {\int }_0^1{\tau }^{\alpha -1}{(1-\tau )}^{\beta -1}d\tau ,\hspace{1em}(\mathrm{Re}(\alpha )>0,\hspace{1em}}\mathrm{Re}(\beta )>0).$$

(52)

Therefore, by using Inequality (51) and Equation (52), we get

$${‖e_n(t)‖}_2^2\le {{\displaystyle {\int }_0^1\left({\displaystyle \sum _{k=0}^n{\displaystyle \sum _{n=N+1}^{\infty }·C_1\left|c_n\right|\left(\begin{array}{c}n\\ k\end{array}\right)\left|G_{n-k}\right|B(1-\alpha ,1+\beta +k)t^{1-\alpha +\beta +k}}}\right)}}^{2}dt.$$

(53)

and

$${‖e_n(t)‖}_2\le \sqrt{{\displaystyle \sum _{k=0}^n{\displaystyle \sum _{n=N+1}^{\infty }\frac{1}{2(-\alpha +\beta +k)+3}{\left(C_1\left|c_n\right|\left(\begin{array}{c}n\\ k\end{array}\right)\left|G_{n-k}\right|B(1-\alpha ,1+\beta +k)\right)}^2}}}.$$

(54)

5. Illustrative Examples

In this section, two numerical examples are performed to check the perfection of the proposed method as well as the accuracy and efficiency of the Genocchi polynomials scheme.

In order to demonstrate the error of a new numerical approach based on Genocchi polynomials, we define the notations as follows:

$$\begin{array}{l}{e}_2\left(N\right)={‖y-y_n‖}_{\infty }=max\left|y-y_n\right|,\\ \hfill 0\le t\le 1\\ e_n(t)=\left|y-y_n\right|,\\ {\xi }_n={\left({\displaystyle {\int }_0^{T}w(t)e_n^2(t)dt}\right)}^{\frac{1}{2}},\end{array}$$

(55)

where $y\left(t\right)\hspace{0.17em}$ is the exact solution and $y_n(t)$ is the approximate function to the proposed method and we have $w\left(t\right)=1$. In our implementation, the calculations are done on a personal computer with core-i5 processor, 2.67 GHZ frequency, and 4 GB memory, and the codes were written in Mathematica 11 software.

Example 1.

We consider the following nonlinear Volterra integral equation which was proposed in [10]:

$$y\left(t\right)=t^{\frac{1}{3}}+\frac{4\mathsf{\Gamma }\left(\frac{4}{3}\right)\mathsf{\Gamma }\left(\frac{13}{6}\right)}{\sqrt{\pi }}{t}^{\frac{3}{2}}-{\displaystyle {\int }_0^t\frac{s^{1/2}{y}^2(s)}{{(t-s)}^{2/3}}ds, \mathrm{t}\in }[0,1].$$

(56)

The exact solution of this equation is $y\left(t\right)=t^{1/3}.$

We solved this equation with the proposed numerical method by using different values of N. The diagonal matrix $\mathsf{\Omega }$ with elements $\frac{\mathsf{\Gamma }\left[1-\alpha \right]\mathsf{\Gamma }\left[m+1+\beta \right]}{\mathsf{\Gamma }\left[m-\alpha +2+\beta \right]}, \mathrm{m}=0,1,\dots ,\mathrm{N},$ and vector $\mathsf{\Pi }$ for $N=5$ are obtain in the following forms:

$$\begin{gathered} \mathsf{\Omega }=\left(\begin{array}{cccccc}2.52393& 0& 0& 0& 0& 0\\ 0& 2.06503& 0& 0& 0& 0\\ 0& 0& 1.82209& 0& 0& 0\\ 0& 0& 0& 1.66364& 0& 0\\ 0& 0& 0& 0& 1.54891& 0\\ 0& 0& 0& 0& 0& 1.4604\end{array}\right), \\ \mathsf{\Pi }={[x^{5/6},x^{11/6},x^{17/6},x^{23/6},x^{29/6},x^{35/6}]}^T. \end{gathered}$$

Also, the unknown vector elements C are as follows:

$$\begin{array}{l}{c}_0=0.529883,c_1=0.598039,c_2=-0.351362,c_3=0.343517,\\ c_4=-0.104667, c_5=0.0717268\end{array}$$

After numerical computations, a system of algebraic nonlinear equations is obtained under the proposed method. Therefore, by solving this system, we obtain the approximate solution for $N=5$ as follows:

$$\begin{array}{lll}{y}_5(t)& =& f(t)-C^T\hspace{0.33em}G\mathsf{\Omega }AG(t)=t^{1/3}-0.151891t^{5/6}+2.18117t^{3/2}-3.56596t^{11/6}\\ & +& 3.71576t^{17/6}-4.02725t^{23/6}+2.47707t^{29/6}-0.628499t^{35/6}.\end{array}$$

According to the error boundaries in Relation (55), we have

$${‖e_5(t)‖}_2\le 0.000598532.$$

Figure 2 is devoted to comparing the exact solution with the approximate solution obtained from the proposed method for $N=5$. Observing Figure 2, overlap of the exact and approximate solutions shows the exactness and correctness of the proposed method. The absolute error functions with $N=5,10,18,20$ are shown in Figure 3, Figure 4, Figure 5, Figure 6. Therefore, these plots quickly explain that the proposed approach has small absolute errors.

We reported the numerical results of the exact and approximate solutions for various values $N$ on the interval $\left[0,1\right]$ in

Table 1. Approximate and exact values of nonlinear Volterra integral equations with $N=5,10,15,20$ for Example 1.

	$\mathit{N}=5$	$\mathit{N}=10$	$\mathit{N}=15$	$\mathit{N}=20$	${\mathit{y}}_{\mathit{E}\mathit{x}\mathit{a}\mathit{c}\mathit{t}}$
0.0	0.000000	0.000000	0.000000	0.000000	0.000000
0.2	0.585076	0.584768	0.584793	0.584797	0.584804
0.4	0.736620	0.736795	0.736802	0.736804	0.736806
0.6	0.843508	0.843427	0.843431	0.843434	0.843433
0.8	0.928164	0.928313	0.928317	0.928319	0.928318
1.0	1.00041	0.99996	1.000001	1.000001	1.000000

. On the other hand, numerical results are showed for different values $N$ in

Table 2. Numerical results of ${\zeta }_N$ for different values $N$ on the interval $[0,1]$ for Example 1.

$\mathit{N}$	${\mathit{\zeta }}_{\mathit{N}}$	Computing Time (s)
5	5.98532 × 10−4	0.321
10	1.14944 × 10−4	0.357
15	4.48214 × 10−5	0.420
20	2.85973 × 10−5	0.451

. The absolute error functions are displayed for various values of $N$ on the interval $\left[0,1\right]$ for this problem in

Table 3. The absolute error function of various values $N$ on the interval $[0,1]$ for Example 1.

$\mathit{t}$	${\mathit{e}}_5(\mathit{t})$	${\mathit{e}}_{10}(\mathit{t})$	${\mathit{e}}_{15}(\mathit{t})$	${\mathit{e}}_{20}(\mathit{t})$
0.0	0.000000000	0.0000000000	0.00000000	0.00000000
0.2	0.000272294	0.0000359627	0.00001089	6.67632 × 10−6
0.4	0.000185829	0.0000111075	3.8548 × 10−6	2.25757 × 10−6
0.6	0.000075540	5.5081 × 10−6	1.83763 × 10−6	9.72768 × 10−6
0.8	0.000153622	4.62581 × 10−6	1.11576 × 10−6	2.18163 × 10−6
1.0	0.000406512	0.0000397521	8.73408× 10−6	9.0017 × 10−6

. Also,

Table 4. Comparison of maximum absolute errors between a new approach approximate solution and Euler’s method on $[0,\epsilon ]$ for Example 1.

Euler’s Method [10]					Our Method (Genocchi Polynomials)
N	$\mathit{\epsilon }=0$	$\mathit{\epsilon }=0.01$	$\mathit{\epsilon }=0.02$	$\mathit{\epsilon }=0.03$	N	$\mathit{\epsilon }=0$	$\mathit{\epsilon }=0.01$	$\mathit{\epsilon }=0.02$	$\mathit{\epsilon }=0.03$
	${\mathit{e}}_{\infty }(\mathit{N})$	${\mathit{e}}_{\infty }(\mathit{N})$	${\mathit{e}}_{\infty }(\mathit{N})$	${\mathit{e}}_{\infty }(\mathit{N})$		${\mathit{e}}_{\infty }(\mathit{N})$	${\mathit{e}}_{\infty }(\mathit{N})$	${\mathit{e}}_{\infty }(\mathit{N})$	${\mathit{e}}_{\infty }(\mathit{N})$
80	0.67 × 10−2	6.60 × 10−3	6.50 × 10−3	6.30 × 10−3	5	0.000	1.851 × 10−3	2.343 × 10−3	2.427 × 10−3
160	3.21 × 10−3	3.10 × 10−3	3,10 × 10−3	3.03 × 10−3	10	0.000	6.595 × 10−4	6.704 × 10−4	6.704 × 10−4
320	1.55 × 10−3	1.50 × 10−3	1.50 × 10−3	1.50 × 10−3	15	0.000	3.193 × 10−4	3.193 × 10−4	3.178 × 10−4
640	753 × 10−4	7.40 × 10−4	7.20 × 10−4	7.20 × 10−4	20	0.000	2.305 × 10−4	2.305 × 10−4	2.305 × 10−4

compares the numerical results of a new proposed numerical approach with Euler’s method [10] for different values of $N$. Also, Table 4 indicates that the new numerical method has better accuracy and efficiency compared to the old method.

Example 2.

Next, we discuss the following Lighthill’s equation which was proposed in [10] and extensively studied in [10,29,30]. The authors employed the iterative method and schemes to solve this integral equation.

$$y\left(t\right)=1-\frac{\sqrt{3}}{\pi }{\displaystyle {\int }_0^t\frac{s^{\frac{1}{3}}{y}^4(s)}{{(t-s)}^{\frac{2}{3}}}ds, \mathrm{t}\in }[0,1].,$$

(57)

The numerical results for this example are obtained by the presented approach for different values of $N$ and are given in

Table 5. Numerical results on the interval $[0,\epsilon ]$, with $\epsilon =0.002$ for Example 2.

$\mathit{N}$	${\mathit{\zeta }}_{\mathit{N}}$	Computing Time (s)
5	1.912914 × 10−4	0.351
10	1.087754 × 10−4	0.402
15	9.106063 × 10−5	0.457
20	7.200394 × 10−5	0.530

and

Table 6. The approximate solutions by different values of N and M for Example 2.

${‖{\mathit{y}}_{\mathit{N}}-{\mathit{y}}_{\mathit{M}}‖}_{\infty }$
$\mathit{t}$	$\mathit{N}=5; \mathrm{M}=7$	$\mathit{N}=7; \mathrm{M}=10$	$\mathit{N}=10; \mathrm{M}=12$	$\mathit{N}=12; \mathrm{M}=13$
0.0000	1.11022 × 10−16	1.12022 × 10−16	0.000000000	0.000000000
0.0004	0.000507344	0.000477524	0.000214749	0.0000875408
0.0008	0.000800212	0.000750437	0.000336102	0.0001366621
0.0012	0.001041861	0.000973492	0.000434214	0.0001761062
0.0016	0.001254042	0.001167461	0.000518585	0.0002097873
0.002	0.001445845	0.001341082	0.000593241	0.000239374

. Also, in

Table 7. Comparison of maximum absolute errors $e_{\infty }(N)={‖y_2-y_N‖}_{ \infty }$ between our method (Genocchi polynomials) and Euler’s method: the Picard iterate $y_2$ was used on $[0,\epsilon ]$ for Example 2.

Euler’s Method [10]				Our Method (Genocchi Polynomials)
N	$\mathit{\epsilon }=0.002$	$\mathit{\epsilon }=0.003$	$\mathit{\epsilon }=0.008$	N	$\mathit{\epsilon }=0.002$	$\mathit{\epsilon }=0.003$	$\mathit{\epsilon }=0.008$
	${\mathit{e}}_{\infty }(\mathit{N})$	${\mathit{e}}_{\infty }(\mathit{N})$	${\mathit{e}}_{\infty }(\mathit{N})$		${\mathit{e}}_{\infty }(\mathit{N})$	${\mathit{e}}_{\infty }(\mathit{N})$	${\mathit{e}}_{\infty }(\mathit{N})$
40	3.60 × 10−2	3.00 × 10−2	1.70 × 10−2	5	6.165 × 10−3	7.441 × 10−3	9.878 × 10−3
80	2.10 × 10−2	1.7 × 10−2	9.10 × 10−3	10	3.378 × 10−3	3.386 × 10−3	4.162 × 10−3
160	1.01 × 10−2	8.4 × 10−3	4.00 × 10−3	12	2.785 × 10−3	3.113 × 10−3	3.222 × 10−3
320	4.00 × 10−3	3.00 × 10−3	1.30 × 10−3	15	2.151 × 10−3	2.311 × 10−3	2.232 × 10−3

, the maximum absolute errors can be compared with those that were achieved by Euler’s method in [10] by different values of $N$ on the interval $[0,\epsilon ]$. We can see that our proposed method is very fast compared to Euler’s method. Figure 7 displays the convergence approximate solutions using our method (Genocchi polynomials) and the Picard iteration $y_2\hspace{0.17em}$ with different values of $N$ on the interval $[0,\epsilon ]$ with $\epsilon =0.002$ for this problem.

6. Conclusions and Future Work

In the study of many nonlinear problems in heat conduction, boundary-layer heat transfer, chemical kinetics, and superfluidity, we are often led to singular Volterra integral equations that are difficult to solve analytically. In this article, a spectral method based on Genocchi polynomials is presented for solving nonlinear Volterra integral equations with weakly singular kernels. An error analysis of the spectral approach has been done. Two numerical examples are provided to confirm the applicability and accuracy of the scheme. Also, the proposed method results have been compared with Euler’s method to show the superiority of the present method with better results in smaller N. For future works, we can use other polynomials like Chebyshev, Lagger, etc. for implementation, and by comparing the archived results, we can expand the present method and implement it on the system of nonlinear Volterra integral equations and nonlinear Volterra integral equations of mix type or the first kind of Volterra integral equations with discontinuous kernels.