Effects of Second-Order Velocity Slip and the Different Spherical Nanoparticles on Nanofluid Flow
Abstract
1. Introduction
2. Mathematical Analysis
3. Boundary Conditions
4. Application of HAM
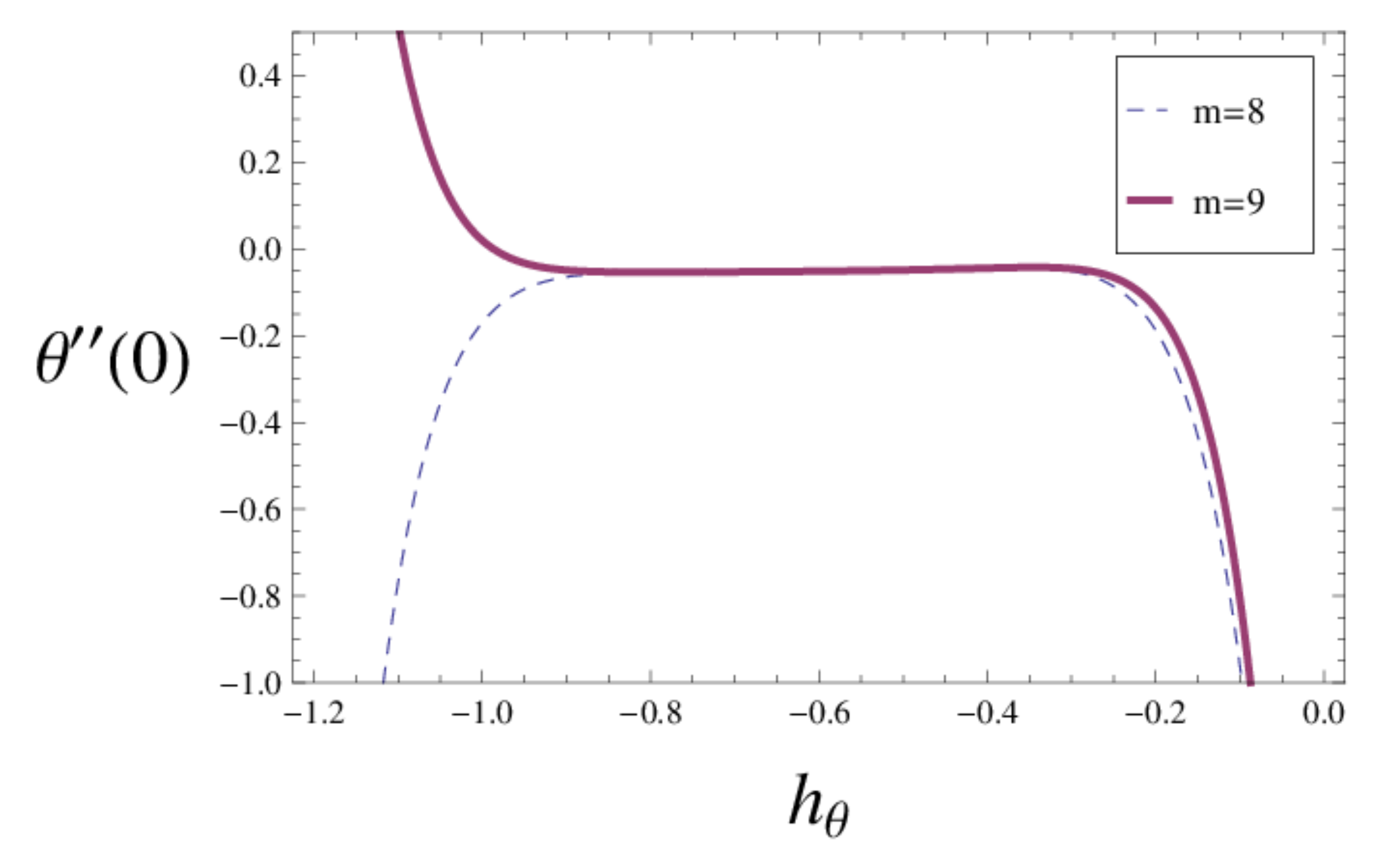
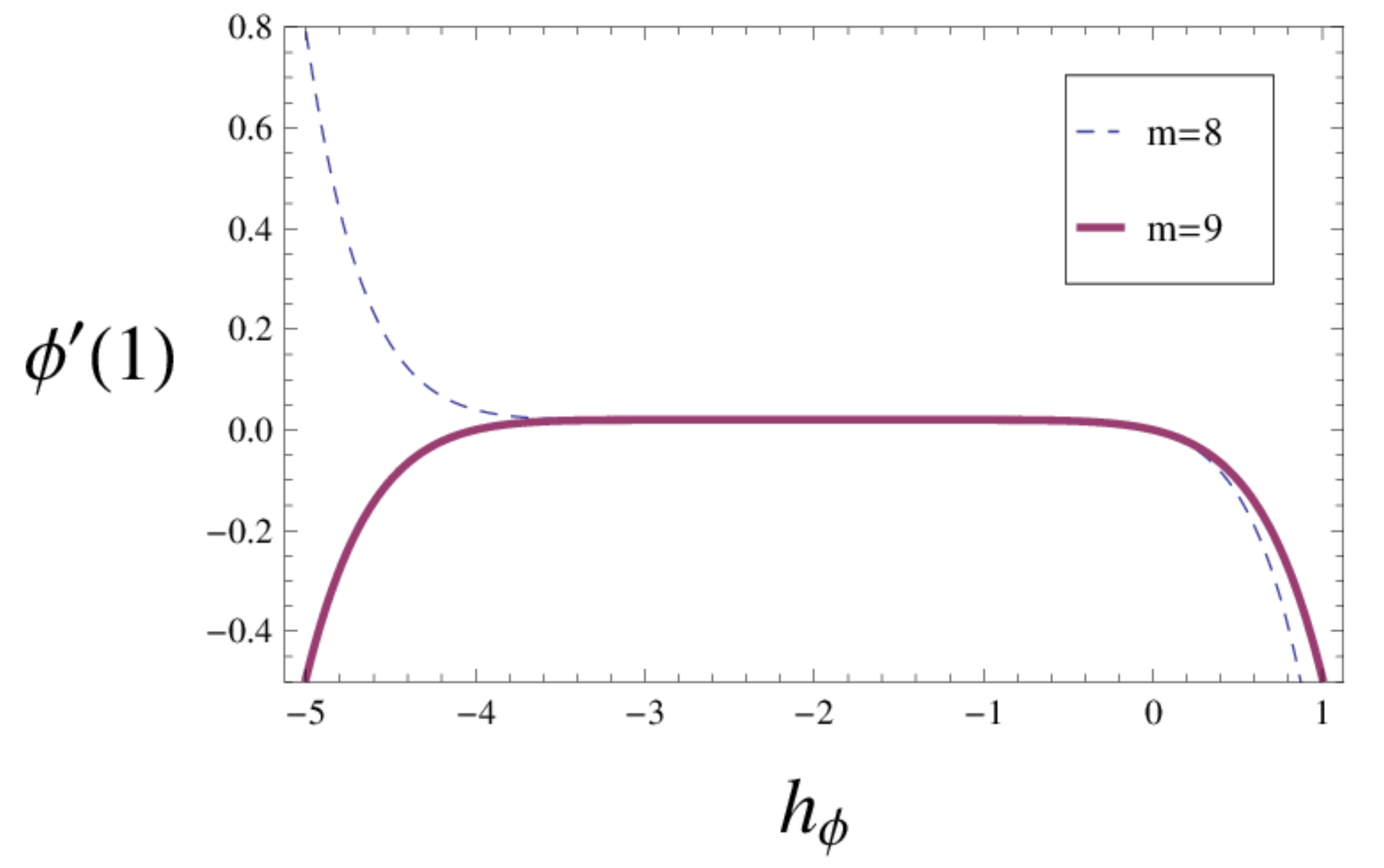
5. Convergence of the HAM Solutions
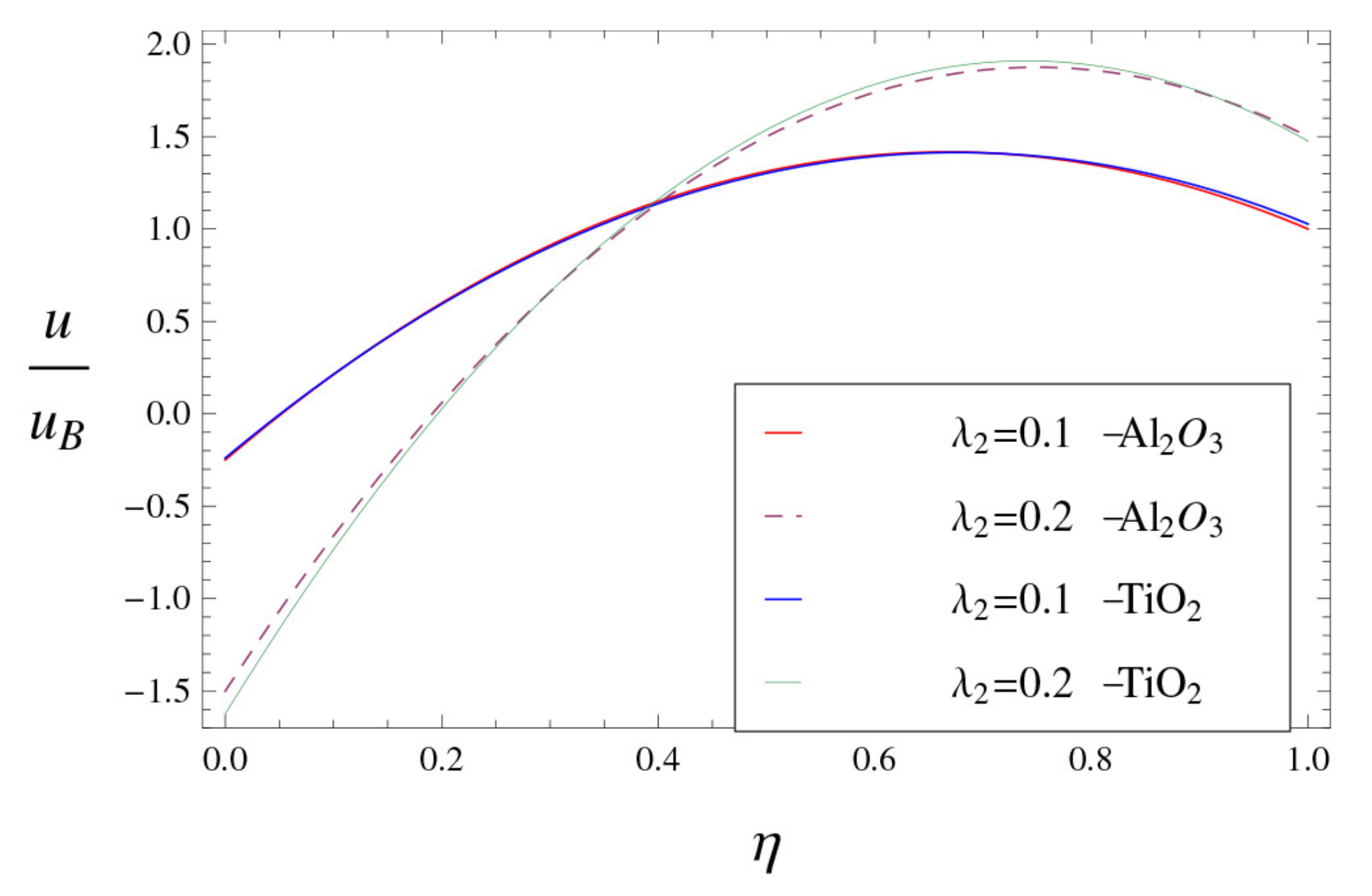
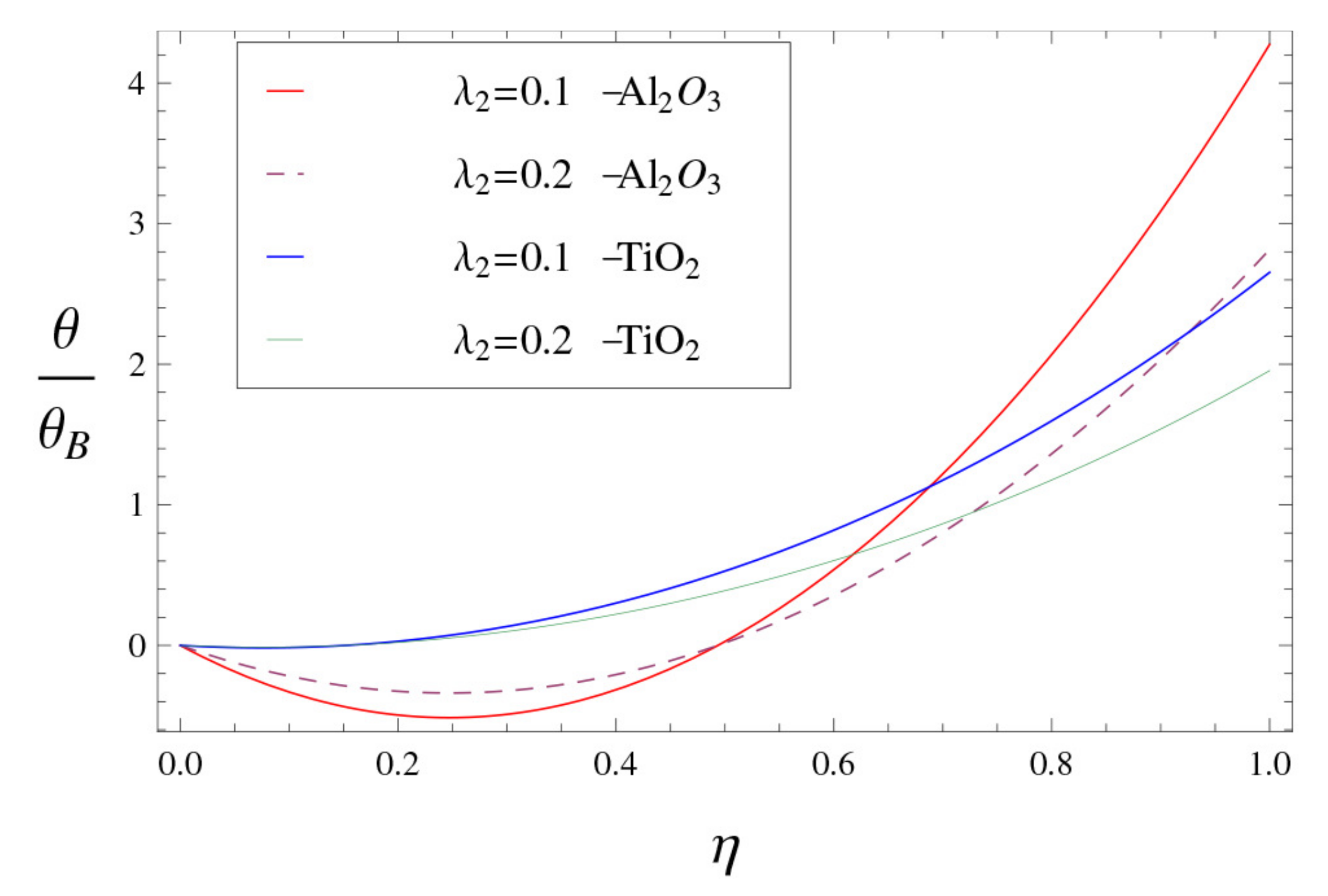
6. Results and Discussion
7. Conclusions
- a
- The semi-analytical relation between and is obtained.
- b
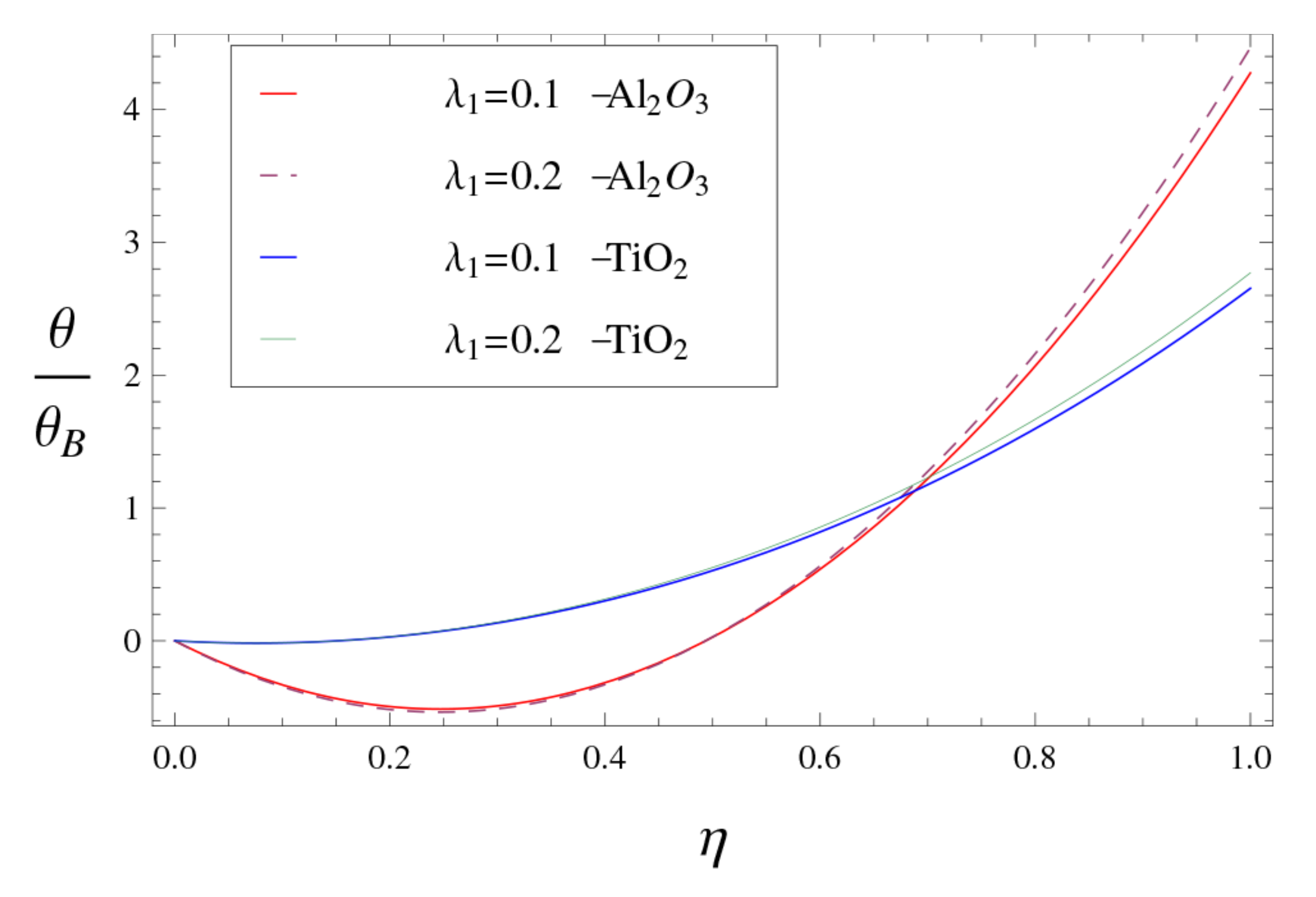
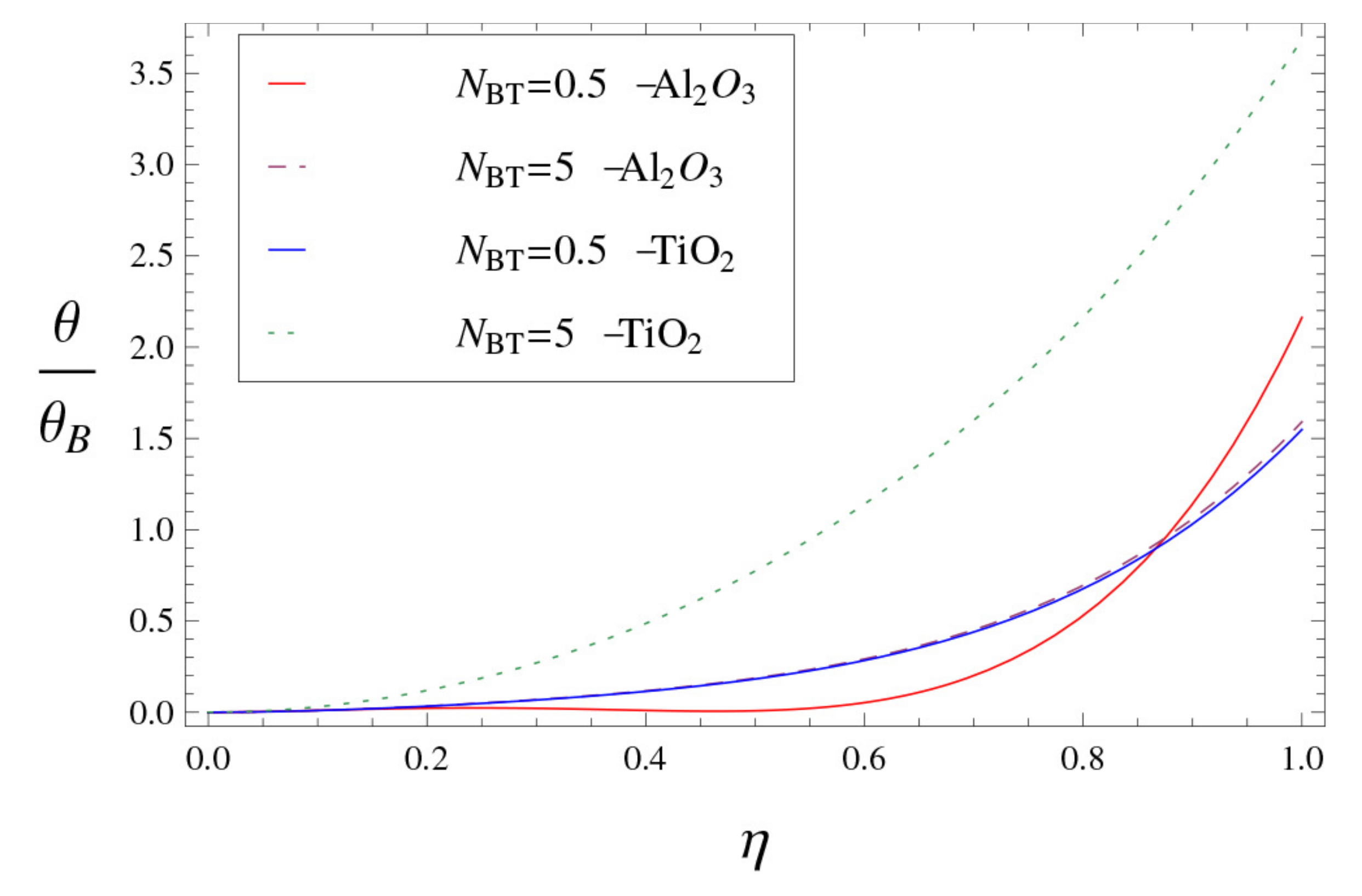
- Both first-order slip parameter and second-order slip parameter have positive effects on of the MHD flow, but nanofluids can transfer heat more efficiently with a second-order slip condition than with a Navier’s condition.
- c
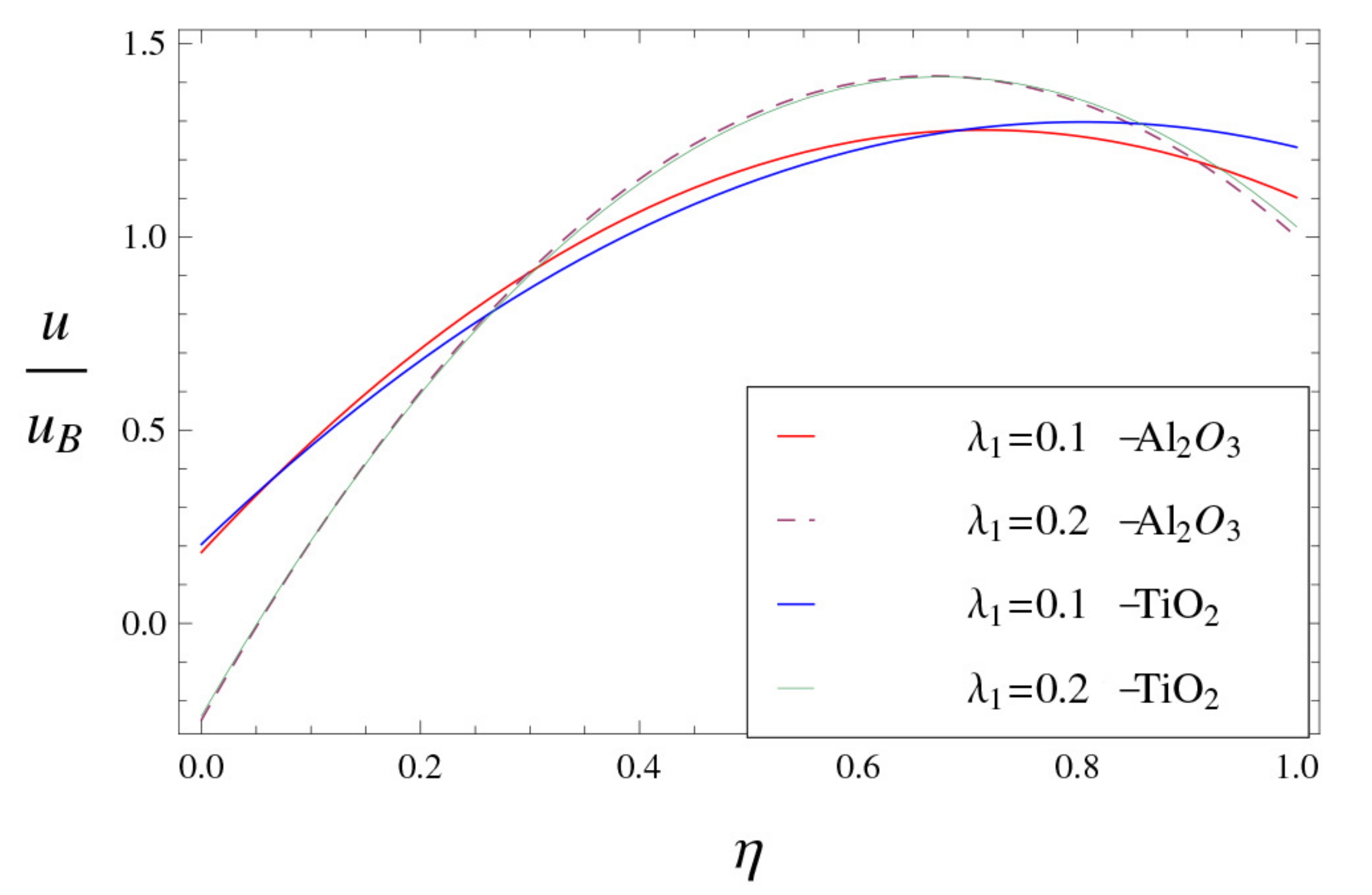
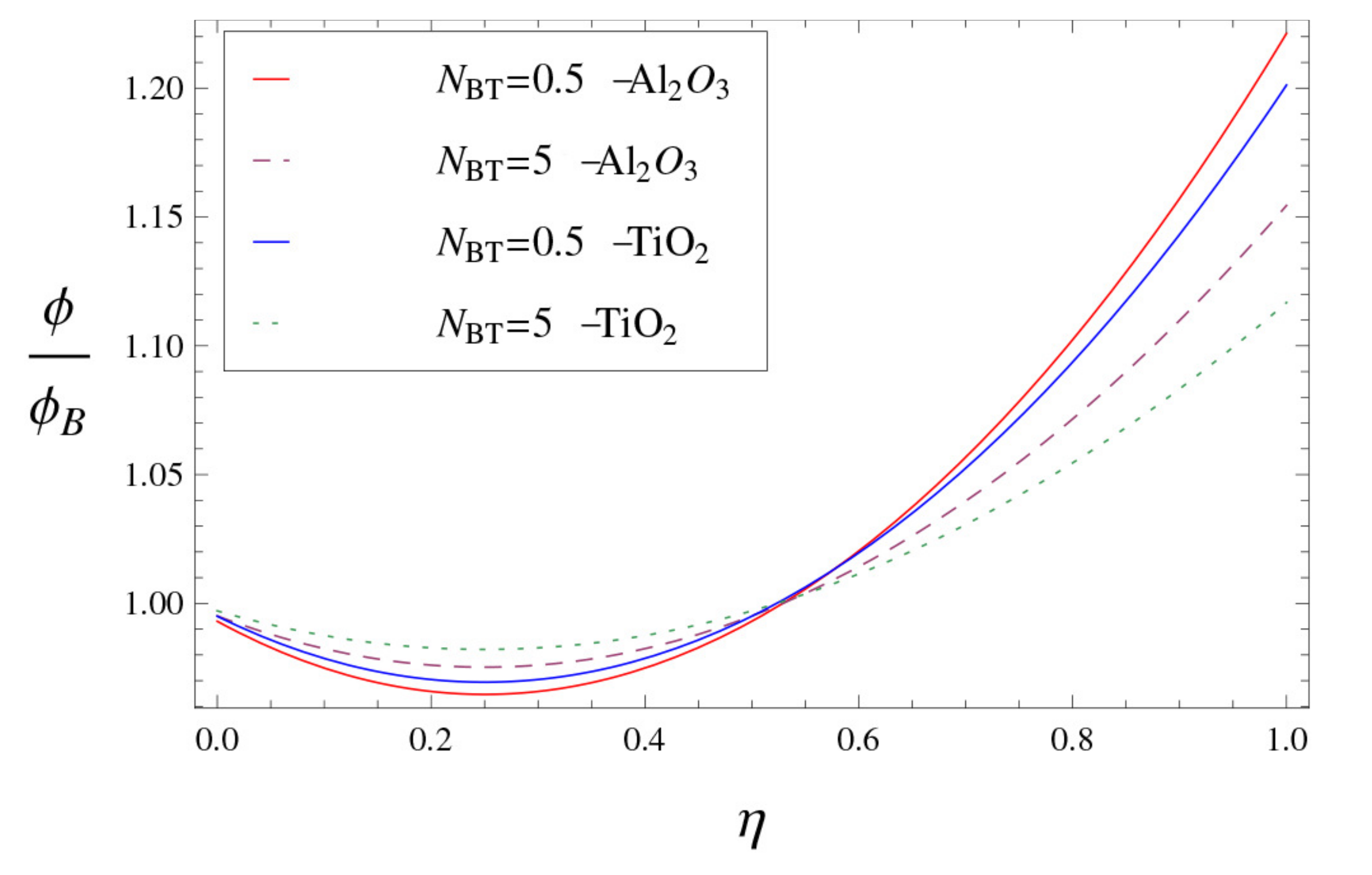
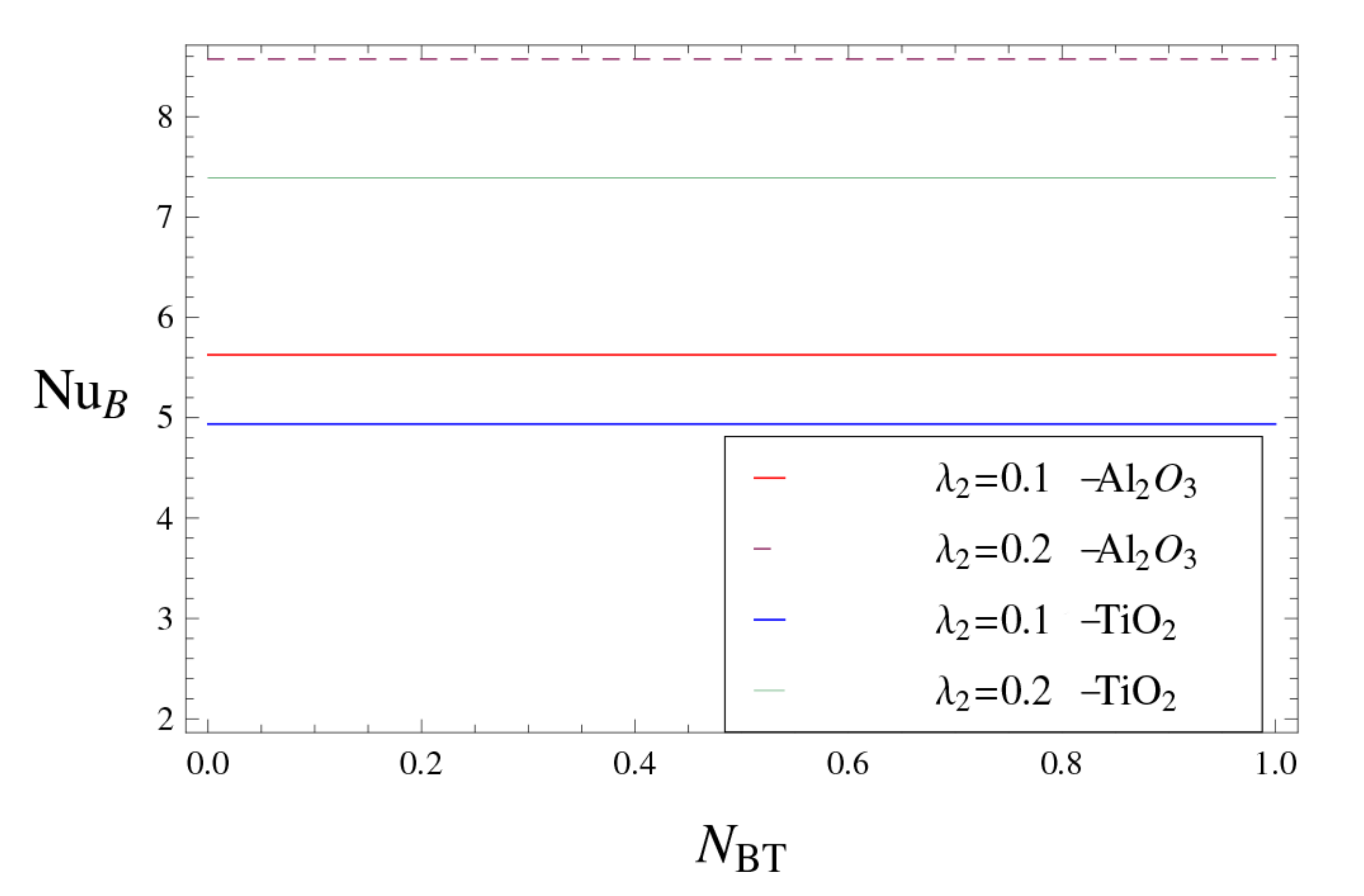
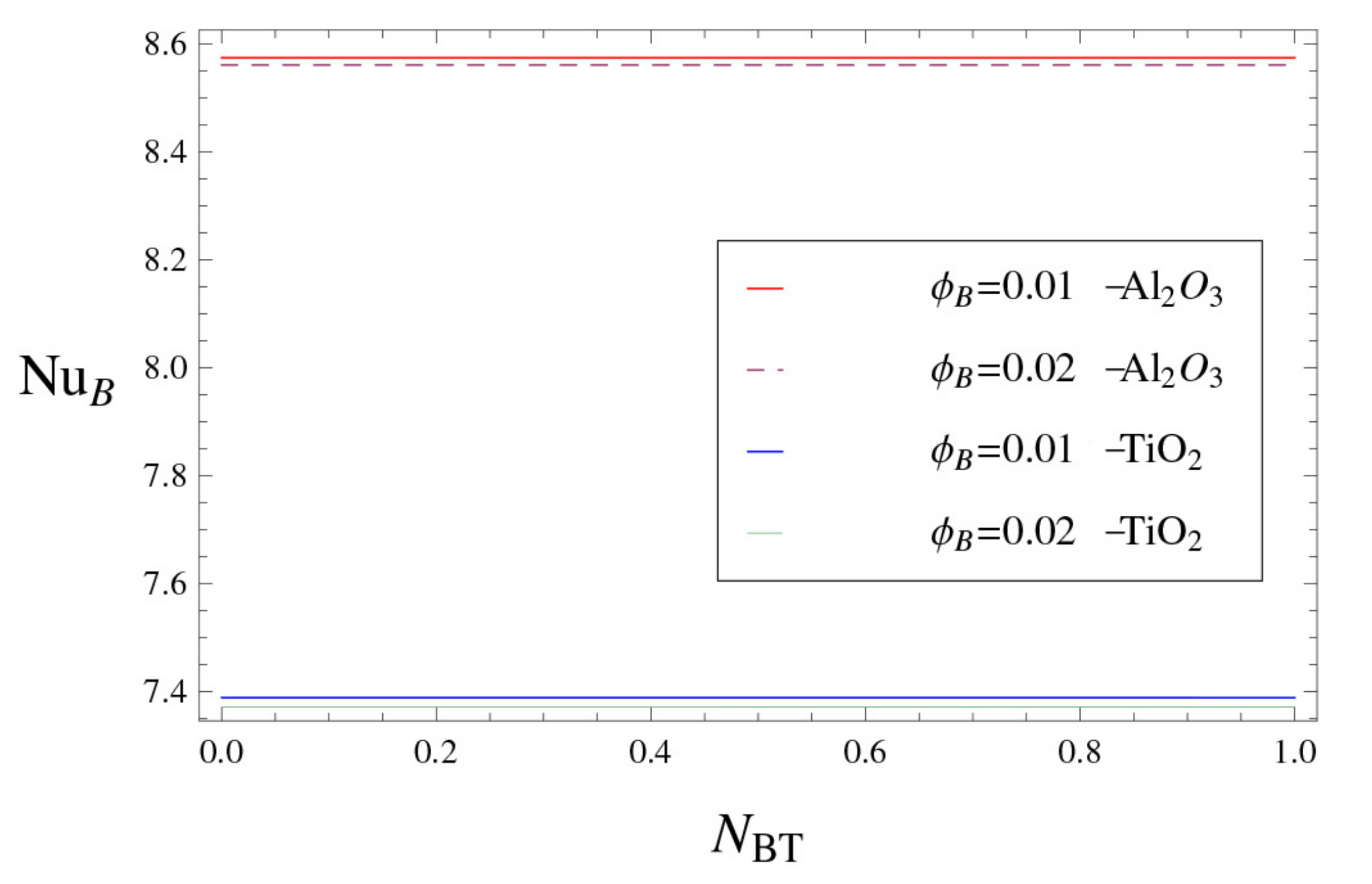
- In the alumina–water nanofluid, is higher than that of titania–water nanofluid.
- d
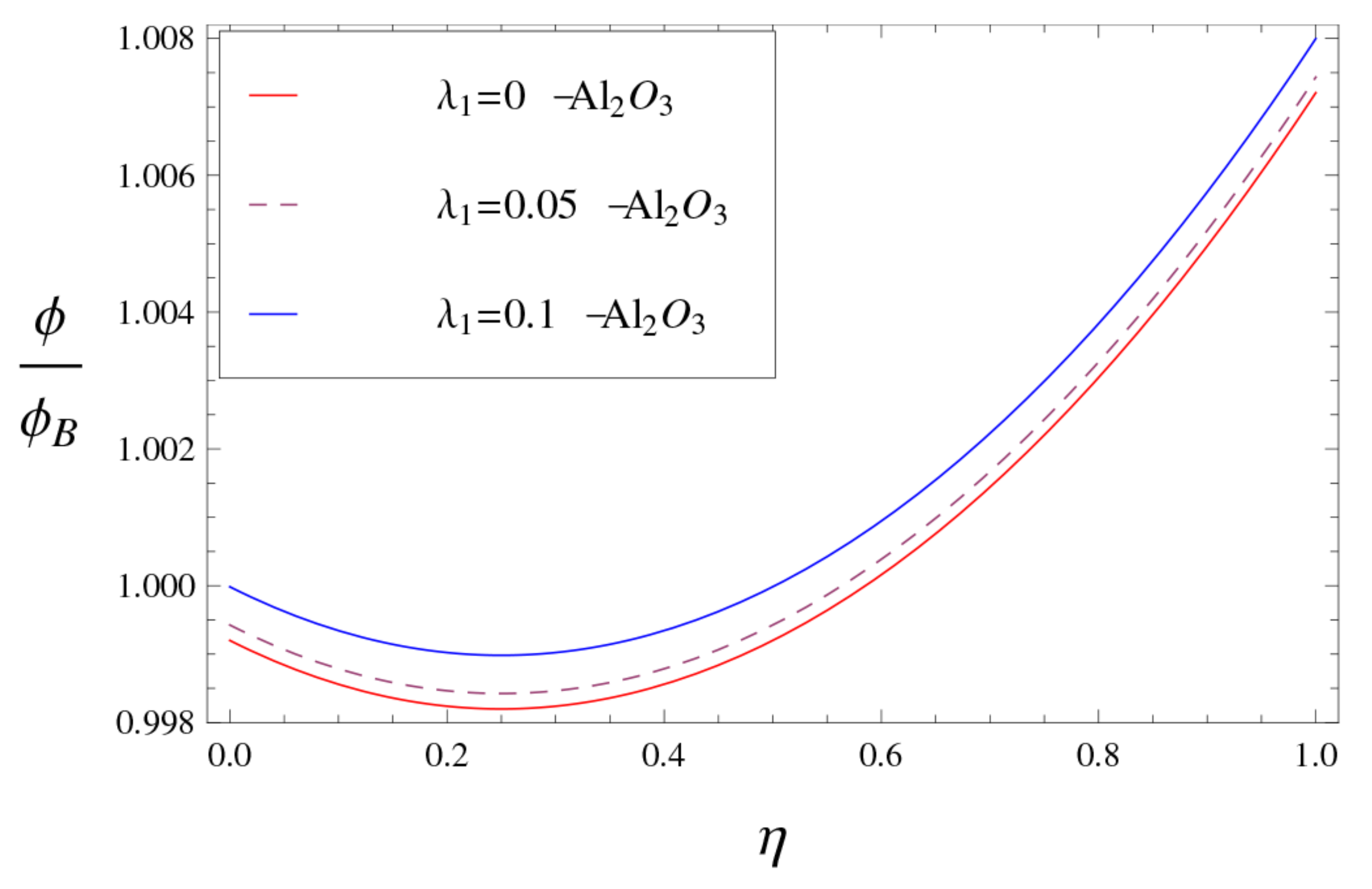
- The positive correlation between slip parameters and is significant for the titania-water nanofluid.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
| Symbol | Description |
| magnetic field strength | |
| specific heat (m/sK) | |
| Brownian motion constant | |
| thermophoresis diffusion coefficient | |
| H | radius (m) |
| h | heat transfer coefficient (W/mK) |
| Hartmann number | |
| dimensionless heat transfer coefficient | |
| k | thermal conductivity (W/mK) |
| free stream temperature | |
| ratio of the Brownian to | |
| thermophoretic diffusivities | |
| non-dimensional pressure drop | |
| Nusselt number | |
| p | pressure (Pa) |
| surface heat flux | |
| radiative heat flux | |
| nanoparticle volume fraction | |
| density | |
| transverse direction | |
| , | slip parameters of velocity |
| B | bulk mean |
| U | axial velocity (m/s) |
| T | temperature (K) |
| k | thermal conductivity |
| dynamic viscosity (kg/m s) | |
| Stefan–Boltzman constant | |
| ratio of wall and fluid temperature | |
| difference to absolute temperature | |
| Subscripts | |
| x, y | coordinate system |
| p | nanoparticle |
| base fluid | |
| i | velocity components |
References
- Li, T.; Liu, B.; Zhou, J.Z.; Xi, W.X.; Huai, X.L.; Zhang, H. A Comparative Study of Cavitation Characteristics of Nano-Fluid and Deionized Water in Micro-Channels. Mathematics 2020, 11, 310. [Google Scholar] [CrossRef] [PubMed]
- Duan, Z.P.; Lv, X.; Ma, H.H.; Su, L.B.; Zhang, M.Q. Analysis of Flow Characteristics and Pressure Drop for an Impinging Plate Fin Heat Sink with Elliptic Bottom Profiles. Appl. Sci. 2020, 10, 225. [Google Scholar] [CrossRef]
- Buongiorno, J. Convective transport in nanofluids. J. Heat Transf. 2006, 128, 240–250. [Google Scholar] [CrossRef]
- Yang, C.; Wang, Q.L.; Nakayama, A.; Qiu, T. Effect of temperature jump on forced convective transport of nanofluids in the continuum flow and slip flow regimes. Chem. Eng. Sci. 2015, 137, 730–739. [Google Scholar] [CrossRef]
- Hedayati, F.; Domairry, G. Effects of nanoparticle migration and asymmetric heating on mixed convection of TiO2-H2O nanofluid inside a vertical microchannel. Powder Technol. 2015, 272, 250–259. [Google Scholar] [CrossRef]
- Andhare, R.S.; Shooshtari, A.; Dessiatoun, S.V.; Ohadi, M.M. Heat transfer and pressure drop characteristics of a flat plate manifold microchannel heat exchanger in counter flow configuration. Appl. Thermal Eng. 2016, 96, 178–189. [Google Scholar] [CrossRef]
- Ooi, E.H.; Popov, V. Numerical study of on the natural convection in Cu-water nanofluid. Int. J. Thermal Sci. 2013, 65, 178–188. [Google Scholar] [CrossRef]
- Ravnik, J.; Šušnjara, A.; Tibaut, J.; Poljak, D.; Cvetkovi, M. Stochastic modelling of nanofluids using the fast Boundary-Domain Integral Method. Eng. Anal. Boundary Elem. 2019, 107, 185–197. [Google Scholar] [CrossRef]
- Maxwell, J.C. Temperature. On Stresses in Rarefied Gases Arising from Inequalities of Temperature. Philos. Trans. R. Soc. 1879, 170, 231–256. [Google Scholar]
- Kou, Z.H.; Bai, M.L. Effects of wall slip and temperature jump on heat and mass transfer characteristics of an evaporating thin film. Int. Commun. Heat Mass Transf. 2011, 38, 874–878. [Google Scholar] [CrossRef]
- Avramenko, A.A.; Tyrinov, A.I.; Shevchuk, I.V.; Dmitrenko, N.P.; Kravchuk, A.V.; Shevchuk, V.I. Mixed convection in a vertical circular microchannel. Int. J. Therm. Sci. 2017, 121, 1–12. [Google Scholar] [CrossRef]
- Thompson, P.A.; Troian, S.M. A general boundary condition for liquid flowat solid surfaces. Nature 1997, 389, 360–362. [Google Scholar] [CrossRef]
- Beskok, A.; Karniadakis, G.E. A model for flows in channels, pipes, and ducts at micro and nano scales. Microsc. Thermophys. Eng. 1999, 3, 43–77. [Google Scholar]
- Wu, L.A. A slip model for rarefied gas flows at arbitrary Knudsen number. Appl. Phys. Lett. 2008, 93, 253103. [Google Scholar] [CrossRef]
- Zhu, J.; Xu, Y.X.; Hang, X. A Non-Newtonian Magnetohydrodynamics (MHD) Nanofluid Flow and Heat Transfer with Nonlinear Slip and Temperature Jump. Mathematics 2019, 7, 1199. [Google Scholar] [CrossRef]
- Almutairi, F.; Khaled, S.M.; Ebaid, A. MHD Flow of Nanofluid with Homogeneous-Heterogeneous Reactions in a Porous Medium under the influence of Second-Order Velocity. Mathematics 2019, 7, 220. [Google Scholar] [CrossRef]
- Noeiaghdam, S.; Dreglea, A.; He, J.H.; Avazzadeh, Z.; Suleman, M.; Araghi, M.A.F.; Sidorov, D.N.; Sidorov, N. Error Estimation of the Homotopy Perturbation Method to Solve Second Kind Volterra Integral Equations with Piecewise Smooth Kernels: Application of the CADNA Library. Symmetry 2020, 12, 1730. [Google Scholar] [CrossRef]
- Nobari, M.R.H.; Gharali, K. A numerical study of flow and heat transfer in internally finned rotating straight pipes and stationary curved pipes. Int. J. Heat Mass Transf. 2005, 49, 1185–1194. [Google Scholar] [CrossRef]
- Ganga, B.; Ansari, S.M.Y.; Ganesh, N.V.; Abdul Hakeem, A.K. MHD flow of Boungiorno model nanofluid over a vertical plate with internal heat generation/absorption. Propuls. Power Res. 2016, 5, 211–222. [Google Scholar] [CrossRef]
- Zhu, J.; Wang, S.N.; Zheng, L.C.; Zhang, X.X. Heat transfer of nanofluids considering nanoparticle migration and second-order slip velocity. Appl. Math. Mech. 2016, 38, 125–136. [Google Scholar] [CrossRef]
- Moein, S.; Mohsen, K. Study of water based nanofluid flows in annular tubes using numerical simulation and sensitivity analysis. Heat Mass Transf. 2018, 54, 2995–3014. [Google Scholar]
- Liao, S.J. On the homotopy analysis method for nonlinear problems. Appl. Math. Comput. 2004, 147, 499–513. [Google Scholar] [CrossRef]
- Fan, T. Applications of Homotopy Analysis Method in Boundary Layer Flow and Nanofluid Flow Problems. Ph.D. Thesis, Shanghai Jiao Tong University, Shanghai, China, 2012. (In Chinese). [Google Scholar]
- Yang, C.; Li, W.; Sano, Y.; Mochizuki, M.; Nakayama, A. On the anomalous convective heat transfer enhancement in nanofluids: A theoretical answer to the nanofluids controversy. J. Heat Transf. 2013, 135, 054504. [Google Scholar] [CrossRef]



| BVPh2.0 | HAM | Relative Error(%) | |
|---|---|---|---|
| 0.01 | −0.00286834 | −0.00286673 | 0.05624769 |
| 0.02 | −0.00396349 | −0.00394892 | 0.36760532 |
| 0.03 | −0.00527046 | −0.00529243 | 0.33803511 |
| 0.04 | −0.00678941 | −0.00671253 | 1.13235171 |
| Yang et al. [24] | HAM | Relative Error(%) | |
|---|---|---|---|
| 0.1 | 7.26823 | 7.26679 | 0.01981 |
| 0.2 | 7.55883 | 7.55889 | 0.00079 |
| 0.3 | 7.69768 | 7.69418 | 0.04547 |
| 0.4 | 7.79492 | 7.79163 | 0.04225 |
| 0.5 | 7.85227 | 7.85200 | 0.00344 |
| 0.6 | 7.90000 | 7.90338 | 0.04278 |
| 0.7 | 7.94920 | 7.94526 | 0.04956 |
| 0.8 | 7.95957 | 7.95947 | 0.00126 |
| 0.9 | 7.97313 | 7.97791 | 0.05995 |
| 1 | 8.04496 | 8.04478 | 0.00224 |
| 2 | 8.12940 | 8.12983 | 0.00529 |
| 10 | 8.21841 | 8.21630 | 0.02567 |
| Types of Fluids | |||||
|---|---|---|---|---|---|
| -Water | -Water | ||||
| 0.1 | 0.1 | 0.5 | 0.01 | 0.000127706 | 0.000129222 |
| 0.2 | 0.000131924 | 0.014154800 | |||
| 0.2 | 0.000179880 | 0.020517000 | |||
| 10 | 0.000127722 | 0.000127916 | |||
| 0.04 | 0.000119804 | 0.000127917 | |||
| Types of Fluids | |||||
|---|---|---|---|---|---|
| -Water | -Water | ||||
| 0.1 | 0.1 | 0.5 | 0.01 | 5.62714 | 4.93726 |
| 0.2 | 8.57429 | 7.38838 | |||
| 0.2 | 8.95671 | 7.71938 | |||
| 10 | 8.69342 | 7.40811 | |||
| 0.04 | 8.56113 | 7.37139 | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, J.; Liu, Y.; Cao, J. Effects of Second-Order Velocity Slip and the Different Spherical Nanoparticles on Nanofluid Flow. Symmetry 2021, 13, 64. https://doi.org/10.3390/sym13010064
Zhu J, Liu Y, Cao J. Effects of Second-Order Velocity Slip and the Different Spherical Nanoparticles on Nanofluid Flow. Symmetry. 2021; 13(1):64. https://doi.org/10.3390/sym13010064
Chicago/Turabian StyleZhu, Jing, Ye Liu, and Jiahui Cao. 2021. "Effects of Second-Order Velocity Slip and the Different Spherical Nanoparticles on Nanofluid Flow" Symmetry 13, no. 1: 64. https://doi.org/10.3390/sym13010064
APA StyleZhu, J., Liu, Y., & Cao, J. (2021). Effects of Second-Order Velocity Slip and the Different Spherical Nanoparticles on Nanofluid Flow. Symmetry, 13(1), 64. https://doi.org/10.3390/sym13010064




