Abstract
Having the best solution for Vehicle Routing Problem (VRP) is still in demand. Beside, Cuckoo Search (CS) is a popular metaheuristic based on the reproductive strategy of the Cuckoo species and has been successfully applied in various optimizations, including Capacitated Vehicle Routing Problem (CVRP). Although CS and hybrid CS have been proposed for CVRP, the performance of CS is far from the state-of-art. Therefore, this study proposes a hybrid CS with Simulated Annealing (SA) algorithm for the CVRP, consisting of three improvements—the investigation of 12 neighborhood structures, three selections strategy and hybrid it with SA. The experiment was conducted using 16 instances of the Augerat benchmark dataset. The results show that 6 out of 12 neighborhood structures were the best and the disruptive selection strategy is the best strategy. The experiments’ results showed that the proposed method could find optimal and near-optimal solutions compared with state-of-the-art algorithms.
1. Introduction
Having the best solution for the vehicle routing problem (VRP) is challenging. It is categorized as a combinatorial optimization problem related to operations research, algorithm theory, and computational complexity theory, which use mathematical and scientific studies with a robust experiment to obtain a reliable solution. The VRP aims to optimize the delivery routing by finding the least-cost (distance, time) route [1]. Determining the optimal solution for VRP without violating specific limitations is also known as capacitated VRP (CVRP) [2] or NP-hard problem [3]. Several metaheuristics have been developed to solve the CVRP that can be classified into two main categories: single-based and population-based. Single-based solutions such as tabu search [4] and simulated annealing (SA) [5] have the ability to exploit the search space in a short time but also have some limitations such as weak exploration as Lévy flight artificial bee colony algorithm. Population-based solutions such as the genetic algorithm (GA) [6], particle swarm optimization (PSO) [7,8,9,10], water flow-like algorithm [11,12] and membrane algorithm [13] are more concerned with exploration rather than exploitation but have limitations in terms of premature convergence and low convergence speed. Enhancement of perturbation based variable neighborhood search with adaptive selection mechanism is also proposed to address the capacitated vehicle routing problem [14]. Hybridization between a population-based and a single-based metaheuristic has been proposed for the CVRP to overcome these two categories’ limitations [15].
Recently, a metaheuristic called Cuckoo Search (CS) has emerged in the literature, which is based on the reproduction strategy of the cuckoo species and the Lévy flight behavior of some birds and fruit flies [16]. The CS has been successfully applied to a wide range of optimization problems, such as selecting relevant genes in drug microarray data [17] and heart disease prediction [18]. For example, Reference [19] proved that CS outperforms other metaheuristics in speed and accuracy in solving the traveling salesman problem (TSP). Later, the CS algorithm also solves the problem of global-support parametric surface approximation for reverse engineering applications [20]. Furthermore, CS is applied to other VRP variants, as Reference [21] proposed CS to solve the VRP with a heterogeneous fleet with mixed backhauls and time windows.
Initial work on CS has been applied for CVRP [2,22,23]. However, the performance is far from the optimal solution. Therefore, this work proposes utilizing CS to solve the CVRP. Four things motivate to use CS: (1) CS is population-based and similar to GA and PSO but it uses some sort of elitism and/or selection similar to that used in harmony search [16], (2) CS is local search components that assist it to attempt to achieve a balance between exploration and exploitation, (3) CS is very simple and has some similarities with hill-climbing and only a few parameters need to be adjusted [24] and (4) CS uses a Lévy flight randomization strategy, which preserves the search space step length (whether large or small) so there is a better balance between exploration and exploitation [16,25]. Traditionally, Gaussian distribution is used for this purpose. The importance of the Lévy flight strategy in various combinatorial optimization problems has been addressed by others [26,27,28,29,30].
The CS has a stronger ability to find good quality solutions than GA and PSO, particularly for non-heavily constrained and continuous problems, such as welded beam design problems [25] and spring designs [31], constrained optimization problems such as business optimization applications [32] the single-objective optimum synthesis of a six-bar double dwell linkage [33] and for phase equilibrium and stability calculations [34]. It is because CS has fewer parameters. Moreover, it has a fine balance of randomization and intensification using Lévy flight [16].
However, CS has limitations when applied to heavily constrained optimization problems, such as web service composition [35], the job scheduling problem [36], multi-objective scheduling problem [37], flow shop scheduling problem [38] and TSP [39], due to its stochastic characteristic in exploring the search space. Some researchers have tried to accelerate the rate of convergence, which generally appears in many metaheuristics, whilst others have tried to achieve a better balance between exploration and exploitation [40]. CS performance improvements have been attempted by considering a variety of aspects. For instance, Reference [41] used a crossover strategy so that a solution could gain part of the other solution’s properties while [42] enhanced CS by modifying Lévy flight using Mantegna’s and McCulloch’s algorithm. Several comprehensive surveys can also be referred for CS modifications [25,43,44,45,46].
Enhancement of the metaheuristic exploration process may involve the usage of neighborhood structures [47,48]. Many neighborhood structures for solving the CVRP have been proposed [49], some neighborhood structures may work well only at the early search, whilst others may perform well towards the end [47]. Reference [50] argued that a meta-level optimization problem is the finding process of suitable neighborhood structures for choosing the actual next neighbor. Recently, Reference [22] applied basic CS to CVRP, the proposed CS employed 2-opt and double bridge as neighborhood structures. However, the result is far from the state-of-art solution. On the other hand, the algorithm performs very fast computational time. Reference [23] has proposed CS for solving patient transportation problems, which is a kind of CVRP with consideration of reducing transportation emissions. The algorithm initialized host nest using saving heuristic, which is enhanced with 3-opt and used two neighborhood structures known as 2-opt and double-bridge moves. The result performed better for some of the state-of-art algorithms. However, the algorithm shows its efficiency. Another type of cuckoo algorithm has been applied to CVRP for optimization, which is not focus of this work [51].
The CS uses a random selection strategy but has a limitation to explore unfruitful areas in the search space. Reference [19] solved the issue by enhancing the selection strategy by categorizing the eggs based on their fitness. A good selection strategy has to be biased towards finding better solutions. In this case, the population may be driven towards better solutions much more quickly. Moreover, the worse solution will not be eliminated and could have a chance of being selected [52]. One of the major reasons for adopting a hybridization strategy when designing a metaheuristic is that it can provide a good balance between exploration and exploitation [50,53]. The original CS lacks effective communication between the individual eggs (solutions) and an attempt was made to overcome this limitation by employing a hybrid methodology [15]. In fact, many studies have addressed this issue by using hybridization techniques [26,27,28,29,30,54]. Moreover, Reference [55] has proposed a hybrid CS with intelligent water drops to solve CVRP. The algorithm has reached all optimal solutions and outperforms three instances compare with the state-of-art algorithm. However, the evaluation used the Christofides benchmark dataset. Therefore, this study aims to hybridize CS with another metaheuristic to exploit the search space for finding good quality solutions.
However, the adaptation of any metaheuristic involves a trade-off between exploration and exploitation, both of which must ideally be optimized. The main objectives to CS in this work is the enhancement of exploration and exploitation through the following:
- Adopting a suitable multiple neighborhood structure strategy to improve CS exploration and to help the algorithm to escape from local optima by observe the behaviors of a random sequence of 12 neighborhood structures and then select the most dominant ones to form the best sequence.
- Adopting a suitable selection strategy for exploring the search space to find new solutions and enhance CS exploitation by investigating three selection strategies, namely tournament, rank and disruptive, to find the best-performing one.
- Combining the advantages of CS with those of SA to improve their ability to cooperatively explore the search space and quickly find good solutions within a small region of the search space and also to prevent deterioration.
- Lastly, evaluate the proposed hybrid CS with SA against other state-of-art methods based on average, standard deviation and computational time. The algorithm is furthermore evaluated using Freidman, Holm and Hochberg test, to identify whether there was a significant difference between the proposed algorithm and the best methods in the literature.
The remainder of this paper is organized as follows: we discuss the basic CS, our propose hybrid CS and explain how it can be applied to the CVRP. We present the results of our experiments that were conducted to select the most suitable components for the proposed CS and then compare the performance of the proposed hybrid CS, which we call Hybrid Cuckoo Search with Simulated Annealing (HCS-SA), with that of state-of-the-art methods by way of computational experiments. Finally, we conclude and suggest areas for further research.
2. Related Work
2.1. CVRP Description
In CVRP, a fleet of K vehicles with homogeneous capacity Q is available for serving customers. The single depot and customers are defined as a set of node N = {0, …, n}, where node 0 represents the depot and the other nodes represent the customers. Each vehicle trip must start from and end at the depot. Each customer i with known demand di is visited by an exact one vehicle trip. The total demand assigned to each vehicle trip must not exceed the vehicle capacity Q. dij > 0 corresponds to the travel distance from node i and node j. The objective of the CVRP problem is to determine a set of vehicle trips serving all customers while minimizing the total travel distance [2].
2.2. Standard Cuckoo Search
Brood parasitism is an interesting feature of the cuckoo bird, in which a female cuckoo lays her eggs in another nest of the observed bird and lets the host bird hatch and brood the young cuckoo chicks. The cuckoo adapting its eggs like a host bird in terms of patterns, shapes and colors to increase the probability of a new cuckoo being born and reducing the probability of the host bird abandoning the eggs [16]. The behavior of the cuckoo in its search for a suitable nest is represented by a combination of CS with Lévy flight [56]. Lévy flight represents a random walk model that is characterized by step lengths that obey a power-law distribution. Studies have shown that hunters search for prey by following a Lévy flight pattern, which commonly consists of small random steps followed in the long term by large jumps [57].
The CS was recently developed by Yang and Deb [16] and was initially designed to solve multimodal functions by following the rules that each cuckoo lays one egg at a time and selects a nest randomly, the best nest with the highest quality egg can pass onto the new generations and the number of host nests is fixed and the egg laid by a cuckoo can be discovered by the host bird with a probability pa ≤ [0, 1].
A cuckoo i generates a new solution via Lévy flight, according to Equation (1):
where α is the step size that follows the Lévy distribution that is shown in Equation (2):
which has an infinite variance with an infinite mean [16] and s is a step size drawn from a Lévy distribution. The Lévy flight is described by Reference [58] as a special type of random walk whose step length in not constant, rather are chosen from a probability distribution with a power-law tail, this means that very large step lengths are possible. The potential of using Lévy flight to enhance met-heuristic is reported in various studies [59,60,61].
In CS, cuckoos are abstracted as entities that each has an associated solution (i.e., an egg) of the optimization problem that they try to place in a solution container (i.e., the host bird’s nest). Table 1 provides an analogy between the behavior of the cuckoo in nature and the artificial behavior of the CS. A detailed description of the basic CS for solving the CVRP is presented in Figure 1 [62].

Table 1.
The analogy between natural cuckoo bird behavior and cuckoo search.

Figure 1.
Standard Cuckoo Search (CS).
3. Proposed Method
3.1. Cuckoo Search for CVRP
To adapt CS to the CVRP these notions will appear in the discussion of the following three main elements: egg, nest and search space, which extend the work of Reference [19]. These key elements can have important implications for combinatorial problems.
3.1.1. The Egg
Assuming that a cuckoo lays a single egg in one nest, we can say that one egg in a nest is a solution represented by one individual in the population. An egg can also be one new candidate solution laid by a cuckoo for a place/location reserved by an individual in the population, while the nest is the container of that new cuckoo egg. In the CVRP, one egg is the equivalent of multiple Hamiltonian cycles of served routes that start and end at the central depot, as shown in Figure 2.
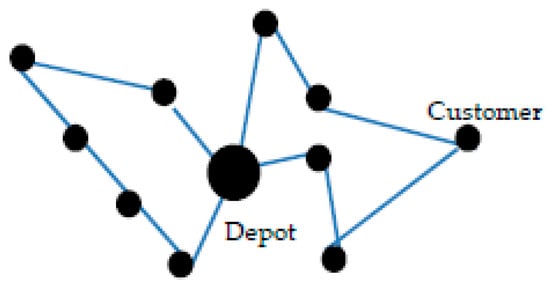
Figure 2.
The egg appears as a multiple Hamiltonian cycle route.
The egg representation adopted in this study can be described as follows—assume a CVRP with n clients and v available vehicles for delivery, then the number 0 denotes the depot and 1, 2, …, n denotes the clients. Based on the v vehicle at the depot, so each egg has at most the v distribution path (route), every path (route) starts at the depot and stops at the depot. Possible routes are shown in Figure 3.

Figure 3.
Egg (solution) representation.
3.1.2. The Nest
In CS, the number of nests is fixed and this number represents the size of the population. A nest is a container of an individual of the population and its abandonment involves its egg being replaced in the population by a new one. By projecting these features on to the CVRP, we can say that a nest is shown as an individual in the population with its Hamiltonian cycle route. Obviously, a nest can have multiple eggs for future extensions but in this study, each nest contains only one egg.
3.1.3. The Search Space
In the CVRP, the visited customers on each route have fixed coordinates; however, the visiting order between the customers can be changed either within the same route or between different routes. The search space in the CVRP is a set of points (customers). Each point is representative of a route that appears as a potential solution. These solutions are positioned in space according to the order of their customers. Since the coordinates of customers are fixed, the movements are based on the order of visited customers. There are several neighborhoods structure, methods, operators, or perturbations that generate a new solution from another existing solution by changing the order of visited customers.
In the adaptation of CS to CVRP, one possible perturbation that can be used to change the order of visited customers is the REINSERTION, SHIFT-1-0, K-SHIFT and EXCHANGE neighborhoods structure. However, REINSERTION, SHIFT-1-0 is used for small steps, while larges jumps are made by SWAP-2-2 and K-SHIFT. Moving a solution to another in the search space (combinatorial space) is made by small steps in a small area around the current solution. Therefore, carrying out several steps leads to additional solutions that are farther away. However, if we want to change the area of search and point to another far area, the solution is perturbed by K-SHIFT and EXCHANGE neighborhood structures.
3.2. Propose Discrete Hybrid Cuckoo Search
In this section, we present the proposed hybrid discrete CS with SA to emulate cuckoo behavior in nature. The main purpose of improving CS is to balance exploration and exploitation to find a better quality solution in less time. In nature, there is what could be likened to an arms race between host birds and cuckoo, where host birds evolve defenses and cuckoos respond with trickery to increase their eggs’ chance of survival [63]. For this reason, cuckoo birds always try to adapt their eggs to appear similar in pattern, shape and color to those of the host bird species. This arms race serves as an inspiration to improve CS in this research. The proposed improvements are summarized in the four phase, that is, the first phase is starts race when the host bird lays eggs that are enhanced in terms of their pattern, shape and color. This step represents the generation of the initial population in CS and for this purpose, a sequential insertion heuristic is used. The second phase is the enhancements of the host bird eggs puts more pressure on the cuckoo bird to respond with trickery to increase its own eggs’ chance of survival. For this purpose, two components are investigated (neighborhood structures and acceptance criteria) to identify a suitable neighborhood structure strategy. The third phase is the cuckoo bird in nature has some kind of surveillance to decide which host nest is the best choice in which to lay its eggs. For this purpose, three selection strategies are investigated in order to find the most suitable one. The last phase is the cuckoo chick starts to throw out the host eggs to get rid of competition for food by using SA when the cuckoo egg is hatched. Thus, a kind of local search is performed around the current solution.
The general pseudo-code for the proposed CS is presented in Figure 4. Note that the act of laying eggs involves the cuckoo bird egg (new solution) and the act of selecting eggs involves the host bird egg (old solution). Moreover, the nest always has one egg in it, which means that the selection and lying of the egg in that nest actually relate to the same egg, which changes from a host to a cuckoo egg.

Figure 4.
Proposed hybrid CS.
As shown in Figure 4, CS starts with an initial solution (empty host nest) and then an initial population is generated using a sequential insertion heuristic (lines 5–7). The number of generated solutions in the population is equal to the number of laid host nest eggs. Then the host nest eggs are evaluated by the fitness function (line 8). After the initialization is finished and the host bird’s nests are built with eggs in them, the cuckoo bird arrives to lay its egg in one of the host bird’s nests, which is described in the pseudo-code as the iterative stage (lines 13–27). The cuckoo bird starts to select a host bird nest in which to lay its egg (this act of laying the egg can be described as replacing the current (host) egg with a new, hopefully improved (cuckoo) one). The selection is made by using one of the selection strategies, which ranks the host bird eggs in the population according to the selection probability (in the basic CS, the solutions are ranked based on just the fitness value). The host bird egg that has the highest rank is selected based on that selection strategy for local exploration. Later, the selected egg is improved by the neighborhood structures.
In the natural world, to increase its chance of surviving and hatching to become a bird, a cuckoo bird egg has to imitate the host bird egg in the pattern, color and shape. The cuckoo bird must adapt with nature and develop this imitation and this behavior is represented in line 17 of the pseudo-code, where a local search mechanism is employed to explore the neighbor solutions of the selected host bird egg, which will lead to further improvement in the pattern, color and shape of the selected egg. In this study, SA is used for this purpose. The improved cuckoo bird egg is then compared to its previous state (host bird egg); if its pattern, color and shape are better than the previous egg it is accepted, otherwise it is discarded (lines 19–22). When the host bird goes to the nest, it starts to find the alien (cuckoo) eggs, the discovery of which depends on parameter pa. The discovered cuckoo eggs are destroyed or the nest is abandoned, in this case, a Lévy flight is used to replace the worse cuckoo eggs by applying neighborhood structures followed by the acceptance criterion (lines 23–25). Finally, all the host nest eggs are ranked based on their fitness value (line 27) and the iterative improvements stage starts again.
3.2.1. Initialization of Host Nest Using Sequential Cheapest Insertion Heuristic
In the context of the CVRP, the initial host bird eggs are generated using a sequential cheapest insertion heuristic, whereby the customer with the minimum traveling cost is sequentially inserted into its respective route until all the vehicles are full. The main aim is to build initial quality solutions using relatively simple and fast schemes.
3.2.2. Selection of Host Nest Egg to Lay a New Cuckoo Egg
The basic CS uses a random selection strategy. This does not fully reflect the behavior of the cuckoo bird in nature, which is based on selecting the most apparently similar eggs in the pattern, color and shape to increase the survival of the egg. Therefore, we incorporate a more advanced selection strategy to emulate this behavior better. In the proposed approach, the calculation of the selection probability is based on the fitness of solution for each egg is based on one of three selection strategies. However, after the calculation of these probabilities is obtained, the solution selection is made based on roulette wheel selection, as shown in Figure 5.

Figure 5.
Pseudo code for selection strategy.
Tournament Selection
Tournament selection is a selection process in which a number of eggs (Ntour) from the population are chosen at random and then a comparison is made depending on their fitness in order to choose the best egg. Parameter Ntour is called the tournament size. Normally, tournaments are held only between two eggs (binary tournament) but the generalization is possible to an arbitrary group. Tournament selection gives eggs with high fitness a greater chance to survive [64]. In this study, we select two eggs from the population and compare their fitness values, then assign one score coded as (a) to the better egg. This process is repeated for all the eggs in the population, as shown in Figure 6, where fi is the fitness value of i = 0 … n and n is the population size [65].

Figure 6.
Tournament selection strategy.
After calculating the value of (a) for all the eggs, the selection probability for each egg is calculated by using Equation (3):
Rank Selection
In rank selection, eggs are sorted in descending order based on the fitness value. An index k value is given to each egg from the best to the worst, that is, for the best fitness, k = 1, whilst for the worst fitness, k = n, where n is the population size and N is the maximum number of iterations. Finally, the selection probability is calculated by using Equation (4) [66]:
Disruptive Selection
The disruptive selection gives higher and lower quality eggs the chance of being selected by changing the definition of the fitness function as in Equation (5):
where fi is the fitness function and ft is the average value of the fitness function fi of the individuals in the population.
3.2.3. Best Sequence of Neighborhood Structure and Lévy Flight
A multi-neighborhood structure is used to improve the cuckoo bird’s eggs’ imitation of the host bird eggs in the nests in terms of pattern, color and shape and thus give them a good chance of survival. The neighborhood structure consists of seven inter-routes (where a change occurs between two routes) and five intra-routes (where a change occurs within the same route), that is, 12 neighborhood structures in total, as shown in Table 2. Five of the seven inter-routes are based on the λ-interchange scheme [67], which involves exchanging up to λ customers between two routes. In this study, λ = 2 is considered due to the high computational cost associated with large λ.

Table 2.
Neighborhood structures.
To avoid generating infeasible solutions, we include the following two restrictions, that is, checking the vehicle capacity before adding a new customer and adding another restriction to avoid emptying the vehicle of the customer, whereby at least one customer is retained to be served by a particular vehicle. The above neighborhood structures need to be linked to the step length generated by the Lévy flight. Lévy flight is generated by a probability density function that has a power-law tail. The Cauchy distribution is often used for this purpose [68]. The method we use to generate a random number from a Lévy distribution is shown in Figure 7.

Figure 7.
Lévy flight via Cauchy distribution.
In this study, the adaptation of CS for the discrete CVRP is similar to the neighborhood structure adaptation for the TSP in Reference [69]. The 12 neighborhood structures are each associated with a step length generated by Lévy flight that can be categorized into small (more frequent), medium (most frequent) and large (less frequent) steps. Thus, the eggs’ pattern, color and shape are changed according to neighborhood structures for each category: small (SHIFT-1-0, SWAP-1-1, SHIFT-2-0, REINSERTION and OR-OPT2), medium (OR-OPT3, TWO-OPT, EXCHANGE and SWAP-2-1, Whilst SWAP-2-2) and large (CROSS, K-SHIFT). To facilitate control over the size of the steps, an interval between 0 and 1 is used. Therefore, according to the value given by the Lévy flight in this interval, we can choose the appropriate step length as follows:
If the value of Lévy is:
- [0, i], one step of a small neighborhood structure is performed.
- [(k−1) × i, k × i], one step of a medium neighborhood structure is performed.
- [k × i, 1], a big neighborhood step is performed.
The value of i in this process is I = (1/(n + 1)), where n is the maximum number of steps and k is {0, ..., n}. So, if we assume that n = 12, then i = 0.07, thus the interval is divided into 12 parts, as listed in Table 3.

Table 3.
Lévy flight associations with neighborhood structures.
The association of these steps with the neighborhood structures is set without any prior knowledge. However, it is better to sequence them based on experimental knowledge in order to identify the most successful neighborhood that has a high impact on improving the solutions. Therefore, an experimental investigation of these neighborhood structures was carried out to identify their effectiveness in improving the solution.
3.2.4. Improve the Egg by Simulated Annealing as a Local Search
In this study, each selected egg is further improved using SA as a local search, whereby we employed the same neighborhood structures mechanism in the previous Section 3.2.3. However, only one neighborhood structure is fired at each iteration based on levy flight. In order to avoid getting trapped in local minima, the fundamental idea is to allow moves to solutions with objective function values that are worse than the objective function value of the current solution. Such a move is often called an uphill-move. At each iteration a solution s’ is generated and later it is randomly chosen. If f(s’) is better than f(s) (i.e., has a lower objective function value), then s’ is accepted as the new current solution. Otherwise, if the move from s to s’ is a worse solution, s’ is accepted with a probability calculated using Equation (6):
Usually, this probability is computed following the Boltzmann distribution, where Δf = f(s’) − f(s) is the difference in quality between the previous and the newly generated solution and t is the current temperature. The temperature is reduced iteratively by the geometric scheduled g(t) = βt, where β is the cooling rate (β < 1). The search process is repeated until the termination criterion is met.
4. Experiment Design
The proposed algorithm consists of three investigation process. The first is to identify a suitable neighborhood strategy. The second identifies the selection strategy in which three selections strategy was investigated and later investigated the performance of proposed hybrid CS with SA. Experiments were conducted to evaluate the performance of the proposed CS on 16 instances Augerat benchmark [9], which can be downloaded from www.branchandcut.org/VRP/data/. In the instances, the total number of customers varies from 30 to 135 and the total number of vehicles varies from 3 to 10. The locations of customers appear in some instances in clusters, whilst in other problems, the customers are randomly scattered or semi-clustered. Experiments were performed on a 3.2 GHz Intel Core i3 CPU and the heuristics were coded using C++ in a Microsoft Visual Studio 2013 environment.
The following details of these instances are presented in Table 4:

Table 4.
Characteristic of benchmark dataset.
- Number of vehicles and customers (column 2 and 3)
- The capacity of each vehicle (column 4)
- Tightness of each problem instance (column 5), which is computed by
- Best-known solution (BKS) of each instance (column 6).
The best (Min.), average (Avg.) and worst (Max.) solution and the standard deviation (Std.) were computed 31 independent runs on each instance, along with the average computational time in seconds required to reach the final best solutions. The best solutions found by the proposed algorithm that was equal to the BKS are shown in bold in the tables in this section. The basic discrete CS parameters were optimized based on the Taguchi method, which is part of the initial stage in this study published in reference [2], the number of iterations equaled 200, the fraction of worse nests to be discarded was 0.1 and there were 50 nests.
Simulated annealing has three parameters: initial temperature, final temperature and cooling schedule. Table 5 shows the parameter values that were used in this study. The final temperature and cooling schedule were set based on a suggestion in Reference [70], whilst the value of the initial temperature was set based on a preliminary experiment in which three different values of the initial temperature were measured. Four instances (A-n33-k5, B-n35-k5, E-n51-k5 and P-n101-k4) of different sizes were chosen to conduct this experiment. The result of the preliminary experiment is summarized in Table 6. The SA performed better when the initial temperature was set to 100.

Table 5.
Parameter Setting for Simulated Annealing (SA).

Table 6.
The average solution quality of different initial temperatures.
Three experiments were performed in this study:
- Experiment 1: First, we investigated the performance of the 12 neighborhood structures to identify the best set of neighborhoods among them and then we formed a sequence based on the knowledge obtained. Second, we investigated which of two acceptance criteria (best, first) was the most suitable for improving the solution. All the neighborhood is evaluated and the best neighborhood is chosen. We were then able to create a neighborhood-enhanced CS (NE-CS) whose performance we compared with that of the basic CS.
- Experiment 2: We investigated three selection strategies and combined the best-performing one (which we named Discrete Cuckoo Search or Dis-CS) with NE-CS and compared its performance with the output from the first experiment.
- Experiment 3: We hybridized CS with SA (which we named HCS-SA) and compared its performance with the output from the second experiment.
5. Experiment Result
5.1. Results of Comparison of Neighborhood Structures
First, we investigated the performance of the neighborhood structures on a random generated solution. The results obtained by the CS on 11 independent runs for each instance were averaged. The results of the experiment are summarized in Table 7, which shows the average neighborhood structure frequency (avg neighborhood frequency) along with the average actual improvement of each neighborhood structure. The frequency was calculated by taking into account all the executions until the termination criterion was met. Based on this frequency, we ranked each neighborhood structure according to its successful percentage rate in improving the solution. It can be seen from the table that REINSERTION achieved the highest percentage of success, whereas K-SHIFT had the lowest percentage. The lowest percentage indicates that the algorithm became stuck in local optima and therefore the neighborhood structure was unable to improve the solution any further.

Table 7.
Percentage of successful neighborhood structures.
It can be seen from Table 7 that the neighborhood structures REINSERTION, TWO-OPT, EXCHANGE, OR-OPT2, SHIFT-1-0 and OR-OPT3 are the most successful structures in the algorithm with a percentage success rate of 99.9%, 99.6%, 99%, 97.4%, 94.8% and 94.8%, respectively. Most of these neighborhoods are intra-route (REINSERTION, TWO-OPT, EXCHANGE, OR-OPT2 and OR-OPT3); only one inter-route neighborhood structure (SHIFT-1-0) was able to achieve a comparable result. The three neighborhoods that were least successful in improving the solutions were K-SHIFT, SHIFT-2-0 and SWAP-2-2 with 44%, 58.6% and 62.3%, respectively.
Based on this finding, a neighborhood structure sequence called ‘best sequence’ was selected. The three best neighborhood structures were chosen from each category (intra- and inter-route) as the aim was to not concentrate on particular categories of neighborhood structure to better explore the solution search space. The best sequences are REINSERTION, SHIFT-1-0, TWO-OPT, SWAP-1-1, EXCHANGE and SWAP-1-2.
5.2. Results of Comparison of Accepting Criteria
We investigate the efficacy of two acceptance criteria by applying them to four instances of different sizes: A-n33-k5 and B-n35-k5, which are small-sized instances; E-n51-k5, which is medium-sized; and P-n101-k4, which is large. The two acceptance criteria were best and first. Best, where the algorithm picks the best improvement neighborhood after examining all the neighborhoods of the current solution. First, where the algorithm picks the first improvement neighborhood of the current solution. The result of the experiment after 11 runs is shown in Figure 8, Figure 9, Figure 10 and Figure 11. Figure 8 and Figure 9 show the small A-n33-k5 and B-35-k5 instances, respectively, whilst Figure 10 shows the medium E-n51-k5 instance and Figure 11 the large P-n101-k4 instance.
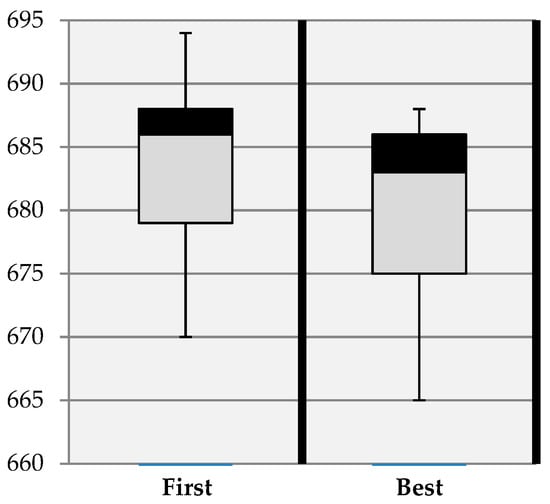
Figure 8.
Acceptance criteria applied to instance A-n33-k5.
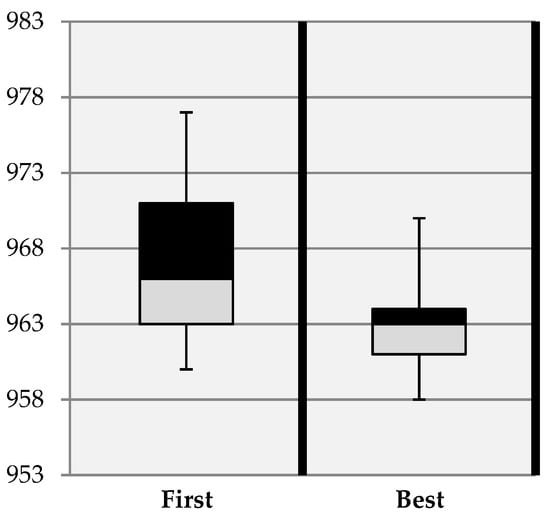
Figure 9.
Acceptance criteria applied on instance B-n35-k5.
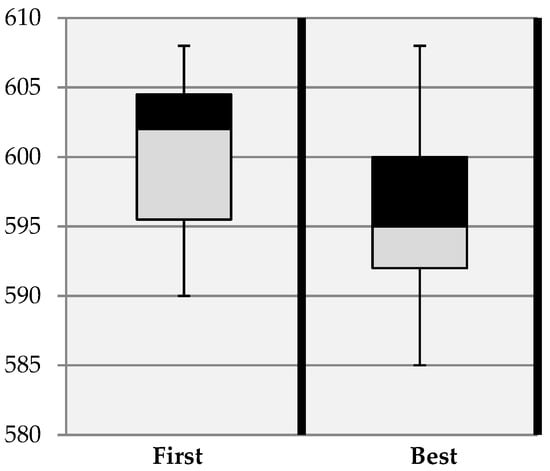
Figure 10.
Acceptance criteria applied on instance E-n51-k5.
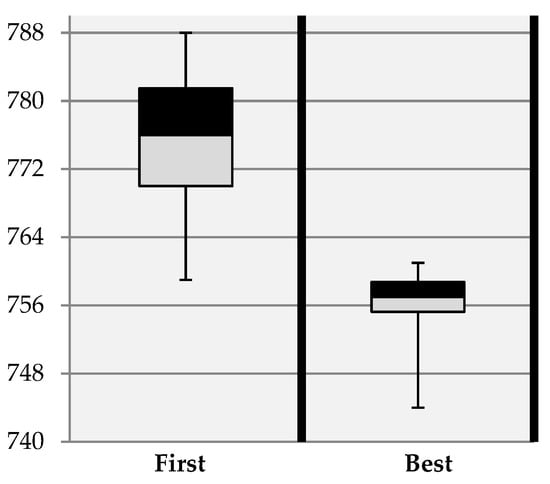
Figure 11.
Acceptance criteria applied on instance P-n101-k4.
Clearly, the Best acceptance criterion achieved the best average objective for the four instances. It was also able to achieve an optimal solution across all instances than the First acceptance criterion. Moreover, the Best acceptance criterion was able to get a near to optimal solution (the lowest line) for two instances, A-n33-k5 and B-n35-k5, as shown in Figure 8 and Figure 9, respectively. Therefore, the Best acceptance criterion was chosen to further investigate the performance of the proposed algorithm.
5.3. Result of Comparison of NE-CS with Basic CS
The result of a comparison of the basic CS with the above CS enhanced by the best sequence of neighborhood structures and Best acceptance criterion, which we named neighborhood-enhanced CS (NE-CS), is summarized in Table 8. From Table 8, it can be seen that NE-CS was able to get a near-optimal solution for most of the instances based on the (Min.) value. The result shows the sensitivity of the algorithm to the neighborhood structures and the positive impact that this has on the search process. Furthermore, the result shows that the proposed NE-CS is much more stable than the basic CS for all instances based on the (Std.) value. Therefore, we can conclude that NE-CS has the ability to explore the search space more efficiently than the basic CS. Also, in terms of computational time, NE-CS outperformed the basic CS for all instances.

Table 8.
The computational result using Basic CS and neighborhood-enhanced CS (NE-CS).
We also performed a Wilcoxon test to determine whether there is a significant difference between the two methods, with a confidence level of 95%. The results are presented in Table 9. The p-values indicate that there were significant differences in 13 out of 16 instances.

Table 9.
p-value results for NE-CS vs. Basic CS.
5.4. Result of Comparison of Selection Strategies
Next, we compared the performance of the NE-CS when modified by three different selection strategies, namely tournament, rank and disruptive, which were named Tour-CS, Rank-CS and Dis-CS, respectively. The result of this comparison is summarized in Table 10. Note that the computational time is not reported because it is similar for all three-selection strategies.

Table 10.
Result of comparison of performance of NE-CS, Tour-CS, Rank-CS and Dis-CS.
It is clear from the table that Dis-CS outperformed the other algorithms. It was able to obtain the BKS for six out of 16 instances (A-n33-k5, B-n46-k7, B-n35-k5, E-n30-k3, F-n72-k4 and M-n101-k10). On the other hand, Tour-CS obtained the BKS for two out of 16 instances (B-n35-k5 and E-n30-k3) and Rank-CS obtained the BKS for three out of 16 instances (A-n33-k5, B-n35-k5 and B-n45-k5). We believe that the better performance of the disruptive strategy is due to its ability to achieve a balance between the selection of worse and better solutions in the population with a small bias towards the better ones; it tries to improve most of the solutions whether they are worse or have high fitness concurrently. The other two selection strategies (tournament and rank) are biased much more towards high-fitness solutions. However, all three-selection strategies outperformed the random selection strategy used by NE-CS. Moreover, the Dis-CS was able to outperform the NE-CS in five instances.
To illustrate the superior performance of Dis-CS, Figure 12 provides boxplots for a range of instance sizes (A-n33-k5, B-n35-k5, E-n51-k5 and P-n101-k4). It is clear from the figure that the disruptive selection strategy performed better than the original random selection strategy for all four instances. Moreover, in the case of B-n35-k5 and P-n101-k4 even the worst solution obtained by the disruptive selection strategy was better than the best obtained by the random selection strategy. The disruptive selection strategy also outperformed the tournament and rank selection strategies. Lastly, the algorithm performed very well on the large instance, P-n101-k4, when using the disruptive selection strategy.
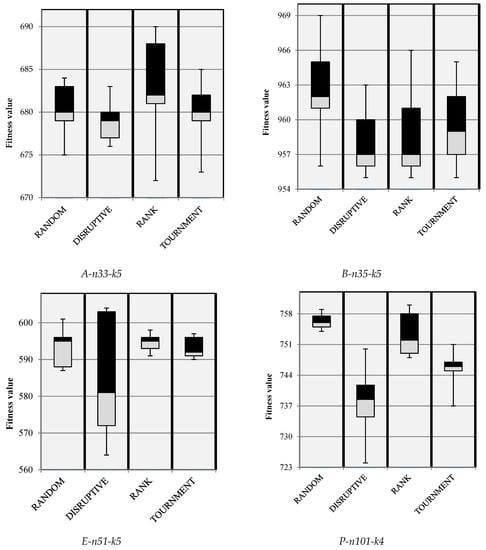
Figure 12.
Boxplots for Random, Disruptive, Rank and Tournament Selection Strategies.
We also conducted a Freidman test to examine whether there was any significant difference between the algorithm with the best-performing selection strategy (Dis-CS) and the other two proposed algorithms, with a significance level of 95%. Table 11 shows the p-value results of the statistical test.

Table 11.
p-value results for Dis-CS vs. Tour-CS and Rank-CS.
We also carried out statistical analysis to identify the rank of each algorithm by conducting a Friedman test followed by Holm and Hochberg tests as post-hoc methods to obtain the adjusted p-value for each comparison when the control algorithm was Dis-CS. Table 12 summarizes the ranking obtained by the Friedman test (the lowest is the best) and Table 13 provides the results of the Holm and Hochberg tests. Table 12 shows that Dis-CS ranked first, followed by Tour-CS and Rank-CS, respectively. The p-value computed by the Friedman test was 0.000017, which was below the significant interval of 95% and thus indicates that there were significant differences between the observed results. Table 12 shows that the Holm and Hochberg procedures revealed significant differences when Dis-CS was the control algorithm. The comparison showed that Dis-CS was better than Rank-CS and Tour-CS with a confidence level of α = 0.05 (2/3 algorithms).

Table 12.
Average ranking of algorithms based on Friedman test.

Table 13.
Adjusted p-values (Friedman).
5.5. Result of Comparison of HCS-SA with Dis-CS
Finally, we compared Dis-CS with HCS-SA in order to ascertain whether hybridization would improve performance more than the best-performing selection strategy. Table 14 presents the results of this comparison. It can be seen from the table that HCS-SA obtained a better result in 12 out of 16 instances. Moreover, it performed better than Dis-CS in all of the instances in terms of Avg., Std. and Max., values when the search ended. In the case of the medium- and large-sized instances (A-n60-k9, B-n45-k5, B-n68-k9, E-n51-k5 and P-n76-k4), HCS-SA found the BKS.

Table 14.
Result of comparison of performance of Dis-CS and HCS-SA.
5.6. Result of Comparison of HCS-SA with State-of-the-Art Methods
In order to further assess the performance of HCS-SA, we compared it with the following eight state-of-the-art approaches: Discrete Particle Swarm Optimization-Simulated Annealing (DPSO-SA) [9], Particle Swarm Optimization-Second Representation (PSO-SR-2) [8], Capacitated Particle Swam Optimization-Simulated Annealing (CPSO-SA) [7], Particle Swarm Optimization-Ant Colony Optimization (PSO-ACO) [71], Improved Quantum Evolution Algorithm (IQEA) [72], Capacitated Routing Problem using an island model based genetic algorithm (CGA) [73], improved golden ball algorithm (IGB) [74] and Intelligent Water Drops (IWD) [75]. Table 15 shows the results of the comparison based on the objective function value (quality). It can be seen from Table 15 that the solution quality achieved by HCS-SA is better than that of all the other methods. The HCS-SA algorithm was able to obtain exactly the same value as the BKS for 13 out of the 16 instances (A-n33-k5, A-n46-k7, A-n60-k9, B-n35-k5, B-n45-k5, B-n68-k9, E-n30-k3, E-n51-k5, F-n72-k4, M-n101-k10, M-n121-k7, P-n76-k4 and P-n101-k4). Moreover, it also obtained solutions that were very close to the BKS for some other instances (B-n78-k10, E-n76-k7 and F-n135-k7).

Table 15.
Comparison of performance of HCS-SA and state-of-the-art methods.
We also compared the computational time of HCS-SA with that of the five state-of-the-art methods for which data was available (DPSO-SA, PSO-SR-2, CPSO-SA, PSO-ACO and IQEA). As can be seen from Table 16 and Table 17, HCS-SA was faster than two methods (DPSO-SA and IQEA) for most instances, which represents around 11 out of 16 instances (approx. 68%). On the other hand, the proposed HCS-SA was slower than the other methods. This result was further analyzed using the percentage of improvement, the result of which showed that some of the instances significantly improved (such as A-n60-k9, B-n45-k5, B-n68-k9, B-n78-k10, E-n30-k3, E-n51-k5 and M-n121-k7) while others saw less improvement (such as A-n35-k5 and E-n51-k5).

Table 16.
Computational times of HCS-SA and state-of-the-art methods.

Table 17.
Percentage improvement in time of HCS-SA and state-of-the-art methods.
The performance of HCS-SA was further analyzed by using statistical tests to identify whether there was a significant difference between the proposed algorithm and the best methods in the literature. Only two methods (PSO-ACO and IQEA) reported the data necessary for this test. First, we employed a Freidman’s test to identify the rank and then we applied Holm and Hochberg tests as post-hoc methods to obtain the adjusted p-value for each comparison between the control algorithm (the best-performing one) and the other two methods. Table 18 summarizes the average ranking (the lower the better) obtained by the Freidman’s test and Table 19 presents the results of the Holm and Hochberg tests.

Table 18.
Average ranking of algorithms based on Friedman test.

Table 19.
Adjusted p-values (Friedman).
Table 18 shows that the PSO-ACO ranked first, followed by HCS-SA and IQEA, respectively. The p-value obtained by the Friedman test was 0.000004, which is below the significance interval of 95% (α = 0.05). This shows that there was a significant difference between the observed results. Furthermore, Table 19 shows that the control method (PSO-ACO) outperformed the proposed method HCS-SA at the critical level of 0.05 (adjusted p-value < 0.05). The results of the Holm and Hochberg statistical tests suggest that HCS-SA is not better than PSO-ACO. However, the results in Table 13 show that HCS-SA outperformed PSO-ACO on one instance and produced a comparable performance across all the other instances.
6. Discussion
As mentioned earlier, this paper has proposed a hybrid HCS-SA for CVRP, however, it has been developed with various stages, as shown in Table 20. The higher –ve value mean the proposed algorithm performed far better. The first, improvement basic CS based on neighborhood structures (NE-CS). It has improved the mean up to 3%, reduced standard deviation up to 20 and reduced computation time up to 17 s. Furthermore, the Freidman test showed NE-CS was significantly improved (p-value < 0.05) compared to basic CS in all instances. The second is improvement using a selection strategy known as Dis-CS. Dis-CS has improved the mean up to 2%, 4% and 4% compare to NE-CS, Tour-DS and Rank-DS respectively. The Freidman test also shows Dis-CS has significantly improved for all instances compare with NE-CS, Tour-CS and Rank-CS except E-30-n3 and B-n45-k5. Besides, it has increased most of the standard deviation and computational time. The third improvement is hybrid with SA, in which it has improved the mean up to 6%, reduced standard deviation up to 8.9, however, it has increased the computational time between 21.65 s to 1999 s. The comparison result between HCS-SA with the state-of-art algorithms shown it has either obtained the same or outperformed for most instances from 0.3 up to 72, except for E-n78-k10 and E-n76-k7 instances, however still better compare with algorithm IWD and IQEA. In terms of computational time, HCS-SA appears to even have performed better on some algorithms such as DIPSO-SA and IQEA but on HCS-SA losses against other algorithms for all problem instances.

Table 20.
Comparison of performance and computational time of HCS-SA and state-of-the-art methods.
7. Conclusions
This study introduced hybrid CS with SA for CVRP that consists of three improvements strategy. The first strategy is to improve the CS exploration of search space by avoiding the trap in local optima using 12 multiple neighborhood structure strategies. However, only six multiple neighborhood structures are enough to obtain the best solution as it has improved both the cost and computational time. The second strategy is to further increase the CS exploration using three selection strategies as the disruptive strategy shown the best solution. The result showed it has significantly improved the solution, however it also increased computational time as well. Therefore, the third strategy aims to improve the exploitation of Disruptive CS ability by hybridizing with SA by targeting of having higher improvement solution with less increase its complexity. The result shown that the HCS-SA has outperformed compared with the state-of-art algorithms includes with other CS improvement. Even though the complexity of HCS-SA is higher compare with most of the state-of-the-art algorithms. However, the complexity of HCS-SA is far less compared with the state of art improvement CS for CVRP. We found that the exploitation strategy has given a higher impact on CS improvement compare with the two exploration strategies. So, it can be concluded that the strategy to maximize the exploration first follows by exploitation as the best strategy for CVRP’s CS improvement. With such a result, we believe the proposed algorithm can be applied to other variants of routing problems as well, such as VRP with time windows [76,77,78], VRP for hazardous materials transportation [79], dynamic vehicle routing problem [80], weighted vehicle routing problem [81], split delivery vehicle routing problem [82] and VRP with outsourcing and profit balancing [83].
Author Contributions
Conceptualization, M.A. (Mansour Alssager), Z.A.O. and M.A. (Masri Ayob); Data curation, M.A. (Mansour Alssager) and Z.A.O.; Formal analysis, M.A. (Mansour Alssager) and Z.A.O.; Funding acquisition, Z.A.O.; Investigation, M.A. (Mansour Alssager) and Z.A.O.; Methodology, M.A. (Mansour Alssager) and Z.A.O.; Project administration, Z.A.O.; Resources, M.A. (Mansour Alssager) and Z.A.O.; Software, M.A. (Mansour Alssager); Supervision, Z.A.O. and M.A. (Masri Ayob); Validation, M.A. (Masri Ayob), R.M. and H.Y.; Visualization, M.A. (Masri Ayob), R.M. and H.Y.; Writing—original draft, M.A. (Mansour Alssager) and Z.A.O.; Writing—review & editing, M.A. (Masri Ayob), R.M. and H.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Universiti Kebangsaan Malaysia under Grant FRGS/1/2019/ICT02/UKM/2/7 and DCP2017-2017-015/4.
Acknowledgments
The authors express highly appreciation to all members at the Center of Artificial Intelligence Technology, UKM providing facilities and guidance on this research for three years.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Altabeeb, A.M.; Mohsen, A.M.; Ghallab, A. An improved hybrid firefly algorithm for capacitated vehicle routing problem. Appl. Soft Comput. 2019, 84, 105728. [Google Scholar] [CrossRef]
- Alssager, M.; Othman, Z.A. Taguchi-based Parameter Setting of Cuckoo Search Algorithm for Capacitated Vehicle Routing Problem. In Lecture Notes in Electrical Engineering; Springer: Berlin/Heidelberg, Germany, 2016; Volume 387, pp. 71–79. [Google Scholar]
- Kesavan, V.; Kamalakannan, R.; Sudhakarapandian, R.; Sivakumar, P. Heuristic and meta-heuristic algorithms for solving medium and large scale sized cellular manufacturing system NP-hard problems: A comprehensive review. Mater. Today Proc. 2020, 21, 66–72. [Google Scholar] [CrossRef]
- Li, G.; Li, J. An Improved Tabu Search Algorithm for the Stochastic Vehicle Routing Problem with Soft Time Windows. IEEE Access 2020, 8, 158115–158124. [Google Scholar] [CrossRef]
- Yu, V.F.; Redi, A.A.N.P.; Hidayat, Y.A.; Wibowo, O.J. A simulated annealing heuristic for the hybrid vehicle routing problem. Appl. Soft Comput. 2017, 53, 119–132. [Google Scholar] [CrossRef]
- Costa, P.R.D.O.D.; Mauceri, S.; Carroll, P.; Pallonetto, F. A Genetic Algorithm for a Green Vehicle Routing Problem. Electron. Notes Discret. Math. 2018, 64, 65–74. [Google Scholar] [CrossRef]
- Kim, B.-I.; Son, S.-J. A probability matrix based particle swarm optimization for the capacitated vehicle routing problem. J. Intell. Manuf. 2012, 23, 1119–1126. [Google Scholar] [CrossRef]
- Ai, T.J.; Kachitvichyanukul, V. Particle swarm optimization and two solution representations for solving the capacitated vehicle routing problem. Comput. Ind. Eng. 2009, 56, 380–387. [Google Scholar] [CrossRef]
- Chen, A.-L.; Yang, G.-K.; Wu, Z.-M. Hybrid discrete particle swarm optimization algorithm for capacitated vehicle routing problem. J. Zhejiang Univ. A 2006, 7, 607–614. [Google Scholar] [CrossRef]
- Hannan, M.; Akhtar, M.; Begum, R.A.; Basri, H.; Hussain, A.; Scavino, E. Capacitated vehicle-routing problem model for scheduled solid waste collection and route optimization using PSO algorithm. Waste Manag. 2018, 71, 31–41. [Google Scholar] [CrossRef]
- Zainudin, S.; Kerwad, M.M.; Othman, Z.A. A water flow-like algorithm for capacitated vehicle routing problem. J. Theor. Appl. Inf. Technol. 2015, 77, 125–135. [Google Scholar]
- Kerwad, M.M.; Othman, Z.A.; Zainudin, S. Improved water flow-like algorithm for capacitated vehicle routing problem. J. Theor. Appl. Inf. Technol. 2018, 96, 4836–4853. [Google Scholar]
- Niu, Y.; Wang, S.; He, J.; Xiao, J. A novel membrane algorithm for capacitated vehicle routing problem. Soft Comput. 2015, 19, 471–482. [Google Scholar] [CrossRef]
- Faiz, A.; Subiyanto, S.; Arief, U.M. An efficient meta-heuristic algorithm for solving capacitated vehicle routing problem. Int. J. Adv. Intell. Inf. 2018, 4, 212–225. [Google Scholar] [CrossRef]
- Ghodrati, A.; Lotfi, S. A Hybrid CS/PSO Algorithm for Global Optimization. In Proceedings of the Asian Conference on Intelligent Information and Database Systems; Springer: Berlin/Heidelberg, Germany, 2012; Volume 7198, pp. 89–98. [Google Scholar]
- Yang, X.-S.; Deb, S. Cuckoo Search via Lévy flights. In Proceedings of the 2009 World Congress on Nature & Biologically Inspired Computing (NaBIC), Coimbatore, India, 9–11 December 2009; pp. 210–214. [Google Scholar]
- Mohamed, N.S.; Zainudin, S.; Othman, Z.A. Metaheuristic approach for an enhanced mRMR filter method for classification using drug response microarray data. Expert Syst. Appl. 2017, 90, 224–231. [Google Scholar] [CrossRef]
- Usman, A.M.; Yusof, U.K.; Naim, S. Cuckoo inspired algorithms for feature selection in heart disease prediction. Int. J. Adv. Intell. Inf. 2018, 4, 95–106. [Google Scholar] [CrossRef]
- Ouaarab, A.; Ahiod, B.; Yang, X.-S. Improved and Discrete Cuckoo Search for Solving the Travelling Salesman Problem. In Decision Diagrams for Optimization; Springer: Berlin/Heidelberg, Germany, 2013; Volume 516, pp. 63–84. [Google Scholar]
- Iglesias, A.; Gálvez, A.; Suarez, P.; Shinya, M.; Yoshida, N.; Otero, C.; Manchado, C.; Gomez-Jauregui, V. Cuckoo Search Algorithm with Lévy Flights for Global-Support Parametric Surface Approximation in Reverse Engineering. Symmetry 2018, 10, 58. [Google Scholar] [CrossRef]
- Meryem, B.; Abdelmadjid, B. Resolving a vehicle routing problem with heterogeneous fleet, mixed backhauls and time windows using cuckoo behaviour approach. Int. J. Oper. Res. 2015, 24, 132. [Google Scholar] [CrossRef]
- Santillan, J.H.; Tapucar, S.; Manliguez, C.; Calag, V. Cuckoo search via Lévy flights for the capacitated vehicle routing problem. J. Ind. Eng. Int. 2017, 14, 293–304. [Google Scholar] [CrossRef]
- Xiao, L.; Dridi, M.; El Hassani, A.H.; Fei, H.; Lin, W. An Improved Cuckoo Search for a Patient Transportation Problem with Consideration of Reducing Transport Emissions. Sustainability 2018, 10, 793. [Google Scholar] [CrossRef]
- Cordeau, J.-F.; Gendreau, M.; Laporte, G.; Potvin, J.-Y.; Semet, F. A guide to vehicle routing heuristics. J. Oper. Res. Soc. 2002, 53, 512–522. [Google Scholar] [CrossRef]
- Yang, X.S.; Deb, S. Engineering optimisation by cuckoo search. Int. J. Math. Model. Numer. Optim. 2010, 1, 330. [Google Scholar] [CrossRef]
- Xie, J.; Zhou, Y.Q.; Chen, H. A Novel Bat Algorithm Based on Differential Operator and Lévy Flights Trajectory. Comput. Intell. Neurosci. 2013, 2013, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Pavlyukevich, I. Lévy flights, non-local search and simulated annealing. J. Comput. Phys. 2007, 226, 1830–1844. [Google Scholar] [CrossRef]
- Gutowski, M. Lévy flights as an underlying mechanism for global optimization algorithms. arXiv 2001, arXiv:math-ph/0106003. [Google Scholar]
- Wang, G.; Guo, L.; Gandomi, A.H.; Cao, L.; Alavi, A.H.; Duan, H.; Li, J. Lévy-Flight Krill Herd Algorithm. Math. Probl. Eng. 2013, 2013, 1–14. [Google Scholar] [CrossRef]
- Yang, X.-S.; Deb, S. Eagle Strategy Using Lévy Walk and Firefly Algorithms for Stochastic Optimization. In Recent Advances in Computational Optimization; Springer: Berlin/Heidelberg, Germany, 2010; pp. 101–111. [Google Scholar]
- Gandomi, A.H.; Yang, X.-S.; Alavi, A.H. Erratum to: Cuckoo search algorithm: A metaheuristic approach to solve structural optimization problems. Eng. Comput. 2013, 29, 245. [Google Scholar] [CrossRef]
- Akhtar, M.; Hannan, M.; Begum, R.A.; Basri, H.; Scavino, E. Backtracking search algorithm in CVRP models for efficient solid waste collection and route optimization. Waste Manag. 2017, 61, 117–128. [Google Scholar] [CrossRef]
- Bulatović, R.R.; Đorđević, S.R.; Đorđević, V.S. Cuckoo Search algorithm: A metaheuristic approach to solving the problem of optimum synthesis of a six-bar double dwell linkage. Mech. Mach. Theory 2013, 61, 1–13. [Google Scholar] [CrossRef]
- Bhargava, V.; Fateen, S.-E.K.; Bonilla-Petriciolet, A. Cuckoo Search: A new nature-inspired optimization method for phase equilibrium calculations. Fluid Phase Equilibria 2013, 337, 191–200. [Google Scholar] [CrossRef]
- Salomie, I.; Chifu, V.R.; Pop, C.B. Hybridization of Cuckoo Search and Firefly Algorithms for Selecting the Optimal Solution in Semantic Web Service Composition. In Decision Diagrams for Optimization; Springer: Berlin/Heidelberg, Germany, 2013; Volume 516, pp. 217–243. [Google Scholar]
- Laha, D.; Gupta, J.N. An improved cuckoo search algorithm for scheduling jobs on identical parallel machines. Comput. Ind. Eng. 2018, 126, 348–360. [Google Scholar] [CrossRef]
- Yasin, Z.M.; Aziz, N.F.A.; Salim, N.A.; Wahab, N.A.; Rahmat, N.A. Optimal Economic Load Dispatch using Multiobjective Cuckoo Search Algorithm. Indones. J. Electr. Eng. Comput. Sci. 2018, 12, 168. [Google Scholar] [CrossRef]
- Marichelvam, M.K.; Prabaharan, T.; Yang, X. Improved cuckoo search algorithm for hybrid flow shop scheduling problems to minimize makespan. Appl. Soft Comput. 2014, 19, 93–101. [Google Scholar] [CrossRef]
- Ouaarab, A.; Ahiod, B.; Yang, X.-S. Random-key cuckoo search for the travelling salesman problem. Soft Comput. 2015, 19, 1099–1106. [Google Scholar] [CrossRef]
- Lin, J.H.; Lee, I.H. Emotional chaotic cuckoo search for the reconstruction of chaotic dynamics. In Proceedings of the 11th WSEAS International Conference on Mathematical Methods, Computational Techniques and Intelligent Systems and Cybernetics (CIMMACS’12), Singapore, 11–13 May 2012; pp. 123–128. [Google Scholar]
- Walton, S.; Hassan, O.; Morgan, K.; Brown, M. Modified cuckoo search: A new gradient free optimisation algorithm. Chaos Solitons Fractals 2011, 44, 710–718. [Google Scholar] [CrossRef]
- Soneji, H.; Sanghvi, R.C. Towards the improvement of Cuckoo search algorithm. In Proceedings of the 2012 World Congress on Information and Communication Technologies, Trivandrum, India, 30 October–2 November 2012; Institute of Electrical and Electronics Engineers (IEEE): Piscataway, NJ, USA, 2012; pp. 878–883. [Google Scholar]
- Joshi, A.; Kulkarni, O.; Kakandikar, G.; Nandedkar, V. Cuckoo Search Optimization—A Review. Mater. Today Proc. 2017, 4, 7262–7269. [Google Scholar] [CrossRef]
- Shehab, M.; Khader, A.T.; Al-Betar, M.A. A survey on applications and variants of the cuckoo search algorithm. Appl. Soft Comput. 2017, 61, 1041–1059. [Google Scholar] [CrossRef]
- Fister, I.; Yang, X.-S.; Fister, D. Cuckoo Search: A Brief Literature Review. In Recent Advances in Computational Optimization; Springer: Berlin/Heidelberg, Germany, 2013; pp. 49–62. [Google Scholar]
- Yang, X.-S.; Deb, S. Cuckoo search: Recent advances and applications. Neural Comput. Appl. 2014, 24, 169–174. [Google Scholar] [CrossRef]
- Hansen, P.; Mladenović, N. Variable neighborhood search: Principles and applications. Eur. J. Oper. Res. 2001, 130, 449–467. [Google Scholar] [CrossRef]
- Abdullah, S.; Turabieh, H. On the use of multi neighbourhood structures within a Tabu-based memetic approach to university timetabling problems. Inf. Sci. 2012, 191, 146–168. [Google Scholar] [CrossRef]
- Gendreau, M.; Hertz, A.; Laporte, G. New Insertion and Postoptimization Procedures for the Traveling Salesman Problem. Oper. Res. 1992, 40, 1086–1094. [Google Scholar] [CrossRef]
- Hoos, H.H.; Stützle, T. Stochastic Local Search: Foundations & Applications; Stoch. Local Search; Morgan Kaufmann: Burlington, MA, USA, 2005; pp. 61–112. [Google Scholar]
- Goli, A.; Aazami, A.; Jabbarzadeh, A. Accelerated Cuckoo Optimization Algorithm for Capacitated Vehicle Routing Problem in Competitive Conditions. Int. J. Artif. Intell. 2018, 16, 88–112. [Google Scholar]
- Alzaqebah, M.; Abdullah, S. Hybrid Artificial Bee Colony Search Algorithm Based on Disruptive Selection for Examination Timetabling Problems. In Proceedings of the International Conference on Combinatorial Optimization and Applications; Springer: Berlin/Heidelberg, Germany, 2011; pp. 31–45. [Google Scholar]
- Lozano, M.; Cordon, O. Hybrid metaheuristics with evolutionary algorithms specializing in intensification and diversification: Overview and progress report. Comput. Oper. Res. 2010, 37, 481–497. [Google Scholar] [CrossRef]
- Yang, X.-S. Firefly Algorithm, Lévy Flights and Global Optimization. In Research and Development in Intelligent Systems XXVI; Springer: Berlin/Heidelberg, Germany, 2010; pp. 209–218. [Google Scholar]
- Teymourian, E.; Kayvanfar, V.; Komaki, G.; Zandieh, M. Enhanced intelligent water drops and cuckoo search algorithms for solving the capacitated vehicle routing problem. Inf. Sci. 2016, 334, 354–378. [Google Scholar] [CrossRef]
- Jaddi, N.S.; Abdullah, S.; Malek, M.A. Master-Leader-Slave Cuckoo Search with Parameter Control for ANN Optimization and Its Real-World Application to Water Quality Prediction. PLoS ONE 2017, 12, e0170372. [Google Scholar] [CrossRef]
- Ilunga-Mbuyamba, E.; Cruz-Duarte, J.M.; Avina-Cervantes, J.G.; Correa-Cely, C.R.; Lindner, D.; Chalopin, C. Active contours driven by Cuckoo Search strategy for brain tumour images segmentation. Expert Syst. Appl. 2016, 56, 59–68. [Google Scholar] [CrossRef]
- Viswanathan, G.M.; Afanasyev, V.; Buldyrev, S.V.; Murphy, E.J.; Prince, P.A.; Stanley, H. Lévy flight search patterns of wandering albatrosses. Nat. Cell Biol. 1996, 381, 413–415. [Google Scholar] [CrossRef]
- Amirsadri, S.; Mousavirad, S.J.; Ebrahimpour-Komleh, H. A Levy flight-based grey wolf optimizer combined with back-propagation algorithm for neural network training. Neural Comput. Appl. 2017, 30, 3707–3720. [Google Scholar] [CrossRef]
- Hakli, H.; Uğuz, H. A novel particle swarm optimization algorithm with Levy flight. Appl. Soft Comput. 2014, 23, 333–345. [Google Scholar] [CrossRef]
- Sharma, H.; Bansal, J.C.; Arya, K.V.; Yang, X.-S. Lévy flight artificial bee colony algorithm. Int. J. Syst. Sci. 2016, 47, 2652–2670. [Google Scholar] [CrossRef]
- Alssager, M.; Othman, Z.A. Cuckoo search algorithm for capacitated vehicle routing problem. J. Theor. Appl. Inf. Technol. 2016, 88, 11–19. [Google Scholar]
- Sterling, K.B. Cuckoo: Cheating by nature. Choice Rev. Online 2015, 53, 53. [Google Scholar] [CrossRef]
- Blickle, T.; Thiele, L. A mathematical analysis of tournament selection. In Proceedings of the 6th International Conference on Genetic Algorithms; Morgan Kaufmann Publishers Inc.: San Francisco, CA, USA, 1995; pp. 9–16. ISBN 1558603700. [Google Scholar]
- Bao, L.; Zeng, J.-C. Comparison and Analysis of the Selection Mechanism in the Artificial Bee Colony Algorithm. In Proceedings of the 2009 Ninth International Conference on Hybrid Intelligent Systems, Shenyang, China, 12–14 August 2009; Institute of Electrical and Electronics Engineers (IEEE): Piscataway, NJ, USA, 2009; Volume 1, pp. 411–416. [Google Scholar]
- Song, A.; Lu, J. Ranking based adaptive evolutionary operator genetic algorithm. Tien Tzu Hsueh Pao 1999, 27, 85–88. [Google Scholar]
- Osman, I.H. Metastrategy simulated annealing and tabu search algorithms for the vehicle routing problem. Ann. Oper. Res. 1993, 41, 421–451. [Google Scholar] [CrossRef]
- Husselmann, A.V.; Hawick, K.A. Levy flights for particle swarm optimisation algorithms on graphical processing units. Parallel Cloud Comput. 2013, 2, 32–40. [Google Scholar]
- Ouaarab, A.; Ahiod, B.; Yang, X.-S. Discrete cuckoo search algorithm for the travelling salesman problem. Neural Comput. Appl. 2014, 24, 1659–1669. [Google Scholar] [CrossRef]
- Burke, E.K.; Kendall, G. Search Methodologies; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Kao, Y.; Chen, M.-H.; Huang, Y.-T. A Hybrid Algorithm Based on ACO and PSO for Capacitated Vehicle Routing Problems. Math. Probl. Eng. 2012, 2012, 1–17. [Google Scholar] [CrossRef]
- Cui, L.; Wang, L.; Deng, J.; Zhang, J. A New Improved Quantum Evolution Algorithm with Local Search Procedure for Capacitated Vehicle Routing Problem. Math. Probl. Eng. 2013, 2013, 1–17. [Google Scholar] [CrossRef]
- Ammi, M.; Chikhi, S. An island model based genetic algorithm for solving the capacitated vehicle routing problem. In Proceedings of the 6th International Conference of Soft Computing and Pattern Recognition (SoCPaR), Tunis, Tunisia, 11–14 August 2014; Institute of Electrical and Electronics Engineers (IEEE): Piscataway, NJ, USA, 2014; pp. 342–347. [Google Scholar]
- Ruttanateerawichien, K.; Kurutach, W.; Pichpibul, T. An Improved Golden Ball Algorithm for the Capacitated Vehicle Routing Problem. In Cyberspace Data and Intelligence, and Cyber-Living, Syndrome, and Health; Springer Science and Business Media LLC: Berlin/Heidelberg, Germany, 2014; Volume 472, pp. 341–356. [Google Scholar]
- Wedyan, A.; Narayanan, A. Solving capacitated vehicle routing problem using intelligent water drops algorithm. In Proceedings of the 10th International Conference on Natural Computation (ICNC), Xiamen, China, 19–21 August 2014; Institute of Electrical and Electronics Engineers (IEEE): Piscataway, NJ, USA, 2014; pp. 469–474. [Google Scholar]
- Rizkallah, L.W.; Ahmed, M.F.; Darwish, N.M. SMT-LH: A New Satisfiability Modulo Theory-Based Technique for Solving Vehicle Routing Problem with Time Window Constraints. Comput. J. 2019. [Google Scholar] [CrossRef]
- Wang, J.; Ren, W.; Zhang, Z.; Huang, H.; Zhou, Y. A Hybrid Multiobjective Memetic Algorithm for Multiobjective Periodic Vehicle Routing Problem with Time Windows. IEEE Trans. Syst. Man Cybern. Syst. 2020, 50, 4732–4745. [Google Scholar] [CrossRef]
- Khoo, T.-S.; Mohammad, B.B.; Wong, V.-H.; Tay, Y.-H.; Nair, M.B. A Two-Phase Distributed Ruin-and-Recreate Genetic Algorithm for Solving the Vehicle Routing Problem with Time Windows. IEEE Access 2020, 8, 169851–169871. [Google Scholar] [CrossRef]
- Zhao, L.; Cao, N. Fuzzy Random Chance-Constrained Programming Model for the Vehicle Routing Problem of Hazardous Materials Transportation. Symmetry 2020, 12, 1208. [Google Scholar] [CrossRef]
- Kucharska, E. Dynamic Vehicle Routing Problem—Predictive and Unexpected Customer Availability. Symmetry 2019, 11, 546. [Google Scholar] [CrossRef]
- Wang, X.; Shao, S.; Tang, J. Iterative Local-Search Heuristic for Weighted Vehicle Routing Problem. IEEE Trans. Intell. Transp. Syst. 2020, 1–11. [Google Scholar] [CrossRef]
- Mehlawat, M.K.; Gupta, P.; Khaitan, A.; Pedrycz, W. A Hybrid Intelligent Approach to Integrated Fuzzy Multiple Depot Capacitated Green Vehicle Routing Problem with Split Delivery and Vehicle Selection. IEEE Trans. Fuzzy Syst. 2020, 28, 1155–1166. [Google Scholar] [CrossRef]
- Zhang, Z.; Qin, H.; Li, Y. Multi-Objective Optimization for the Vehicle Routing Problem with Outsourcing and Profit Balancing. IEEE Trans. Intell. Transp. Syst. 2020, 21, 1987–2001. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).