A New S-Box Generation Method and Advanced Design Based on Combined Chaotic System
Abstract
:1. Introduction
- Our paper proposes a new combined chaotic system and analyzes its dynamic behavior.
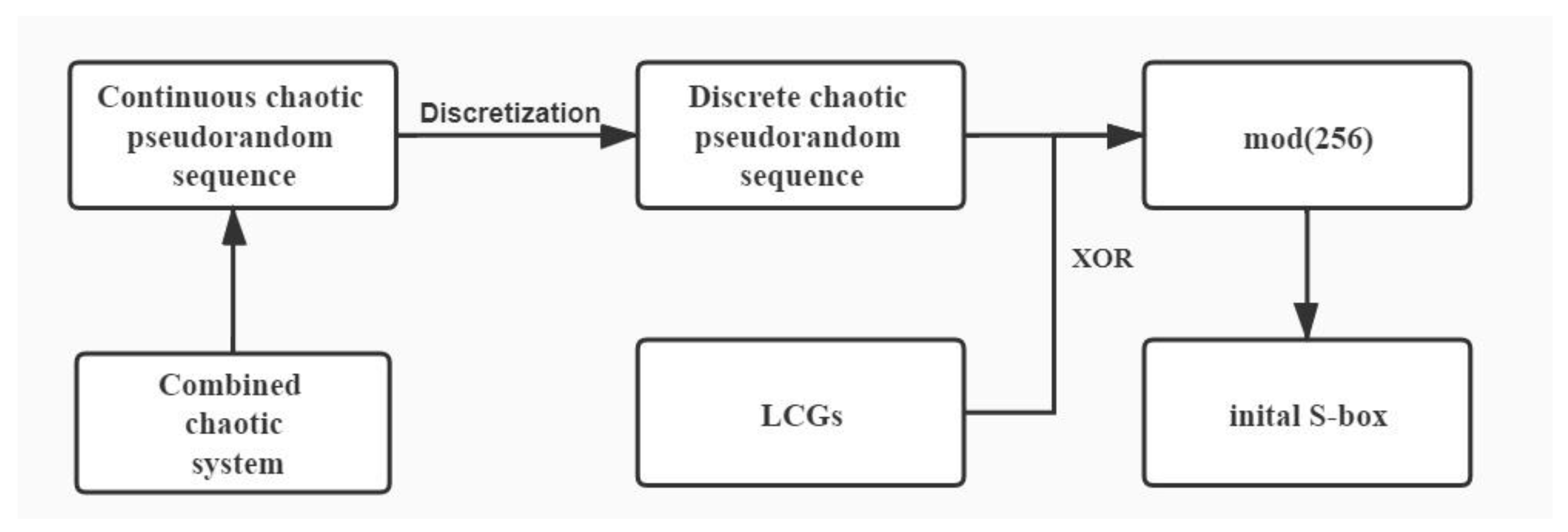
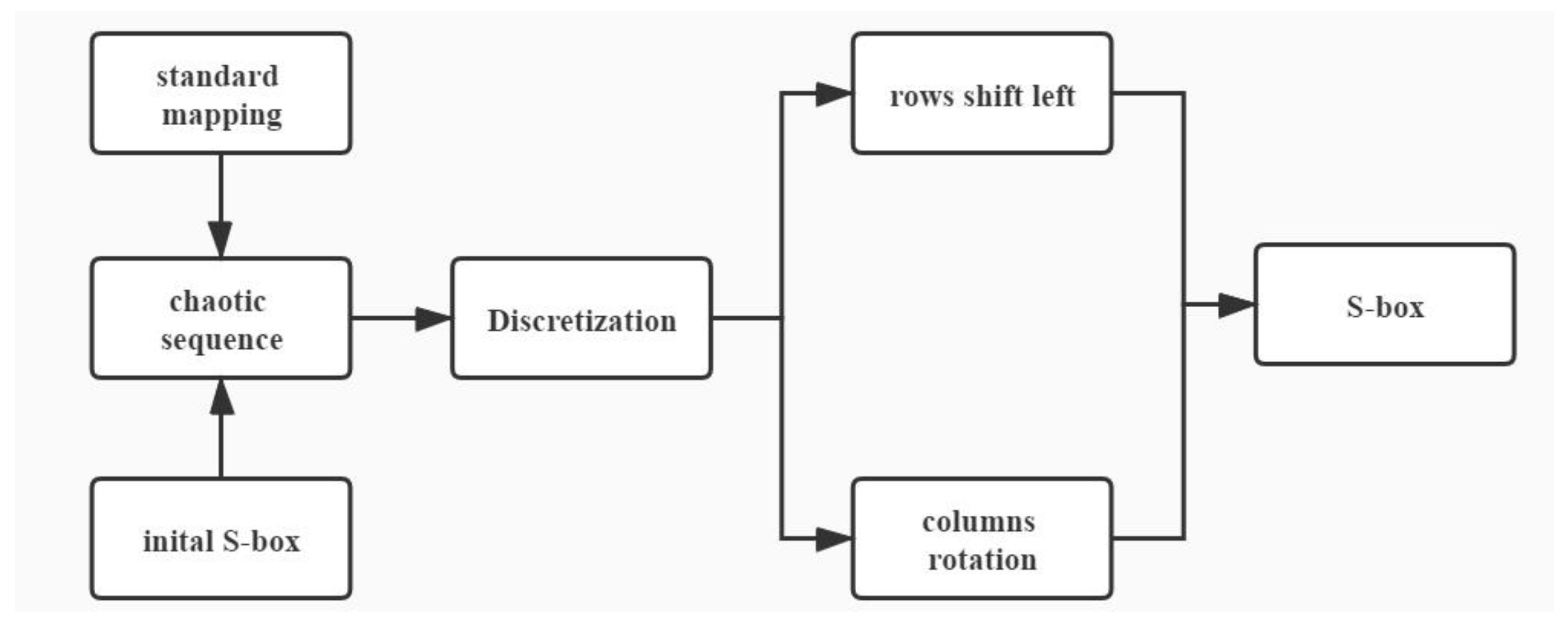
- We construct S-Box by combining the generated pseudo-random sequence with the linear congruence random number generator, and the standard mapping is introduced to scramble the initial S-box.
- The S-box optimization method based on advanced genetic algorithm is proposed in this paper.
- Through a lot of security analysis experiment and comparison with other papers, the optimized S-box has better cryptography characteristics and can resist linear attacks and differential attacks.
2. Related Work
2.1. Review of S-Box
2.2. Review of Genetic Algorithm
3. Chaotic System Analysis
- Lyapunov exponent of the combined chaotic system
- Bifurcation diagram of the combined system
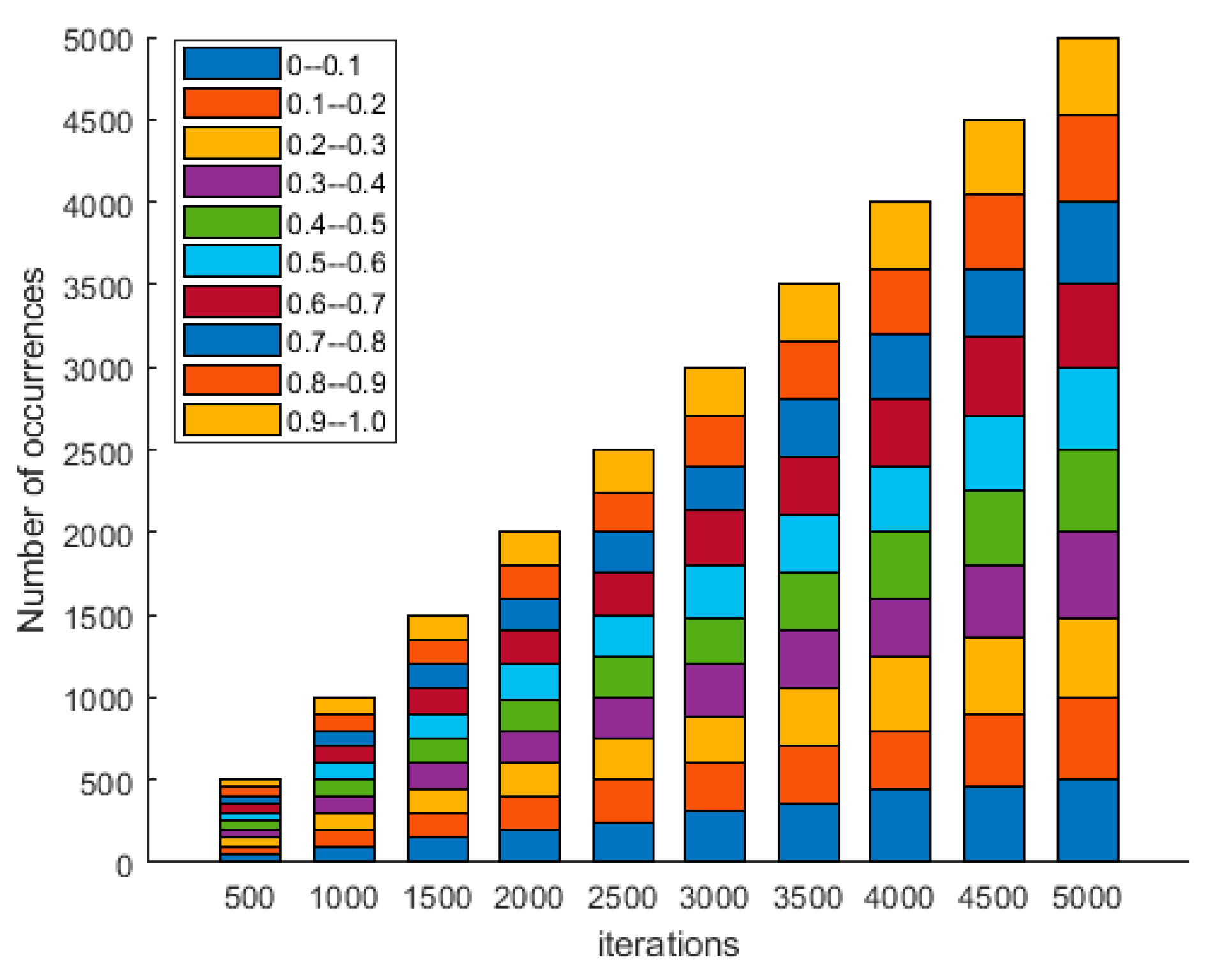
- Sequence uniformity
- Initial value sensitivity
4. S-Box Generation Method Based on Combined Chaotic System
4.1. Construction of S-Box
4.2. Scrambling of S-Box
4.3. Security Analysis of Chaotic Pseudo-Random Sequences
5. S-Box Optimization Based on Advanced Genetic Algorithm
5.1. Traditional Genetic Algorithm
5.2. The Design of S-Boxes Optimization Based on Advanced GA
5.2.1. Adaptive S-Boxes Coding
5.2.2. Advanced Fitness Function
5.2.3. Advanced Selection Operator
5.2.4. Advanced Crossover Operator
5.2.5. Advanced Mutation Operator
5.3. The Design of S-Boxes Optimization Based on Advanced GA
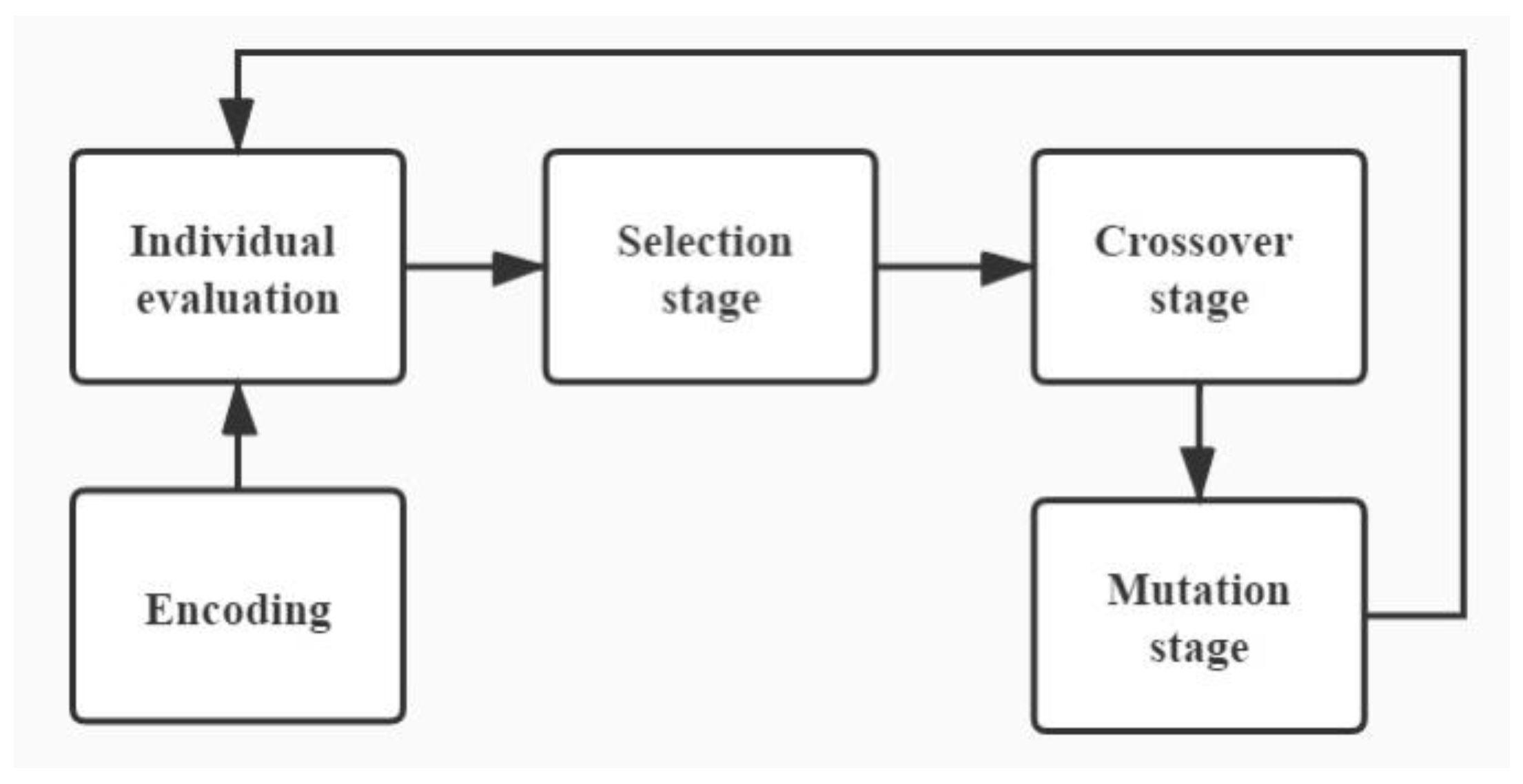
- Step 1: Initialization
- Step 2: Individual evaluation
- Step 3: Selection stage
- Step 4: Crossover stage
- Step 5: Mutation stage
- Step 6: Termination condition determination
| Algorithm 1 TThe pseudo code of chaotic s-box optimization |
| Input: The initial S-box population {S}, Q, T, , , , , , |
| Output: The optimal S-box Sp; |
| 1: read the initial S-box {S}; |
| 2: sort(F({S})); |
| 3: while(m < Q && n < T) do |
| 4: if(m/Q <= 3/5) |
| 5: pa = ; |
| 6: N1 = pa × T; |
| 7: else pa = ; |
| 8: N1 = pa × T; |
| 9: end if; |
| 10: Selection(N1); |
| 11: if() |
| 12: pb = ; |
| 13: N2 = pb × T; |
| 14: else pb = ; |
| 15: N2 = pb × T; |
| 16: end if; |
| 17: Obtain S1: F(S1) = max(F{S}); |
| 18: Obtain S2: i = Floor(T × x’); |
| 19: S’ = Crossover(S1,S2); |
| 20: add S’ to {S}; |
| 21: if(pc == ) |
| 22: N3 = pc × T |
| 23: else N3 = *T; |
| 24: end if; |
| 25: Obtain Si: i = Floor(T × x’); |
| 26: Change(X1 + i,X2 + i):X1 = Floor(N2 × x’’); X2 = Floor((N2-1) × x′); |
| 27: SEED←max(F{Si}); |
| 28: end while; |
| 29: Sp←SEED; |
| 30: return Sp; |
5.4. Proposed S-Boxes
6. Performance Analysis
6.1. Nonlinear Criterion
6.2. The Strict Avalanche Criterion (SAC)
6.3. Equiprobable Input/Output XOR Distribution
6.4. The Output Bits Independence Criterion
6.5. Linear Approximation Probability
6.6. Performance Comparation
- The average nonlinearity of the constructed S-box-based construction method in Section 3 is 107.5, and the optimized S-box based on the advanced GA in Section 4 is 110.75, which is better than all other S-box algorithms except for literature 16 and 19. Therefore, our S-box has very good nonlinear characteristics and can resist linear attacks.
- The SAC value of S-box in this paper is 0.0019 different from 0.5000, and the performance is better than that of references 17, 18, 19, 22, 23, 24. The performance of the optimized S-box is better than that of all other S-box algorithms except for reference 24.
- The value of the XOR distribution of equiprobable input/output of our constructed S-box is 0.03900 and the optimized S-box is 0.01560, which illustrates resistance to differential cryptanalysis.
- The BIC-nonlinearity of our constructed S-box is 105.75 and the BIC-SAC is 0.5005. The BIC-nonlinearity of optimized S-box is 110.02 and the BIC-SAC is 0.5005, which illustrates good output bits independence.
- The LP of our constructed S-box is 0.0629 and the optimized S-box is 0.0156, which illustrates resistance to liner cryptanalysis.
- In conclusion, both the constructed S-box and optimized S-box have a good performance in nonlinear criterion, the strict avalanche criterion, differential uniformity, the output bits independence criterion and linear approximation probability.
7. Comprehensive Analysis of Proposed Method
- The S-box of proposed method is determined in advance, which can ensure the quality of optimization.
- The proposed optimization algorithm controls the degree of optimization through the fitness function; therefore, we can obtain the satisfactory S-box by controlling the fitness function.
8. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Adams, C.; Tavares, S. The structured design of cryptographically good S-boxes. J. Cryptol. 1990, 3, 27–41. [Google Scholar] [CrossRef]
- Abdulsalam, A.A. Keystream Generator Based On Simulated Annealing. J. Appl. Comput. Sci. Math. 2011, 5, 48–53. [Google Scholar]
- Sreelaja, N.K.; Pai, G.A.V. Stream cipher for binary image encryption using Ant Colony Optimization based key generation. Appl. Soft Comput. 2012, 12, 2879–2895. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, Z.; Zhang, L.Y.; Feng, J.; Gao, J.; Lei, P. A genetic algorithm for constructing bijective substitution boxes with high nonlinearity. Inf. Sci. 2020, 523, 152–166. [Google Scholar] [CrossRef]
- Pathak, V.K.; Singh, A.K.; Singh, R.; Chaudhary, H. A modified algorithm of Particle Swarm Optimization for form error evaluation. Tm-Tech. Mess. 2017, 84, 272–292. [Google Scholar] [CrossRef]
- Tian, Y.; Lu, Z. Chaotic S-box: Intertwining Logistic Map and Bacterial Foraging Optimization. Math. Probems Eng. 2017. [Google Scholar] [CrossRef]
- Khan, M.F.; Ahmed, A.; Saleem, K. A Novel Cryptographic Substitution Box Design Using Gaussian Distribution. IEEE Access 2019, 7, 15999–16007. [Google Scholar] [CrossRef]
- Khan, M.A.; Ali, A.; Jeoti, V.; Manzoor, S. A Chaos-Based Substitution Box (S-Box) Design with Improved Differential Approximation Probability (DP). Iran. J. Sci. Technol. Trans. Electr. Eng. 2018, 42, 219–238. [Google Scholar] [CrossRef]
- Isa, H.; Jamil, N.; Zaba, M.R. Construction of Cryptographically Strong S-Boxes Inspired by Bee Waggle Dance. New Gener. Comput. 2016, 34, 221–238. [Google Scholar] [CrossRef]
- Rafiq, A.; Khan, M. Construction of new S-boxes based on triangle groups and its applications in copyright protection. Multimed. Tools Appl. 2019, 78, 15527–15544. [Google Scholar] [CrossRef]
- Ahmad, M.; Doja, M.N.; Sufyan Beg, M.M. ABC Optimization Based Construction of Strong Substitution-Boxes. Wirel. Pers. Commun. 2018, 101, 1715–1729. [Google Scholar] [CrossRef]
- Zahid, A.H.; Arshad, M.J. An Innovative Design of Substitution-Boxes Using Cubic Polynomial Mapping. Symmetry 2019, 11, 437. [Google Scholar] [CrossRef] [Green Version]
- Shahzad, I.; Mushtaq, Q.; Razaq, A. Construction of New S-Box Using Action of Quotient of the Modular Group for Multimedia Security. Secur. Commun. Netw. 2019, 2019, 2847801. [Google Scholar] [CrossRef] [Green Version]
- Belazi, A.; El-Latif, A.A.A. A simple yet efficient s-box method based on chaotic sine map. Optik 2017, 130, 1438–1444. [Google Scholar] [CrossRef]
- Çavuşoğlu, Ü.; Zengin, A.; Pehlivan, I.; Kaçar, S. A novel approach for strong s-box generation algorithm design based on chaotic scaled zhongtang system. Nonlinear Dyn. 2017, 87, 1081–1094. [Google Scholar] [CrossRef]
- Guesmi, R.; Farah, M.A.; Kachouri, A.; Samet, M. A novel design of Chaos based S-Boxes using genetic algorithm techniques. In Proceedings of the 2014 IEEE/ACS 11th International Conference on Computer Systems and Applications (AICCSA), Doha, Qatar, 10–13 November 2014; pp. 678–684. [Google Scholar]
- Ilvanov, G.; Nikolov, N.; Nikova, S. Reversed genetic algorithms for generation of bijectives-boxes with good cryptographic properties. Cryptogr. Commun. 2016, 8, 247–276. [Google Scholar]
- Wang, Y.; Wong, K.W.; Li, C.; Li, Y. A novel method to design S-box based on chaotic map and genetic algorithm. Phys. Lett. A 2012, 376, 827–833. [Google Scholar] [CrossRef]
- Cui, L.; Cao, Y. A new S-box structure named affine power-affine. Int. J. Innov. Comput. Inf. Control 2007, 3, 751–759. [Google Scholar]
- Wang, Y.; Lei, P.; Wong, K.-W. A method for constructing bijective S-box with high nonlinearity based on chaos and optimization. Int. J. Bifurc. Chaos 2015, 25, 1550127. [Google Scholar] [CrossRef]
- Belazi, A.; Abd El-Latif, A.A.; Diaconu, A.V.; Rhouma, R.; Belghith, S. Chaos-based partial image encryption scheme based on linear fractional and lifting wavelet transforms. Opt. Lasers Eng. 2017, 88, 37–50. [Google Scholar] [CrossRef]
- Lambic, D. A new discrete-space chaotic map based on the multiplication of integer numbers and its application in S-box design. Nonlinear Dyn. 2020, 1–13. [Google Scholar] [CrossRef]
- Wang, X.; Çavuşoğlu, Ü.; Kacar, S.; Akgul, A.; Pham, V.T.; Jafari, S.; Alsaadi, F.E.; Nguyen, X.Q. S-box based image encryption application using a chaotic system without equilibrium. Appl. Sci. 2019, 9, 781. [Google Scholar] [CrossRef] [Green Version]
- Ozkaynak, F. Construction of robust substitution boxes based on chaotic systems. Neural Comput. Appl. 2019, 31, 3317–3326. [Google Scholar] [CrossRef]
- Ullah, A.; Jamal, S.S.; Shah, T. A novel scheme for image encryption using substitution box and chaotic system. Nonlinear Dyn. 2018, 91, 359–370. [Google Scholar] [CrossRef]
- Daemen, J.; Rijmen, V. Design of Rijndael: AES—Advanced Encryption Standard; Springer Science and Business Media: Berlin, Germany, 2002. [Google Scholar]




| Test Suite | Pass Rate | p-Value | Result |
|---|---|---|---|
| Frequency | 0.97 | 0.5748 | SUCCESS |
| Block Frequency | 1.00 | 0.6253 | SUCCESS |
| Cumulative | 0.98 | 0.8712 | SUCCESS |
| Runs | 0.99 | 0.1623 | SUCCESS |
| Lonest Run | 1.00 | 0.3458 | SUCCESS |
| Rank | 0.99 | 0.5182 | SUCCESS |
| FFT | 0.97 | 0.7923 | SUCCESS |
| Non-Overlapping Template | 1.00 | 0.8322 | SUCCESS |
| Overlapping Template | 1.00 | 0.6573 | SUCCESS |
| Universal | 1.00 | 0.8812 | SUCCESS |
| Approximate Entropy | 0.99 | 0.1678 | SUCCESS |
| Random Excursion | 0.97 | 0.5893 | SUCCESS |
| Random Excursions Variant | 1.00 | 0.7694 | SUCCESS |
| Serial | 1.00 | 0.6199 | SUCCESS |
| Serial | 0.99 | 0.0765 | SUCCESS |
| Linear Complexity | 1.00 | 0.8192 | SUCCESS |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 244 | 83 | 117 | 150 | 190 | 111 | 102 | 17 | 128 | 200 | 92 | 223 | 247 | 174 | 198 | 147 |
| 1 | 241 | 47 | 95 | 71 | 184 | 242 | 113 | 48 | 30 | 135 | 50 | 10 | 202 | 110 | 22 | 203 |
| 2 | 101 | 44 | 53 | 13 | 140 | 28 | 58 | 168 | 196 | 132 | 199 | 70 | 11 | 206 | 252 | 177 |
| 3 | 98 | 90 | 89 | 109 | 66 | 61 | 169 | 170 | 214 | 20 | 136 | 2 | 232 | 130 | 154 | 126 |
| 4 | 246 | 158 | 67 | 39 | 51 | 76 | 87 | 1 | 139 | 37 | 121 | 176 | 24 | 185 | 178 | 157 |
| 5 | 175 | 14 | 212 | 225 | 46 | 12 | 219 | 142 | 29 | 226 | 0 | 81 | 179 | 243 | 127 | 153 |
| 6 | 165 | 205 | 119 | 180 | 217 | 97 | 118 | 112 | 64 | 159 | 94 | 255 | 77 | 249 | 134 | 171 |
| 7 | 211 | 65 | 181 | 43 | 161 | 57 | 99 | 201 | 108 | 115 | 155 | 187 | 123 | 208 | 173 | 124 |
| 8 | 238 | 222 | 248 | 216 | 182 | 237 | 152 | 25 | 250 | 143 | 146 | 172 | 18 | 194 | 5 | 207 |
| 9 | 192 | 239 | 8 | 254 | 221 | 80 | 35 | 75 | 195 | 21 | 229 | 213 | 62 | 224 | 42 | 82 |
| A | 149 | 68 | 114 | 86 | 15 | 27 | 245 | 144 | 227 | 88 | 105 | 141 | 72 | 38 | 210 | 162 |
| B | 122 | 56 | 73 | 236 | 19 | 103 | 7 | 129 | 233 | 209 | 52 | 54 | 133 | 163 | 93 | 34 |
| C | 36 | 107 | 186 | 55 | 125 | 191 | 106 | 45 | 69 | 60 | 85 | 91 | 116 | 240 | 218 | 131 |
| D | 220 | 74 | 145 | 49 | 151 | 164 | 230 | 26 | 31 | 79 | 197 | 84 | 253 | 23 | 6 | 137 |
| E | 96 | 166 | 183 | 59 | 167 | 251 | 120 | 148 | 189 | 160 | 231 | 215 | 235 | 33 | 228 | 234 |
| F | 9 | 193 | 3 | 188 | 204 | 104 | 32 | 4 | 40 | 156 | 78 | 63 | 16 | 41 | 138 | 100 |
| - | 110 | 109 | 107 | 108 | 112 | 108 | 109 |
|---|---|---|---|---|---|---|---|
| 113 | - | 108 | 110 | 108 | 109 | 112 | 106 |
| 109 | 105 | - | 116 | 108 | 110 | 109 | 114 |
| 114 | 107 | 109 | - | 106 | 117 | 109 | 109 |
| 112 | 109 | 108 | 107 | - | 110 | 109 | 110 |
| 108 | 112 | 107 | 106 | 112 | - | 114 | 110 |
| 114 | 109 | 112 | 110 | 109 | 109 | - | 112 |
| 117 | 111 | 109 | 110 | 109 | 113 | 112 | - |
| - | 0.503887 | 0.498913 | 0.506238 | 0.502119 | 0.493289 | 0.494276 | 0.500157 |
|---|---|---|---|---|---|---|---|
| 0.507813 | - | 0.496994 | 0.506836 | 0.507813 | 0.492811 | 0.506602 | 0.495117 |
| 0.480469 | 0.503672 | - | 0.496094 | 0.500376 | 0.499871 | 0.501728 | 0.499572 |
| 0.500497 | 0.502930 | - | 0.500198 | 0.500492 | 0.498081 | 0.498814 | |
| 0.499882 | 0.499871 | 0.500836 | 0.507831 | - | 0.501001 | 0.500321 | 0.500427 |
| 0.501813 | 0.500501 | 0.501121 | 0.500192 | 0.501036 | - | 0.500492 | 0.500513 |
| 0.500499 | 0.500507 | 0.500177 | 0.499213 | 0.499172 | 0.499925 | - | 0.498210 |
| 0.500130 | 0.500498 | 0.499918 | 0.500116 | 0.500091 | 0.500492 | 0.499981 | - |
| S-Boxes | Average Nonlinearity | SAC | DP | BIC- Nonlinearity | BIC- SAC | LP |
|---|---|---|---|---|---|---|
| Constructed S-box | 107.25 | 0.5019 | 0.03900 | 105.75 | 0.5005 | 0.0629 |
| Optimized S-box | 110.75 | 0.5005 | 0.01560 | 110.02 | 0.5005 | 0.0156 |
| Cui [19] | 112.00 | 0.5007 | 0.01560 | 112 | 0.4997 | 0.0156 |
| Çavusoglu [17] | 106.25 | 0.5039 | 0.03910 | 103.35 | 0.5059 | 0.0791 |
| Wang [20] | 110.50 | 0.4937 | 0.03910 | 103.85 | 0.5033 | 0.0625 |
| Belazi [21] | 112.00 | 0.5115 | 0.03130 | 103.78 | 0.4982 | 0.0479 |
| Lambic [22] | 106.75 | 0.5010 | 0.03910 | 104.07 | 0.5005 | 0.0706 |
| X. Wang [23] | 106.75 | 0.4998 | 0.03910 | 104.14 | 0.4998 | 0.0706 |
| Ozkaynak [24] | 106.75 | 0.4971 | 0.03910 | 102.92 | 0.5008 | 0.0791 |
| Ullah [25] | 106.00 | 0.5034 | 0.04690 | 105.28 | 0.4980 | 0.0627 |
| AES [26] | 107.25 | 0.5049 | 0.01560 | 112 | 0.5046 | 0.0706 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, D.; Tong, X.; Zhang, M.; Wang, Z. A New S-Box Generation Method and Advanced Design Based on Combined Chaotic System. Symmetry 2020, 12, 2087. https://doi.org/10.3390/sym12122087
Zhu D, Tong X, Zhang M, Wang Z. A New S-Box Generation Method and Advanced Design Based on Combined Chaotic System. Symmetry. 2020; 12(12):2087. https://doi.org/10.3390/sym12122087
Chicago/Turabian StyleZhu, Ding, Xiaojun Tong, Miao Zhang, and Zhu Wang. 2020. "A New S-Box Generation Method and Advanced Design Based on Combined Chaotic System" Symmetry 12, no. 12: 2087. https://doi.org/10.3390/sym12122087
APA StyleZhu, D., Tong, X., Zhang, M., & Wang, Z. (2020). A New S-Box Generation Method and Advanced Design Based on Combined Chaotic System. Symmetry, 12(12), 2087. https://doi.org/10.3390/sym12122087





