Design of Fuzzy TS-PDC Controller for Electrical Power System via Rules Reduction Approach
Abstract
:1. Introduction
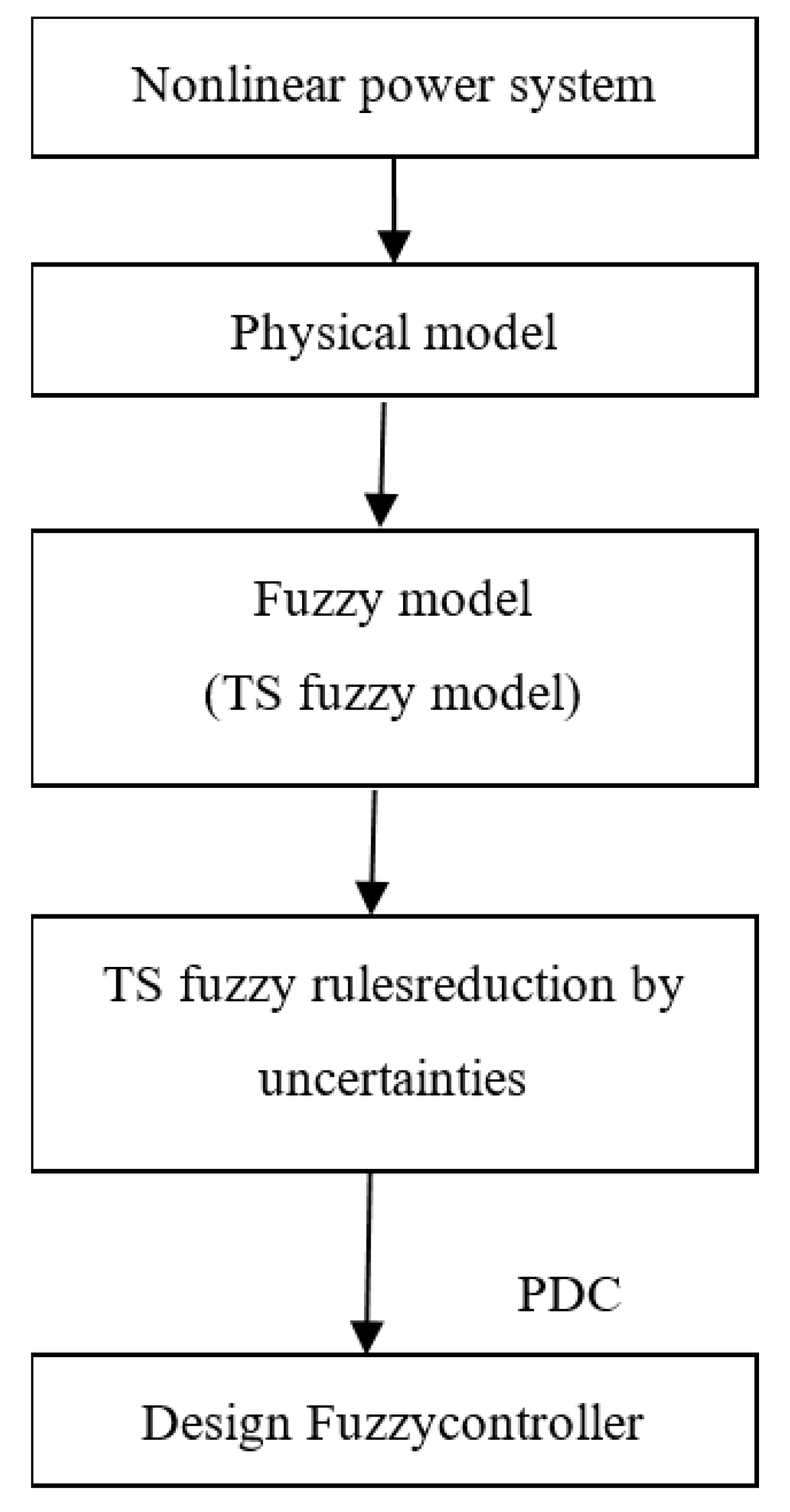
2. Materials and Methods
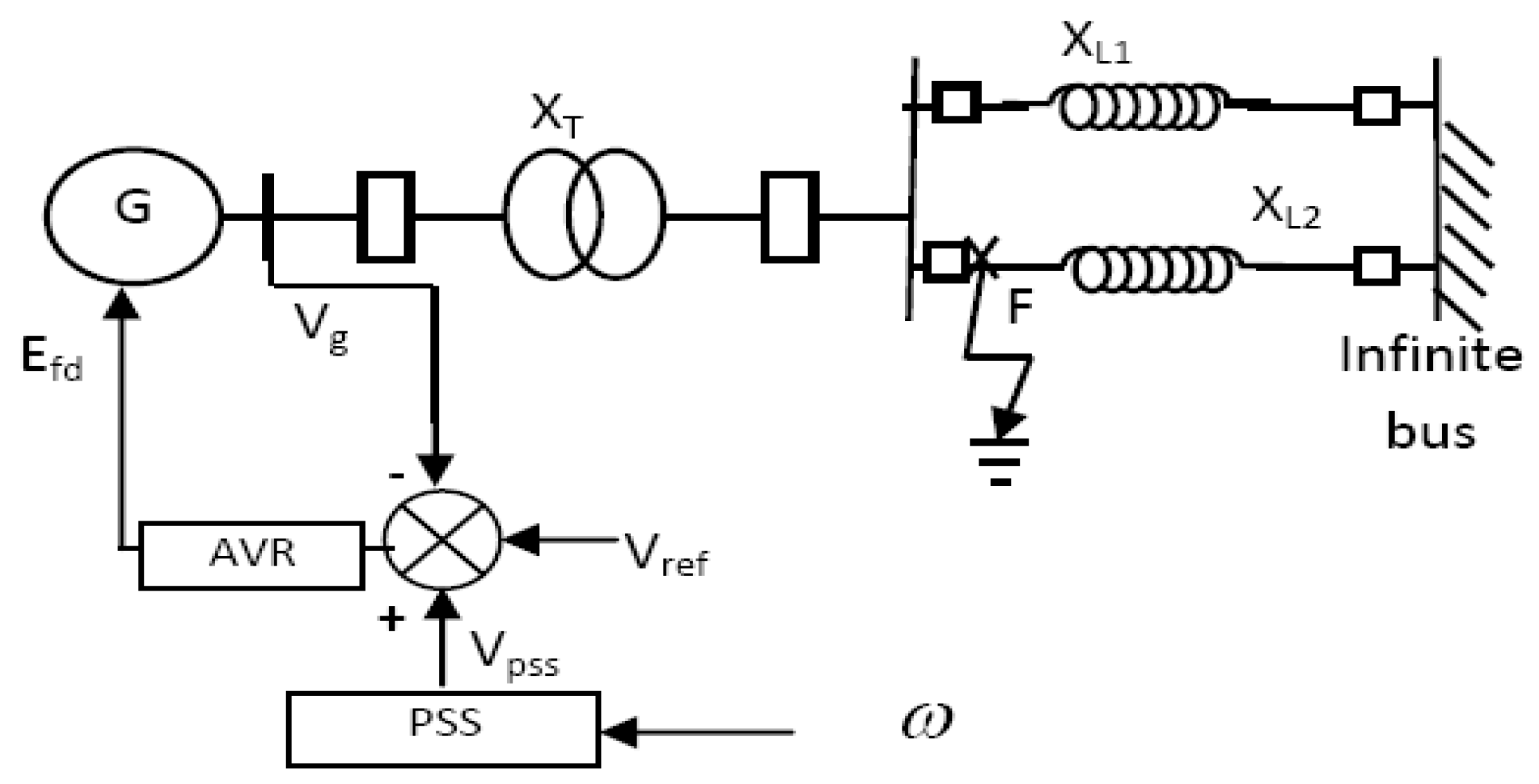
2.1. Power Network Modeling
2.2. Fuzzy Model Stabilization
2.2.1. T-S Fuzzy Model
2.2.2. PDC Fuzzy Controller Design
2.3. TS Fuzzy Rules Reduction by Uncertainties
2.3.1. Uncertain TS Fuzzy Model
2.3.2. System Stability and Robustness with Uncertainties
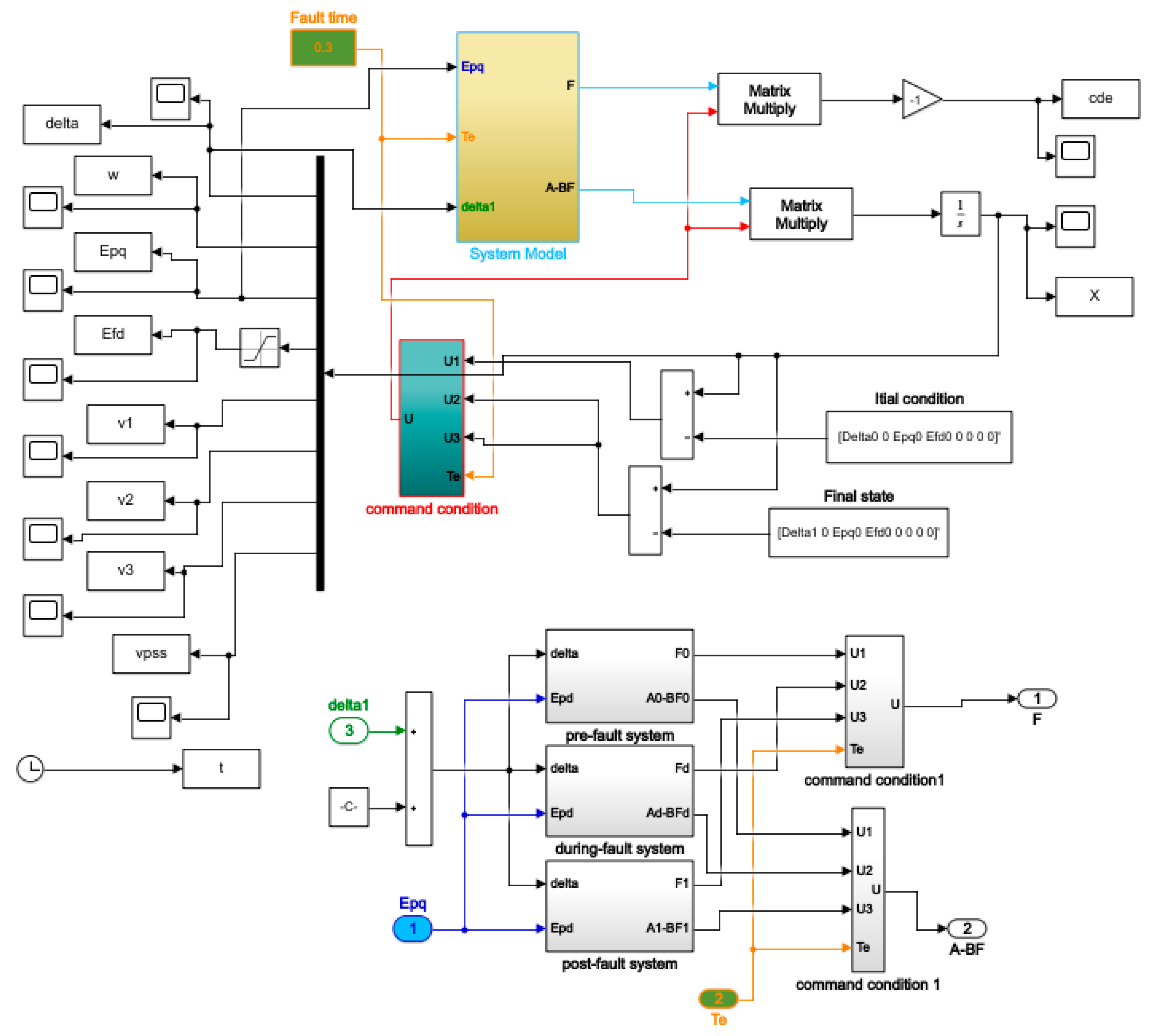
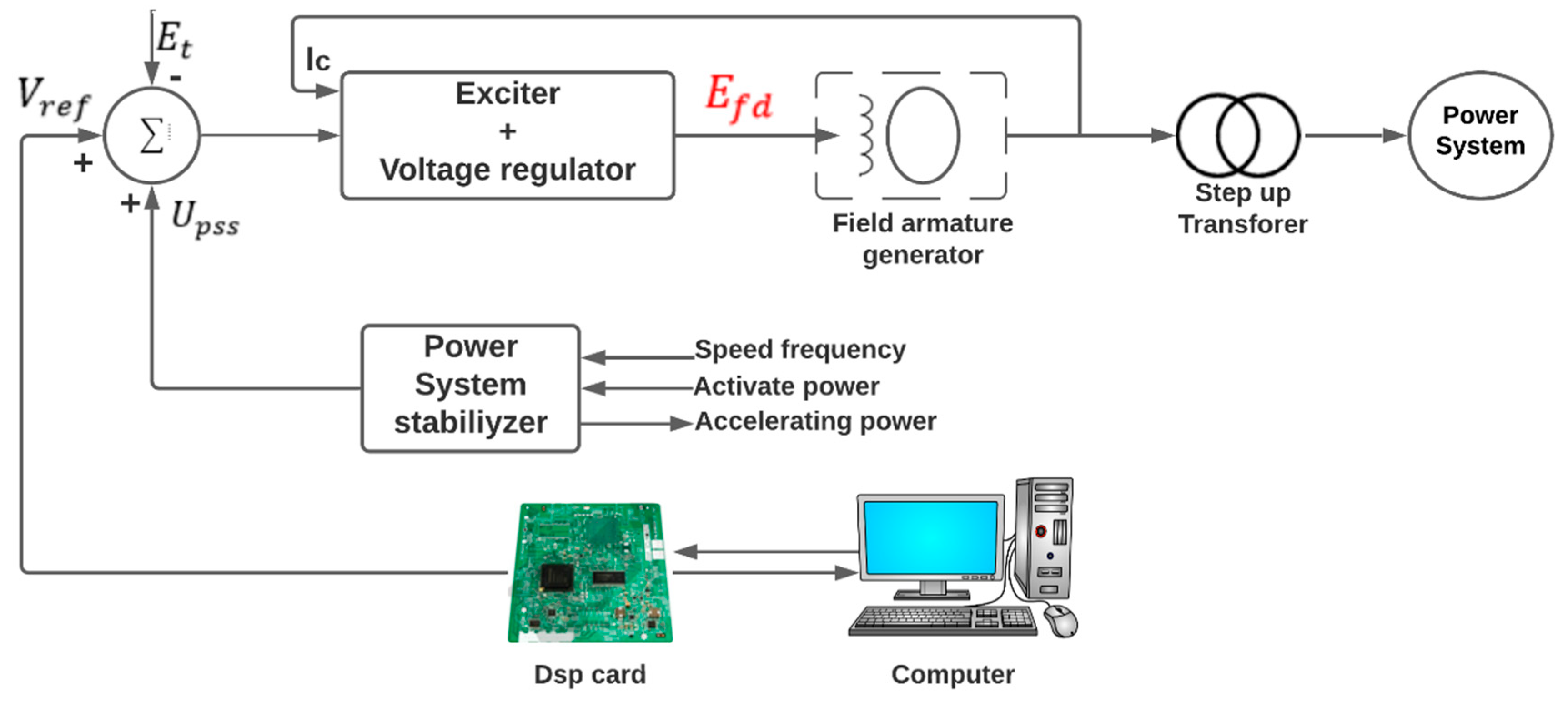
2.4. Application: Stabilization of SMIB Power System by T-S Fuzzy PDC Controller
2.4.1. System Test
2.4.2. Construction of T-S Fuzzy Model for SMIB Power System
2.4.3. Nonlinearities Reduction by Uncertainties
- ▪
- For the firstnonlinearities we can write with : , where:
- ▪
- For the second nonlinearities we can write with : , where:
- ▪
- For the third nonlinearities we can write with : , where:Using a single nonlinearity, two rules were obtained, the model is:
- Rule 1.ifis. Then.
- Rule 2.ifis. Then, where:
2.4.4. Taylor Linearization
- Pre-fault state:with
- During fault state:The equilibrium point during the fault is the same after the fault elimination. Then,with
- Post-fault state:with
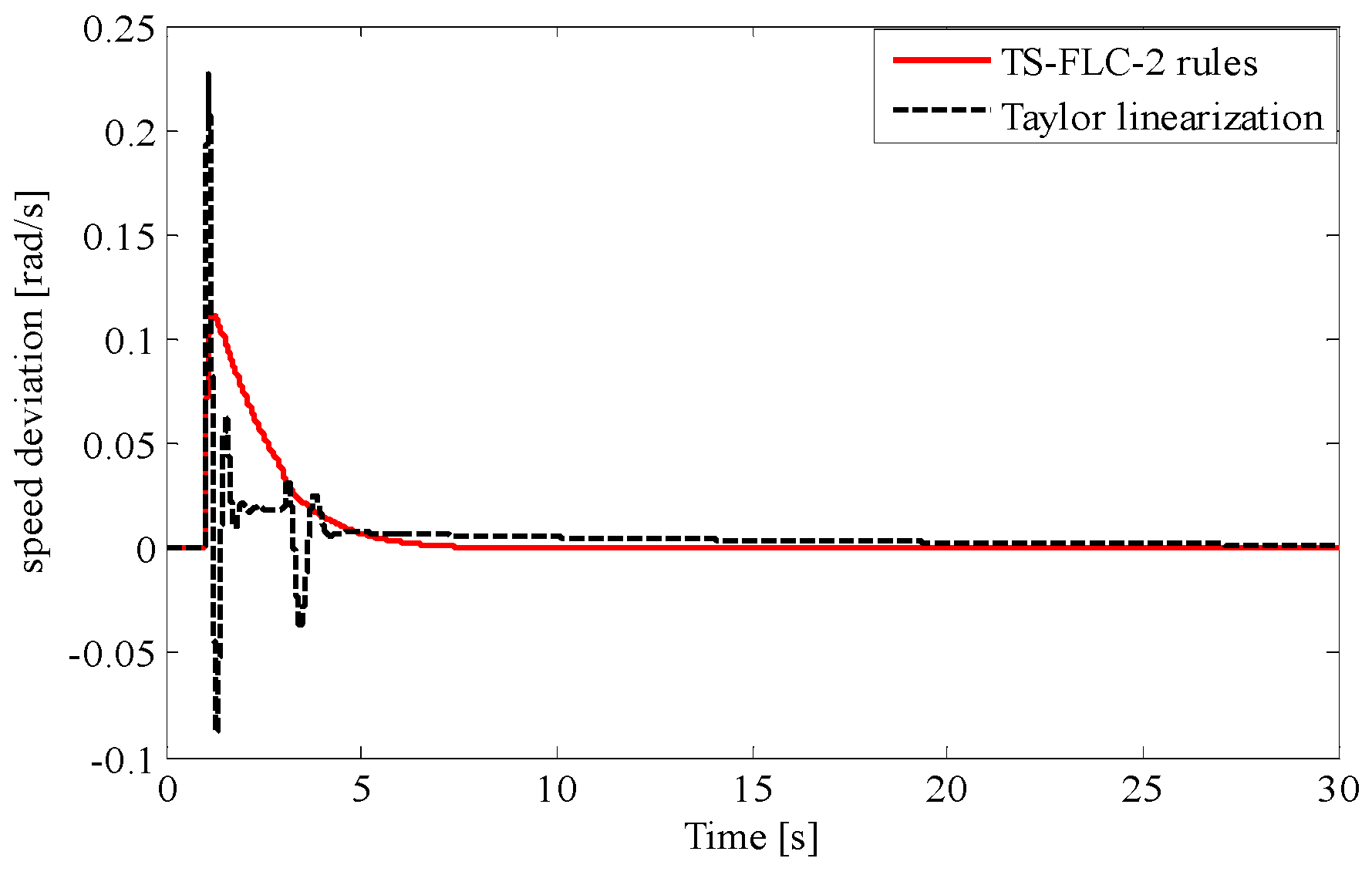
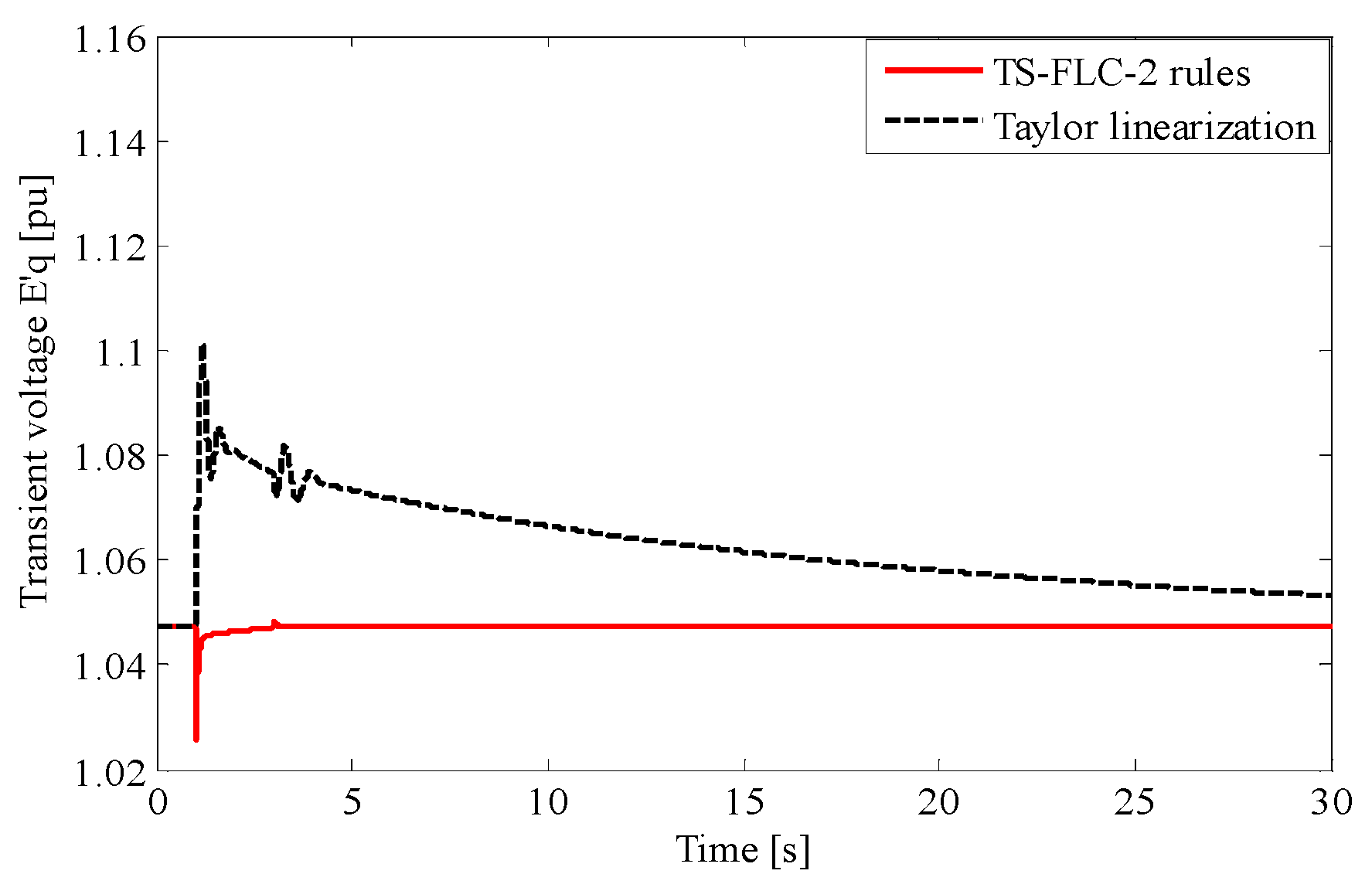
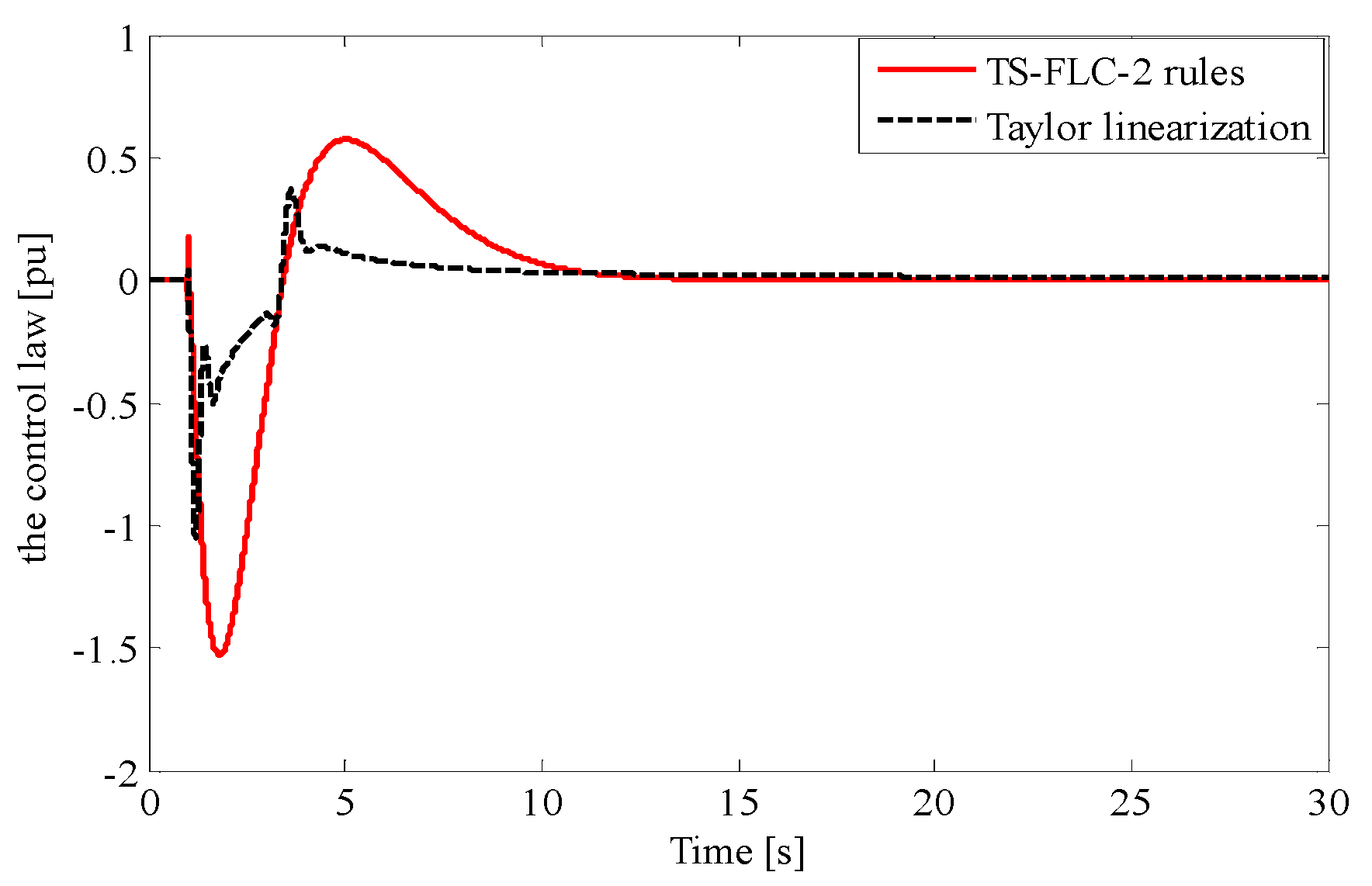
3. Results
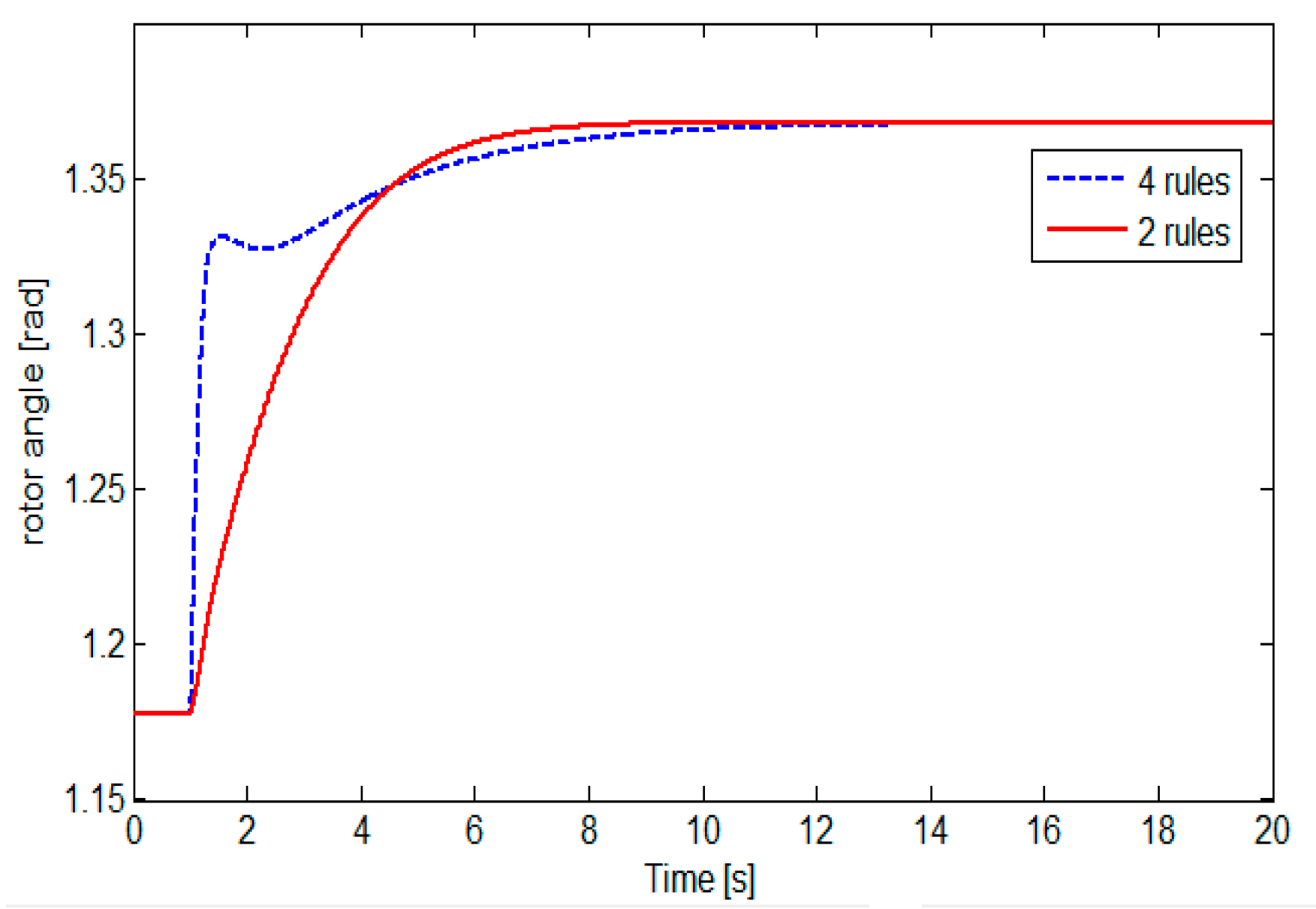
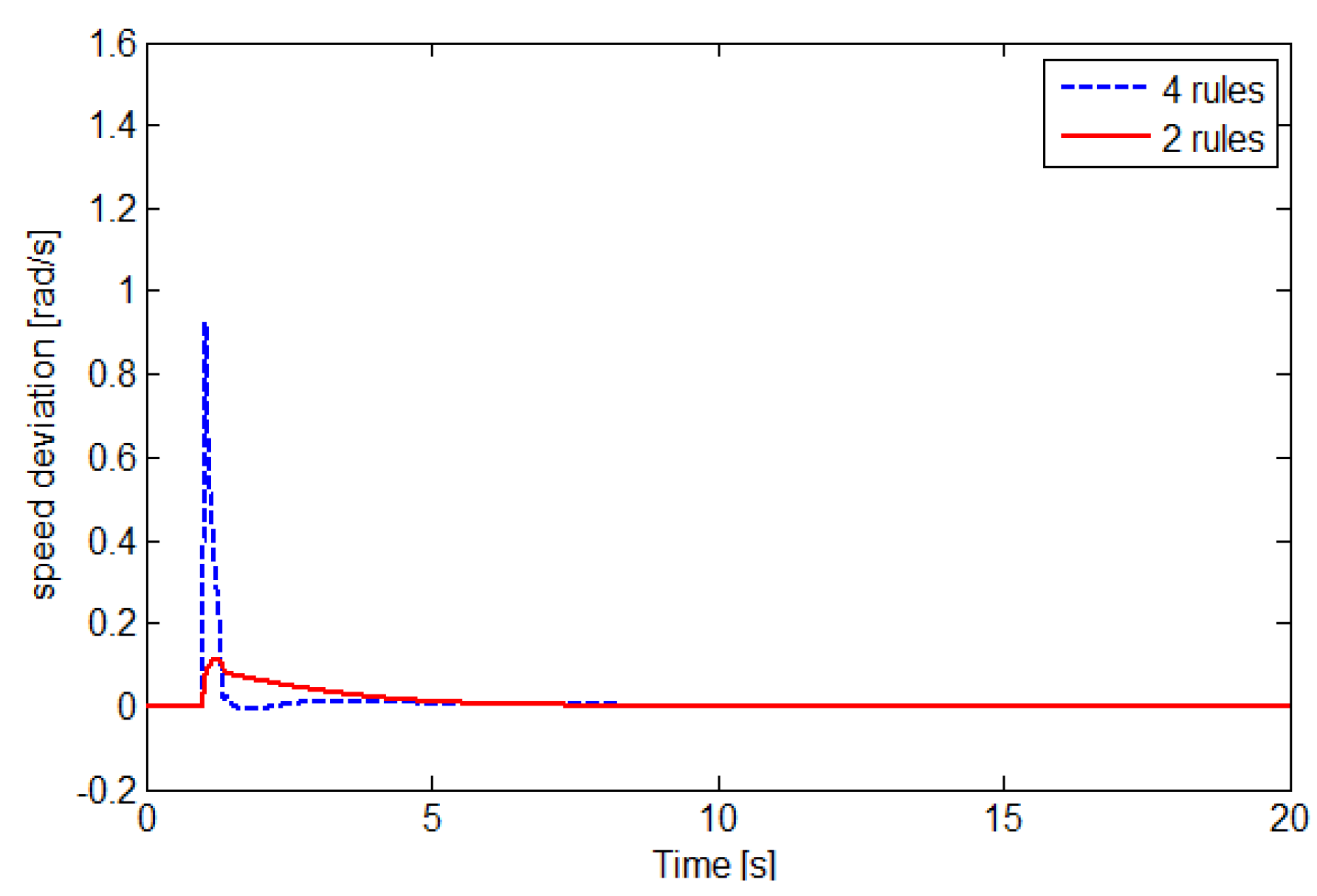
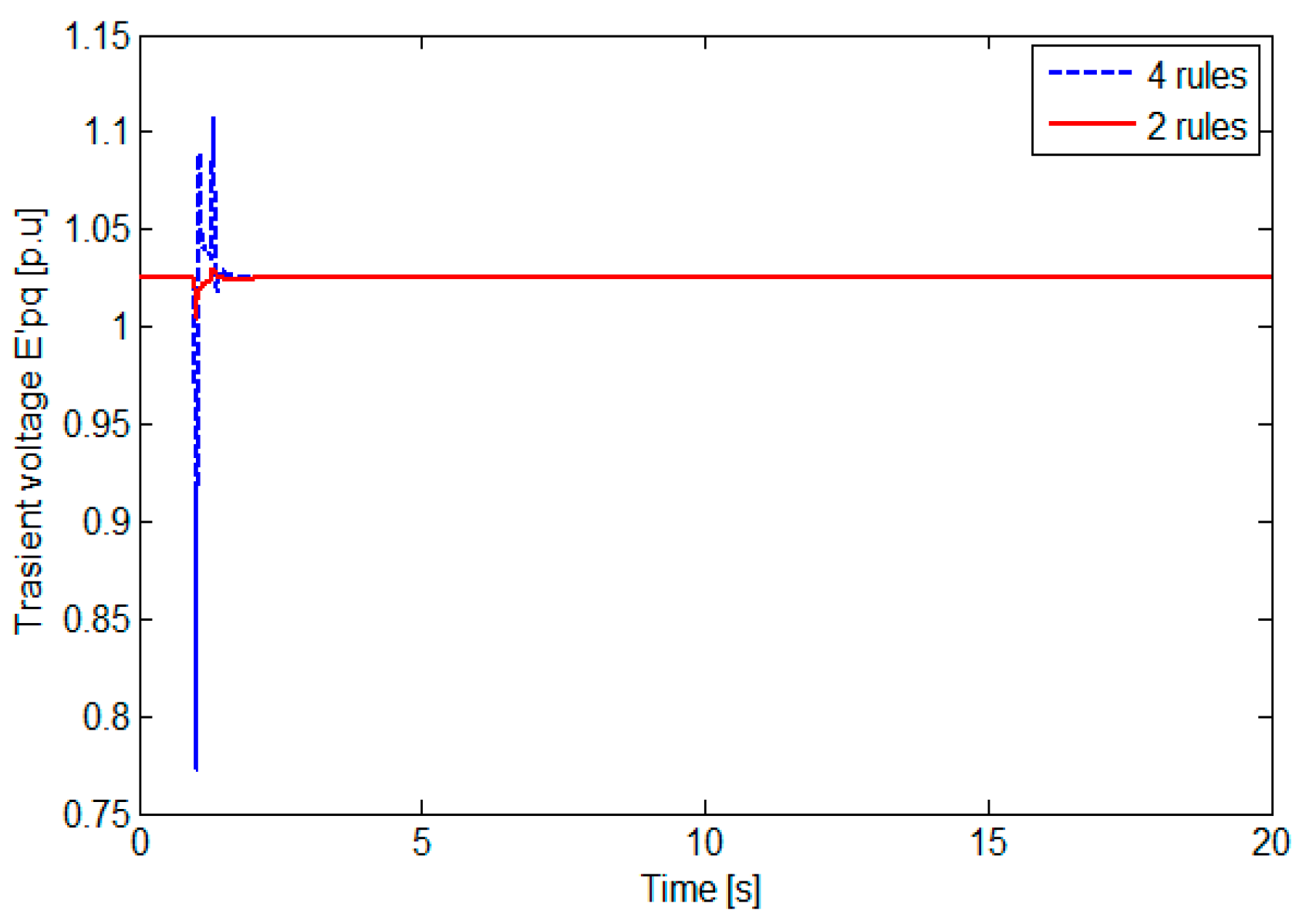
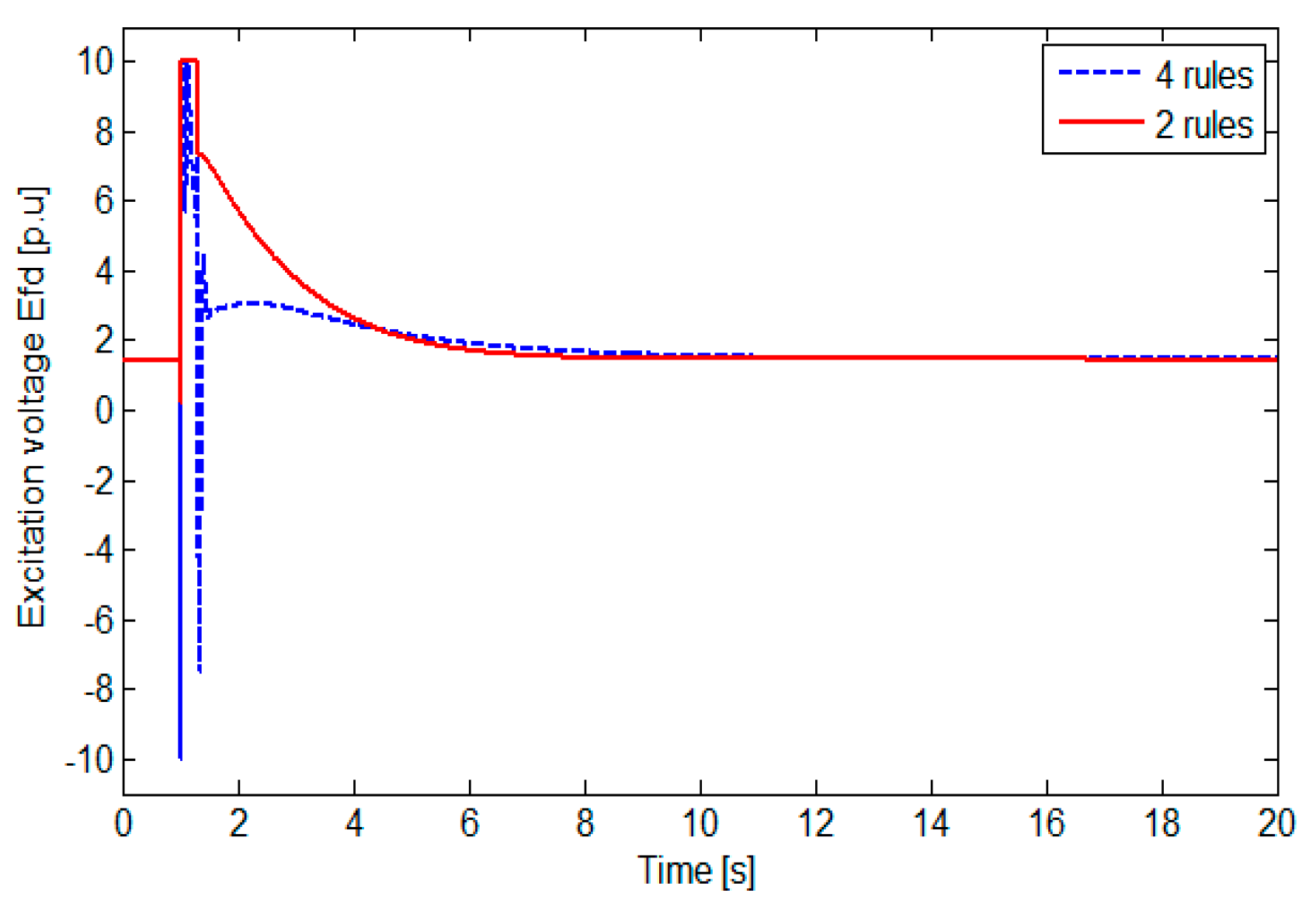
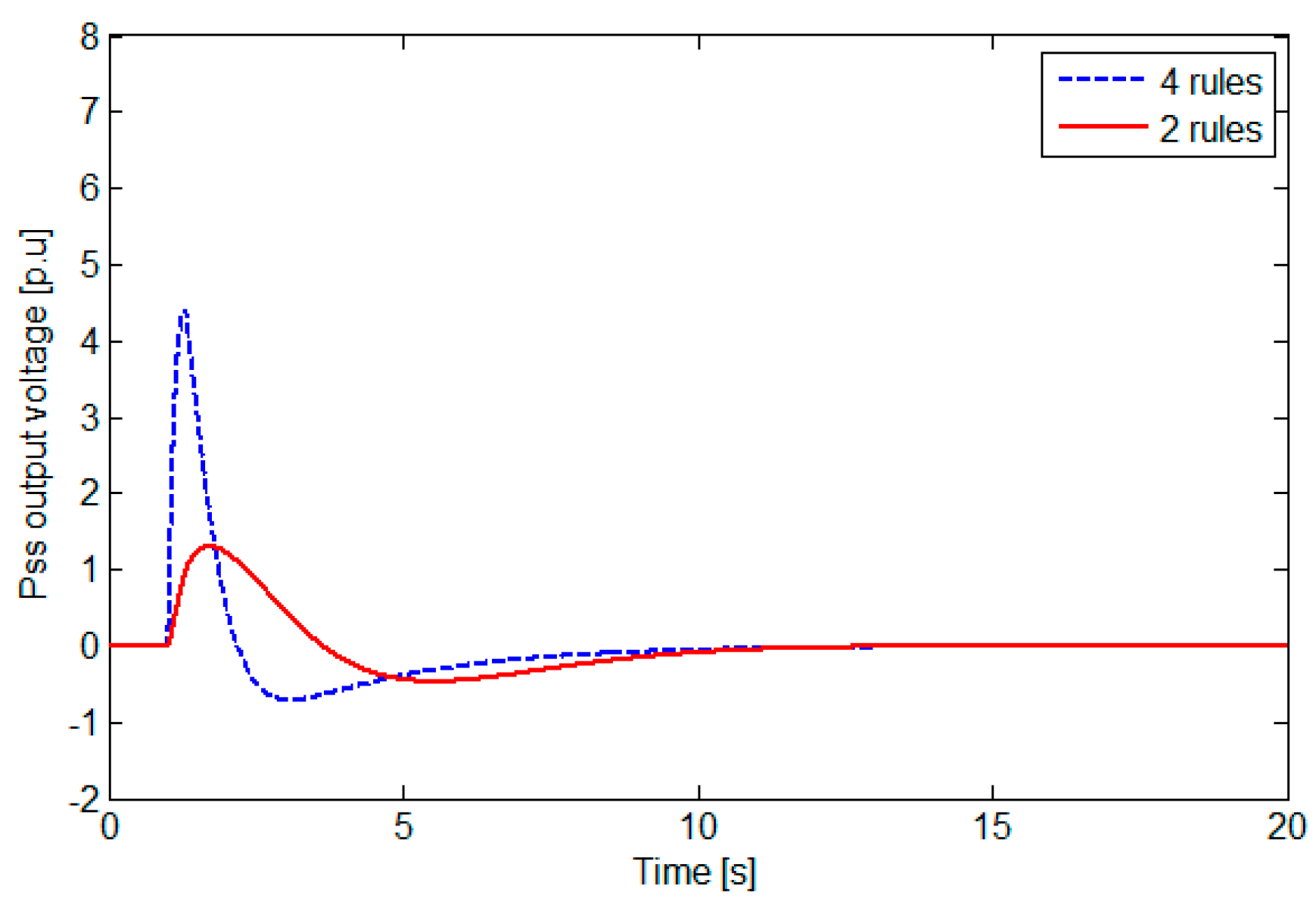
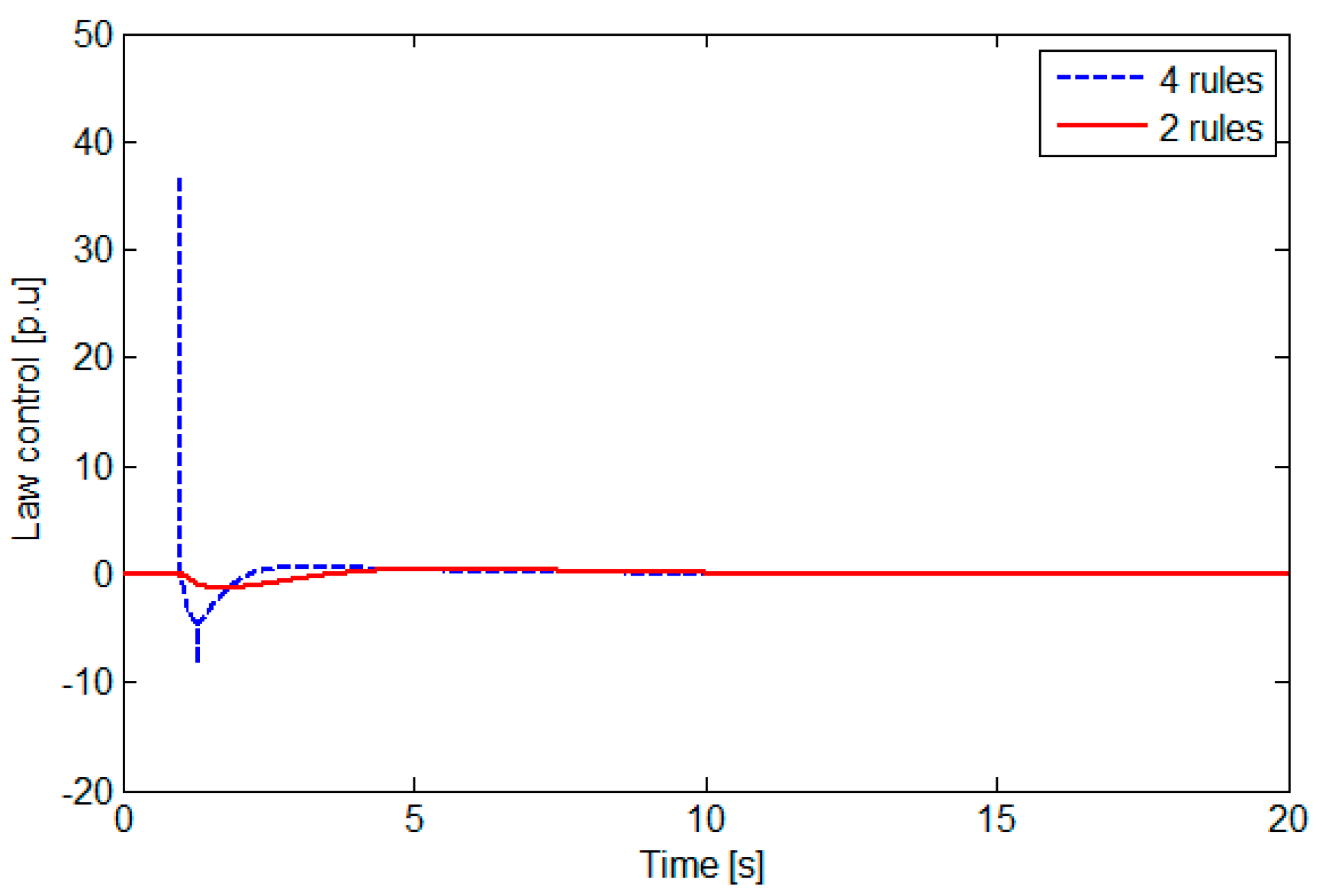
3.1. Comparison: One Nonlinearity (Two-Rule Model) and Two Nonlinearities (Four-Rule Model)
3.2. TS Fuzzy PDC Controller Law
- For the Pre-fault state the control law is:
- During fault state the control law is:
- For the Post-fault state the control law is:
- Pre-fault state:
- During fault state:
- Post-fault state:
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| δ | Power angle of the generator, radian |
| ω | Rotor speed of the generator, radian/s |
| Pm | Mechanical power, p.u |
| KD | Damping constant, p.u |
| H | Inertia constant, p.u |
| Td0′ | Direct axis transient short circuit time constant, s |
| Pe | Active electrical power produced by the generator, p.u |
| Eq′ | Transient EMF in the quadratic axis of the generator, p.u |
| Efd | Equivalent EMF in the excitation system, p.u |
| Vt | Generator terminal voltage, p.u |
| VB | Infinite bus voltage, p.u |
| XT | Reactance of the transformer, p.u |
| XL | Reactance of the transmission line, p.u |
| Xd | Direct axis reactance of the generator, p.u |
| Xd′ | Direct axis transient reactance of the generator, p.u |
| Xq | Quadratic axis reactance of the generator, p.u |
| Vref | Voltage reference [pu] |
| Vpss | PSS output voltage [pu] |
| Ta | Time constant of the AVR, s |
| Ka | Gain of the AVR, p.u. |
| Tω | Time constant of the PSS, s |
| Kω | Gain of the PSS, p.u. |
| T1, T2 | Lead-block time constant of PSS, s |
| T3, T4 | Lag-block time constant of PSS, s |
| V1, V2 and V3 | Intermediate variables of the PSS model |
References
- Eremia, M.; Shahidehpour, M. Handbook of Electrical Power System Dynamics: Modeling, Stability, and Control; Wiley-IEEE Press: Hoboken, NJ, USA, 2013. [Google Scholar]
- Kahouli, O.; Jebali, M.; Alshammari, B.; Abdallah, H.H. PSS design for damping low-frequency oscillations in a multi-machine power system with penetration of renewable power generations. IET Renew. Power Gener. 2019, 13, 116–127. [Google Scholar] [CrossRef]
- Gordon, M.; Hill, D.J. Global transient stability and voltage regulation for power systems. In Power and Energy Society General Meeting-Conversion and Delivery of Electrical Energy in the 21st Century; IEEE: Pittsburgh, PA, USA, 2008. [Google Scholar]
- Abbadi, A.; Hamidia, F.; Morsli, A.; Tlemcani, A. Optimal voltage controller using t-s fuzzy model for multimachine power systems. Nonlinear Dyn. Syst. Theory 2019, 19, 217–226. [Google Scholar]
- Roy, T.K.; Mahmud, M.A.; Shen, W.X. Robust nonlinear adaptive backstepping excitation controller design for rejecting external disturbances in multimachine power systems. Int. J. Electr. Power Energy Syst. 2017, 84, 76–86. [Google Scholar] [CrossRef]
- Amoozegar, D. DSTATCOM modelling for voltage stability with fuzzy logic PI current controller. Int. J. Electr. Power Energy Syst. 2016, 76, 129–135. [Google Scholar] [CrossRef]
- Yousefian, R.; Kamalasadan, S. A Lyapunov function based optimal hybrid power system controller for improved transient stability. Electr. Power Syst. Res. 2016, 137, 6–15. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Zhao, J.; Dimirovski, G.M.; Dimirovski, G.M. Robust adaptive control for a single-machine infinite-bus power system with an SVC. Control Eng. Pract. 2014, 30, 132–139. [Google Scholar] [CrossRef]
- Fan, B.; Yang, Q.; Wang, K. Adaptive excitation control of power systems with time-varying constraints. In Proceedings of the 12th World Congress on Intelligent Control and Automation, Guilin, China, 12–15 June 2016. [Google Scholar] [CrossRef]
- Kundur, P. Power System Stability and Control; McGraw-Hill: New York, NY, USA, 1994. [Google Scholar]
- Salah, R.B.; Djebali, M.; Kahouli, O.; Bouchoucha, C.; Hadj Abdallah, H. Small Signal stability of the tunisian interconnected power system. In Proceedings of the 15th International Conference on Sciences and Techniques of Automatic Control & Computer Engineering, STA’2014, Sousse, Tunisia, 21–23 December 2014. [Google Scholar] [CrossRef]
- Salah, R.B.; Kahoul, O.; HadjAbdallah, H. A nonlinear Takagi-Sugeno fuzzy logic control for single machine power system. Int. J. Adv. Manuf. Technol. 2017, 90, 575–590. [Google Scholar] [CrossRef]
- Morère, Y. Mise en Œuvre de Lois de Commande Pour les Modèles Flous de Type Takagi-Sugeno. Ph.D. Thesis, Université de Valenciennes et du Hainaut-Cambrésis, Valenciennes, France, 2001. [Google Scholar]
- Benzaouia, A.; El Hajjaji, A. Advanced Takagi-Sugeno Fuzzy Systems; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Hu, G.; Liu, X.; Wang, L.; Li, H. An extended approach to controller design of continuous-time Takagi–Sugeno fuzzy model. J. Intell. Fuzzy Syst. 2018, 34, 2235–2246. [Google Scholar] [CrossRef]
- Tanaka, K.; Wang, H.O. Fuzzy Control Systems Design and Analysis; John Wiley & Sons: Hoboken, NJ, USA, 2001. [Google Scholar]
- Zheng, X.; Wang, X.; Yin, Y. Stability analysis and constrained fuzzy tracking control of positive nonlinear systems. Nonlinear Dyn. 2016, 83, 2509–2522. [Google Scholar] [CrossRef]
- Yang, F.; Zhang, H.; Wang, Y. An enhanced input-delay approach to sampled-data stabilization of T-S fuzzy systems via mixed convex combination. Nonlinear Dyn. 2014, 75, 501–512. [Google Scholar] [CrossRef]
- Chiu, C.H.; Peng, Y.F. Design of takagi-sugeno fuzzy control scheme for real world system control. Sustainability 2019, 11, 3855. [Google Scholar] [CrossRef] [Green Version]
- Chang, W.; Wang, W.J. H∞ Fuzzy control synthesis for a large-scale system with a reduced number of LMIs. IEEE Trans. Fuzzy Syst. 2015, 23, 1197–1210. [Google Scholar] [CrossRef]
- Ksantini, M.; Ellouze, A.; Delmotte, F. Control of a hydraulic system by means of a fuzzy approach. Int. J. Optim. Control Theor. Appl. 2013, 3, 121–131. [Google Scholar] [CrossRef]
- Ghalehnoie, M.; Akbarzadeh-Tootoonchi, M.R.; Pariz, N. Fuzzy control design for nonlinear impulsive switched systems using a nonlinear Takagi-Sugeno fuzzy model. Trans. Inst. Meas. Control 2020, 42, 1700–1711. [Google Scholar] [CrossRef]
- Oke, P.; Nguang, S.K. Robust H∞ Takagi–Sugeno fuzzy output-feedback control for differential speed steering vehicles. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2020, 234, 2822–2835. [Google Scholar] [CrossRef]
- Sung, H.C.; Park, J.B. Robust fuzzy control for a hybrid magnetic bearings: The relaxed stabilization condition approach. Nonlinear Dyn. 2016, 85, 2487–2496. [Google Scholar] [CrossRef]
- José, V. T–S Fuzzy bibo stabilisation of non-linear systems under persistent perturbations using fuzzy lyapunov functions and non-pdc control laws. Int. J. Appl. Math. Comput. Sci. 2020, 30, 529–550. [Google Scholar]
- Tanaka, K.; Tanaka, M.; Chen, Y.J.; Wang, H.O. A new sum- of- squares design framework for robust control of polynomial fuzzy system with uncertainties. IEEE Trans. Fuzzy Syst. 2016, 24, 94–110. [Google Scholar] [CrossRef]
- Nguyen, A.T.; Taniguchi, T.; Eciolaza, L.; Campos, V.; Palhares, R.; Sugeno, M. Fuzzy control systems: Past, present and future. IEEE Comput. Intell. Mag. 2019, 14, 56–68. [Google Scholar] [CrossRef]


| Variables | Values | Variables | Values |
|---|---|---|---|
| Pe | 0.9 | XL2 | 0.93 |
| Qe | 0.436 | XT | 0.15 |
| Vt | 1 | Ka | 250 |
| f | 50 | Ta | 0.015 |
| Xd | 1.81 | T1 | 0.9471 |
| Xq | 1.494 | T2 | 1.0175 |
| X′d | 0.3 | T3 | 0.6725 |
| X′q | 0.65 | T4 | 0.6756 |
| T′d0 | 8 | Kw | 45.8373 |
| H | 3.5 | Tw | 1.0871 |
| D | 0.01 | TE | 1 |
| XL1 | 0.5 |
| Variables | Values |
|---|---|
| 1.178 | |
| 0 | |
| 1.0474 | |
| 2.4160 | |
| 0 | |
| 1.368 | |
| 0 | |
| 1.0474 | |
| 2.4160 | |
| 0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alshammari, B.; Ben Salah, R.; Kahouli, O.; Kolsi, L. Design of Fuzzy TS-PDC Controller for Electrical Power System via Rules Reduction Approach. Symmetry 2020, 12, 2068. https://doi.org/10.3390/sym12122068
Alshammari B, Ben Salah R, Kahouli O, Kolsi L. Design of Fuzzy TS-PDC Controller for Electrical Power System via Rules Reduction Approach. Symmetry. 2020; 12(12):2068. https://doi.org/10.3390/sym12122068
Chicago/Turabian StyleAlshammari, Badr, Rim Ben Salah, Omar Kahouli, and Lioua Kolsi. 2020. "Design of Fuzzy TS-PDC Controller for Electrical Power System via Rules Reduction Approach" Symmetry 12, no. 12: 2068. https://doi.org/10.3390/sym12122068
APA StyleAlshammari, B., Ben Salah, R., Kahouli, O., & Kolsi, L. (2020). Design of Fuzzy TS-PDC Controller for Electrical Power System via Rules Reduction Approach. Symmetry, 12(12), 2068. https://doi.org/10.3390/sym12122068







