Zhang–Zhang Polynomials of Ribbons

Abstract

We report a closed-form formula for the Zhang–Zhang polynomial (also known as ZZ polynomial or Clar covering polynomial) of an important class of elementary peri-condensed benzenoids $Rb\left(n_1,n_2,m_1,m_2\right)$, usually referred to as ribbons. A straightforward derivation is based on the recently developed interface theory of benzenoids [Langner and Witek, MATCH Commun. Math. Comput. Chem. 2020, 84, 143–176]. The discovered formula provides compact expressions for various topological invariants of $Rb\left(n_1,n_2,m_1,m_2\right)$: the number of Kekulé structures, the number of Clar covers, its Clar number, and the number of Clar structures. The last two classes of elementary benzenoids, for which closed-form ZZ polynomial formulas remain to be found, are hexagonal flakes $O\left(k,m,n\right)$ and oblate rectangles $Or\left(m,n\right)$.

1. Introduction

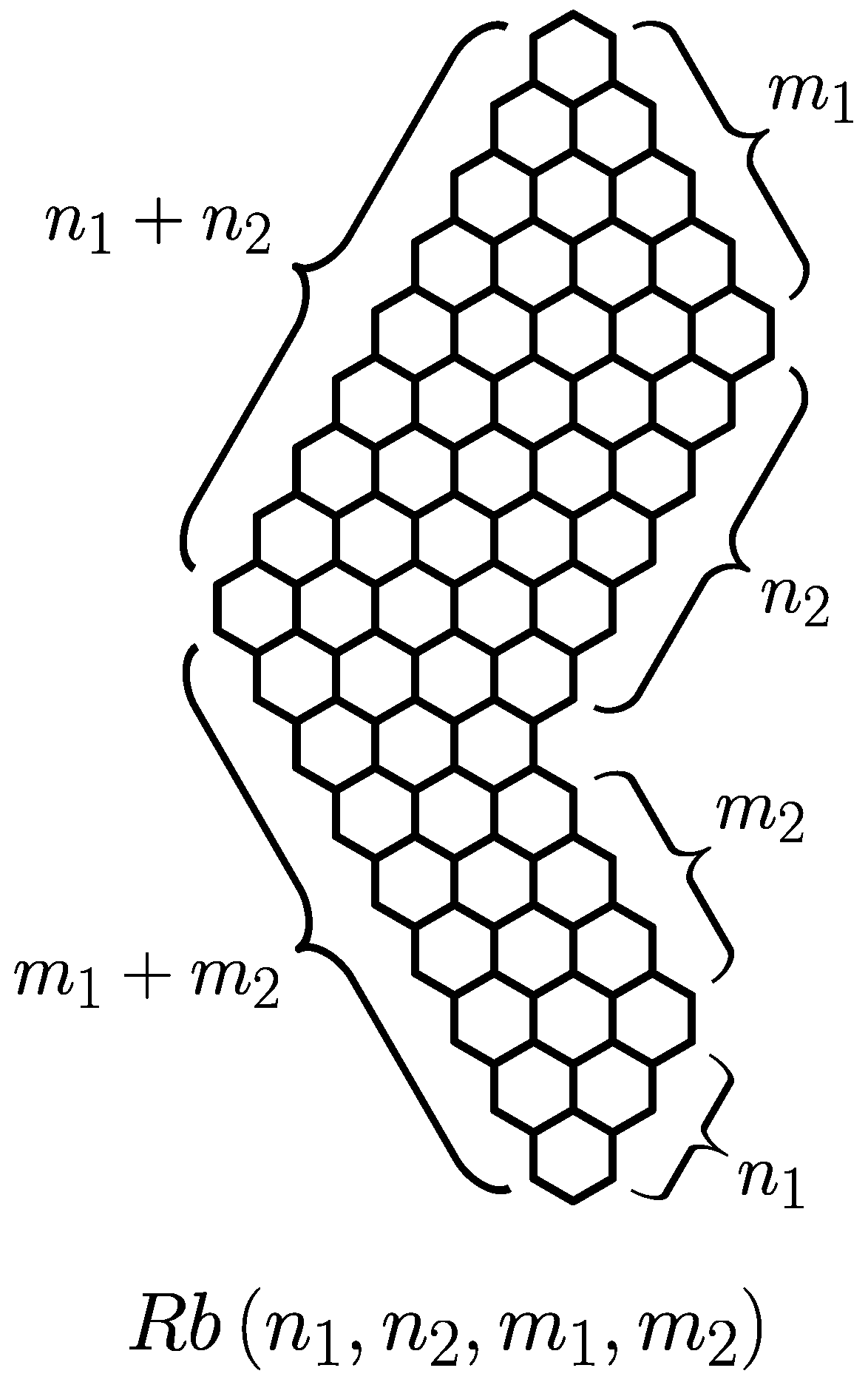
Consider a regular peri-condensed benzenoid depicted in Figure 1, which can be fully characterized by specifying four structural parameters: $n_1$, $n_2$, $m_1$, and $m_2$. Structures of this type constitute an important class of elementary peri-condensed benzenoids and occupy a pronounced position in the general theory of Clar covers among other, highly symmetric structures such as parallelograms $M\left(m,n\right)$ [1,2,3,4], parallelogram chains [5,6], hexagons $O\left(k,m,n\right)$ [1,7,8,9,10,11,12,13], oblate and prolate rectangles $Or\left(m,n\right)$ [9,10,14] and $Pr\left(m,n\right)$ [9,15,16], multiple zigzag chains $Z\left(m,n\right)$ [17], chevrons $Ch\left(k,m,n\right)$ [1,4,9,18], generalized chevrons $Ch\left(k,m,n_1,n_2\right)$ [4], and m-tier regular benzenoid strips [19,20]. In situations when $m_1=n_1$, the structure shown in Figure 1 is traditionally referred to as a ribbon or a V-shaped benzenoid, and has been symbolically denoted by $V\left(k,m,n\right)$ [18,21,22], where $k=m_1=n_1$, $m=m_1+m_2$, and $n=n_1+n_2$. Here, we consider a wider class of ribbons, allowing the parameters $m_1$ and $n_1$ to be different. We still refer to these structures as ribbons, but we represent them by a new symbol $Rb\left(n_1,n_2,m_1,m_2\right)$ capable of accommodating the extra new parameter in contrast to $V\left(k,m,n\right)$. The Clar theory of generalized ribbons $Rb\left(n_1,n_2,m_1,m_2\right)$—which we attempt to construct in the current paper—clearly encompasses the Clar theory of regular ribbons $V\left(k,m,n\right)$, similarly as before we were able to show [4] that the Clar theory of generalized chevrons $Ch\left(k,m,n_1,n_2\right)$ includes as a special case the Clar theory of regular chevrons $Ch\left(k,m,n\right)$. The questions we want to answer in the current paper are: $\left(i\right)$ How many Kekulé structures exist for $Rb\left(n_1,n_2,m_1,m_2\right)$? $\left(ii\right)$ How many Clar covers can be constructed for $Rb\left(n_1,n_2,m_1,m_2\right)$? $\left(iii\right)$ What is the Clar number of $Rb\left(n_1,n_2,m_1,m_2\right)$? $\left(iv\right)$ How many Clar structures can be constructed for $Rb\left(n_1,n_2,m_1,m_2\right)$? $\left(v\right)$ What is the ZZ polynomial of $Rb\left(n_1,n_2,m_1,m_2\right)$? Note that the solution to the last problem is sufficient for answering all the questions posed here, justifying the title and the scope of the current paper.

Stimulated by an anonymous referee’s request, we would like to discuss briefly what kinds of other topological invariants could be useful for characterizing physical and chemical properties of benzenoids. The departure point for our divagations is the structure of the valence bond wave function corresponding to the ground state of these molecules, which can be considered as a linear combination of many Slater determinants (or more generally: configuration state functions (CSFs) obtained from Slater determinants by appropriate linear combinations aiming at modeling proper spin quantum number). In such a model, a single CSF would correspond to a single Kekulé structure or a Clar cover of a given benzenoid. Two natural extensions to such a valence-bond CSF base can be perceived. The first extension corresponds to the extended conjugated circuit model introduced in the chemical graph theory community by Trinajstić and collaborators [23,24] and including not only double bonds (i.e., $K_2$ subgraphs) and aromatic rings (i.e., $C_6$ subgraphs) in the description of valence resonance structures of benzenoids, but also larger cycles ($C_{10}$, $C_{14}$, etc.). Following this idea, Žigert Pleteršek conceived a generalized Zhang–Zhang polynomial, which is also capable of enumerating larger cycles [25]. We believe that these generalized Clar covers can constitute an important class of topological invariants for benzenoids. At the moment, generalized ZZ polynomials have not been reported for any class of benzenoids and no correlation with energetics and properties of benzenoids has been studied. The second extension can be associated with radical resonance structures. It is well known that many benzenoids display pronounced radical character [26,27]. Including the biradical and tetraradical Kekulé structures and Clar covers in the graph-theoretical analysis of Kekuléan benzenoids and single radical and triradical resonance structures in the analysis of non-Kekuléan benzenoids can yield a completely new information about those structures and permit their better description in the valence bond language. Initial applications of the new version of ZZDecomposer [28] to study spin populations in benzenoids shows that using such radical Clar covers allows one to achieve very close correlation with spin populations determined from quantum chemical calculations.

2. Preliminaries

A benzenoid is a planar hydrocarbon B consisting of fused benzene rings. From a theoretical graph point, B is defined as a two-connected finite plane graph such that every interior face is a regular hexagon [29]. A Kekulé structure K is a resonance structure of B constructed using only double bonds [30]. A Clar cover C is a resonance structure of B constructed using double bonds and aromatic Clar sextets [31]. From a theoretical graph point, a Kekulé structure K is a spanning subgraph of B all the components of which are $K_2$ and a Clar cover C is a spanning subgraph of B, the components of which are either $K_2$ or hexagons $C_6$. Note that most difficulties originating from this double terminology can be circumvented if one establishes two correspondences: a complete graph on two vertices $K_2\equiv$ double bond and a cycle graph on six vertices $C_6\equiv$ aromatic Clar sextet. The maximal number of hexagons $C_6$ that can be accommodated in C is referred to as the Clar number $Cl$ of B [31,32]. The Clar covers with $Cl$ aromatic sextets $C_6$ are referred to as the Clar structures of B [31,32]. The Clar covers with k aromatic sextets $C_6$ are referred to as the Clar covers of order k. If we represent the number of Clar covers of order k for B by $c_k$, we can define a combinatorial polynomial

$$\mathrm{ZZ}\left(\mathit{B},x\right)=\sum _{k=0}^{Cl}{c}_k{x}^k$$

(1)

usually referred to as the Clar covering polynomial of B, the Zhang–Zhang polynomial of B, or the ZZ polynomial of B. [15,33,34,35] Clearly, the ZZ polynomial of B has the following inviting properties:

• The number of Kekulé structures of B is given by $K\left\{\mathit{B}\right\}=c_0=\mathrm{ZZ}\left(\mathit{B},0\right)$.
• The number of Clar covers of B is given by $C\left\{\mathit{B}\right\}=c_0+\cdots +c_{Cl}=\mathrm{ZZ}\left(\mathit{B},1\right)$.
• The Clar number of B is given by $Cl=deg\left(\mathrm{ZZ}\left(\mathit{B},x\right)\right)$.
• The number of Clar structures of B is given by $c_{Cl}=\mathrm{coeff}\left(\mathrm{ZZ}\left(\mathit{B},x\right),x^{Cl}\right)$.

These relations demonstrate the claim made at the end of Section 1, where we have written that determination of the ZZ polynomial of B answers most graph-theoretically relevant questions about B. Zhang and Zhang were able to demonstrate that the ZZ polynomials possess a rich structure of recursive decomposition properties [15,33,34], which enable their fast and robust computations in practical applications. (See, for example, Properties 1–7 in [3].) Consequently, the ZZ polynomial of an arbitrary benzenoid B or fullerene [36] can be efficiently computed using recursive decomposition algorithms [3,14,37] or determined using interface theory of benzenoids [38,39,40,41]. A useful practical tool for determination of ZZ polynomials is ZZDecomposer [10,37]. With this freely downloadable [28,42] software, one can conveniently define a graph representation corresponding to a given benzenoid B using a mouse drawing pad and subsequently use it to find the ZZ polynomial of B, generate the set of Clar covers of B, and determine its structural similarity to other, related benzenoids.

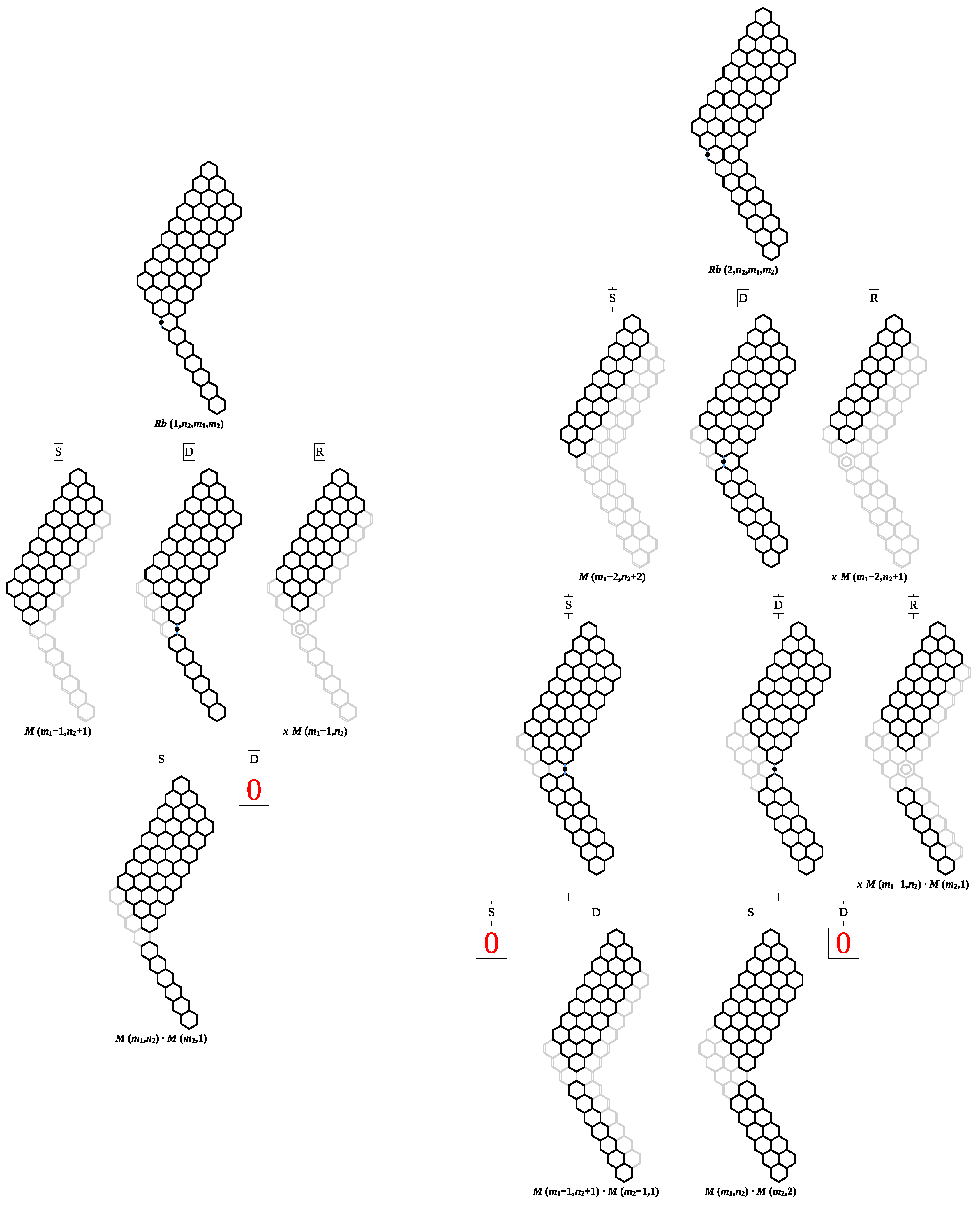
In the most typical depth-decomposition mode of ZZDecomposer, used below in Figure 2 to prove Equations (2) and (3), ZZDecomposer generates a recurrence relation for the analyzed benzenoid structure, which relates its ZZ polynomial to the ZZ polynomials of structurally related benzenoids and often allows for determination of closed-form formulas for the whole family of structurally similar benzenoids. Another useful feature of ZZDecomposer is generating vector graphics that can be easily incorporated in publications.

3. Heuristic Determination of the ZZ Polynomial from Recurrence Relations

Before presenting a formal derivation of the ZZ polynomial for the ribbon $Rb\left(n_1,n_2,m_1,m_2\right)$ in Section 4, first we discuss here a heuristic reasoning suggesting how such formulas can be discovered for a general benzenoid B. This goal can be readily achieved using the ZZDecomposer described in Section 2 by considering the first two members of this family of structures, $Rb\left(1,n_2,m_1,m_2\right)$ and $Rb\left(2,n_2,m_1,m_2\right)$, and performing their multi-step recursive decompositions with respect to the covering character of the vertical edges depicted in blue (with a black dot) in Figure 2.

The process of assigning to these edges single bond covering $\begin{array}{|c|}\hline \mathrm{S}\\ \hline\end{array}$, double bond covering $\begin{array}{|c|}\hline \mathrm{D}\\ \hline\end{array}$, or aromatic ring covering $\begin{array}{|c|}\hline \mathrm{R}\\ \hline\end{array}$, as it is demonstrated in Figure 2, allows us to partition the set of Clar covers of $Rb\left(1,n_2,m_1,m_2\right)$ and $Rb\left(2,n_2,m_1,m_2\right)$ into three and five subsets, respectively, each of them consisting of a region of fixed bonds separating parallelogram-shaped regions with not-fixed bonds. Consequently, the ZZ polynomials of $Rb\left(1,n_2,m_1,m_2\right)$ and $Rb\left(2,n_2,m_1,m_2\right)$ can be expressed as sums of products of ZZ polynomials of the parallelogram-shaped regions over all the subsets. Moreover, the formulas can be written compactly in terms of the ZZ polynomials of the parallelograms $M\left(m,n\right)$ as

$$\begin{array}{ccc}\hfill \mathrm{ZZ}\left(Rb\left(1,n_2,m_1,m_2\right),x\right)& =& \mathrm{ZZ}\left(M\left(m_1,n_2\right),x\right)·\mathrm{ZZ}\left(M\left(m_2,1\right),x\right)\hfill \\ & +& \mathrm{ZZ}\left(M\left(m_1-1,n_2+1\right),x\right)+x\mathrm{ZZ}\left(M\left(m_1-1,n_2\right),x\right)\hfill \end{array}$$

(2)

and

$$\begin{array}{ccc}\hfill \mathrm{ZZ}\left(Rb\left(2,n_2,m_1,m_2\right),x\right)& =& \mathrm{ZZ}\left(M\left(m_1,n_2\right),x\right)·\mathrm{ZZ}\left(M\left(m_2,2\right),x\right)\hfill \\ & +& \mathrm{ZZ}\left(M\left(m_1-1,n_2+1\right),x\right)·\mathrm{ZZ}\left(M\left(m_2+1,1\right),x\right)\hfill \\ & +& x\mathrm{ZZ}\left(M\left(m_1-1,n_2\right),x\right)·\mathrm{ZZ}\left(M\left(m_2,1\right),x\right)\hfill \\ & +& \mathrm{ZZ}\left(M\left(m_1-2,n_2+2\right),x\right)+x\mathrm{ZZ}\left(M\left(m_1-2,n_2+1\right),x\right)\hfill \end{array}$$

(3)

It is easy to notice regularities and patterns in these formulas. Remembering that $\mathrm{ZZ}\left(M\left(m,0\right),x\right)=1$, we can rewrite Equations (2) and (3) for situations when $n_1\le m_1$ in the following form

$$\begin{array}{c}\mathrm{ZZ}\left(Rb\left(n_1,n_2,m_1,m_2\right),x\right)=\hfill \\ {\displaystyle \sum _{k=0}^{n_1}}\mathrm{ZZ}\left(M\left(m_1-k,n_2+k\right),x\right)·\mathrm{ZZ}\left(M\left(m_2+k,n_1-k\right),x\right)+\hfill \\ +x{\displaystyle \sum _{k=1}^{n_1}}\mathrm{ZZ}\left(M\left(m_1-k,n_2-1+k\right),x\right)·\mathrm{ZZ}\left(M\left(m_2-1+k,n_1-k\right),x\right)\hfill \end{array}$$

(4)

The final generalization applies to situations when $n_1>m_1$. It is clear that the ZZ polynomials of $Rb\left(n_1,n_2,m_1,m_2\right)$ and $Rb\left(m_1,m_2,n_1,n_2\right)$ should be identical as there is a clear (horizontal mirror reflection) isomorphism between the sets of Clar covers of both structures. Indeed, Equation (4) reflects this symmetry except for the upper summations limits; it is easy to see that the appropriate change relies on replacing $n_1$ by $min\left(n_1,m_1\right)$. Consequently, the general formula for the ZZ polynomial of $Rb\left(n_1,n_2,m_1,m_2\right)$ must have the following symmetric form

$$\mathrm{ZZ}\left(Rb\left(n_1,n_2,m_1,m_2\right),x\right)=$$

(5)

$$\sum _{k=0}^{min\left(n_1,m_1\right)}\mathrm{ZZ}\left(M\left(m_1-k,n_2+k\right),x\right)·\mathrm{ZZ}\left(M\left(m_2+k,n_1-k\right),x\right)+$$

(6)

$$+x\sum _{k=1}^{min\left(n_1,m_1\right)}\mathrm{ZZ}\left(M\left(m_1-k,n_2-1+k\right),x\right)·\mathrm{ZZ}\left(M\left(m_2-1+k,n_1-k\right),x\right)$$

(7)

This formula can be further simplified by substituting an explicit form of the ZZ polynomial for the parallelogram $M\left(m,n\right)$

$$\mathrm{ZZ}\left(M\left(m,n\right),x\right)={}_2{F}_1\left[\begin{array}{c}-m,-n\\ 1\end{array};1+x\right]=\sum _{j=0}^{min\left(m,n\right)}\left(\genfrac{}{}{0pt}{}{m}{j}\right)\left(\genfrac{}{}{0pt}{}{n}{j}\right){\left(1+x\right)}^j$$

(8)

Introducing this formula into Equation (5), we obtain

$$\begin{array}{c}\mathrm{ZZ}\left(Rb\left(n_1,n_2,m_1,m_2\right),x\right)=\hfill \\ {\displaystyle \sum _{k=0}^{min\left(n_1,m_1\right)}}{}_2{F}_1\left[\begin{array}{c}-m_1+k,-n_2-k\\ 1\end{array};1+x\right]{}_2{F}_1\left[\begin{array}{c}-n_1+k,-m_2-k\\ 1\end{array};1+x\right]+\hfill \\ +x{\displaystyle \sum _{k=1}^{min\left(n_1,m_1\right)}}{}_2{F}_1\left[\begin{array}{c}-m_1+k,-n_2+1-k\\ 1\end{array};1+x\right]{}_2{F}_1\left[\begin{array}{c}-n_1+k,-m_2+1-k\\ 1\end{array};1+x\right]\hfill \end{array}$$

(9)

or

$$\begin{array}{c}\mathrm{ZZ}\left(Rb\left(n_1,n_2,m_1,m_2\right),x\right)=\hfill \\ {\displaystyle \sum _{k=0}^{min\left(n_1,m_1\right)}}{\displaystyle \sum _{j=0}^{m_1-k}}{\displaystyle \sum _{i=0}^{n_1-k}}\left(\genfrac{}{}{0pt}{}{m_1-k}{j}\right)\left(\genfrac{}{}{0pt}{}{n_2+k}{j}\right)\left(\genfrac{}{}{0pt}{}{m_2+k}{i}\right)\left(\genfrac{}{}{0pt}{}{n_1-k}{i}\right){\left(1+x\right)}^{i+j}+\hfill \\ +x{\displaystyle \sum _{k=1}^{min\left(n_1,m_1\right)}}{\displaystyle \sum _{j=0}^{m_1-k}}{\displaystyle \sum _{i=0}^{n_1-k}}\left(\genfrac{}{}{0pt}{}{m_1-k}{j}\right)\left(\genfrac{}{}{0pt}{}{n_2-1+k}{j}\right)\left(\genfrac{}{}{0pt}{}{m_2-1+k}{i}\right)\left(\genfrac{}{}{0pt}{}{n_1-k}{i}\right){\left(1+x\right)}^{i+j}\hfill \end{array}$$

(10)

Numerical experiments performed with ZZDecomposer for various values of the parameters $n_1$, $n_2$, $m_1$, and $m_2$ show that formulas given by Equations (9) and (10) are indeed correct. Formal demonstration of correctness of Equations (9) and (10) is presented in the next section; the proof is based on the recently developed interface theory of benzenoids [40,41].

As we mentioned earlier, the ribbon $Rb\left(n_1,n_2,m_1,m_2\right)$ has been also denoted in the earlier literature by the symbol $V\left(k,m,n\right)$, where $k=m_1=n_1$, $m=m_1+m_2$, and $n=n_1+n_2$ or by $V\left(k_1,k_2,m,n\right)$, where $k_1=n_1$, $k_2=m_1$, $m=m_1+m_2$, and $n=n_1+n_2$. Therefore, for consistency, we also give explicit formulas for the ZZ polynomials of $V\left(k,m,n\right)$ and $V\left(k_1,k_2,m,n\right)$ using their structural parameters in the formulas. We have

$$\begin{array}{c}\mathrm{ZZ}\left(V\left(k,m,n\right),x\right)=\hfill \\ {\displaystyle \sum _{s=0}^k}{\displaystyle \sum _{j=0}^{k-s}}{\displaystyle \sum _{i=0}^{k-s}}\left(\genfrac{}{}{0pt}{}{k-s}{j}\right)\left(\genfrac{}{}{0pt}{}{n-k+s}{j}\right)\left(\genfrac{}{}{0pt}{}{m-k+s}{i}\right)\left(\genfrac{}{}{0pt}{}{k-s}{i}\right){\left(1+x\right)}^{i+j}+\hfill \\ +x{\displaystyle \sum _{s=1}^k}{\displaystyle \sum _{j=0}^{k-s}}{\displaystyle \sum _{i=0}^{k-s}}\left(\genfrac{}{}{0pt}{}{k-s}{j}\right)\left(\genfrac{}{}{0pt}{}{n-k-1+s}{j}\right)\left(\genfrac{}{}{0pt}{}{m-k-1+s}{i}\right)\left(\genfrac{}{}{0pt}{}{k-s}{i}\right){\left(1+x\right)}^{i+j}\hfill \end{array}$$

(11)

and

$$\begin{array}{c}\mathrm{ZZ}\left(V\left(k_1,k_2,m,n\right),x\right)=\hfill \\ {\displaystyle \sum _{k=0}^{min\left(k_1,k_2\right)}}{\displaystyle \sum _{j=0}^{k_2-k}}{\displaystyle \sum _{i=0}^{k_1-k}}\left(\genfrac{}{}{0pt}{}{k_2-k}{j}\right)\left(\genfrac{}{}{0pt}{}{n-k_1+k}{j}\right)\left(\genfrac{}{}{0pt}{}{m-k_2+k}{i}\right)\left(\genfrac{}{}{0pt}{}{k_1-k}{i}\right){\left(1+x\right)}^{i+j}+\hfill \\ +{\displaystyle x\sum _{k=1}^{min\left(k_1,k_2\right)}}{\displaystyle \sum _{j=0}^{k_2-k}}{\displaystyle \sum _{i=0}^{k_1-k}}\left(\genfrac{}{}{0pt}{}{k_2-k}{j}\right)\left(\genfrac{}{}{0pt}{}{n-k_1-1+k}{j}\right)\left(\genfrac{}{}{0pt}{}{m-k_2-1+k}{i}\right)\left(\genfrac{}{}{0pt}{}{k_1-k}{i}\right){\left(1+x\right)}^{i+j}.\hfill \end{array}$$

(12)

Note that analogous formulas for the number of Kekulé structures given by Cyvin and Gutman (as Equation (19) of [21]) have both of the inner summations evaluated to a closed binomial form. This is indeed possible for Kekulé structures, for which $x=0$, where the following binomial identity (Equation (5.22) of [43]) can be used.

$$\sum _{j=0}^b\left(\genfrac{}{}{0pt}{}{b}{j}\right)\left(\genfrac{}{}{0pt}{}{v-b}{j}\right)=\left(\genfrac{}{}{0pt}{}{v}{b}\right)$$

(13)

In the case of the ZZ polynomial, Equation (13) takes on the following form

$$\sum _{j=0}^b\left(\genfrac{}{}{0pt}{}{b}{j}\right)\left(\genfrac{}{}{0pt}{}{v-b}{j}\right){\left(1+x\right)}^j={}_2{F}_1\left[\begin{array}{c}-b,-v+b\\ 1\end{array};1+x\right]$$

which renders Equations (11) and (12) in the hypergeometric form analogous to Equation (9). These hypergeometric functions reduce to the obvious polynomial form or to Jacobi polynomials, and no other functional identities exist that would allow to express them as some well-known functions.

4. Formal Derivation of the ZZ Polynomial from the Interface Theory of Benzenoids

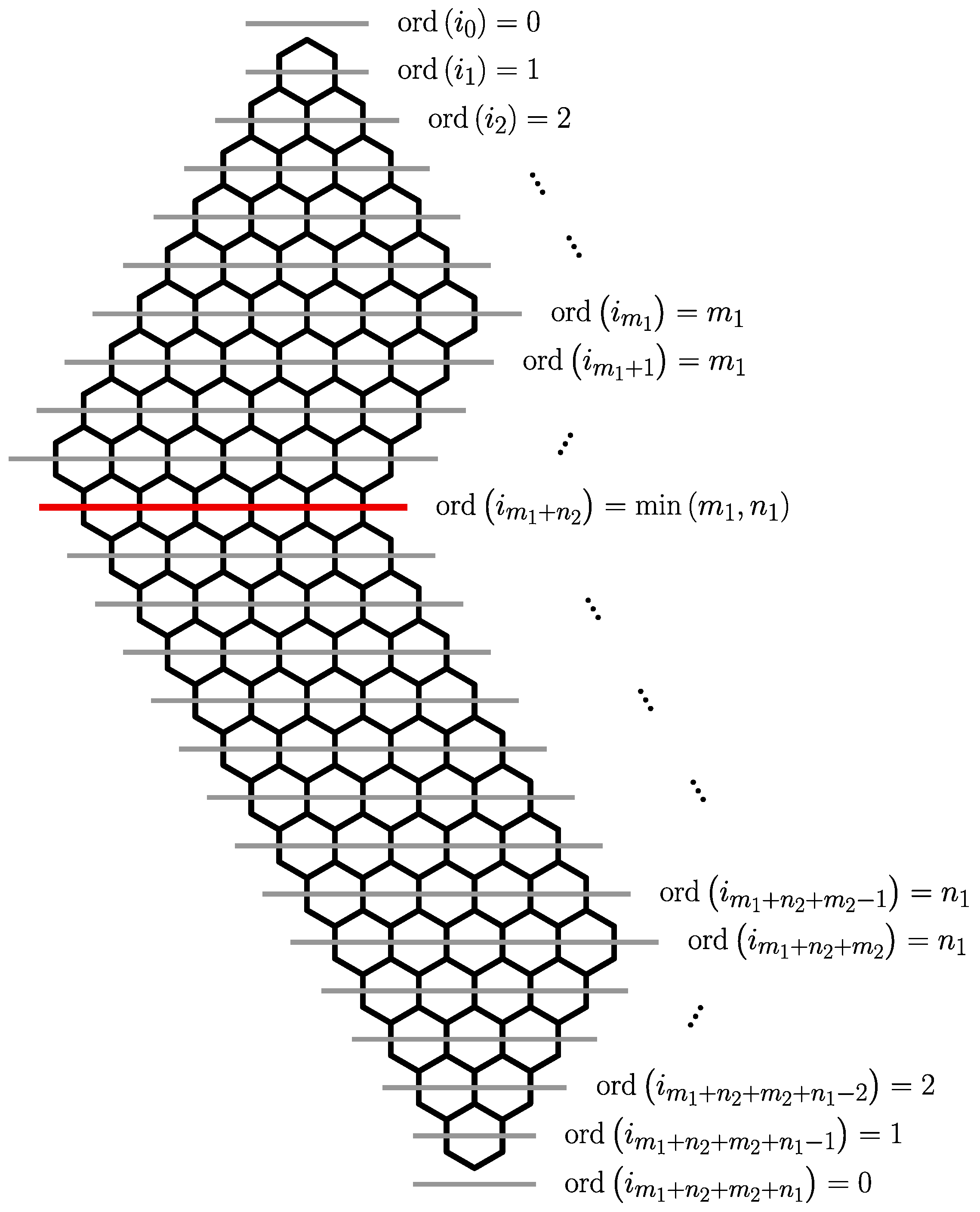
Consider the ribbon $\mathit{B}\equiv Rb\left(n_1,n_2,m_1,m_2\right)$ in the orientation shown in Figure 1. We introduce a system of $m_1+n_2+m_2+n_1-1$ elementary cuts $I_k$ intersecting the vertical edges of $\mathit{B}$ in the way shown in Figure 3. The set of vertical edges intersected by the elementary cut $I_k$ is referred to as the interface $i_k$ of $\mathit{B}$. It is convenient to augment the set $\left\{i_1,\dots ,i_{m_1+n_2+m_2+n_1-1}\right\}$ of interfaces by two empty interfaces, $i_0$ and $i_{m_1+n_2+m_2+n_1}$, located, respectively, above and below $\mathit{B}$.

Let us further refer to all the edges and vertices of $\mathit{B}$ located (at least partially) between the elementary cuts $I_{k-1}$ and $I_k$ as the fragment $f_k$ of $\mathit{B}$. We augment the set of fragments with two additional fragments: $f_1$ including all edges and vertices located (at least partially) above the elementary cut $I_1$ and $f_{m_1+n_2+m_2+n_1}$ including all edges and vertices located (at least partially) below the elementary cut $I_{m_1+n_2+m_2+n_1-1}$. It is clear from these definitions that for $1\le k\le m_1+n_2+m_2+n_1$

• $i_{k-1}\subset f_k$ is the upper interface of $f_k$,
• $i_k\subset f_k$ is the lower interface of $f_k$.

Consider now a fragment $f_k\subset \mathit{B}$ together with its upper interface $i_{k-1}$ and its lower interface $i_k$. Denote by $e_{\mathrm{first}}$ the left-most vertical edge of $f_k$, and by $e_{\mathrm{last}}$, the right-most vertical edge of $f_k$. We can now define the function shape as follows

$$\mathrm{shape}\left(f_k\right)=\left\{\begin{array}{cc}\mathtt{W}\hfill & \mathrm{when}{e}_{\mathrm{first}}\in i_k\mathrm{and}{e}_{\mathrm{last}}\in i_k\hfill \\ \mathtt{N}\hfill & \mathrm{when}{e}_{\mathrm{first}}\in i_{k-1}\mathrm{and}{e}_{\mathrm{last}}\in i_{k-1}\hfill \\ \mathtt{R}\hfill & \mathrm{when}{e}_{\mathrm{first}}\in i_{k-1}\mathrm{and}{e}_{\mathrm{last}}\in i_k\hfill \\ \mathtt{L}\hfill & \mathrm{when}{e}_{\mathrm{first}}\in i_k\mathrm{and}{e}_{\mathrm{last}}\in i_{k-1}\hfill \end{array}\right.$$

(14)

The symbols $\mathtt{W}$, $\mathtt{N}$, $\mathtt{R}$, and $\mathtt{L}$ describe the shape geometrically (respectively: wider, narrower, to-the-right, and to-the-left) of each fragment.

Using this terminology, it is possible to apply the function shape to $\mathit{B}=\left(f_1,f_2,\dots ,f_{m_1+n_2+m_2+n_1}\right)$, simply by mapping it to the sequence of its fragments. For example, the shape of the structure shown in Figure 1 is specified by the following sequence

$$\mathrm{shape}\left(Rb\left(3,6,5,4\right)\right)=\mathtt{WWWWWLLLLNNRRRRNNN}$$

(15)

Let us now consider an arbitrary Clar cover $\mathit{C}$ of $\mathit{B}$. For every edge e of $\mathit{B}$, we define a covering order function $\mathrm{ord}\left(e\right)$ as follows

$$\mathrm{ord}\left(e\right)=\left\{\begin{array}{cc}1\hfill & \mathrm{when}\exists K_2\subset \mathit{C}:e\in K_2\hfill \\ \frac{1}{2}\hfill & \mathrm{when}\exists C_6\subset \mathit{C}:e\in C_6\hfill \\ 0\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

(16)

This definition can be naturally extended to covering order of interfaces by defining the order of the interface $\mathrm{ord}\left(i\right)$ as

$$\mathrm{ord}\left(i\right)=\sum _{e\in i}\mathrm{ord}\left(e\right).$$

(17)

The interfaces $i_0$ and $i_{m_1+n_2+m_2+n_1}$ are empty, thus

$$\mathrm{ord}\left(i_0\right)=0=\mathrm{ord}\left(i_{m_1+n_2+m_2+n_1}\right).$$

(18)

It turns out that the orders of the remaining interfaces can be conveniently computed in an iterative fashion using:

Theorem 1

(First rule of interface theory: interface order criterion [40,41]). Let $\mathit{C}$ be some Clar cover of a benzenoid $\mathit{B}$. Let $f_k$ be a fragment of $\mathit{B}$, and let $i_{k-1}$ and $i_k$ be the upper and lower interfaces of $f_k$, respectively. The following conditions are always satisfied.

(a)

If $f_k$ has the shape $\mathtt{W}$, then$\mathrm{ord}\left(i_k\right)=\mathrm{ord}\left(i_{k-1}\right)+1$.

(b)

If $f_k$ has the shape $\mathtt{N}$, then$\mathrm{ord}\left(i_k\right)=\mathrm{ord}\left(i_{k-1}\right)-1$.

(c)

If $f_k$ has the shape $\mathtt{R}$ or $\mathtt{L}$, then$\mathrm{ord}\left(i_k\right)=\mathrm{ord}\left(i_{k-1}\right)$.

The interface orders determined this way starting with $\mathrm{ord}\left(i_0\right)=0$ depend only on the shape of $\mathit{B}$ and are independent of the choice of $\mathit{C}$. Therefore, the interface orders are identical for every Clar cover $\mathit{C}$. It is straightforward to show that the interface orders of $Rb\left(3,6,5,4\right)$ shown in Figure 1 are specified by the following sequence

$$\left(\mathrm{ord}\left(i_0\right),\dots ,\mathrm{ord}\left(i_{m_1+n_2+m_2+n_1}\right)\right)=\left(0,1,2,3,4,5,5,5,5,5,4,3,3,3,3,3,2,1,0\right)$$

and the interface orders of $Rb\left(5,9,4,6\right)$ shown in Figure 3 are specified by the following sequence

$$\left(\mathrm{ord}\left(i_0\right),\dots ,\mathrm{ord}\left(i_{m_1+n_2+m_2+n_1}\right)\right)=\left(0,1,2,3,4,\underset{10\mathrm{times}}{\underbrace{5}},\underset{4\mathrm{times}}{\underbrace{6}},5,4,3,2,1,0\right)$$

Let us now consider in detail the interface $i_{m_1+n_2}$ of $Rb\left(n_1,n_2,m_1,m_2\right)$. Application of Theorem 1 to $i_{m_1+n_2}$ shows that $\mathrm{ord}\left(i_{m_1+n_2}\right)=N\equiv min\left(m_1,n_1\right)$. At the same time simple geometrical considerations show that $i_{m_1+n_2}$ consists of $N+1$ vertical edges $e_0,\dots ,e_N$, where the numbering proceeds from right to left. Since

$$\mathrm{ord}\left(i_{m_1+n_2}\right)=\sum _{k=0}^N\mathrm{ord}\left(e_k\right)=N$$

(19)

and since each $\mathrm{ord}\left(e_k\right)$ can take on only three values: 0, $\frac{1}{2}$, and 1, the interface order $\mathrm{ord}\left(i_{m_1+n_2}\right)=N$ can be created from the interface edges orders $\mathrm{ord}\left(e_k\right)$ only in two possible ways

$$\begin{array}{ccc}\hfill N& =& \underset{N\mathrm{times}}{\underbrace{1+\dots +1}}+\underset{1\mathrm{time}}{\underbrace{0}}\hfill \end{array}$$

(20)

$$\begin{array}{ccc}\hfill N& =& \underset{N-1\mathrm{times}}{\underbrace{1+\dots +1}}+\underset{2\mathrm{times}}{\underbrace{\frac{1}{2}+\frac{1}{2}}}\hfill \end{array}$$

(21)

The first of these two choices, described by Equation (20), correspond to Clar covers in which the interface $i_{m_1+n_2}$ is composed of N double bonds and 1 single bond. Clearly, there exist $N+1$ distinct classes of Clar covers fulfilling this condition; in each distinct class, the single bond is located at the position $e_k$ with $k\in \left\{0,\dots ,N\right\}$. Each of such distinct classes corresponds to a single summand in Equation (6). The second of these choices, described by Equation (21), correspond to Clar covers in which the interface $i_{m_1+n_2}$ is composed of $N-1$ double bonds and 2 aromatic bonds belonging to the same hexagon $C_6$. Clearly, there exist N distinct classes of Clar covers fulfilling this condition; in each distinct class, the hexagon $C_6$ is located at the positions $e_{k-1}$ and $e_k$ with $k\in \left\{1,\dots ,N\right\}$. Each of such distinct classes corresponds to a single summand in Equation (7). To complete the proof of Equation (5) it remains to be demonstrated that for each of these distinct classes of Clar covers, the covering orders of edges in the interface $i_{m_1+n_2}$ induce a fixed-bond region in $\mathit{B}$ separating two not-fixed-bond regions, each of them in the shape of a parallelogram.

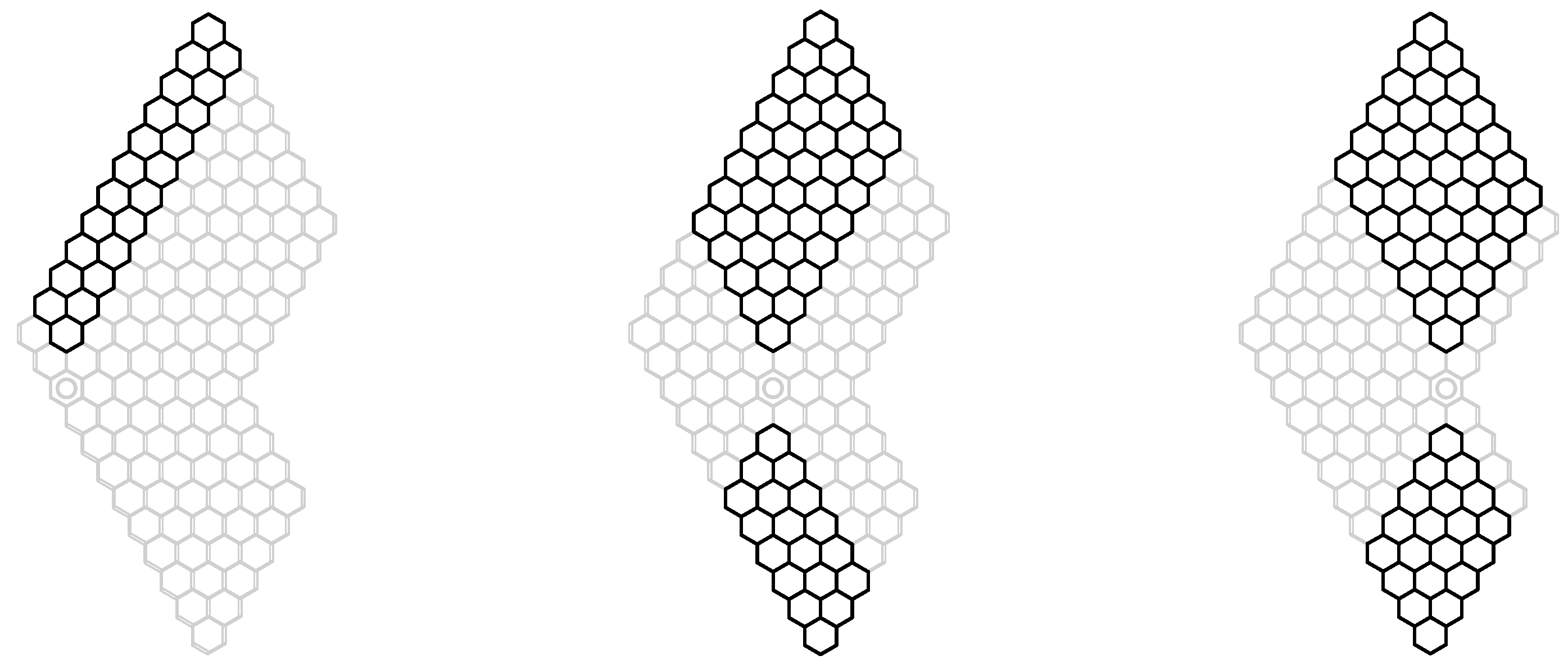
Let us first consider a class of Clar covers of $\mathit{B}$ corresponding to Equation (20) with a single bond in the position $e_k$ of the interface $i_{m_1+n_2}$ and double bonds in its remaining positions. Figure 4 shows that the systems of double bonds in the interface $i_{m_1+n_2}$ propagates down and up in $\mathit{B}$, uniquely deciding the covering orders for a large portion of this structure. Each Clar cover belonging to this class shares this region of fixed bonds. However, there remain two disconnected regions in $\mathit{B}$, each in the shape of a parallelogram, for which the covering characters are not determined by the covering of the interface $i_{m_1+n_2}$. The sizes of these two parallelograms are determined by the structural parameters $n_1$, $n_2$, $m_1$, and $m_2$ and the location k of the single bond. It is easy to see that the upper parallelogram is $M\left(m_1-k,n_2+k\right)$ and the lower one is $M\left(m_2+k,n_1-k\right)$. The product of the ZZ polynomials of these two parallelograms

$$\mathrm{ZZ}\left(M\left(m_1-k,n_2+k\right),x\right)·\mathrm{ZZ}\left(M\left(m_2+k,n_1-k\right),x\right)$$

describes the contribution of this class of Clar covers to the ZZ polynomial of $\mathit{B}$. The sum of these contributions for $k\in \left\{0,\dots ,N\right\}$ reproduces Equation (6).

Let us now consider a class of Clar covers of $\mathit{B}$ corresponding to Equation (21) with a hexagon $C_6$ located at the positions $e_{k-1}$ and $e_k$ of the interface $i_{m_1+n_2}$ and double bonds in its remaining positions. Figure 5 shows that the covered bonds in the interface $i_{m_1+n_2}$ induce a system of double bonds in the interfaces $i_{m_1+n_2-1}$ and $i_{m_1+n_2+1}$, which propagate down and up in $\mathit{B}$, again uniquely deciding the covering orders for a large portion of this structure. Each Clar cover belonging to this class shares this region of fixed bonds. Again, there remain two disconnected regions in $\mathit{B}$, each in the shape of a parallelogram, for which the covering characters are not determined by the covering of the interface $i_{m_1+n_2}$. The sizes of these two parallelograms are determined by the structural parameters $n_1$, $n_2$, $m_1$, and $m_2$ and the location k of the Clar sextet. It is again easy to see that the upper parallelogram is $M\left(m_1-k,n_2-1+k\right)$ and the lower one is $M\left(m_2-1+k,n_1-k\right)$. The product of the ZZ polynomials of these two parallelograms

$$\mathrm{ZZ}\left(M\left(m_1-k,n_2-1+k\right),x\right)·\mathrm{ZZ}\left(M\left(m_2-1+k,n_1-k\right),x\right)$$

describes the contribution of this class of Clar covers to the ZZ polynomial of $\mathit{B}$. The sum of these contributions—multiplied by a factor x to account for the additional Clar sextet at location k—for $k\in \left\{1,\dots ,N\right\}$ reproduces Equation (7) and concludes the proof of Equation (5).

5. Discussion and Conclusions

We have derived a closed-form formula for the ZZ polynomial of ribbons $\mathit{B}\equiv Rb\left(n_1,n_2,m_1,m_2\right)$, an important class of elementary peri-condensed benzenoids. The formal demonstration of its correctness is based on the recently developed interface theory of benzenoids. The discovered formula

$$\begin{array}{c}\mathrm{ZZ}\left(\mathit{B},x\right)=\hfill \\ {\displaystyle \sum _{k=0}^{min\left(n_1,m_1\right)}}{\displaystyle \sum _{j=0}^{m_1-k}}{\displaystyle \sum _{i=0}^{n_1-k}}\left(\genfrac{}{}{0pt}{}{m_1-k}{j}\right)\left(\genfrac{}{}{0pt}{}{n_2+k}{j}\right)\left(\genfrac{}{}{0pt}{}{m_2+k}{i}\right)\left(\genfrac{}{}{0pt}{}{n_1-k}{i}\right){\left(1+x\right)}^{i+j}+\hfill \\ +x{\displaystyle \sum _{k=1}^{min\left(n_1,m_1\right)}}{\displaystyle \sum _{j=0}^{m_1-k}}{\displaystyle \sum _{i=0}^{n_1-k}}\left(\genfrac{}{}{0pt}{}{m_1-k}{j}\right)\left(\genfrac{}{}{0pt}{}{n_2-1+k}{j}\right)\left(\genfrac{}{}{0pt}{}{m_2-1+k}{i}\right)\left(\genfrac{}{}{0pt}{}{n_1-k}{i}\right){\left(1+x\right)}^{i+j}\hfill \end{array}$$

uniquely determines the most important topological invariants of $Rb\left(n_1,n_2,m_1,m_2\right)$:

• The number of Kekulé structures

  $$K\left\{\mathit{B}\right\}=\sum _{k=0}^{min\left(n_1,m_1\right)}\sum _{j=0}^{m_1-k}\sum _{i=0}^{n_1-k}\left(\genfrac{}{}{0pt}{}{m_1-k}{j}\right)\left(\genfrac{}{}{0pt}{}{n_2+k}{j}\right)\left(\genfrac{}{}{0pt}{}{m_2+k}{i}\right)\left(\genfrac{}{}{0pt}{}{n_1-k}{i}\right)$$
• The number of Clar covers

  $$C\left\{\mathit{B}\right\}=\sum _{k=0}^{min\left(n_1,m_1\right)}\sum _{j=0}^{m_1-k}\sum _{i=0}^{n_1-k}\left(\genfrac{}{}{0pt}{}{m_1-k}{j}\right)\left(\genfrac{}{}{0pt}{}{n_2+k}{j}\right)\left(\genfrac{}{}{0pt}{}{m_2+k}{i}\right)\left(\genfrac{}{}{0pt}{}{n_1-k}{i}\right)2^{i+j}$$

  $$+\sum _{k=1}^{min\left(n_1,m_1\right)}\sum _{j=0}^{m_1-k}\sum _{i=0}^{n_1-k}\left(\genfrac{}{}{0pt}{}{m_1-k}{j}\right)\left(\genfrac{}{}{0pt}{}{n_2-1+k}{j}\right)\left(\genfrac{}{}{0pt}{}{m_2-1+k}{i}\right)\left(\genfrac{}{}{0pt}{}{n_1-k}{i}\right)2^{i+j}$$
• The Clar number $Cl=deg\left(\mathrm{ZZ}\left(\mathit{B},x\right)\right)$,
• And the number of Clar structures equal to $\mathrm{coeff}\left(\mathrm{ZZ}\left(\mathit{B},x\right),x^{Cl}\right)$.

Interestingly, it is straightforward to obtain the Clar number of $Rb\left(n_1,n_2,m_1,m_2\right)$ and the number of Clar structures of $Rb\left(n_1,n_2,m_1,m_2\right)$ directly from the ZZ polynomial, but it seems to be a formidable task to extract these two quantities directly from the structural constants $n_1$, $n_2$, $m_1$, and $m_2$. For example, at the moment, the most compact formula for $Cl$ in terms of the structural constants $n_1$, $n_2$, $m_1$, and $m_2$ that we are aware of is given by the following expression

$$Cl=max\left(C{l}_{\mathrm{s}},C{l}_{\mathrm{r}}\right),$$

(22)

where

$$\begin{array}{ccc}\hfill C{l}_{\mathrm{s}}& =& \underset{k\in \left\{0,\dots ,min\left(m_1,n_1\right)\right\}}{max}\left(min\left(m_1-k,n_2+k\right)+min\left(n_1-k,m_2+k\right)\right)\hfill \end{array}$$

(23)

$$\begin{array}{ccc}\hfill C{l}_{\mathrm{r}}& =& \underset{k\in \left\{1,\dots ,min\left(m_1,n_1\right)\right\}}{max}\left(1+min\left(m_1-k,n_2-1+k\right)+min\left(n_1-k,m_2-1+k\right)\right)\hfill \end{array}$$

(24)

Both of these terms are needed, as the following examples show. For $Rb\left(1,2,2,3\right)$, we have $C{l}_{\mathrm{s}}=3$ and $C{l}_{\mathrm{r}}=2$, so $Cl=C{l}_{\mathrm{s}}.$ For $Rb\left(3,1,2,2\right)$, we have $C{l}_{\mathrm{s}}=3$ and $C{l}_{\mathrm{r}}=4$, so $Cl=C{l}_{\mathrm{r}}.$ We believe that Equations (22)–(24) cannot be simplified much. Therefore, it should be very instructive to see this expression for researchers who try to determine Clar numbers of simple benzenoids directly from geometrical considerations. The structural complexity of this formula suggests that transforming relatively easy geometrical constructs into an algebraic expression can be cumbersome.

The last two classes of elementary peri-condensed benzenoids, for which closed-form ZZ polynomial formulas remain to be found, are hexagonal flakes $O\left(k,m,n\right)$ and oblate rectangles $Or\left(m,n\right)$. We hope that our results will stimulate mathematicians and mathematically-oriented chemists to discover these two last missing formulas. A possible departure point for such investigations can be the interface theory of benzenoids [38,39,40,41] or the recently discovered equivalence between the ZZ polynomials of regular benzenoid strips and the extended strict order polynomials of certain posets associated with those benzenoids [44,45]. Yet another convenient departure point for discovering a general closed form of ZZ polynomials of $O\left(k,m,n\right)$ (and by extension, also for $Or\left(m,n\right)$), can be our recently accepted study reporting structural parameters-based closed-form formula for hexagonal graphene flakes $O\left(k,m,n\right)$ with $k,m = 1–7$ and arbitrary n [13]. Ultimate general formulas of that kind are still unknown.