Clar Covers of Overlapping Benzenoids: Case of Two Identically-Oriented Parallelograms
Abstract
1. Introduction
2. Counting Clar Covers
- Kekulé count ,
- Clar count ,
- Clar number ,
- the number of Clar formulas ,
- and the first Herndon number [22].
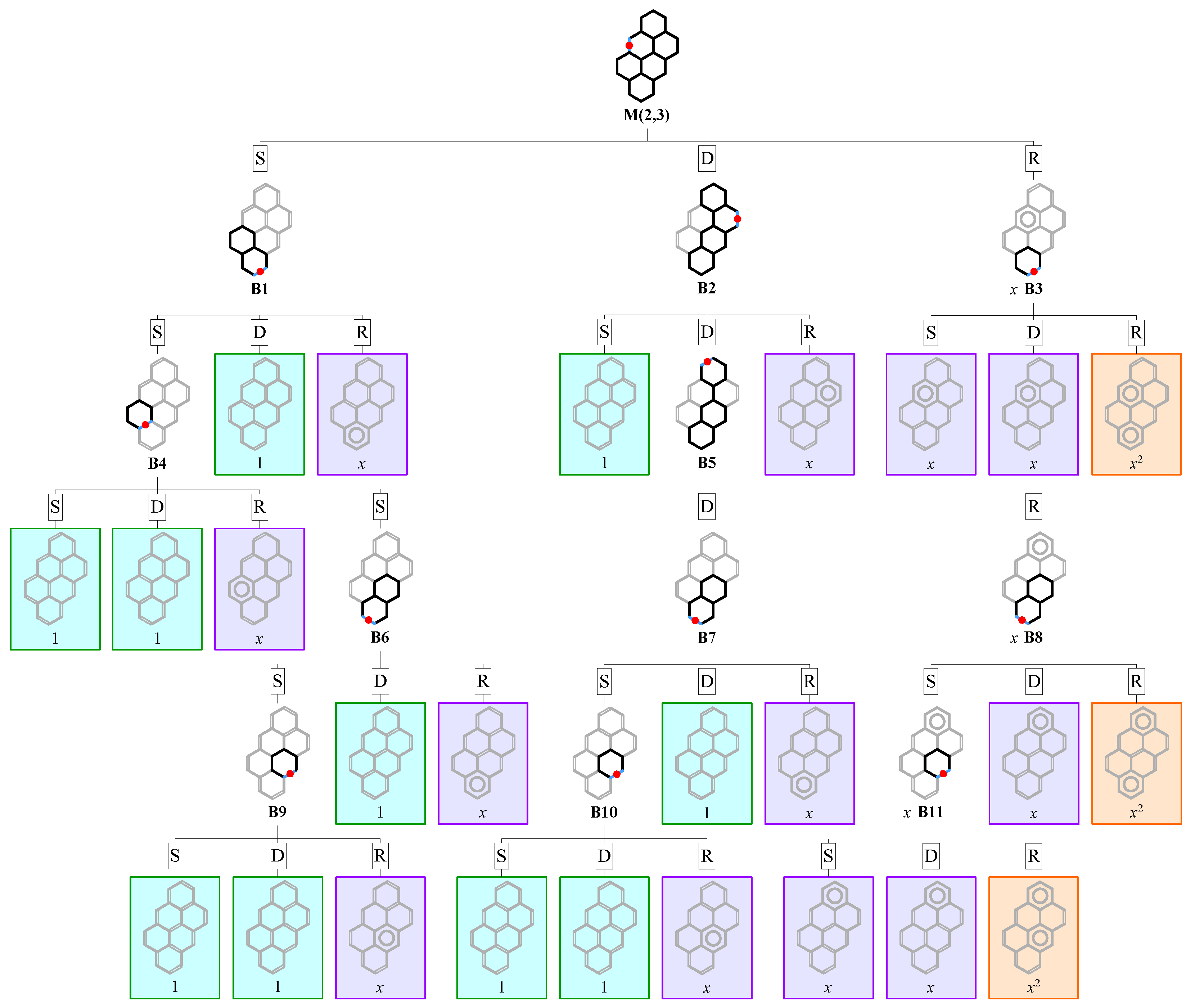
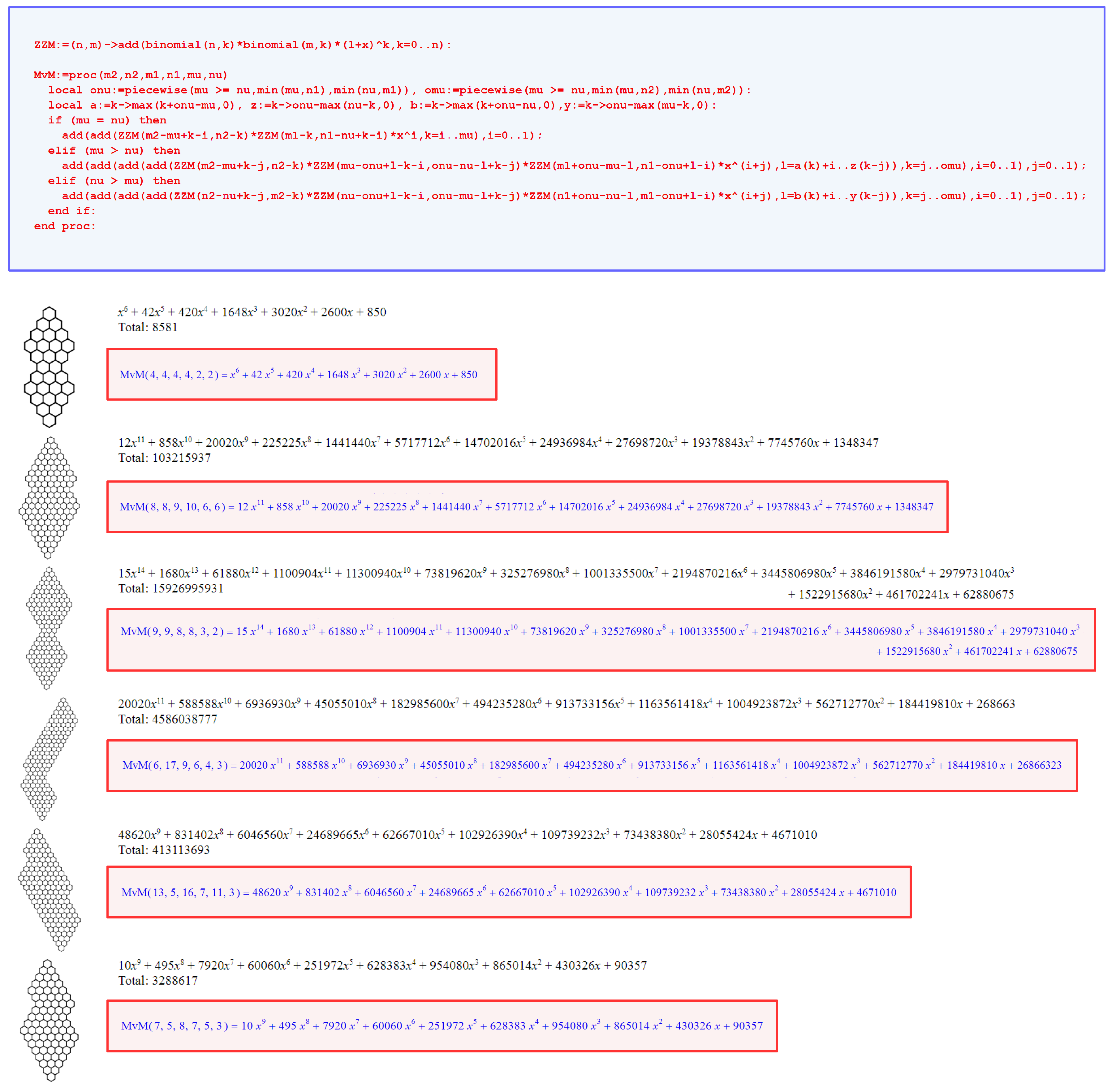
3. ZZ Polynomials of Complex Benzenoid Structures
4. Results
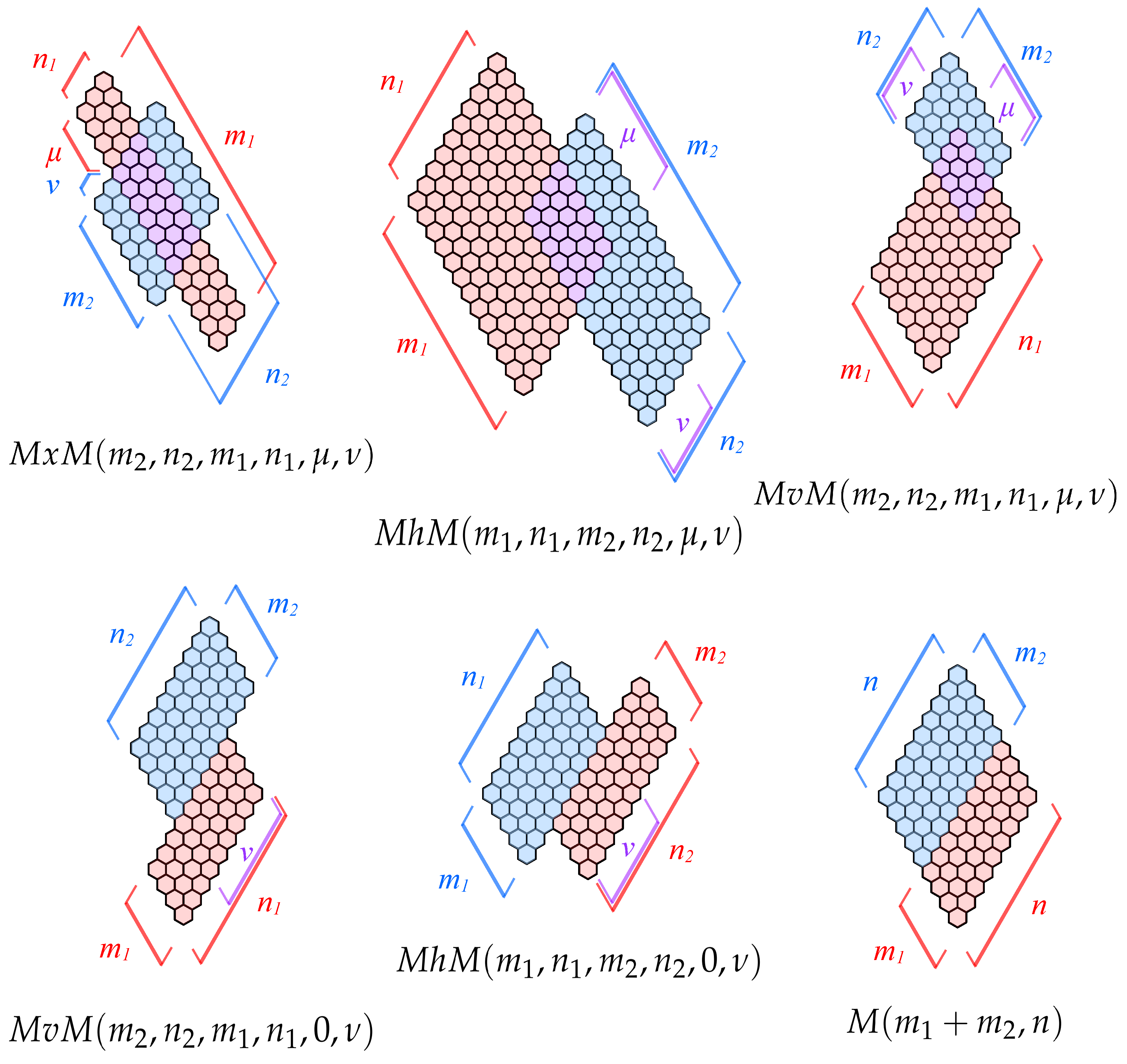
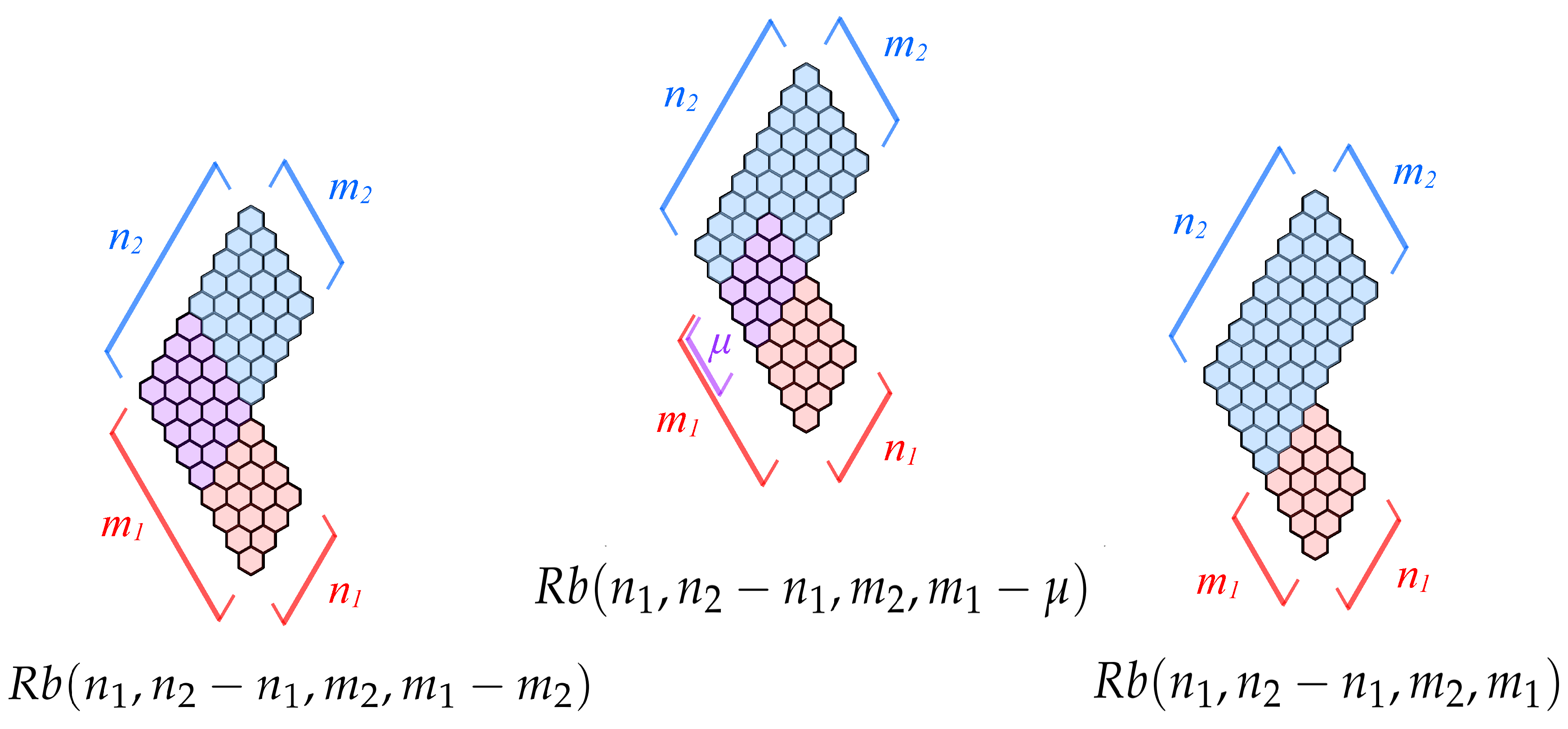
4.1. Ribbons , , and
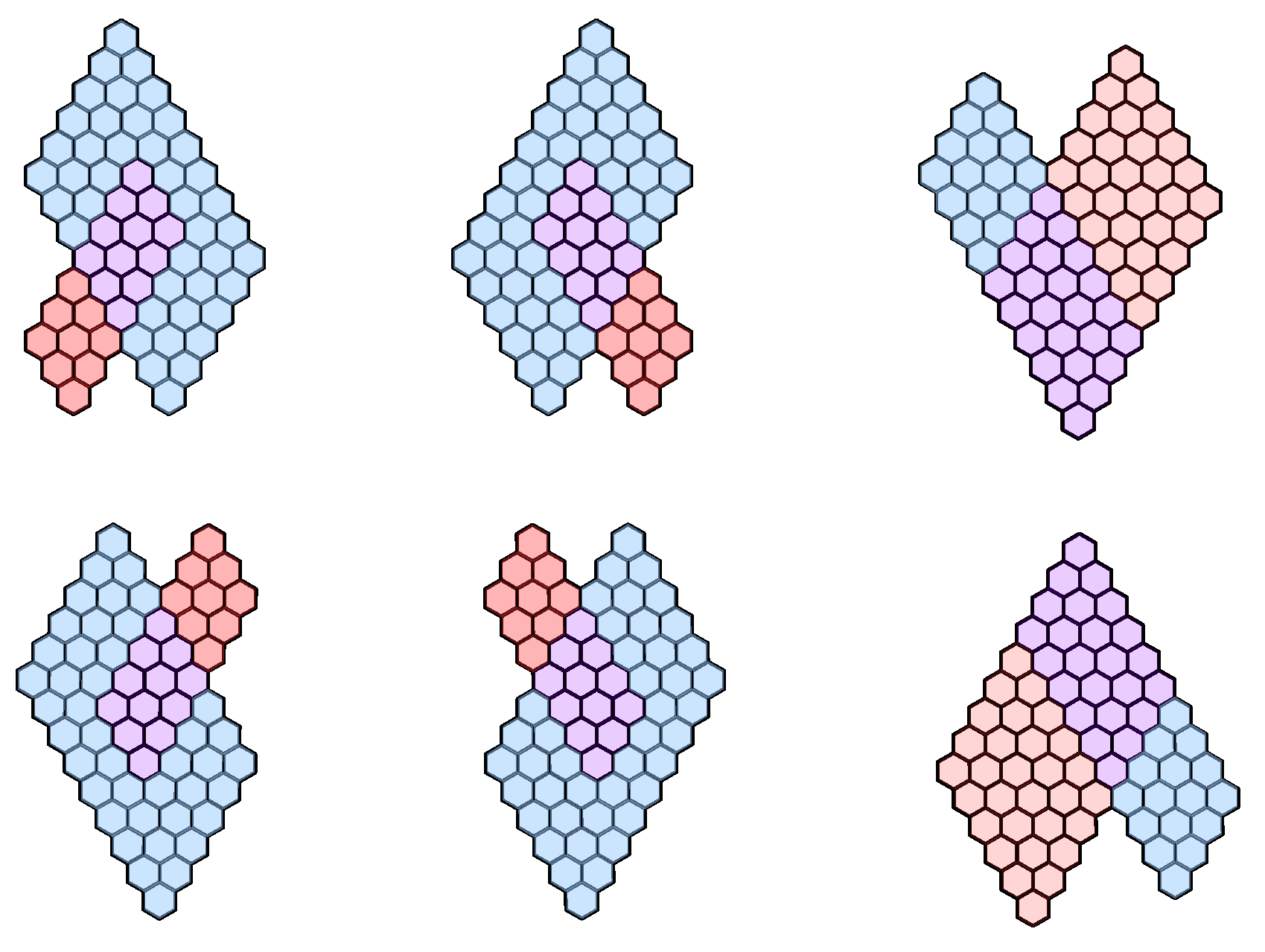
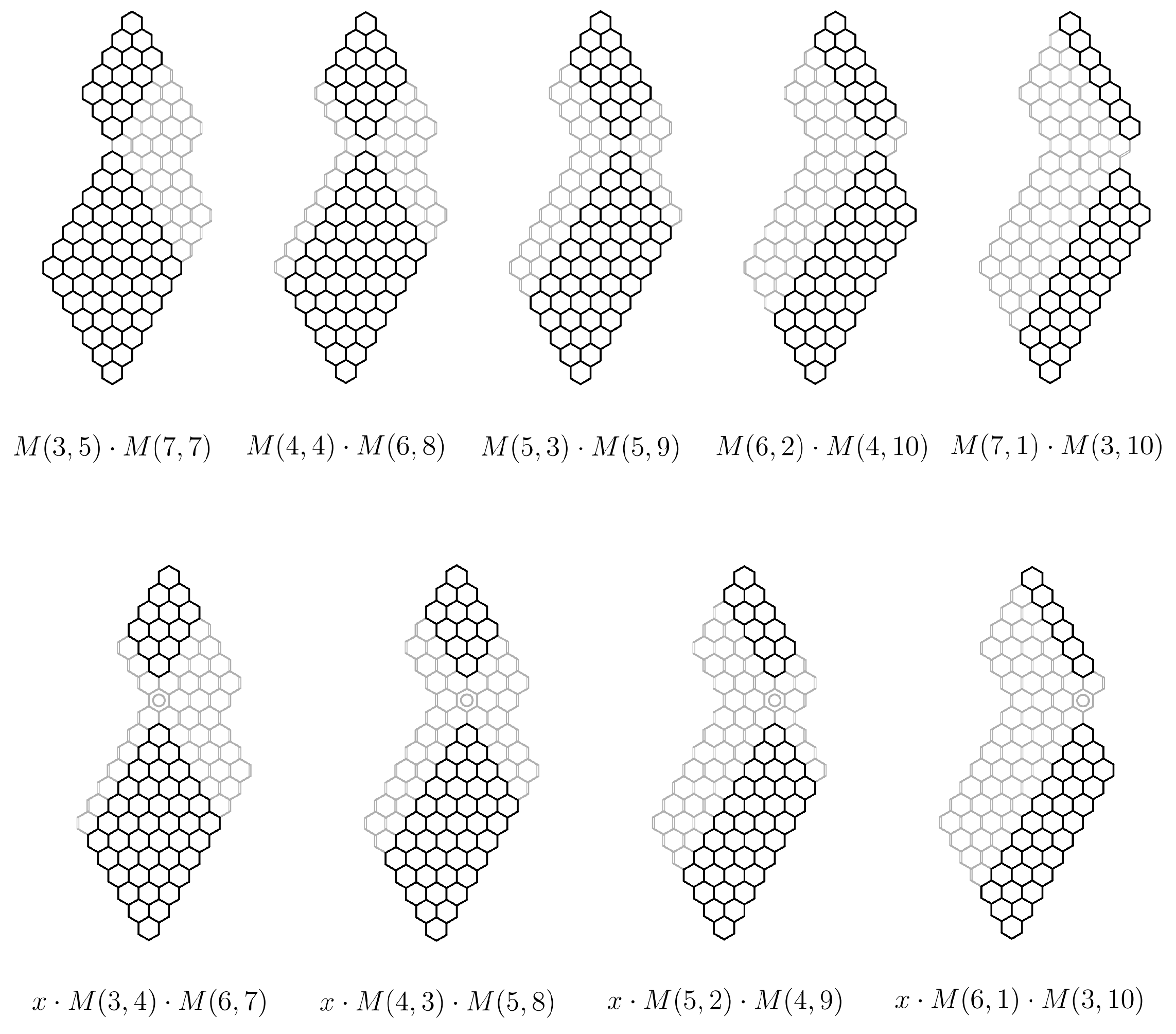
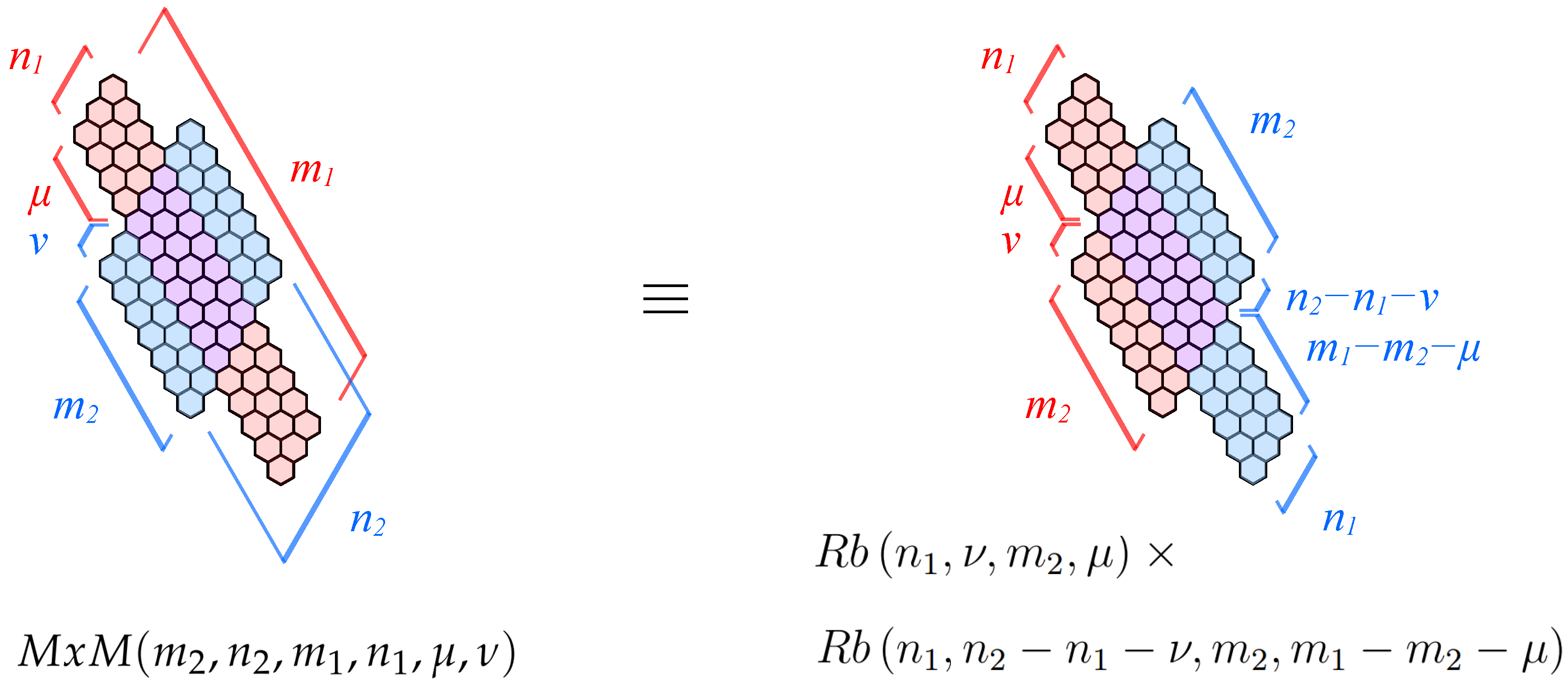
4.2. Two Vertically Overlapping Parallelograms
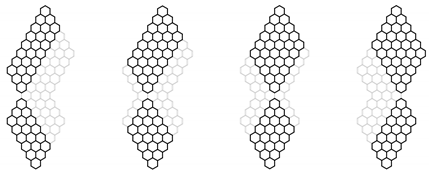
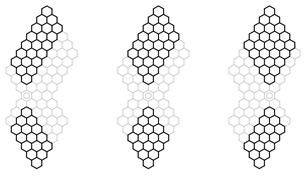
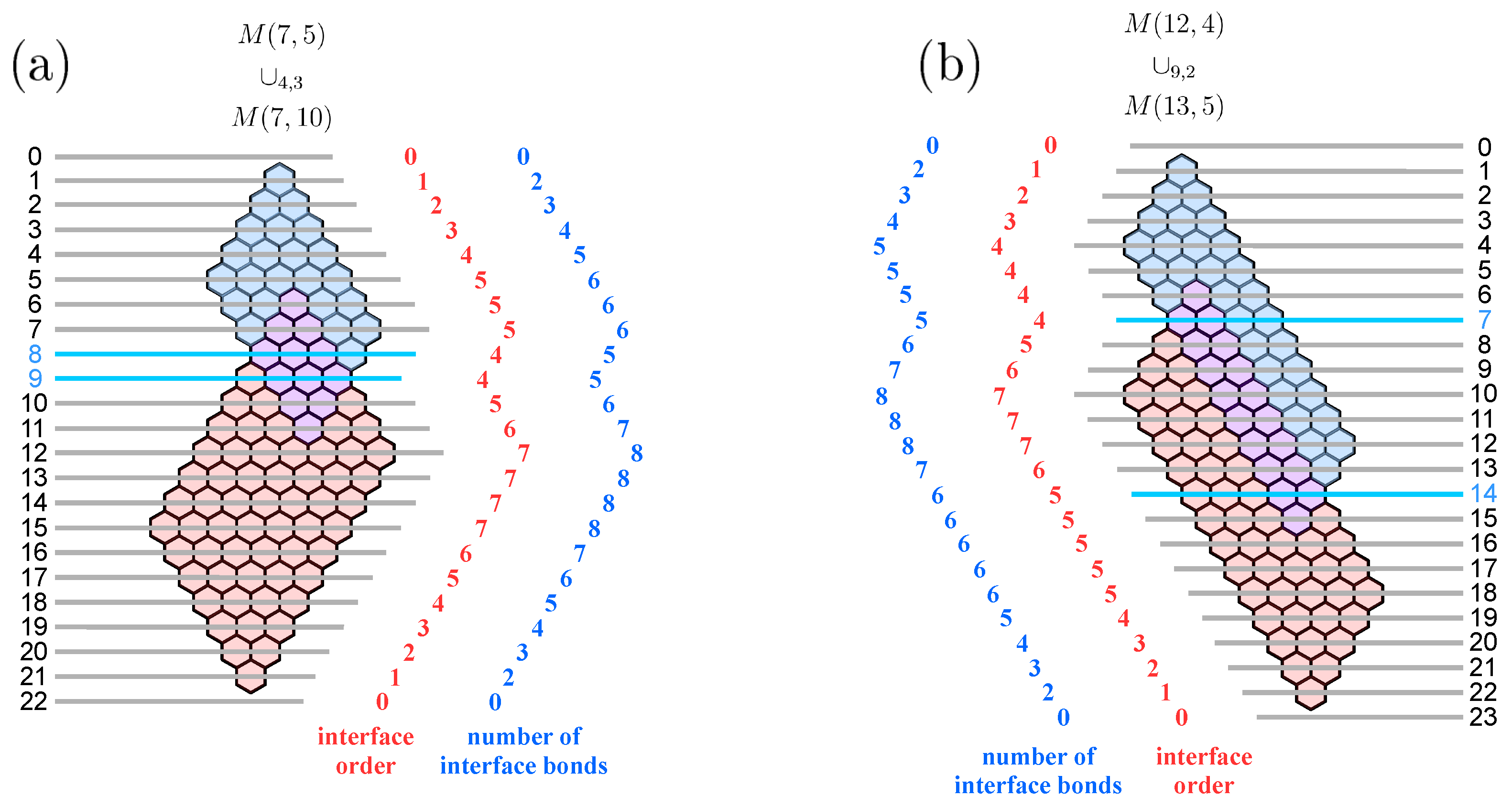
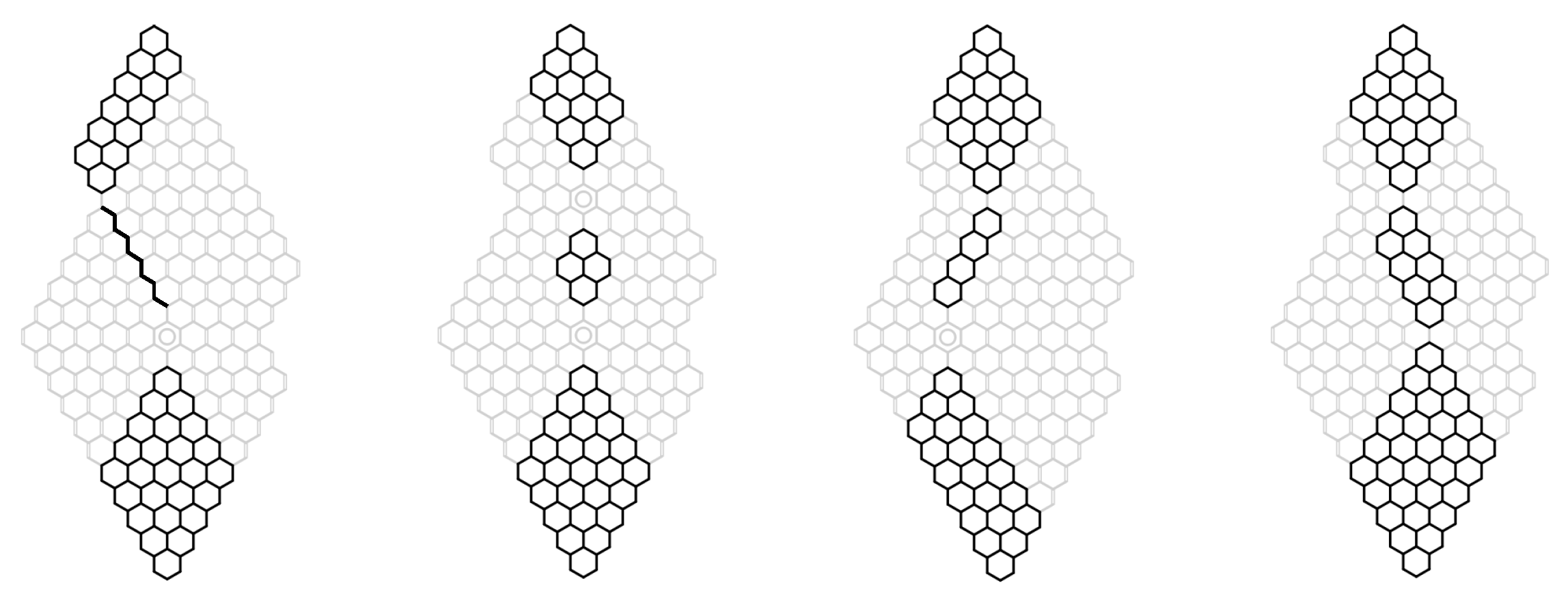
- We introduce in a system of parallel horizontal lines referred to as the elementary cuts in the way shown in Figure 5. Each such elementary cut is perpendicular to some vertical edges of and dissects them into halves. The number of elementary cuts introduced in this way is . For convenience, we augment this system with two additional elementary cuts, and in the way shown in Figure 5.
- The set of vertical edges of intersected by the elementary cut is referred to as the interface . Each edge belonging to the interface is referred to as an interface bond. Simple geometrical considerations allow establishing that the number of interfaces in is . It is beneficial to augment this set again with two additional empty interfaces and in the way shown in Figure 5.
- The set of edges of located at least partially between the elementary cuts and is referred to as the fragment . has fragments.
- For , is the upper interface of and is the lower interface of .
- Interface bonds in each fragment are numbered from left to right. The leftmost interface edge in is referred to as and the the rightmost interface edge in , as .
- Each fragment can be assigned an attribute of shape (, , , and ), which is defined in the following wayFollowing this convention, it is possible to assign the attribute of shape to the whole structure , simply by listing the shape of each fragment from the top to the bottom. For example, the shape sequences for the two structures in Figure 5 are: (a) and (b) .
- Let us now consider an arbitrary Clar cover of . For every interface edge e in , we define a covering order function , which assumes the following valueswhere and denote the sets of edges of and , respectively. We refer to a bond e with covering order 0 as a single bond, a bond e with covering order 1 as a double bond, and a bond e with covering order as an aromatic bond.
- The concept of covering order (or briefly: order) can be naturally extended to interfaces. We define the covering order of the interface i as
- Since the interface is empty, we naturally have . The orders of the remaining interfaces can be recursively computed from the First rule of interface theory [51,52], which for an arbitrary Clar cover relates the covering order of the interface to the covering order of the interface and the shape of the fragment in the following way
- (a)
- If has the shape , then .
- (b)
- If has the shape , then .
- (c)
- If has the shape or , then .
- The interface orders obtained in this way are actually independent of the choice of the Clar cover , as they are completely determined by the condition and the shape sequence . Therefore, the interface orders are identical for every Clar cover of and can be treated as an inherent property of allowing enumerating and constructing the set of Clar covers of . The interface covering orders computed in this way are listed in red for the two structures shown in Figure 5.
- The number of interface bonds in every non-empty interface of is larger by 1 from the order of this interface, , as can be easily seen from Figure 5. This property holds for a general structure of this type, as both the interface orders and the numbers of interface bonds in consecutive interfaces depend in the same manner on the shape of the fragment between the interfaces, except for the first and the last fragment.
- An explicit formula for the interface order as a function of the interface number k is somewhat cumbersome. It can be shown thatwherewhere , , and correspond to the order of the same interface in the pristine structures , , and , respectively.

- Let us assume that a partition was selected for with the single bond in position . Somewhat involved geometric considerations show that the range of indices of non-fixed interface bonds in associated with this choice is given by .
- Consequently, a single bond in interface in position k permits placing a single bond in interface in position or permits placing an aromatic ring in hexagon .
- Let us assume now that a partition was selected for with the aromatic ring in hexagon . Again, geometric considerations show that the range of indices of non-fixed interface bonds in associated with this choice of covering for is given by .
- Consequently, an aromatic ring in hexagon k of interface permits placing a single bond in interface in position or permits placing an aromatic ring in hexagon .
4.3. Two Horizontally Overlapping Parallelograms
4.4. Two Intersecting Parallelograms
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Tang, M.; Yu, Q.; Wang, Z.; Zhang, C.; Sun, B.; Yi, Y.; Zhang, F.L. Synthesis of Polycyclic Aromatic Hydrocarbons (PAHs) via a Transient Directing Group. Org. Lett. 2018, 23, 7620–7623. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Xu, Z.; Si, W.; Oniwa, K.; Bao, M.; Yamamoto, Y.; Jin, T. Synthesis of extended polycyclic aromatic hydrocarbons by oxidative tandem spirocyclization and 1,2-aryl migration. Nat. Commun. 2017, 8, 15073. [Google Scholar] [CrossRef] [PubMed]
- Lemmens, A.K.; Rap, D.B.; Thunnissen, J.M.M.; Willemsen, B.; Rijs, A.M. Polycyclic aromatic hydrocarbon formation chemistry in a plasma jet revealed by IR-UV action spectroscopy. Nat. Commun. 2020, 11, 269. [Google Scholar] [CrossRef] [PubMed]
- Tsuge, M.; Bahou, M.; Wu, Y.J.; Allamandola, L.; Lee, Y.P. The infrared spectrum of protonated ovalene in solid para-hydrogen and its possible contribution to interstellar unidentified infrared emission. Astrophys. J. 2016, 825, 28864–28871. [Google Scholar] [CrossRef]
- Sundararajan, P.; Tsuge, M.; Baba, M.; Sakurai, H.; Lee, Y.P. Infrared spectrum of hydrogenated corannulene rim-HC20H10 isolated in solid para-hydrogen. J. Chem. Phys. 2019, 151, 044304. [Google Scholar] [CrossRef]
- Jacobson, R.S.; Korte, A.R.; Vertes, A.; Miller, J.H. The Molecular Composition of Soot. Angew. Chem. Int. Ed. 2020, 59, 4484–4490. [Google Scholar] [CrossRef]
- Zhang, L.; Yang, L.; Zhou, Q.; Zhang, X.; Xing, W.; Wei, Y.; Hu, M.; Zhao, L.; Toriba, A.; Hayakawa, K.; et al. Size distribution of particulate polycyclic aromatic hydrocarbons in fresh combustion smoke and ambient air: A review. J. Environ. Sci. 2020, 88, 370–384. [Google Scholar] [CrossRef]
- Rybolt, T.R.; Black, C.B. Polycyclic Aromatic Hydrocarbon Molecule-Surface Binding Energies in Site Specific Graphene Bilayer Nanopores: A Puzzle-ene Force Field Calculation. Graphene 2017, 6, 72–84. [Google Scholar] [CrossRef][Green Version]
- Nsibande, S.A.; Montaseri, H.; Forbes, P.B.C. Advances in the application of nanomaterial-based sensors for detection of polycyclic aromatic hydrocarbons in aquatic systems. Trends Anal. Chem. 2019, 115, 52–69. [Google Scholar] [CrossRef]
- Lammel, G. Polycyclic Aromatic Compounds in the Atmosphere—A Review Identifying Research Needs. Polycycl. Aromat. Compd. 2015, 35, 316–329. [Google Scholar] [CrossRef]
- Szulejko, J.E.; Kim, K.H.; Brown, R.J.C.; Bae, M.S. Review of progress in solvent-extraction techniques for the determination of polyaromatic hydrocarbons as airborne pollutants. Trends Anal. Chem. 2014, 61, 40–48. [Google Scholar] [CrossRef]
- Yang, X.J.; Glaser, R.; Li, A.; Zhong, J.X. The carriers of the unidentified infrared emission features: Clues from polycyclic aromatic hydrocarbons with aliphatic sidegroups. New Astron. Rev. 2017, 77, 1–22. [Google Scholar] [CrossRef]
- Boersma, C.; Bauschlicher, C.W., Jr.; Allamandola, L.J.; Ricca, A.; Peeters, E.; Tielens, A.G.G.M. The 15–20 μm PAH emission features: Probes of individual PAHs? Astron. Astrophys. 2010, 511, A32. [Google Scholar] [CrossRef]
- Karton, A. How Reliable Is DFT in Predicting Relative Energies ofPolycyclic Aromatic Hydrocarbon Isomers? Comparison of Functionals from Different Rungs of Jacob’s Ladder. J. Comput. Chem. 2017, 38, 370–382. [Google Scholar] [CrossRef] [PubMed]
- Liu, P.; Zhang, Y.; Li, Z.; Bennett, A.; Lin, H.; Sarathy, S.M.; Roberts, W.L. Computational study of polycyclic aromatic hydrocarbons growth by vinylacetylene addition. Combust. Flame 2019, 202, 276–291. [Google Scholar] [CrossRef]
- Gutman, I.; Cyvin, S.J. Introduction to the Theory of Benzenoid Hydrocarbons; Springer: Berlin, Germany, 1989. [Google Scholar]
- Randić, M. Aromaticity of Polycyclic Conjugated Hydrocarbons. Chem. Rev. 2003, 103, 3449–3606. [Google Scholar] [CrossRef]
- Zhang, F.; Zhang, H.; Liu, Y. The Clar covering polynomial of hexagonal systems. II. An application to resonance energy of condensed aromatic hydrocarbons. Chin. J. Chem. 1996, 14, 321–325. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, F. The Clar covering polynomial of hexagonal systems I. Discret. Appl. Math. 1996, 69, 147–167. [Google Scholar] [CrossRef]
- Zhang, H. The Clar covering polynomial of hexagonal systems with an application to chromatic polynomials. Discret. Math. 1997, 172, 163–173. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, F. The Clar covering polynomial of hexagonal systems III. Discret. Math. 2000, 212, 261–269. [Google Scholar] [CrossRef]
- Herndon, W.C. Thermochemical parameters for benzenoid hydrocarbons. Thermochim. Acta 1974, 8, 225–237. [Google Scholar] [CrossRef]
- Chou, C.P.; Witek, H.A. An algorithm and FORTRAN program for automatic calculations of the Zhang-Zhang polynomial of benzenoids. MATCH Commun. Math. Comput. Chem. 2012, 68, 3–30. [Google Scholar]
- Gutman, I.; Furtula, B.; Balaban, A.T. Algorithm for simultaneous calculations of Kekulé and Clar structure counts, and Clar number of benzenoid molecules. Polycycl. Aromat. Compd. 2006, 26, 17–35. [Google Scholar] [CrossRef]
- Chou, C.P.; Witek, H.A. ZZDecomposer: A Graphical Toolkit for Analyzing the Zhang-Zhang Polynomials of Benzenoid Structures. MATCH Commun. Math. Comput. Chem. 2014, 71, 741–764. [Google Scholar]
- Chou, C.P.; Witek, H.A. ZZDecomposer. 2017. Available online: https://bitbucket.org/solccp/zzdecomposer_binary/downloads/ (accessed on 30 July 2020).
- Chen, H.; Chou, C.P.; Witek, H.A. ZZDecomposer. 2019. Available online: https://bitbucket.org/peggydbc1217/zzdecomposer_hsi/downloads/ (accessed on 30 July 2020).
- Witek, H.A.; Kang, J.S. ZZ polynomials for isomers of (5,6)-fullerenes Cn with n = 20–50. Symmetry 2020, 12, 1483. [Google Scholar] [CrossRef]
- Chen, D.; Deng, H.; Guo, Q. Zhang-Zhang polynomials of a class of pericondensed benzenoid graphs. MATCH Commun. Math. Comput. Chem. 2010, 63, 401–410. [Google Scholar]
- Guo, Q.; Deng, H.; Chen, D. Zhang-Zhang polynomials of cyclo-polyphenacenes. J. Math. Chem. 2009, 46, 347–362. [Google Scholar] [CrossRef]
- Chou, C.P.; Witek, H.A. Comment on ‘Zhang-Zhang polynomials of cyclo polyphenacenes’ by Q. Guo, H. Deng, and D. Chen. J. Math. Chem. 2012, 50, 1031–1033. [Google Scholar] [CrossRef]
- Gutman, I.; Borovićanin, B. Zhang-Zhang polynomial of multiple linear hexagonal chains. Z. Naturforschung A 2006, 61, 73–77. [Google Scholar] [CrossRef]
- Chou, C.P.; Witek, H.A. Closed-Form Formulas for the Zhang-Zhang Polynomials of Benzenoid Structures: Chevrons and Generalized Chevrons. MATCH Commun. Math. Comput. Chem. 2014, 72, 105–124. [Google Scholar]
- Chou, C.P.; Witek, H.A. Zhang-Zhang polynomials of various classes of benzenoid systems. MATCH Commun. Math. Comput. Chem. 2012, 68, 31–64. [Google Scholar]
- Chou, C.P.; Witek, H.A. Determination of Zhang-Zhang Polynomials for Various Classes of Benzenoid Systems: Non-Heuristic Approach. MATCH Commun. Math. Comput. Chem. 2014, 72, 75–104. [Google Scholar]
- Chou, C.P.; Kang, J.S.; Witek, H.A. Closed-form formulas for the Zhang–Zhang polynomials of benzenoid structures: Prolate rectangles and their generalizations. Discret. Appl. Math. 2016, 198, 101–108. [Google Scholar] [CrossRef]
- Witek, H.A.; Moś, G.; Chou, C.P. Zhang-Zhang Polynomials of Regular 3- and 4-tier Benzenoid Strips. MATCH Commun. Math. Comput. Chem. 2015, 73, 427–442. [Google Scholar]
- Witek, H.A.; Langner, J.; Moś, G.; Chou, C.P. Zhang–Zhang Polynomials of Regular 5-tier Benzenoid Strips. MATCH Commun. Math. Comput. Chem. 2017, 78, 487–504. [Google Scholar]
- Chou, C.P.; Witek, H.A. Two Examples for the Application of the ZZDecomposer: Zigzag-Edge Coronoids and Fenestrenes. MATCH Commun. Math. Comput. Chem. 2015, 73, 421–426. [Google Scholar]
- Langner, J.; Witek, H.A.; Moś, G. Zhang-Zhang Polynomials of Multiple Zigzag Chains. MATCH Commun. Math. Comput. Chem. 2018, 80, 245–265. [Google Scholar]
- He, B.H.; Witek, H.A. Clar theory for hexagonal benzenoids with corner defects. MATCH Commun. Math. Comput. Chem. 2021, 85. in press. [Google Scholar]
- He, B.H.; Chou, C.P.; Langner, J.; Witek, H.A. Zhang-Zhang Polynomials of Ribbons. Discret. Appl. Math. 2020. submitted. [Google Scholar]
- Bodroža, O.; Gutman, I.; Cyvin, S.J.; Tošić, R. Number of Kekulé structures of hexagon-shaped benzenoids. J. Math. Chem. 1988, 2, 287–298. [Google Scholar] [CrossRef]
- He, B.H.; Langner, J.; Witek, H.A. Hexagonal flakes as fused parallelograms: A determinantal formula for Zhang-Zhang polynomials of the O(2,m,n) benzenoids. J. Chin. Chem. Soc. 2021. submitted. [Google Scholar]
- He, B.H.; Langner, J.; Witek, H.A. Can the John-Sachs theory of Kekulé structures be extended to enumerate Clar covers of benzenoids. MATCH Commun. Math. Comput. Chem. 2021. to be submitted. [Google Scholar]
- Zhang, H.; Ji, N.; Yao, H. Transfer-matrix Calculations of the Clar Covering Polynomial of Hexagonal Systems. MATCH Commun. Math. Comput. Chem. 2010, 63, 379–392. [Google Scholar]
- Zhang, H.; Shiu, W.C.; Sun, P.K. A relation between Clar covering polynomial and cube polynomial. MATCH Commun. Math. Comput. Chem. 2013, 70, 477–492. [Google Scholar]
- Berlič, M.; Tratnik, N.; Žigert Pleteršek, P. Equivalence of Zhang-Zhang polynomial and cube polynomial for spherical benzenoid systems. MATCH Commun. Math. Comput. Chem. 2015, 73, 443–456. [Google Scholar]
- Žigert Pleteršek, P. Equivalence of the Generalized Zhang-Zhang Polynomial and the Generalized Cube Polynomial. MATCH Commun. Math. Comput. Chem. 2018, 80, 215–226. [Google Scholar]
- Langner, J.; Witek, H.A. Equivalence between Clar Covering Polynomials of Single Zigzag Chains and Tiling Polynomials of 2×n Rectangles. Discret. Appl. Math. 2018, 243, 297–303. [Google Scholar] [CrossRef]
- Langner, J.; Witek, H.A. Interface Theory of Benzenoids. MATCH Commun. Math. Comput. Chem. 2020, 84, 143–176. [Google Scholar]
- Langner, J.; Witek, H.A. Interface Theory of Benzenoids: Basic applications. MATCH Commun. Math. Comput. Chem. 2020, 84, 177–215. [Google Scholar]
- Langner, J.; Witek, H.A. Algorithm for generating generalized resonance structures of single zigzag chains based on interface theory. J. Math. Chem. 2018, 56, 1393–1406. [Google Scholar] [CrossRef]
- Langner, J.; Witek, H.A. Connectivity Graphs for Single Zigzag Chains and their Application for Computing ZZ Polynomials. Croat. Chem. Acta 2017, 90, 391–400. [Google Scholar] [CrossRef]
- Li, G.; Pei, Y.; Wang, Y. Clar covering polynomials with only real zeros. MATCH Commun. Math. Comput. Chem. 2020, 84, 217–228. [Google Scholar]
- He, B.H.; Witek, H.A. Enumeration of Clar covers of parallelogram chains. Discret. Appl. Math. 2021. submitted. [Google Scholar]
- Cyvin, S.J.; Gutman, I. Topological properties of benzenoid hydrocarbons: Part XLIV. Obvious and concealed non-Kekuléan benzenoids. J. Mol. Stcruct. Theochem. 1987, 150, 157–169. [Google Scholar] [CrossRef]
- Cyvin, S.J.; Gutman, I. Kekulé Structures in Benzenoid Hydrocarbons; Springer: Berlin, Germany, 1988. [Google Scholar]
- Gordon, M.; Davison, W.H.T. Theory of Resonance Topology of Fully Aromatic Hydrocarbons. I. J. Chem. Phys. 1952, 20, 428–435. [Google Scholar] [CrossRef]
- Sachs, H. Perfect matchings in hexagonal systems. Combinatorica 1984, 4, 89–99. [Google Scholar] [CrossRef]
- John, P.; Rempel, J. Counting Perfect Matchings in Hexagonal Systems. In Graphs, Hypergraphs and Applications, Proceedings of the International Conference on Graph Theory, Eyba, Germany, 1–5 October 1984; Texte zur Mathematik 73; Teubner: Leipzig, Germany, 1985; pp. 72–79. [Google Scholar]
- John, P.; Sachs, H. Calculating the number of perfect matchings and Pauling’s bond orders in hexagonal systems whose inner dual is a tree. In Graphs, Hypergraphs and Applications, Proceedings of the International Conference on Graph Theory, Eyba, Germany, 1–5 October 1984; Texte zur Mathematik 73; Teubner: Leipzig, Germany, 1985; pp. 80–91. [Google Scholar]
- Gutman, I.; Cyvin, S.J. A new method for the enumeration of Kekulé structures. Chem. Phys. Lett. 1987, 136, 137–140. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Witek, H.A.; Langner, J. Clar Covers of Overlapping Benzenoids: Case of Two Identically-Oriented Parallelograms. Symmetry 2020, 12, 1599. https://doi.org/10.3390/sym12101599
Witek HA, Langner J. Clar Covers of Overlapping Benzenoids: Case of Two Identically-Oriented Parallelograms. Symmetry. 2020; 12(10):1599. https://doi.org/10.3390/sym12101599
Chicago/Turabian StyleWitek, Henryk A., and Johanna Langner. 2020. "Clar Covers of Overlapping Benzenoids: Case of Two Identically-Oriented Parallelograms" Symmetry 12, no. 10: 1599. https://doi.org/10.3390/sym12101599
APA StyleWitek, H. A., & Langner, J. (2020). Clar Covers of Overlapping Benzenoids: Case of Two Identically-Oriented Parallelograms. Symmetry, 12(10), 1599. https://doi.org/10.3390/sym12101599




