Critical Solutions of Scalarized Black Holes
Abstract
1. Introduction
2. EMs Theory
3. Limit of Cold Black Holes
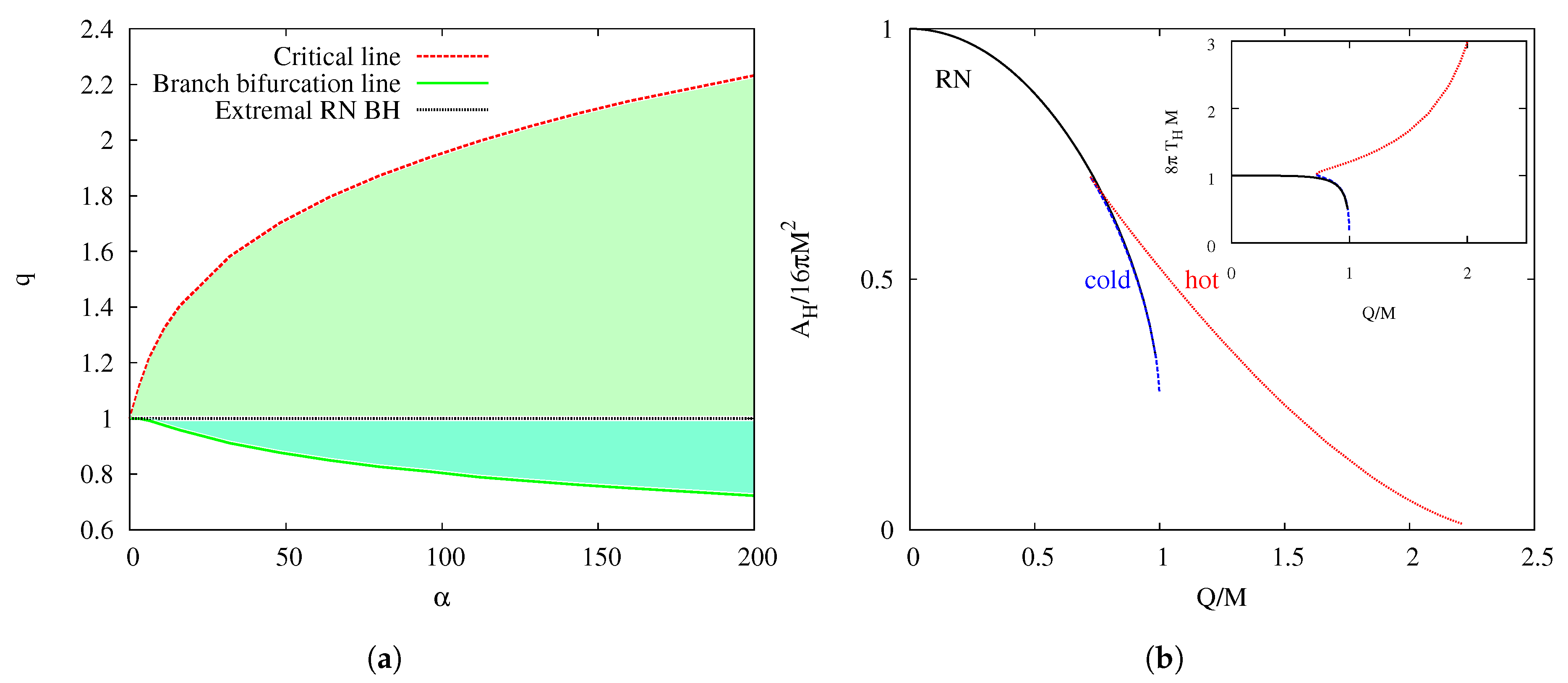
3.1. Branches of Black Holes
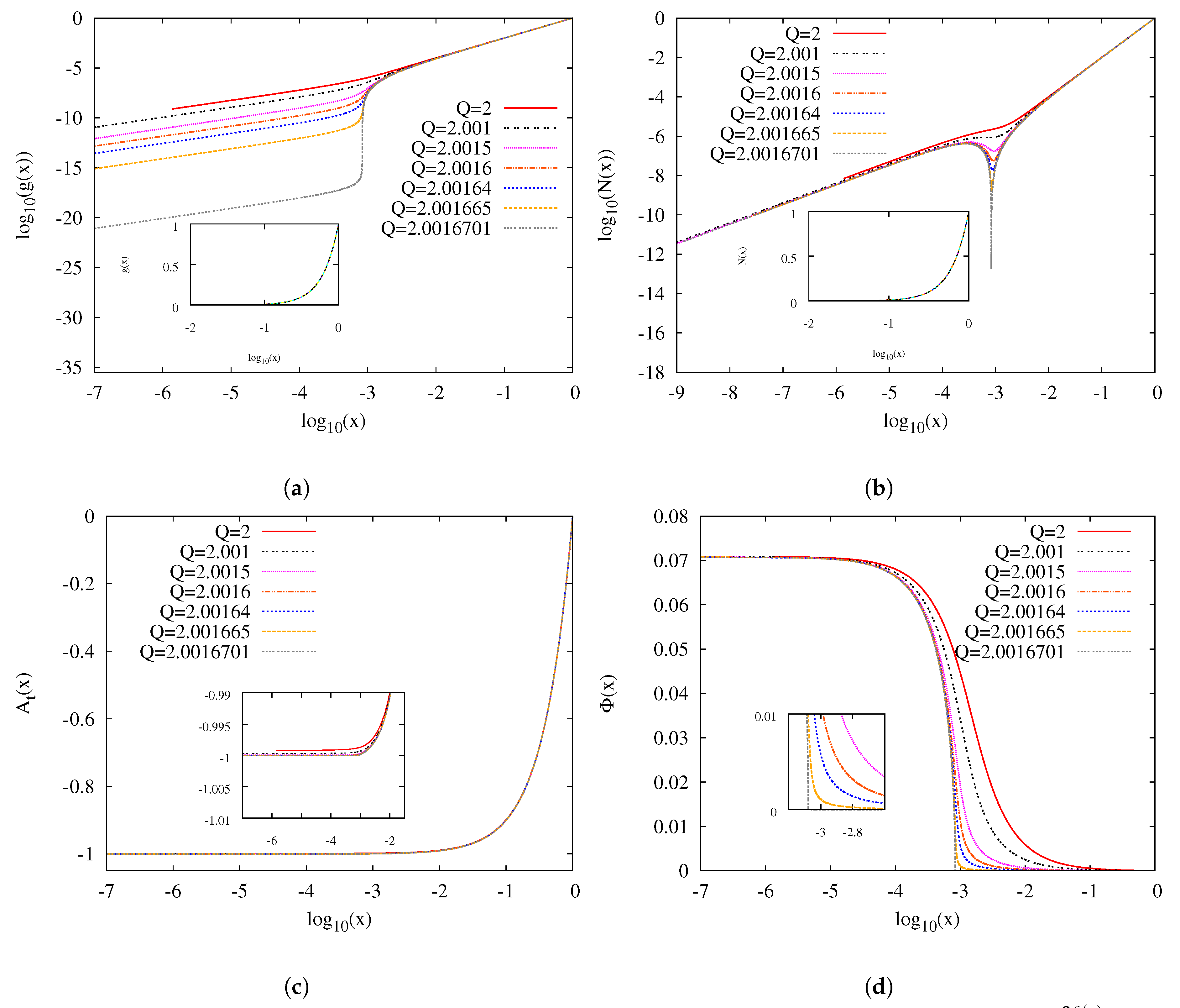
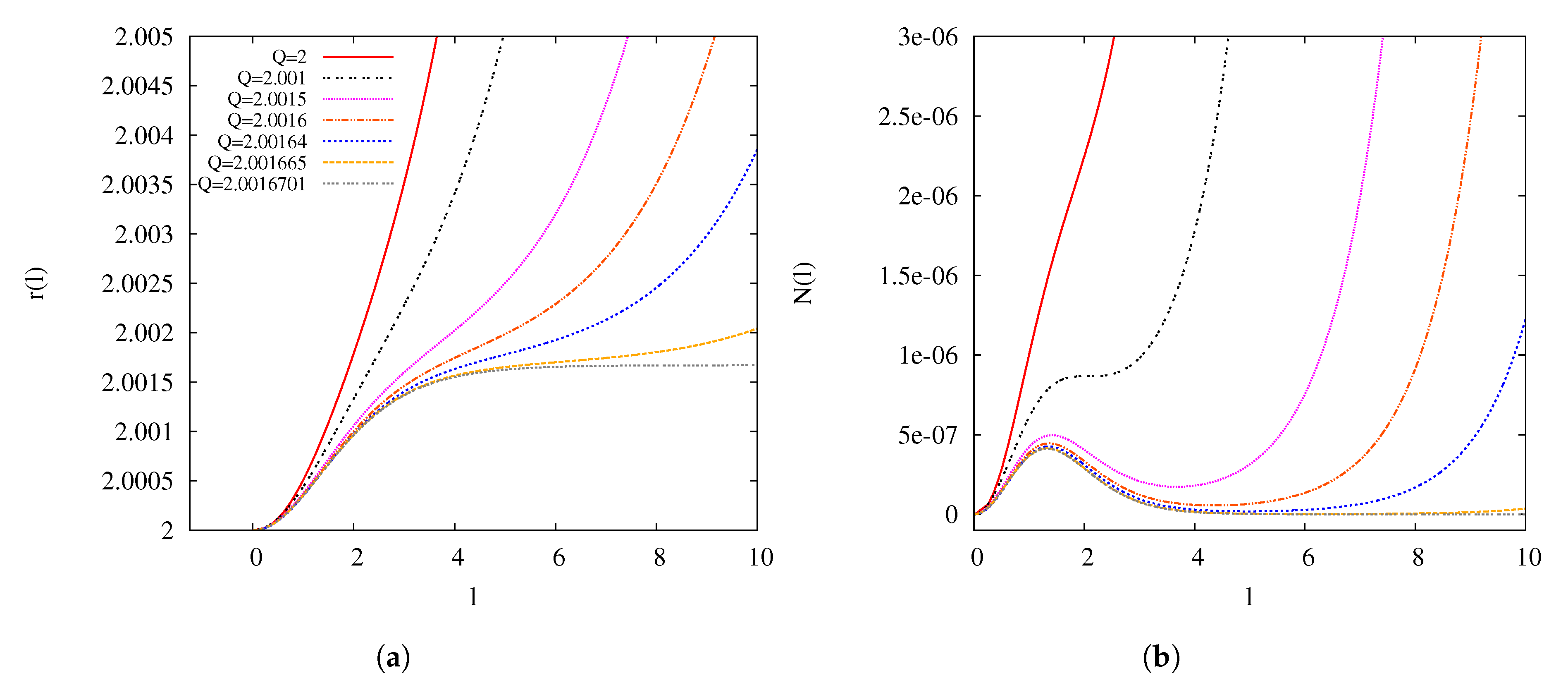
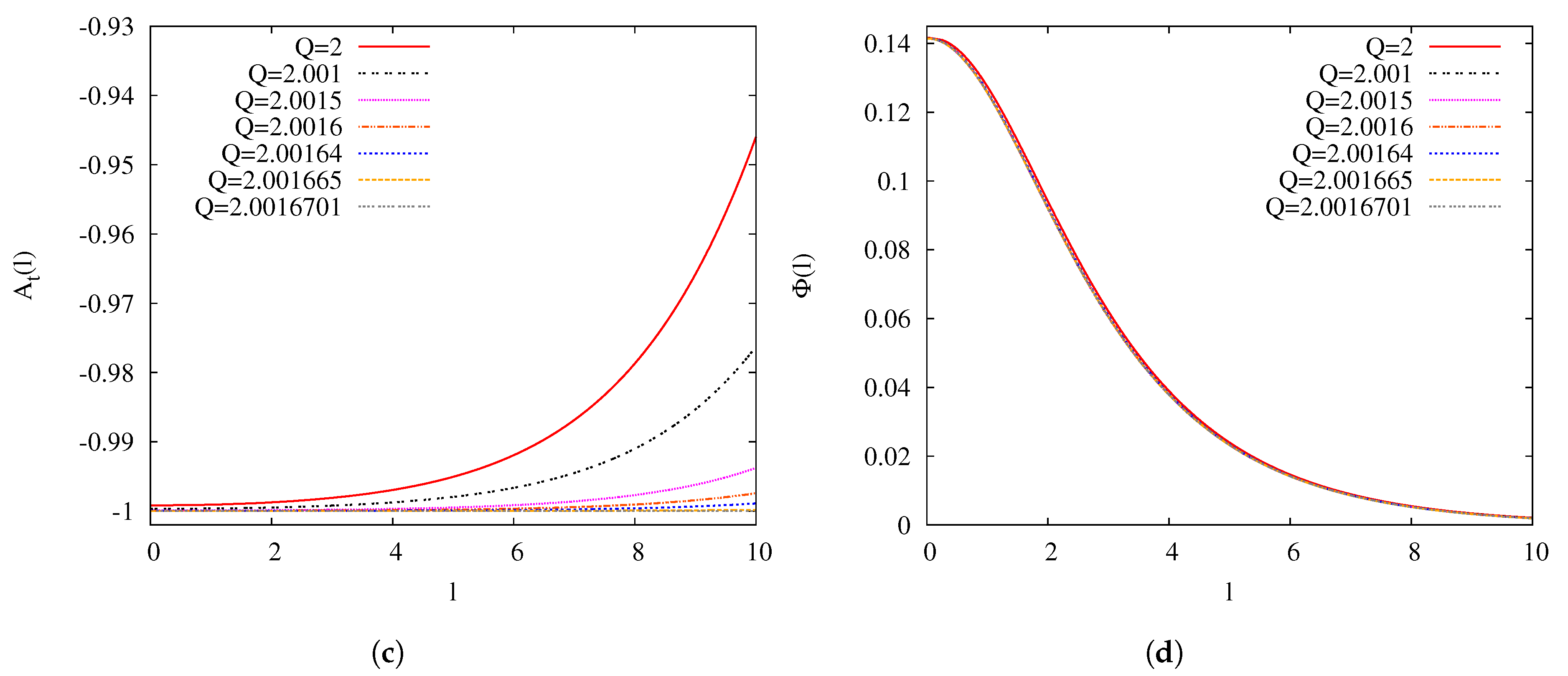
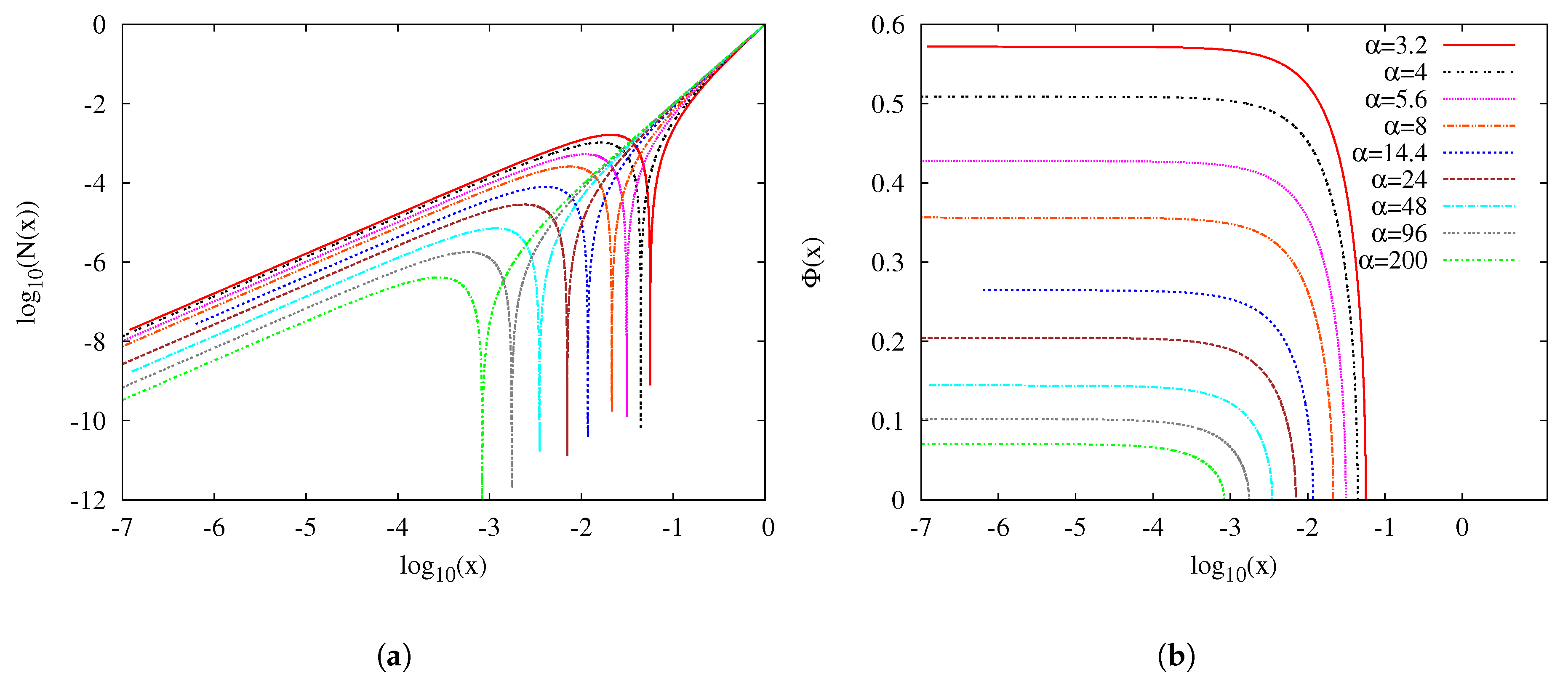
3.2. Approach to the Critical Solution for
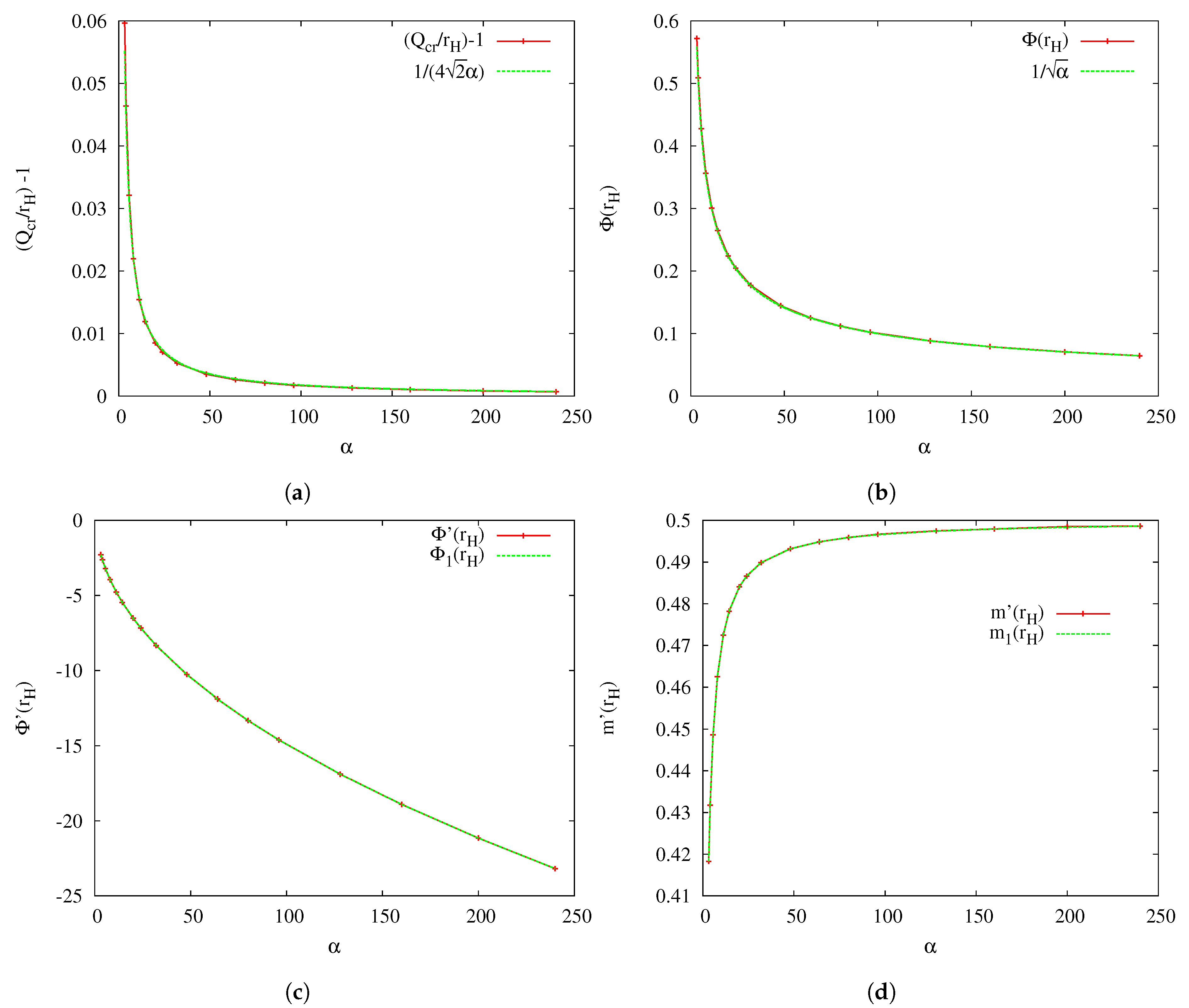
3.3. -Dependence of the Critical Solution
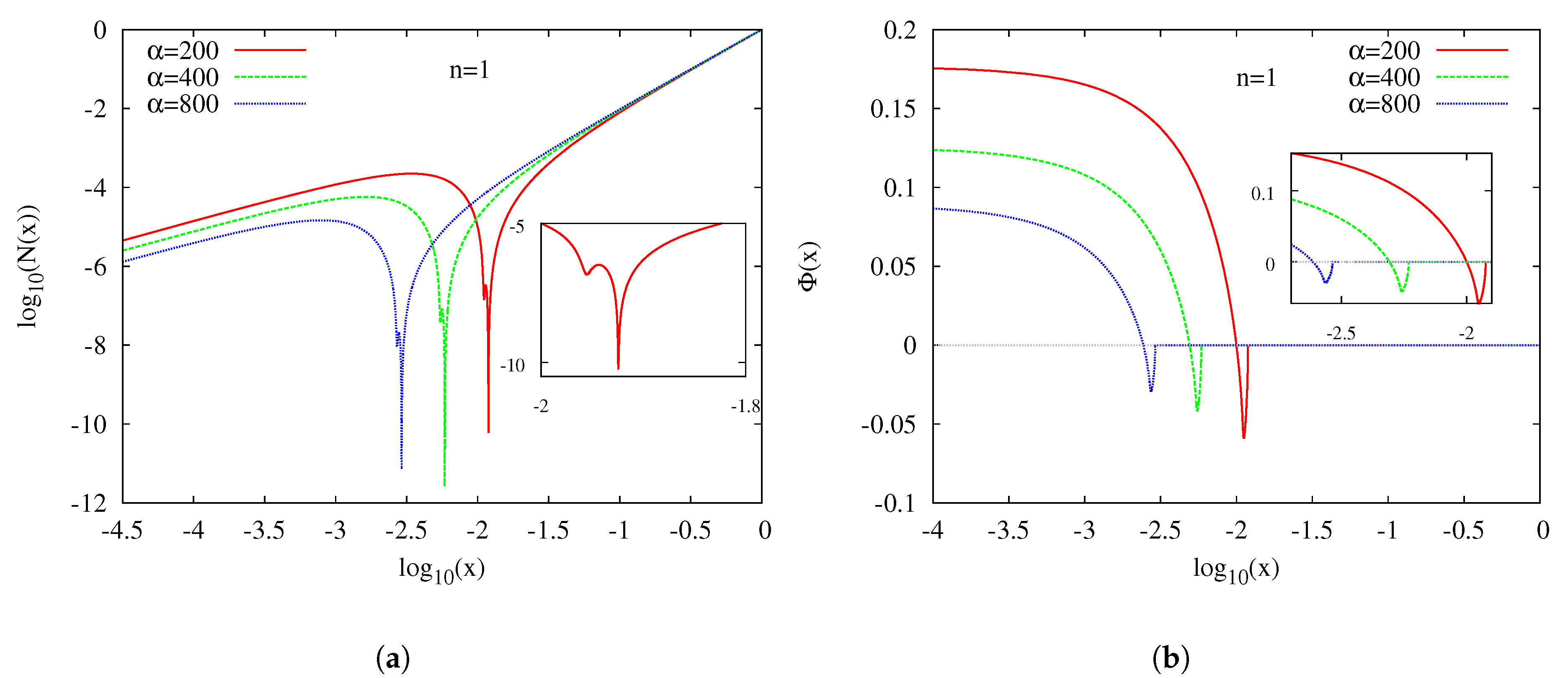
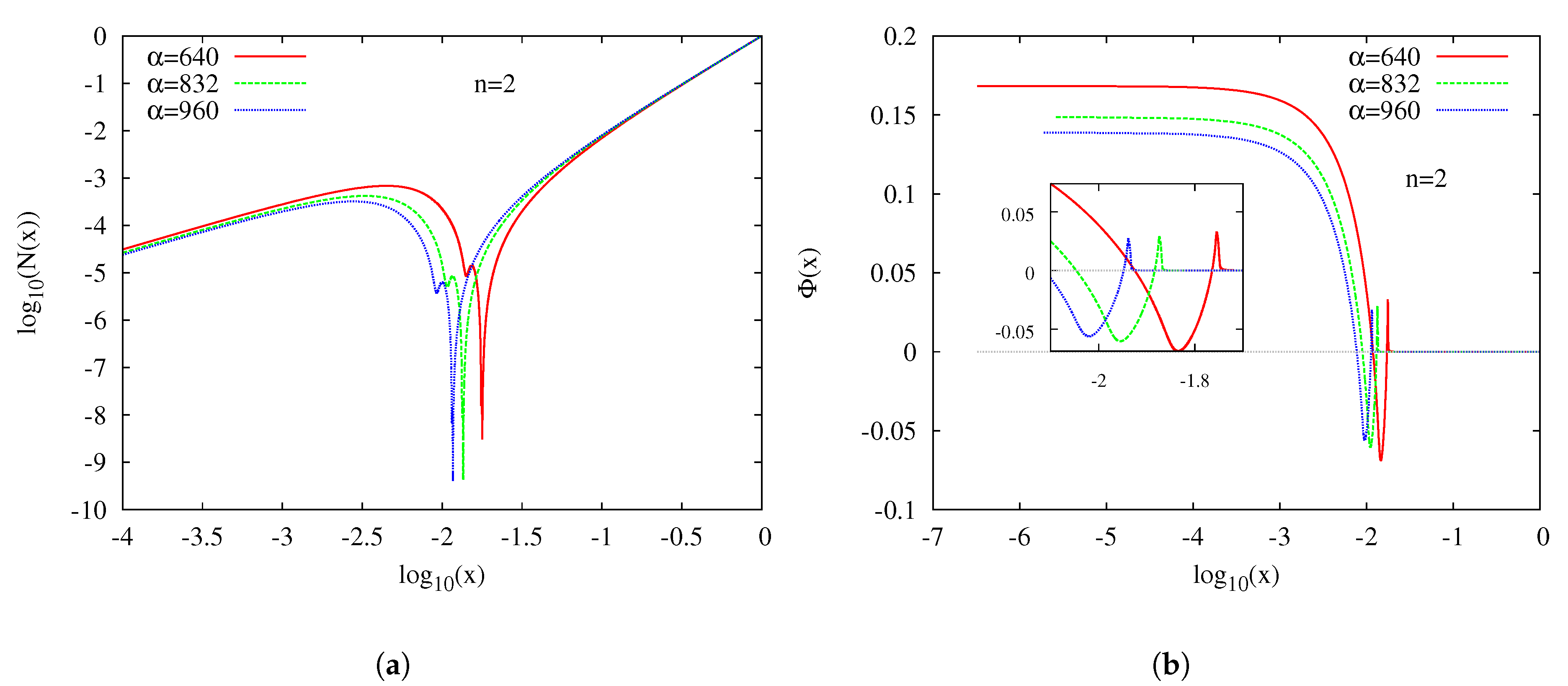
4. Excited Solutions
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Doneva, D.D.; Yazadjiev, S.S. New Gauss-Bonnet Black Holes with Curvature-Induced Scalarization in Extended Scalar-Tensor Theories. Phys. Rev. Lett. 2018, 120, 131103. [Google Scholar] [CrossRef] [PubMed]
- Antoniou, G.; Bakopoulos, A.; Kanti, P. Evasion of No-Hair Theorems and Novel Black-Hole Solutions in Gauss-Bonnet Theories. Phys. Rev. Lett. 2018, 120, 131102. [Google Scholar] [CrossRef] [PubMed]
- Silva, H.O.; Sakstein, J.; Gualtieri, L.; Sotiriou, T.P.; Berti, E. Spontaneous scalarization of black holes and compact stars from a Gauss-Bonnet coupling. Phys. Rev. Lett. 2018, 120, 131104. [Google Scholar] [CrossRef] [PubMed]
- Antoniou, G.; Bakopoulos, A.; Kanti, P. Black-Hole Solutions with Scalar Hair in Einstein-Scalar- Gauss-Bonnet Theories. Phys. Rev. D 2018, 97, 084037. [Google Scholar] [CrossRef]
- Blázquez-Salcedo, J.L.; Doneva, D.D.; Kunz, J.; Yazadjiev, S.S. Radial perturbations of the scalarized Einstein-Gauss-Bonnet black holes. Phys. Rev. D 2018, 98, 084011. [Google Scholar] [CrossRef]
- Doneva, D.D.; Kiorpelidi, S.; Nedkova, P.G.; Papantonopoulos, E.; Yazadjiev, S.S. Charged Gauss-Bonnet black holes with curvature induced scalarization in the extended scalar-tensor theories. Phys. Rev. D 2018, 98, 104056. [Google Scholar] [CrossRef]
- Minamitsuji, M.; Ikeda, T. Scalarized black holes in the presence of the coupling to Gauss-Bonnet gravity. Phys. Rev. D 2019, 99, 044017. [Google Scholar] [CrossRef]
- Silva, H.O.; Macedo, C.F.; Sotiriou, T.P.; Gualtieri, L.; Sakstein, J.; Berti, E. Stability of scalarized black hole solutions in scalar-Gauss-Bonnet gravity. Phys. Rev. D 2019, 99, 064011. [Google Scholar] [CrossRef]
- Brihaye, Y.; Ducobu, L. Hairy black holes, boson stars and non-minimal coupling to curvature invariants. Phys. Lett. B 2019, 795, 135–143. [Google Scholar] [CrossRef]
- Doneva, D.D.; Staykov, K.V.; Yazadjiev, S.S. Gauss-Bonnet black holes with a massive scalar field. Phys. Rev. D 2019, 99, 104045. [Google Scholar] [CrossRef]
- Myung, Y.S.; Zou, D.C. Black holes in Gauss–Bonnet and Chern–Simons-scalar theory. Int. J. Mod. Phys. D 2019, 28, 1950114. [Google Scholar] [CrossRef]
- Cunha, P.V.; Herdeiro, C.A.; Radu, E. Spontaneously Scalarized Kerr Black Holes in Extended Scalar-Tensor- Gauss-Bonnet Gravity. Phys. Rev. Lett. 2019, 123, 011101. [Google Scholar] [CrossRef] [PubMed]
- Macedo, C.F.; Sakstein, J.; Berti, E.; Gualtieri, L.; Silva, H.O.; Sotiriou, T.P. Self-interactions and Spontaneous Black Hole Scalarization. Phys. Rev. D 2019, 99, 104041. [Google Scholar] [CrossRef]
- Hod, S. Spontaneous scalarization of Gauss-Bonnet black holes: Analytic treatment in the linearized regime. Phys. Rev. D 2019, 100, 064039. [Google Scholar] [CrossRef]
- Collodel, L.G.; Kleihaus, B.; Kunz, J.; Berti, E. Spinning and excited black holes in Einstein-scalar- Gauss–Bonnet theory. Class. Quantum Gravity 2020, 37, 075018. [Google Scholar] [CrossRef]
- Bakopoulos, A.; Kanti, P.; Pappas, N. Large and ultracompact Gauss-Bonnet black holes with a self-interacting scalar field. Phys. Rev. D 2020, 101, 084059. [Google Scholar] [CrossRef]
- Blázquez-Salcedo, J.L.; Doneva, D.D.; Kahlen, S.; Kunz, J.; Nedkova, P.; Yazadjiev, S.S. Axial perturbations of the scalarized Einstein-Gauss-Bonnet black holes. Phys. Rev. D 2020, 101, 104006. [Google Scholar] [CrossRef]
- Blázquez-Salcedo, J.L.; Doneva, D.D.; Kahlen, S.; Kunz, J.; Nedkova, P.; Yazadjiev, S.S. Polar quasinormal modes of the scalarized Einstein-Gauss-Bonnet black holes. arXiv 2020, arXiv:2006.06006. [Google Scholar] [CrossRef]
- Dima, A.; Barausse, E.; Franchini, N.; Sotiriou, T.P. Spin-induced black hole spontaneous scalarization. arXiv 2020, arXiv:2006.03095. [Google Scholar]
- Doneva, D.D.; Collodel, L.G.; Krüger, C.J.; Yazadjiev, S.S. Black hole scalarization induced by the spin – 2+1 time evolution. Phys. Rev. D 2020, 102, 104027. [Google Scholar] [CrossRef]
- Berti, E.; Collodel, L.G.; Kleihaus, B.; Kunz, J. Spin-induced black-hole scalarization in Einstein-scalar-Gauss- Bonnet theory. arXiv 2020, arXiv:2009.03905. [Google Scholar]
- Herdeiro, C.A.; Radu, E.; Silva, H.O.; Sotiriou, T.P.; Yunes, N. Spin-induced scalarized black holes. arXiv 2020, arXiv:2009.03904. [Google Scholar]
- Herdeiro, C.A.; Radu, E.; Sanchis-Gual, N.; Font, J.A. Spontaneous Scalarization of Charged Black Holes. Phys. Rev. Lett. 2018, 121, 101102. [Google Scholar] [CrossRef] [PubMed]
- Myung, Y.S.; Zou, D.C. Instability of Reissner–Nordström black hole in Einstein–Maxwell–scalar theory. Eur. Phys. J. C 2019, 79, 273. [Google Scholar] [CrossRef]
- Boskovic, M.; Brito, R.; Cardoso, V.; Ikeda, T.; Witek, H. Axionic instabilities and new black hole solutions. Phys. Rev. D 2019, 99, 035006. [Google Scholar] [CrossRef]
- Myung, Y.S.; Zou, D.C. Quasinormal modes of scalarized black holes in the Einstein–Maxwell–Scalar theory. Phys. Lett. B 2019, 790, 400–407. [Google Scholar] [CrossRef]
- Fernandes, P.G.; Herdeiro, C.A.; Pombo, A.M.; Radu, E.; Sanchis-Gual, N. Spontaneous Scalarisation of Charged Black Holes: Coupling Dependence and Dynamical Features. Class. Quantum Gravity 2020, 36, 134002, Erratum: Class. Quantum Gravity 2020, 37, 049501. [Google Scholar] [CrossRef]
- Brihaye, Y.; Hartmann, B. Spontaneous scalarization of charged black holes at the approach to extremality. Phys. Lett. B 2019, 792, 244–250. [Google Scholar] [CrossRef]
- Herdeiro, C.A.; Oliveira, J.M. On the inexistence of solitons in Einstein–Maxwell–scalar models. Class. Quantum Gravity 2019, 36, 105015. [Google Scholar] [CrossRef]
- Myung, Y.S.; Zou, D.C. Stability of scalarized charged black holes in the Einstein–Maxwell–scalar theory. Eur. Phys. J. C 2019, 79, 641. [Google Scholar] [CrossRef]
- Astefanesei, D.; Herdeiro, C.; Pombo, A.; Radu, E. Einstein–Maxwell–scalar black holes: Classes of solutions, dyons and extremality. JHEP 2019, 10, 078. [Google Scholar] [CrossRef]
- Konoplya, R.; Zhidenko, A. Analytical representation for metrics of scalarized Einstein-Maxwell black holes and their shadows. Phys. Rev. D 2019, 100, 044015. [Google Scholar] [CrossRef]
- Fernandes, P.G.; Herdeiro, C.A.; Pombo, A.M.; Radu, E.; Sanchis-Gual, N. Charged black holes with axionic-type couplings: Classes of solutions and dynamical scalarization. Phys. Rev. D 2019, 100, 084045. [Google Scholar] [CrossRef]
- Herdeiro, C.A.; Oliveira, J.M. On the inexistence of self-gravitating solitons in generalised axion electrodynamics. Phys. Lett. B 2020, 800, 135076. [Google Scholar] [CrossRef]
- Zou, D.C.; Myung, Y.S. Scalarized charged black holes with scalar mass term. Phys. Rev. D 2019, 100, 124055. [Google Scholar] [CrossRef]
- Brihaye, Y.; Herdeiro, C.; Radu, E. Black Hole Spontaneous Scalarisation with a Positive Cosmological Constant. Phys. Lett. B 2020, 802, 135269. [Google Scholar] [CrossRef]
- Astefanesei, D.; Blázquez-Salcedo, J.L.; Herdeiro, C.; Radu, E.; Sanchis-Gual, N. Dynamically and thermodynamically stable black holes in Einstein-Maxwell-dilaton gravity. JHEP 2020, 7, 063. [Google Scholar] [CrossRef]
- Blázquez-Salcedo, J.L.; Herdeiro, C.A.; Kunz, J.; Pombo, A.M.; Radu, E. Einstein–Maxwell–scalar black holes: The hot, the cold and the bald. Phys. Lett. B 2020, 806, 135493. [Google Scholar] [CrossRef]
- Blázquez-Salcedo, J.L.; Herdeiro, C.A.; Kahlen, S.; Kunz, J.; Pombo, A.M.; Radu, E. Quasinormal modes of hot, cold and bald Einstein–Maxwell–scalar black holes. arXiv 2020, arXiv:2008.11744. [Google Scholar]
- Astefanesei, D.; Blázquez-Salcedo, J.L.; Gómez, F.; Rojas, R. Thermodynamically stable asymptotically flat hairy black holes with a dilaton potential: The general case. arXiv 2020, arXiv:2009.01854. [Google Scholar] [CrossRef]
- Gibbons, G.; Maeda, K.i. Black Holes and Membranes in Higher Dimensional Theories with Dilaton Fields. Nucl. Phys. B 1988, 298, 741–775. [Google Scholar] [CrossRef]
- Kanti, P.; Mavromatos, N.; Rizos, J.; Tamvakis, K.; Winstanley, E. Dilatonic black holes in higher curvature string gravity. Phys. Rev. D 1996, 54, 5049–5058. [Google Scholar] [CrossRef] [PubMed]
- Volkov, M.S.; Gal’tsov, D.V. Gravitating nonAbelian solitons and black holes with Yang-Mills fields. Phys. Rep. 1999, 319, 1–83. [Google Scholar] [CrossRef]
- Gal’tsov, D. Gravitating lumps. In Proceedings of the 16th International Conference on General Relativity and Gravitation (GR16), Durban, South Africa, 15–21 July 2001; pp. 142–161. [Google Scholar] [CrossRef]
- Kleihaus, B.; Kunz, J.; Navarro-Lerida, F. Rotating black holes with non-Abelian hair. Class. Quantum Gravity 2016, 33, 234002. [Google Scholar] [CrossRef]
- Lee, K.M.; Nair, V.; Weinberg, E.J. Black holes in magnetic monopoles. Phys. Rev. D 1992, 45, 2751–2761. [Google Scholar] [CrossRef] [PubMed]
- Breitenlohner, P.; Forgacs, P.; Maison, D. Gravitating monopole solutions. Nucl. Phys. B 1992, 383, 357–376. [Google Scholar] [CrossRef]
- Breitenlohner, P.; Forgacs, P.; Maison, D. Gravitating monopole solutions. 2. Nucl. Phys. B 1995, 442, 126–156. [Google Scholar] [CrossRef]
- Ridgway, S.; Weinberg, E.J. Instabilities of magnetically charged black holes. Phys. Rev. D 1995, 51, 638–646. [Google Scholar] [CrossRef]
- Brihaye, Y.; Hartmann, B.; Kunz, J. Gravitating dyons and dyonic black holes. Phys. Lett. B 1998, 441, 77–82. [Google Scholar] [CrossRef]
- Hartmann, B.; Kleihaus, B.; Kunz, J. Gravitationally bound monopoles. Phys. Rev. Lett. 2001, 86, 1422–1425. [Google Scholar] [CrossRef]
- Hartmann, B.; Kleihaus, B.; Kunz, J. Axially symmetric monopoles and black holes in Einstein-Yang- Mills-Higgs theory. Phys. Rev. D 2002, 65, 024027. [Google Scholar] [CrossRef]
- Ascher, U.; Christiansen, J.; Russell, R. A Collocation Solver for Mixed Order Systems of Boundary Value Problems. Math. Comput. 1979, 33, 659–679. [Google Scholar] [CrossRef]
- Brihaye, Y.; Hartmann, B. Strong gravity effects of charged Q-clouds and inflating black holes. arXiv 2020, arXiv:2009.08293. [Google Scholar]
- Brihaye, Y.; Cônsole, F.; Hartmann, B. Inflation inside non-topological defects and scalar black holes. arXiv 2020, arXiv:2010.15625. [Google Scholar]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Blázquez-Salcedo, J.L.; Kahlen, S.; Kunz, J. Critical Solutions of Scalarized Black Holes. Symmetry 2020, 12, 2057. https://doi.org/10.3390/sym12122057
Blázquez-Salcedo JL, Kahlen S, Kunz J. Critical Solutions of Scalarized Black Holes. Symmetry. 2020; 12(12):2057. https://doi.org/10.3390/sym12122057
Chicago/Turabian StyleBlázquez-Salcedo, Jose Luis, Sarah Kahlen, and Jutta Kunz. 2020. "Critical Solutions of Scalarized Black Holes" Symmetry 12, no. 12: 2057. https://doi.org/10.3390/sym12122057
APA StyleBlázquez-Salcedo, J. L., Kahlen, S., & Kunz, J. (2020). Critical Solutions of Scalarized Black Holes. Symmetry, 12(12), 2057. https://doi.org/10.3390/sym12122057




