Study on the Effects of the Wear-Rings Clearance on the Solid-Liquid Two-Phase Flow Characteristics of Centrifugal Pumps
Abstract
:1. Introduction
2. Method
2.1. Calculation Model
2.2. Meshing and Boundary Conditions
2.3. Governing Equation
2.4. Wear Model
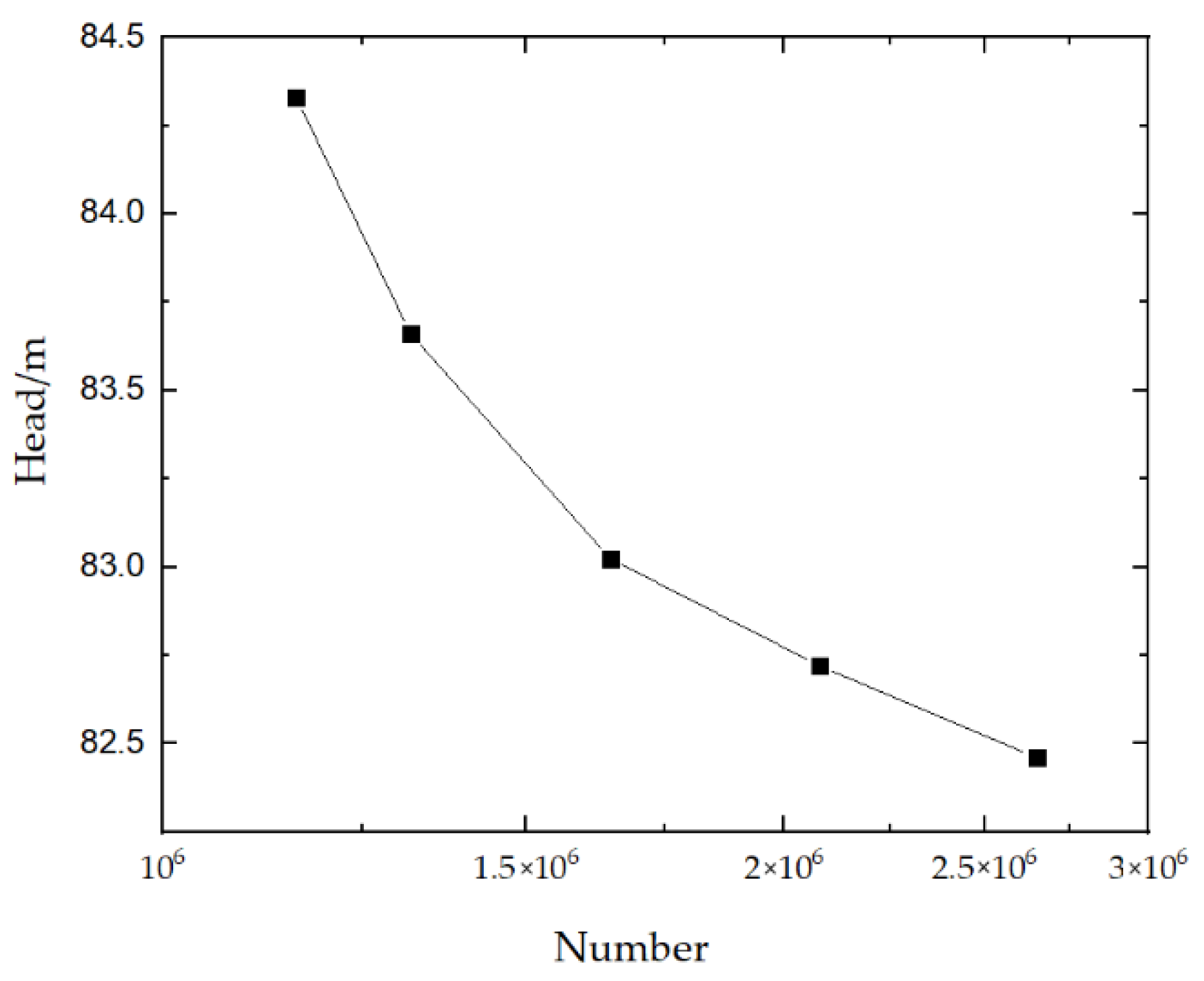
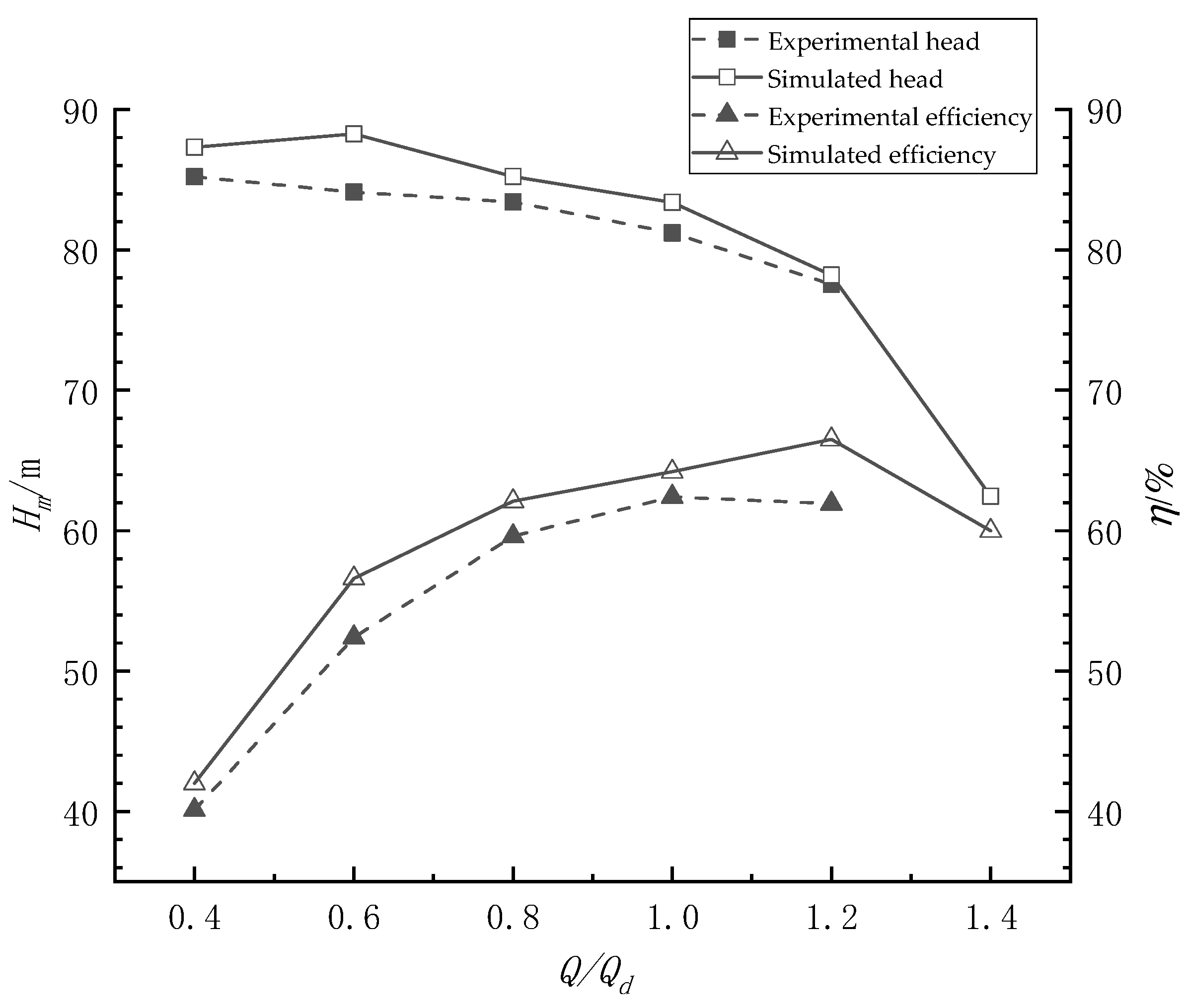
2.5. Verification of a Numerical Simulation Method
3. Results and Discussions
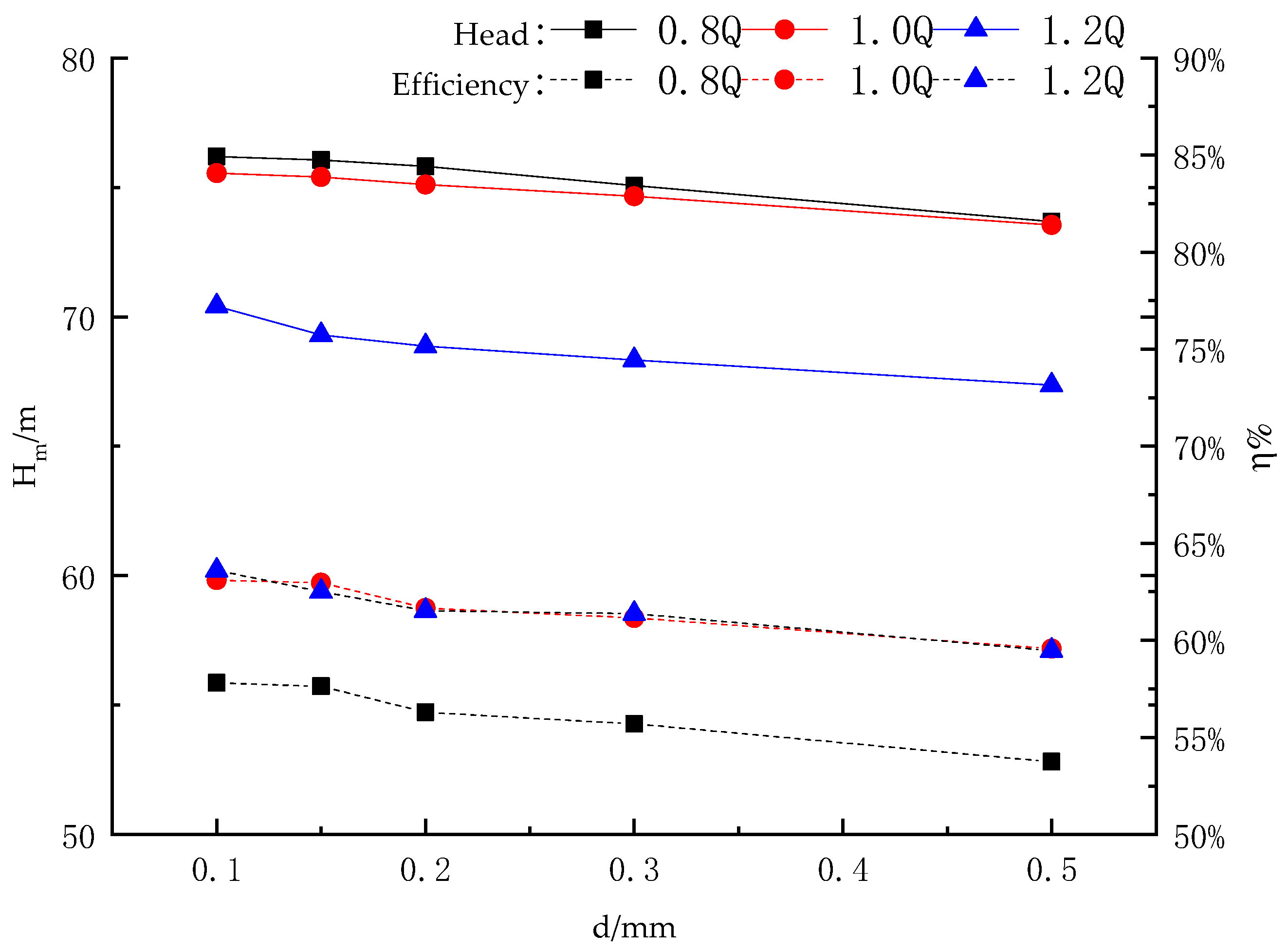
3.1. Effects of Wear-Rings Clearance on External Characteristics of Centrifugal Pump
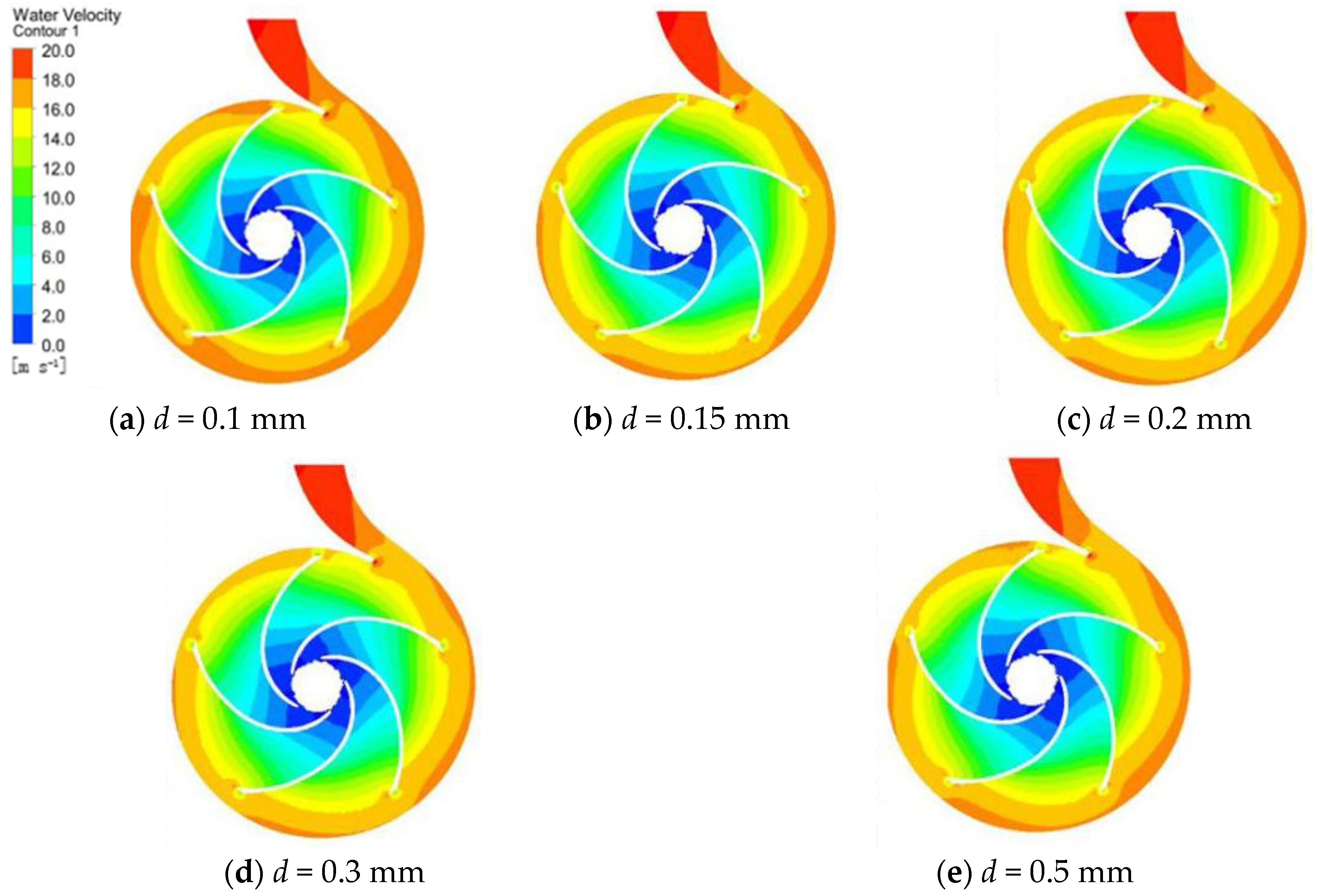
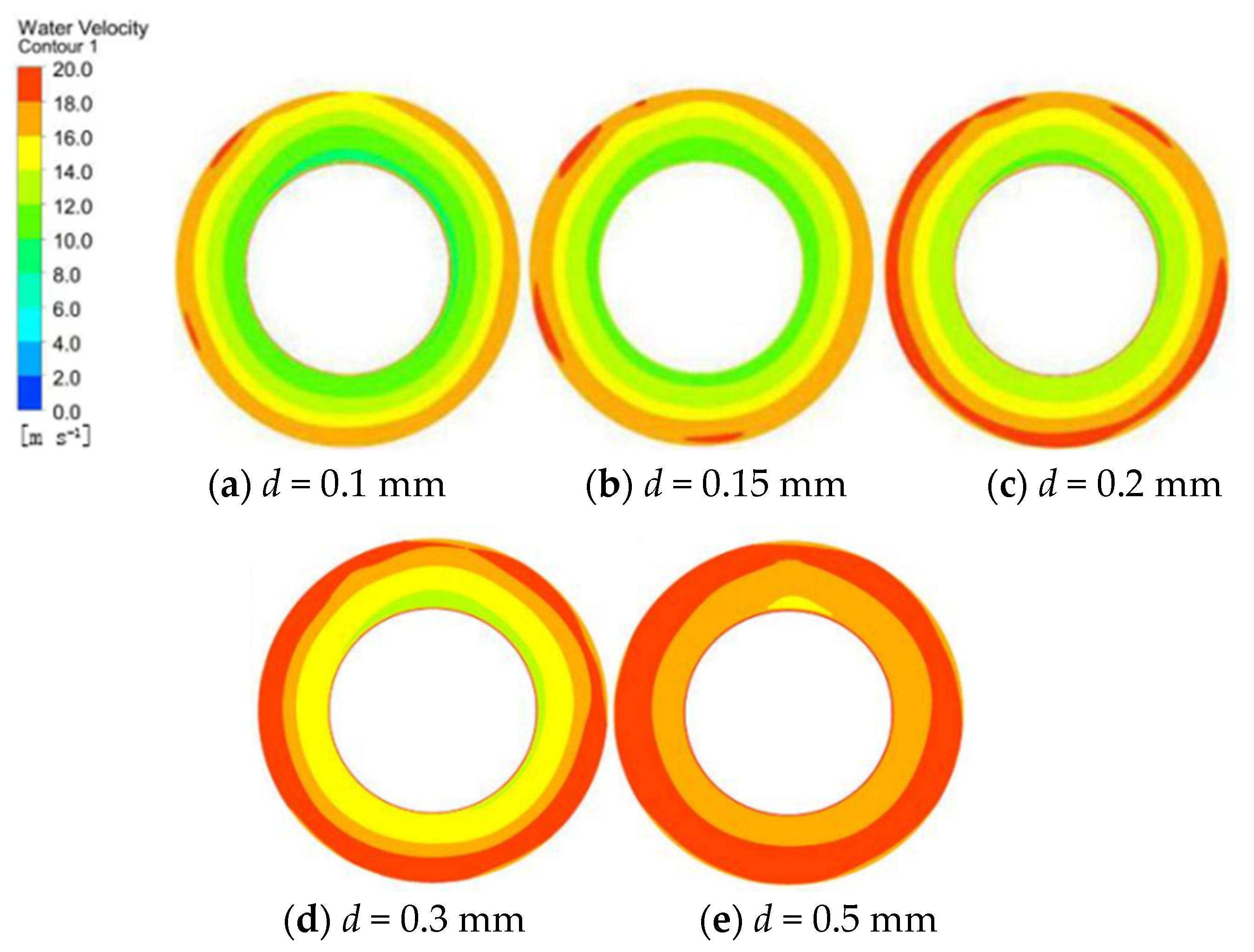
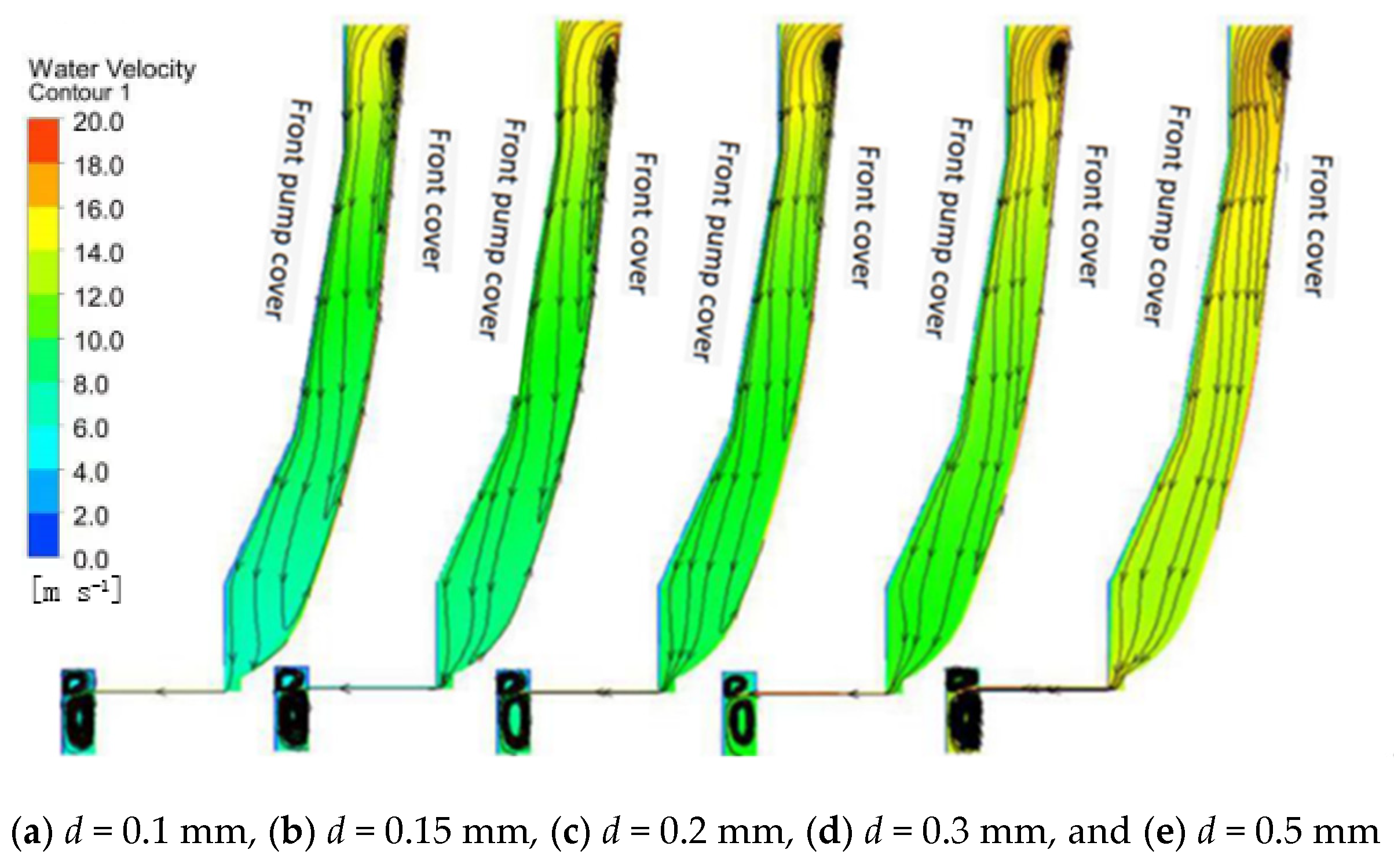
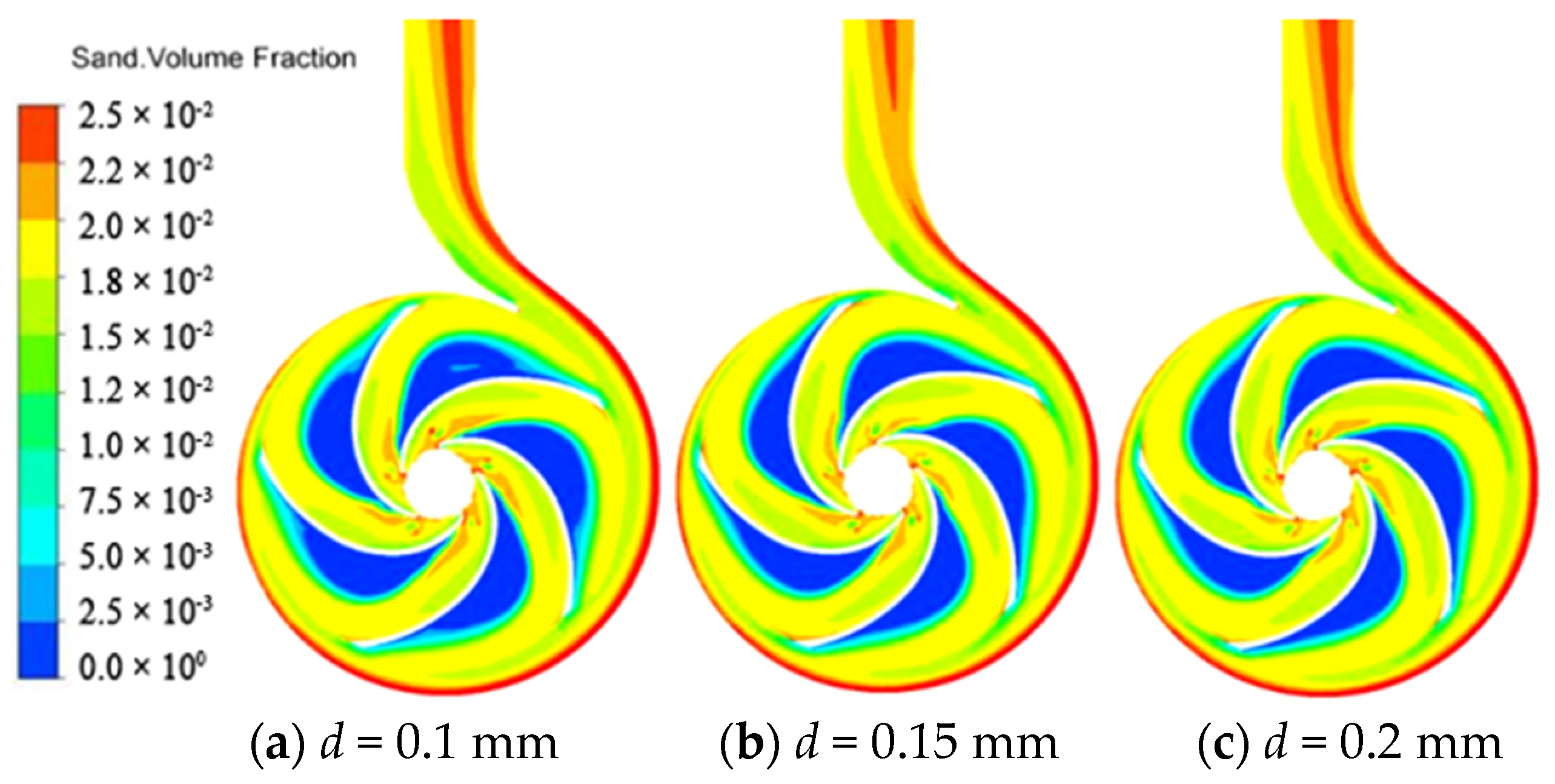
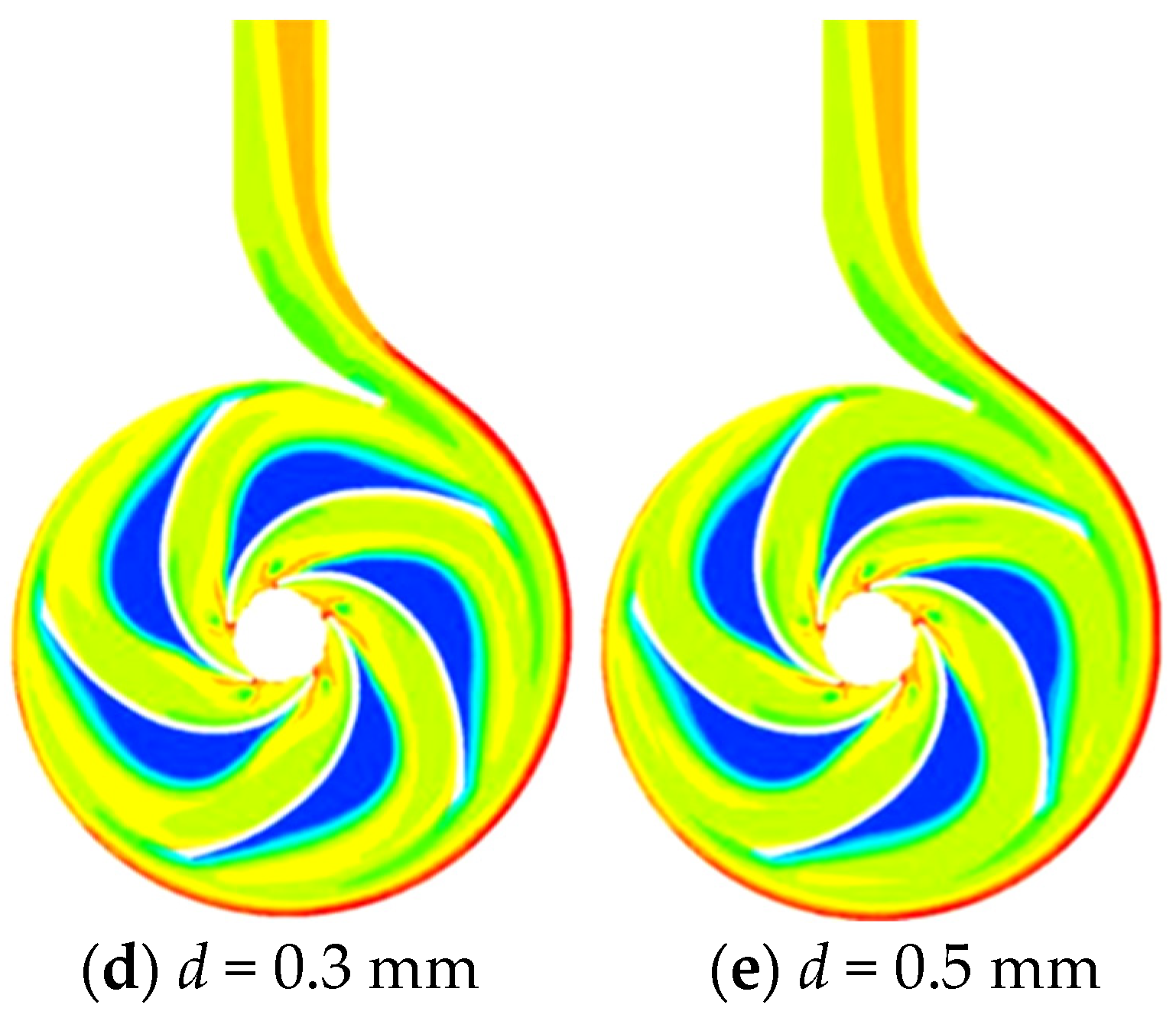
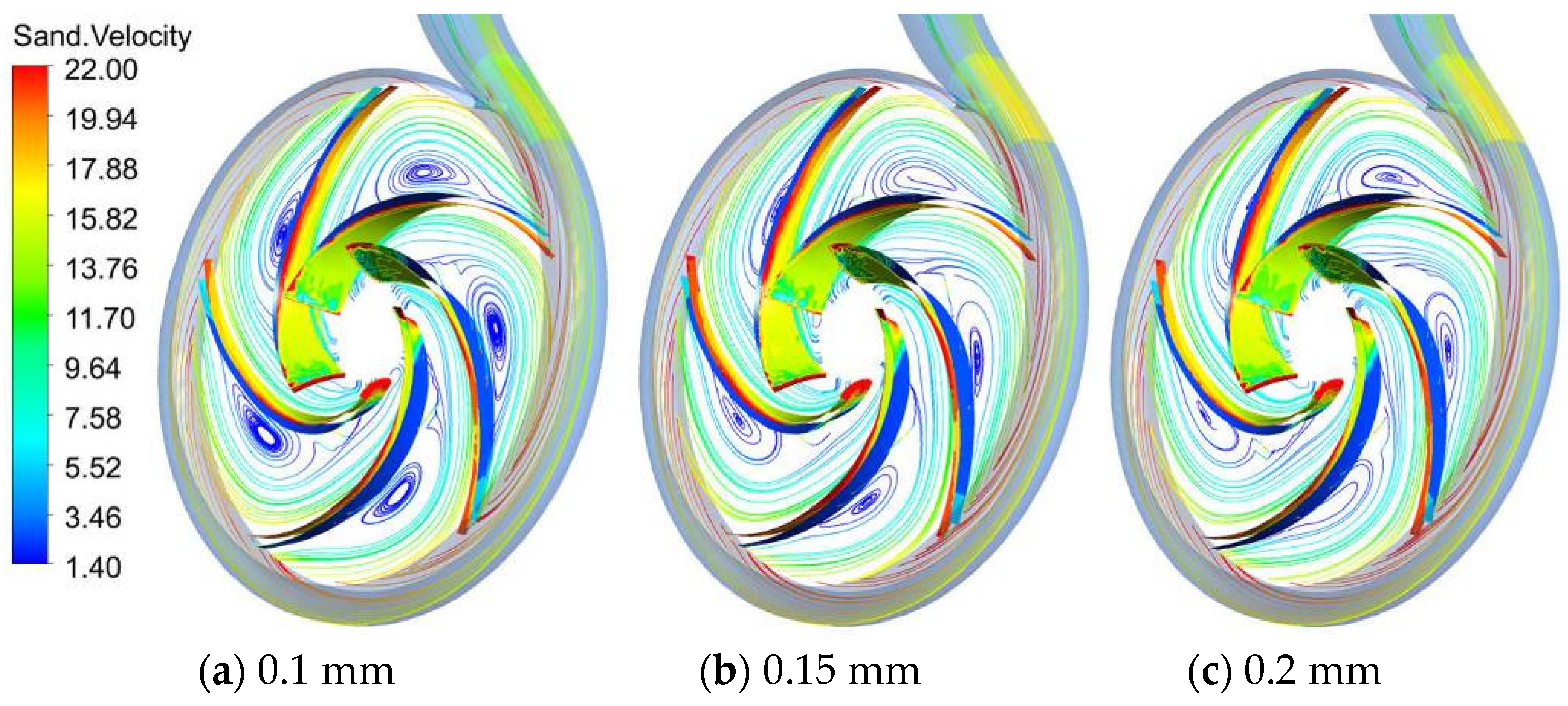
3.2. Unsteady Clearance Flow Analysis
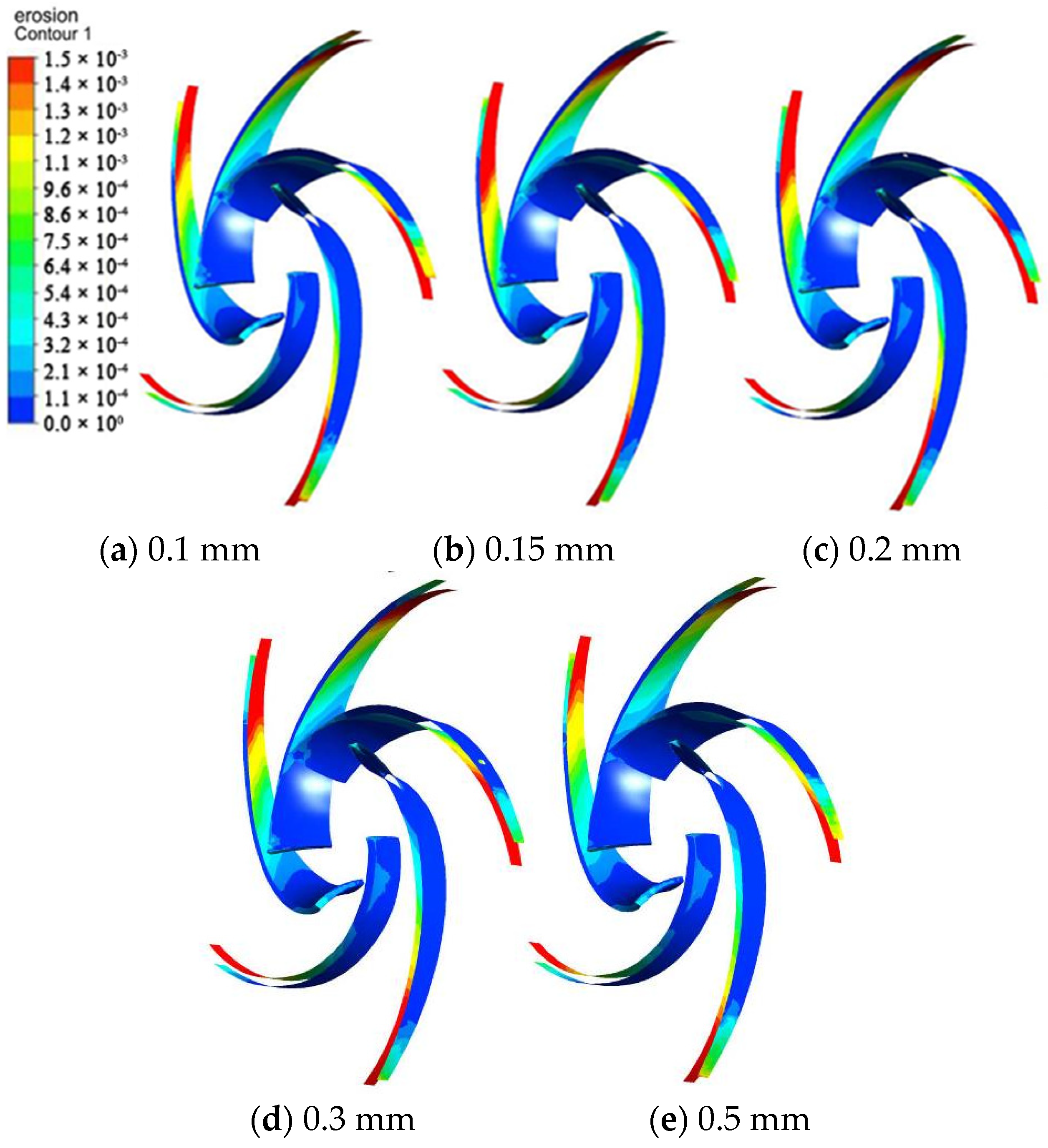
3.3. Wear Characteristics Analysis of the Impeller with a Different Clearance
3.4. Wear Characteristics’ Analysis of the Volute Wall under a Different Clearance
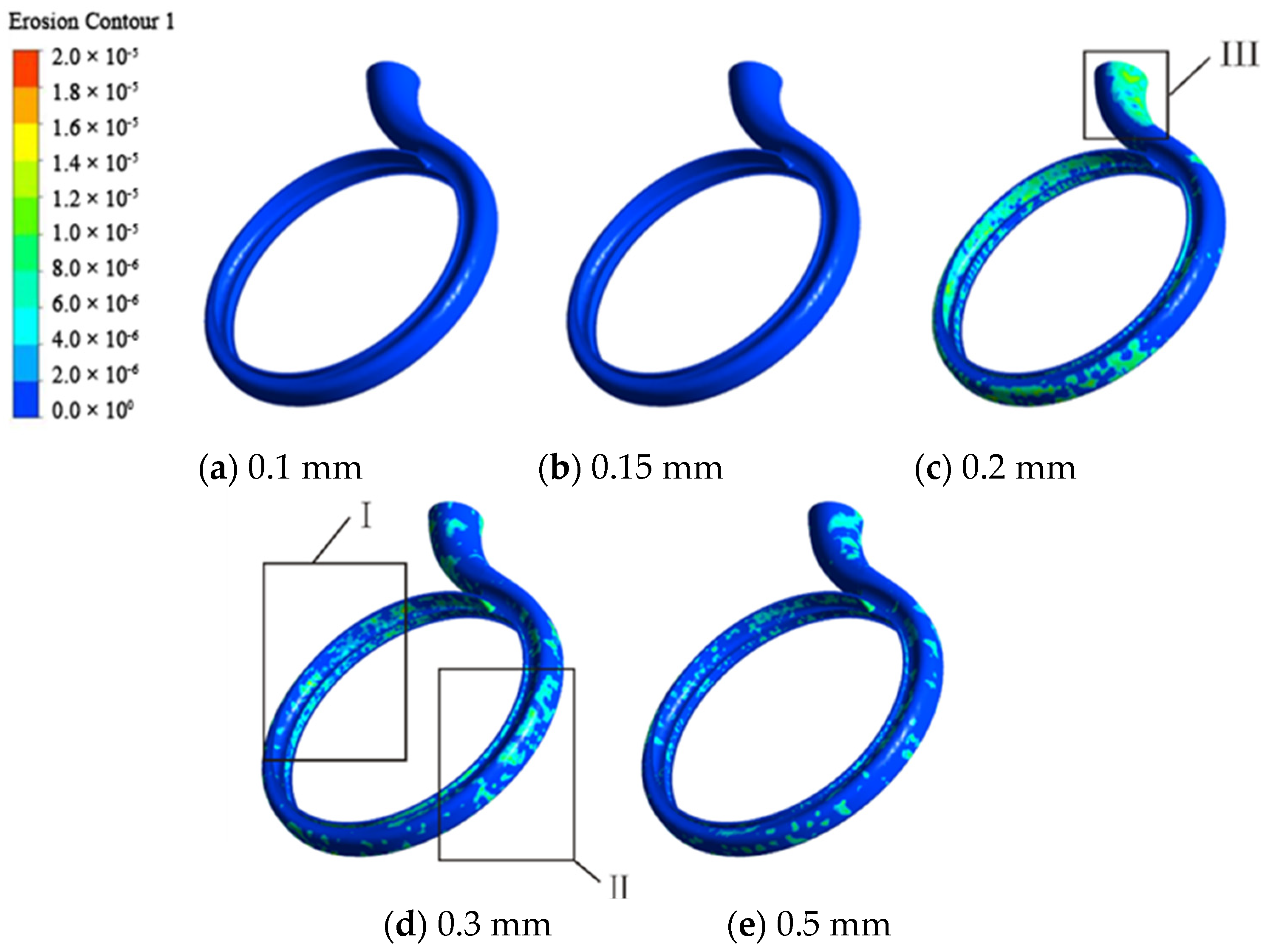
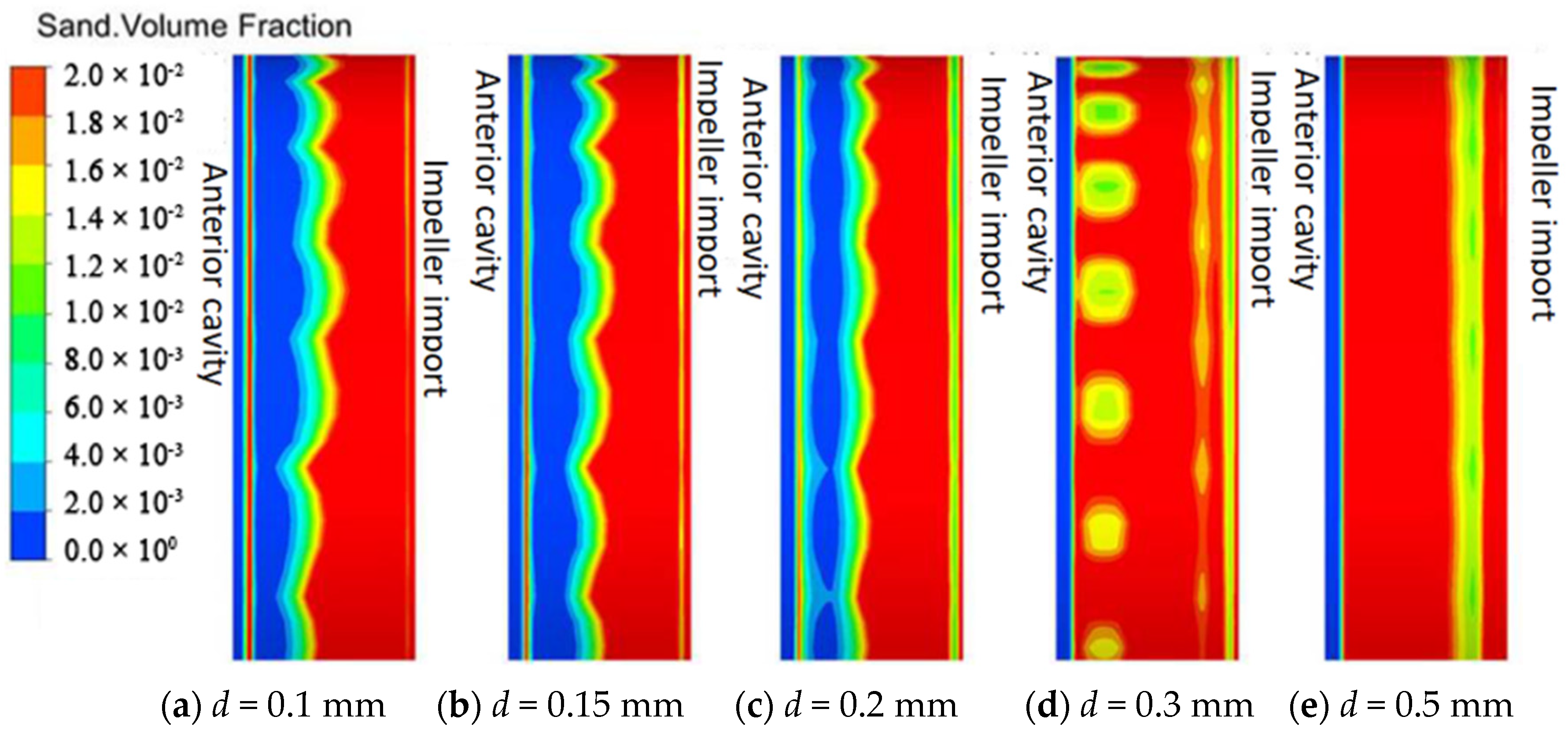
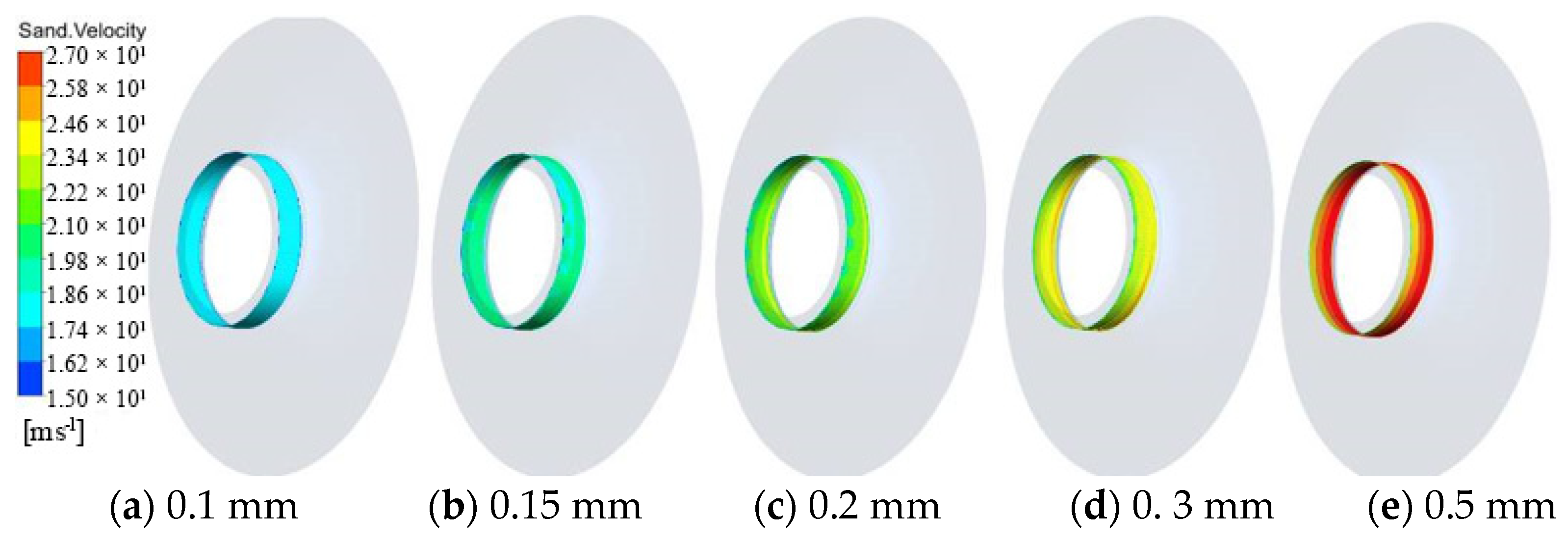
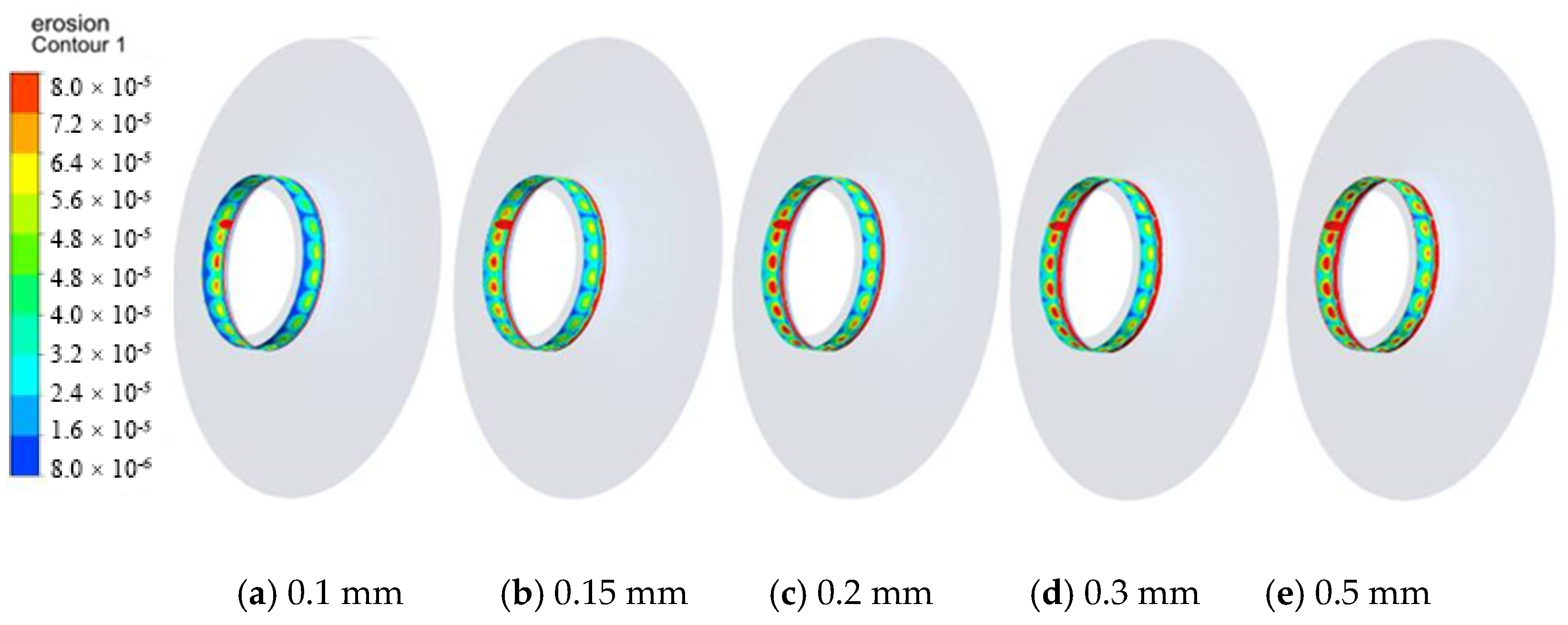
3.5. Wear Characteristics Analysis of Wear-Rings under Different Clearances
4. Conclusions
- (1)
- The wear of the centrifugal pump blade is mainly concentrated in the end and the inlet of the blade because the tip of the blade is moving at a higher speed and the solid particles at the front of the blade have a better positive impact angle. Under the influence of vortexes, the wear at the end of the blade suction surface is very severe, while, that at the front of blade, is more serious.
- (2)
- With the clearance changing, the maximum wear of the blade changes. When the clearance increases from 0.1 mm to 0.15 mm, the maximum wear in the impeller increases. When the clearance increases from 0.15 mm to 0.5 mm, the maximum wear in the impeller decreases because of the leakage of the wear-rings and energy loss.
- (3)
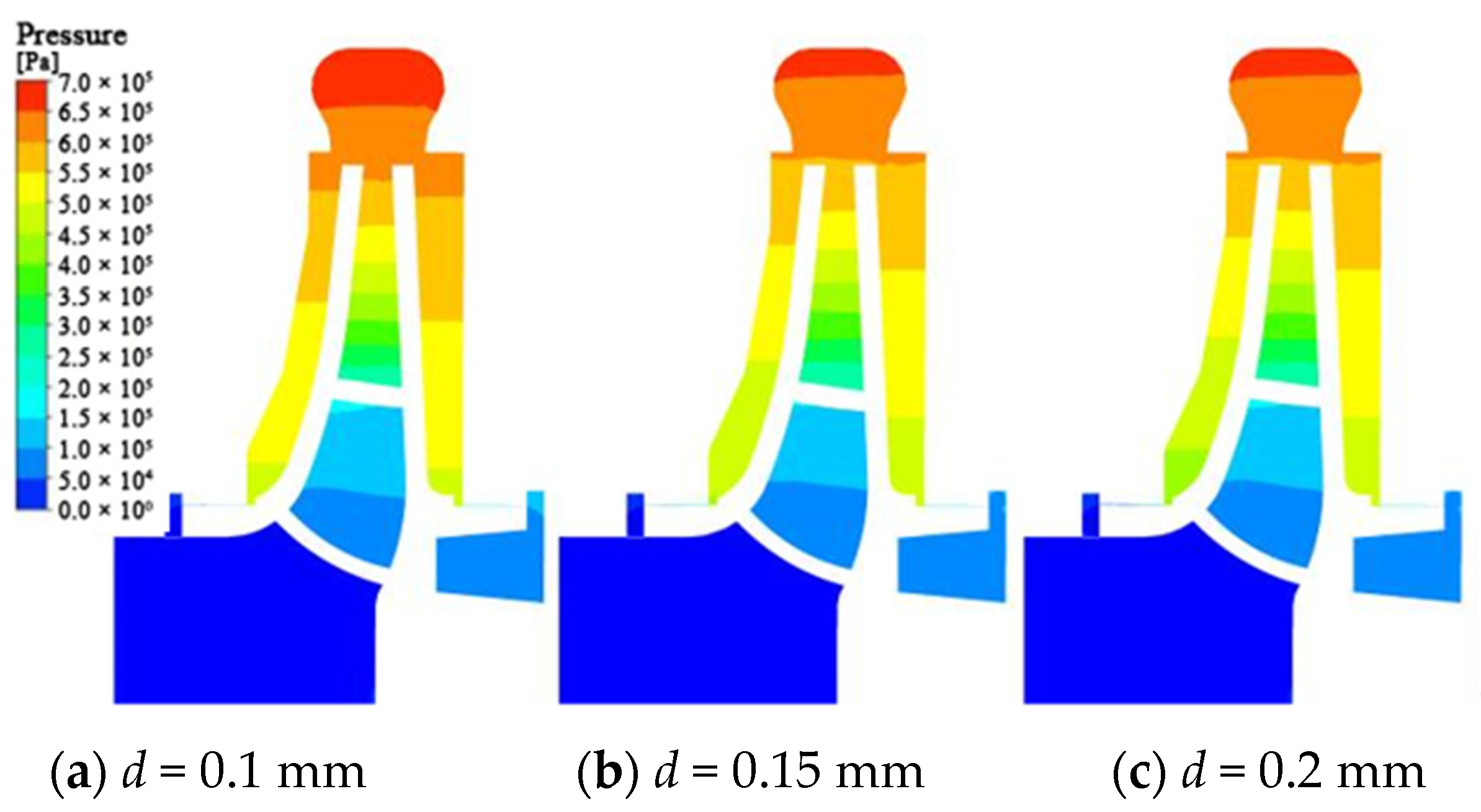
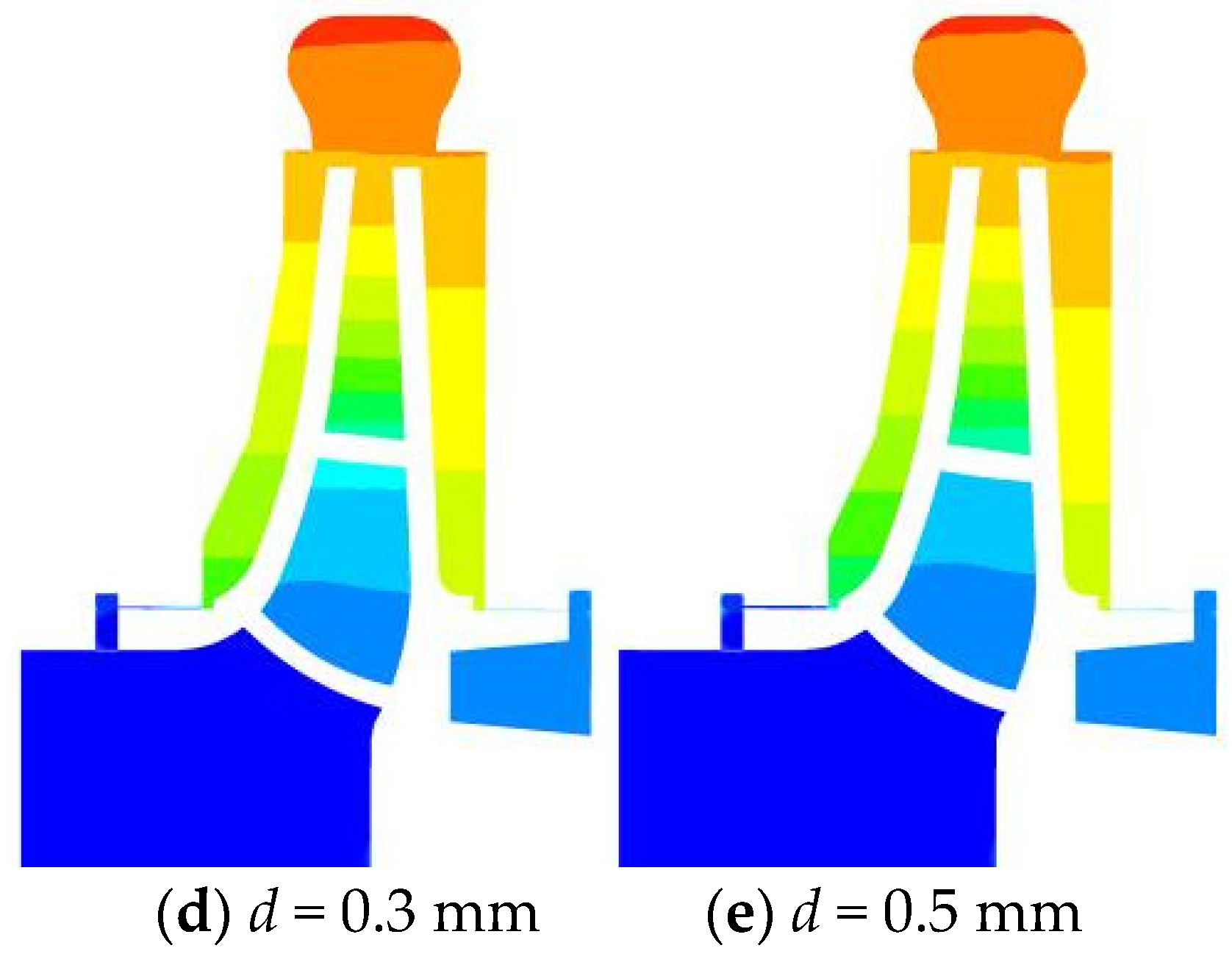
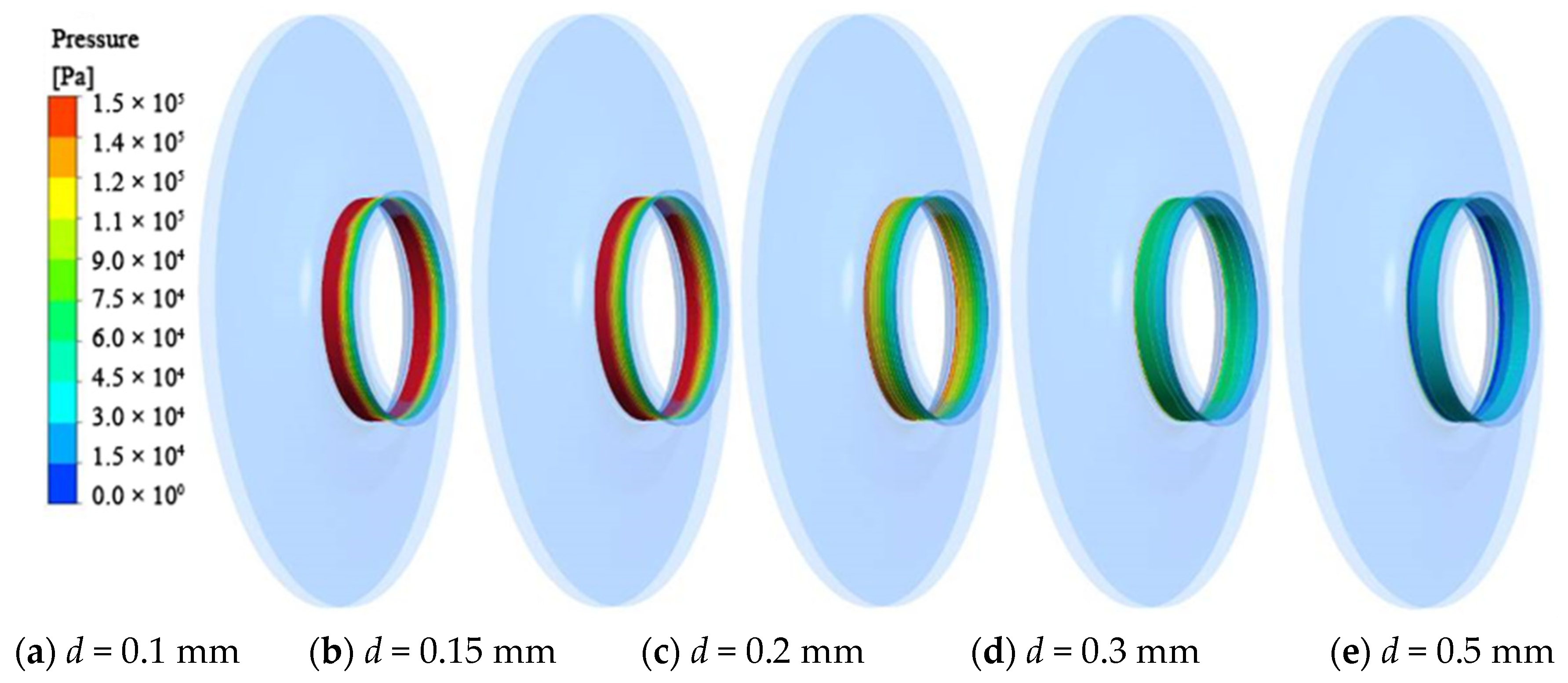
- It can be found through the analysis of the solid distribution and pressure distribution at the wear-rings that the solid distribution presents different distribution states with the change of the clearance. In general, the larger the clearance is, the higher the solid concentration is. The analysis of the impeller’s front cavity shows that the pressure of the front cavity is affected by the change of the clearance, which influences the flow of the fluid and the movement of solid particles in the front cavity.
- (4)
- As the clearance of the wear-rings increases, the wear of the centrifugal pump becomes more significant, and the severe wear area presents a point-like circumferential distribution.
Author Contributions
Funding
Conflicts of Interest
References
- Xie, N.; Battaglia, F.; Pannala, S. Effects of using two- versus three-dimensional computational modeling of fluidized beds: Part II, budget analysis. Powder Technol. 2008, 182, 14–24. [Google Scholar] [CrossRef]
- Wu, B.; Yan, H.Z.; Duan, Y.Q. 3D Numerical Simulation of Turbulent Flow and Wear Characteristics of Slurry Pump. China Mech. Eng. 2009, 20, 719–722. [Google Scholar]
- Liu, J.R.; Xu, Y.G.; Wang, D.M. Numerical analysis of solid-liquid two-phase flow and centrifugal pump impeller. Trans. Chin. Soc. Agric. Mach. 2010, 41, 86–90. [Google Scholar]
- Tao, Y.; Yuan, S.Q.; Zhang, J.F.; Zhang, F.; Tao, J.Q. Numerical Simulation and Experiment on Wear of Slurry Pump Impeller. Trans. Chin. Soc. Agric. Eng. 2014, 30, 63–69. [Google Scholar]
- Li, Y. Numerical Study of Suspended Sediment Movement Near Shore Based on Solid-Liquid Two-Phase Turbulence Theory; Tsinghua University: Beijing, China, 2007. [Google Scholar]
- Annaland, M.V.S.; Bolckers, G.A.; Goldschmidt, M.J.V. Development of a mufti-fluid model for poly-disperse dense gas solid fluidized beds, Part II: Segregation in binary particle mixtures. Chem. Eng. Sci. 2009, 64, 4237–4246. [Google Scholar] [CrossRef]
- Zhang, Z.C. Study on Sediment Wear Characteristics of Double Suction Centrifugal Pumps; Agricultural University: Beijing, China, 2016. [Google Scholar]
- Li, Y.S.; Wei, J.F. Numerical simulation of small particle size solid-liquid two-phase flow in swirl pump. Fluid Mach. 2010, 38, 20–24. [Google Scholar]
- Peng, G.J.; Wang, Z.W.; Fu, S.S. Wear characteristics of centrifugal mud pump overflow parts. J. Drain. Irrig. Mach. Engine 2015, 33, 1013–1018. [Google Scholar]
- Chen, S.; Wang, Z.C.; Lu, F.X. Numerical calculation of impeller wear based on discrete phase model. J. China Univ. Pet. Nat. Sci. Ed. 2015, 3, 143–148. [Google Scholar]
- Tabakoff, W.; Kotwal, R.; Hamed, A. Erosion study of different materials affected by coal ash particles. Wear 1979, 52, 161–173. [Google Scholar] [CrossRef]
- McLaury, B.S. A Model to Predict Solid Particle Erosion in Oil Field Geometries; The University of Tulsa: Tulsa, OK, USA, 1993. [Google Scholar]
- Oka, Y.; Okamura, K.; Yoshida, T. Practical estimation of erosion damage caused by solid particle impact. Part 1: Effect of impact parameters on a predictive equation. Wear 2005, 259, 95–101. [Google Scholar] [CrossRef]
- Oka, Y.; Okamura, K.; Yoshida, T. Practical estimation of erosion damage caused by solid particle impact. Part 2: Mechanical properties of materials directly associated with erosion damage. Wear 2005, 259, 102–109. [Google Scholar] [CrossRef]
- Qian, Z.D.; Wang, Y.; Xie, H. Analysis of the influence of auxiliary vane on the sand abrasion of double-suction centrifugal pump. J. Hydroelectr. Eng. 2012, 31, 232–237. [Google Scholar]
- Huang, J.D.; Zhang, K.T.; Chen, L. Experimental Study on the Wear of Centrifugal Pump Impeller by Water Containing Sand. J. Eng. Thermophys. 1999, 20, 448–452. [Google Scholar]
- Wang, J.Q.; Jiang, W.M.; Kong, F.Y. Numerical simulation of internal flow field and wear characteristics of solid-liquid two-phase flow centrifugal pump. J. Agric. Mach. 2013, 44, 53–66. [Google Scholar]
- Qiaorui, S.; Gérard, B.; Qifeng, J.; Wenting, H.; Asad, A.; Shouqi, Y. Investigation on the Handling Ability of Centrifugal Pumps under Air–Water Two-Phase Inflow: Model and Experimental Validation. Energies 2018, 11, 3048. [Google Scholar]
- Tarek, A.G.; Meftah, H. Gas–Liquid Two-Phase Upward Flow through a Vertical Pipe: Influence of Pressure Drop on the Measurement of Fluid Flow Rate. Energies 2018, 11, 2937. [Google Scholar]
- Wang, W.J.; Li, T.L. Numerical analysis of gas-liquid two-phase flow in jet centrifugal pump. Fluid Mach. 2020, 48, 53–57. [Google Scholar]
- Safa, R.; Goharrizi, A.S. CFD Simulation of an Industrial Hydrocyclone with Eulerian-Eulerian Approach: A Case Study. Int. J. Min. Sci. Technol. 2014, 24, 643–648. [Google Scholar] [CrossRef]
- Swain, S.; Mohanty, S. A 3-Dimensional Eulerian-Eulerian CFD Simulation of a Hydrocyclone. Appl. Math. Model. 2013, 37, 2921–2932. [Google Scholar] [CrossRef]
- Zare, M.; Ashtiani, F.Z.; Fouladitajar, A. CFD Modeling and Simulation of Concentration Polarization in Microfiltration of Oil-Water Emulsions; Application of an Eulerian Multi-phase Model. Desalination 2013, 324, 37–47. [Google Scholar] [CrossRef]
- Kubilay, A.; Derome, D.; Blocken, B.; Carmeliet, J. CFD Simulation and Validation of Wind-Driven Rain on a Building Fa- cade with an Eulerian Multiphase Model. Build. Environ. 2013, 61, 69–81. [Google Scholar] [CrossRef]
- Yu, X.; Hassan, M.; Ocone, R.; Makkawi, Y. A CFD Study of Biomass Pyrolysis in a Downer Reactor Equipped with A Novel Gas- Solid Separator-I: Hydrodynamic Performance. Fuel Process. Technol. 2014, 126, 366–382. [Google Scholar] [CrossRef] [Green Version]
- Zhang, C.; Zhao, T.C.; Liao, N.B.; Xu, S.Y. Numerical simulation study on the internal characteristics and particle distribution of centrifugal pumps under solid-liquid two-phase flow. J. Vac. Sci. Technol. 2019, 39, 870–875. [Google Scholar]
- Huang, S.; Su, X.; Guo, J.; Yue, L. Unsteady Numerical Simula-tion for Gas-Liquid Two-Phase Flow in Self-Priming Process of Centrifugal Pump. Energy Convers. Manag. 2014, 85, 694–700. [Google Scholar] [CrossRef]
- Liu, Z.L.; Zhang, N.; Cheng, X.R.; Shen, L.X.; Zhao, W.G. Analysis of blade wear characteristics of sand-contained underwater single-stage double-suction centrifugal pumps. J. Lanzhou Univ. Technol. 2014, 40, 56–61. [Google Scholar]
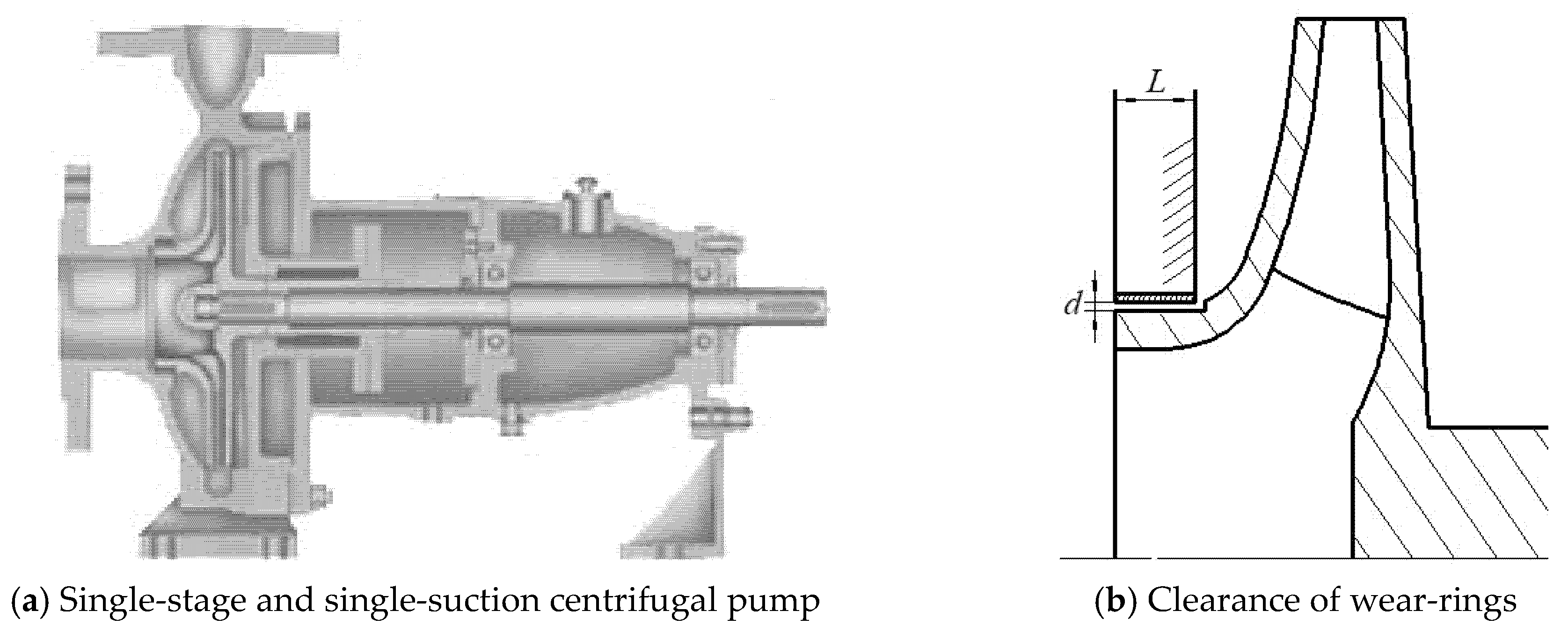




| Parameter | Value |
|---|---|
| Impeller inlet diameter D1 | 80 mm |
| Impeller outer diameter D2 | 250 mm |
| Number of blades Z | 5 |
| Angle of the tongue β | 24° |
| Impeller outlet width b | 6.5 mm |
| Base circle diameter D3 | 260 mm |
| Outlet diameter D4 | 50 mm |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, C.; Liu, J.; Zheng, S.; Huang, B.; Dai, J. Study on the Effects of the Wear-Rings Clearance on the Solid-Liquid Two-Phase Flow Characteristics of Centrifugal Pumps. Symmetry 2020, 12, 2003. https://doi.org/10.3390/sym12122003
Yan C, Liu J, Zheng S, Huang B, Dai J. Study on the Effects of the Wear-Rings Clearance on the Solid-Liquid Two-Phase Flow Characteristics of Centrifugal Pumps. Symmetry. 2020; 12(12):2003. https://doi.org/10.3390/sym12122003
Chicago/Turabian StyleYan, Chaoshou, Jianfei Liu, Shuihua Zheng, Bin Huang, and Jiacheng Dai. 2020. "Study on the Effects of the Wear-Rings Clearance on the Solid-Liquid Two-Phase Flow Characteristics of Centrifugal Pumps" Symmetry 12, no. 12: 2003. https://doi.org/10.3390/sym12122003
APA StyleYan, C., Liu, J., Zheng, S., Huang, B., & Dai, J. (2020). Study on the Effects of the Wear-Rings Clearance on the Solid-Liquid Two-Phase Flow Characteristics of Centrifugal Pumps. Symmetry, 12(12), 2003. https://doi.org/10.3390/sym12122003





